新乡-商丘断裂延津至封丘段新构造期构造样式分析

赵显刚; 李稳; 成万里; 王斐斐

doi:10.11899/zzfy20220203

新乡-商丘断裂延津至封丘段新构造期构造样式分析

doi: 10.11899/zzfy20220203

1.
河南省地震局, 郑州 450016
2.
中国地震局地球物理勘探中心, 郑州 450002

基金项目: 中国地震局地震科技星火计划项目（XH20037）；中央公益性科研院所基本科研业务专项（IGCEA1902）；中国地震局城市活动断层探测与地震危险性评价项目；河南省地震构造探查工程项目

详细信息

作者简介:
赵显刚，男，生于 1973年。高级工程师。主要从事活动构造与工程地震等方面的研究。E-mail：1033245390@qq.com

通讯作者:
成万里，男，生于 1982年。高级工程师。主要从事地震学的研究。E-mail：htuali@126.com

2 中国地震局地球物理勘探中心，2016. 新乡市活动断层探测与地震危险性评价工程报告.
3 中国地震局地球物理勘探中心，2014. 长垣县主城区地震小区划报告.
4 河南省航空物探遥感中心，2013. 河南省内黄隆起区地震概查及资源远景评价报告.
5 河南省航空物探遥感中心，2019. 河南省地震构造探查工程（1）浅层人工地震探测专题报告.
6 中国石油化工股份有限公司中原油田分公司物探研究院，2017. 新乡-商丘断裂石油地震资料分析与解释成果报告.
7 中国地震局地球物理勘探中心，2019. 新乡-商丘断层活动构造探测目标断层人工地震浅层反射剖面探测专题报告.
8 河南省地质矿产勘查开发局第五地质勘查院，2020. 河南省地震构造探查工程（2）-主要断裂活动性鉴定（部分）成果报告.
9 河南省地质调查院，2021. 河南省地震构造探查工程（4）-主要断裂活动性鉴定（部分）成果报告.
10 北京防灾科技有限公司，2021. 新乡-商丘断裂（封丘段）活动性鉴定与定位验收报告.
计量
- 文章访问数: 233
- HTML全文浏览量: 62
- PDF下载量: 86
- 被引次数: 0
出版历程
- 收稿日期: 2022-03-11
- 刊出日期: 2022-06-30

Analysis of Structural Style of Yanjin Fengqiu Section of Xinxiang Shangqiu Fault in Neotectonic Period

1.
Henan Earthquake Agency, Zhengzhou 450016, China
2.
Geophysical Exploration Center, China Earthquake Administratio, Zhengzhou 450002, China

摘要

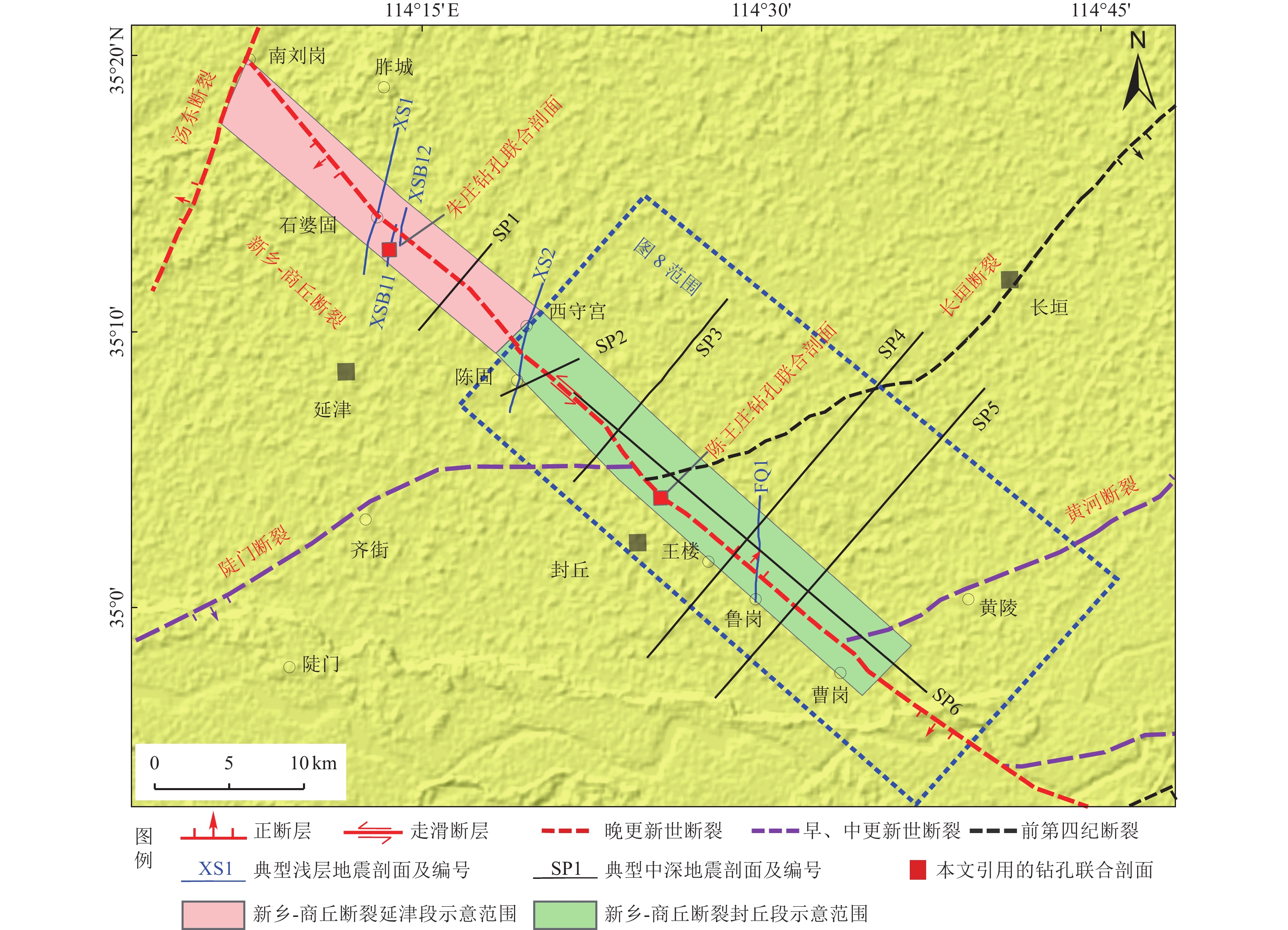
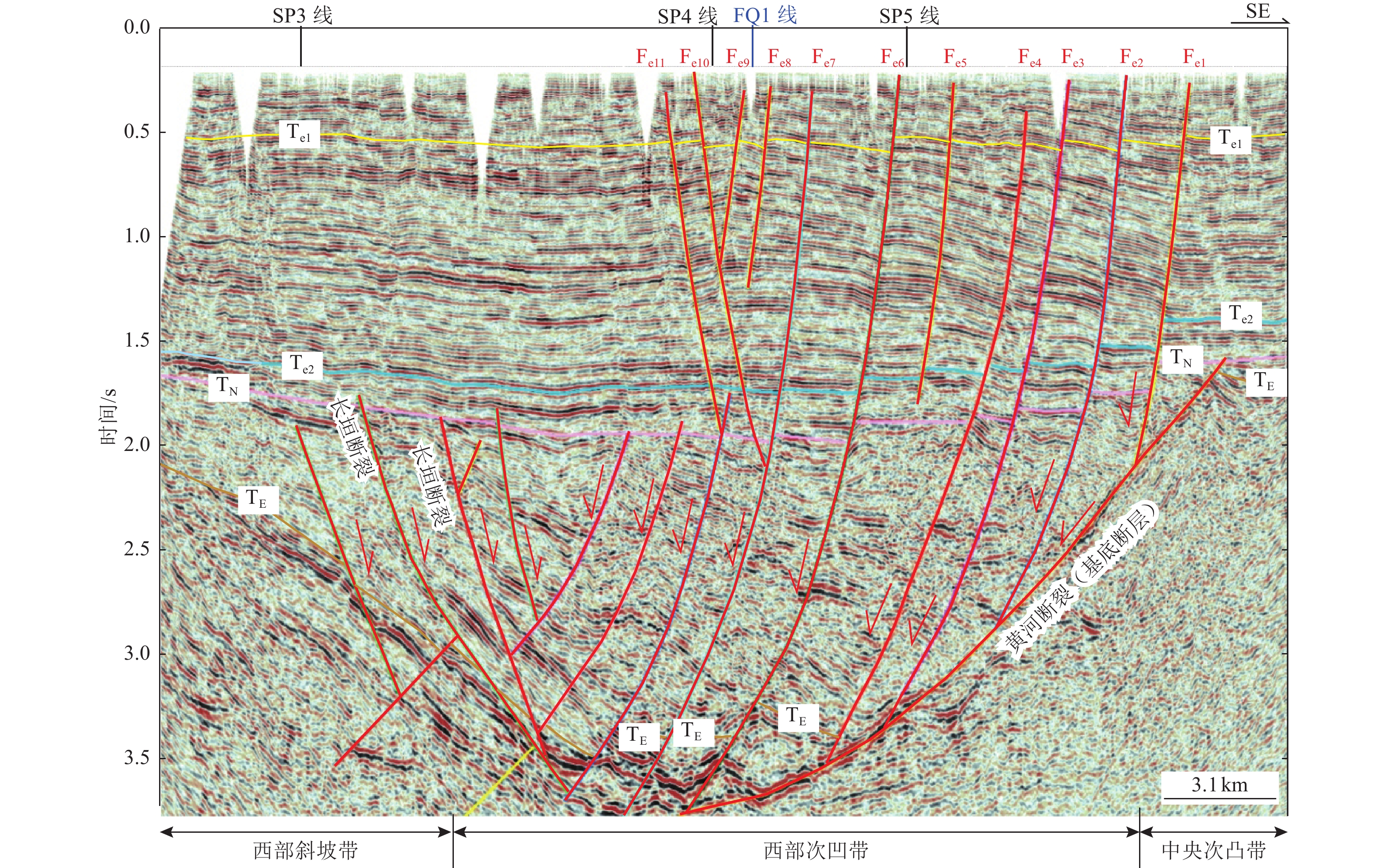
摘要: 新乡-商丘断裂是南华北盆地与渤海湾盆地、鲁西隆起的分界断裂，是一条长期活动的区域性深大断裂。浅层地震勘探与跨断层钻孔联合剖面探测工作已证实该断裂延津至封丘段的最新活动时代为晚更新世，本文通过对典型地震勘探剖面和钻探资料综合分析认为：新乡-商丘断裂延津至封丘段断裂结构复杂，新近纪以来构造样式在不同构造部位有显著差异。延津段在地震勘探剖面上浅部显示为负花状构造；封丘段变化较大，东部在剖面上为多组阶状正断层组合，形成了由断层带控制的构造背斜，平面上表现为NW向排列、走向NNE雁列状断层组合；西部结构单一，自东向西断裂控制的浅部地层变形范围增大，断层带逐步变宽。根据新乡-商丘断裂延津至封丘段剖面上的构造样式与平面上的组合模式，表明该段断裂最新活动具有走滑运动性质。
- 新乡-商丘断裂 /
- 地震勘探 /
- 构造样式
Abstract: The Xinxiang-Shangqiu fault is a regional deep fracture of long-term activity marking the boundary between the South North China Basin and Bohai Bay Basin. The latest active age of the Yanjin to Fenqiu fragment of this fault is of late Pleistocene, which is testified by the joint work of shallow seismic exploration and cross-fault borehole detection. On the basis of the typical seismic exploration profiles and drilling data, we concluded that the Yanjin-Fengqiu fragment of the Xinxiang-Shangqiu fault has a very complicated structure. Since the Neogene time, the different tectonic positions of the Yanjin-Fengqiu fragment have quite different tectonic styles. The Yanjin part has a negative flower structure in the seismic exploration profile. However, the Fengqiu part is structurally quite variable. The eastern segment of the Fengqiu part is composed of multiple scalariform normal faults, which form an anticline controlled by a fault belt. These faults are arranged in the NW direction and in echelon with a strike of NNE direction. The western segment is relatively in simple structure, with increasing deformation scale of the shallow strata controlled by the E-W trending fault. The fault zone of the western segment becomes wider from east to the west. According to the tectonic styles and combination patterns of the profile, we concluded that the Yanjin-Fengqiu fragment of the Xinxiang-Shangqiu fault is of strike-slip characteristics.
- Xinxiang Shangqiu fault /
- Seismic exploration /
- Structural style
注释:

1) 2 中国地震局地球物理勘探中心，2016. 新乡市活动断层探测与地震危险性评价工程报告.

2) 3 中国地震局地球物理勘探中心，2014. 长垣县主城区地震小区划报告.

3) 4 河南省航空物探遥感中心，2013. 河南省内黄隆起区地震概查及资源远景评价报告.

4) 5 河南省航空物探遥感中心，2019. 河南省地震构造探查工程（1）浅层人工地震探测专题报告.

5) 6 中国石油化工股份有限公司中原油田分公司物探研究院，2017. 新乡-商丘断裂石油地震资料分析与解释成果报告.

6) 7 中国地震局地球物理勘探中心，2019. 新乡-商丘断层活动构造探测目标断层人工地震浅层反射剖面探测专题报告.

7) 8 河南省地质矿产勘查开发局第五地质勘查院，2020. 河南省地震构造探查工程（2）-主要断裂活动性鉴定（部分）成果报告.

8) 9 河南省地质调查院，2021. 河南省地震构造探查工程（4）-主要断裂活动性鉴定（部分）成果报告.

9) 10 北京防灾科技有限公司，2021. 新乡-商丘断裂（封丘段）活动性鉴定与定位验收报告.

HTML全文

图 1 新乡-商丘断裂延津至封丘段构造单元划分图

Figure 1. Division of structural units in Yanjin—Fengqiu section of Xinxiang-Shangqiu fault

下载: 全尺寸图片幻灯片

图 2 新乡-商丘断裂延津至封丘段主要地震勘探反射剖面分布

Figure 2. Distribution of main seismic exploration sections of Yanjin—Fengqiu section of Xinxiang-Shangqiu fault

下载: 全尺寸图片幻灯片

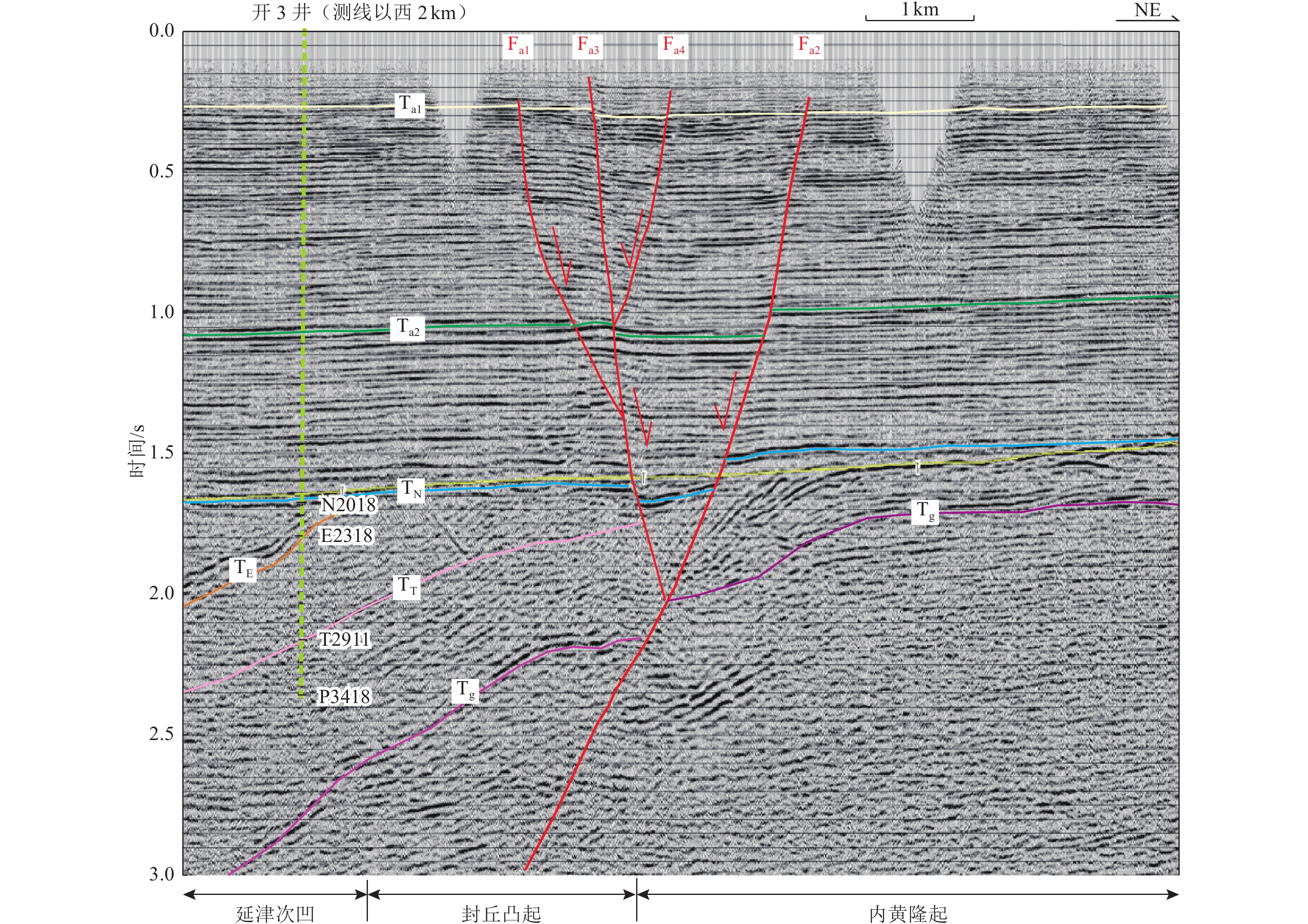
图 3 SP1线偏移时间剖面^③

Figure 3. Time seismic exploration profile of SP1 line

下载: 全尺寸图片幻灯片

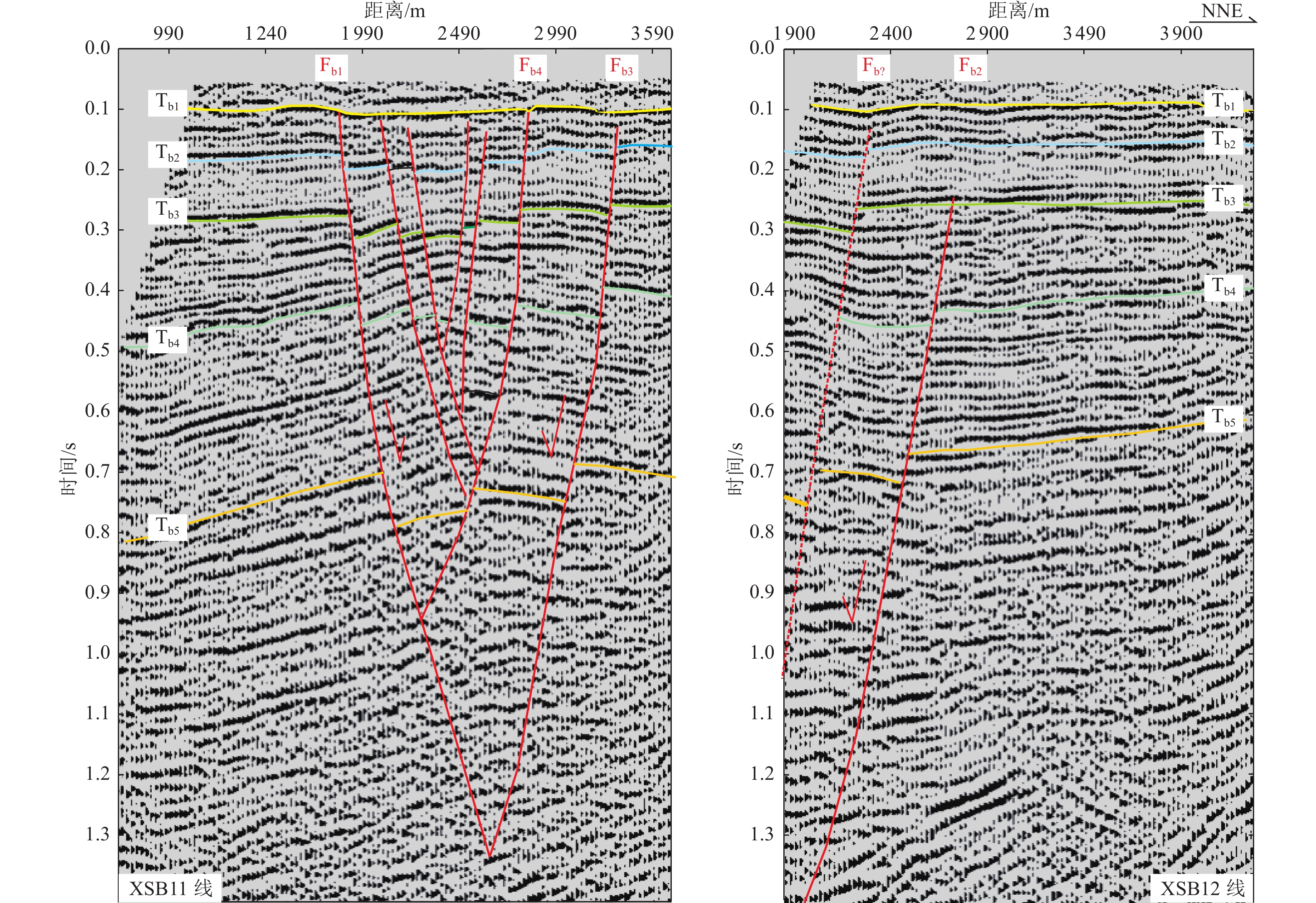
图 4 XSB1线偏移时间剖面图^④

Figure 4. Time profile of XSB1 line offset

下载: 全尺寸图片幻灯片

图 5 SP2线与SP3线偏移时间剖面^⑤

Figure 5. Seismic time profile of line SP2 and line SP3

下载: 全尺寸图片幻灯片

图 6 SP4线与SP5线偏移时间剖面⁶

Figure 6. Seismic time profile of line SP4 and line SP5

下载: 全尺寸图片幻灯片

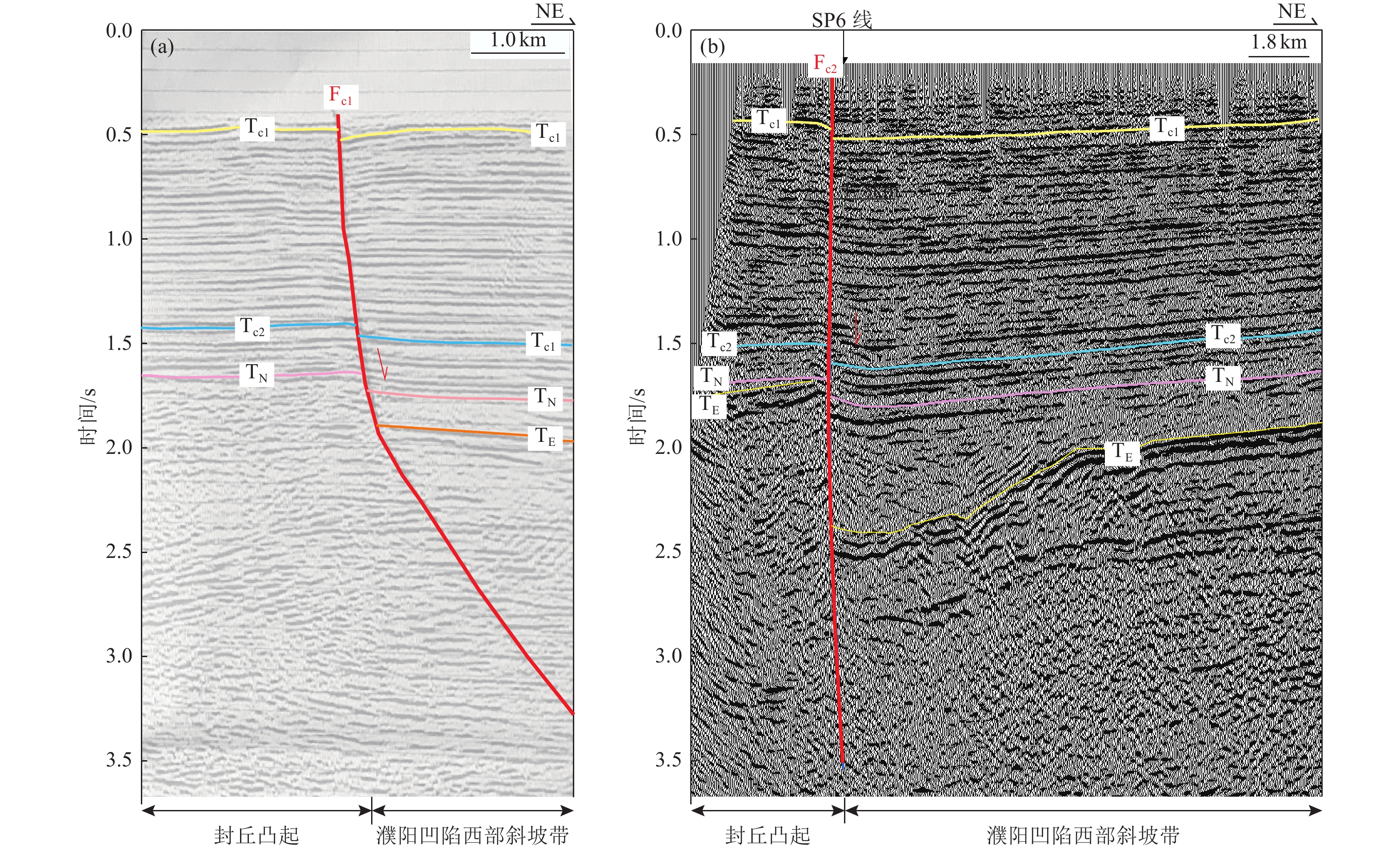
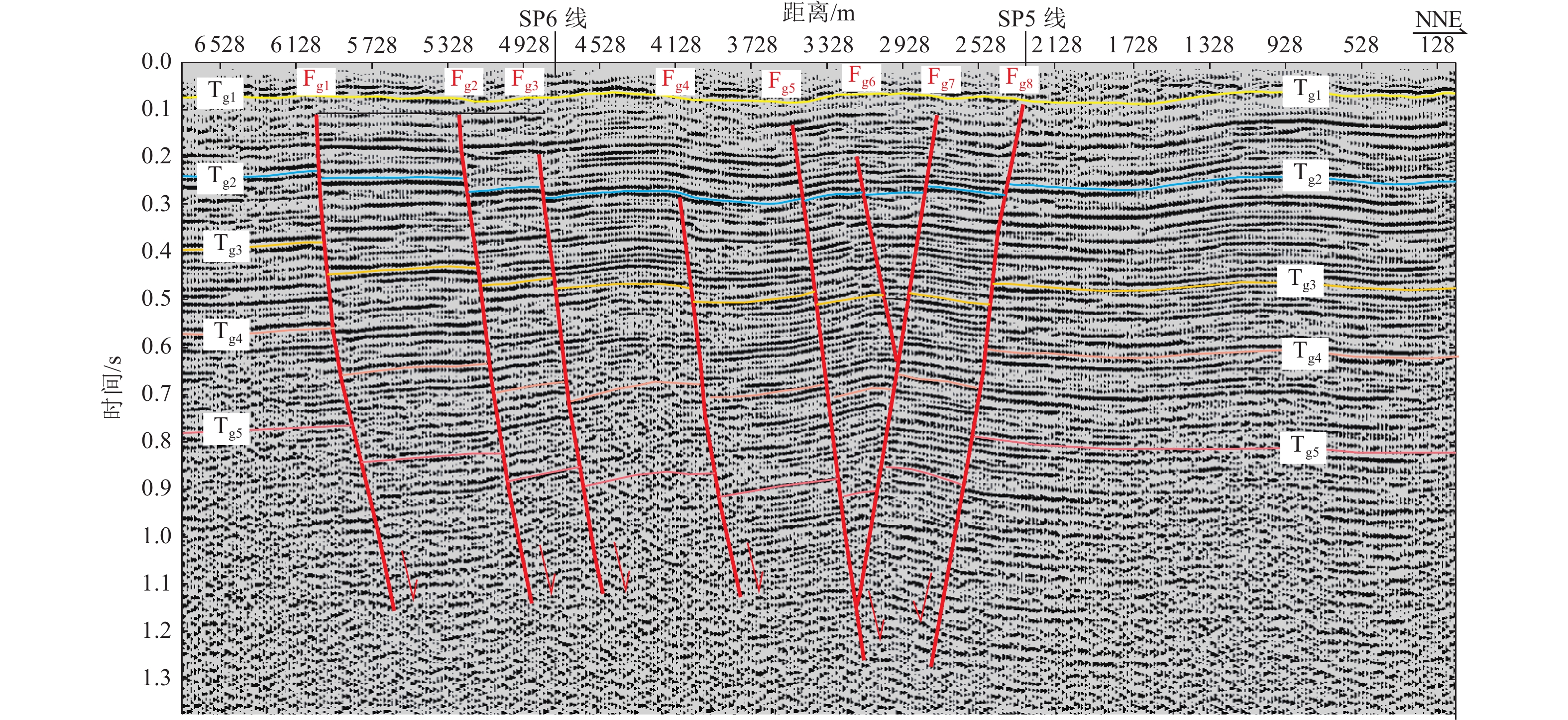
图 7 SP6线偏移时间剖面^⑤

Figure 7. Seismic time profile of line SP6

下载: 全尺寸图片幻灯片

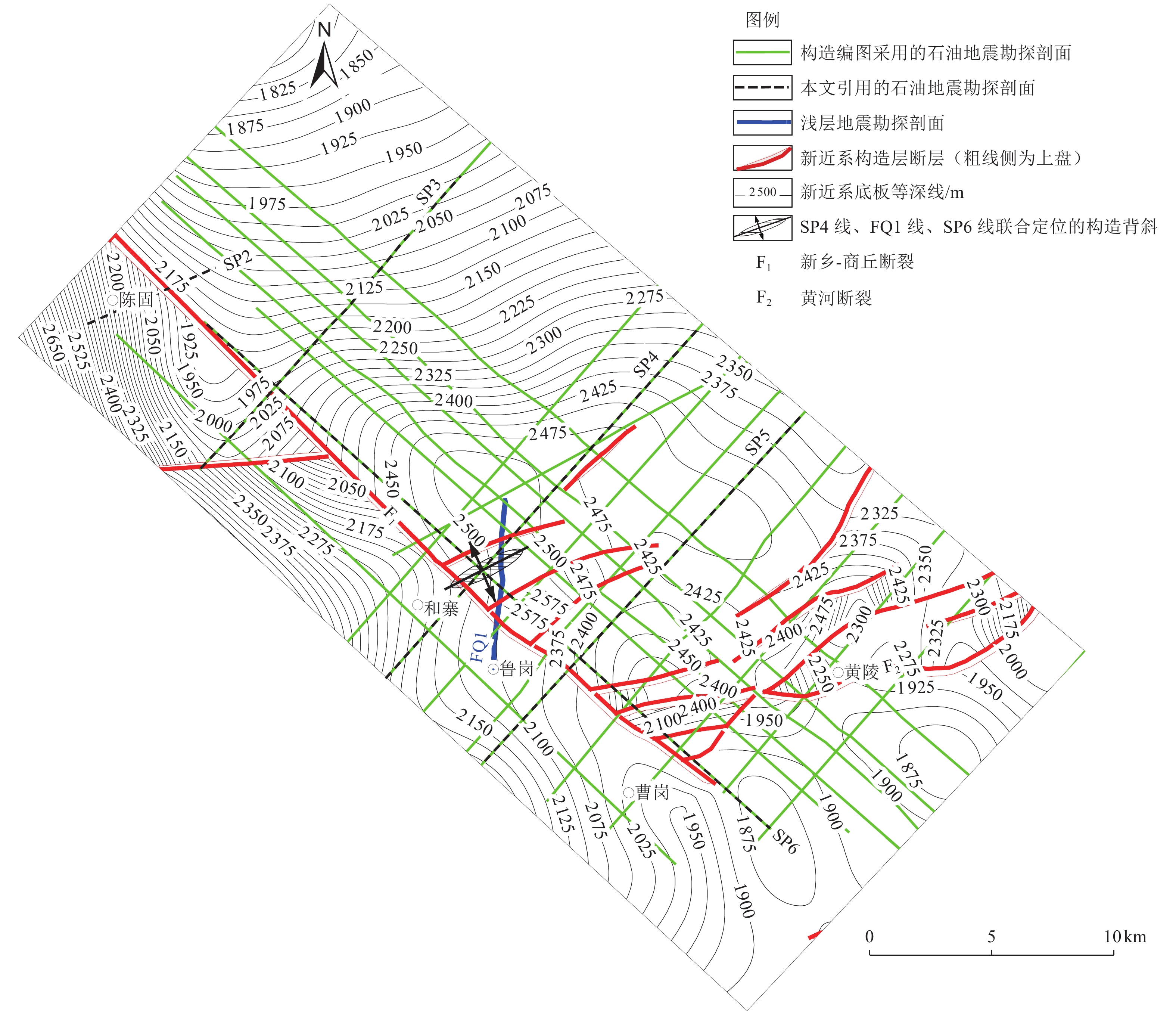
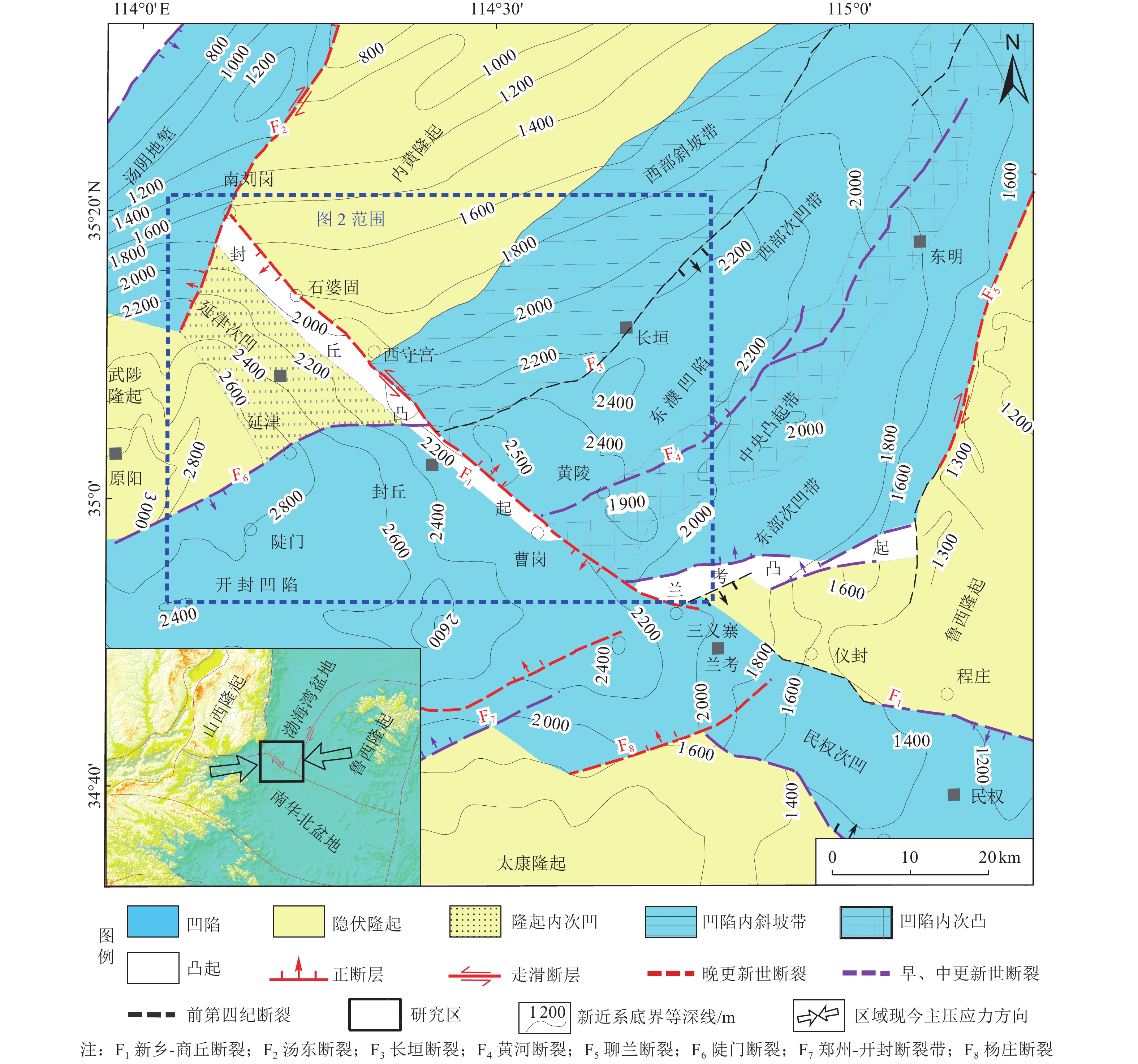
图 8 新乡-商丘断裂与黄河断裂交汇区构造图⁶（位置见图2，构造层为新近系底板，有修改）

Figure 8. Structural map of the intersection area of Xinxiang Shangqiu fault and Yellow River fault (See Fig. 2 for location, the structural layer is the Neogene floor which is modified according)

下载: 全尺寸图片幻灯片

图 9 XS2线偏移时间剖面^④

Figure 9. Shallow seismic exploration section of XS2 line

下载: 全尺寸图片幻灯片

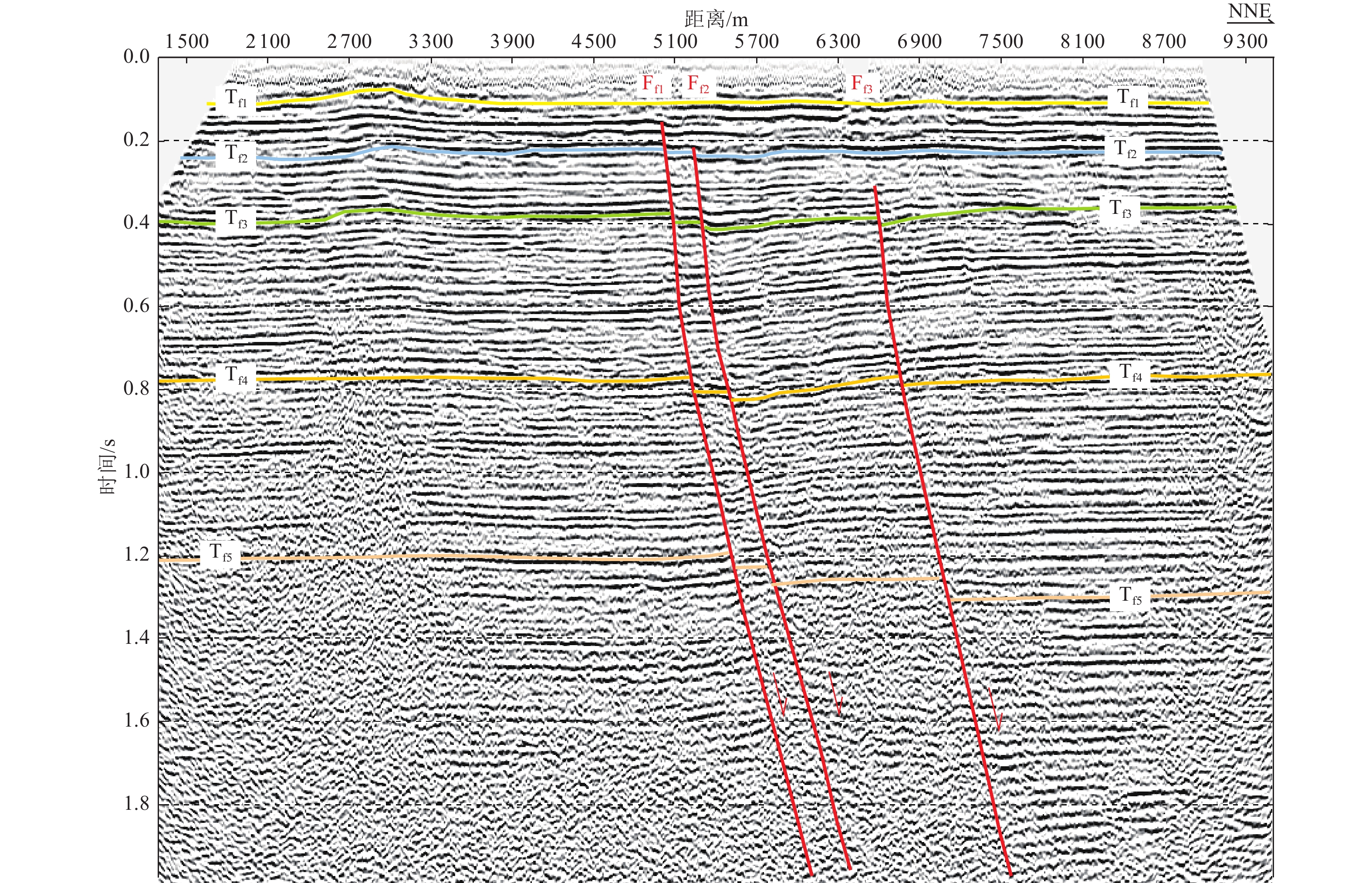
图 10 FQ1线偏移时间剖面^⑥

Figure 10. Shallow seismic exploration section of FQ1 line

下载: 全尺寸图片幻灯片

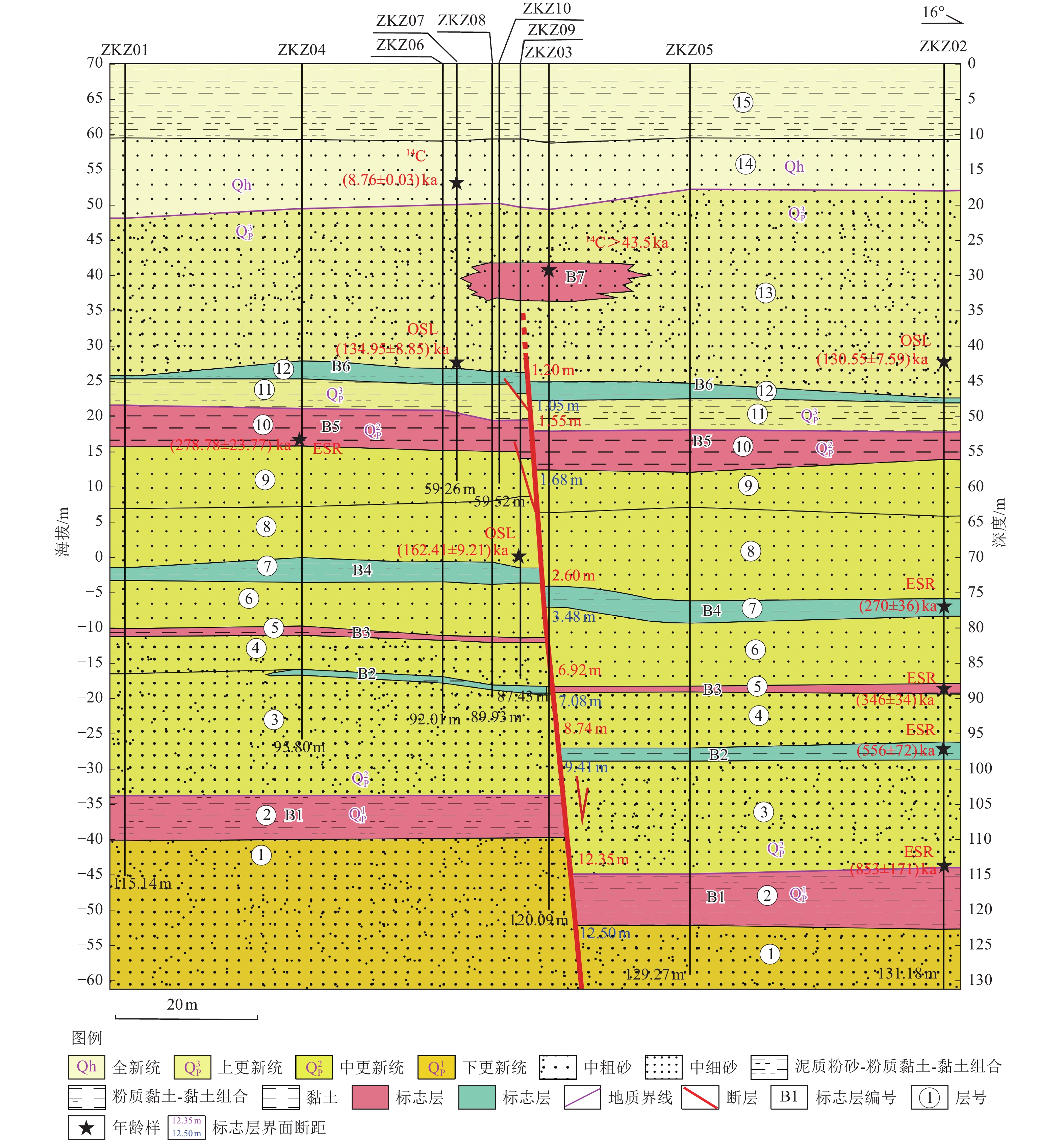
图 11 新乡-商丘断裂延津段朱庄钻孔联合地质剖面^⑧

Figure 11. Combined geological profile of Zhuzhuang borehole in Yanjin section of Xinxiang Shangqiu fault

下载: 全尺寸图片幻灯片

图 12 新乡-商丘断裂封丘段陈王庄钻孔联合地质剖面⁹

Figure 12. Combined geological profile of chenwangzhuang borehole in Fengqiu section of Xinxiang Shangqiu fault

下载: 全尺寸图片幻灯片

表 1 浅层地震勘探基本参数

Table 1. Basic parameters of shallow seismic exploration

序号	线号	长度 /m	道距/m	炮距/m	偏移距/m	接收道数	覆盖次数	采样间隔/ms	记录时间 /s	震源吨位/t
1	XS1	8875	10	20	0	240	60	0.5	3	26
2	XSB1	5795	5	20	0	260	32	0.5	3	26
3	XS2	8100	10	20	0	240	60	0.5	3	26
4	FQ1	7216	4	16	0	220	22	0.5	2	18
注：XSB1线为组合线，由XSB11线与XSB12线组合而成。

下载: 导出CSV

表 2 朱庄钻孔联合剖面测年数据表^⑧

Table 2. Data sheet of combined profile dating of Zhuzhuang borehole

样品编号	样品埋深/m	地层/标志层	所处构造位置	测试方法	距今年龄/ka
ZKZ07¹⁴C01	16.55	层⑮	上覆地层	¹⁴C	8.76±0.03
ZKZ03¹⁴C02	28.26	层⑬/B7	上覆地层	¹⁴C	＞43.50
ZKZ02OSL03	42.38	层⑬	上覆地层	OSL	130.55±7.59
ZKZ07OSL01	43.98	层⑫/B6	断层下盘	OSL	134.95±8.85
ZKZ04OSL02	54.18	层⑨	断层下盘	OSL	278.78±23.77
ZKZ09OSL01	72.45	层⑦/B4	断层下盘	OSL	162.41±9.21
ZKZ02ESR01	77.40	层⑦/B4	断层上盘	ESR	270±36
ZKZ02ESR02	88.70	层⑤/B3	断层上盘	ESR	346±34
ZKZ02ESR03	96.59	层③/B2	断层上盘	ESR	556±72
ZKZ02ESR05	117.43	层①	断层上盘	ESR	853±171
注：¹⁴C样品年龄测试由美国Beta实验室完成；OSL、ESR样品年龄测试由北京光释光实验室有限公司完成。

下载: 导出CSV

表 3 陈王庄钻孔联合剖面测年数据表^⑧

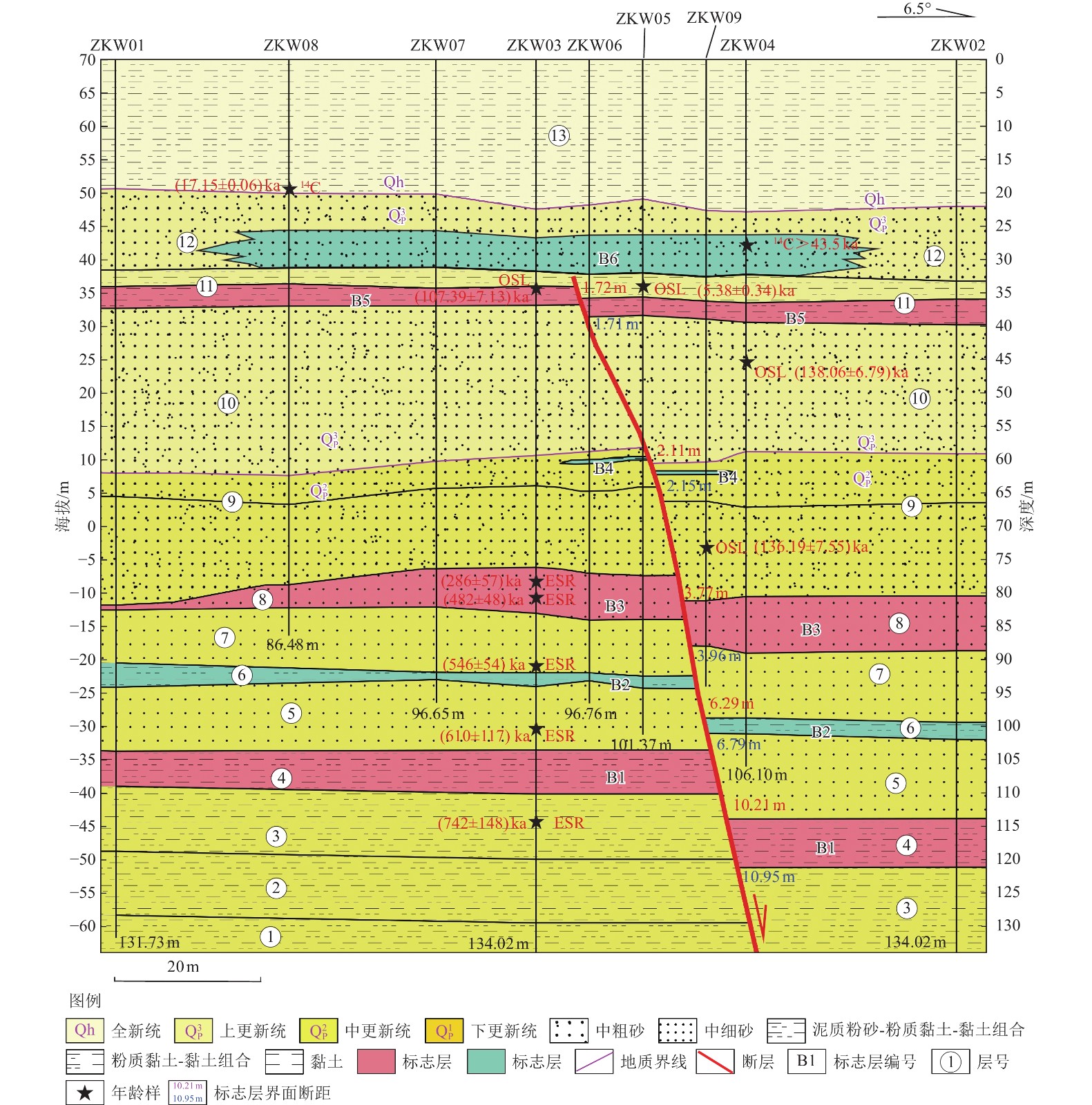
Table 3. Data sheet of combined profile dating of Chenwangzhuang borehole

样品编号	样品埋深/m	地层/标志层	所处构造位置	测试方法	距今年龄/ka
ZKW08¹⁴C01	18.84	层⑬	上覆地层	¹⁴C	17.15±0.06
ZKW04¹⁴C01	25.05	层⑫	上覆地层	¹⁴C	＞43.5
ZKW05OSL02	32.34	层⑪	断层上盘	OSL	5.38±0.34
ZKW03OSL02	33.75	层⑪	断层下盘	OSL	107.39±7.13
ZKW04OSL02	45.96	层⑩	断层上盘	OSL	138.06±6.79
ZKW09OSL02	73.58	层⑨	断层上盘	OSL	136.19±7.55
ZKW03ESR01	77.14	层⑧/B3	断层下盘	ESR	286±57
ZKW03ESR02	82.21	层⑧/B3	断层下盘	ESR	482±48
ZKW03ESR04	93.10	层⑥/B2	断层下盘	ESR	546±54
ZKW03ESR05	101.97	层⑤	断层下盘	ESR	610±117
ZKW03ESR06	120.49	层②	断层下盘	ESR	742±148
注：¹⁴C样品年龄测试由美国Beta实验室完成；OSL、ESR样品年龄测试由北京光释光实验室有限公司完成。

下载: 导出CSV

参考文献(12)

[1]	侯江飞, 邢磊, 张扬等, 2021. 新乡—商丘断裂延津段浅部地层结构特征研究. 工程地球物理学报, 18（4）: 486—494 doi: 10.3969/j.issn.1672-7940.2021.04.0011 Hou J. F. , Xing L. , Zhang Y. , et al. , 2021. The shallow structural characteristics of the Yanjin section of Xinxiang—Shangqiu fault. Chinese Journal of Engineering Geophysics, 18(4): 486—494. (in Chinese) doi: 10.3969/j.issn.1672-7940.2021.04.0011
[2]	李艳友, 漆家福, 周赏, 2017. 走滑构造差异变形特征及其主控因素分析——基于砂箱模拟实验. 石油实验地质, 39（5）: 711—715 doi: 10.11781/sysydz201705711 Li Y. Y. , Qi J. F. , Zhou S. , 2017. Differential deformation and its main controls on strike-slip structures: evidence from sandbox experiments. Petroleum Geology & Experiment, 39(5): 711—715. (in Chinese) doi: 10.11781/sysydz201705711
[3]	刘尧兴, 周庆, 荆制国, 2001. 豫北地区新构造活动特征及中长期地震预测研究. 西安: 西安地质出版社.
[4]	马宝军, 漆家福, 于福生, 2017. 东濮凹陷构造变形的物理模拟研究. 地球学报, 38（3）: 430—438 doi: 10.3975/cagsb.2017.03.13 Ma B. J. , Qi J. F. , Yu F. S. , 2017. An analysis of physical modeling of tectonic deformation in Dongpu sag. Acta Geoscientica Sinica, 38(3): 430—438. (in Chinese) doi: 10.3975/cagsb.2017.03.13
[5]	王定一, 汤锡元, 陈乃明, 1994. 开封坳陷构造特征、形成演化与油气远景. 石油学报, 15（2）: 39—47 doi: 10.3321/j.issn:0253-2697.1994.02.005 Wang D. Y. , Tang X. Y. , Chen N. M. , 1994. Structural features, evolution and oil and gas prospects of Kai Feng depression. Acta Petrolei Sinica, 15(2): 39—47. (in Chinese) doi: 10.3321/j.issn:0253-2697.1994.02.005
[6]	王志铄, 2017. 河南省地震构造特征. 北京: 地质出版社.
[7]	谢智, 谢健健, 王磊等, 2010. 豫北地区地震活动性研究. 华南地震, 30（3）: 42—52 doi: 10.3969/j.issn.1001-8662.2010.03.006 Xie Z. , Xie J. J. , Wang L. , et al. , 2010. Study on earthquake activity in Yubei region. South China Journal of Seismology, 30(3): 42—52. (in Chinese) doi: 10.3969/j.issn.1001-8662.2010.03.006
[8]	徐汉林, 赵宗举, 杨以宁等, 2003. 南华北盆地构造格局及构造样式. 地球学报, 24（1）: 27—33 doi: 10.3321/j.issn:1006-3021.2003.01.005 Xu H. L. , Zhao Z. J. , Yang Y. N. , et al. , 2003. Structural pattern and structural style of the southern North China basin. Acta Geoscientica Sinica, 24(1): 27—33. (in Chinese) doi: 10.3321/j.issn:1006-3021.2003.01.005
[9]	许立青, 李三忠, 索艳慧等, 2013. 华北地块南部断裂体系新构造活动特征. 地学前缘, 20（4）: 75—87 Xu L. Q. , Li S. Z. , Suo Y. H. , et al. , 2013. Neotectonic activity and its kinematics of fault system in the south of North China block. Earth Science Frontiers, 20(4): 75—87. (in Chinese)
[10]	许忠淮, 汪素云, 黄雨蕊等, 1989. 由大量的地震资料推断的我国大陆构造应力场. 地球物理学报, 32（6）: 636—647 doi: 10.3321/j.issn:0001-5733.1989.06.004 Xu Z. H. , Wang S. Y. , Huang Y. R. , et al. , 1989. The tectonic stress field of Chinese continent deduced from a great number of earthquakes. Chinese Journal of Geophysics, 32(6): 636—647. (in Chinese) doi: 10.3321/j.issn:0001-5733.1989.06.004
[11]	张扬, 王志铄, 周栋梁等, 2018. 南华北盆地沈丘凹陷新构造时期断裂活动特征. 地震地磁观测与研究, 39（5）: 30—38 doi: 10.3969/j.issn.1003-3246.2018.05.005 Zhang Y. , Wang Z. S. , Zhou D. L. , et al. , 2018. Shenqiu depression faults movement characteristics in southern North China basin during the neotectonic period. Seismological and Geomagnetic Observation and Research, 39(5): 30—38. (in Chinese) doi: 10.3969/j.issn.1003-3246.2018.05.005
[12]	张扬, 贺承广, 鲁人齐等, 2021. 新乡—商丘断裂延津段活动特征与晚第四纪地层沉积关系研究. 地质论评, 67（S1）: 11—14 doi: 10.16509/j.georeview.2021.s1.005 Zhang Y. , He C. G. , Lu R. Q. , et al. , 2021. Relationship of the activity characteristics in the Yanjin segment of the Xinxiang-Shangqiu fault and the late-quaternary stratigraphic sedimentary. Geological Review, 67(S1): 11—14. (in Chinese) doi: 10.16509/j.georeview.2021.s1.005