Borehole Seismometer Azimuth Detection in Jiangsu Seismic Network
-
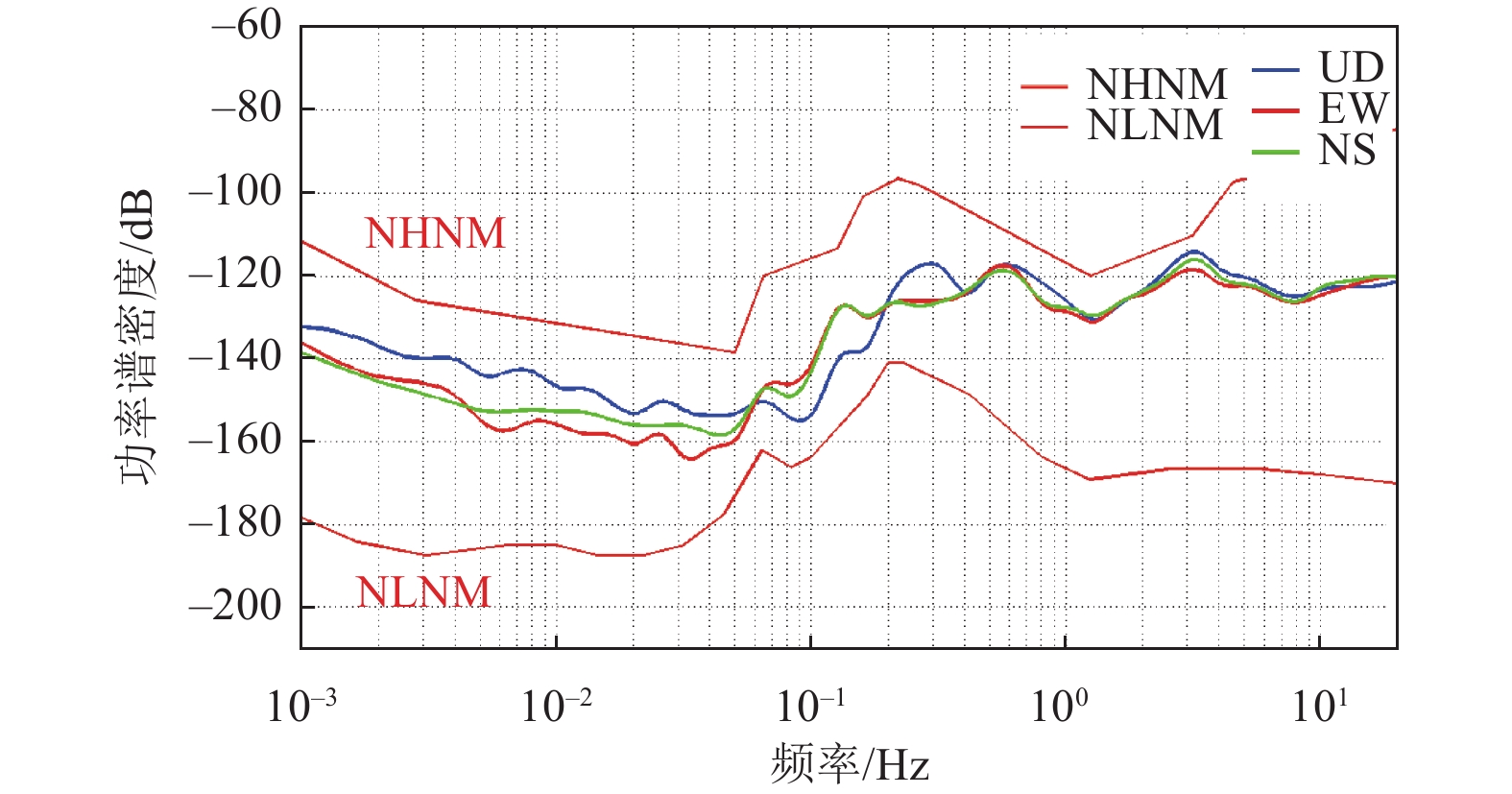
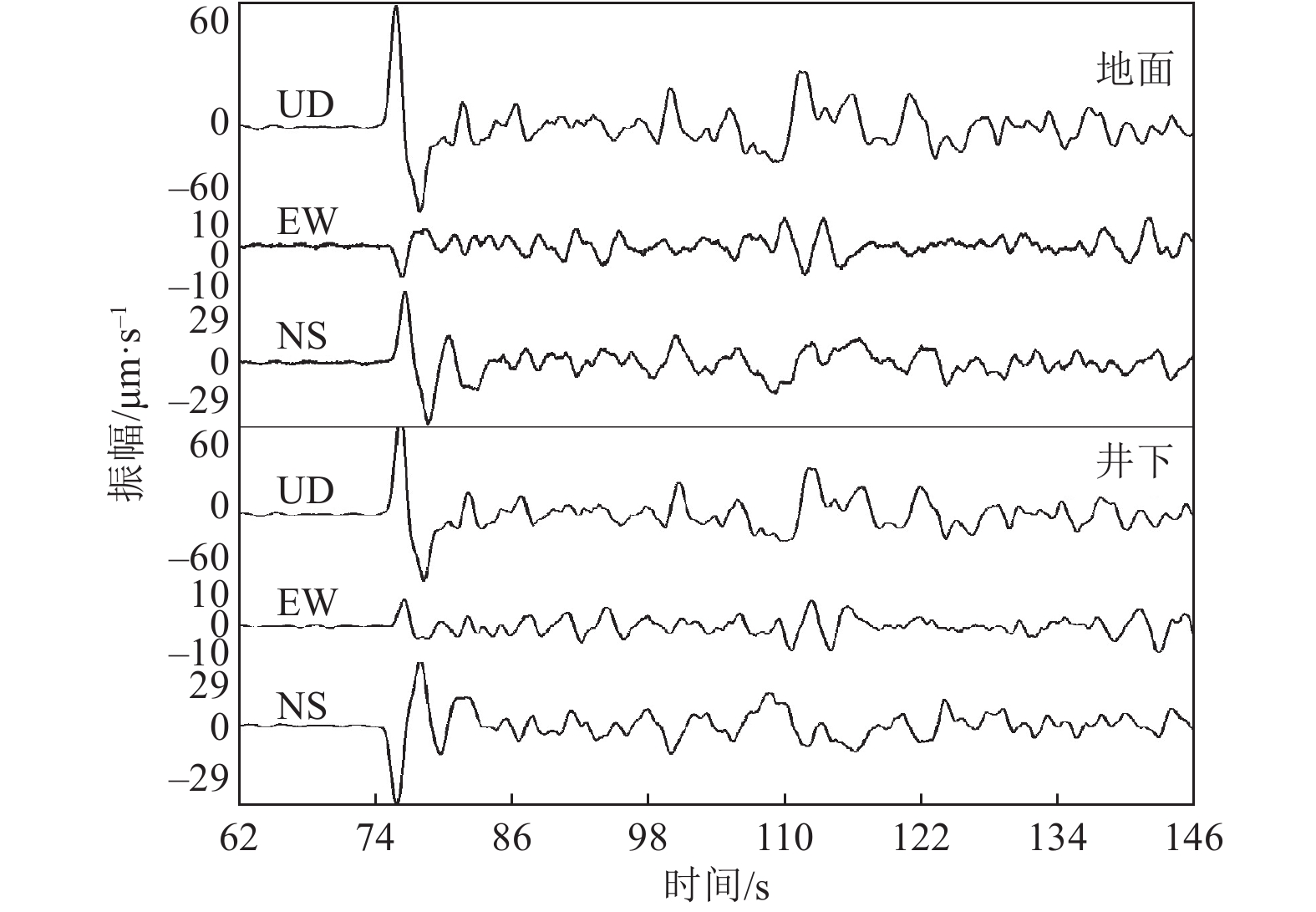
摘要: 为获取江苏省测震台网井下地震计精确方位角，架设地面参考地震计，将其精确指北，并与井下地震计检测结果进行对比，利用相关分析法计算22个深井台站精度较高的方位角。研究结果表明，受多因素制约，井下地震计检测结果普遍偏差较大，部分台站水平向分量几乎反向，如提井，需重新进行方位角检测；地面与井下地震计同频带有利于提高相关性，从而获取高精度检测结果；利用不同频带地震计进行井下地震计方位角检测时，对较宽频带地震计进行仿真处理尤为重要；溧阳2台站新建井下地震计检测结果表明相关分析法可应用于井下地震计方位角检测；尽可能选择台基噪声功率谱密度曲线具有明显波峰频段作为滤波频段，有利于提高地面与井下地震计观测数据相关性，提高方位角检测精度。Abstract: In order to obtain the accurate azimuth angles of borehole seismometer in Jiangsu seismic network, the ground reference seismometer is set up to accurately point north accurately. Comparative observation between ground and borehole seismometer has been done . Accurate azimuths of 22 borehole seismometers were obtained, and we draw the following conclusions: The azimuth angle deviations of borehole seismometer are generally large due to the restriction of many factors, and the horizontal components of some stations are almost reversed. Remount of borehole seismometer must changes the azimuth, so the azimuth detection must be carried out again.The same frequency band between ground and borehole seismometers is beneficial to improve the correlation and obtain higher precision detection results.The comparison observation of different frequency band seismometers needs to be simulated. Azimuth detection of Liyang 2 borehole seismometer proves that the correlation analysis method is feasible to detect the azimuth of borehole seismometer. The frequency band with obvious peak on the power spectrum curve of the background noise is selected as the filtering frequency band as far as possible, which is beneficial to improve the correlation between ground and borehole seismometer observation data and improve the accuracy of azimuth detection.
-
引言
2022年1月8日青海省海北州门源县发生MS6.9地震（图1），震中位于37.77°N，101.26°E，震源深度10 km。发震断裂为青藏高原北东缘祁连-海原断裂中西段的冷龙岭断裂，震中位于断裂南侧3～4 km（Yuan等，2013；李智敏等，2022）。本次地震产生了以左旋走滑为主的同震地表破裂带。破裂带分为南、北支，分别沿托莱山断裂东端和冷龙岭断裂西端展布，总长约27 km（潘家伟等，2022）。南支破裂带最大左行水平位错量约85 cm，北支破裂带最大左行水平位错量约3.7 m。
门源地震虽未造成人员伤亡，但使冷龙岭断裂西端产生破裂带，破裂带与兰新铁路相交（图1），对铁路大桥和隧道造成了严重破坏,其中大梁隧道被本次地震破裂带直接错断，受损最严重（图2）。在距地震破裂带稍远处，地震对隧道的破坏以外墙和拱顶开裂、剥落、掉块及变形为主（图2（a））。在地震破裂带与隧道交汇处，隧道被断裂左旋水平错动约2 m（图2（b）），这一水平错动使隧道在短期内难以修复，造成巨大的经济损失。拟定隧道修复方案时，需对冷龙岭断裂未来强震的水平位错量进行评估，为隧道抗震设计提供参考。
活断层同震位错量是铁路、隧道、油气管线等长线路工程抗断设计中的关键性参数（曹毅渊等，2019）。目前，我国工程地震界普遍采用确定性方法评估活断层同震位错量，即通过活断层最大潜在地震震级和震级与最大位错量的经验关系估算对应的最大位错量。然而目前人类对地震的认识水平有限，发震断层震级分布、破裂长度、位错分布等均存在较大的不确定性。因此，地震学家尝试借鉴经典的概率地震危险性分析理论，采用概率性方法评价断层未来一段时间内可能的位错分布情况，即概率断层位错危险性分析（Probabilistic Fault Displacement Hazard Analysis, PFDHA）（Youngs等，2003）。概率断层位错危险性分析理论和方法已被国内外学者广泛应用于断层同震位错量评估中（冉洪流等，2004a，2004b；Chen等，2011；Petersen等，2011；荆旭，2019；Valentini等，2021；吴果等，2022）。
本文基于近年来冷龙岭断裂的最新地震活动性研究成果，选取适当的平均地震复发间隔、最大震级等参数，进而采用确定性方法和概率断层位错危险性分析方法对冷龙岭断裂未来强震的水平位错量进行评估。本研究可为大梁隧道修复工程提供参考，为其他长线路工程抗断设计提供技术支撑。
1. 冷龙岭断裂地震活动参数
冷龙岭断裂在青藏高原东北缘的构造变形中起着重要的转换调节作用（Gaudemer等，1995）。断裂西端与托莱山断裂呈左阶斜列分布，东端与天桥沟-黄羊川断裂及金强河断裂相接（李智敏等，2022）。断裂晚第四纪主要表现为左旋走滑运动，地震活动强烈（郭鹏等，2017）。
郭鹏（2019）通过探槽开挖和放射性碳定年技术揭示了冷龙岭断裂最近发生的6次古地震事件和形成时代，由新到老的年龄分别为438—350 a BP以来、2 951—1 155 a BP、4 016—3 609 a BP、5 325—4 476 a BP、7 284—6 690 a BP和8 483—7 989 a BP。6次古地震事件的平均复发间隔为（1 640±570） a，相应变异系数为0.34。
冷龙岭断裂在我国第五代地震动参数区划图中位于六盘山—祁连山地震带的冷龙岭潜在震源区内（潘华等，2013）。冷龙岭潜在震源区震级上限为M7.5，所在地震带的b值为0.75，本文采用以上参数开展相关研究。
2. 水平位错量评估
2.1 确定性方法与评估结果
确定性方法是将断裂最大潜在地震震级代入震级与最大位错量的经验关系式，从而估算对应的最大位错量Dm。对于本研究，Dm特指最大水平位错量。已有学者基于不同数据集拟合了不同的经验关系式。考虑不确定性因素影响，本文同时引用邓起东等（1992）、冉洪流（2011）、Wells等（1994）提出的关系式。
邓起东等（1992）建立的适用于我国青藏地区走滑断层的震级与最大位错量关系为：
$$ \log （{D_{\text{m}}}） = - 3.37 + 0.53M，{\text{ }}\sigma {\text{ = 0}}{\text{.33}}，{R^{\text{2}}}{\text{ = 0}}{\text{.60}} $$ (1) 式中，M为震级，σ为标准差，R2为相关系数。
冉洪流（2011）建立的适用于我国西部地区走滑断层的震级与最大位错量关系式为：
$$ \log （{D_{\text{m}}}） = - 1.791 + 0.324M，{\text{ }}\sigma {\text{ = 0}}{\text{.22}}，{R^{\text{2}}}{\text{ = 0}}{\text{.57}} $$ (2) 国际上应用最广泛的是Wells等（1994）提出的关系式：
$$ \log （{D_{\text{m}}}） = - 7.03 + 1.03{M_{\text{w}}}，{\text{ }}\sigma {\text{ = 0}}{\text{.34 }}，{R^{\text{2}}}{\text{ = 0}}{\text{.90}} $$ (3) 式中，MW为矩震级。
由于Wells等（1994）的关系式是基于矩震级，因此需将我国工程地震界常用的面波震级转换为矩震级（张力方等，2013；吴果等，2014；谢卓娟等，2020）。本文引用Cheng等（2017）拟合的适用于我国大陆地区的震级转换关系，当MS≥7.0时：
$$ {M_{\text{w}}} = {{ - }}2.42 + 1.28{M_{\text{S}}}，{\text{ }}\sigma {\text{ = 0}}{\text{.14}}，{R^{\text{2}}}{\text{ = 0}}{\text{.61}} $$ (4) 式中，MS为面波震级。
与冷龙岭断裂最大潜在地震震级对应的矩震级为Mw7.18，最大水平位错量计算结果如表1所示。
表 1 确定性方法给出的水平位错量评估结果Table 1. Assessment results of horizontal displacement by deterministic method2.2 概率性方法与评估结果
2.2.1 基本原理
评估断裂同震位错量的过程中面临多个关键环节的不确定性，本文给出的震级与最大位错量的经验关系式均带有一定标准差，即存在不确定性。经验关系式的不确定性影响计算结果（吴果等，2022），而该影响在确定性方法中往往被忽视。此外，确定性方法未考虑断裂震级分布，默认采用最大潜在地震震级估算对应的最大位错量，这种方法可能会造成结果过于保守（孙建宝，2002）。事实上，大震产生的同震位错量大，复发间隔长；小震产生的同震位错量小，复发间隔小于大震。因此，断裂上大、小地震之间的频度关系（震级分布）与未来一定时段内可能发生的同震位错量直接相关。
冷龙岭断裂平均复发间隔为（1 640±570）a，存在较大的不确定性。此外，2022年门源地震震级为MS6.9，小于M7.5，同样引起了显著的同震位错。这说明可能导致冷龙岭断裂错动的地震存在较大的震级范围。综上，冷龙岭断裂在复发间隔和发震震级上均存在较大的不确定性，且不符合经典的特征地震模型。因此，本研究在上述确定性方法的基础上，进行冷龙岭断裂概率断层位错危险性分析。
在概率断层位错危险性分析中，需同时考虑震级分布、震级与破裂尺度的经验关系、同震位错沿断层走向分布等的不确定性。概率断层位错危险性分析结果形式类似于概率地震危险性分析（Petersen等，2011；潘华等，2017），以不同预设位错量对应的超越概率表示，不仅针对最大同震位错量。吴果等（2022）给出了概率断层位错危险性分析完整表达形式，但其涉及的环节较多、形式较复杂。
本文基于现有资料和认知水平，对概率断层位错危险性分析模型进行适当简化：①郭鹏（2019）基于错断地貌和古地震探槽研究给出了断裂平均复发间隔，隐含有平均每隔一定年限地震破裂穿过1次该位置的含义。因此，本研究不考虑分段破裂、级联破裂等复杂过程，且不考虑这些过程涉及的破裂传播距离、破裂能否传播到目标点的问题。②实际震例中位错量是沿断层走向变化的，以2008年汶川地震为例，地震在北川段产生的平均垂直位错量为3～4 m，而最大位错量为（6.5±0.5） m（Xu等，2009）。然而，Wesnousky（2008）收集了全球多次地震的地表破裂数据，发现不同地震的位错分布规律差异巨大。基于上述原因，同时考虑到冷龙岭断裂运动性质是以左旋走滑为主，本研究暂不考虑位错量随地震破裂走向变化的复杂情形。③本研究假设同震位错全部分布在单一主干断裂上，暂不考虑同震位错中一部分被分配到主干断裂以外分支断裂的情形（Chen等，2011）。
在此基础上，基于断层上不同震级档地震之间相互独立且年发生率极低的假设，可得到概率断层位错危险性分析模型的表达形式。对于某条断层上的任意目标点，断层上发生的地震在该点产生的位错量d大于等于预设位错量d0的年发生概率为：
$$ \lambda （d \geqslant {d_0}） = {{n}}（{m_0}） \cdot \int_{{m_0}}^{{m_{\rm{u}}}} {{\rm{P}}（d \geqslant {d_0}|m） \cdot f（m）dm} $$ (5) 式中，m0和mu分别为断层起算震级和最大潜在地震震级；n（m0）为断层起算震级m0以上地震年发生率；f（m）为断层震级概率密度函数；P（d≥d0|m）为断层上发生m级地震时，在目标点处产生的位错量大于等于预设位错量的概率，P（d≥d0|m）取决于震级与最大位错量的经验关系式及其不确定性。
在概率地震危险性分析中，当超越概率水平非常低时，地震动衰减关系的不确定性校正过程可能会产生失去物理意义的过大值（Zhang等，2021）。在对震级与最大同震位错量的经验关系式进行不确定性校正时，同样需增加适当的约束条件（吴果等，2022）。本研究参考经典概率地震危险性分析方法，使用经验关系式时将结果限制在3倍标准差以内。此外，历史上我国西部地区记录到的最大同震位错量为14 m，由1931年新疆富蕴8级地震产生（新疆维吾尔自治区地震局，1985）。因此本文将考虑标准差后的最大位错量限制在14 m以内。
2.2.2 震级分布模型
潘家伟等（2022）指出在青藏高原地区通常矩震级Mw≥7的地震才会产生同震地表破裂，7级以下地震不产生明显同震地表破裂（顾功叙，1983），因此本研究将M7.0作为起算震级，最大潜在地震震级为M7.5，M7.0～M7.5之间的震级概率密度函数可通过地震带的b值约束。
假设起算震级以上地震年发生率服从泊松模型。泊松模型是现行概率地震危险性分析的基础模型，其假设时间上先后发生的地震之间是相互独立的。假设断层上地震年发生率为λ，则实际发生的地震数X为k次的概率为：
$$ {\rm{P}}\left( {{{X}} = {{k}}} \right){{ = }}\frac{{{\lambda ^{{k}}}}}{{{{k}}!}}{{\rm{e}}^{ - \lambda }}，{{ k}} 为自然数 $$ (6) 对于本研究而言，
$\lambda $ 即起算震级以上地震年发生率n（m0），其等于平均复发间隔的倒数，约为0.000 61。对该参数进行简单验证，采用我国第五代地震动参数区划图中六盘山—祁连山地震带的地震活动参数、冷龙岭潜在震源区的空间分布函数（潘华等，2013）、潜在震源区中冷龙岭断裂和托莱山断裂的长度比例，可推算出冷龙岭断裂M7.0以上地震年发生率约为0.000 58，其与0.000 61接近。进一步可得到断裂在ΔT年内的发震概率为：
$$ {\rm{P}}\left(\Delta T\right){=1-}{\rm{P}}{\left({X}={0}\right)}^{\Delta T}{{=1-{\rm{e}}}}^{{-}\lambda \cdot \Delta T} $$ (7) 2.2.3 评估结果
基于概率断层位错危险性分析方法原理，平均复发间隔取1 640 a，分别计算50年超越概率2%、100年超越概率2%和100年超越概率1%的水平位错量（表2），对应的重现周期分别为2 475 a、4 950 a和9 950 a。冷龙岭断裂的平均复发间隔T为（1 640±570） a，不确定性较大。为考虑该不确定性的影响，将T取下限值1 070 a后再次计算，对应的平均值*结果如表2所示。
表 2 概率断层位错危险性分析得到的水平位错量评估结果Table 2. Assessment results of horizontal displacement by probabilistic fault displacement hazard analysis3. 评估结果综合分析
（1）采用不同震级与最大位错量的经验关系式，确定性方法评估结果显示出较大差异，根据冉洪流（2011）给出的关系式计算得到的水平位错量最大，为4.36 m，根据Wells等（1994）给出的关系式计算得到的水平位错量最小，为2.32 m。概率断层位错危险性分析结果受所用经验关系式的影响显著，可知采用确定性方法和概率性方法时均须同时采用多组经验关系式，以考虑结果的不确定性。
（2）当超越概率水平为50年2%、100年2%和100年1%时，概率断层位错危险性分析结果均值分别为1.82 m、3.17 m、4.61 m，可知评估结果随着超越概率的降低而增大，这与概率地震危险性分析中地震动随超越概率的变化规律一致。概率断层位错危险性分析可根据工程设施的重要程度和设计使用寿命，提供不同超越概率水平的位错参数，较确定性方法更灵活。
（3）考虑平均复发间隔的不确定性，将其由1 640 a改为下限值1 070 a时，概率断层位错危险性分析结果有所增大，平均值的放大倍数随着超越概率的降低而减小，这说明断裂的平均复发间隔对高超越概率下的概率断层位错危险性分析结果影响更显著。
（4）总体上，确定性方法评估结果介于100年超越概率2%和100年超越概率1%的概率断层位错危险性分析结果之间，明显大于50年超越概率2%的概率断层位错危险性分析结果。然而，如果断裂的平均复发间隔缩短至下限值1 070 a，100年超越概率2%的概率断层位错危险性分析结果将略大于确定性方法评估结果。考虑到大部分工程设施的抗震设防要求均低于100年超越概率1%的结果，此时确定性方法评估结果具备一定保守性。同时，确定性方法还具备简单易行的优点，这是其被广泛采用的原因之一。但对于跨越地震活跃断层的重要设施，开展概率断层位错危险性分析有助于认识评估结果的不确定性，且存在提供更保守的评估结果可能性。
（5）本文模型进行了一定简化，还有众多潜在的不确定性值得进一步探讨，如Guo等（2019）的研究认为冷龙岭断裂上最大潜在地震震级可达Mw7.5～Mw7.8，大于本研究所用的MS7.5。此外，Guo等（2019）认为历史上冷龙岭断裂的同震位错量是沿着断层走向变化的，在发生本次地震的断裂西端位置约为3 m。
在现有技术水平下，断裂未来强震的同震位错量评价仍面临诸多不确定性。因此，本文虽提供了不同方法的计算结果，但最终的取舍和决策仍需要专家判断。如果开展更深入的研究，可建立逻辑树，以减小认知不确定性的影响（Youngs等，2003）。
4. 结论
本文基于冷龙岭断裂最新的地震活动参数研究成果，同时采用确定性方法和概率断层位错危险性分析方法评估了该断裂未来强震的水平位错量，得出以下结论：
（1）不同研究者提供的震级与最大位错量的经验关系式之间差异较大，对于确定性方法评估结果和概率断层位错危险性分析结果均有显著影响，建议同时采用多组关系式，以考虑不确定性。
（2）通常确定性方法仅提供单一的位错量评估结果，而概率断层位错危险性分析结果随着超越概率的降低而增大，可供不同重要程度和设计使用寿命的工程设施选择相应的抗断参数。
（3）确定性方法评估结果介于概率断层位错危险性分析结果中100年超越概率2%和100年超越概率1%之间，显著大于50年超越概率2%的结果。这说明确定性方法提供的同震位错量评估结果对于大部分工程设施而言是偏保守的。然而，随着断裂平均复发间隔的缩短，概率断层位错危险性分析结果会进一步增大。因此，对于地震活动十分活跃的断层，有必要开展概率断层位错危险性分析，以提供更保守的评估结果。
（4）本文基于现有资料和研究程度，对概率断层位错危险性分析中的破裂传播过程和位错分布模型进行了简化，后续需开展更深入的研究。在现有技术水平下，断裂未来强震的同震位错量评价过程中仍有诸多不确定性难以避免，不同方法评估结果的取舍仍需要专家的主观决策。在条件允许时可建立逻辑树，以减小认知不确定性的影响。
致谢 感谢中国地震局地质研究所郭鹏副研究员对本文提供地震地质数据和相应的解释，感谢审稿人给予的专业修改建议，感谢编辑老师对本文的润色。
-
图 2 射阳台站井下地震计台基噪声功率谱密度曲线
Figure 2. Borehole seismometer power spectrum curve of Sheyang station
表 1 井下地震台基本信息
Table 1. The fundamental information of borehole seismic stations
台站名 代码 台基岩性 安装深度/m 安装方式 地震计型号 频带范围 数采型号 采样率/Hz 沛县 PX 石英砂 280 卡壁 JDF-2 20 s～20 Hz EDAS-24IP 100 280 卡壁 GL-S60B 60 s～50 Hz EDAS-24GN 100 淮安 HUA 松散沉积层 315 卡壁 JDF-2 20 s～50 Hz EDAS-24IP 100 315 卡壁 GL-S60B 60 s～50 Hz EDAS-24GN 100 海安 HA 松散沉积层 425 卡壁 JDF-3 120 s～50 Hz EDAS-24GN 100 425 卡壁 GL-S60B 60 s～50 Hz EDAS-24GN 100 大丰 DF 松散沉积层 409 卡壁 JDF-3 120 s～50 Hz EDAS-24GN 100 409 卡壁 GL-S60B 60 s～50 Hz EDAS-24GN 100 阳光岛 YGD 基岩 530 卡壁 JDF-3 120 s～50 Hz EDAS-24GN 100 530 卡壁 GL-S60B 60 s～50 Hz EDAS-24GN 100 泰州 TZ 沉积岩 500 落底 GL-S60B 60 s～50 Hz EDAS-24GN 100 盐城 YC 松散沉积层 410 卡壁 GL-S60B 60 s～50 Hz EDAS-24GN 100 宝应 BY 石英砂 450 卡壁 CMG-3TB 120 s～50 Hz EDAS-24GN 100 射阳 SY 松散沉积层 460 卡壁 GL-S60B 60 s～50 Hz EDAS-24GN 100 如东 RD 灰岩 450 落底 GL-S60B 60 s～50 Hz EDAS-24GN 100 启东 QD 灰岩 410 落底 GL-S60B 60 s～50 Hz EDAS-24GN 100 溧阳 LY 安山玄武岩 80 落底 GL-S60B 60 s～50 Hz EDAS-24GN 100 溧阳2 LY2 安山玄武岩 203 落底 GL-S60B 60 s～50 Hz EDAS-24GN 100 高邮 GY 松散沉积层 452 落底 GL-S60B 60 s～50 Hz EDAS-24GN 100 南通 NT 石英砂 159 卡壁 GL-S60B 60 s～50 Hz EDAS-24GN 100 兴化 XH 混合花岗岩 490 落底 GL-S60B 60 s～50 Hz EDAS-24GN 100 兴化2 XH2 混合花岗岩 510 卡壁 GL-CS60B 60 s～50 Hz EDAS-24GN 100 涟水 LAS 石英岩 400 落底 GL-S60B 60 s～50 Hz EDAS-24GN 100 丰县 FX 石英砂 405 落底 GL-S60B 60 s～50 Hz EDAS-24GN 100 李堡 LIB 松散沉积层 450 落底 GL-CS60B 60 s～50 Hz EDAS-24GN 100 坪山 PIS 泥岩 425 落底 GL-S60B 60 s～50 Hz EDAS-24GN 100 扬中 YAZ 泥岩 416 落底 GL-CS60B 60 s～50 Hz EDAS-24GN 100 
下载: 导出CSV
表 2 地面参考地震计参数
Table 2. The parameters of ground referenceseismometer
地震计型号 地震计序列号 频带范围 电压灵敏度/ V·m−1·s−1 UD分向 EW分向 NS分向 GL-S120 G14408VS 120 s～50 Hz 1 993.76 1 986.20 1 994.00 GL-S60 G11842VS 60 s～50 Hz 2 002.26 2 000.32 2 005.64
下载: 导出CSV
表 3 井下地震计方位角检测结果
Table 3. The azimuth detection results of borehole seismometers
台站名 测试地震计型号 参考地震计型号 滤波频带/Hz 参考地震计方位角/° 测试地震计方位角/° 校正后井下方位角/° 相关系数 沛县 JDF-2 GL-S60 0.2～0.3 359.9 186.2 186.1 0.921 89 淮安 JDF-2 GL-S60 0.2～0.3 359.6 166.7 166.3 0.895 56 GL-S60B GL-S60 0.2～0.3 0.1 50.2 50.1 0.992 51 海安 JDF-3 GL-S120 0.2～0.3 359.9 146.2 146.1 0.814 48 GL-S60B GL-S60 0.2～0.3 359.9 314.8 314.7 0.997 47 大丰 JDF-3 GL-S120 0.2～0.3 359.8 184.1 183.9 0.831 92 GL-S60B GL-S60 0.2～0.3 0.1 122.3 122.4 0.990 79 阳光岛 JDF-3 GL-S120 0.2～0.3 0.2 162.4 162.6 0.800 07 GL-S60B GL-S60 0.2～0.3 359.6 340.6 340.2 0.960 31 泰州 GL-S60B GL-S120 0.2～0.3 0.0 −4.5 −4.5 0.928 45 盐城 GL-S60B GL-S120 0.2～0.3 0.0 −137.3 −137.3 0.900 50 宝应 CMG-3TB GL-S120 0.2～0.3 359.8 6.8 6.6 0.963 71 射阳 GL-S60B GL-S60 0.1～0.2 359.6 346.0 345.6 0.968 96 如东 GL-S60B GL-S60 0.2～0.3 0.3 329.9 330.2 0.937 37 启东 GL-S60B GL-S60 0.2～0.3 0.0 6.2 6.2 0.823 46 溧阳 GL-S60B GL-S60 0.2～0.3 0.3 −2.2 −1.9 0.917 73 溧阳2 GL-S60B GL-S60 0.2～0.3 0.0 176.5 176.5 0.997 48 高邮 GL-S60B GL-S60 0.2～0.3 359.8 299.5 299.3 0.975 95 南通 GL-S60B GL-S120 0.2～0.3 359.5 347.4 346.9 0.997 02 兴化 GL-S60B GL-S60 0.2～0.3 359.3 84.3 83.6 0.988 24 兴化2 GL-CS60B GL-S60 0.2～0.3 0.0 299.9 299.9 0.990 08 涟水 GL-S60B GL-S60 0.2～0.3 0.0 233.3 233.3 0.938 00 丰县 GL-S60B GL-S60 0.2～0.3 0.0 301.8 301.8 0.956 90 李堡 GL-CS60B GL-S60 0.2～0.3 359.6 147.5 147.1 0.998 01 坪山 GL-S60B GL-S60 0.2～0.3 0.1 86.6 86.7 0.979 15 扬中 GL-CS60B GL-S60 0.2～0.3 0.6 211.8 212.4 0.996 99
下载: 导出CSV
表 4 沛县、淮安台站24 h平均检测结果
Table 4. 24-hour average azimuth detection results of Peixian、Huaian
台站 状态 东西向分量 南北向分量 平均值 相对方位角/º 相关系数 相对方位角/º 相关系数 相对方位角/º 相关系数 沛县 仿真 185.3 0.882 14 187.0 0.961 63 186.1 0.921 89 未仿真 188.0 0.697 36 186.0 0.962 12 186.8 0.829 74 淮安 仿真 164.7 0.846 90 168.6 0.944 21 166.3 0.895 56 未仿真 160.1 0.729 65 169.1 0.955 54 164.6 0.842 60
下载: 导出CSV
-
[1] 陈继锋, 李亮, 李少睿等, 2016. 甘肃省测震台网地震台站地震计方位角检验与校正. 地震工程学报, 38（3）: 460-465 doi: 10.3969/j.issn.1000-0844.2016.03.018Chen J. F. , Li L. , Li S. R. , et al. , 2016. Check and correction of seismometer azimuth for Gansu seismic network stations. China Earthquake Engineering Journal, 38(3): 460-465. (in Chinese) doi: 10.3969/j.issn.1000-0844.2016.03.018 [2] 樊晓春, 李伟, 孙君嵩等, 2020. 垂向地电阻率观测装置系数的计算——以江宁地震台为例. 震灾防御技术, 15（3）: 651—657 doi: 10.11899/zzfy20200320Fan X. C. , Li W. , Sun J. S. , et al. , 2020. Calculation of configuration coefficient in the vertical geo-resistivity observation -taking the Jiangning seismic station as an example. Technology for Earthquake Disaster Prevention, 15(3): 651—657. (in Chinese) doi: 10.11899/zzfy20200320 [3] 宫杰, 胡米东, 康清清等, 2019. 江苏地区同频带井下地震计地震监测能力对比. 地震地磁观测与研究, 40（6）: 93-99 doi: 10.3969/j.issn.1003-3246.2019.06.014Gong J. , Hu M. D. , Kang Q. Q. , et al. , 2019. Comparative analysis of monitoring capability of underground seismometer in the same frequency band in Jiangsu. Seismological and Geomagnetic Observation and Research, 40(6): 93-99. (in Chinese) doi: 10.3969/j.issn.1003-3246.2019.06.014 [4] 宫杰, 居海华, 鲍海英等, 2020. 地震流动观测防护罩集成优化与效果分析. 震灾防御技术, 15（4）: 855-867 doi: 10.11899/zzfy20200420Gong J. , Ju H. H. , Bao H. Y. , et al. , 2020. Integration optimization and effect analysis of earthquake flow observation shield. Technology for Earthquake Disaster Prevention, 15(4): 855-867. (in Chinese) doi: 10.11899/zzfy20200420 [5] 贾媛, 李杰, 朱成林等, 2020. 青岛地震台钻孔体应变异常变化因素分析. 震灾防御技术, 15（1）: 224—233 doi: 10.11899/zzfy20200123Jia Y. , Li J. , Zhu C. L. , et al. , 2020. Analysis of the abnormal variation factors of the borehole volumetric strain at Qingdao seismic station. Technology for Earthquake Disaster Prevention, 15(1): 224—233. (in Chinese) doi: 10.11899/zzfy20200123 [6] 李少睿, 董平江, 罗治国, 2012. 测震仪器定向方法探讨. 地震地磁观测与研究, 33（5）: 250-254 doi: 10.3969/j.issn.1003-3246.2012.05/06.047Li S. R. , Dong P. J. , Luo Z. G. , 2012. Discussion on the measurement methods of seismic instrument orientiation. Seismological and Geomagnetic Observation and Research, 33(5): 250-254. (in Chinese) doi: 10.3969/j.issn.1003-3246.2012.05/06.047 [7] 李少睿, 毛国良, 王党席等, 2016. 井下地震计方位角检测技术应用研究. 地球物理学报, 59（1）: 299-310 doi: 10.6038/cjg20160125Li S. R. , Mao G. L. , Wang D. X. , et al. , 2016. Research on the application of borehole seismometer azimuth detection technology. Chinese Journal of Geophysics, 59(1): 299-310. (in Chinese) doi: 10.6038/cjg20160125 [8] 李少睿, 惠少兴, 董平江, 2020. 利用同台址地脉动记录检测井下地震计水平向方位角. 地震研究, 43（1）: 71-78 doi: 10.3969/j.issn.1000-0666.2020.01.009Li S. R. , Hui S. X. , Dong P. J. , 2020. Borehole seismometer horizontal azimuth detection by using microtremors data at the same station. Journal of Seismological Research, 43(1): 71-78. (in Chinese) doi: 10.3969/j.issn.1000-0666.2020.01.009 [9] 谢剑波, 2014. 地震记录的时间域反褶积、仿真及在地震计方位角相对测量中的应用. 地球物理学报, 57（1）: 167-178 doi: 10.6038/cjg20140115Xie J. B. , 2014. Deconvolution, simulation of seismic records in the time domain and application in the relative measurements of seismometer orientation. Chinese Journal of Geophysics, 57(1): 167-178. (in Chinese) doi: 10.6038/cjg20140115 [10] 张明, 陈军辉, 严俊峰等, 2019. 浙江省测震观测台网井下地震计方位角检测与校正. 地震地磁观测与研究, 40（4）: 125-129 doi: 10.3969/j.issn.1003-3246.2019.04.019Zhang M. , Chen J. H. , Yan J. F. , et al. , 2019. Detection and correction of azimuth of borehole seismograph in Zhejiang seismic network. Seismological and Geomagnetic Observation and Research, 40(4): 125-129. (in Chinese) doi: 10.3969/j.issn.1003-3246.2019.04.019 [11] Aster R. C. , Shearer P. M. , 1991. High-frequency borehole seismograms recorded in the San Jacinto fault zone, Southern California. Part 1. Polarizations. Bulletin of the Seismological Society of America, 81(4): 1057-1080. doi: 10.1785/BSSA0810041057 [12] Lacoss R. T. , Kelly E. J. , Toksöz M. N. , 1969. Estimation of seismic noise structure using arrays. Geophysics, 34(1): 21—38. doi: 10.1190/1.1439995 [13] Niu F. L. , Li J. , 2011. Component azimuths of the CEArray stations estimated from P-wave particle motion. Earthquake Science, 24(1): 3-13. doi: 10.1007/s11589-011-0764-8 [14] Peterson J. R., 1993. Observations and modeling of seismic background noise. U. S. Geological Survey Open-File Report. 93-322. 期刊类型引用(1)
1. 张敏，宫杰，立凯，张扬，居海华，胡光武. 南京地震台甚宽频地震计观测性能研究. 华南地震. 2024(03): 51-58 . 
百度学术其他类型引用(0)
-
下载:
点击查看大图
计量
- 文章访问数: 224
- HTML全文浏览量: 53
- PDF下载量: 17
- 被引次数: 1
