Design and Application of A Deformation Time-frequency Analysis Software Package Based on MATLAB
-
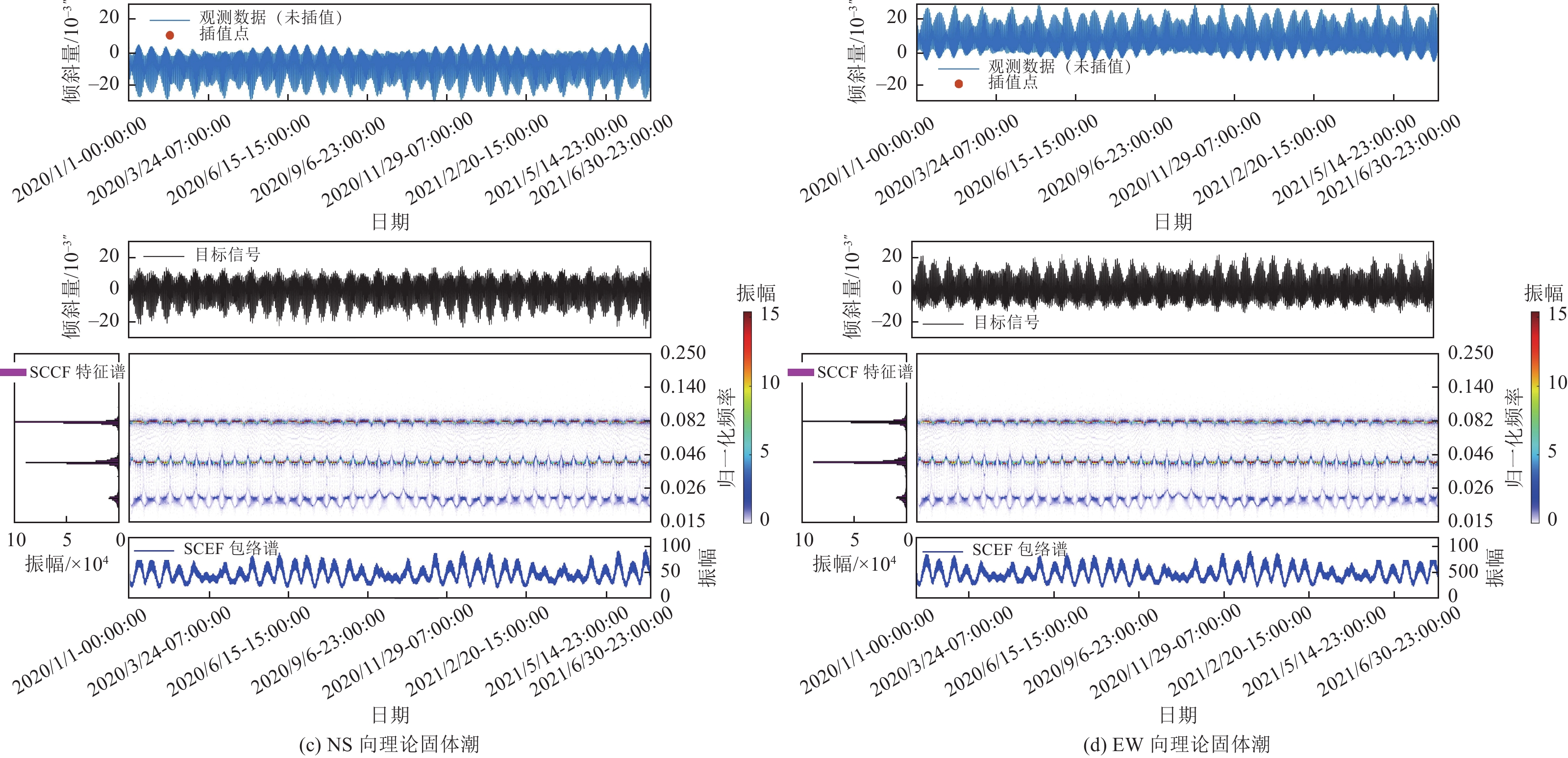
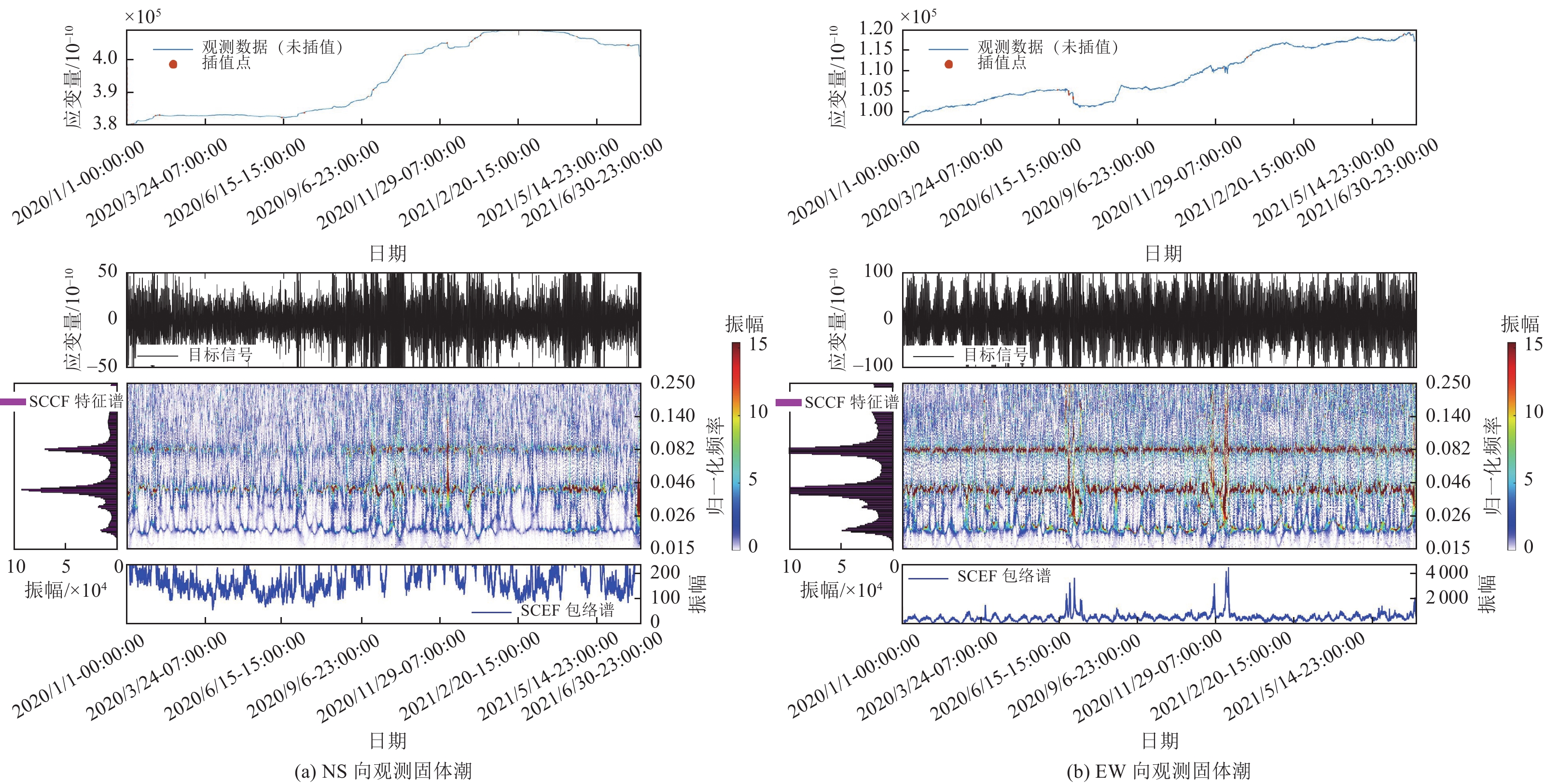
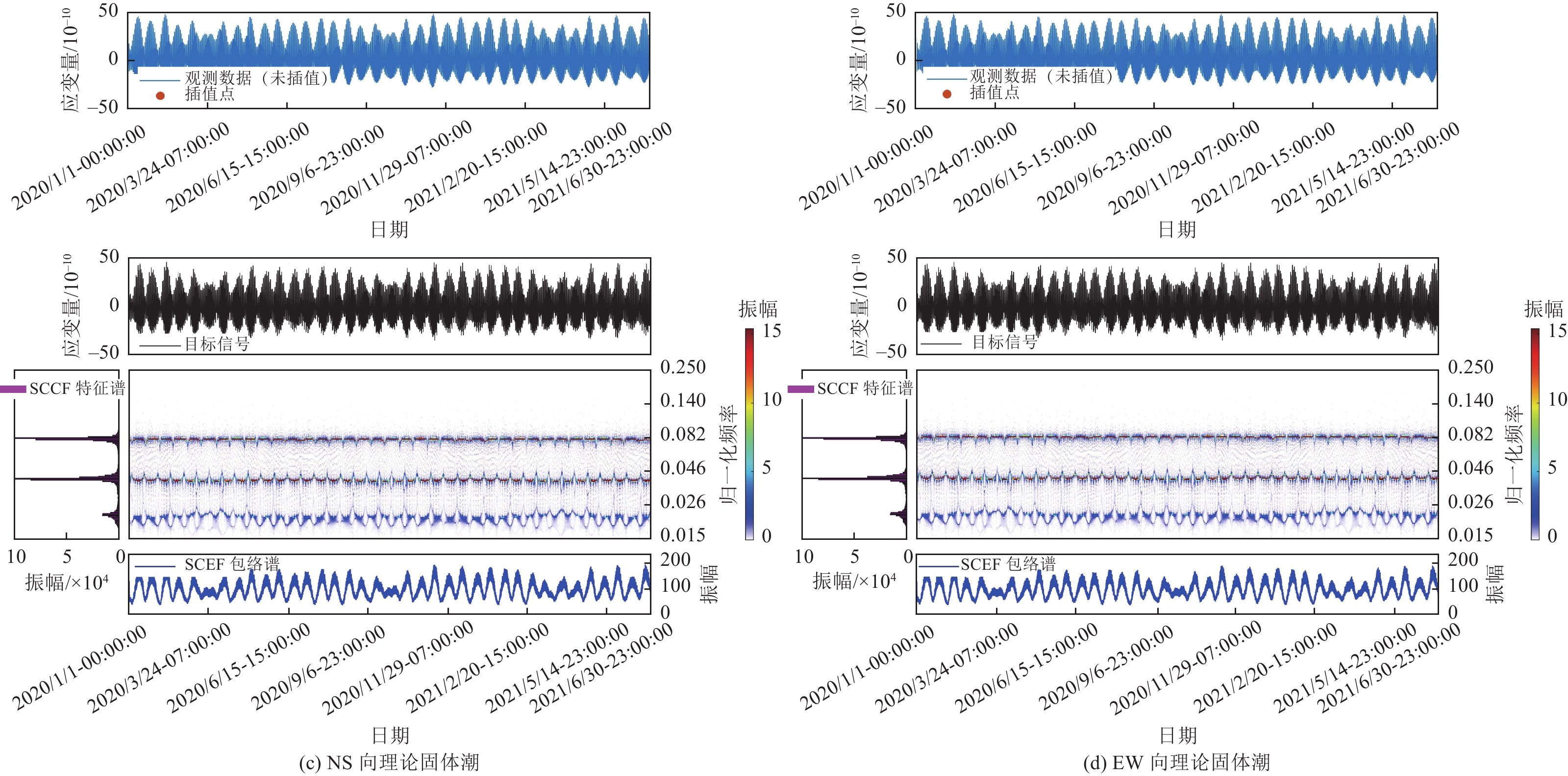
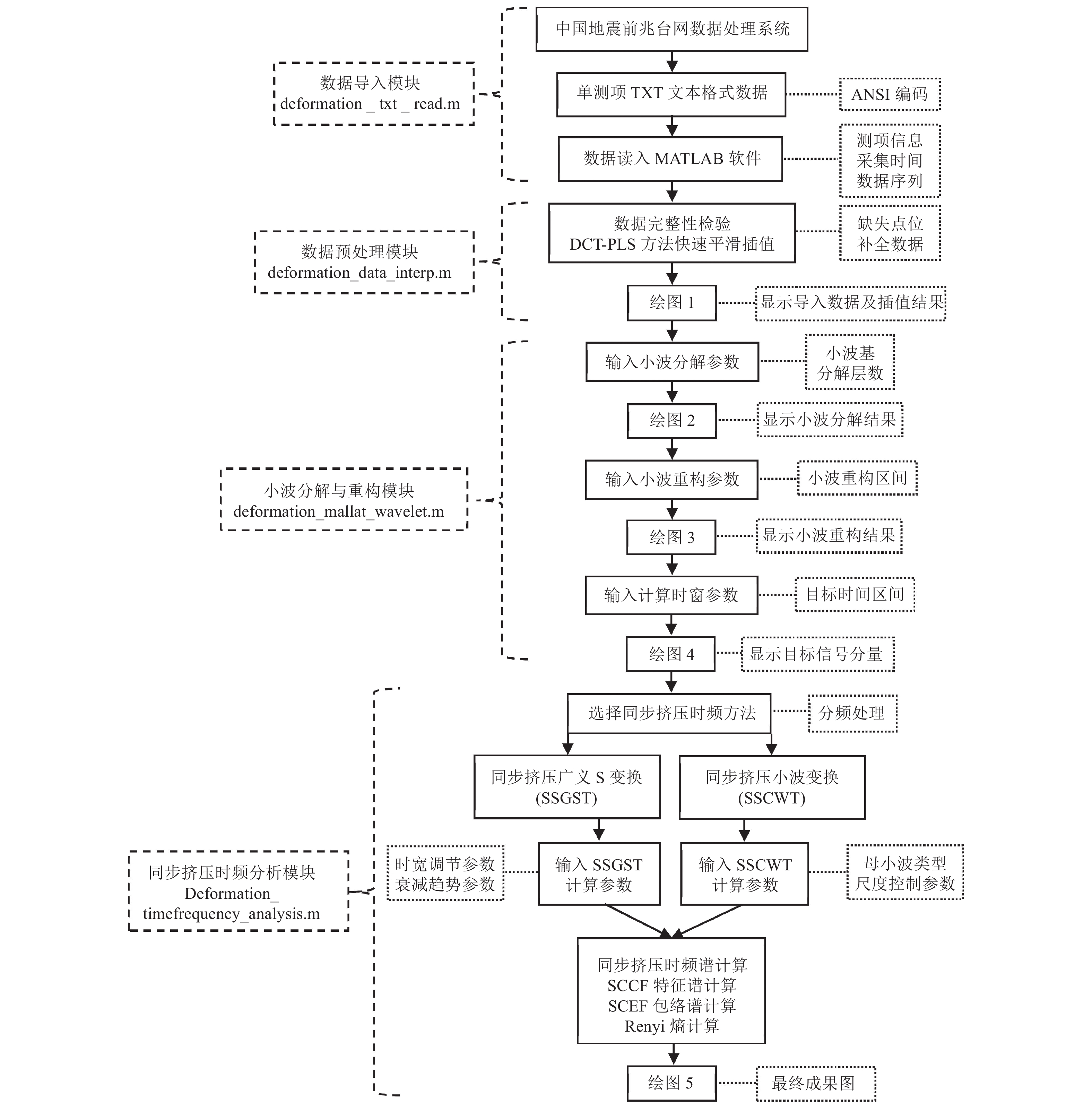
摘要: 为方便台站工作人员快速准确分析定点形变观测数据的时频响应特征，利用MATLAB软件研发了基于小波分析和同步挤压时频变换的交互式数据处理与成图软件包。该软件包遵循模块化设计原则，利用导入模块读取从中国地震前兆台网数据处理系统下载的原始数据，利用预处理模块对缺失数据进行插值补全，利用小波分解与重构模块从原始数据中提取待分析的目标信号分量，利用同步挤压时频分析模块对提取目标进行高精度时频分析，并在各模块关键节点中增加绘图功能，全部处理过程采用绘图-参数输入-绘图交互的方式进行，参数灵活可调，且每步计算结果直观清晰。应用该软件包对2020年1月至2021年6月西昌小庙台DSQ型水管仪和SS-Y型伸缩仪整时值采样数据进行固体潮时频计算，并与理论固体潮时频结果进行对比，结合时频辅助分析方法，从时频谱角度初步评价了2套仪器观测资料的质量情况，为台站日常数据跟踪分析提供了参考。Abstract: In order to facilitate the station staff to effectively and accurately analyze the time-frequency characteristics of the fixed point deformation data, we provide an interactive data processing and mapping software package of wavelet decomposition and synchrosqueezing time-frequency transform based on MATLAB. The package follows the principle of modularization and includes such modules as the import module reading the original data from the txt file downloaded by QZProcess, the preprocess module interpolating the missing original data, the wavelet decomposition and reconstruction module extracting the target signal component from the original data and the synchrosqueezing transform module carrying out high precision time-frequency results of the extracted target signal. Since the mapping functions are integrated into modules and the whole flow is operated interactively, the calculation parameters are adjustable and the result of each step is intuitive. We use the proposed software package to process the hourly sampling data for DSQ and SS-Y of Xiaomiao station from Jan,2020 to June,2021. The processing results of earth tide signal qualitatively evaluate the quality of observation, and also providing useful reference for precursory data tracking and analysis.
-
引言
随着我国交通基础建设的持续深入发展，穿越黏滑断层的隧道不断涌现，如在建的雅康高速二郎山隧道穿越保凰活动断裂，成兰铁路诸隧道穿越龙门山活动断裂等。在2008年汶川地震中，都映高速部分隧道，其所穿越的黏滑断层在强震诱发下发生黏滑错动，造成错动段隧道结构和围岩严重破坏，甚至出现了隧道整体垮塌的严重震害（图 1），这对灾后救援和灾后重建工作造成了严重影响（四川省交通厅公路规划勘察设计研究院，2008；于海英等，2008）。如何提高断层黏滑错动时隧道结构的安全性和稳定性是亟待研究和解决的关键技术问题之一。
图 1 龙溪隧道黏滑断层段隧道整体垮塌Figure 1. Collapse of stick-slip fracture section in Longxi tunnel目前，黏滑断层隧道的减错措施主要有二衬设置减错缝和初支与二衬之间设置减错层2种。设置减错缝可减小隧道结构的纵向刚度，提高了隧道结构适应断层黏滑错动所产生相对变位的性能；设置减错层可减小隧道结构的横向刚度，消减了传递至二衬结构的强制位移。
国内外专家、学者对穿越黏滑断层隧道的减错技术做了部分研究，主要有：穿越活动断层隧道震害特征及震害机理（高孟潭等，2008；崔光耀等，2013a；何川等，2014）；断层错动下围岩与隧道结构的位移和应力变化（赵伯明等，2009；李玉江等，2013）；不同倾角、错距下断层黏滑错动对山岭隧道洞身结构的受力特性（熊炜等，2010；蒋建平等，2011；刘学增等，2014；张理平等，2017）；设置不同减错缝的减错效果（崔光耀等，2013b；李学峰等，2014；信春雷等，2015）；设置不同减错层的减错效果（崔光耀等，2013c）等。以上研究在穿越黏滑断层隧道断层错动机制，设置减错缝不同间距、减错层不同厚度减错效果方面做了部分工作，但均未对穿越黏滑断层隧道设置减错缝不同缝宽、减错层不同刚度的减错效果进行研究。本文依托都汶高速友谊隧道F1黏滑断层段，对黏滑断层隧道设置不同缝宽减错缝、不同刚度减错层的减错效果进行研究，以期能够促进穿越黏滑断层隧道减错技术的发展。
1. 研究情况
1.1 友谊隧道F1黏滑断层段工程概况
1.1.1 工程地质
隧址区位于纸厂沟与小桃沟之间的山体内，受断层和岩性影响，节理裂隙较发育，岩体较破碎。
F1黏滑断层为挤压性逆断层，隧道洞身穿F1黏滑断层而过，走向北东，倾向北西，倾角60°，破碎带宽度0.5—2.0m，断层破碎带主要由糜棱岩、碎块岩组成，Ⅴ级围岩。上下盘岩体均为Ⅴ级围岩。
1.1.2 支护结构设计
隧道支护结构为复合式衬砌，跨度×高度＝9.4m×8.0m；隧道初支采用C25喷射混凝土，厚度25cm，二衬采用C25模筑混凝土，厚度40cm。
1.2 计算情况
1.2.1 计算模型
以友谊隧道F1黏滑断层段为研究背景，利用FLAC3D有限差分数值模拟软件建立计算模型，隧道埋深为40m，隧底围岩厚40m，左右两侧宽度取5倍隧道跨度，约60m，纵向开挖长度100m。本次计算采用brick单元，其中围岩单元47550个，衬砌单元6820个。计算时围岩按弹塑性材料考虑，衬砌则按弹性材料考虑。减错缝采用12m设缝间距（崔光耀等，2013b），减错层厚度采用10cm（崔光耀等，2013c）。通过在上盘围岩施加位移荷载来模拟断层错动，位移荷载通过施加速度来实现，错距10cm。
1.2.2 计算参数
施工中减错缝主要采用止水带进行连接，减错层一般采用橡胶板（王帅帅等，2016），围岩根据勘测资料选取Ⅴ级围岩。计算模型物理力学参数如表 1所示。
表 1 计算模型参数Table 1. Parameters of calculation model参数 重度/kN·m-3 弹性模量/MPa 泊松比 黏聚力/MPa 内摩擦角/° 围岩 20 15000 0.40 0.10 24 C25喷射混凝土 22 23000 0.20 C25模注混凝土 25 28000 0.20 减错缝 6 10 0.45 减错层 10 0—2000 0.45 1.2.3 计算工况
本文主要研究减错缝不同缝宽、减错层不同刚度对减错效果的影响规律，计算工况如表 2所示。
表 2 计算工况Table 2. Calculation condition工况 计算内容 备注 1 无减错措施 2 施设减错缝 缝宽分别为：5cm、10cm、15cm、20cm 3 施设减错层 弹模分别为：2.5MPa、5MPa、10MPa、20MPa、50MPa、100MPa、200MPa、500MPa、1000MPa、2000MPa 1.2.4 监测布置
计算模型上盘设4个监测断面、下盘设3个监测断面，每个监测断面设置8个监测点，监测布置如图 2所示。
2. 减错缝宽度对减错效果的影响分析
2.1 结构内力
提取各工况错动完成时的各监测断面计算数据，以缝宽10cm为例进行内力分析。轴力、弯矩的计算按照公式（1）、（2）计算（中华人民共和国交通部，2004）。监测断面最大轴力值见表 3，监测断面最大弯矩值见表 4。
表 3 监测断面最大轴力（单位：kN）Table 3. Maximum axial force of monitoring section (unit: kN)工况 距断层距离/m -22 -10 -2 2 10 22 34 无减错措施 -6468 -9754 -14884 -13376 -13341 -9551 -3702 缝宽10cm -5917 -9133 -14857 -13395 -12558 -8646 -3153 注：距断层距离正值为上盘，负值为下盘，其它同理。 表 4 监测断面最大弯矩（单位：kN·m）Table 4. Maximum bending moment of monitoring section (unit: kN·m)工况 距断层距离/m -22 -10 -2 2 10 22 34 无减错措施 -60.2 -142.1 -217.6 -185.0 -121.9 -45.1 -126.7 缝宽10cm -61.3 -140.2 276.1 -200.5 -127.7 48.5 -116.6 轴力、弯矩计算公式为：
$$ N=\frac{1}{2}E({\varepsilon _内}+{\varepsilon _外})bh $$ (1) $$ M=\frac{1}{{12}}E({\varepsilon _内}-{\varepsilon _外})b{h^2} $$ (2) 式中，b为截面宽度（m），取1m；h为截面厚度（m）；E为弹性模量（MPa）；${\varepsilon _内}$、${\varepsilon _外}$为结构内、外侧应变；N为结构轴力（N）；M为弯矩（N·m）；后同。
由表 3可知，施设减错缝与无减错措施工况监测断面最大轴力值均呈现压应力状态，且沿隧道纵向分布趋势相似，最大值均出现在下盘靠近断层的断面，其中无减错措施工况值为-14884kN，施设减错缝工况值为-14857kN；随着监测断面与断层的距离增大，监测断面最大轴力呈下降趋势。由各监测断面最大轴力整体分析可知，施设减错缝工况监测断面最大轴力略小于无减错措施工况。
由表 4可知，无减错措施工况监测断面最大弯矩均表现为外侧受拉，施设减错缝改变了隧道结构受力，出现内侧受拉部位；监测断面最大弯矩值均出现在下盘靠近断层的断面，其中不设减错缝工况值为-217.6kN·m，施设减错缝工况值为276.1kN·m。由各监测断面最大弯矩整体分析可知，施设减错缝工况监测断面最大弯矩略大于无减错措施工况。
轴力、弯矩指标主要用于结构设计，单一分析轴力、弯矩不能综合体现结构的力学性能。隧道支护的结构安全性可由安全系数（综合考虑了轴力、弯矩等指标）体现。
2.2 结构安全系数
提取各工况错动完成时的内力计算数据进行安全系数分析，安全系数K按照公式（3）、（4）计算（中华人民共和国交通部，2004）。以缝宽10cm进行安全系数分析，监测断面最小安全系数见表 5。
$$ KN \le \varphi \alpha{R_{\rm{a}}}bh $$ (3) $$ KN \le \varphi \frac{{1.75{R_1}bh}}{{6{e_0}/h - 1}} $$ (4) 表 5 监测断面最小安全系数Table 5. Minimum safety factor of monitoring section工况 距断层距离/m -22 -10 -2 2 10 22 34 无减错措施 1.933 1.282 0.840 0.935 0.937 1.309 3.377 缝宽10cm 2.112 1.326 0.841 0.933 0.995 1.446 3.964 式中，Ra为混凝土抗压极限强度（MPa）；Rl为混凝土抗拉极限强度（MPa）；φ为构件纵向弯曲系数；α为轴向力偏心影响系数；e0为轴向力对截面的偏心距（m）。
由表 5可知，施设减错缝与无减错措施工况监测断面最小安全系数沿隧道纵向分布趋势相似，最小值均出现在下盘靠近断层监测断面，其中无减错措施工况安全系数最小值为0.840，施设减错缝工况安全系数最小值为0.841；随着监测断面与断层距离的增大，监测断面最小安全系数呈增大趋势，上盘安全系数整体较下盘小。由各监测断面最小安全系数整体分析可知，施设减错缝工况监测断面最小安全系数略大于无减错措施工况。
2.3 减错效果
根据安全系数分析各工况减错效果，减错效果可按式（5）进行计算，各工况减错效果如图 3所示。
$$ \lambda= \frac{{{K_1}-{K_0}}}{{{K_0}}} \times 100\% $$ (5) 式中：λ为减错效果；K0为无减错措施工况监测断面最小安全系数；K1为施设减错缝工况监测断面最小安全系数。
由图 3可知，各工况减错效果沿隧道纵向分布趋势相似，随着监测断面与断层的距离增大，上下盘减错效果整体呈上升趋势，且上盘减错效果较下盘整体更好，其中上盘减错效果最大为24.50%，下盘减错效果最大为9.26%。随着减错缝宽度的增加，隧道上盘减错效果变好，下盘缝宽10—15cm时减错效果最好，主要由于断层黏滑错动对上盘的影响远大于下盘。减错缝宽度的增加适应了断层黏滑错动造成的上盘强制位移，断层黏滑错动的能量得到一定程度的释放，从而提高了上盘隧道的结构安全性，可以设想，对于隧道上盘部分存在最优减错缝宽度；减错缝宽度的增加虽然适应了断层黏滑错动造成的下盘强制位移，但由于抵御断层黏滑错动对下盘影响所需减错缝缝宽为10—15cm，当缝宽增加到20cm时，下盘隧道整体刚度的下降对下盘隧道的结构安全性造成了不利影响，致使减错效果下降。
3. 减错层弹性模量对减错效果的影响分析
3.1 结构内力
提取各工况错动完成时各监测断面的计算数据，以减错层弹性模量为2.5MPa为例进行内力分析。监测断面最大轴力值见表 6，监测断面最大弯矩值见表 7。
表 6 监测断面最大轴力（单位：kN）Table 6. Maximum axial force of monitoring section (unit: kN)工况 距断层距离/m -21 -11 -2 2 11 21 32 无减错措施 -6515 -10663 -17049 -14062 -12114 -7572 -3777 减错层弹模（2.5MPa） -5557 -7014 -8375 -8981 -8490 -6154 -3788 表 7 监测断面最大弯矩（单位：kN·m）Table 7. Maximum bending moment of monitoring section (unit: kN·m)工况 距断层距离/m -21 -11 -2 2 11 21 32 无减错措施 -78.5 -155.9 -218 -187.2 -100.3 -46.8 -35.9 减错层弹模（2.5MPa） -173.4 -269 -254.1 -217.1 -108.0 -59.3 -42.7 由表 6可知，施设减错层与无减错措施工况监测断面最大轴力值均呈现压应力状态，且沿隧道纵向分布趋势相似，最大值均出现在上下盘靠近断层的断面，其中无减错措施工况值为-17049kN，施设减错层工况值为-8981kN；随着监测断面与断层距离的增大，监测断面最大轴力呈下降趋势。由各监测断面最大轴力整体分析可知，施设减错层工况监测断面最大轴力小于无减错措施工况。
由表 7可知，施设减错层与无减错措施工况监测断面最大弯矩值均表现为外侧受拉；无减错措施工况监测断面最大弯矩值出现在下盘靠近断层的断面，其值为-218kN·m，施设减错层监测断面最大弯矩值出现在下盘距离断层11m处，其值为-269kN·m。由各监测断面最大弯矩整体分析可知，施设减错层工况监测断面最大弯矩大于无减错措施工况。
3.2 结构安全系数
提取各工况错动完成时各监测断面的计算数据，以减错层弹性模量为2.5MPa为例进行安全系数分析，监测断面最小安全系数见表 8。
表 8 监测断面最小安全系数Table 8. Minimum safety factor of monitoring section工况 距断层距离/m -21 -11 -2 2 11 21 32 无减错措施 1.919 1.172 0.733 0.889 1.032 1.651 3.310 减错层弹模（2.5MPa） 2.455 1.798 1.505 1.583 1.592 2.031 3.399 由表 8可知，施设减错层与无减错措施工况监测断面最小安全系数沿隧道纵向分布趋势相似，最小值均出现在下盘靠近断层监测的断面，其中无减错措施工况最小安全系数最小值为0.733，施设减错层工况最小安全系数最小值为1.505；随着监测断面与断层距离的增大，监测断面最小安全系数呈增大趋势，上盘安全系数整体较下盘小。由各监测断面最小安全系数整体分析可知，施设减错层工况监测断面最小安全系数大于无减错措施工况。
3.3 减错效果
根据安全系数分析各工况减错效果，减错效果计算方法同式（5），各工况减错效果如图 4所示。
由图 4可知，各工况减错效果沿隧道纵向分布趋势相似，随着监测断面与断层距离的增大，上下盘减错效果整体呈下降趋势，且下盘减错效果较上盘整体略好，其中下盘减错效果最大为105.32%，上盘减错效果最大为78.07%；当减错层弹性模量增加到一定程度（约100MPa），减错效果趋于稳定。
4. 结论
（1）断层黏滑错动对隧道上盘的影响远大于下盘，上盘部分是黏滑断层隧道减错设防设计的重点段落。
（2）减错缝对上盘部分隧道结构的减错效果优于下盘，其中上盘减错效果最大为24.50%，下盘减错效果最大为9.26%；减错层对下盘部分隧道结构的减错效果略优于上盘，其中下盘减错效果最大为105.32%，上盘减错效果最大为78.07%。
（3）随着减错缝宽度的增加，隧道上盘减错效果变好，下盘缝宽10—15cm减错效果最好，主要是由于断层黏滑错动对上盘的影响远大于下盘。减错缝宽度的增加适应了断层黏滑错动造成的上盘强制位移，断层黏滑错动的能量得到一定程度的释放，从而提高了上盘隧道的结构安全性，可以设想，对于隧道上盘部分存在最优减错缝宽度；减错缝宽度的增加虽然适应了断层黏滑错动造成的下盘强制位移，由于抵御断层黏滑错动对下盘影响所需减错缝缝宽为10—15cm，当缝宽增加到20cm时，下盘隧道整体刚度的下降对下盘隧道的结构安全性造成了不利影响，致使减错效果下降。
（4）随着减错层弹性模量的增加，隧道上下盘减错效果降低；当减错层弹性模量增加到一定程度（约100MPa），减错效果趋于稳定。
-
图 1 软件总体处理框架流程
Figure 1. General processing framework and flow of the software package
3 小庙台2020年1月至2021年6月DSQ型水管仪观测固体潮与理论固体潮时频结果对比
3. Comparison of time-frequency results between observed and theoretical earth tide of DSQ data of Xiaomiao seismic station from Jan, 2020 to June,2021
4 小庙台2020年1月至2021年6月SS-Y型伸缩仪观测固体潮与理论固体潮时频结果对比
4. Comparison of time-frequency results between observed and theoretical earth tide of SS-Y data of Xiaomiao seismic station from Jan,2020 to June,2021
表 1 软件包所用方法及基本定义
Table 1. Summary of methods and basic definitions of the software package
类型 方法名称 基本定义 备注 信号分解方法 小波分析
（DWT）${A}_{j}s\left(t\right)={A}_{j+1}s\left(t\right)+{D}_{j+1}s\left(t\right),j=\mathrm{0,1},\cdots ,N$ $ s\left(t\right) $为原始信号，$ N $为分解层数，$ {A}_{j}s\left(t\right) $为第$ j $阶低频趋势分量，$ {D}_{j}s\left(t\right) $为第$ j $阶高频细节分量 时频前处理
方法连续小波变换
（CWT）$ C W T\left(a,\tau \right)=\left\langle{s,{\psi }_{a,\tau }}\right\rangle={\displaystyle\int }_{-\infty }^{+\infty }s\left(t\right){a}^{-\frac{1}{2}}{\psi }^{*}\left(\dfrac{t-\tau }{a}\right){\rm{d}}t $ $ {a}^{-\frac{1}{2}}\psi \left(\dfrac{t-\tau }{a}\right) $为母小波族，$ a $为小波尺度因子，$ \tau $为时间平移因子 广义S变换
（GST）$ G S T\left(f,t\right)={\displaystyle\int }_{-\infty }^{+\infty }s\left(\tau \right)\dfrac{{\left|f\right|}^{\lambda }}{\sqrt{2{\text{π}} }\rho }{\rm{e}}^{-\dfrac{{\left(\tau -t\right)}^{2}{f}^{2\lambda }}{2{\rho }^{2}}}{\rm{e}}^{-j2{\text{π}} \tau }{\rm{d}}\tau $ $ \dfrac{\left|f\right|}{\sqrt{2{\text{π}} }}{\rm{e}}^{-\dfrac{{t}^{2}{f}^{2}}{2}} $为Gauss窗，$ \lambda $为时宽调节参数，$ \rho $为衰减趋势调节参数 时频后处理
方法同步挤压小波变换（SSCWT） $ S S C W T\left({\omega }_{l},\tau \right)={\Delta \omega }^{-1}\displaystyle\sum _{{a}_{k}:\left|C W T\left(a,\tau \right)-{\omega }_{l}\right|\leqslant \Delta \omega /2}C W T\left(a,\tau \right){{a}_{k}}^{-3/2}\left({\Delta a}_{k}\right) $ $ C W T\left(a,\tau \right) $为CWT时频谱，$ {a}_{k} $为第$ k $个离散化尺度，$ {\omega }_{l} $为点$ l $处离散化频率值 同步挤压广义S变换（SSGST） $ S S G S T\left({\tilde f}_{l},t\right)={(\Delta {\tilde f}_{l})}^{-1}\displaystyle\sum _{{f}_{k}:\left|{\tilde f}_{l}\left({f}_{k},t\right)-{\tilde f}_{l}\right|\leqslant \Delta {\tilde f}_{l}/2}\left|GST\left({f}_{k},t\right)\right|{f}_{k}\Delta {f}_{k} $ $ GST\left({f}_{k},t\right) $为GST时频谱，$ {f}_{k} $为离散频点，$ {\tilde f}_{l} $为挤压中心频率，$ \Delta {\tilde f}_{l} $为挤压带宽 辅助分析
方法叠加幅值特征函数（SCCF） $ S C C F\left(t\right)=\displaystyle\sum _{t=1}^{N}\left|TFR(f,t)\right|f=1,\cdots ,M $ $ TFR(f,t)\in {\boldsymbol{C}}^{M\cdot N} $，为时频谱矩阵 叠加系数包络函数（SCEF） $ S C E F\left(f\right)=\displaystyle\sum _{f=1}^{M}\left|E(f,t)\right|t=1,\cdots ,N $ $ E(f,t) $为频率点$ f $处时频谱系数的包络函数 信息熵（Renyi） $ {H}_{a}\left(T F R\right)=\dfrac{1}{1-a}{\mathrm{log}}_{2}\displaystyle\iint T F R(f,t){\rm{d}}t{\rm{d}}f $ $ a $为Renyi熵的阶次，一般取3，$ {H}_{a} $为熵值 
下载: 导出CSV
表 2 软件包所含函数程序与功能
Table 2. Summary of programs and functions of the software package
函数（脚本）名称 所属功能模块 主要功能描述 Main_func.m 主脚本程序 封装全部功能模块函数，执行全计算流程 deformation_txt_read.m 数据导入模块 导入TXT文件中原始数据及测项信息 deformation_data_interp.m 数据预处理模块 利用DCT-PLS方法平滑插值缺失数据 deformation_mallat_wavelet.m 小波分解与重构模块 利用DWT分解并提取待分析目标信号 deformation_timefrequency_analysis.m 同步挤压时频分析模块 分频计算SSCWT或SSGST时频谱，并计算SCCF函数、
SCEF函数、Renyi熵等辅助分析项dctpls_smoothn.m 模块子调用函数 封装DCT-PLS插值方法实现算法 sscwt_tfrs.m 模块子调用函数 封装SSCWT时频方法实现算法 ssgst_tfrs.m 模块子调用函数 封装SSGST时频方法实现算法
下载: 导出CSV
表 3 观测固体潮与理论固体潮时频谱Renyi熵值
Table 3. The Renyi entropy of observed earth tide and theoretical earth tide
项目 DSQ（NS向） DSQ（EW向） SS-Y（NS向） SS-Y（EW向） 观测固体潮时频谱Renyi熵值 6.26 5.56 8.44 8.17 理论固体潮时频谱Renyi熵值 5.50 5.50 5.13 5.13 Renyi熵误差 0.76 0.06 3.31 3.04
下载: 导出CSV
-
[1] 蔡佩蕊, 陈伟, 林立峰等, 2020. 基于STFT方法对沿海宽频带倾斜仪的噪声分析. 地震工程学报, 42（2）: 396—402 doi: 10.3969/j.issn.1000-0844.2020.02.396Cai P. R. , Chen W. , Lin L. F. , et al. , 2020. Noise analysis of coastal broadband tiltmeter based on STFT method. China Earthquake Engineering Journal, 42(2): 396—402. (in Chinese) doi: 10.3969/j.issn.1000-0844.2020.02.396 [2] 侯跃伟, 赵兵, 田韬, 2015. 基于Daubechies小波分析的南京数字化钻孔形变震前变化特征研究. 震灾防御技术, 10（2）: 388—396 doi: 10.11899/zzfy20150219Hou Y. W. , Zhao B. , Tian T. , 2015. Anomalies characteristics of digital data of borehole deformation before the earthquakes at the nanjing region based on daubechies wavelet analysis. Technology for Earthquake Disaster Prevention, 10(2): 388—396. (in Chinese) doi: 10.11899/zzfy20150219 [3] 黄昱丞, 郑晓东, 栾奕等, 2018. 地震信号线性与非线性时频分析方法对比. 石油地球物理勘探, 53（5）: 975—989Huang Y. C. , Zheng X. D. , Luan Y. , et al. , 2018. Comparison of linear and nonlinear time-frequency analysis on seismic signals. Oil Geophysical Prospecting, 53(5): 975—989. (in Chinese) [4] 孔祥瑞, 翟丽娜, 李梦莹等, 2018. 经验模态分解法在高频形变干扰分析中的应用. 防灾减灾学报, 34（4）: 34—37Kong X. R. , Zhai L. N. , Li M. Y. , et al. , 2018. Application of empirical mode decomposition method to analysis of high-frequency deformation interference. Journal of Disaster Prevention and Reduction, 34(4): 34—37. (in Chinese) [5] 李娜, 冯建刚, 张博等, 2020. 天水钻孔应变可靠性分析及映震效能检验. 地震工程学报, 42（5）: 1111—1116 doi: 10.3969/j.issn.1000-0844.2020.05.1111Li N. , Feng J. G. , Zhang B. , et al. , 2020. Reliability analysis of borehole strain meters and test of earthquake-reflecting efficacy in Tianshui. China Earthquake Engineering Journal, 42(5): 1111—1116. (in Chinese) doi: 10.3969/j.issn.1000-0844.2020.05.1111 [6] 刘建明, 李志海, 孙甲宁等, 2016. 基于小波分析提取地倾斜异常特征. 地震, 36（1）: 38—48 doi: 10.3969/j.issn.1000-3274.2016.01.005Liu J. M. , Li Z. H. , Sun J. N. , et al. , 2016. Extraction of ground tilt anormalies based on wavelet analysis. Earthquake, 36(1): 38—48. (in Chinese) doi: 10.3969/j.issn.1000-3274.2016.01.005 [7] 吕品姬, 赵斌, 陈志遥等, 2011. 小波分解-STFT方法在地形变观测数据中的应用. 大地测量与地球动力学, 31（5）: 136—140Lv P. J. , Zhao B. , Chen Z. Y. , et al. , 2011. Application of wavelet-decomposition and STFT method in continuous deformation observation analysis. Journal of Geodesy and Geodynamics, 31(5): 136—140. (in Chinese) [8] 孟庆筱, 吕健, 李进武等, 2018. 基于S变换的唐山四分量钻孔应力时频特征分析. 大地测量与地球动力学, 38（11）: 1202—1206Meng Q. X. , Lv J. , Li J. W. , et al. , 2018. Analysis of time-frequency characteristics of four-components borehole stress at tangshan station based on S-transform. Journal of Geodesy and Geodynamics, 38(11): 1202—1206. (in Chinese) [9] 潘晓, 曹思远, 徐彦凯等, 2020. 基于同步挤压小波变换的烃类识别技术. 地球物理学报, 63（11）: 4176—4187 doi: 10.6038/cjg2020M0663Pan X. , Cao S. Y. , Xu Y. K. , et al. , 2020. The hydrocarbon detection technology based on synchrosqueezing wavelet transform. Chinese Journal of Geophysics, 63(11): 4176—4187. (in Chinese) doi: 10.6038/cjg2020M0663 [10] 平建军, 张永仙, 单连君等, 2013. 地震前兆信息量计算软件研制及其操作说明. 震灾防御技术, 8（4）: 397—407 doi: 10.3969/j.issn.1673-5722.2013.04.007Ping J. J. , Zhang Y. X. , Shan L. J. , et al. , 2013. Software for earthquake precursor information extracting and analysis. Technology for Earthquake Disaster Prevention, 8(4): 397—407. (in Chinese) doi: 10.3969/j.issn.1673-5722.2013.04.007 [11] 孙伶俐, 李明, 蒋玲霞等, 2013. 湖北省潮汐形变观测异常及干扰识别. 大地测量与地球动力学, 33（S1）: 36—40Sun L. L. , Li M. , Jiang L. X. , et al. , 2013. Anomaly recognition of tidal deformation and disturbance factors in Hubei Province. Journal of Geodesy and Geodynamics, 33(S1): 36—40. (in Chinese) [12] 王宁, 吴云, 张燕, 2014. 时频分析方法在形变数据中的应用研究. 地震工程学报, 36（2）: 413—420 doi: 10.3969/j.issn.1000-0844.2014.02.0413Wang N. , Wu Y. , Zhang Y. , 2014. The application of time-frequency analysis methods in deformation data. China Earthquake Engineering Journal, 36(2): 413—420. (in Chinese) doi: 10.3969/j.issn.1000-0844.2014.02.0413 [13] 魏学强, 袁洪克, 秦晶晶等, 2016. 广义S变换地震信号时频分析. 震灾防御技术, 11（4）: 808—813 doi: 10.11899/zzfy20160411Wei X. Q. , Yuan H. K. , Qin J. J. , et al. , 2016. The time-frequency analysis of seismic data using generalized S transform. Technology for Earthquake Disaster Prevention, 11(4): 808—813. (in Chinese) doi: 10.11899/zzfy20160411 [14] 武善艺, 刘琦, 龚丽文等, 2018.2008年汶川MS8.0地震前定点形变高频异常特征的研究. 地震, 38（2）: 145—156Wu S. Y. , Liu Q. , Gong L. W. , et al. , 2018. High-frequency anormaly characteristics of fixed-point deformation before the 2008 Wenchuan MS8.0 earthquake. Earthquake, 38(2): 145—156. (in Chinese) [15] 严海滔, 黄饶, 周怀来等, 2019. 同步挤压广义S变换在南海油气识别中的应用. 地球物理学进展, 34（3）: 1229—1235 doi: 10.6038/pg2019CC0143Yan H. T. , Huang R. , Zhou H. L. , et al. , 2019. Application of Nanhai oil and gas identification based on synchrosqueezing generalized S transform. Progress in Geophysics, 34(3): 1229—1235. (in Chinese) doi: 10.6038/pg2019CC0143 [16] 杨千里, 王婷婷, 边银菊, 2020. 基于广义S变换的地震与爆炸识别. 地震学报, 42（5）: 613—628Yang Q. L. , Wang T. T. , Bian Y. J. , 2020. Recognition of earthquakes and explosions based on generalized S transform. Acta Seismologica Sinica, 42(5): 613—628. (in Chinese) [17] 张桂欣, 郝振纯, 祝善友等, 2016. AMSR2缺失数据重建及其土壤湿度反演精度评价. 农业工程学报, 32（20）: 137—143 doi: 10.11975/j.issn.1002-6819.2016.20.018Zhang G. X. , Hao Z. C. , Zhu S. Y. , et al. , 2016. Missing data reconstruction and evaluation of retrieval precision for AMSR2 soil moisture. Transactions of the Chinese Society of Agricultural Engineering, 32(20): 137—143. (in Chinese) doi: 10.11975/j.issn.1002-6819.2016.20.018 [18] 张维辰, 朱凯光, 池成全等, 2019. 基于小波变换的2013年芦山MS7.0地震前姑咱台钻孔应变异常时频分析. 地震学报, 41（2）: 230—238Zhang W. C. , Zhu K. G. , Chi C. Q. , et al. , 2019. Time-frequency analyses for borehole strain anomaly at guzan station before 2013 Lushan MS7.0 earthquake based on wavelet transform. Acta Seismologica Sinica, 41(2): 230—238. (in Chinese) [19] 张小艳, 熊峰, 王旭东等, 2019. 内蒙古中部地区形变主要干扰的时频响应特征分析. 中国地震, 35（4）: 718—725 doi: 10.3969/j.issn.1001-4683.2019.04.012Zhang X. Y. , Xiong F. , Wang X. D. , et al. , 2019. Analysis of time-frequency response characteristics for main deformation disturbances in central Inner Mongolia. Earthquake Research in China, 35(4): 718—725. (in Chinese) doi: 10.3969/j.issn.1001-4683.2019.04.012 [20] 张中旭, 李智蓉, 2020. 小波分析方法在定点形变日常跟踪中的应用研究. 云南大学学报（自然科学版）, 42（6）: 1121—1128Zhang Z. X. , Li Z. R. , 2020. Application of wavelet analysis method in daily tracking of fixed-point deformation. Journal of Yunnan University (Natural Sciences Edition), 42(6): 1121—1128. (in Chinese) [21] 赵佳佳, 陈志遥, 张燕等, 2017. 奇异谱分析在倾斜应变数据处理中的应用研究. 大地测量与地球动力学, 37（5）: 541—545Zhao J. J. , Chen Z. Y. , Zhang Y. , et al. , 2017. Research on application of singular spectrum analysis in data processing of earth tilt and strain. Journal of Geodesy and Geodynamics, 37(5): 541—545. (in Chinese) [22] Mallat S. G. , 1989. A theory for multiresolution signal decomposition: the wavelet representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 11(7): 674—693. doi: 10.1109/34.192463 [23] Mousavi S. M. , Langston C. A. , Horton S. P. , 2016. Automatic microseismic denoising and onset detection using the synchrosqueezed continuous wavelet transform. Geophysics, 81(4): V341—V355. doi: 10.1190/geo2015-0598.1 期刊类型引用(1)
1. 侯跃伟，刘孝峰，杜存鹏. 定点形变数据可视化分析系统的研制及应用. 地震地磁观测与研究. 2023(06): 154-162 . 
百度学术其他类型引用(0)
-
下载:
点击查看大图
计量
- 文章访问数: 207
- HTML全文浏览量: 82
- PDF下载量: 36
- 被引次数: 1
