Positioning Accuracy Analysis of the New Portable Industry-level Unmanned Aerial Vehicle Phantom 4RTK
-
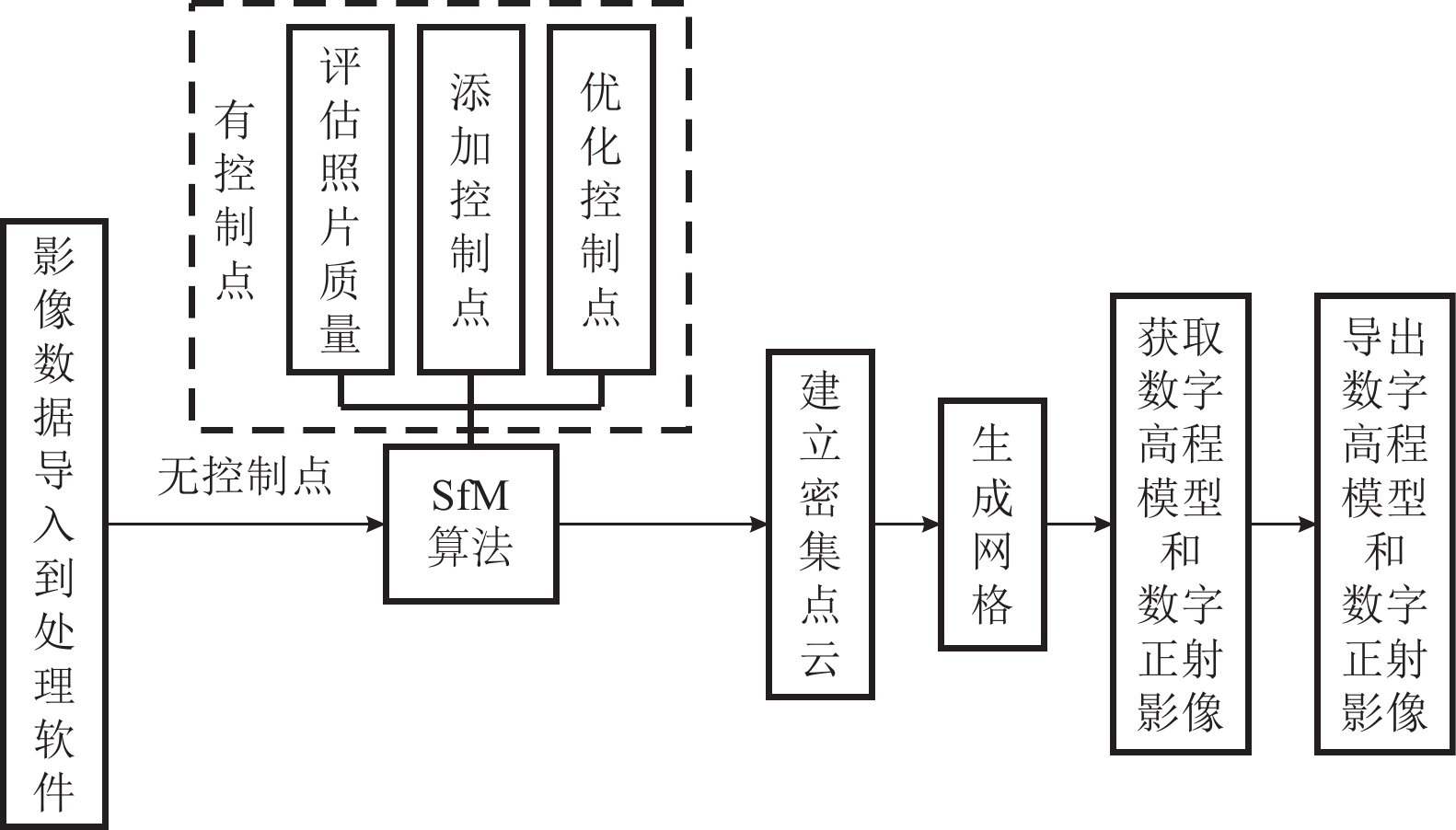
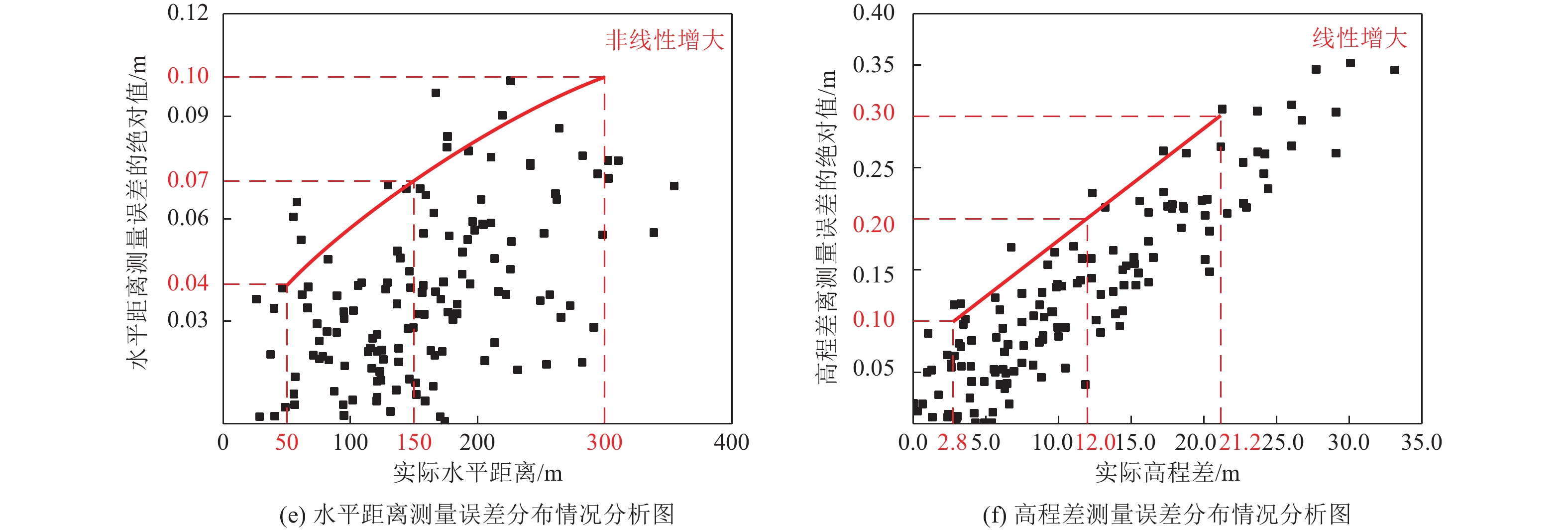
摘要: 本文针对新型便携式行业级无人机精灵4RTK开展了实测数据的定位精度分析，从有、无控制点情况下的绝对定位精度和无控制点情况下的相对定位精度2方面入手，详细计算后者水平距离和高程差的测量误差，探讨网络RTK技术的无控制点情况在活动构造中的应用。结果表明，无人机精灵4RTK在天气较晴朗、飞行高度100 m、镜头角度正射向下、旁向和航向重叠率均为70%等实测条件下，有控制点情况下水平位置和高程测量误差均<4.5 cm，无控制点情况下水平位置测量误差<0.60 m、高程测量误差<1.90 m；无控制点情况下，当实际水平距离<300 m时，水平距离测量误差<0.100 m，当高程差<2.8 m时，高程差测量误差<0.100 m；以复合运动性质的发震断层为例，初步探讨认为无人机精灵4RTK的网络RTK技术在无控制点情况下提取活动构造的定量参数时，其水平位移量精度能够达到厘米级，垂直位错量精度可能达不到厘米级，当垂直位错量小于8.0 m时，精度能够达到0.157 m。Abstract: This paper carried out a study on positioning accuracy of measured data for the new portableindustry-level unmanned aerial vehicle Phantom 4RTK. Starting from the absolute positioning accuracy with and without control points and relative positioning accuracy without control points aspects, the measurement errors of the horizontal distance and elevation difference of the latter are calculated in detail, and the application of the network RTK technology without control points in active tectonics is discussed. The results show that the horizontal position and elevation measurement errors of unmanned aerial vehicle Phantom 4RTK are less than 4.5 cm with control points under the measured conditions of sunny weather, flying altitude of 100 m, camera angle downwards, lateral and course overlap rate of 70%. Without control points,the measurement errors of horizontal position and elevation are less than 4.5 cm, in the case of no control points the horizontal position measurement error is less than 0.60 m, and the elevation measurement error is less than 1.90 m. In the case of no control points, when the actual horizontal distance is less than 300 m, the horizontal distance measurement error is less than 0.100 m, when the elevation difference is less than 2.8 m, the elevation difference measurement error is less than 0.100 m. Taking causative faults of composite motion as an example, this paper preliminarily discussed that the network RTK technology based on Phantom 4RTK can extract the quantitative parameters of the active tectonics without control points, the accuracy of the horizontal displacement can reach centimeter level, but the accuracy of the vertical dislocation may not reach centimeter level, when the vertical dislocation is less than 8.0 m, the accuracy can reach 0.157 m.
-
引言
对地震动特征规律的分析是地震工程学科研究的主要问题 (刘启方等，2006)。近几十年来国内外发生了多次破坏性地震，对所获得地震动记录进行分析，不难看出位于发震断层附近区域内的地震动具有许多独特性质，例如竖向效应。竖向效应是指近断层区域内竖向地震作用远远超过规范所规定的值的现象，国内外众多地震的强震记录显示竖向地震峰值是水平向的1/2—2/3(Ambraseys等，2003)，我国《建筑抗震设计规范》(GB 50011—2010) 规定竖向地震影响系数为水平向的65%(中华人民共和国国家标准，2010)，但在许多地震灾害中的近断层区域内出现了竖向地震动高于水平向地震动的现象 (冉志杰等，2012；赵国辉等，2008；周锡元等，2006；Niazi等，1991)。
中国大陆强震台网于2008年3月投入运行，在2008年5月12日汶川特大地震中获得了丰富的近断层强震记录，为相关问题的研究提供了重要的基础数据。通过对强震记录的分析发现近断层地震动竖向与水平分量之比最高达到了1.4(谢俊举等，2010；于海英等，2008)。但是已有的对于竖向效应问题的研究主要集中于对地震动动力特性的分析，关于地震动对工程结构影响的分析较少，尤其缺少对影响效应的定量分析。
本文基于此研究背景，选取汶川地震近断层强震记录为基础数据，以单自由度体系P-Δ效应为研究目标，对近断层竖向地震动所产生的P-Δ效应进行分析研究，对于工程结构的抗震问题具有一定的意义。
1. P-Δ效应的计算方法
已有研究表明，P-Δ效应产生的放大作用是竖向地震导致结构破坏的主要原因之一 (贺秋梅等，2014；刘启方等，2006)。根据结构抗震思想，大多数工程结构在进行抗震设计时都需要转化为等效的单自由度体系的叠加进行分析 (胡聿贤，2006；李宏男，2013；梁炯丰等，2013)，所以本文对单自由度体系竖向地震作用下的P-Δ效应进行分析。
1.1 P-Δ效应概念描述
P-Δ效应是指体系在动力荷载作用下，由于其竖向作用使体系结构产生动力附加弯矩的过程，相当于在体系上附加了一个水平地震作用，其原理如图 1所示 (胡聿贤，2006；袁一凡等，2012)。图中m表示质量，P(t) 表示体系在某一时刻承受的水平动力荷载，F(t) 表示体系在某一时刻承受的竖向荷载，包括重力以及竖向动力荷载等。
根据其基本原理，对于地震作用下的单自由度体系，在考虑了竖向地震作用后就变成了具有2个方向自由度的双自由度体系。由于地震所产生的运动以水平运动为主，故本文分析时不考虑竖向地震作用造成的竖向相对运动，因此该体系在某一时刻承受的竖向荷载作用为重力与竖向地震作用引起的惯性力。
强震仪所获得的地震加速度以av(t) 表示，同时竖直方向以加速度向上为正、向下为负，根据其基本原理P-Δ效应等效出的水平地震作用如下式 (1) 所示：
$$ {P_0}(t) = m\left[ {g + {a_v}(t)} \right] \cdot \frac{{u(t)}}{H} $$ (1) 式中，u(t) 为体系在某时刻的位移大小，H为体系高度，P0(t) 为与竖向地震作用等效的水平地震作用。
1.2 P-Δ效应的计算方法
将P-Δ效应所产生的附加水平动力作用带入动平衡方程，则得到考虑P-Δ效应的动力平衡方程，表达如下：
$$ m\ddot u{\rm{(}}t{\rm{)}} + c\dot u{\rm{(}}t{\rm{)}} + ku{\rm{(}}t{\rm{)}} = m\; \cdot \;\left[ {g + {a_v}{\rm{(}}t{\rm{)}}} \right]\; \cdot \;\frac{{u{\rm{(}}t{\rm{)}}}}{H} + m{a_h}{\rm{(}}t{\rm{)}} $$ (2) 式中，c是单自由度体系阻尼系数，k是回复力系数，ah(t) 是水平地震加速度。
式 (2) 可以根据杜哈密积分进行简化求解，进而求得考虑P-Δ效应的单自由度体系的地震反应，从而进一步求得P-Δ效应的放大作用，具体方法为：
(1) 按照地震动力时间步利用杜哈密积分求得每一时间步时刻的水平地震作用动力反应，即得到u(ti) 与ü(ti)；
(2) 根据每一时间步的水平位移按照公式 (3) 计算竖向荷载所产生的等效水平地震作用，利用杜哈密积分求解等效水平地震作用所产生的附加地震反应：ü0(ti)
$$ {\ddot u_0}({t_i}) = \left[ {g + {a_v}(t)} \right]\; \cdot \;\frac{{u(t)}}{H} $$ (3) (3) 据所计算出的水平地震反应ü(t) 与附加地震反应ü0(t)，按照公式 (4) 计算P-Δ效应所产生的放大作用，式中β为效应放大系数，越大表征所产生放大作用越强。
$$ \beta = \frac{{\ddot u(t) + {{\ddot u}_0}(t)}}{{\ddot u(t)}} $$ (4) 2. 竖向地震动P-Δ效应放大作用的分析
为分析近断层竖向地震动P-Δ效应放大作用的特点，本文分别选取汶川地震中近断层与中远场强震记录，按上述方法分析计算实际地震动所产生P-Δ效应的放大系数，并与中远程强震记录对比分析。
2.1 强震数据的选取
按近断层定义，本文先选取汶川地震中发震断层附近20个强震台站的强震记录，台站的断层距小于60km，具体信息见表 1。再选取位于中远场的20个强震台站的强震记录，台站的断层距大于100km，具体信息见表 2。强震记录来源于中国地震局工程力学研究所下属的中国强震台网中心数据库。
表 1 所选取强震记录的近场台站信息Table 1. The information of near-site stations selected in the study编号 51MZQ 51JYH 51PXZ 51AXT 51JYD 51SFB 51MXN 51WCW 51MXT 51JYC 断层距/km 7.17 13.6 21.05 25.89 26.43 26.73 27.09 27.72 27.77 30.54 编号 51DXY 51DYB 51LXT 51QLY 51LXM 51PWM 51LXS 51GYZ 51BXZ 51XJD 断层距/km 31.19 34.33 46.4 49.17 49.18 51.28 51.58 55.15 57.75 59.09 表 2 所选取强震记录的中远场台站信息Table 2. The information of remote stations selected in the study编号 51HSD 51CXQ 51YAS 51JZB 62SHW 51JZZ 51TQL 51HYQ 51HYJ 51LDD 断层距/km 104.5 104.7 111.1 114.2 121.1 125.4 137.2 155.4 163 177.1 编号 51SMW 51LDL 62TSH 51SMM 51MBD 51YXX 51YXZ 51SMC 51LDS 51MNL 断层距/km 188.7 190.9 191.4 211.5 222.2 249.2 262.2 272.9 278.5 300.4 为充分表达研究目的，给出了汶川地震发震断层与所选取近断层强震台站的空间分布，如图 2所示。
2.2 P-Δ效应放大系数计算结果
对于任意台站，所获得强震记录分为水平向 (EW、NS) 与竖直向 (UD)，所以任意台站可以获得2个P-Δ效应放大系数。分别计算所选取近断层与中远场强震台站记录的放大系数，并将计算结果绘制成频率直方图，如图 3所示。计算中，结合大多数工程结构的动力特点，其单自由度体系阻尼比选择为0.05，自振周期分别取1s、2s与3s。
图 3 不同自振周期P-Δ效应的放大系数Figure 3. Amplification factor for P-Δ effect of different natural period对比近断层与中远场强震台站记录所计算出的放大系数，从整体上可以看出：对于近断层所获得的强震记录其P-Δ效应放大系数值较大，而中远场的P-Δ效应放大系数值较小；对于中远场地震动，其地震作用的水平分量本身就较弱，故其竖向地震动所产生的P-Δ效应可以忽略。因此竖向地震动所产生P-Δ效应的放大作用是近断层地震动所产生动力作用的主要特点，对于近断层地震动应分析其所产生的P-Δ效应。
2.3 放大系数的统计分析
地震动具有很强的不确定性 (Niazi等，1991)，为对建筑抗震设计提供具体参考，在完成对所选取强震记录初步分析后，应对多条强震记录的初步分析结果进行统计规律分析。
基于所得到的20个近断层台站获得的强震记录，计算得到不同自振周期条件下P-Δ效应的放大系数。利用概率图工具分析放大系数服从的概率分布，如图 4所示 (自振周期为1s)。根据分析，放大系数服从正态分布。进一步计算不同自振周期单自由度体系放大系数的统计参数，计算结果如表 3所示。
表 3 放大系数的统计参数Table 3. Statistical parameter of amplification factor自振周期/s 1 2 3 均值 1.012 1.229 1.701 方差 0.002 0.014 0.063 从表 3可以看出，对于同一自振周期的单自由度体系，其放大系数的离散性较小，放大系数主要分布于均值附近，且主要受单自由度体系自振周期的影响，自振周期越大，其P-Δ效应放大系数越高。为此，可以认为，在近断层区域内，竖向地震动所产生P-Δ效应的放大作用具有普遍性，其放大作用主要受自振周期大小的影响。
3. P-Δ效应放大系数谱的建立
3.1 放大系数谱的建立思路
在近断层范围内竖向地震引起的P-Δ效应会产生普遍放大作用，其放大系数主要受自振周期的影响，因此可以参考地震动反应谱的基本思想建立P-Δ效应放大系数谱，以获得竖向地震动P-Δ效应的放大作用与体系自振周期的关系。以上分析可知，当体系自振周期一定时P-Δ效应放大系数的离散性较小，所以可以用自振周期为一定时不同台站强震记录放大系数的均值作为P-Δ效应放大系数的代表值，从而建立放大系数谱，建立步骤如下：
(1) 设定不同的自振周期，分别为Tk=0.02×k(k=1，2，…，200)。
(2) 对于所设定的不同的自振周期，分别计算每个台站地震记录的P-Δ效应放大系数，即得到βi(Tk)，其表示第i个台站的强震记录在自振周期为Tk时的P-Δ效应放大系数。
(3) 当体系自振周期为Tk时，求得不同台站强震记录放大系数的均值，即u[β(Tk)]，进而求得不同自振周期条件下，其放大系数的均值u[β(Tk)]。
(4) 绘制放大系数曲线，横坐标为Tk，纵坐标为u[β(Tk)]，基于所得曲线利用最小二乘法拟合，得到规准化后的放大系数谱。
3.2 放大系数谱的建立
建立近断层竖向地震P-Δ效应的放大系数谱，需先求得Tk-u[β(Tk)]曲线，然后进行最小二乘拟合。为了方便工程应用，拟合函数选用线性函数进行。从Tk-u[β(Tk)]曲线中可以看出，在自振周期Tk < 2s时放大系数几乎都小于1.1，曲线趋近于一条斜率为零的直线，在自振周期Tk > 2s时放大系数β > 1.1，P-Δ效应具有明显的放大作用，β随Tk的变化趋近于单调上升的线性函数曲线，所以对放大系数规准谱曲线以Tk=2s为分界点进行分段拟合。利用最小二乘法进行分段拟合并经过简化处理得到规准化后的放大系数谱，如图 5所示。
图 5 竖向地震动P-Δ效应的放大系数谱Figure 5. Amplification spectra of P-Δ effect for vertical ground motion进一步拟合放大系数谱的数学关系，其关系表达式为式 (5)：
$$ \beta = \left\{ \begin{array}{l} {\rm{1}}.{\rm{05}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {\rm{0s}}< {T_k} \le {\rm{1}}.7{\rm{s}}\\ {\rm{0}}.{\rm{6}} \times {T_k} + {\rm{0}}.{\rm{03}},\;\;\;\;{\rm{1}}.{\rm{7s}}\; < {T_k} \le {\rm{4s}} \end{array} \right. $$ (5) 此公式可为近断层区域内抗震设计问题中考虑竖向地震作用P-Δ效应的参考公式，在结构抗震设计中可以与反应谱结合使用。
4. 结语
本文以汶川大地震近断层的强震数据为基础，对近断层竖向地震动所产生的P-Δ效应进行分析，结果如下：
(1) 汶川地震中相比于中远场区域，近断层区域内竖向地震作用所产生的P-Δ效应具有明显的放大作用，并且具有普遍性。P-Δ效应放大系数主要受体系自振周期的影响，当自振周期一定时，不同地震动的放大系数服从正态分布并且离散性较小，主要分布于均值附近。
(2) 建立了放大系数随体系自振周期变化的放大系数谱，从而为结构抗震设计提供了参考依据；认为在可能发生强烈地震的活断层附近区域内，结构抗震设计过程中应该考虑竖向地震动所产生P-Δ效应引起的放大作用，放大系数按照规准后的放大系数谱曲线确定，在结构抗震设计中，放大系数谱可以与反应谱结合使用。
(3) 由于中国大陆地区强震记录数量的限制，本文仅仅选择了汶川地震的近断层强震记录；随着近断层强震数据的增多，应根据发震断层与地质构造特点，建立适用于不同区域、不同地质场地条件的放大系数谱，从而使其在工程应用中日益完善。
-
图 1 Trimble R8差分GPS、地面控制点和检查点、航线规划
Figure 1. Trimble R8 differential GPS, ground control points and checkpoints, route planning
图 3 有控制点情况下误差分布直方图及正态分布曲线
Figure 3. Histogram and normal distribution curve of error distribution of variables at control points and checkpoints with control point
图 4 无控制点情况下检查点各变量误差分布直方图及正态分布曲线
Figure 4. Histogram and normal distribution curve of error distribution of each variable at checkpoint without control point
5 无控制点情况下水平距离和高程差测量误差分析
5. Measurement error analysis of horizontal distance and elevation difference without control point
表 1 有控制点情况下的误差分析结果
Table 1. Error analysis results of control points and checkpoints with control point
控制点
编号X误差
/cmY误差
/cmXY误差
/cmZ误差
/cm检查点
编号X误差
/cmY误差
/cmXY误差
/cmZ误差
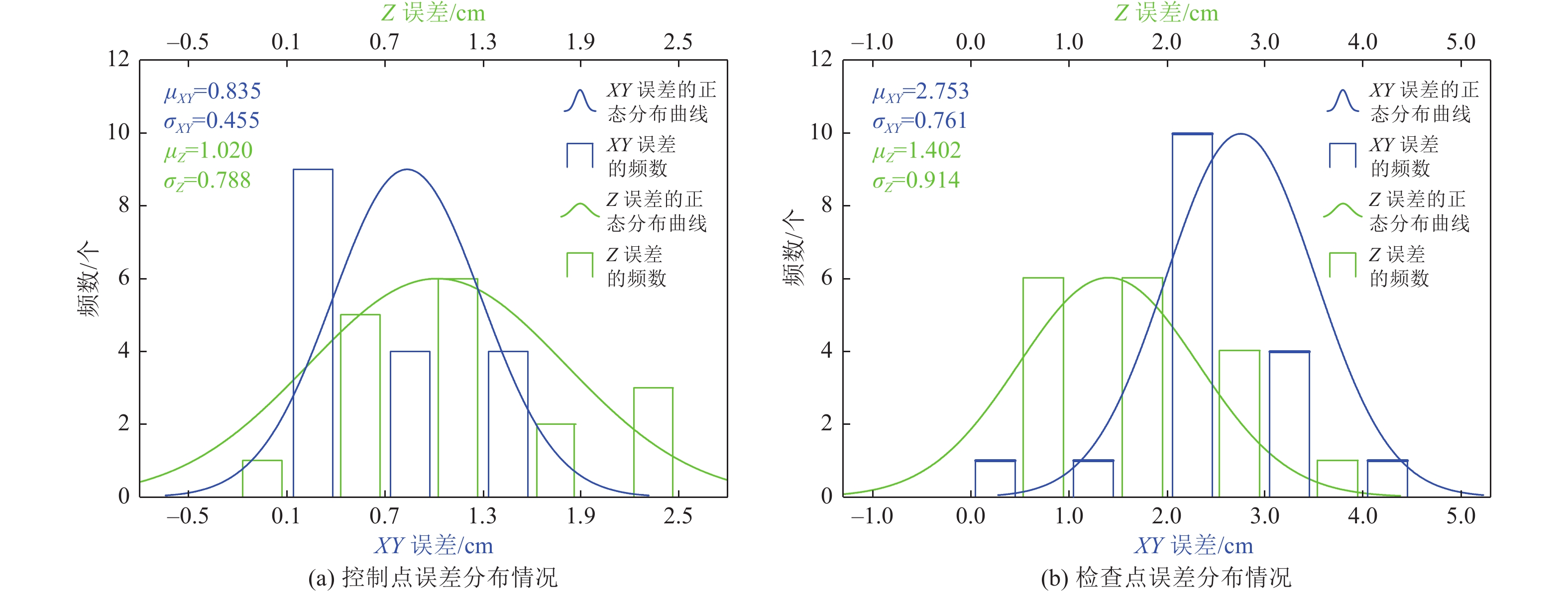
/cmK1 0.143 0.821 0.834 −0.208 J1 2.172 3.695 4.286 0.100 K2 −0.312 0.237 0.778 −0.345 J2 1.748 1.973 2.636 −0.700 K3 −0.330 −0.034 0.692 1.548 J3 −2.530 −1.634 3.012 −1.716 K4 −0.244 0.236 0.395 −2.303 J4 −1.683 −1.625 2.339 −1.579 K5 1.133 −0.313 0.529 0.219 J5 2.161 2.327 3.176 3.300 K6 0.597 1.411 1.757 2.349 J6 −1.740 −1.534 2.320 −1.538 K7 −0.623 −0.029 0.619 0.212 J7 −1.620 −2.188 2.722 1.500 K8 1.017 0.068 1.420 1.066 J8 −2.629 −0.314 2.648 1.000 K9 −1.255 0.402 0.445 1.018 J9 −3.329 −1.302 3.575 2.300 K10 −0.705 −0.328 0.392 −0.299 J10 1.424 2.337 2.737 −0.200 K11 −0.051 −0.690 0.331 −0.764 J11 −2.310 −2.935 3.735 1.500 K12 −0.324 −0.225 0.339 −0.958 J12 −2.764 −1.033 2.951 1.500 K13 −0.005 −0.529 1.176 −1.112 J13 0.808 0.240 0.843 2.300 K14 0.379 −1.716 1.532 −1.883 J14 −1.872 −2.067 2.789 −1.400 K15 −0.422 0.454 0.624 2.221 J15 0.970 2.121 2.332 −0.300 K16 1.300 0.572 1.019 −0.026 J16 −0.241 1.862 1.878 2.200 K17 −0.295 −0.333 1.318 −0.810 J17 −0.310 2.805 2.822 1.200 均值 0.537 0.494 0.835 1.020 均值 1.783 1.882 2.753 1.402 中误差 0.670 0.666 0.945 1.274 中误差 1.964 2.065 2.850 1.643 注：控制点和检查点的X误差、Y误差和Z误差均值为其绝对值的均值。 
下载: 导出CSV
表 2 无控制点情况下检查点误差分析结果
Table 2. Error analysis results of checkpoint without control point
检查点
序号X误差
/mY误差
/mXY误差
/mZ误差
/m检查点
序号X误差
/mY误差
/mXY误差
/mZ误差
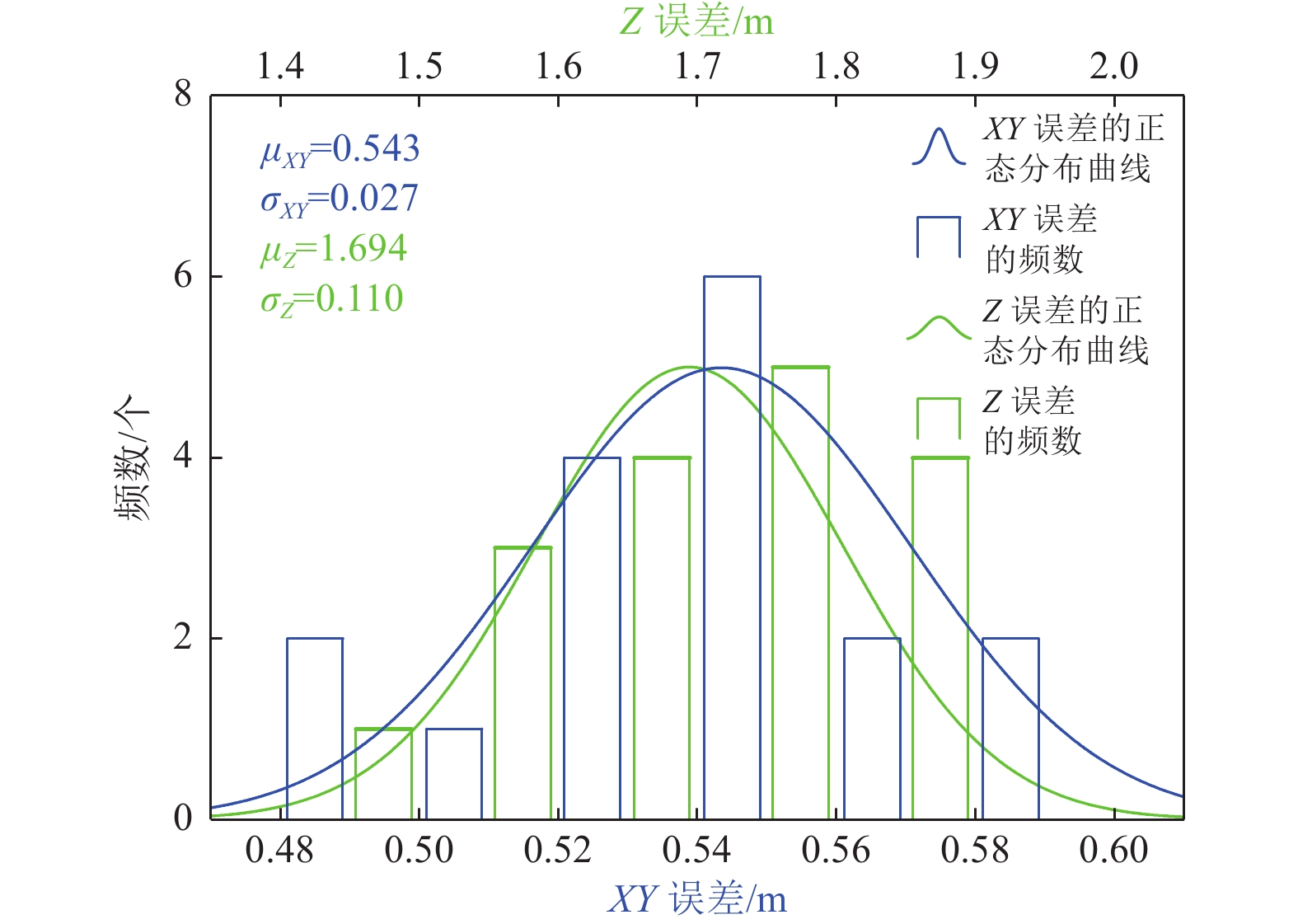
/mJ1 −0.352 −0.423 0.550 −1.843 J11 −0.318 −0.453 0.553 −1.637 J2 −0.328 −0.416 0.530 −1.707 J12 −0.321 −0.444 0.548 −1.631 J3 −0.361 −0.460 0.585 −1.716 J13 −0.274 −0.415 0.497 −1.578 J4 −0.339 −0.443 0.558 −1.579 J14 −0.281 −0.450 0.530 −1.804 J5 −0.299 −0.384 0.487 −1.497 J15 −0.281 −0.450 0.531 −1.842 J6 −0.306 −0.430 0.528 −1.538 J16 −0.340 −0.445 0.560 −1.849 J7 −0.313 −0.451 0.549 −1.632 J17 −0.360 −0.432 0.562 −1.793 J8 −0.348 −0.453 0.572 −1.741 均值 0.320 0.439 0.543 1.694 J9 −0.325 −0.482 0.582 −1.726 中误差 0.321 0.439 0.544 1.698 J10 −0.293 −0.425 0.517 −1.688 注：控制点和检查点的X误差、Y误差和Z误差均值为其绝对值的均值。
下载: 导出CSV
表 3 强震造成地表破裂的参数表
Table 3. Parameter table of surface rupture caused by strong earthquake
序号 发震时间 地点 震级/M 发震断层性质 地表破裂 水平位移量/m 垂直位错量/m 1 1607-07-12 甘肃酒泉 7¼ 逆—左旋 3.0 1.0 2 1679-09-02 三河平谷 8 右旋—正 3.9 3.2 3 1709-10-14 宁夏中卫南 7½ 逆—左旋 5.0～6.0 1.0～2.0 4 1713-02-26 云南寻甸 6¾ 正—左旋 2.3 2.0 5 1739-01-03 宁夏银川、平罗 8 正—右旋 1.5 0.9 6 1902-08-22 新疆阿图什 8¼ 左旋—逆 20.0 5.0 7 1920-12-16 宁夏海原 8.5 逆—左旋 10.0～11.0 7.0～8.0 8 1927-05-23 甘肃古浪 8.0 逆—左旋 6.0 7.1 9 1933-08-25 四川叠溪 7.5 逆—左旋 5.0 3.0～4.0 10 1937-01-07 青海托索湖 7.5 逆—左旋 8.0 5.0～6.0 11 1947-03-17 青海达日 7.7 逆—左旋 5.0～10.0 5.0～6.0 12 1951-11-18 西藏当雄 8.0 正—右旋 7.3 1.5 13 1952-08-18 西藏那曲西南 7.5 左旋—正 5.0 5.5 14 1954-02-11 甘肃山丹 7¼ 右旋—正 2.9～4.0 1.0～1.2 15 1970-01-05 云南通海 7.8 逆—右旋 3.3 0.5 16 1985-08-23 新疆乌恰 7.4 右旋—逆 1.6 1.6 17 1996-02-03 云南丽江 7.0 左旋—正 0.3 0.3 18 2008-03-21 新疆于田 7.3 左旋—正 1.8 2.0 19 2008-05-12 四川汶川 8.0 右旋—逆 4.0～5.0 4.0～5.0 20 2021-5-22 青海玛多 7.4 逆—左旋 2.9～4.0 1.0～2.0 注：数据源自张维岐等，1988；邓起东等，1989；国家地震局地质研究所等，1990；黄静宜，2016；潘家伟等，2021；王未来等，2021。
下载: 导出CSV
-
[1] 程理, 苏刚, 李光涛等, 2019. 云南中甸-大具断裂上新发现的地震地表破裂带. 震灾防御技术, 14（4）: 797—809 doi: 10.11899/zzfy20190411Cheng L. , Su G. , Li G. T. , et al. , 2019. New finding of earthquake surface rupture on Zhongdian-Daju fault. Technology for Earthquake Disaster Prevention, 14(4): 797—809. (in Chinese) doi: 10.11899/zzfy20190411 [2] 邓起东, 张维岐, 张培震等, 1989. 海原走滑断裂带及其尾端挤压构造. 地震地质, 11（1）: 1—14.Deng Q. D. , Zhang W. Q. , Zhang P. Z. , et al. , 1989. Haiyuan strike-slip fault zone and its compressional structures of the end. Seismology and Geology, 11(1): 1—14. (in Chinese) [3] 邓起东, 于贵华, 叶文华, 1992. 地震地表破裂参数与震级关系的研究. 北京: 地震出版社.Deng Q. D. , Yu G. H. , Ye W. H. , 1992. Relationship between earthquake magnitude and parameters of surface ruptures associated with historical earthquakes. Beijing: Seismological Press. (in Chinese) [4] 国家地震局地质研究所, 宁夏回族自治区地震局, 1990. 海原活动断裂带. 北京: 地震出版社. [5] 李伟, 张红月, 孙衍建等, 2021. 地区级实景三维模型色彩均衡方法实验. 山东国土资源, 37（7）: 86—90Li W. , Zhang H. Y. , Sun Y. J. , et al. , 2021. Experiment on color equalization method of regional real scene 3D model. ShangDong Land and Resources, 37(7): 86—90. (in Chinese) [6] 黄静宜, 2016. 强震地表破裂评估方法研究. 哈尔滨: 中国地震局工程力学研究所.Huang J. Y., 2016. Research on the method for evaluating the earthquake surface rupture. Harbin: Institute of Engineering Mechanics, China Earthquake Administration. (in Chinese) [7] 李冀, 熊晶, 熊保颂等, 2021. 便携式消费级无人机相机标定有效性评估. 测绘通报, （4）: 131—135Li J. , Xiong J. , Xiong B. S. , et al. , 2021. Effectiveness evaluation of camera calibration for portable consumer UAV. Bulletin of Surveying and Mapping, (4): 131—135. (in Chinese) [8] 刘超, 雷启云, 余思汗等, 2021a. 基于无人机摄影测量技术的地震地表破裂带定量参数提取——以1709年中卫南M7½地震为例. 地震学报, 43（1）: 113—123Liu C. , Lei Q. Y. , Yu S. H. , et al. , 2021a. Using UAV photogrammetry technology to extract the quantitative parameters of earthquake surface rupture zone: a case study of the southern Zhongwei M7½ earthquake in 1709. Acta Seismologica Sinica, 43(1): 113—123. (in Chinese) [9] 刘超, 杜鹏, 王银等, 2021b. 基于无人机摄影测量技术研究有无地面控制点的差异性在地震方面的应用. 华南地震, 41（1）: 84—93Liu C. , Du P. , Wang Y. , et al. , 2021b. Research on the application of the difference with or without ground control points in earthquake based on UAV photogrammetry technology. South China Journal of Seismology, 41(1): 84—93. (in Chinese) [10] 潘家伟, 白明坤, 李超等, 2021.2021年5月22日青海玛多MS7.4地震地表破裂带及发震构造. 地质学报, 95（6）: 1655—1670 doi: 10.3969/j.issn.0001-5717.2021.06.001Pan J. W. , Bai M. K. , Li C. , et al. , 2021. Coseismic surface rupture and seismogenic structure of the 2021-05-22 Maduo (Qinghai) MS7.4 earthquake. Acta Geologica Sinica, 95(6): 1655—1670. (in Chinese) doi: 10.3969/j.issn.0001-5717.2021.06.001 [11] 王未来, 房立华, 吴建平等, 2021. 2021年青海玛多MS7.4地震序列精定位研究. 中国科学: 地球科学, 51（7）: 1193—1202.Wang W. L., Fang L. H., Wu J. P., et al., 2021. Aftershock sequence relocation of the 2021 MS7.4 Maduo earthquake, Qinghai, China. Science China Earth Sciences, 64（8）: 1371—1380. (in Chinese) [12] 魏占玉, Ramon A, 何宏林等, 2015. 基于SfM方法的高密度点云数据生成及精度分析. 地震地质, 37（2）: 636—648 doi: 10.3969/j.issn.0253-4967.2015.02.024Wei Z. Y. , Ramon A. , He H. L. , et al. , 2015. Accuracy analysis of terrain point cloud acquired by “Structure from Motion” using aerial photos. Seismology and Geology, 37(2): 636—648. (in Chinese) doi: 10.3969/j.issn.0253-4967.2015.02.024 [13] 熊保颂, 2020. 基于便携式无人机SfM方法的活动构造地貌位错测量应用研究. 武汉: 中国地震局地震研究所.Xiong B. S., 2020. Offset measurement along active fault based on portable UAV and structure from motion. Wuhan: Institute of Seismology, China Earthquake Administration. (in Chinese) [14] 熊保颂, 李雪, 2020. 基于便携式无人机SfM方法的活动构造地貌位错测量——以阿尔金断裂中段为例. 科学技术与工程, 20（26）: 10848—10855. doi: 10.3969/j.issn.1671-1815.2020.26.044Xiong B. S. , Li X. , 2020. Offset measurement along active fault based on portable unmanned aerial vehicle and structure from motion: a case study of the middle section in Altyn-Tagh fault. Science Technology and Engineering, 20(26): 10848—10855. (in Chinese) doi: 10.3969/j.issn.1671-1815.2020.26.044 [15] 张维岐, 焦德成, 柴炽章等, 1988. 宁夏香山-天景山弧形断裂带新活动特征及1709年中卫南7½级地震形变带. 地震地质, 10（3）: 12—20Zhang W. Q. , Jiao D. C. , Chai C. Z. , et al. , 1988. Neotectonic features of the Xiangshan-Tianjingshan arc fracture zone and the seismic deformation zone of 1709 south of Zhongwei M=7½ earthquake. Seismology and Geology, 10(3): 12—20. (in Chinese) [16] 赵云景, 龚绪才, 杜文俊等, 2015. PhotoScan Pro软件在无人机应急航摄中的应用. 国土资源遥感, 27（4）;179—182.Zhao Y. J., Gong X. C., Du W. J., et al., 2015. UAV imagery data processing for emergency response based on PhotoScan Pro. Remote Sensing for Land & Resources, 27（4）: 179—182. (in Chinese) [17] 中国地震局, 2019. DB/T 71—2018 活动断层探察 断错地貌测量. 北京: 中国标准出版社.China Earthquake Administration, 2019. DB/T 71—2018 Active fault survey—Measurement of faulted landform. Beijing: Standards Press of China. (in Chinese) [18] James M. R. , Robson S. , 2012. Straightforward reconstruction of 3D surfaces and topography with a camera: Accuracy and geoscience application. Journal of Geophysical Research: Earth Surface, 117(F3): F03017. [19] Lucieer A. , De Jong S. M. , Turner D. , 2014. Mapping landslide displacements using Structure from Motion (SfM) and image correlation of multi-temporal UAV photography. Progress in Physical Geography: Earth and Environment, 38(1): 97—116. [20] Ryan J. C. , Hubbard A. L. , Box J. E. , et al. , 2015. UAV photogrammetry and structure from motion to assess calving dynamics at Store Glacier, a large outlet draining the Greenland ice sheet. The Cryosphere, 9(1): 1—11. [21] Snavely N. , Seitz S. M. , Szeliski R. , 2008. Modeling the world from internet photo collections. International Journal of Computer Vision, 80(2): 189—210. 期刊类型引用(2)
1. 刘岚，张可颖，张宸瑞，陈远，章迪. 面向防灾减灾场景的无人机高精度定位系统. 测绘科学. 2024(02): 108-114 . 
百度学术2. 陆玉霞，胡方涛. 无人机RTK联合EGM2008高程异常改正的精度分析与应用. 水利科技与经济. 2024(07): 142-147 . 百度学术其他类型引用(1)
-
下载:
点击查看大图
计量
- 文章访问数: 237
- HTML全文浏览量: 74
- PDF下载量: 19
- 被引次数: 3
