Analysis of Vertical Accuracy Based on Network/Base Station RTK-SfM Data
-
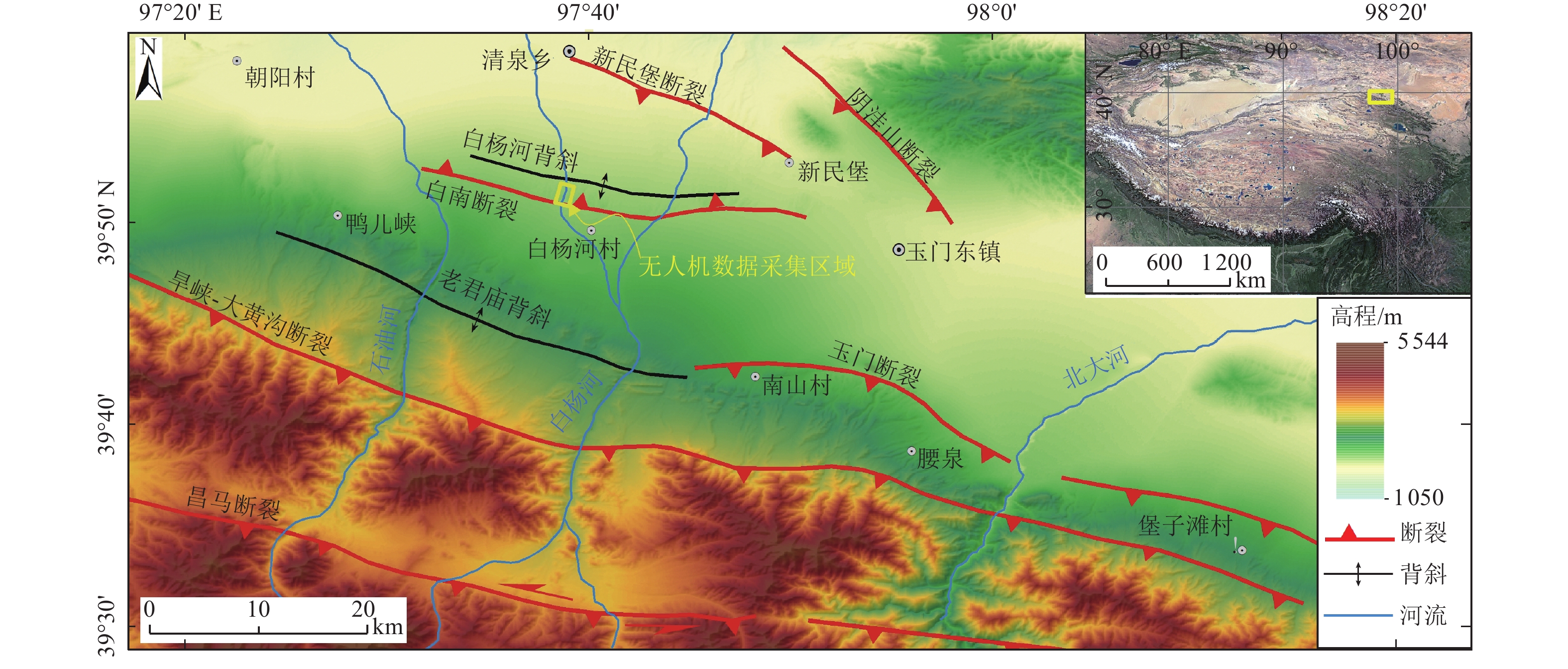
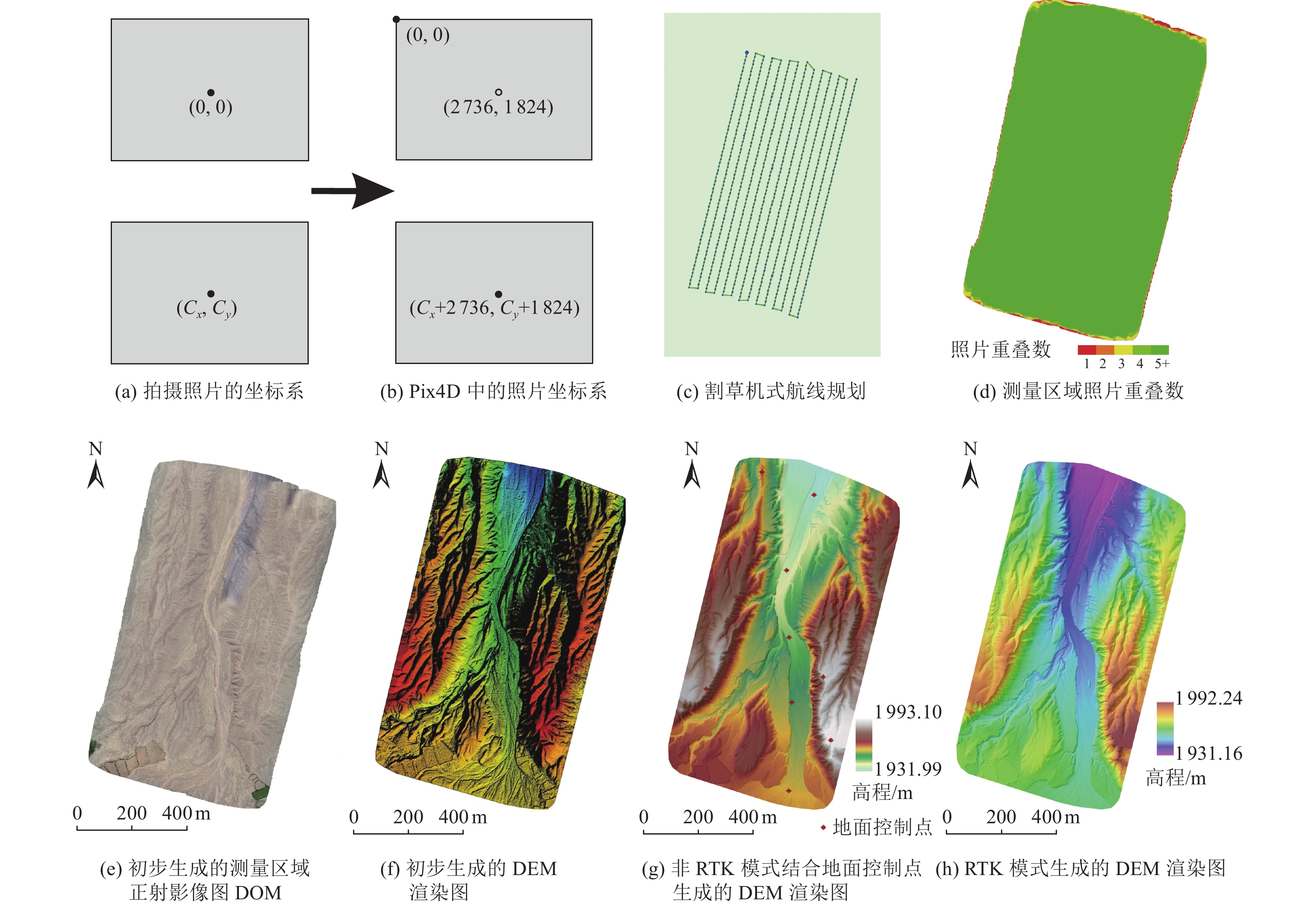
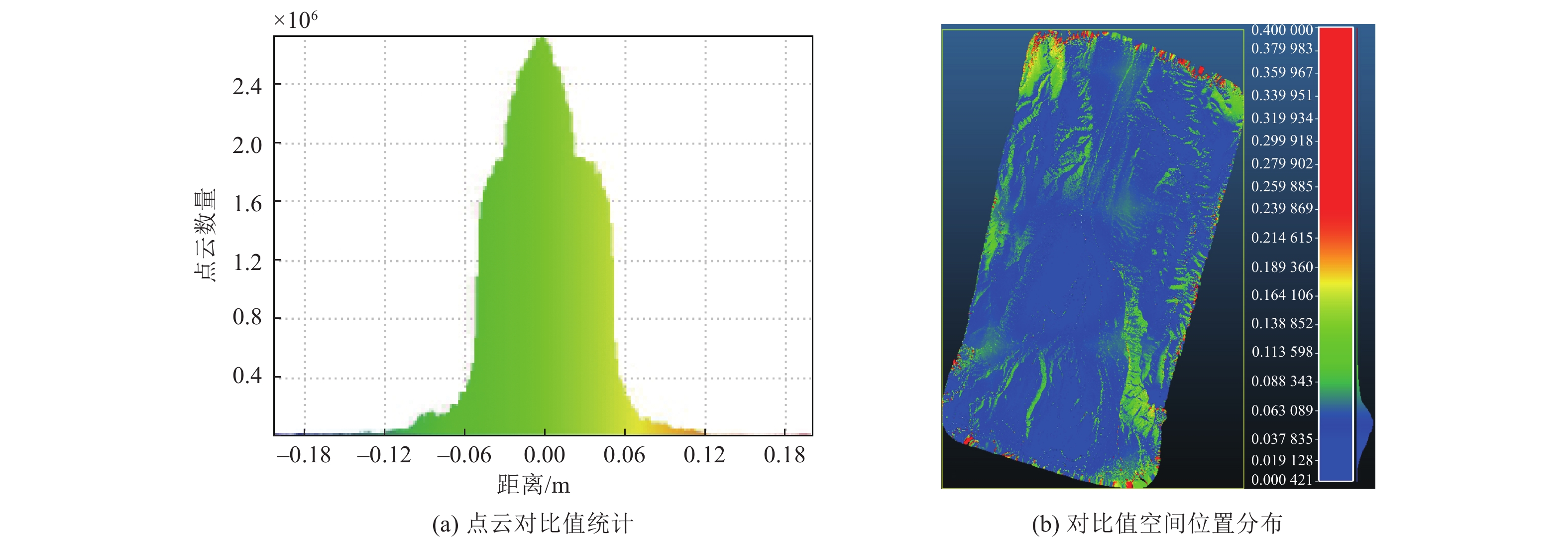
摘要: 移动摄影测量技术SfM（Structure from Motion）的发展使活动构造研究中快速获得野外中小区域内高精度DEM数据更便捷，DEM数据精度是目前活动构造与测量领域较关注的问题。本文通过对比非RTK模式无人机摄影测量并结合地面控制点（GCPs）生成的SfM DEM数据与基于RTK移动摄影测量技术获取的RTK-SfM DEM数据差异，重点分析搭载RTK模块的移动摄影测量技术获取的DEM数据在垂向上的精度。数据采集、处理与对比结果表明：在添加地面控制点后的非RTK模式无人机摄影测量生成的DEM数据中，除测量区域边缘照片较少而产生畸变外，大部分地区畸变率较小；基于移动RTK技术摄影测量获取的高程数据畸变率更小，且与非RTK模式无人机摄影结合地面控制点生成的高程数据存在约0.85 m的系统高程误差，减去该误差后，点云对比结果表明二者95%以上的点垂向误差均＜0.05 m；搭载RTK模块的移动摄影测量技术获取的DEM数据在垂向上具有更高的精度，且节省了时间与人工成本。
-
关键词:
- 活动构造 /
- 移动摄影测量技术 /
- RTK-SfM DEM /
- 垂向误差 /
- 测量精度
Abstract: The development of Structure from Motion (SfM) technology makes it more convenient to obtain high precision DEM data in small and medium-sized areas quickly in the field of active tectonics research. The accuracy of DEM data is a major concern in the field of active tectonics and surveying. By comparing the SfM DEM data generated by non-RTK model UVA technology combined with ground control point (GCPs) and RTK-SfM DEM data obtained based on RTK SfM technology, this paper focuses on analyzing the vertical accuracy of DEM data obtained by SfM technology equipped with RTK module. The results of data acquisition, processing and comparison show that in the DEM data generated by non-RTK model SfM technology with the GCPs, the distortion rate is small in most areas except the distortion caused by fewer photos at the edge of the measurement area. The DEM data obtained by RTK-SfM has a smaller distortion rate, and the data generated by non-RTK SfM combined with GCPs has a system elevation error of about 0.85 m. After subtracting the system error, the point cloud comparison results show that more than 95% of the vertical errors of both are less than 0.05 m. The DEM data obtained by SfM technology equipped with RTK module has better vertical accuracy and saves time and labor cost.-
Key words:
- Active tectonics /
- SfM technology /
- RTK-SfM DEM /
- Vertical error /
- Accuracy of surveying
1) 2 CloudCompare user manual（Version 2.6.1），2015. -
引言
城市地球物理探测与传统的地球物理勘查差别很大，城市地质环境是被人类活动改造过的自然环境，实际情况会更加复杂。地下除地层、构造等天然地质体以外，还有地下管网系统、地下轨道交通、地下储存库等地下综合体。此外，城市地球物理场是动态演化的，在城市化前后甚至还会发生更加显著的变化（陈颙等，2003）。因此，城市地球物理探测具有探测深度浅、探测精度要求高、干扰因素多、场地受限等特点（李万伦等，2018）。目前国内外对目标层埋深仅有几十米（甚至十几米）的超浅层地震勘探经验不多，理论研究也不够深入。从地表至地下几十米的深度范围是各种人工地震勘探的盲区，但它对断层定位和活动性研究意义重大，近年来由于工程建设和防灾减灾的需要，已经开展了不少浅层地震勘探实践和技术研究（朱金芳等，2005）。在城市活断层探测中，用于第四纪覆盖区的活断层探测方法可分为地质学方法和地球物理方法，浅层或超浅层地震方法是地球物理方法调查城市活动断层研究中的重要手段之一（邓起东，2002；邓起东等，2003）。由于浅层地质条件以及新构造运动的特点，浅层或超浅层地震方法与常规地震勘探中采用的方法不完全相同。合理的数据采集方案是获得高分辨率地震剖面的重要基础；对浅层地震波传播速度的研究为数据处理中速度参考值的确定提供了理论依据。近年来，国内外浅层反射地震方法在城市活断层调查中的研究及其实例也相继发表，前人的研究成果反映了浅层地震方法的研究水平正在不断提高（Williams等，1995；潘纪顺等，2002；方盛明等，2002；刘保金等，2002；徐明才等，2005；段生全等，2005；杨晓平等，2007）。在利用浅层地震勘探方法确定隐伏活断层位置及其上断点埋深等工作中，一些地球物理工作者从地震波的激发、数据采集方法、室内资料处理与解释方法等方面进行了有益的探索，并取得了许多宝贵的经验，使得城市活断层浅层地震探测剖面质量和断层定位精度不断提高（何正勤等，2010；李大虎等，2010；杨歧焱等, 2015, 2016；许汉刚等，2016）。
青岛市地处胶东半岛西南部、黄海之滨，新构造运动以隆升为主，缺失第三系和第四系下部。第四纪晚期，受构造作用和海平面上升影响，接受十几米至二十余米厚以砂粘土为主的晚更新世—全新世河、海堆积物，直接覆盖于风化基岩（多为花岗岩）之上。东南部主要为花岗岩组成的低山丘陵，基岩在长期风化作用下形成了一定厚度的风化壳，并在山麓等和缓地带堆积有风化-坡积物，沿海港湾有第四纪晚期河海沉积；西北部主要是第四纪晚期的河海堆积平原或海湾，沉积有10—30m厚的第四系。因此，青岛市地震勘探属于超浅层地震勘探范畴。区域内发育若干北北东向断裂，活动性不甚强烈，地质地貌表现不很清楚，许多段落隐伏于第四系之下，断层的准确位置和活动性都不十分可靠（图 1）。与其他地区的有利探测环境相比，青岛市第四系很薄，横向物性变化大，垂向分层性差。对于不同的地震地质条件和探测目的，必须采用合理的野外采集方法和采集参数，因此，在一个新工区进行正式数据采集之前，应认真进行数据采集参数试验（何正勤等，2007）。本文通过在青岛王哥庄断裂上进行不同观测系统和采集参数的对比试验，获得了几米至二十几米深度范围内高分辨率的地震剖面，为隐伏活动断层位置及断层上断点的确定、钻孔剖面的布设和断层活动性的判定提供了可靠的科学依据。
图 1 青岛地区地质构造图Figure 1. Simplified geological map of the Qingdao areaF1：沧口断裂；F2：青岛山断裂；F3：劈石口断裂；F4：王哥庄断裂；F5：马山-王哥庄断裂1. 青岛地区地质构造概况
青岛及邻近地区在大地构造上属华北地台胶辽断隆，基底为元古代的变质岩系，经吕梁运动固结形成；古生代开始为地台发育时期，长期处于构造隆起状态，缺失古生代至三叠纪地层，致使结晶基底大面积出露。总体而言，青岛及邻近地区山势不高，以低山、丘陵和平原为主，海拔较高的山峰多为孤立分布，大致以沧口断裂为界划分为西北、东南2个不同的地貌分区。西北部地势较低，多为海湾、第四系冲洪积平原。由于新构造时期鲁东地区以隆升运动为主，青岛及邻近地区第四纪地层发育不良。许多地区基岩出露，部分地区沉积有晚更新世及全新世堆积物，局部地区发育有中更新世晚期的沉积物。市区东南部主要为花岗岩组成的低山丘陵，在山麓等和缓地带堆积有较厚的风化、坡积物，沿海港湾有第四纪晚期河海堆积；西北部是中生代地层组成的准平原和第四纪河海堆积平原（或海湾），沉积较厚的第四系，最大厚度近30米。
2. 超浅层地震勘探
2.1 青岛地区超浅层地震勘探的特点
（1）目的层比较浅，有效反射波大多在70ms以内，在反射波出现的时窗内，各种干扰波、特别是声波和面波很强，在接收反射波的后几道，出现折射波和反射波混合的情况，严重影响了有效反射波。
（2）在近震源处，震源干扰波条带内干扰严重，很难获取有效波，不同波阻抗界面形成的反射信号幅度远远小于干扰波振幅。
（3）青岛及附近地区沉积结构和地层厚度横向变化大，反射波速度和频率受此影响较大。
（4）青岛及附近地区覆盖层较薄，第四系底界面通常只有一个较强的风化界面，由于风化地层的风化程度是渐变的，风化基岩之间波阻抗差较小，第四系内部垂向分层差。基岩顶部常有数米厚的风化壳，有些基岩面甚至更浅，风化基岩与上覆地层之间的波阻抗差也不是很明显。
2.2 观测系统的设计和采集参数的选取
针对上述地震勘探特点，本文选取王哥庄断层（图 1中F4断裂）为实验对象，为了获得王哥庄断层从近地表至第四系底界面（深约30m）深度范围内的地震剖面，对同一深度范围按照探测精度由低到高的工作思路，在同一地震测线上采用不同的方法技术和探测参数，不同探测参数的地震剖面分别命名为TEST-a和TEST-b。地震数据采集使用德国DMT公司生产的SUMMIT数字地震仪，地震波激发采用了人工夯击和人工锤击，针对同一探测深度、不同精度的探测要求，采用的观测系统参数、地震波激发和数据采集参数见表 1。
表 1 观测系统参数和地震采集参数表Table 1. Survey parameters and seismic data acquisition details剖面编号 道间距/m 偏移距/m 接收道数 覆盖次数 激发震源 检波器固有频率/Hz 采样间隔/ms 记录长度/ms TEST-a 3 6 24 6 人工夯击 60 0.25 256 TEST-b 1 7 24 12 人工锤击 100 0.25 256 在不同道间距的超浅层地震记录上（图 2），图 2（a）、图 2（b）分别是TEST-a、TEST-b对应的超浅层地震共炮点记录。对比图 2（a）和图 2（b）可以看出，采用较大道间距、较小偏移距以及能量较大的震源可以获得一组很清楚的反射波组，但是近震源受干扰波影响严重，在超浅层不能获取有效反射波；采用较小道间距、较大偏移距以及能量较小震源，可以获取超浅层有效反射波，也可以减轻震源干扰波的影响，但是能量较弱，反射波信号相对变弱。
图 2 不同道间距的超浅层地震共炮点记录Figure 2. The common-shot gather of ultra-shallow seismic records in different trace intervals采用较小道间距和较弱震源，可以获取超浅层有效反射波，且垂向分层较好。由于采用小排列接收，道间距越小反射波能量衰减也越慢，因此受震源干扰波影响也变的越小，但是面波比较发育。由此可见，较小道间距和较小偏移距有利于保护反射波，延缓反射波的衰减，但是也带来了面波发育的问题；在保证探测深度要求的前提下，较弱的震源有利于避开震源干扰波的影响。
2.3 超浅层地震数据处理中的方法
采用Promax地震反射处理系统处理地震数据。在数据处理过程中，由于获得的原始记录的反射波近震源干扰严重，远震源反射波能量较强、干扰能量较弱等特点，因此选取记录信噪比高的远震反射波，可最大限度地提高地震资料的分辨率。其数据处理流程和方法主要包括：道编辑、静校正、真振幅恢复、地表一致性振幅处理、地表一致性反褶积、二维随机噪音衰减、f-k滤波、正常时差校正（NMO）、共中心点（CMP）叠加、叠后频率带通滤波和叠后剖面去噪等。
本文利用不同的滤波和处理方法来提高地震数据信噪比，图 3为同一记录数据在不同情况下进行f-k滤波获得的对比分析结果和频谱分析结果。其中，图 3（a）为原始数据和相对应的谱分析结果，可以看出在超浅层地震勘探中，地震反射波受浅层折射、面波和声波的影响，反射波信号相对较弱（图中红色圆圈），信噪比不高，通过频谱分析则显示地震数据主频有2个频段：50Hz和100Hz；图 3（b）为对原始数据应用f-k滤波后的结果及其频谱分析，由图可见应用f-k滤波后，数据中面波和声波得到有效减弱，反射波信号得到加强，信噪比也得到提高，频谱分析显示数据主频为100Hz，同时结果还显示面波频率范围与有效地震反射波接近，滤波困难，数据信噪比低；图 3（c）通过切除数据前几道信号，避免了近道面波对反射波的干扰，再进行f-k滤波，反射波信号明显增强，信噪比也得到进一步提高。对比结果表明，在浅层或超浅层地震勘探中，在取得信噪比较高的情况下，再对地震数据进行f-k滤波可以有效去除干扰波，提高地震反射波的信噪比。
图 3 原始数据及不同信噪比下的f-k滤波对比及其频谱分析图（一）Figure 3. Analysis between f-k filtering under different signal-to-noise ratio data and corresponding spectrum2.4 超浅层地震剖面特征
图 4、图 5分别是TEST-a、TEST-b测线经过数据处理后的地震反射时间及地质解释剖面（图中方向左西右东）。在图 4地震反射时间剖面中，丰富的地层界面反射波组出现在剖面100ms以上的时间范围内，存在1组起伏变化的反射波组，由2—3个强相位组成；在图 5地震反射时间剖面中，丰富的地层界面反射波组出现在剖面60ms以上的时间范围内，存在2组起伏变化的反射波组，分别由2—3个强相位组成。根据剖面上反射波同相轴的横向变化特征和上下反射波组关系，在该测线剖面上解释了1个断点，在图 4和图 5中标识为F。断层F位于TEST-a测线CDP423#和TEST-b测线CDP87#处，反射波同相轴出现了错动，断层为倾向西、高倾角逆断层，根据测区地质资料，判断该断层为王哥庄断裂。
图 4 TEST-a地震反射时间及地质解释剖面Figure 4. Stack time section of seismic reflection and the interpretation in TEST-a
图 5 TEST-b地震反射时间及地质解释剖面Figure 5. Stack time section of seismic reflection and the interpretation in TEST-b对比TEST-a、TEST-b测线的地震反射波叠加剖面发现，TEST-b测线在超浅层部分，特别是30ms以上部分有清晰的反射同相轴，说明小道距在超浅层地震勘探中，能揭示更多的断层结构细节。
3. 钻孔地质剖面及综合解
在王哥庄北TEST-a测线CDP423#和TEST-b测线CDP87#处的王哥庄断裂断点附近，布设了1组深19.1—23.5m、相邻孔距5—10m的钻孔（ZK1—ZK7），发现在ZK2与ZK6之间基岩顶面和第四系底部被断层错断4m左右，西升东降（图 6）。由图 6可见，除底部层位外，第四系各个层位均连续分布，未受断层构造变动，根据前期第四纪地层划分结果（包括测年结果），这套地层应为上更新统。因此，该处王哥庄断裂在晚更新世早期仍在活动。
图 6 TEST-a和TEST-b测线王哥庄断裂钻孔联合地质剖面Figure 6. The drilling geological section of WGZ fracture combined with the TEST-a and TEST-b survey lines4. 结论与讨论
（1）本文从城市活断层探测的角度出发，利用地质学、地球物理学等学科中的相关理论和方法，探讨超浅层地震在复杂地质构造背景下获得有效探测结果的前提条件。综合分析青岛地区地震勘探资料发现：①要依据扩展排列试验并参考观测系统参数选择原则，选好最小和最大偏移距，在超浅层探测中，近震源道记录中反射波与干扰波很难分辨，需要一定的偏移距才能将其分辨清楚；②最大偏移距不能过大，由于目标层埋深很浅，若排列长度过大，记录的多为折射波，所以需要采用短排列、小道间距进行数据采集。
（2）在对超浅层地震数据采集技术、资料处理与解释方法进行系统研究的基础上，以可清晰分辨出断层位置的典型剖面为例，证明在选择合适的观测系统和数据处理方法基础上，超浅层地震反射波法可以获取深度仅有十几米的地层反射信号，且大部分反射剖面都可较清楚地揭示出超浅部断层位置和断层特征。青岛王哥庄断裂地震勘探研究结果显示，超浅层地震反射方法在城市活断层探测中，特别是沿海覆盖层较浅的区域具有良好的应用前景。
（3）在对青岛王哥庄断裂超浅层地震反射时间剖面开展研究和解释的基础上，结合典型断点的钻孔联合剖面探测资料，研究了王哥庄断裂的准确位置、几何结构和活动性。研究表明，王哥庄断裂晚更新世以来可能也是活动的。
-
图 2 测量区域及其周围构造
Figure 2. Schematic diagram of the survey area and its surrounding tectonics
图 3 测量用无人机及地面控制点采集系统
Figure 3. UAV for surveying and ground control point acquisition system
图 5 SfM-DEM与RTK-SfM DEM点云对比统计及误差空间分布
Figure 5. Point cloud comparison statistics and error spatial distribution between SFM-DEM and RTK-SFM DEM
图 6 基于DEM分析结果与野外调查结果的阶地划分及DGPS测线分布
Figure 6. River terraces division and DGPS lines distribution based on DEM analysis and field investigation
图 7 DGPS、SfM DEM、RTK-SfM DEM高程数据对比
Figure 7. Comparison of three elevation data of DGPS, SfM DEM and RTK-SFM DEM
图 8 去除系统误差后DGPS数据与2种方式生成的DEM数据之间差值的正态分布
Figure 8. Normal distribution of the difference between DGPS data and DEM generated by the two methods after removing systematic error
表 1 初步对比点云转换矩阵数据
Table 1. Preliminary comparison point cloud transformation matrix table
x y z RMS 1.000 0.000 0.000 0.565 −0.000 1.000 0.000 0.509 −0.000 −0.000 1.000 0.851 0.000 0.000 0.000 1.000 
下载: 导出CSV
表 2 3种高程数据差值的平均值
Table 2. Average value of difference of three elevation data
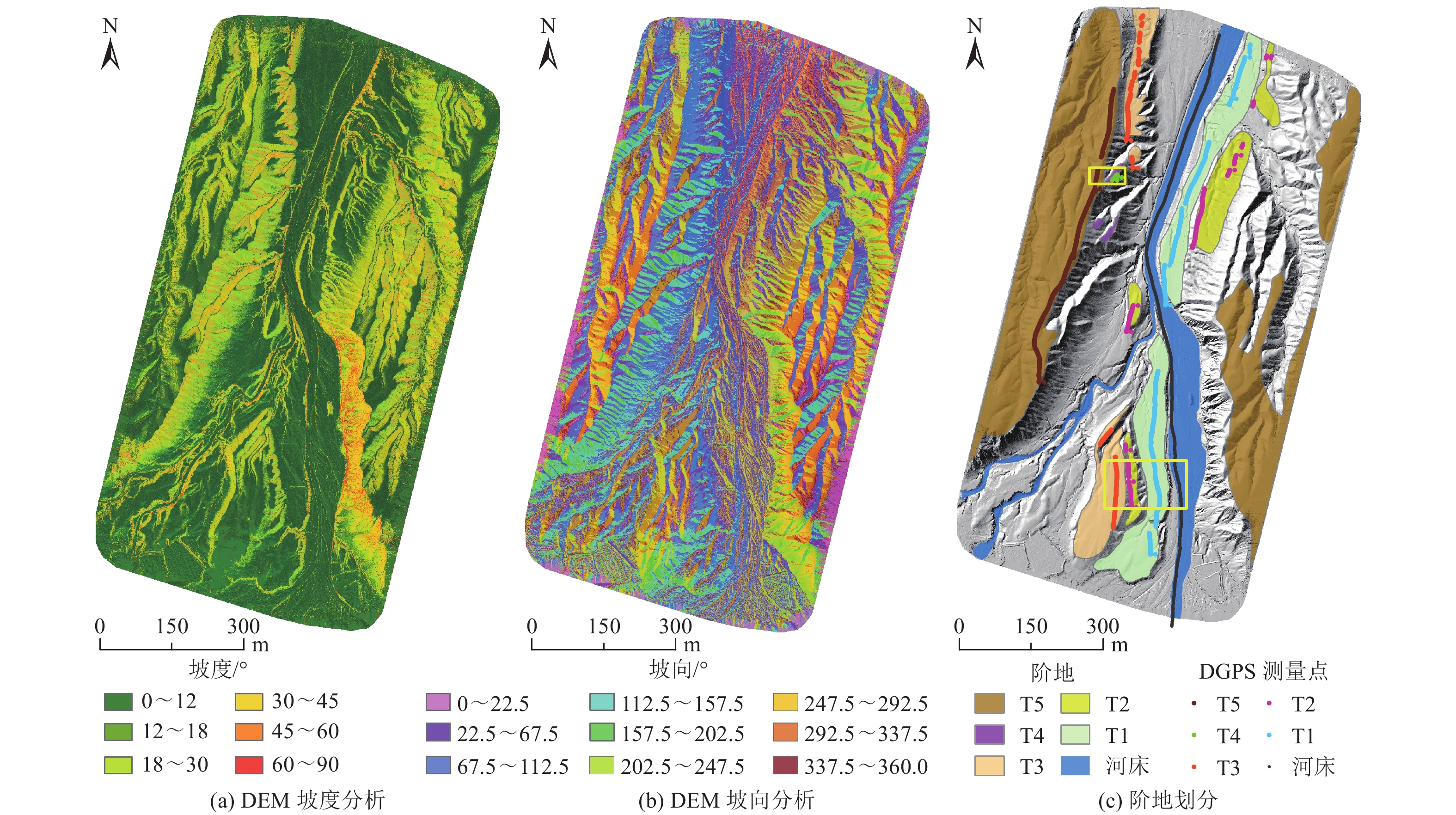
测线 DGPS与SfM DEM差值/m DGPS与RTK-SfM DEM差值/m 河床 0.44648900 1.25817214 T1 0.51727922 1.33264908 T2 0.56253832 1.39865517 T3 0.54695363 1.33524765 T4 0.61002861 1.38761910 T5 0.56203093 1.47095521 平均值 0.540886618 1.36388305
下载: 导出CSV
表 3 去除系统误差后3种高程数据差值平均值与标准差
Table 3. Average difference and standard deviation of three elevation data after removing systematic error
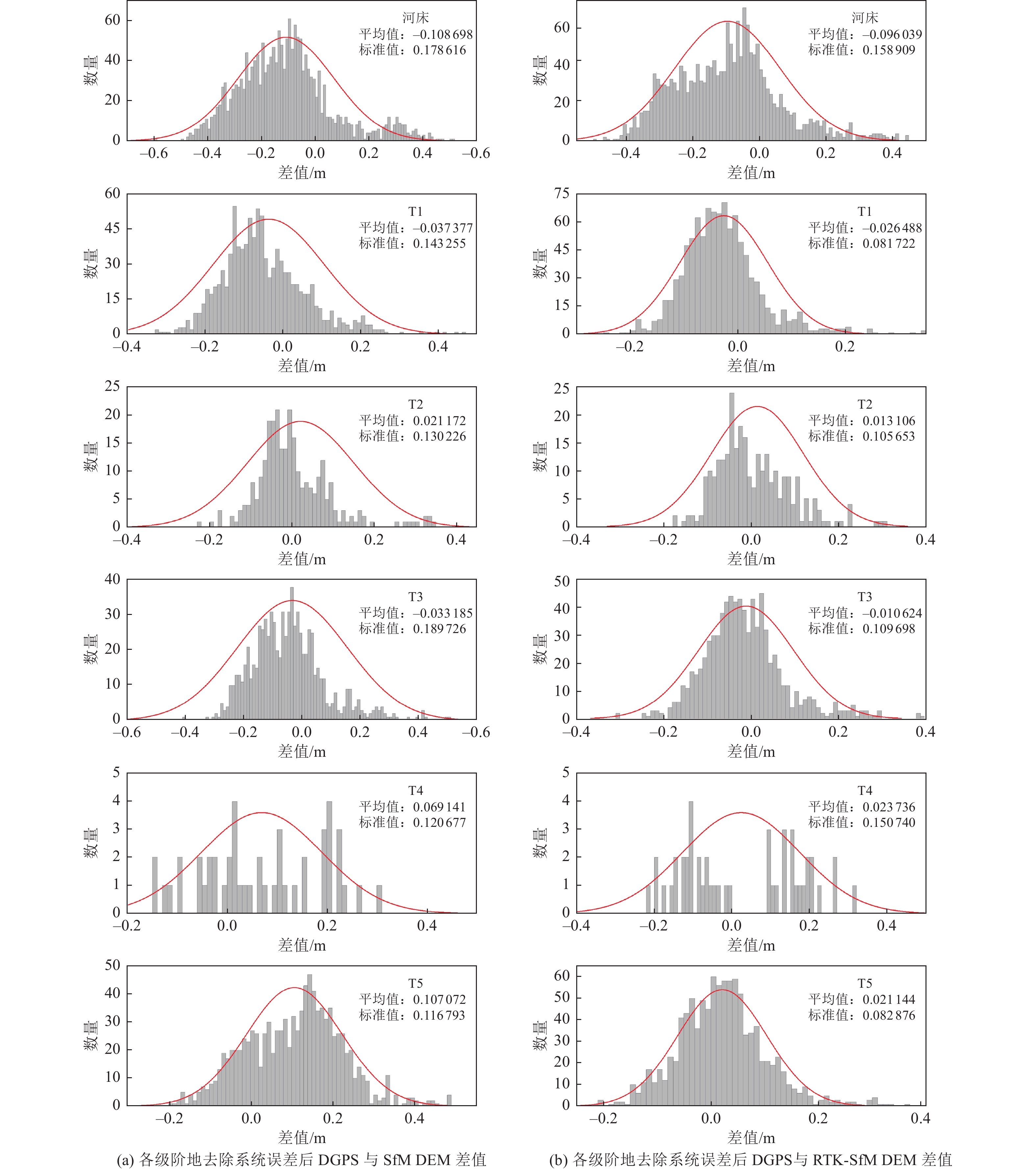
测线 DGPS与SfM DEM差值/m DGPS与RTK-SfM DEM差值/m 平均值 标准差 平均值 标准差 河床 −0.108 698 0.178 616 −0.096 039 0.158 909 T1 −0.037 377 0.143 255 −0.026 488 0.081 722 T2 0.021 172 0.130 226 0.013 106 0.105 653 T3 −0.033 185 0.189 726 −0.010 624 0.109 698 T4 0.069 141 0.120 677 0.023 736 0.150 740 T5 0.107 072 0.116 793 0.021 144 0.082 876
下载: 导出CSV
-
[1] 艾明, 毕海芸, 郑文俊等, 2018. 利用无人机摄影测量技术提取活动构造定量参数. 地震地质, 40（6）: 1276—1293Ai M. , Bi H. Y. , Zheng W. J. , et al. , 2018. Using unmanned aerial vehicle photogrammetry technology to obtain quantitative parameters of active tectonics. Seismology and Geology, 40(6): 1276—1293. (in Chinese) [2] 陈涛, 张培震, 刘静等, 2014. 机载激光雷达技术与海原断裂带的精细地貌定量化研究. 科学通报, 59（14）: 1293—1304.Chen T. , Zhang P. Z. , Liu J. , et al. , 2014. Quantitative study of tectonic geomorphology along Haiyuan fault based on airborne LiDAR. Chinese Science Bulletin, 59（20）: 2396—2409. (in Chinese) [3] 陈志雄, 2008. 基于图像配准的SIFT算法研究与实现. 武汉: 武汉理工大学.Chen Z. X. , 2008. The SIFT research and implementation based on the image registration. Wuhan: Wuhan University of Technology. (in Chinese) [4] 邓起东, 陈立春, 冉勇康, 2004. 活动构造定量研究与应用. 地学前缘, 11（4）: 383—392 doi: 10.3321/j.issn:1005-2321.2004.04.005Deng Q. D. , Chen L. C. , Ran Y. K. , 2004. Quantitative studies and applications of active tectonics. Earth Science Frontiers, 11(4): 383—392. (in Chinese) doi: 10.3321/j.issn:1005-2321.2004.04.005 [5] 高帅坡, 冉勇康, 吴富峣等, 2017. 利用无人机摄影测量技术提取复杂冲积扇面构造活动信息——以新疆巴里坤盆地南缘冲积扇面为例. 地震地质, 39（4）: 793—804 doi: 10.3969/j.issn.0253-4967.2017.04.013Gao S. P. , Ran Y. K. , Wu F. Y. , et al. , 2017. Using UAV photogrammetry technology to extract information of tectonic activity of complex alluvial fan——A case study of an alluvial fan in the southern margin of Barkol Basin. Seismology and Geology, 39(4): 793—804 (in Chinese). doi: 10.3969/j.issn.0253-4967.2017.04.013 [6] 赖旭东, 李咏旭, 陈佩奇等, 2017. 机载激光雷达技术现状及展望. 地理空间信息, 15（8）: 1—4 doi: 10.3969/j.issn.1672-4623.2017.08.001Lai X. D. , Li Y. X. , Chen P. Q. , et al. , 2017. Current status and outlook of LiDAR technology. Geospatial Information, 15(8): 1—4. (in Chinese) doi: 10.3969/j.issn.1672-4623.2017.08.001 [7] 李美燕, 2014. 基于改进SFM方法的航空摄影测量应用研究. 南宁: 广西大学.Li M. Y., 2014. Research on the application of improved SFM in aerial photogrammetry. Nanning: Guangxi University. (in Chinese) [8] 刘静, 陈涛, 张培震等, 2013. 机载激光雷达扫描揭示海原断裂带微地貌的精细结构. 科学通报, 58（1）: 41—45 doi: 10.1360/972012-1526Liu J. , Chen T. , Zhang P. Z. , et al. , 2013. Illuminating the active Haiyuan Fault, China by airborne light detection and ranging. Chinese Science Bulletin, 58(1): 41—45. (in Chinese) doi: 10.1360/972012-1526 [9] 刘睿, 李安, 张世民等, 2017. 白杨河阶地揭示的北祁连山西段晚第四纪构造变形. 地震地质, 39（6）: 1237—1255 doi: 10.3969/j.issn.0253-4967.2017.06.010Liu R. , Li A. , Zhang S. M. , et al. , 2017. The late quaternary tectonic deformation revealed by the terraces on the Baiyang river in the northern Qilian Mountains. Seismology and Geology, 39(6): 1237—1255. (in Chinese) doi: 10.3969/j.issn.0253-4967.2017.06.010 [10] 罗达, 林杭生, 金钊等, 2019. 无人机数字摄影测量与激光雷达在地形地貌与地表覆盖研究中的应用及比较. 地球环境学报, 10（3）: 213—226Luo D. , Lin H. S. , Jin Z. , et al. , 2019. Applications of UAV digital aerial photogrammetry and LiDAR in geomorphology and land cover research. Journal of Earth Environment, 10(3): 213—226. (in Chinese) [11] 闵伟, 张培震, 何文贵等, 2002. 酒西盆地断层活动特征及古地震研究. 地震地质, 24（1）: 35—44 doi: 10.3969/j.issn.0253-4967.2002.01.004Min W. , Zhang P. Z. , He W. G. , et al. , 2002. Research on the active faults and paleoearthquakes in the western Jiuquan basin. Seismology and Geology, 24(1): 35—44. (in Chinese) doi: 10.3969/j.issn.0253-4967.2002.01.004 [12] 佘金星, 程多祥, 刘飞等, 2018. 机载激光雷达技术在地质灾害调查中的应用——以四川九寨沟7.0级地震为例. 中国地震, 34（3）: 435—444 doi: 10.3969/j.issn.1001-4683.2018.03.005She J. X. , Cheng D. X. , Liu F. , et al. , 2018. Application of airborne LiDAR technology in geological disaster investigation—taking the Jiuzhaigou MS7.0 earthquake in Sichuan province as an example. Earthquake Research in China, 34(3): 435—444. (in Chinese) doi: 10.3969/j.issn.1001-4683.2018.03.005 [13] 王朋涛, 邵延秀, 张会平等, 2016. sUAV摄影技术在活动构造研究中的应用——以海原断裂骟马沟为例. 第四纪研究, 36（2）: 433—442 doi: 10.11928/j.issn.1001-7410.2016.02.18Wang P. T. , Shao Y. X. , Zhang H. P. , et al. , 2016. The application of sUAV photogrammetry in active tectonics: Shanmagou site of Haiyuan Fault, for example. Quaternary Sciences, 36(2): 433—442. (in Chinese) doi: 10.11928/j.issn.1001-7410.2016.02.18 [14] 魏占玉, Ramon A. , 何宏林等, 2015. 基于SfM方法的高密度点云数据生成及精度分析. 地震地质, 37（2）: 636—648 doi: 10.3969/j.issn.0253-4967.2015.02.024Wei Z. Y. , Ramon A. , He H. L. , et al. , 2015. Accuracy analysis of terrain point cloud acquired by “Structure from Motion” using aerial photos. Seismology and Geology, 37(2): 636—648. (in Chinese) doi: 10.3969/j.issn.0253-4967.2015.02.024 [15] 杨海波, 杨晓平, 黄雄南等, 2016. 移动摄影测量数据与差分GPS数据的对比分析——以祁连山北麓洪水坝河东岸断层陡坎为例. 地震地质, 38（4）: 1030—1046 doi: 10.3969/j.issn.0253-4967.2016.04.018Yang H. B. , Yang X. P. , Huang X. N. , et al. , 2016. Data comparative analysis between SFM data and DGPS data: a case study from fault scarp in the east bank of Hongshuiba river, northern margin of the Qilian Shan. Seismology and Geology, 38(4): 1030—1046. (in Chinese) doi: 10.3969/j.issn.0253-4967.2016.04.018 [16] 杨艳伟, 2009. 基于SIFT特征点的图像拼接技术研究. 西安: 西安电子科技大学.Yang Y. W., 2009. Research on image mosaic based on SIFT feature points. Xi’an: Xidian University. (in Chinese) [17] 张志文, 任俊杰, 章小龙, 2021. 高精度无人机航测在2021年玛多7.4级地震地表破裂精细研究中的应用. 震灾防御技术, 16（3）: 437—447Zhang Z. W. , Ren J. J. , Zhang X. L. , 2021. Application of high-precision UAV aerial survey in the detailed study of surface rupture of Maduo MS7.4 earthquake in 2021. Technology for Earthquake Disaster Prevention, 16(3): 437—447. (in Chinese) [18] 郑辉, 2010. 基于SIFT特征的全景图像拼接算法研究. 武汉: 武汉科技大学.Zheng H., 2010. Research of panorama image mosaic algorithm based on SIFT feature. Wuhan: Wuhan University of Science and Technology. (in Chinese) [19] Arrowsmith J. R. , Zielke O. , 2009. Tectonic geomorphology of the San Andreas Fault zone from high resolution topography: an example from the Cholame segment. Geomorphology, 113(1—2): 70—81. doi: 10.1016/j.geomorph.2009.01.002 [20] Bemis S. P. , Micklethwaite S. , Turner D. , et al. , 2014. Ground-based and UAV-Based photogrammetry: a multi-scale, high-resolution mapping tool for structural geology and paleoseismology. Journal of Structural Geology, 69: 163—178. doi: 10.1016/j.jsg.2014.10.007 [21] Bi H. Y. , Zheng W. J. , Ren Z. K. , et al. , 2017. Using an unmanned aerial vehicle for topography mapping of the fault zone based on structure from motion photogrammetry. International Journal of Remote Sensing, 38(8—10): 2495—2510. doi: 10.1080/01431161.2016.1249308 [22] Fonstad M. A. , Dietrich J. T. , Courville B. C. , et al. , 2013. Topographic structure from motion: a new development in photogrammetric measurement. Earth Surface Processes and Landforms, 38(4): 421—430. doi: 10.1002/esp.3366 [23] Harwin S. , Lucieer A. , 2012. Assessing the accuracy of georeferenced point clouds produced via multi-view stereopsis from unmanned aerial vehicle (UAV) imagery. Remote Sensing, 4(6): 1573—1599. doi: 10.3390/rs4061573 [24] Hudnut K. W. , Borsa A. , Glennie C. , et al. , 2002. High-resolution topography along surface rupture of the 16 October 1999 hector mine, California, earthquake (MW 7.1) from airborne laser swath mapping. Bulletin of the Seismological Society of America, 92(4): 1570—1576. doi: 10.1785/0120000934 [25] James M. R. , Robson S. , 2012. Straightforward reconstruction of 3D surfaces and topography with a camera: accuracy and geoscience application. Journal of Geophysical Research, 117(F3): F03017. [26] Javernick L. , Brasington J. , Caruso B. , 2014. Modeling the topography of shallow braided rivers using Structure-from-Motion photogrammetry. Geomorphology, 213: 166—182. doi: 10.1016/j.geomorph.2014.01.006 [27] Johnson K. , Nissen E. , Saripalli S. , et al. , 2014. Rapid mapping of ultrafine fault zone topography with structure from motion. Geosphere, 10(5): 969—986. doi: 10.1130/GES01017.1 [28] Lowe D. G. , 2004. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision, 60(2): 91—110. doi: 10.1023/B:VISI.0000029664.99615.94 [29] Lucieer A. , de Jong S. M. , Turner D. , 2014. Mapping landslide displacements using Structure from Motion (SfM) and image correlation of multi-temporal UAV photography. Progress in Physical Geography: Earth and Environment, 38(1): 97—116. doi: 10.1177/0309133313515293 [30] Mancini F. , Dubbini M. , Gattelli M. , et al. , 2013. Using unmanned aerial vehicles (UAV) for high-resolution reconstruction of topography: the structure from motion approach on coastal environments. Remote Sensing, 5(12): 6880—6898. doi: 10.3390/rs5126880 [31] Okyay U. , Telling J. , Glennie C. L. , et al. , 2019. Airborne lidar change detection: an overview of Earth sciences applications. Earth-Science Reviews, 198: 102929. doi: 10.1016/j.earscirev.2019.102929 [32] Tomasi C. , Kanade T. , 1992. Shape and motion from image streams under orthography: a factorization method. International Journal of Computer Vision, 9(2): 137—154. doi: 10.1007/BF00129684 [33] Ullman S. , 1979. The interpretation of structure from motion. Proceedings of the Royal Society B: Biological Sciences, 203(1153): 405—426. [34] Wei Y. M. , Kang L. , Yang B. , et al. , 2013. Applications of structure from motion: a survey. Journal of Zhejiang University SCIENCE C, 14(7): 486—494. doi: 10.1631/jzus.CIDE1302 [35] Westoby M. J. , Brasington J. , Glasser N. F. , et al. , 2012. ‘Structure-from-Motion’ photogrammetry: a low-cost, effective tool for geoscience applications. Geomorphology, 179: 300—314. doi: 10.1016/j.geomorph.2012.08.021 [36] Zielke O. , Arrowsmith J. R. , Grant Ludwig L. , et al. , 2012. High-resolution topography-derived offsets along the 1857 Fort Tejon earthquake rupture trace, San Andreas fault. Bulletin of the Seismological Society of America, 102(3): 1135—1154. doi: 10.1785/0120110230 期刊类型引用(3)
1. 徐伟，程理，李光涛，陈文龙. 马雅雪山断裂金强河段晚第四纪断错地貌及滑动速率确定. 震灾防御技术. 2024(03): 457-467 . 
本站查看2. 李彦锋，杨延斌，杨岩，杨树宏，杨超. RTK技术在云南高海拔山区架空输电线路多旋翼无人机自动巡检中的应用. 云南电业. 2024(06): 36-39 . 百度学术3. 丁锐. 城市规划测绘在数字化城市建设中的应用. 中国高新科技. 2023(07): 155-157+160 . 百度学术其他类型引用(0)
-
下载:
点击查看大图
计量
- 文章访问数: 335
- HTML全文浏览量: 91
- PDF下载量: 96
- 被引次数: 3
