Behavior of High Ductility FRP-confined Large-size Concrete Columns Under Axial Compression
-
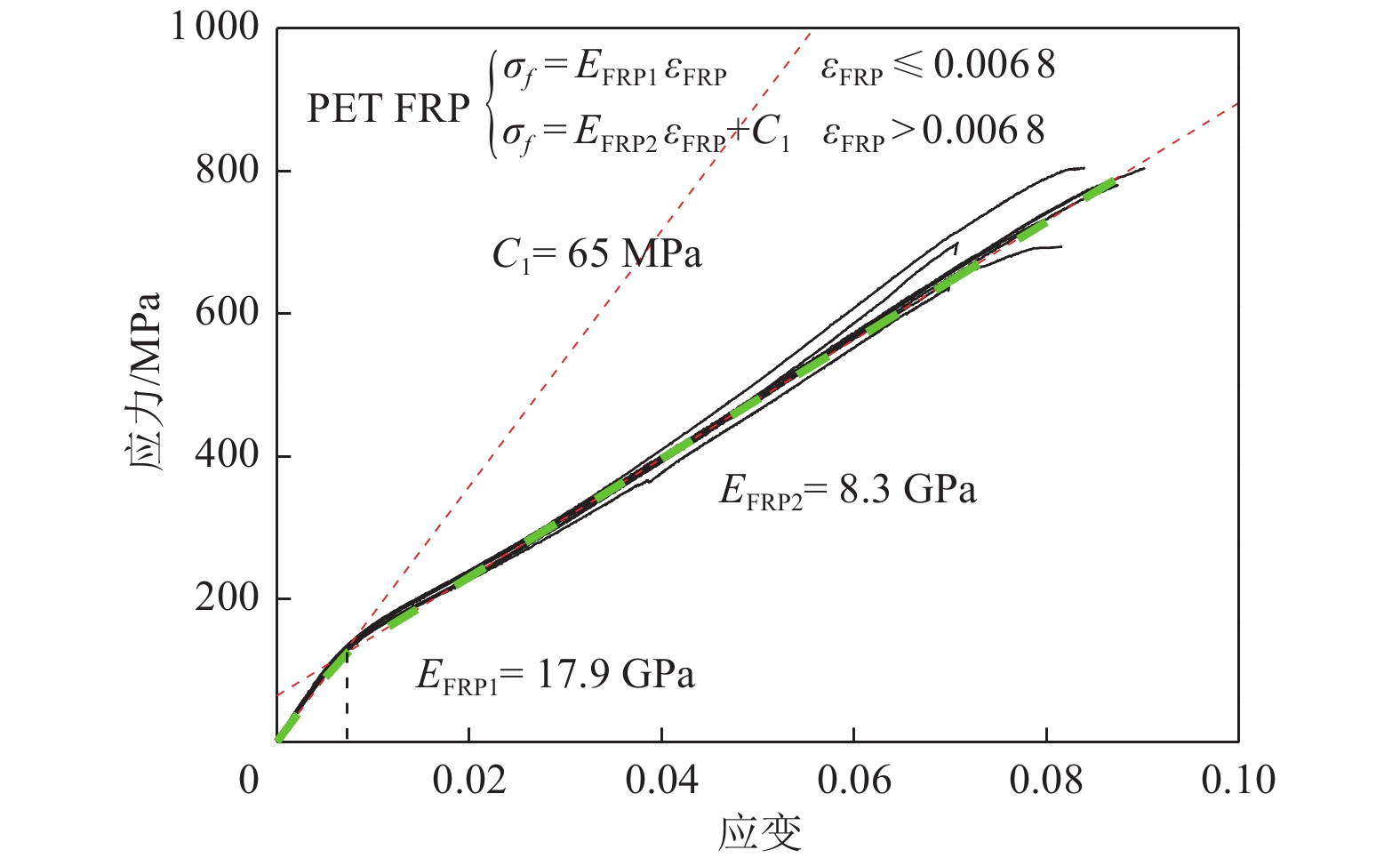
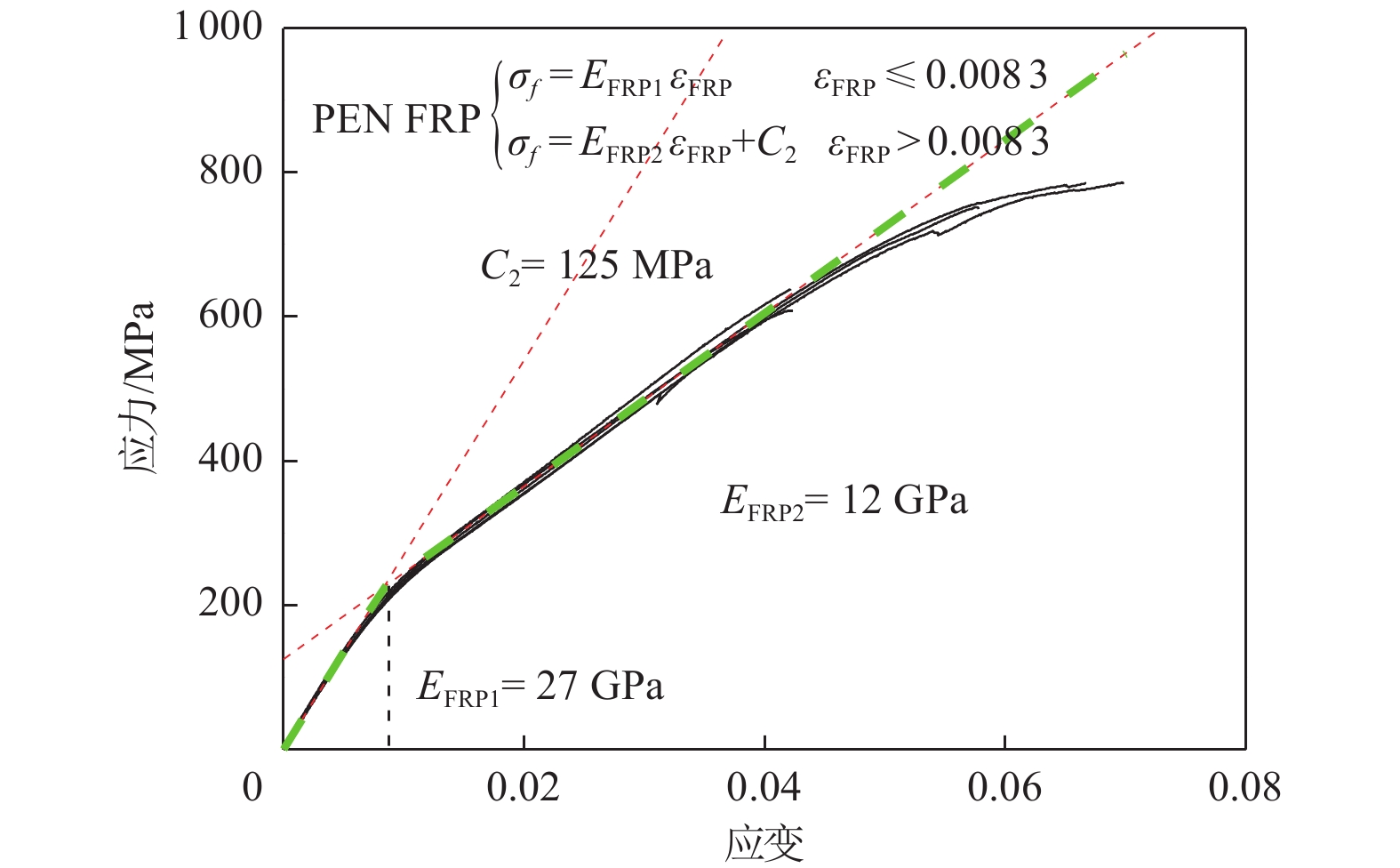
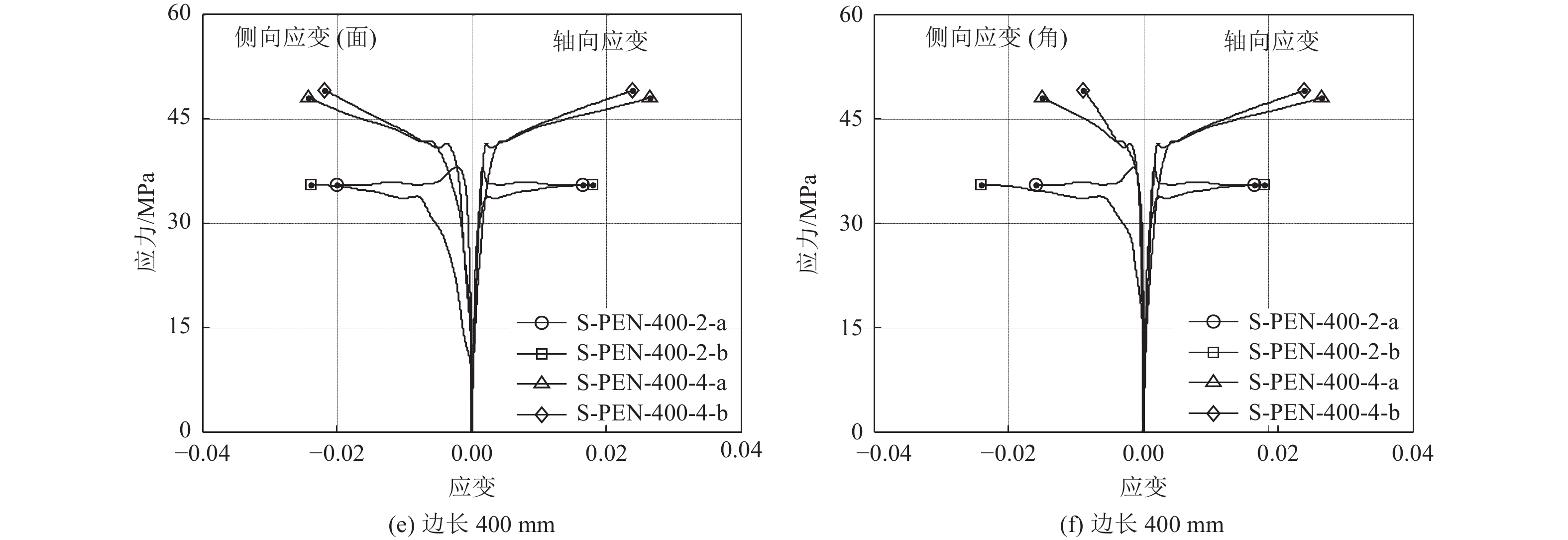
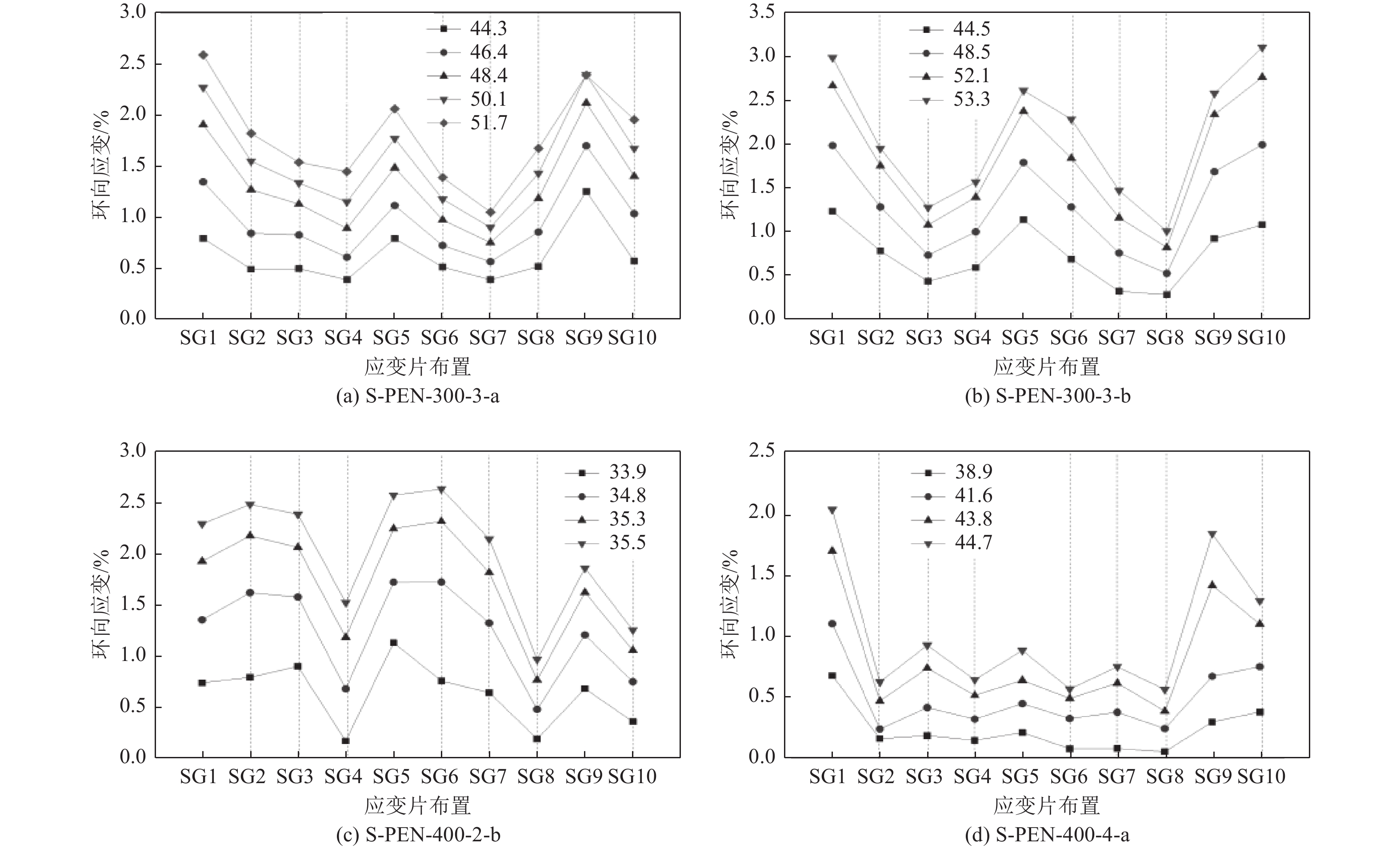
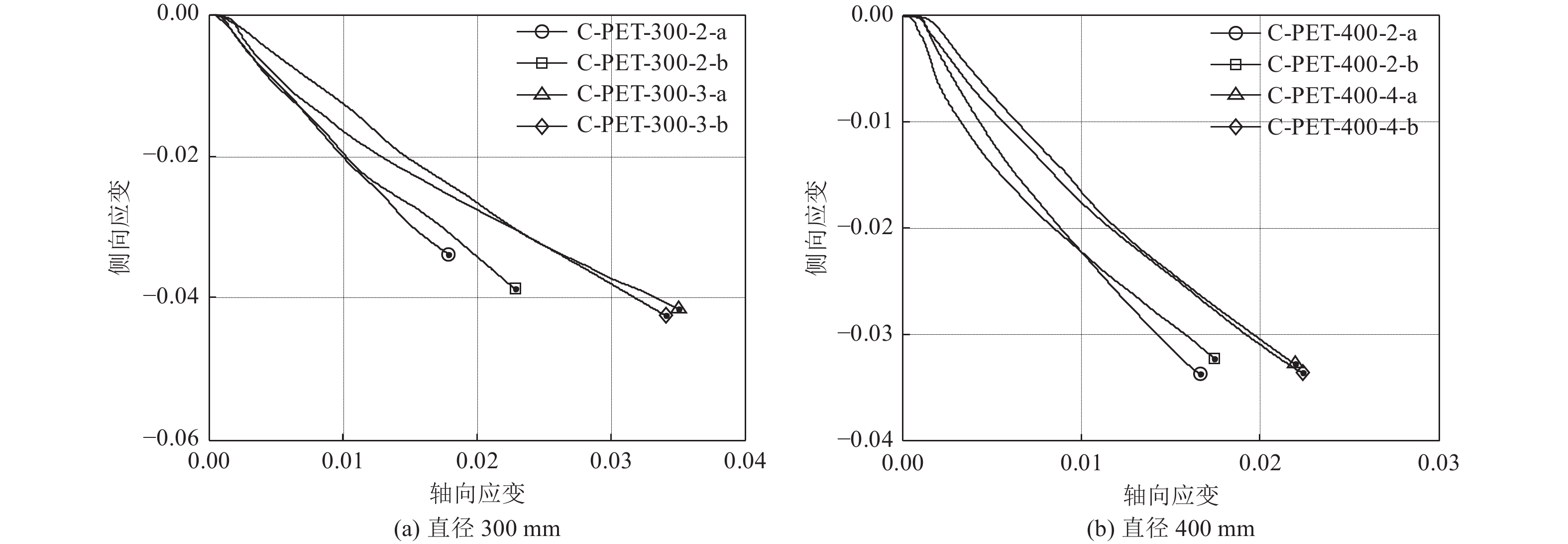
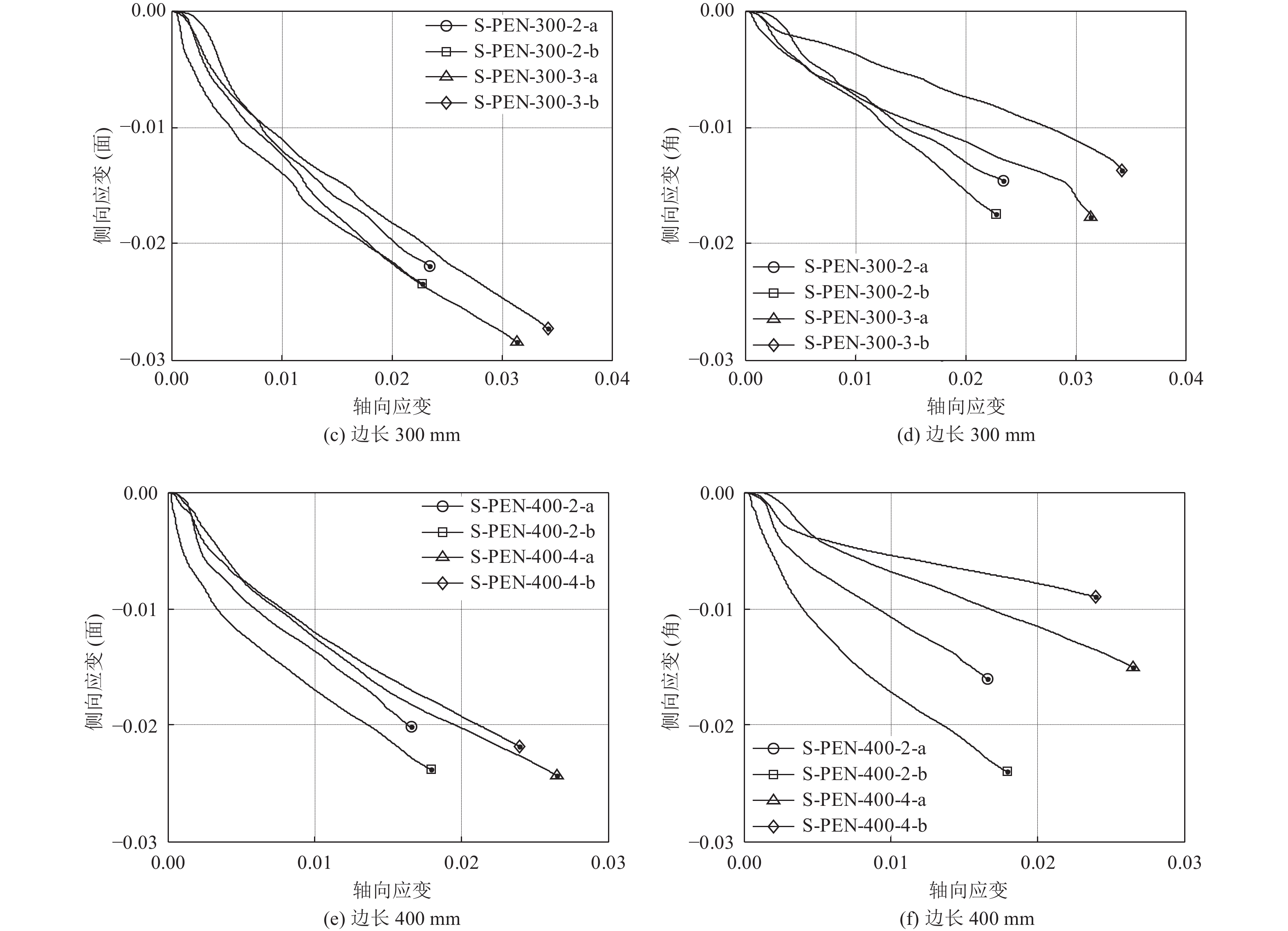
摘要: 现有纤维增强复合材料（FRP）约束混凝土短柱的研究多基于小尺寸试件，对大尺寸试件的研究较少。聚对苯二甲酸乙二醇酯纤维增强复合材料（PET FRP）和聚萘二甲酸乙二醇酯纤维增强复合材料（PEN FRP）是由回收废弃塑料制成的环保型高延性FRP。高延性FRP具有超过5%的断裂应变，超过传统FRP断裂应变（1.5～3%）。本研究对8个PET FRP约束混凝土圆柱（直径300、400 mm试件各4个）与8个PEN FRP约束混凝土方柱（边长300、400 mm试件各4个）进行轴压力学性能试验，研究构件截面形状、FRP层数等参数对试件轴压力学性能的影响。试验结果表明：高延性FRP约束混凝土柱应力-应变曲线由3个不同的部分组成；部分高延性FRP约束混凝土柱应力-应变曲线第2段出现了下降段，与约束刚度较小有关；相同尺寸的试件，随着高延性FRP层数（厚度）的增加，试件承载力提高，延性更好；对于PEN FRP约束混凝土方柱，在同一轴向变形、高度区域处，环向面应变较环向角应变大，且环向面应变的增加值大于角区域；采用现有高延性FRP约束混凝土柱模型，对约束圆形和方形混凝土柱轴压力学性能提供相对合理的预测。Abstract: Most of the existing researches on fiber reinforced polymer (FRP) composite-confined concrete short columns are based on small size specimens, and large-size columns have not been fully studied. PET (Polyethylene Terephthalate) FRP and PEN (Polyethylene Naphthalene) FRP are environmentally friendly large rupture strain FRPs made from recycled waste plastic. Compared with traditional FRP, high ductility FRP materials have a fracture strain larger than 5%, which is far larger than that of traditional FRP materials with the value of 1.5～3%. In recent years, high ductility FRP has become a research hotspot all over the world. In this paper, the axial compressive behavior of 8 PET FRP-confined concrete columns and 8 PEN FRP-confined concrete columns were experimentally studied. The main research parameters included the shape of specimens and the number of FRP layers. Results show that the stress-strain curve of high ductility FRP-confined concrete columns has three different parts; the second part of stress-strain curve of partially high ductility FRP-confined concrete columns appears a descending section, which is related to the small constraint stiffness; the bearing capacity and ductility of same size specimens increase with the increase of FRP thickness; The middle strain is larger than corner strain of PEN FRP-confined concrete square columns at the same axial deformation. Moreover, the existing stress strain models for high ductility FRP-confined concrete were evaluated with the test results.
-
引言
近年来，频繁的地震灾害造成了巨大的人员伤亡和经济损失，选择可靠的加固方法对既有混凝土结构进行加固与维护变得尤为重要。随着经济和技术的发展，高性能材料大量涌现。纤维增强复合材料（Fiber Reinforced Polymer，简称FRP）以其轻质、高强、耐腐蚀、施工方便等优点，在混凝土结构加固中得到越来越广泛的应用（Hollaway等，2008；Teng等，2002；Xiao等，2009）。聚对苯二甲酸乙二醇酯纤维增强复合材料（Polyethylene Terephthalate Fiber Reinforced Polymer，简称PET FRP）和聚萘二甲酸乙二醇酯纤维增强复合材料（Polyethylene Naphthalene Fiber Reinforced Polymer，简称PEN FRP）以其断裂应变较大（ >5%）的特点，弥补了传统FRP断裂应变较小（1.5～3%）的不足。与传统FRP相比，高延性FRP由回收废弃塑料制成，价格相对低廉，且符合绿色环保发展理念（Han等，2020）。由于高延性特点，高延性FRP加固柱可避免发生脆性破坏。因此，在混凝土结构抗震加固中，高延性FRP成为传统碳纤维增强复合材料（Carbon Fiber Reinforced Polymer，简称CFRP）的可替代方案。
随着建筑材料科学的发展，结构跨度、高度及形式越来越多样化，混凝土结构主体各部分和构件尺寸逐渐增大。然而，FRP约束混凝土柱轴压力学性能研究多基于小尺寸试件，对FRP约束混凝土大尺寸柱破坏机理和力学性能的研究较少（蔡静，2015；龙跃凌等，2010；邓宗才等，2019；Dai等，2011；Han等，2020；Ozbakkaloglu等，2013；Saleem等，2016；Wang等，2008；Zeng等，2018）。因此，需进一步对FRP约束混凝土大尺寸柱进行研究。为此，本文对8个PET FRP约束混凝土圆柱（直径300、400 mm试件各4个）和8个PEN FRP约束混凝土方柱（边长300、400 mm试件各4个）进行试验研究和理论分析，以期为实际工程提供理论依据。
1. 试验概况
1.1 试件设计
本文以构件截面形状及FRP层数为参数，试件长细比均为2，截面尺寸如图1所示，编号及参数如表1所示。试件编号中“C”表示圆柱，“S”表示方柱，“PET”表示PET FRP，“PEN”表示PEN FRP，“300”表示试件直径或边长为300 mm，“400”表示试件直径或边长为400 mm，“2”表示FRP为2层，“3”表示FRP为3层，“4”表示FRP为4层，“a，b”表示2个完全相同的试件。
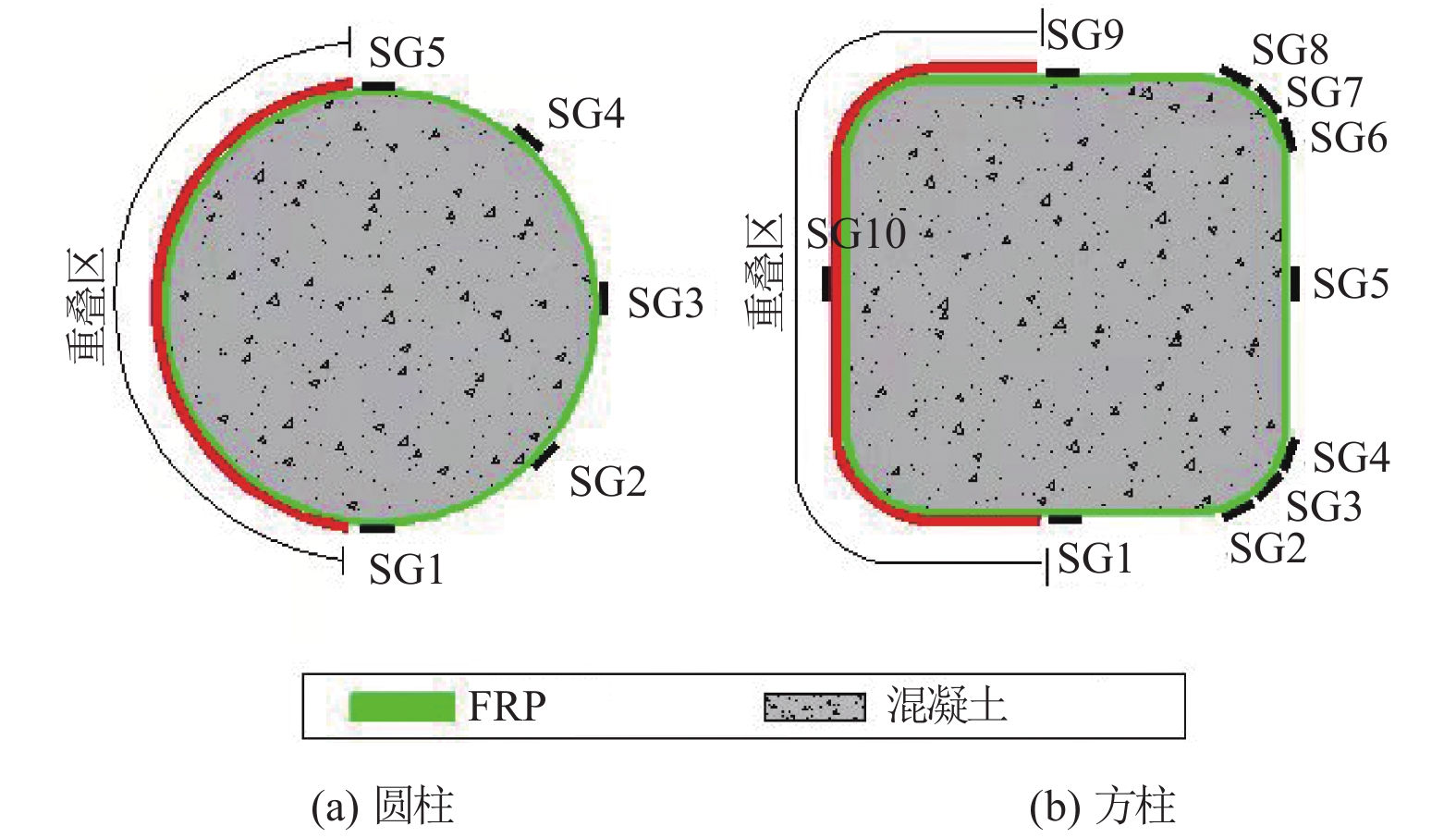
表 1 试件编号及参数Table 1. Details of specimens试件编号 直径或边长/mm 高度/mm 角半径/mm 材料类型 FRP层数/层 C-PET-300-2-a,b 300 600 — PET FRP 2 C-PET-300-3-a,b 300 600 — PET FRP 3 C-PET-400-2-a,b 400 800 — PET FRP 2 C-PET-400-4-a,b 400 800 — PET FRP 4
S-PEN-300-2-a,b
300
600
60
PEN FRP
2
S-PEN-300-3-a,b
300
600
60
PEN FRP
3
S-PEN-400-2-a,b
400
800
80
PEN FRP
2
S-PEN-400-4-a,b
400
800
80
PEN FRP
41.2 材料性能
1.2.1 混凝土
所有试件均使用当地制造商提供的同批预拌混凝土进行浇筑。试块按标准养护28 d后，根据ASTM标准（ASTM C469，2002），在北京工业大学结构实验室进行抗压强度试验，测得素混凝土标准圆柱平均抗压强度
$ f_{{\rm{co}}}' $ 为33.3 MPa，本文将未约束混凝土的峰值应变εco取0.225%，该值由下式计算得到（Popovics，1973）：$$ {\varepsilon _{{\rm{co}}}} = 9.37 \times {10^{ - 4}}\sqrt[{4}]{{f_{{\rm{co}}}^\prime }} $$ (1) 1.2.2 CFRP及胶体力学性能
CFRP由北京卡本工程技术研究所有限公司生产，PET FRP和PEN FRP从日本Maeda Kosen公司购买，胶体由上海三悠树脂有限公司生产。CFRP、PET FRP和PEN FRP名义厚度分别为0.111、0.841、1.272 mm，抗拉强度分别为3972、740、790 MPa，伸长率分别为1.77 %、8.3 %、5.8 %。CFRP弹性模量为245.5 GPa，PET FRP和PEN FRP第1阶段弹性模量分别为17.9、27.0 GPa，第2阶段弹性模量分别为8.3、12.0 GPa。
按照ASTM标准（ASTM D3039M，2008），对PET FRP和PEN FRP进行平板拉伸试验，如图2、3所示。PET FRP和PEN FRP拉伸应力-应变曲线分别如图4、5所示，可知曲线表现出近似双折线的应力-应变关系。
1.3 试件制作
试件制作步骤如下：（1）准备模具，将模具固定在模板上，并做好模具底部防水工作；（2）浇筑混凝土；（3）养护成型，拆模；（4）湿铺法包裹纤维布，纤维布搭接长度为试件周长的1/2，防止接口处因黏结不牢影响构件加固效果；（5）各试件上、下端分别采用60、100 mm宽CFRP进行加固，防止加载过程中出现端部破坏现象。
1.4 量测方案
采用YAM-72000J型电液伺服试验机进行加载，选择位移控制加载方式，加载速率为0.6 mm/min。为避免FRP突然断裂损坏试验机器，圆柱试件在外包PET FRP环向应变最大值达3.5 %时终止试验，方柱试件在外包PEN FRP环向应变最大值达2.2 %时终止试验。各试件使用3对LVDT位移传感器进行轴向位移测量，其中1对用于测量试件整体轴向变形，另外2对均匀放置在接近试件四角位置的位移架上，用于测量试件中部区域范围内的轴向变形，如图6所示，所有试验数据均由采集仪记录。
试件环向应变均采用长度为20 mm的电阻式应变片进行测量，应变片（编号SG1～SG10）布置如图7所示。
2. 试验结果与分析
2.1 主要试验结果
基于同批压爆的小尺寸试件得到的经验及试验过程中遇到的情况，调整得到终止试验时的PET FRP与PEN FRP环向应变最大值。总之，在保证实验室安全的前提下，尽量使试件加载时间更久，试验曲线更长。试验结束后的试件如图8所示，主要试验结果如表2、3所示。表2、3中fcu ′ 为试件极限应力，取试验终止时的应力；εcu表示试件极限轴向应变；εh,rup表示试件环向断裂应变；εh,c表示方柱试件2个角上环向断裂应变的平均值；εh,s表示方柱试件3个面上环向断裂应变的平均值；在混凝土中，压应力和压应变符号为正；在FRP中，拉伸应力和拉伸应变符号为正；应力表示轴向荷载与截面面积的比值；应变表示测区竖向位移与卡距的比值。
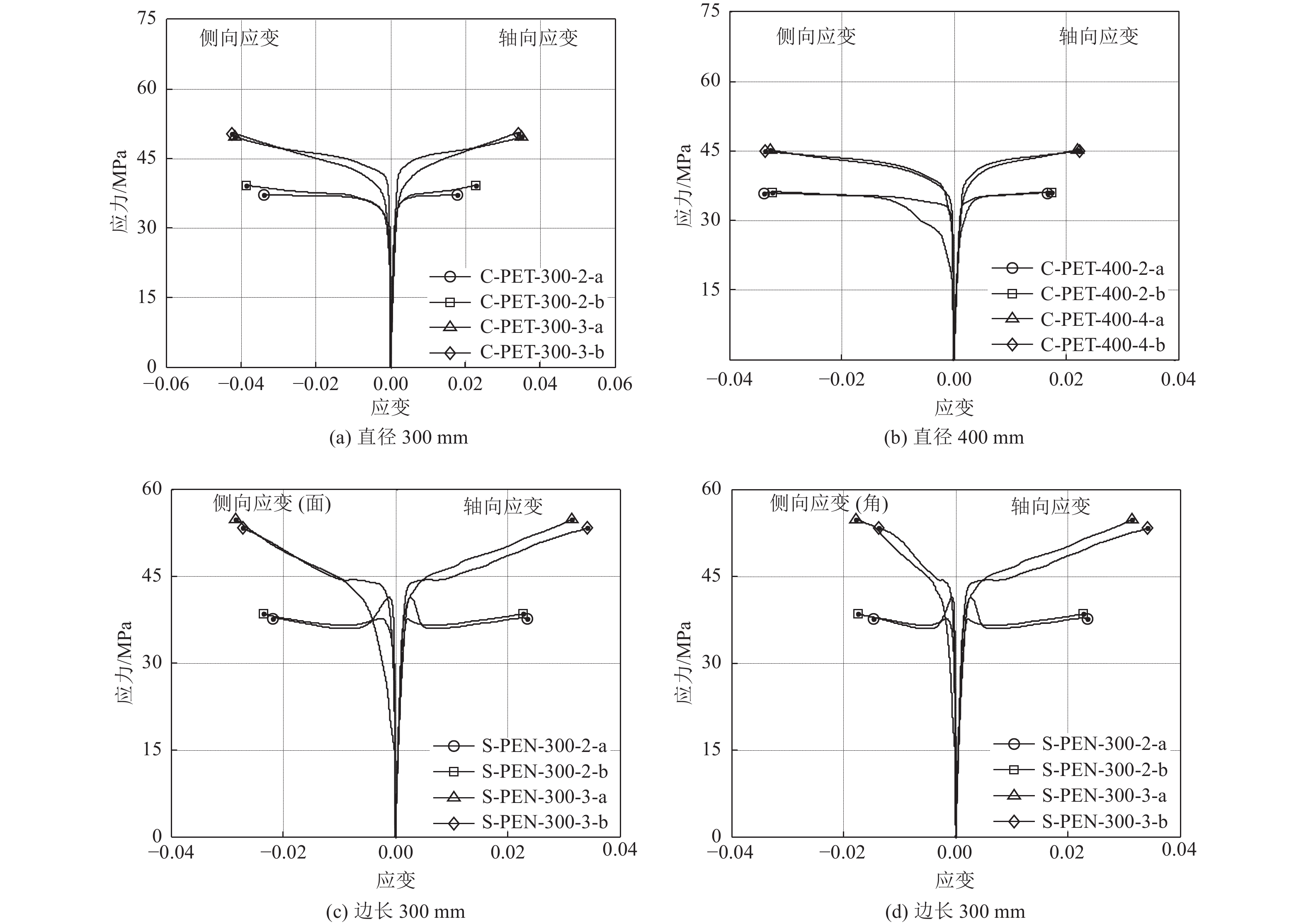
表 2 圆柱主要试验结果Table 2. Key results of circular column tests试件编号 fcu ′ /MPa εcu/% εh,rup/% 最大环向应变对应的应变片编号 C-PET-300-2-a 37.2 1.79 3.38 SG1 C-PET-300-2-b 39.2 2.28 3.86 SG5 C-PET-300-3-a
49.6
3.51
4.16
SG1C-PET-300-3-b 50.4 3.41 4.24 SG4 C-PET-400-2-a 35.9 1.67 3.38 SG1 C-PET-400-2-b 36.2 1.75 3.23 SG2 C-PET-400-4-a 45.2 2.19 3.28 SG5 C-PET-400-4-b 45.0 2.24 3.36 SG1 表 3 方柱主要试验结果Table 3. Key results of square column tests试件编号 fcu ′ /MPa εcu/% εh,c/% εh,s/% 最大环向应变对应的应变片编号 S-PEN-300-2-a 37.6 2.34 1.46 2.19 SG9 S-PEN-300-2-b 38.4 2.28 1.75 2.34 SG1 S-PEN-300-3-a 54.8 3.14 1.77 2.84 SG1 S-PEN-300-3-b 53.3 3.42 1.37 2.73 SG1 S-PEN-400-2-a 35.5 1.66 1.60 2.01 SG9 S-PEN-400-2-b 35.5 1.79 2.40 2.38 SG5 S-PEN-400-4-a 47.9 2.64 1.50 2.43 SG9 S-PEN-400-4-b 49.0 2.39 0.90 2.18 SG1 2.2 混凝土柱轴向应力-应变曲线
试件轴向应力-应变曲线如图9所示，其中侧向应变εl显示在坐标原点左边，轴向应变εc显示在坐标原点右边。由图9可知，FRP可显著提高混凝土柱极限抗压强度和延性。
2.3 环向应变分布
对于FRP约束混凝土柱，FRP提供的横向约束为被动约束，仅在核心混凝土膨胀时横向约束才会增加。部分方柱试件环向应变分布如图10所示，其中，SG3、SG7对应角，SG10对应重叠区。由于方柱4个角部位出现应力集中，所以方柱沿周长方向受力不均匀。由图10可知，同一高度区域，面中部环向应变大于角部环向应变。
高延性FRP约束混凝土柱轴向应变和环向面应变、角应变之间的关系如图11所示。与传统FRP相比，高延性FRP约束混凝土柱由于断裂应变大的特性表现出较大的轴向和环向变形。对于圆柱，应变取为PET FRP圆周方向上叠合区之外的5个应变点的平均值；对于方柱，面上应变取为PEN FRP周长方向叠合区之外的3个平面内测点的平均值，角部应变取为2个角部测点的平均值。
3. 模型适用性研究
3.1 基于刚度的高延性FRP设计模型
Bai等（2019）刚度设计模型认为高延性FRP约束混凝土柱的应力-应变曲线由3部分组成：第1部分为抛物线段，第2、3部分为直线段。直线段具有不同的轴向刚度。
对于高延性FRP强约束混凝土柱
$\left( {{E_2} \geqslant 0} \right) $ ：$$ {\sigma _{\rm{c}}} = \left\{ {\begin{array}{*{20}{l}} {{E_{\rm{c}}}{\varepsilon _{\rm{c}}} - \dfrac{{{{\left( {{E_{\rm{c}}} - {E_2}} \right)}^2}}}{{4{{f}_{{\rm{co}}}'}}}{\varepsilon _{\text{c}}^2} \quad,{\text{ 0}} \leqslant {\varepsilon _{\rm{c}}} \leqslant {\varepsilon _{\rm{t}}}} \\ \begin{gathered} {{f}_{{\rm{co}}}'} + {E_2}{\varepsilon _{\rm{c}}} \quad\quad\quad\quad \;\;\;\;,{\text{ }}{\varepsilon _{\rm{t}}} \leqslant {\varepsilon _{\rm{c}}} \leqslant \varepsilon _{\rm{t}}^* \hfill \\ \sigma _{\rm{t}}^* + E_2^*({\varepsilon _{\rm{c}}}{{ - }}\varepsilon _{\rm{t}}^*) {\text{ }} \quad\quad\;\;\,,\,\, \varepsilon _{\rm{t}}^* \leqslant {\varepsilon _{\rm{c}}} \leqslant {\varepsilon _{\rm{cu}}} \hfill \\ \end{gathered} \end{array}} \right.{\text{ }} $$ (2) 式中，σc为FRP约束混凝土轴向应力；εc为FRP约束混凝土轴向应变；Ec为未约束混凝土初始弹性模量；E2为第2部分直线段斜率；
$E_2^* $ 为第3部分直线段斜率；$\varepsilon _{\rm{t}} $ 为第1部分抛物线段与第2部分直线段连接处的轴向应变；$\sigma_{\rm{t}}^* $ 和$\varepsilon _{\rm{t}}^* $ 分别为第2、3部分直线段连接处的轴向应力和轴向应变。同样地，对于高延性FRP弱约束混凝土柱
$\left( {{E_2} < 0} \right) $ ：$$ {\sigma _{\rm{c}}} = \left\{ {\begin{array}{*{20}{l}} {{E_{\rm{c}}}{\varepsilon _{\rm{c}}} - \dfrac{{E_{\rm{c}}^2}}{{4{{f}_{{\rm{co}}}'}}}\varepsilon _{\rm{c}}^2 \quad\quad\;,\;{\text{0}} \leqslant {\varepsilon _{\rm{c}}} \leqslant {\varepsilon _{\rm{t}}}} \\ \begin{gathered} {{f}_{{\rm{co}}}'} + {E_2}{\varepsilon _{\rm{c}}}{\text{ }} \quad\quad\quad\;\;,\; {\varepsilon _{\rm{t}}} \leqslant {\varepsilon _{\rm{c}}} \leqslant \varepsilon _{\rm{t}}^* \hfill \\ \sigma _{\rm{t}}^* + E_2^*({\varepsilon _{\rm{c}}}{{ - }}\varepsilon _{\rm{t}}^*{\text{) }} \quad\;\,,\; \varepsilon _{\rm{t}}^* \leqslant {\varepsilon _{\rm{c}}} \leqslant {\varepsilon _{\rm{cu}}} \hfill \\ \end{gathered} \end{array}} \right.{\text{ }}{\text{ }} $$ (3) FRP对混凝土的约束应力σl为：
$$ {\sigma _{\rm{l}}} = \frac{{{E_{{\rm{FRP}}}}{t_{{\rm{FRP}}}}{\varepsilon _{\rm{h}}}}}{R} $$ (4) 式中，EFRP和tFRP分别为FRP弹性模量和厚度；εh为混凝土柱轴压测试中FRP环向应变；R为混凝土圆柱半径。
约束刚度定义为约束刚度比（2EFRPtFRP/D，D为圆柱直径）与未约束混凝土强度
$f_{{\rm{co}}}' $ 的比值：$$ \rho = \frac{{2{E_{{\rm{FRP}}}}{t_{{\rm{FRP}}}}}}{{D{{f}_{{\rm{co}}}'}}} $$ (5) εco由下式给出：
$$ {\varepsilon _{{\rm{co}}}} = \frac{{2{{f}_{{\rm{co}}}'}}}{{{E_{\rm{i}}}}} $$ (6) 式中，Ei为未约束混凝土初始弹性模量，取值与Ec同。
新的膨胀模型为：
$$ \frac{{{\varepsilon _{\rm{c}}}}}{{{\varepsilon _{{\rm{co}}}}}} = \left( {1.0 + 8.0\frac{{{\sigma _{\rm{l}}}}}{{{{f}_{{\rm{co}}}'}}}} \right) \cdot \left[ {0.97{\text{0}}{{\left( {\frac{{ - {\varepsilon _{\rm{l}}}}}{{{\varepsilon _{{\rm{co}}}}}}} \right)}^{0.43{\text{1}}}} + 0.06{\text{7}}\left( {\frac{{ - {\varepsilon _{\rm{l}}}}}{{{\varepsilon _{{\rm{co}}}}}}} \right)} \right] $$ (7) 式中，εl为FRP约束混凝土侧向应变。
通过回归分析建立以下方程：
$$ \dfrac{{{E_2}}}{{{{f}_{{\rm{co}}}'}}} = - 259.8{\rho ^{ - 0.5}} + 108.5 $$ (8) $$ \frac{{E_2^*}}{{{{f}_{{\rm{co}}}'}}} = - 57.7{({\rho ^*})^{ - 0.5}} + 38.1 $$ (9) 式中，ρ为第2部分直线段约束刚度；ρ*为第3部分直线段约束刚度。
εt表达式如下：
$$ {\varepsilon _{\rm{t}}} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{2{{f}_{{\rm{co}}}'}}}{{{E_{\rm{c}}} - {E_2}}}}&{\left( {{E_2} \geqslant 0} \right)} \\ {\dfrac{{2{{f}_{{\rm{co}}}'}\left( {{E_{\rm{c}}} - {E_2}} \right)}}{{E_c^2}}}&{\left( {{E_2} < 0} \right)} \end{array}} \right. $$ (10) 第1部分抛物线段与第2部分直线段连接处的轴向应力σt表达式如下：
$$ {\sigma _{\rm{t}}} = \left\{ {\begin{array}{*{20}{l}} {{{f}_{{\rm{co}}}'} + {E_2}{\varepsilon _{\rm{t}}}}&{\left( {{E_2} \geqslant 0} \right)} \\ {{E_{\rm{c}}}{\varepsilon _{\rm{t}}} - \dfrac{{E_{\rm{c}}^2}}{{4{{f}_{{\rm{co}}}'}}}\varepsilon _{\rm{t}}^2}&{\left( {{{\rm{E}}_2} < 0} \right)} \end{array}} \right. $$ (11) 3.2 Pimanmas等模型
Pimanmas等（2019）模型由3部组成，即应力-应变曲线达峰值前的上升段、强度软化区的下降段、应力达最低点后的上升段。本文仅给出决定该模型曲线形状的主要公式。
（1）应力-应变曲线达峰值前的上升段
此阶段表达式如下：
$$ {f_{\rm{c}}} = {E_{\rm{c}}}{\varepsilon _{\rm{c}}}\left[ {1 - \frac{1}{n}{{\left( {\frac{{{\varepsilon _{\rm{c}}}}}{{{\varepsilon _{{\rm{c}}1}}}}} \right)}^{n - 1}}} \right]{\text{ ， }} 0 <\varepsilon_{{\rm{c}}}<\varepsilon_{{\rm{c}}1} $$ (12) $$ n = \frac{{{E_{\rm{c}}}{\varepsilon _{{\rm{c}}1}}}}{{{E_{\rm{c}}}{\varepsilon _{{\rm{c}}1}} - {f_{{\rm{c}}1}}}} $$ (13) $$ \frac{{{f_{{\rm{c}}1}}}}{{{{f}_{{\rm{co}}}'}}} = 1 + 0.48{\left( {\frac{{{f_{{\rm{la}}}}}}{{{{f}_{{\rm{co}}}'}}}} \right)^{0.5}} $$ (14) $$ \frac{{{\varepsilon _{{\rm{c}}1}}}}{{{\varepsilon _{{\rm{co}}}}}} = 1 + 80{\varepsilon _{{\rm{fu}}}}\left( {\frac{{{f_{{\rm{la}}}}}}{{{{f}_{{\rm{co}}}'}}}} \right) $$ (15) 式中，εc1为峰值应变；fc1为峰值应力；n为系数；fla为FRP实际的最大环向约束应力；εfu为平板拉伸试验测得的FRP极限拉伸断裂应变平均值。
（2）应力-应变曲线强度软化区的下降段
此阶段第1部分表达式如下：
$$ {f_{\rm{c}}} = \frac{{K{f_{{\rm{c}}1}}\left( {\dfrac{{{\varepsilon _{\rm{c}}}}}{{{\varepsilon _{{\rm{c}}1}}}}} \right)}}{{1 + A\left( {\dfrac{{{\varepsilon _{\rm{c}}}}}{{{\varepsilon _{{\rm{c}}1}}}}} \right) + B{{\left( {\dfrac{{{\varepsilon _{\rm{c}}}}}{{{\varepsilon _{{\rm{c}}1}}}}} \right)}^2} + C{{\left( {\dfrac{{{\varepsilon _{\rm{c}}}}}{{{\varepsilon _{{\rm{c}}1}}}}} \right)}^3}}}{\text{，}} \varepsilon_{\mathrm{c1}}<\varepsilon_{{\rm{c}}}<\varepsilon_{\mathrm{cs}} $$ (16) $$ A=C+K-2 $$ (17) $$ B=1-2 C $$ (18) $$ C=K \frac{\left(K_{\sigma}-1\right)}{\left(K_{\varepsilon }-1\right)^{2}}-\frac{1}{K_{\varepsilon}} $$ (19) $$ K=\frac{E_{{\rm{c}}}}{E_{{\rm{sec}}}} $$ (20) $$ E_{{\rm{sec}}}=\frac{f_{{\rm{c}}1}}{\varepsilon _{{\rm{c}} 1}} $$ (21) $$ K_{\varepsilon }=\frac{\varepsilon_{{\rm{c s}}}}{\varepsilon_{{\rm{c}} 1}} $$ (22) $$ \frac{{{\varepsilon _{{\rm{cs}}}}}}{{{\varepsilon _{{\rm{co}}}}}} = 5.47 + 84.6{\varepsilon _{{\rm{fu}}}}\left( {\frac{{{f_{{\rm{la}}}}}}{{{{f}_{{\rm{co}}}'}}}} \right) $$ (23) $$ K_{\sigma }=\frac{f_{{\rm{c}} 1}}{f_{{\rm{cs}}}} $$ (24) $$ \frac{{{f_{{\rm{cs}}}}}}{{{{f}_{{\rm{co}}}'}}} = 0.53 + 1.65\left( {\frac{{{f_{{\rm{la}}}}}}{{{{f}_{{\rm{co}}}'}}}} \right) $$ (25) 式中，K为刚度比，取无约束混凝土的初始弹性模量（Ec）与割线模量（Esec）的比值；Kε为应变比，取峰值后下降段斜率最大点（拐点）的应变（εcs）与峰值应变（εc1）的比值；Kσ为应力比，取峰值应力（fc1）与峰值后下降段斜率最大点的应力（fcs）的比值。
此阶段第2部分表达式如下：
$$ f_{{\rm{c}}}=f_{{\rm{cs}}}-E_{{\rm{s}}}\left(\varepsilon_{{\rm{c}} 2}-\varepsilon_{{\rm{cs}}}\right) {\text{，}} \varepsilon_{{\rm{cs}}} < \varepsilon_{{\rm{c}}}< \varepsilon_{{\rm{c}} 2} $$ (26) $$ {E_{\rm{s}}} = \frac{{{f_{{\rm{cs}}}} - {f_{{\rm{c2}}}}}}{{{\varepsilon _{{\rm{c2}}}} - {\varepsilon _{{\rm{cs}}}}}} $$ (27) $$ \frac{{{f_{{\rm{c2}}}}}}{{{{f}_{{\rm{co}}}'}}} = 0.448 + 1.83\left( {\frac{{{f_{{\rm{la}}}}}}{{{{f}_{{\rm{co}}}'}}}} \right) $$ (28) $$ \frac{{{\varepsilon _{{\rm{c}}2}}}}{{{\varepsilon _{{\rm{co}}}}}} = 1 + 45.91{\varepsilon _{{\rm{fu}}}}{\left( {\frac{{{f_{{\rm{la}}}}}}{{{{f}_{{\rm{co}}}'}}}} \right)^{ - 0.5}} $$ (29) 式中，Es为峰值后下降段斜率最大点（拐点）应力（fcs）与曲线最低点应力（fc2）之间的割线模量；εc2为下降段最低点应变。
（3）应力-应变曲线应力达最低点后的上升段
此阶段表达式如下：
$$ {f_{\rm{c}}} = {f_{{\rm{c}}2}} + {E_{\rm{a}}}\left( {{\varepsilon _{{\rm{cu}}}} - {\varepsilon _{{\rm{c}}2}}} \right) {\text{，}} \varepsilon_{{\rm{c}}2} < \varepsilon_{{\rm{c}}}< \varepsilon_{{\rm{c u}}} $$ (30) $$ {E_{\rm{a}}} = \frac{{f_{{\rm{cu}}}' - {f_{{\rm{c}}2}}}}{{{\varepsilon _{{\rm{cu}}}} - {\varepsilon _{{\rm{c}}2}}}} $$ (31) $$ \frac{{{{f}_{{\rm{c}}{\text{u}}}'}}}{{{{f}_{{\rm{co}}}'}}} = 0.56 + 3.33\left( {\frac{{{f_{{\rm{la}}}}}}{{{{f}_{{\rm{co}}}'}}}} \right) $$ (32) $$ \frac{{{\varepsilon _{{\rm{cu}}}}}}{{{\varepsilon _{{\rm{co}}}}}} = 1 + 537{\varepsilon _{{\rm{fu}}}}{\left( {\frac{{{f_{{\rm{la}}}}}}{{{{f}_{{\rm{co}}}'}}}} \right)^{0.25}}{\left( {0.5 + \frac{{2r}}{b}} \right)^{ - 1.1}} $$ (33) 式中，Ea为极限轴向应力（
$f_{{\rm{cu}}}'$ ）与最低点应力（fc2）之间的割线模量；$f_{{\rm{cu}}}'$ 为极限轴向应力。模型预测结果与试验结果的对比如图12所示。由图12可知，Bai等（2019）刚度设计模型和Pimanmas等（2019）模型可合理预测试验曲线，模型准确性较高；Bai等（2019）刚度设计模型预测曲线略低于试验曲线，略低估了试件极限应力，因此该模型可用于大尺寸圆柱保守设计；Pimanmas等（2019）模型预测曲线略低于试验曲线，略高估了试件极限应力和极限应变，这是由于该模型中实际环向断裂应变是由平板拉伸试验测得的FRP极限拉伸断裂应变平均值乘有效因子得到的。
4. 结论
（1）高延性FRP约束大尺寸混凝土柱应力-应变曲线由3个不同的部分组成，第1部分上升段与无侧限混凝土相似，峰值强度略高于无侧限强度。第2部分过渡区趋势受约束刚度的影响较大，约束刚度较低的试件具有应变软化行为，而约束刚度较大的试件倾向于表现出应变硬化行为。第3部分曲线开始再次上升，直至FRP被拉断，试件破坏。
（2）相同尺寸的试件，随着高延性FRP层数（厚度）的增加，高延性FRP包裹柱的承载力提高，延性更好。
（3）由于方柱沿周长方向受力不均匀，在同一轴向变形、高度区域处，PEN FRP约束混凝土方柱面上中部环向应变较角部环向应变大，且面上中间区域环向应变增加值大于角区域。
（4）采用现有的高延性FRP约束混凝土本构模型，对高延性FRP约束圆柱、方柱进行了评估。结果表明，Bai等（2019）刚度设计模型和Pimanmas等（2019）模型预测结果与试验结果较吻合，该模型可为实际工程应用提供相对合理的预测。
-
表 1 试件编号及参数
Table 1. Details of specimens
试件编号 直径或边长/mm 高度/mm 角半径/mm 材料类型 FRP层数/层 C-PET-300-2-a,b 300 600 — PET FRP 2 C-PET-300-3-a,b 300 600 — PET FRP 3 C-PET-400-2-a,b 400 800 — PET FRP 2 C-PET-400-4-a,b 400 800 — PET FRP 4
S-PEN-300-2-a,b
300
600
60
PEN FRP
2
S-PEN-300-3-a,b
300
600
60
PEN FRP
3
S-PEN-400-2-a,b
400
800
80
PEN FRP
2
S-PEN-400-4-a,b
400
800
80
PEN FRP
4
下载: 导出CSV
表 2 圆柱主要试验结果
Table 2. Key results of circular column tests
试件编号 fcu ′ /MPa εcu/% εh,rup/% 最大环向应变对应的应变片编号 C-PET-300-2-a 37.2 1.79 3.38 SG1 C-PET-300-2-b 39.2 2.28 3.86 SG5 C-PET-300-3-a
49.6
3.51
4.16
SG1C-PET-300-3-b 50.4 3.41 4.24 SG4 C-PET-400-2-a 35.9 1.67 3.38 SG1 C-PET-400-2-b 36.2 1.75 3.23 SG2 C-PET-400-4-a 45.2 2.19 3.28 SG5 C-PET-400-4-b 45.0 2.24 3.36 SG1
下载: 导出CSV
表 3 方柱主要试验结果
Table 3. Key results of square column tests
试件编号 fcu ′ /MPa εcu/% εh,c/% εh,s/% 最大环向应变对应的应变片编号 S-PEN-300-2-a 37.6 2.34 1.46 2.19 SG9 S-PEN-300-2-b 38.4 2.28 1.75 2.34 SG1 S-PEN-300-3-a 54.8 3.14 1.77 2.84 SG1 S-PEN-300-3-b 53.3 3.42 1.37 2.73 SG1 S-PEN-400-2-a 35.5 1.66 1.60 2.01 SG9 S-PEN-400-2-b 35.5 1.79 2.40 2.38 SG5 S-PEN-400-4-a 47.9 2.64 1.50 2.43 SG9 S-PEN-400-4-b 49.0 2.39 0.90 2.18 SG1
下载: 导出CSV
-
[1] 蔡静, 2015. 大尺寸CFRP约束混凝土方柱的轴心抗压试验研究. 湖南大学硕士论文.Cai J, 2015. Experimental research on large-scale square concrete columns confined with wrapped CFRP under axial compressive. Hunan University. (in Chinese) [2] 邓宗才, 顾佳培, 2019. FRP管约束活性粉末混凝土方柱抗震性能研究. 震灾防御技术, 14(4): 769—780 doi: 10.11899/zzfy20190408Deng Z. C. , Gu J. P. , 2019. Research on seismic performance of reactive powder concrete square columns confined with FRP tubes. Technology for Earthquake Disaster Prevention, 14(4): 769—780. (in Chinese) doi: 10.11899/zzfy20190408 [3] 龙跃凌, 戴建国, 2010. 新型大断裂应变FRP约束混凝土圆柱的轴压性能. 混凝土, 07: 44-47Long Y L, Dai J G, 2010. Behavior of circular concrete columns confined by new-typed large rupture strain FRP under axial compression. Concrete, 07: 44-47. (in Chinese) [4] ASTM, 2002. Standard test method for static modulus of elasticity and poission’s ratio of concrete in compression ASTM C469. American Society for Testing and Materials. [5] ASTM, 2008. D3039/D3039M. Standard test method for tensile properties of polymer matrix composite materials, American Society for Testing and Materials. [6] Bai Y L, Dai J G, Mohammadi M, Lin G, Mei S J, 2019. Stiffness-based design-oriented compressive stress-strain model for large-rupture-strain (LRS) FRP-confined concrete. Composites Structures, 223: 110953. doi: 10.1016/j.compstruct.2019.110953 [7] Dai J G, Bai Y L, Teng J G, 2011. Behavior and modeling of concrete confined with FRP composites of large deformability[J]. Journal of Composites for Construction, 15(6): 963-973. doi: 10.1061/(ASCE)CC.1943-5614.0000230 [8] Han Q, Yuan W Y, Bai Y L, Du X L, 2020. Compressive behavior of large rupture strain (LRS) FRP-confined square concrete columns: experimental study and model evaluation. Materials and Structures, 53: 59. doi: 10.1617/s11527-020-01495-8 [9] Han Q, Yuan W Y, Ozbakkaloglu T, and Bai Y L, 2020. Compressive behavior for recycled aggregate concrete confined with recycled polyethylene naphthalate composites. Constr. Build. Mater, 261: 120498. doi: 10.1016/j.conbuildmat.2020.120498 [10] Hollaway L C, Teng J G, 2008. Strengthening and rehabilitation of civil infrastructures using fibre- reinforced polymer (FRP) composites. Cambridge, UK: Woodhead Publishing. [11] Ozbakkaloglu T, Lim J C, Vincent T, 2013. FRP-confined concrete in circular sections: Review and assessment of stress-strain models. Engineering Structures, 49: 1068-1088. doi: 10.1016/j.engstruct.2012.06.010 [12] Pimanmas A, Saleem S, 2019. Evaluation of existing stress-strain models and modeling of PET FRP-confined concrete. J Mater Civ Eng, 31(12): 04019303. doi: 10.1061/(ASCE)MT.1943-5533.0002941 [13] Popovics S, 1973. A numerical approach to the complete stress-strain curve of concrete. Cement and concrete research, 3(5), 583-599. doi: 10.1016/0008-8846(73)90096-3 [14] Saleem S, Hussain Q, Pimanmas A, 2016. Compressive Behavior of PET FRP-Confined Circular, Square, and Rectangular Concrete Columns. Journal of Composites for Construction, 21(3): 04016097. [15] Teng J G, Chen J F, Smith S T, et al. FRP-strengthened RC structures. John Wiley & Sons, Ltd; 2002. [16] Wang L M, Wu Y F, 2008. Effect of corner radius on the performance of CFRP confined square concrete columns: Test. Engineering Structures, 30(2): 493-505. doi: 10.1016/j.engstruct.2007.04.016 [17] Xiao Y, 2009. Applications of FRP composites in concrete columns. Advance in Structural Enginerring, 7(4), 335-343. [18] Zeng J J, Lin G, Teng J G, Li LJ, 2018. Behavior of large-scale FRP-confined rectangular RC columns under axial compression. Engineering Structures, (174): 629-645. -
下载:
点击查看大图
计量
- 文章访问数: 271
- HTML全文浏览量: 66
- PDF下载量: 6
- 被引次数: 0
