An Approach and Experiments for Human Respiratory Signal Recognition based on UWB Radar and Support Vector Machine
-
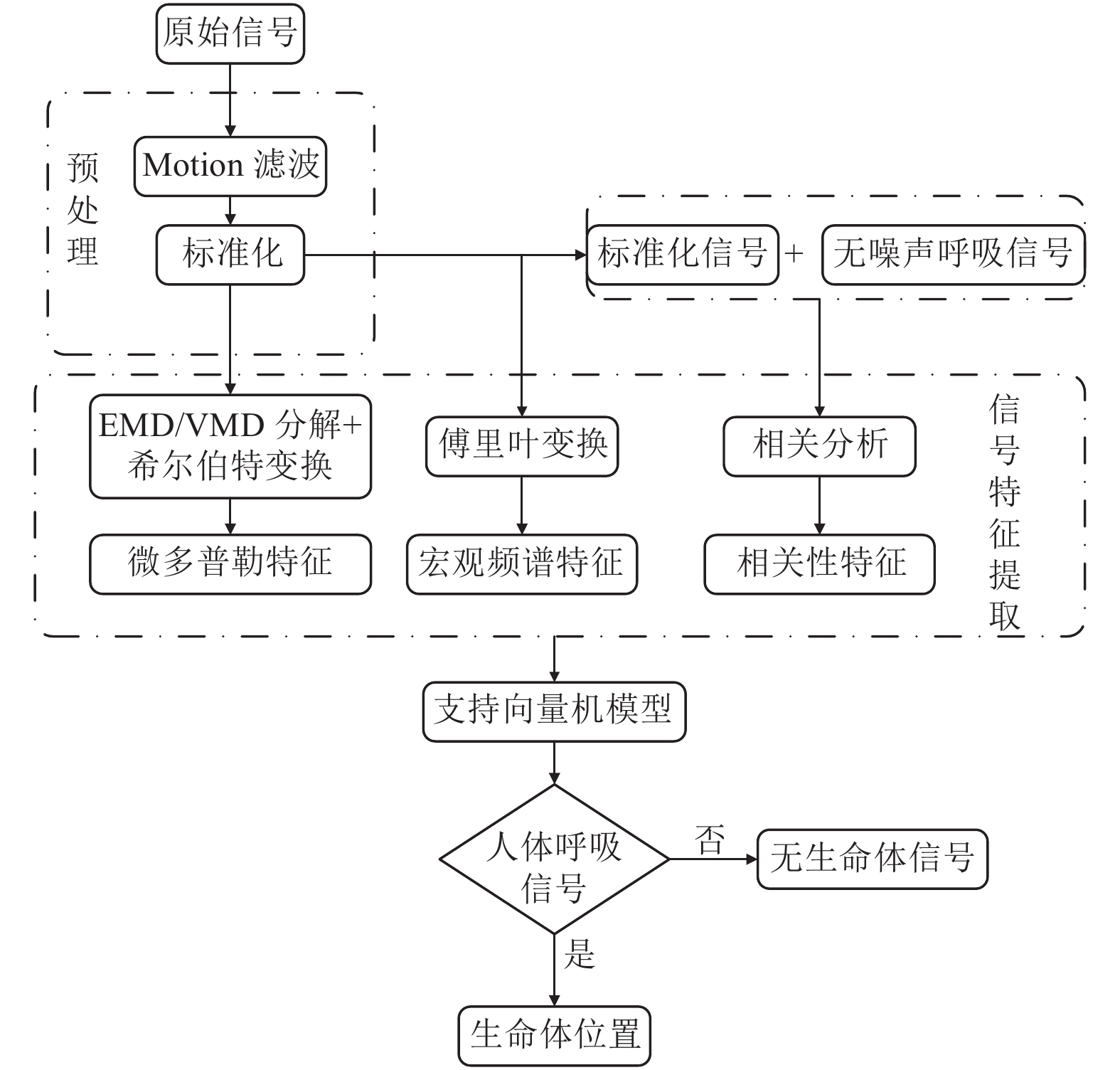
摘要: 与常规雷达相比，超宽带雷达具有距离分辨力高、近距离盲区小、穿透性强、目标识别率高等特点，已被广泛应用于灾后搜寻、救援工作中，以对受困生命体征目标进行生命探测。为实现使用超宽带雷达对受困生命体征目标的识别定位，本研究提出基于信号多特征提取技术及支持向量机模型的人体呼吸信号识别方法。首先，使用经验模态分解、变分模态分解及希尔伯特变换提取雷达探测信号的微多普勒特征，使用傅里叶变换提取宏观频谱特征，使用相关分析获取相关性特征；然后，以提取的信号特征为输入，使用支持向量机模型对信号进行分类，进而对人体呼吸信号进行识别，对人体位置进行定位。不同障碍物场景下的试验结果表明，本方法可有效识别砖墙、建筑楼板等遮挡物下的受困生命体征目标，并提供其位置信息。Abstract: Compared with conventional radar, the ultra-wideband (UWB) radar has the advantages of high distance resolution, small blind spot at close range, strong penetration, and high target recognition rate. Therefore, it has been widely used in post-disaster Radar-based Life Detecting System. In order to identify and locate the trapped person using UWB radar, a method based on signal multi-feature extraction and support vector machine model for human respiratory signal recognition is proposed in this paper. Firstly, we use empirical mode decomposition, variational mode decomposition, and Hilbert transformation to extract the micro-Doppler characteristics of echo signals use Fourier transformation to extract the spectrum characteristics and use correlation analysis to obtain the correlation characteristics. Then, the signals are classified by a support vector machine model based on these signal features. As a result, the respiratory signal can be identified and the position of the human body can be located. The experimental results obtained from different scenes show that the proposed method can effectively identify the human body which is shielded by brick walls and floor slabs, and the location of the human body can be determined at the same time.
-
Key words:
- Ultra-broadband radar /
- Life detection /
- Signal processing /
- Support vector machine
-
引言
龙门山断裂带位于青藏高原东缘，作为青藏高原向东扩展的边界，其地势险峻，自然灾害频发，一直是国内外研究的热点区域。2008年5月12日和2013年4月20日，在龙门山构造带上发生了汶川MS 8.0和芦山MS 7.0大地震，进一步说明该区域构造活动极为强烈。汶川地震发震断裂为北川-映秀断裂和灌县-江油断裂，分别产生了约240km和72km的地表破裂带。地震前后，各学者对龙门山地区都进行了一定的研究（李传友等，2004；李勇等，2006；周荣军等，2006；Densmore等，2007；刘静等，2008；徐锡伟等，2008），基本认为北川-映秀断裂是逆冲为主兼具走滑的断裂，具有明显分段性；然而区域内人为因素和气候对地形改造迅速，地貌标志保存困难且植被茂密，影响滑动位错和地层年代的定量观测，造成龙门山断裂带运动学特征定量研究的不足。构造活动对区域地貌演化研究具有很大的影响，地貌参数值对几千年至几十万年尺度的构造活动有指示作用（Hack，1973；Kirby等，2012），运用高精度数字高程模型（DEM）与GIS等技术，通过对地貌参数的定量研究，可以获取区域构造活动的信息（何祥丽等，2014；常直杨，2015）。
随着GIS技术的不断发展和DEM数据的获取，国内外学者利用各种地貌参数分析构造活动，这些参数包括了坡度、地形起伏度、河长坡降指数、Hack剖面、流域对称度以及面积高程积分等，定量化的地貌参数可以多维度、全方位地描述与分析构造地貌，并获取构造活动的多层次信息（张会平等，2006a；常直杨，2015）。坡度与地形起伏度是传统描述地貌形态的参数。面积高程积分反映了流域盆地的地貌演化过程，其对构造活动的影响十分敏感。
本研究以北川-映秀断裂及邻区流域为研究对象，区域内河流发育，河流地貌对构造活动的响应敏感，利用ASTER GDEM V2数据，空间分辨率30m，基于ArcMap 10.1水文分析模块对该地区坡度、地形起伏度及面积高程积分进行提取，进而定量研究区域的地貌特征，北川-映秀断裂沿走向运动学特征发生变化，本文依据地貌参数，定量化了新构造活动程度，讨论了北川-映秀断裂走向上及其两侧的参数变化特征、地层岩性和水系的变化，探讨了其与构造活动的关系。
1. 区域概况
龙门山构造带由后山断裂（汶川-茂县）、中央断裂（映秀-北川）、前山断裂（灌县-江油）和山前隐伏断裂等4条逆冲断裂及其所夹持的逆冲楔体组成，其形成过程表现为自后山断裂向东南方向发展的前展式逆冲，受到北川附近的NW向走滑断层及都江堰附近的NW向三江口断裂的切割，龙门山构造带可分为北段、中段和南段。研究区域（图 1）位于龙门山的中北段地区，断裂带沿线分布有新生代沉积物，断裂横穿湔江、沱江、凯江及涪江流域支流安昌河、通口河以及平通河，穿过断裂水系发生大型右旋位错，水系形态受北川-映秀断裂逆冲走滑作用明显。
图 1 龙门山中北段区域构造及地质图Figure 1. Simplified geological map of the central and northern sections of Longmenshan龙门山构造带表现为逆冲推覆模式，逆冲断层下盘产生新的逆冲活动并不断向前陆方向扩展（林茂炳等，1991），区域内自北西—南东方向地层出露由老变新，中段出露大面积元古代岩浆岩，北段出露大面积志留系板岩、凝灰岩，泥盆系泥岩、灰岩、白云岩，向前陆方向，三叠系砂岩、碳酸盐岩和侏罗系砂岩沿断裂走向呈带状展布。北川-映秀断裂处于龙门山中央断裂中段，其南段展布于彭灌杂岩的东南缘，断层两侧地层岩性差异明显，其西侧主要出露彭灌杂岩、下震旦统火山岩，发育一系列飞来峰构造；其东侧为志留系泥质岩和碳酸盐岩建造，泥盆系碳酸盐岩与碎屑岩互层以及上三叠统的须家河组，西侧地层较东侧地层强硬（姚琪等，2012）；北川以北段展布于志留系与泥盆系地层中，表现为变质的下古生界逆冲于未变质的古生界之上（陈社发等，1994）。地层单元上，北川-映秀断裂北西侧与南东侧地层存在明显差异。
2. 数据方法
本研究利用ASTER GDEM V2数据（水平分辨率为30m），流域水系和地貌参数的提取分析均在ArcGIS 10.1平台下完成，地理坐标系统为WGS84。
2.1 坡度与地形起伏度
坡度与地形起伏度是传统的宏观地形分析方法（Scherler等，2014）。坡度指地面的倾斜程度，反应地表物质剥蚀和堆积的发展，能够指示地貌发育阶段及程度。坡度具有一定的临界值，约为30°，超过这个值，则不再随侵蚀速率等因素的增大而增大（Schmidt等，1995）。使用ArcGIS 10.1空间分析中的坡度分析自动生成研究区域坡度图。
地形起伏度为一定区域内最高点和最低点高程之差，它能够反映地面侵蚀程度（Zhang等，2011），间接反映了构造活动的强弱。一般使用公式：
$$ R=H\text{max}-H\text{min} $$ (1) 其中，R表示地形起伏度，Hmax和Hmin分别表示分析窗口内的最大高程值和最小高程值。利用ArcGIS10.1的空间分析模块中的焦点统计工具，采用分析窗口4.28km2（23×23）统计出最大高程值和最小高程值（南希等，2017），再使用栅格计算器计算地形起伏度。
2.2 条带状剖面
条带状剖面可统计一定区域范围内地形高程的最大值、最小值和平均值，用以半定量、定量分析研究区域内山峰、河谷的高程变化以及侵蚀程度（张会平等，2006b；梁明剑等，2014；苏琦等，2016）。相对于线状剖面，条带剖面则可以较为准确地表征地球表面本身具有的面状地形起伏特征。为了比较横向地形变化，利用ArcGIS 10.1沿断裂走向，在3个不同区域沿约130°方向提取5km宽条带状剖面，将高程数据导入Origin 8.1成图。
2.3 面积-高程积分（HI）
面积高程积分是Strahler（1952）提出的定量描述流域内高程的分布、表征未被侵蚀部分体积的1个参数，可以指示区域构造活动差异（Alipoor等，2011；Gao等，2013）。
在1个流域盆地演化的不同阶段，其地貌形态会发生较大的变化。在演化早期阶段，河流侵蚀能力强，地貌以深切河谷为主，流域内高海拔区域较大；随着河流演化进入后期，U形谷发育，流域内低海拔区域的面积逐渐增大。面积-高程积分曲线就是1个表征流域盆地内某一特定高程值之上的面积占全流域面积的比例函数（常直杨等，2014）。
在1个流域盆地内，最高海拔为Hmax，最低海拔为Hmin（一般为河流出口处的海拔值），取H=Hmax - Hmin，h为0—H之间的任意值，a为H—h之间的面积，A为全流域面积（图 2（a））。令x=a/A、y=h/H作图，可得到面积高程积分曲线（图 2（b））。
图 2 面积-高程积分曲线示意图（Singh等，2008）Figure 2. Schematic diagram of area-elevation integral curve (fromh Singh et. al., 2008)图 2（b）中，灰色部分表示流域内未被侵蚀部分的比例，即面积高程积分（HI），是1个表征侵蚀程度的值。其计算公式为：
$$ HI=\int_{0}^{1}{\left(\frac{h}{H} \right)\text{d}\left(\frac{a}{A} \right)}=\int_{0}^{1}{y\text{d}x} $$ (2) 根据 Pike等（1971）的研究，可以简化为：
$$ HI=\frac{H\text{max}-H\text{mean}}{H\text{max}-H\text{min}} $$ (3) 其中，Hmax为流域高程最高值，Hmin为最小值，Hmean为平均值。
由图 2（b）可知，流域积分曲线为上凸型时，其积分值高，流域积分曲线为下凹型时，积分值低。高积分值意味着流域内大部分物质体积未被侵蚀，地形演化时间短，地貌处于幼年期。积分曲线呈上凸型与流域内岩性、构造活动和降雨剥蚀等因素有关。地形演化时间越长，地貌处于老年期，积分曲线呈下凹型。介于凸型及凹型之间，呈凹凸型的则为中年期。依据Strahler（1952）对HI的划分，可分为3级：①幼年期：HI＞0.5；②中年期：0.4≤HI≤0.5；③老年期：HI＜0.4。面积高程积分对构造活动的响应非常敏感，可很好地判断流域盆地内地貌特征及其构造活动响应。
3. 结果分析
面积高程积分的提取在ArcGIS 10.1水文分析模块进行，为了细致分析流域地貌发育特征对于构造活动的差异响应，结合龙门山中北段流域特征，选取阈值7000提取河网，获得1381个亚流域盆地，分别计算各亚流域的HI值，为了更好地反映HI的空间分布特征，对HI值进行克里金插值分析，获取等值分区图。
3.1 宏观地貌分析
龙门山中北段沿断裂横跨断裂两侧，坡度及地形起伏度表现出明显的西高东低的特征。地貌参数沿断裂走向呈现中段高、北段低的特征，且坡度与地形起伏度分布特征具有一致性。龙门山中段坡度与地形起伏度极大，沿北川-映秀断裂两侧参数值差异明显，北西侧坡度达到80°，大部分地区坡度处在临界值之上，跨过断裂坡度值骤减，普遍在40°左右。地形起伏度有相似的递变趋势，北川-映秀断裂北西侧局部地形起伏达到5000m，跨断裂后骤减。龙门山北段坡度与地形起伏值相比中段减少，跨断裂自西向东两侧参数值仍有明显的骤减，大部分地区坡度值处在临界值30°之下，地形起伏在2000—3000m之间，局部达到4000m（图 3）。
图 3 龙门山中北段坡度（a）与地形起伏度分布图（b）Figure 3. Distribution of slope and topographic relief of the middle and north sections of Longmenshan3条条带状剖面反映了沿断裂走向上地形的变化（图 4），图中（a）、（b）、（c）分别代表图 1中AA′、BB′、CC′条带状剖面。龙门山中段平均海拔处于3000m左右，在北川附近平均海拔为2000m左右，再往北段降低至1500m；垂直断裂方向，AA′剖面显示龙门山中段地形起伏相对较大，3条剖面显示地形落差最大处在北川-映秀断裂两侧。
3.2 流域特征分析
龙门山中北段发育多条大型水系，断裂横穿湔江、沱江、凯江及涪江流域支流安昌河、通口河以及平通河，北段水系右旋位错明显（贾营营等，2010）。在流域盆地基础上提取亚流域盆地获取HI值，由图 5可见，HI值呈规律性复杂分布。HI高值（大于0.5）基本出现在断层上盘，流域发育程度低，处于幼年期；前山断裂的下盘HI值（小于0.4）较低，流域发育成熟，处于老年期。龙门山中段HI高值出现在逆冲断裂的上盘且集中分布，在茂汶-安县区段内，HI高值分布靠近前缘且较分散，北段断裂两侧的HI值差异较中段小，沿断裂方向，局部的河谷地区出现HI低值区，灌县-江油断裂上盘出现HI高值区。
图 5 龙门山中北段流域分布图和HI值分布Figure 5. The HI value distribution of the middle and north sections of Longmenshan4. 讨论
地表地形地貌特征主要受控于构造、气候以及岩性等综合性因素。近年来大量的研究认为，在构造非常活跃的地区，断层作用控制的山体隆升是控制区域地貌生长的主要因素（Kirby等，2003；Zhang等，2006；Kirby等，2012）。而在地貌演化中，前人的研究也指出河流地貌参数与气候变化和基岩的抗侵蚀能力有关（赵洪壮等，2010；邵崇建等，2015）。本研究结合龙门山中北段宏观地貌特征与地貌参数，探讨区域地形地貌主控因素及构造活动差异性。
4.1 地貌参数影响因素分析
气候是地貌演化过程中的重要因素，其直接表现形式之一为降水，降水通过影响水系流量进而影响河流对于河道的侵蚀堆积作用，从而控制区域地形的演化（Hartshorn等，2002）。在年均降水量约400mm/a的祁连山地区，前人对降水量与亚流域盆地HI指数做了相关性分析，认为降水量对地貌指数无明显控制（苏琦等, 2016, 2017）。同时HI值具有空间依赖性（郑光佑，2002），在年降水量更高的龙门山地区，邵崇建等（2015）将集水盆地依据高程划分山地、丘陵和平原3种类型，根据同类型地形下的降水与HI指数对比，得出降水不是影响地貌指数的主要因素。
本文利用前人插值获取的全球高分辨降水数据（Hijmans等，2005），获得龙门山地区年平均降水分布图（图 6）。年平均降水沿东南到西北方向递减，900mm/a降水等值线基本与龙门山断裂带平行，研究区域内北川-映秀断裂两侧年均降水量普遍在850—950mm/a之间，局部存在地形雨造成的降水高值区，但是顺降水等值线方向研究区域HI指数变化极大。龙门山地区降水量受地形控制，形成季节性强降雨带，研究区域属于山地与丘陵地形，受到地形雨影响严重（邵崇建等，2015），在不考虑构造活动的前提下，流域内年降水量越多，内部侵蚀越严重，面积-高程积分越小。由图 6可知，研究区域内北川-映秀断裂两侧降水量普遍在800—900mm/a之间，变化不大，然而研究区域所在的山前丘陵地区与山地地区HI指数差异很大。据此认为区域年降水量对地貌指数并无明显控制作用。
图 6 龙门山地区年平均降水分布Figure 6. Annual average precipitation distribution in the Longmenshan area岩性也是控制地貌演化的1个因素。不同岩性的抗侵蚀能力不同，坚硬岩抗侵蚀能力强，风化程度小，易于保留原地地貌，软弱岩抗侵蚀能力弱，风化程度大，易被塑造成新的地貌形态。前人根据岩性及其形成时代对比讨论地形发育情况，认为岩性不是影响HI值的主要因素（苏琦等，2017）。陈彦杰等（2005）以不同流域阈值提取集水盆地地层和活动构造做叠图分析时，发现阈值小于1000m2，HI值受岩性与构造影响；阈值大于2000m2，HI值主要受构造活动影响。在龙门山地区地貌参数研究中，梁欧博等（2018）将岩石依据坚硬程度分为坚硬岩、较硬岩、较软岩、软岩和极软岩5个等级，通过同类型岩性下地貌指数的对比得出岩性并非影响地貌参数的主控因素。
研究区域除龙门山中段出露前寒武系火成岩外，区域内发育志留系碳酸盐岩和砂岩，处于较硬岩与较软岩之间，且跨北川-映秀断裂岩性界限分明。然而在北川-映秀断裂北川和南坝的局部河谷，不同的岩性有相似的HI值。因此岩性与气候并非研究区域内地貌特征的主控因素。
印-亚板块碰撞塑造了青藏高原及其周缘的地质地貌格局，沿龙门山断裂系发生了一系列挤压与右旋变形，形成了其东缘快速变化的地形特征（Burchiel等，2008）。在龙门山地区的地貌学研究中，Kirby等（2003，2008）通过排除岩性、沉积通量及地形雨的影响，认为区域内河道陡峭指数梯度变化反映了构造抬升活动的差异。前人在祁连山及龙门山地区对流域盆地的地貌演化研究中，通过影响因素的相干性分析，也认为HI值的变化反映了构造隆升的差异（梁明剑等, 2013, 2014；李奋生等，2015；苏琦等，2017）。根据上述对岩性及降水量的分析，推测构造活动是区域地形地貌演化的主控因素。
4.2 龙门山中北段构造活动差异性
认为龙门山断裂带第四纪构造活动存在差异是1个普遍的认识。龙门山南段表现为强烈的逆冲活动，南段前陆区发育广阔褶皱构造带，延续至中段龙泉山一带并向北逐渐消亡；中北段构造变形主要发生在山区冲断带，而中段成为构造活动的转换区间，整体上呈现逆冲兼走滑的性质（杨晓平等，1999；马保起等，2005；姜大伟等，2018）。在龙门山地区活动构造研究中，马保起等（2005）根据岷江阶地的变形估算了汶川-茂汶断裂、北川-映秀断裂和灌县-江油断裂晚第四纪平均垂直滑动速率为0.5mm/a、0.3—0.6mm/a和0.2mm/a。前人对整个东缘的断裂地貌进行了研究，在茂汶和映秀两地得到汶川-茂汶断裂和北川-映秀断裂平均垂直滑动速率约为0.84mm/a和0.54mm/a，平均水平滑动速率约为1mm/a，灌县-江油断裂则表现出纯逆冲特征，结合对北段青川断裂走滑运动的研究，得出北段的右旋走滑位错量大于中段，且承担龙门山断裂带大部分右旋走滑分量（马保起等，2005；周荣军等，2006；李勇等，2006；Densmore等，2007；樊春等，2008；徐锡伟等，2008）。
坡度与地形起伏度是地表形态的直观反映，研究区域地形起伏与坡度向盆地内梯度递减，沿断裂走向中段比北段地形起伏大，坡度大，表明了龙门山中段构造抬升活动强烈；北段的地貌参数值均变小且跨断裂没有快速变化，表明了构造抬升活动减弱，这种沿断裂走向与垂直走向上的地貌参数差异与断裂的构造性质及滑动速率值的变化呈现一致性的特点。
龙门山地区大量的低温热年代学研究反映了区域剥蚀速率的差异，根据动态均衡原理，假定地形演化处在1个稳定模式下（England等，1990；Willett等，2002），山地基岩构造抬升速率与剥蚀速率相等。前人在龙门山中段的低温热年代学研究中得到剥蚀速率的空间展布模式，从四川盆地西缘到北川-映秀与汶川-茂汶断裂之间的区域，剥蚀速率从小于0.1km/m.y增长到大于1km/m.y，而后再向高原内部递减（Tian等，2013）。面积-高程积分对区域应力挤压造成的构造隆升反映敏感（郑光佑，2002），龙门山中段逆冲推覆构造形成的构造推覆体表现异常高的HI值，向盆地方向，HI值迅速降低；再向北东方向，断裂上盘HI值相对降低并且更集中在断裂附近，茂汶-北川一带HI值呈过渡状态，HI高值区靠近断裂且向北减弱，前山断裂由于纯逆冲性质，其上盘呈现明显HI高值，北川-南坝一带HI值相对减小，局部的河谷盆地呈现HI低值区。HI高值区表明了构造隆升的强烈，区域内HI值的分布模式也与剥蚀速率的变化呈现一致性。 Tan等（2019）在对龙门山中北段的低温热年代的研究中得到岷山地区剥蚀速率约0.9km/m.y，与龙门山中南段剥蚀速率进行对比，提出了高原东缘最大剥蚀速率带，认为该带是高原向东逆冲活动的边界，结合前人在东缘的构造地貌研究以及上述结果，反映了地貌参数与剥蚀速率和构造抬升变化的一致性，同时龙门山北段构造活动的变化以及所引起的地形地貌因素的响应，表明北段不再是高原东向扩展的边界（Zhang等，2011）。
5. 结论
本文通过ASTER GDEM V2数据系统提取了龙门山中北段地区坡度、地形起伏度、条带状剖面和流域水系及其面积-高程积分等地貌参数，并分析其地质意义，研究结论如下：
（1）构造活动是龙门山中北段地区地貌特征的主控因素，地貌地形特点反映了龙门山断裂带的活动特征。
（2）坡度、地形起伏度和条带状剖面等地貌参数反映了青藏高原东缘龙门山断裂带的逆冲演化过程，地貌参数值呈梯度分布，走向上存在差异；HI值分布图反应构造抬升活动的演化，由龙门山中段的逆冲为主转换为北段逆冲兼走滑的特征，反应龙门山中北段的构造差异性。
致谢: 感谢姜大伟老师在论文写作及修改过程中给予的讨论与意见。 -
图 4 PluseOn440单基站雷达传感器模块及平板天线
Figure 4. P440 monostatic radar module and panel antenna
图 6 无障碍物场景下探测距离为25 m时的识别结果
Figure 6. Detection results of the experiment without obstacles when the human body is 25 m away
图 8 砖墙隔挡场景下探测距离7.24 m时识别结果
Figure 8. Detection results of the experiment with the block of a brick wall when the human body is 7.24 m away
图 10 2层楼板隔挡场景下识别结果
Figure 10. Detection results of the experiment with the block of 2 floorslabs
表 1 训练样本探测环境
Table 1. Scenarios for human detection
障碍物类别 障碍物厚度/cm 探测距离/m 无障碍 — 1、2、3、5、10、15、20 泡沫板 3 1、2、3、5、10、15、20 玻璃 1 1、2、3、5、10、15、20 木门 5 1、2、3、5、10、15、20 砖墙 28 1、2、3、5、10、15、20 
下载: 导出CSV
表 2 平板天线主要技术参数
Table 2. Technical parameters of panel antenna
参数名称 参数值 尺寸/mm 150×150×18 覆盖频段/GHz 3.25～3.75 3 dB角 30° 增益/dB 15
下载: 导出CSV
表 3 无障碍物场景下分类准确度
Table 3. Accuracy of classification in experiments without obstacle
探测距离/m 准确度/% ±10 cm误差 ±30 cm误差 10 87 88 15 82 83 20 89 91 25 97 98 30 95 96
下载: 导出CSV
表 4 砖墙隔挡场景下分类准确度
Table 4. Accuracy of classification in the experiments with the block of brick wall
探测距离/m 障碍物厚度/cm 准确度/% ±10 cm误差 ±30 cm误差 0.24 24 72 72 1.24 24 81 81 3.24 24 72 73 5.24 24 85 86 7.24 24 83 81
下载: 导出CSV
表 5 楼板隔挡场景下探测工况
Table 5. Scenarios for human detection with the block of floorslabs
障碍物
层数障碍物
总厚度/m探测
距离/m探测
时长/min被探测
人员1 0.1 0.50 3 男性1 2 0.2 1.53 3 男性1 1 0.1 0.50 5 男性1 1 0.1 0.50 5 男性2 1 0.1 0.50 5 男性3 2 0.2 1.53 5 男性1 2 0.2 1.53 5 男性2 2 0.2 1.53 5 男性3 2 0.2 1.53 5 男性1
下载: 导出CSV
表 6 楼板隔挡场景下分类准确度
Table 6. Accuracy of classification in the experiments with the block of floorslabs
楼板层数 障碍物厚度/m 探测距离/m 准确度/% ±10 cm误差 ±30 cm误差 1 0.1 0.50 75 78 2 0.2 1.53 73 77
下载: 导出CSV
-
[1] 崔学荣, 杨雷, 李娟等, 2021. 复杂场景下基于UWB雷达的呼吸特征检测算法. 电子测量技术, 44(4): 70—74Cui X. R. , Yang L. , Li J. , et al. , 2021. Respiratory feature detection algorithm based on UWB radar in complex scene. Electronic Measurement Technology, 44(4): 70—74. (in Chinese) [2] 蒋留兵, 魏光萌, 车俐, 2019. 基于卷积神经网络的雷达人体动作识别方法. 计算机应用与软件, 36(11): 168—174, 234 doi: 10.3969/j.issn.1000-386x.2019.11.028Jiang L. B. , Wei G. M. , Che L. , 2019. Human motion recognition method by radar based on CNN. Computer Applications and Software, 36(11): 168—174, 234. (in Chinese) doi: 10.3969/j.issn.1000-386x.2019.11.028 [3] 孙公德, 郭勇, 沈建等, 2017. 分布式超宽带雷达地震被困人员协同探测技术. 震灾防御技术, 12(4): 966—977 doi: 10.11899/zzfy20170424Sun G. D. , Guo Y. , Shen J. , et al. , 2017. Collaborative detection technology for detecting trapped personnel by distributed UWB radar earthquake. Technology for Earthquake Disaster Prevention, 12(4): 966—977. (in Chinese) doi: 10.11899/zzfy20170424 [4] 王亚夫, 梁步阁, 杨德贵等, 2021. 基于CNN的超宽带穿墙雷达静目标数量识别技术. 传感器与微系统, 40(4): 19—22Wang Y. F. , Liang B. G. , Yang D. G. et al. , 2021. Quantity identifying technology for static target of ultra-wideband through-wall radar based on CNN. Transducer and Microsystem Technologies, 40(4): 19—22. (in Chinese) [5] Cortes C. , Vapnik V. , 1995. Support-vector networks. Machine Learning, 20(3): 273—297. [6] Cristianini N. , Shawe-Taylor J. , 2000. An introduction to support vector machines and other kernel-based learning methods. Cambridge: Cambridge University Press. [7] Dragomiretskiy K. , Zosso D. , 2014. Variational mode decomposition. IEEE Transactions on Signal Processing, 62(3): 531—544. doi: 10.1109/TSP.2013.2288675 [8] Gibbs J. E. , 1970. Transmission of information by orthogonal functions. Electronics & Power, 16(4): 138. [9] Harmuth H. , 1969a-09-30. System for the transmission of information by carrier waves over a single conductor: US, 3470324DA. [10] Harmuth H. F. , 1969b. Applications of Walsh functions in communications. IEEE Spectrum, 6(11): 82—91. doi: 10.1109/MSPEC.1969.5214175 [11] Huang N. E. , Shen Z. , Long S. R. , et al. , 1998. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 454(1998): 903—995. [12] Li C. Z. , Cummings J. , Lam J. , et al. , 2009. Radar remote monitoring of vital signs. IEEE Microwave Magazine, 10(1): 47—56. doi: 10.1109/MMM.2008.930675 [13] Li J. , Liu L. B. , Zeng Z. F. , et al. , 2014. Advanced signal processing for vital sign extraction with applications in UWB radar detection of trapped victims in complex environments. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7(3): 783—791. doi: 10.1109/JSTARS.2013.2259801 [14] Luz E. J. D. S. , Schwartz W. R. , Cámara-Chávez G. , et al. , 2016. ECG-based heartbeat classification for arrhythmia detection: a survey. Computer Methods and Programs in Biomedicine, 127: 144—164. doi: 10.1016/j.cmpb.2015.12.008 [15] Ma Y. Y. , Wang P. F. , Huang W. Z. , et al. , 2021. A robust multi-feature based method for distinguishing between humans and pets to ensure signal source in vital signs monitoring using UWB radar. EURASIP Journal on Advances in Signal Processing, 2021(1): 27. doi: 10.1186/s13634-021-00738-2 [16] Ossberger G. , Buchegger T. , Schimback E. , et al. , 2004. Non-invasive respiratory movement detection and monitoring of hidden humans using ultra wideband pulse radar. In: 2004 International Workshop on Ultra Wideband Systems Joint with Conference on Ultra Wideband Systems and Technologies. Kyoto: IEEE, 395—399. [17] Platt J. C. , 1999. Fast training of support vector machines using sequential minimal optimization. In: Schölkopf B. , Burges C. J. C. , Smola A. J. , eds. , Advances in Kernel Methods: Support Vector Learning. Cambridge: MIT Press, 185—208. [18] Ren L. Y. , Wang H. F. , Naishadham K. , et al. , 2016. Phase-based methods for heart rate detection using UWB impulse Doppler radar. IEEE Transactions on Microwave Theory and Techniques, 64(10): 3319—3331. doi: 10.1109/TMTT.2016.2597824 [19] Scalise L. , Primiani V. M. , Russo P. , et al. , 2013. Wireless sensing for the respiratory activity of human beings: measurements and wide-band numerical analysis. International Journal of Antennas and Propagation, 2013: 396459. [20] Tariq A. , Ghafouri-Shiraz H. , 2011. Vital signs detection using Doppler radar and continuous wavelet Transform. In: Proceedings of the 5th European Conference on Antennas and Propagation. Rome: IEEE, 285—288. [21] Withington P. , Fluhler H. , Nag S. , 2003. Enhancing homeland security with advanced UWB sensors. IEEE Microwave Magazine, 4(3): 51—58. doi: 10.1109/MMW.2003.1237477 [22] Wu S. Y. , Tan K. , Xia Z. H. , et al. , 2016. Improved human respiration detection method via ultra-wideband radar in through-wall or other similar conditions. IET Radar, Sonar & Navigation, 10(3): 468—476. [23] Yarovoy A. G. , Ligthart L. P. , Matuzas J. , et al. , 2006. UWB radar for human being detection. IEEE Aerospace and Electronic Systems Magazine, 21(11): 22—26. doi: 10.1109/MAES.2006.284354 -
下载:
点击查看大图
计量
- 文章访问数: 139
- HTML全文浏览量: 100
- PDF下载量: 10
- 被引次数: 0
