基于应变能耗储的钢筋混凝土框架结构地震损伤演化研究

苏佶智; 刘伯权; 宋猛; 马煜东; 黄娇

doi:10.11899/zzfy20210313

基于应变能耗储的钢筋混凝土框架结构地震损伤演化研究

doi: 10.11899/zzfy20210313

苏佶智^1,,
刘伯权^2, ,,
宋猛²,
马煜东²,
黄娇²

1.
国网河北省电力有限公司经济技术研究院, 石家庄 050000
2.
长安大学, 建筑工程学院, 西安 710000

基金项目: 国家自然科学基金项目(51578077)

详细信息

作者简介:
苏佶智，男，生于1989年。博士，工程师。主要从事建筑结构抗震减震研究。E-mail：sujizhi1989@163.com

通讯作者:
刘伯权，男，生于1956年。教授，博士生导师。主要从事建筑结构抗震减震研究。E-mail：bqliu@chd.edu.cn

计量
- 文章访问数: 112
- HTML全文浏览量: 44
- PDF下载量: 4
- 被引次数: 0
出版历程
- 收稿日期: 2021-02-22
- 刊出日期: 2021-09-30

Research on Seismic Damage Evolution of Reinforced Concrete Frame Structures Based on Strain-energy Consumption-storage Theory

1.
State Grid Hebei Economic and Technological Research Institute, Shijiazhuang 050000, China
2.
School of Civil Engineering, Chang’an University, Xi’an 710000, China

摘要

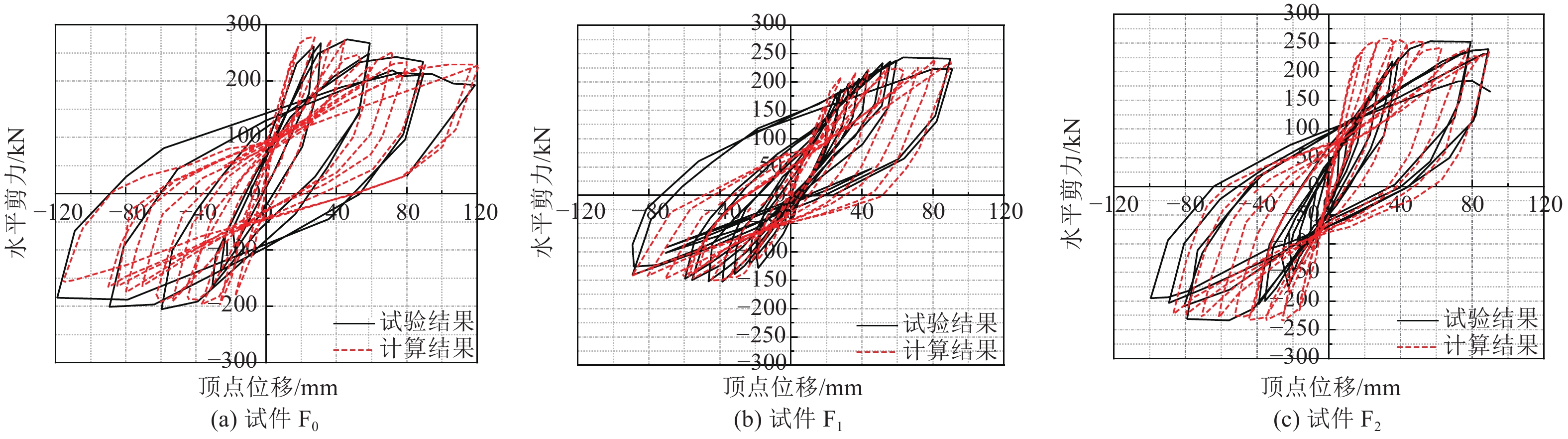
摘要: 结构地震损伤破坏，本质上是地震动输入能量超出结构或构件耗能能力所致。“能量”参数能够综合反映地震动强度、频谱特性以及强震持时对结构破坏的影响，本文基于能量耗散原理建立结构损伤模型，采用有限元软件ABAQUS对3榀单层单跨钢筋混凝土平面框架结构抗震性能进行数值模拟，通过损伤指数量化研究了地震作用下钢筋混凝土框架结构的损伤演化规律。研究表明：基于应变能耗储的结构损伤模型，能够合理有效地反映“位移首超破坏”与“累积损伤破坏”模式，且上、下界收敛；模拟分析得到的滞回曲线和骨架曲线与试验数据吻合较好，数值建模方法适用于以梁、柱构件为主的框架结构抗震性能分析；耗能构件框架梁能够对结构损伤破坏发展和抗震性能劣化起到一定延缓作用，承力构件框架柱的损伤加剧会加速结构抗震性能的劣化；加载幅值较小时，结构依靠混凝土裂缝闭合摩擦消耗能量，“位移首超破坏”所致损伤所占比例较大，随着位移幅值及循环次数的增加，“累积损伤破坏”所致损伤所占比例逐渐增大。
- 能量耗储 /
- 钢筋混凝土框架结构 /
- 损伤演化 /
- 损伤指数模型
Abstract: Structural seismic damage from the scientific facts that the seismic input energy the energy-dissipation capability of structures or components essentially, and the “Energy” parameters can reflect the comprehensive influence of seismic intensity, spectral characteristic and earthquake duration. In this article, a structural damage index model based on energy-consumption theory was established and a numerical simulation study on the seismic behavior of one-story, one-span reinforced concrete plane-frames was conducted with the finite element software ABAQUS. Meanwhile, the seismic damage evolusion rules of RC frame-structures were analysed by quantifying the damage degree. Results show that the structural damage model based on strain-energy consumption-storage theory could describe “first excursion damage” and “cumulative energy damage” effectively, and its upper-lower boundary was absolute convergence. The computational hysteresis-curves and skeleton-curves were consistent with experimental data, and numerical simulation method was applicable for the seismic performance analysis of frame structures mainly consisted with columns and beams. Frame-beams acting as energy-comsumption elements had a positive effects on slowing the structural damage development and seismic performance deterioration, in contrast, the increased damage of frame-columns would accelerate the degradation tendency. The structures consumed the seismic energy through the extension and friction of concrete cracks, therefore, the proportion of first-excursion-damage was larger at early loading stage; the proportion of cumulative-energy-damage gradually increased, along with the displacement amplitude and loading cycles rising.
- Energy dissipation /
- Reinforced concrete frame structure /
- Damage evolusion /
- Damage index model

HTML全文

图 1 基底剪力-顶点位移曲线

Figure 1. Base shear-top displacement curves

下载: 全尺寸图片幻灯片

图 2 结构损伤的划分

Figure 2. Division of the structural damage

下载: 全尺寸图片幻灯片

图 3 结构损伤的二折线简化

Figure 3. Structural damage simplification as two-fold line

下载: 全尺寸图片幻灯片

图 4 试件几何参数及截面配筋示意

Figure 4. Geometric parameters and sectional reinforcements of specimen

下载: 全尺寸图片幻灯片

图 5 纤维梁单元截面示意

Figure 5. Diagram of fiber unit section

下载: 全尺寸图片幻灯片

图 6 混凝土材料滞回本构模型

Figure 6. Hysteretic constitutive model of concrete

下载: 全尺寸图片幻灯片

图 7 钢筋材料滞回本构模型

Figure 7. Hysteretic constitutive model of steel

下载: 全尺寸图片幻灯片

图 8 试验滞回曲线与数值计算滞回曲线对比

Figure 8. Comparison between test hysteresis-curves and computational hysteresis-curves

下载: 全尺寸图片幻灯片

图 9 试验骨架曲线与数值计算骨架曲线对比

Figure 9. Comparison between test skeleton-curves and computational skeleton-curves

下载: 全尺寸图片幻灯片

图 10 试件损伤发展曲线

Figure 10. Damage development curves of test specimen

下载: 全尺寸图片幻灯片

图 11 试件F₀损伤破坏现象

Figure 11. Failure phenomena of specimen F₀

下载: 全尺寸图片幻灯片

图 12 试件F₁损伤破坏现象

Figure 12. Failure phenomena of specimen F₁

下载: 全尺寸图片幻灯片

图 13 试件F₂损伤破坏现象

Figure 13. Failure phenomena of specimen F₂

下载: 全尺寸图片幻灯片

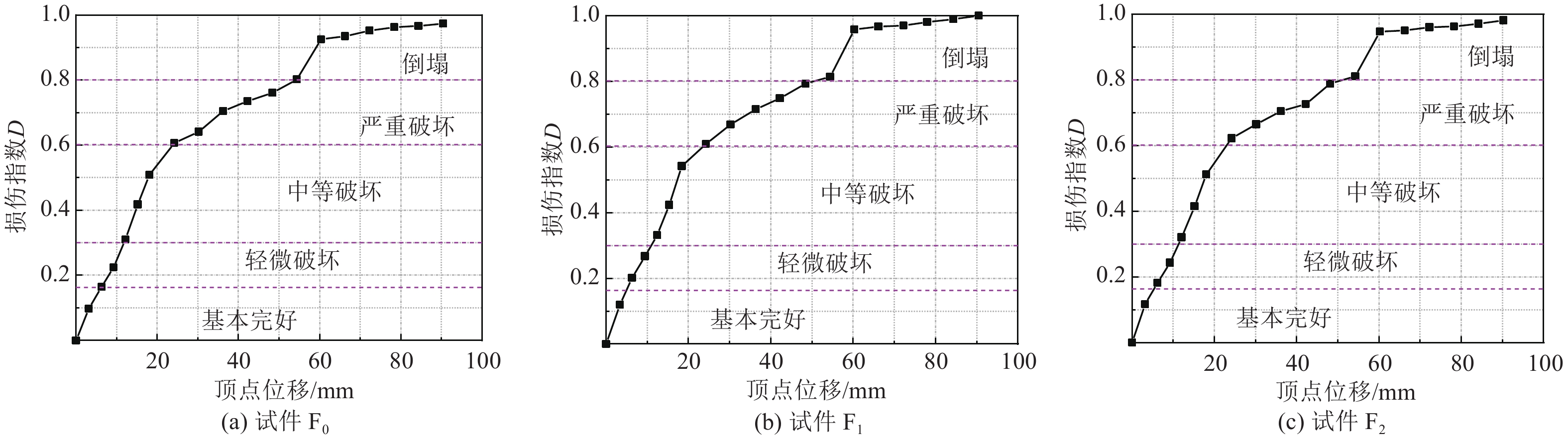
表 1 不同损伤状态对应的损伤指数范围

Table 1. Damage indices corresponding to individual levels

损伤等级	破坏现象描述	损伤指数
基本完好	承重构件完好，个别耗能构件轻微开裂	0.00～0.15
轻微破坏	个别承重构件轻微开裂，个别耗能构件明显破坏	0.15～0.30
中等破坏	多数承重构件轻微开裂、部分明显开裂，个别耗能构件严重破坏	0.30～0.60
严重破坏	多数承重、耗能构件严重破坏	0.60～0.80
倒塌	多数承重构件倒塌，耗能构件普遍破坏	0.80～1.00

下载: 导出CSV

表 2 平面框架各受力阶段的损伤指数

Table 2. Damage indices corresponding to individual loading phases

损伤等级	损伤情况	试件F₀		试件F₁		试件F₂
损伤等级	损伤情况	D_r	D_h	D_r	D_h	D_r	D_h
基本完好	指数	0.0866	0.0107	0.1025	0.0196	0.0982	0.0174
基本完好	比例/%	89	11	84	16	85	15
轻微破坏	指数	0.1789	0.0448	0.2092	0.0591	0.1991	0.0468
轻微破坏	比例/%	80	20	78	22	81	19
中等破坏	指数	0.3109	0.1998	0.3104	0.2343	0.3070	0.2047
中等破坏	比例/%	61	49	57	43	60	40
严重破坏	指数	0.3958	0.3654	0.3651	0.4288	0.3787	0.4104
严重破坏	比例/%	52	48	46	54	48	52
倒塌破坏	指数	0.3496	0.6217	0.3200	0.6800	0.3630	0.6183
倒塌破坏	比例/%	36	64	32	63	37	63

下载: 导出CSV

参考文献(17)

[1]	贺景然, 陈建兵, 任晓丹等, 2021. 基于不同损伤本构模型的钢筋混凝土剪力墙结构数值模拟. 建筑结构学报, 42(6): 139—149. He J. R., Chen J. B., Ren X. D., et al., 2021. Numerical simulation of RC shear wall structure based on different damage constitutive models of concrete. Journal of Building Structures, 42(6): 139—149. (in Chinese)
[2]	李忠献, 陈宇, 李宁, 2014. 基于材料损伤的钢筋混凝土构件损伤模型. 工程力学, 31(6): 53—59. Li Z. X., Chen Y., Li N., 2014. A damage model for reinforced concrete members based on material damage. Engineering Mechanics, 31(6): 53—59. (in Chinese)
[3]	刘文锋, 王来其, 高彦强等, 2014. 高强钢筋混凝土框架抗震性能试验研究. 土木工程学报, 47(11): 64—74. Liu W. F., Wang L. Q., Gao Y. Q., et al., 2014. Experimental study on seismic behavior of high-strength reinforced concrete frame. China Civil Engineering Journal, 47(11): 64—74. (in Chinese)
[4]	刘祖强, 任甭优, 薛建阳等, 2021. 型钢混凝土异形柱框架地震损伤分析. 工程力学, 38(1): 143—153. doi: 10.6052/j.issn.1000-4750.2020.02.0123 Liu Z. Q., Ren B. Y., Xue J. Y., et al., 2021. Seismic damage analysis on steel reinforced concrete frames with special-shaped columns. Engineering Mechanics, 38(1): 143—153. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.02.0123
[5]	吕海霞, 滕军, 李祚华, 2014. 高层建筑结构基于整体稳定的失效判别方法. 建筑科学, 30(1): 61—66, 70. doi: 10.3969/j.issn.1002-8528.2014.01.012 Lv H. X., Teng J., Li Z. H., 2014. Analysis on gravity second-order effects and the overall stability of the high-rise structure. Building Science, 30(1): 61—66, 70. (in Chinese) doi: 10.3969/j.issn.1002-8528.2014.01.012
[6]	吕杨, 徐龙河, 李忠献等, 2010. 基于纤维模型的钢筋混凝土结构动力弹塑性分析. 震灾防御技术, 5(2): 257—262. doi: 10.3969/j.issn.1673-5722.2010.02.014 Lv Y., Xu L. H., Li Z. X., et al., 2010. Dynamic elasto-plastic analysis of reinforced concrete structure based on fiber model. Technology for Earthquake Disaster Prevention, 5(2): 257—262. (in Chinese) doi: 10.3969/j.issn.1673-5722.2010.02.014
[7]	曲哲, 叶列平, 2011. 基于有效累积滞回耗能的钢筋混凝土构件承载力退化模型. 工程力学, 28(6): 45—51. Qu Z., Ye L. P., 2011. Strength deterioration model based on effective hysteretic energy dissipation for RC members under cyclic loading. Engineering Mechanics, 28(6): 45—51. (in Chinese)
[8]	王中阳, 车佳玲, 张尚荣等, 2018. 基于能量方法设计的RC框架结构易损性分析. 震灾防御技术, 13(3): 524-533. doi: 10.11899/zzfy20180304 Wang Z. Y., Che J. L., Zhang S. R., et al., 2018. Seismic fragility analysis of RC frame structure based on energy balance. Technology for Earthquake Disaster Prevention, 13(3): 524—533. (in Chinese) doi: 10.11899/zzfy20180304
[9]	曾武华, 王逢朝, 卓卫东, 2016. 采用变形和能量双重准则的钢筋混凝土桥墩地震损伤模型. 华侨大学学报(自然科学版), 37(4): 441—446. doi: 10.11830/ISSN.1000-5013.201604010 Zeng W. H., Wang F. C., Zhuo W. D., 2016. Deformation and energy-based seismic damage model of reinforced concrete bridge piers. Journal of Huaqiao University (Natural Scicncc), 37(4): 441—446. (in Chinese) doi: 10.11830/ISSN.1000-5013.201604010
[10]	周知, 钱江, 黄维, 2016. 基于修正的Park-Ang损伤模型在钢构件中的应用. 建筑结构学报, 37(S1): 448—454. Zhou Z., Qian J., Huang W., 2016. Application of modified Park-Ang damage model to steel members. Journal of Building Structures, 37(S1): 448—451. (in Chinese)
[11]	Cao S. S., Jiang L. Z., Wei B., 2019. Numerical and experimental investigations on the Park-Ang damage index for high-speed railway bridge piers with flexure failures. Engineering Structures, 201: 109851. doi: 10.1016/j.engstruct.2019.109851
[12]	Clough R. W., Johnston S. B., 1966. Effect of stiffness degradation on earthquake ductility requirements. In: Proceedings of Japan Earthquake Engineering Symposium. Tokyo, 227—232.
[13]	Federal Emergency Management Agency, 2000. Prestandard and commentary for the seismic rehabilitation of buildings. Washington: Federal Emergency Management Agency.
[14]	Iervolino I., Giorgio M., Chioccarelli E., 2016. Markovian modeling of seismic damage accumulation. Earthquake Engineering & Structural Dynamics, 45(3): 441—461.
[15]	Lee J., Kong J., Kim J., 2018. Seismic performance evaluation of steel diagrid buildings. International Journal of Steel Structures, 18(3): 1035—1047. doi: 10.1007/s13296-018-0044-8
[16]	Scott B. D., Park R., Priestley M. J. N., 1982. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates. ACI Structural Journal, 79(1): 13—27.
[17]	Ventura A., Chiaia B., De Biagi V., 2017. Robustness assessment of RC framed structures against progressive collapse. IOP Conference Series: Materials Science and Engineering, 245(3): 032033.