Estimation of Site Amplification Effect Considering the Absorption and Attenuation of Seismic Waves by the Medium
-
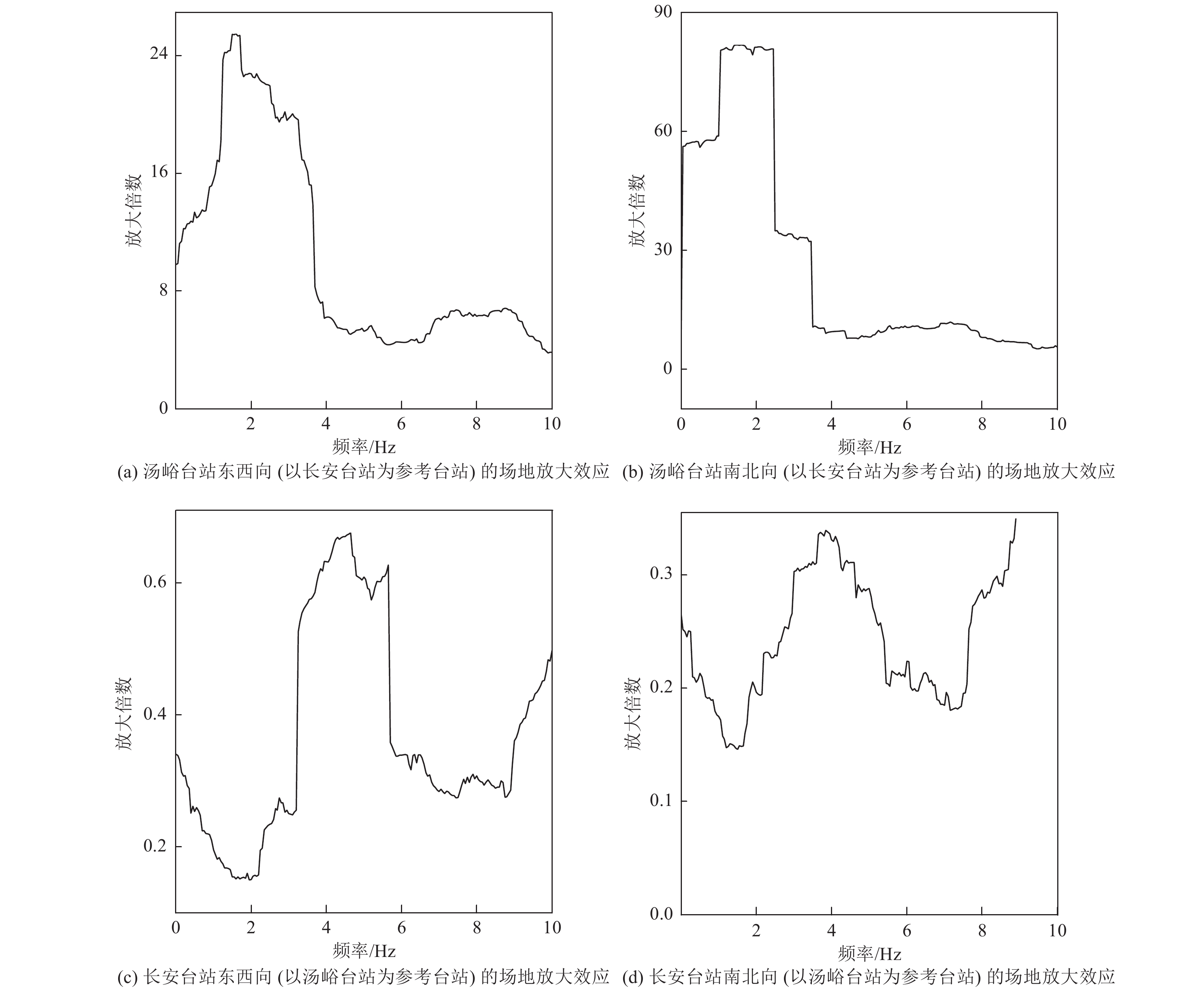
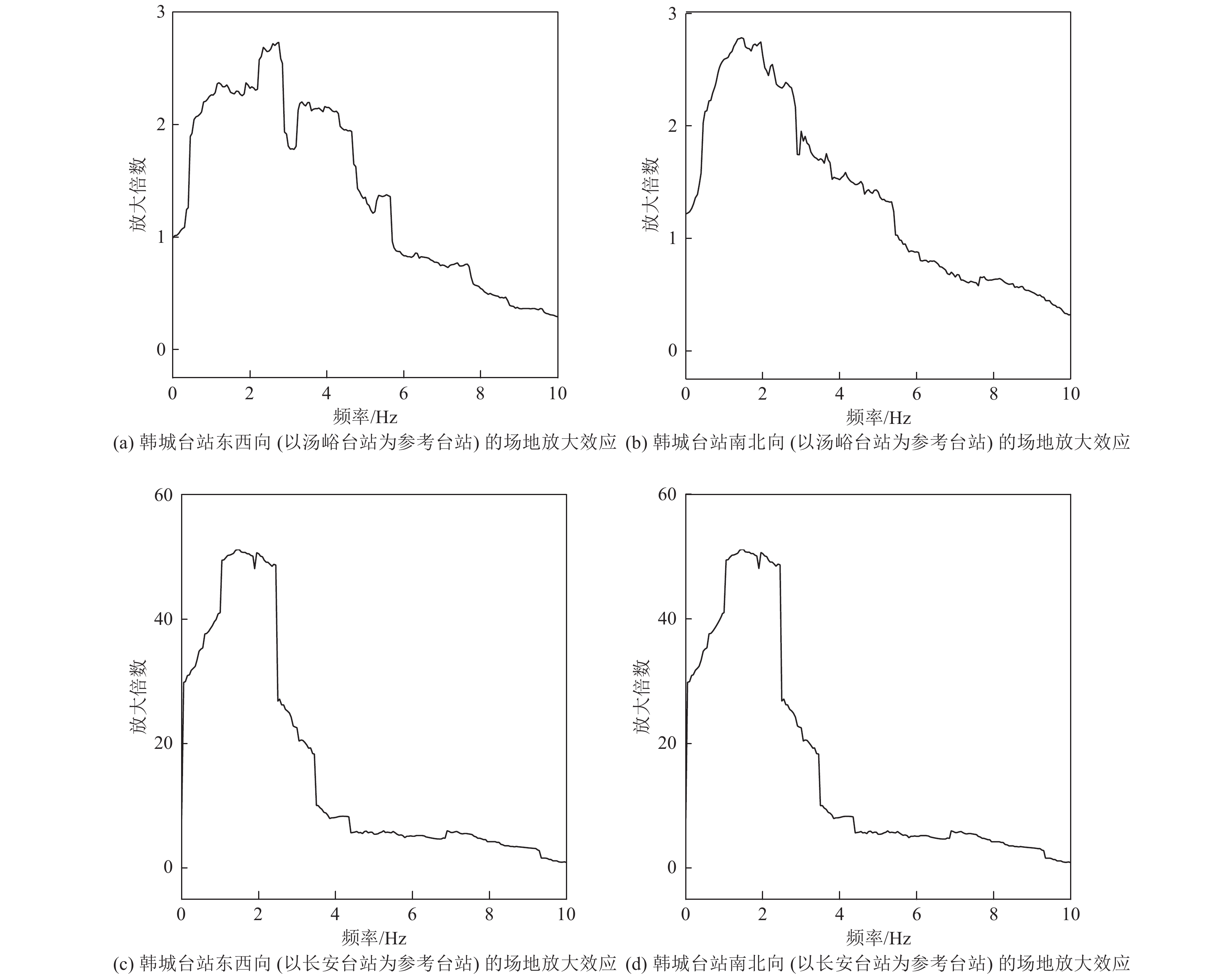
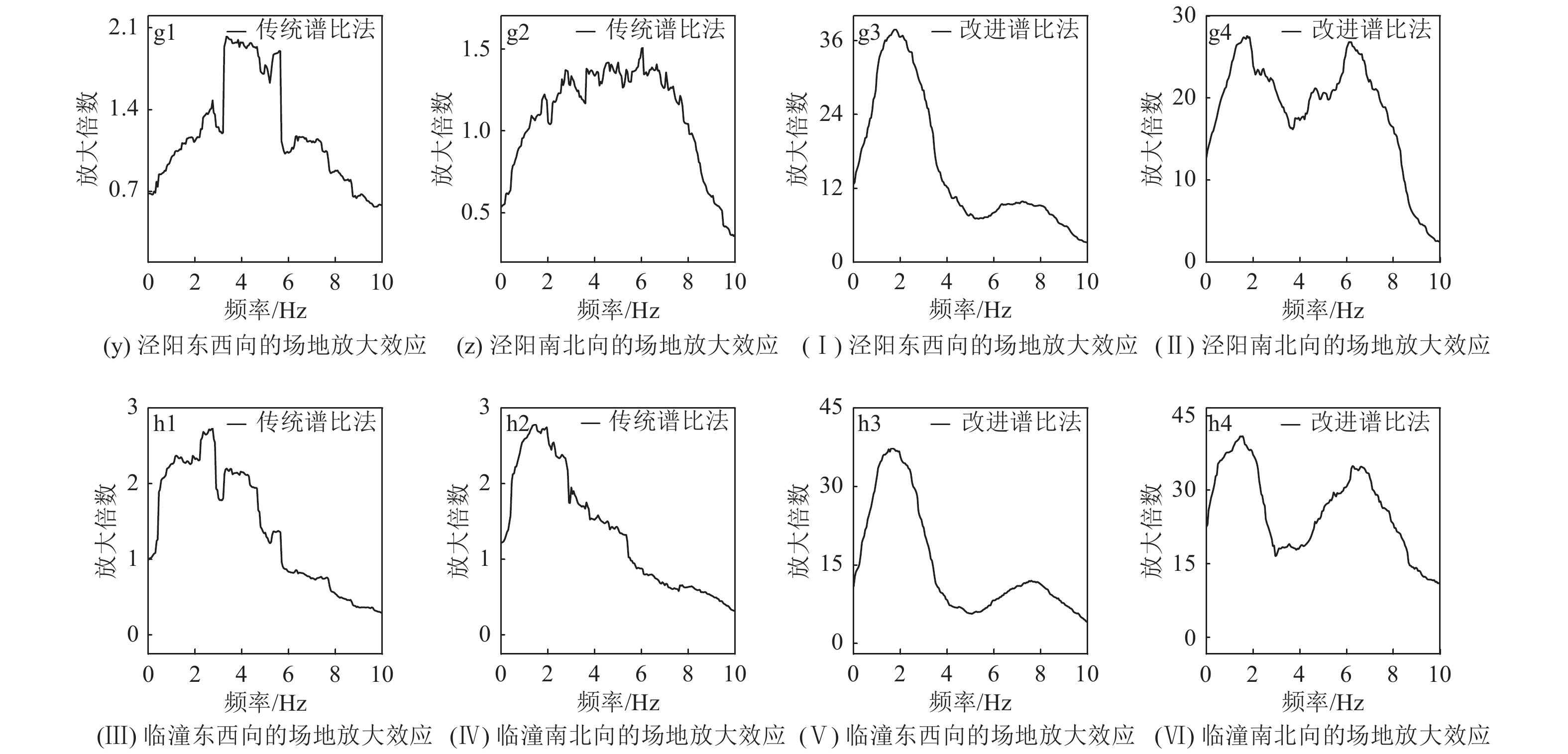
摘要: 当参考场地震源距小于研究场地震源距时，传统谱比法低估了场地放大效应，且参考场地与研究场地震源距相差越大，低估程度越大；当参考场地震源距大于研究场地震源距时，传统谱比法高估了场地放大效应，且参考场地与研究场地震源距相差越大，高估程度越大，计算结果依赖参考场地的选择。上述问题存在的原因是传统谱比法估计场地放大效应时未考虑地震波传播过程中介质的吸收衰减作用，故传统谱比法适用于参考场地与研究场地地质构造类似且震源距相差较小的情况，为此本文通过考虑介质对地震波的吸收衰减作用，提出改进谱比法，可适用于地质构造类似、任意震源距的情况。本文分别采用未改进方法和改进方法估计汶川地震中渭河盆地多个台站场地反应，证实了传统谱比法存在的上述问题。采用改进谱比法估计的场地放大倍数均在2 Hz以下出现1个峰值，且这些峰值多为最大值；采用未改进谱比法估计的场地放大倍数峰值出现的频率多大于2 Hz；改进谱比法可信度较高。Abstract: When the reference field source distance is less than the research field source distance, the traditional spectral ratio method underestimates the site amplification effect. The greater the difference between the two source distances, the greater the degree of underestimation; when the reference field source distance is greater than the research field source distance, the traditional spectral comparison method overestimates the site magnification effect. The greater the distance between the two sources, the greater the degree of overestimation. The calculation result depends on the selection of the reference site. The reason for the above problems is that the traditional spectral ratio method does not consider the absorption and attenuation of the medium during the propagation of seismic waves when estimating the site amplification effect. Therefore, the traditional spectral ratio method is suitable for situations where the geological structure of the research site and the reference site are similar, and the seismic source distance is small. Therefore, we consider the absorption and attenuation of seismic waves by the medium, and propose an improved spectral ratio method, which can be applied to the situation where the geological structure is similar and the source distance is arbitrary. In this paper, the unimproved method and the improved method are used to estimate the field response of multiple stations in the Weihe Basin of the Wenchuan earthquake, which confirms the above-mentioned problems of the traditional spectral ratio method. The site amplification rate estimated by the improved spectral ratio method has a peak below 2 Hz, and most of these peaks are the maximum; the site amplification peak estimated by the uncorrected spectral ratio method occurs with a frequency higher than 2 Hz. The improved spectral ratio method has higher reliability.
-
图 2 汤峪台站和长安台站的场地放大效应
Figure 2. The site amplification effect of Tangyu station and Chang'an station
图 4 用传统谱比法和改进谱比法计算结果对比
Figure 4. The comparison of calculation results between the traditional spectral ratio method and improved spectral ratio method
表 1 地震台站地区沉积物厚度
Table 1. Thickness of sediment at each station
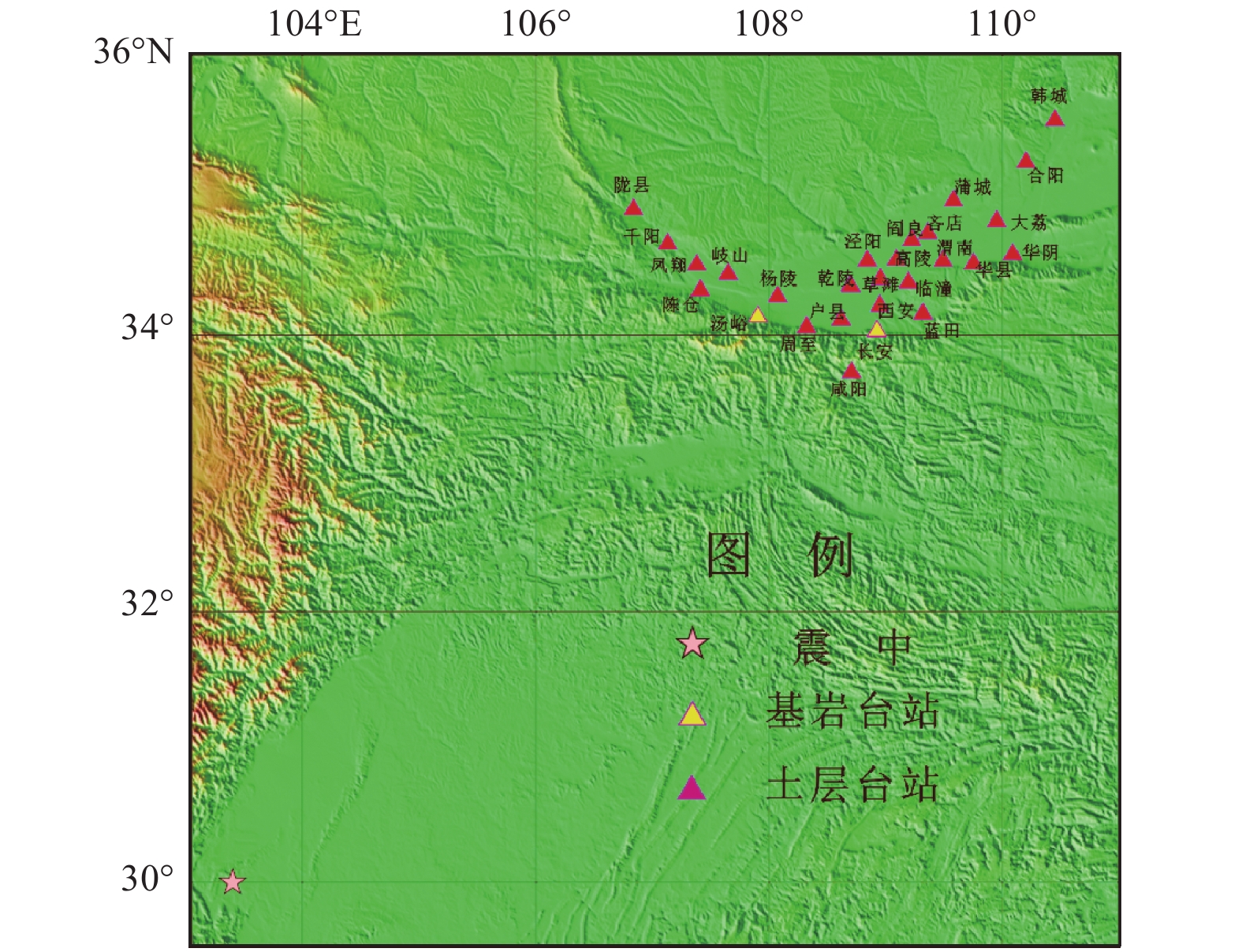
台站 沉积物厚度/m 台站 沉积物厚度/m 台站 沉积物厚度/m 陇县 — 千阳 — 凤翔 100 陈仓 200 岐山 100 杨凌 700 汤峪 0 乾陵 10 户县 800 周至 100 咸阳 600 草滩 700 长安 0 西安 1 200 蓝田 100 泾阳 600 高陵 800 临潼 870 渭南 1 325 阎良 400 吝店 600 华县 800 蒲城 200 华阴 800 大荔 700 合阳 100 韩城 — 
下载: 导出CSV
表 2 地震台站震源距
Table 2. Source distance of the station
台站 震源距/km 台站 震源距/km 台站 震源距/km 陈仓 610 千阳 624 凤翔 624 陇县 632 汤峪 634 周至 646 岐山 647 杨陵 647 户县 670 长安 686 乾陵 694 咸阳 694 西安 701 草滩 715 泾阳 717 临潼 723 蓝田 723 高陵 734 阎良 754 渭南 762 吝店 767 华县 779 蒲城 799 华阴 808 大荔 814 合阳 861 韩城 900
下载: 导出CSV
-
[1] 李世峰, 金瞰昆, 周俊杰, 2008. 资源与工程地球物理勘探. 北京: 化学工业出版社, 114—115. [2] 彭建兵, 1992. 渭河断裂带的构造演化与地震活动. 地震地质, 14(2): 113—120.Peng J. B., 1992. Tectonic evolution and seismicity of Weihe fault zone. Seismology and Geology, 14(2): 113—120. (in Chinese) [3] 王海云, 2011. 渭河盆地中土层场地对地震动的放大作用. 地球物理学报, 54(1): 137—150. doi: 10.3969/j.issn.0001-5733.2011.01.015Wang H. Y., 2011. Amplification effects of soil sites on ground motion in the Weihe basin. Chinese Journal of Geophysics, 54(1): 137—150. (in Chinese) doi: 10.3969/j.issn.0001-5733.2011.01.015 [4] 章文波, 周雍年, 谢礼立, 2001. 场地放大效应的估计. 地震工程与工程振动, 21(4): 1—9. doi: 10.3969/j.issn.1000-1301.2001.04.001Zhang W. B., Zhou Y. N., Xie L. L., 2001. Estimation of absolute site amplification. Earthquake Engineering and Engineering Vibration, 21(4): 1—9. (in Chinese) doi: 10.3969/j.issn.1000-1301.2001.04.001 [5] Andrews D. J., 1982. Separation of source and propagation spectra of Seven Mammoth Lakes aftershocks. In: Proceedings of workshop XVI. Dynamic Characteristics of Faulting Inferred from Recordings of Strong Ground Motion. Lake Tahoe: United States Geological Survey, 82—591. [6] Beresnev I. A., Atkinson G. M., 1998. Stochastic finite-fault modeling of ground motions from the 1994 northridge, California, earthquake. I. Validation on rock sites. Bulletin of the Seismological Society of America, 88(6): 1392—1401. [7] Borcherdt R. D., 1970. Effects of local geology on ground motion near San Francisco Bay. Bulletin of the Seismological Society of America, 60(1): 29—61. [8] Field E. H., Jacob K. H., 1995. A comparison and test of various site-response estimation techniques, including three that are not reference-site dependent. Bulletin of the Seismological Society of America, 85(4): 1127—1143. [9] Hanks T. C., Krawinkler H., 1991. The 1989 Loma Prieta earthquake and its effects: Introduction to the special issue. Bulletin of the Seismological Society of America, 81(5): 1415—1423. doi: 10.1785/BSSA0810051415 [10] Inagaki H., Iai S., Sugano T., et al., 1996. Performance of caisson type quay walls at Kobe port. Soils and Foundations, 36(S): 119—136. [11] Irikura K., 1983. Semi-empirical estimation of strong ground motions during large earthquakes. Bulletin of Disaster Prevention Research Institute, Kyoto Univ, 33(2): 63-104. -
点击查看大图
图(5) / 表(2)
计量
- 文章访问数: 102
- HTML全文浏览量: 56
- PDF下载量: 37
- 被引次数: 0
