Preliminary Study on the Spatial Coherency of Surface Wave
-
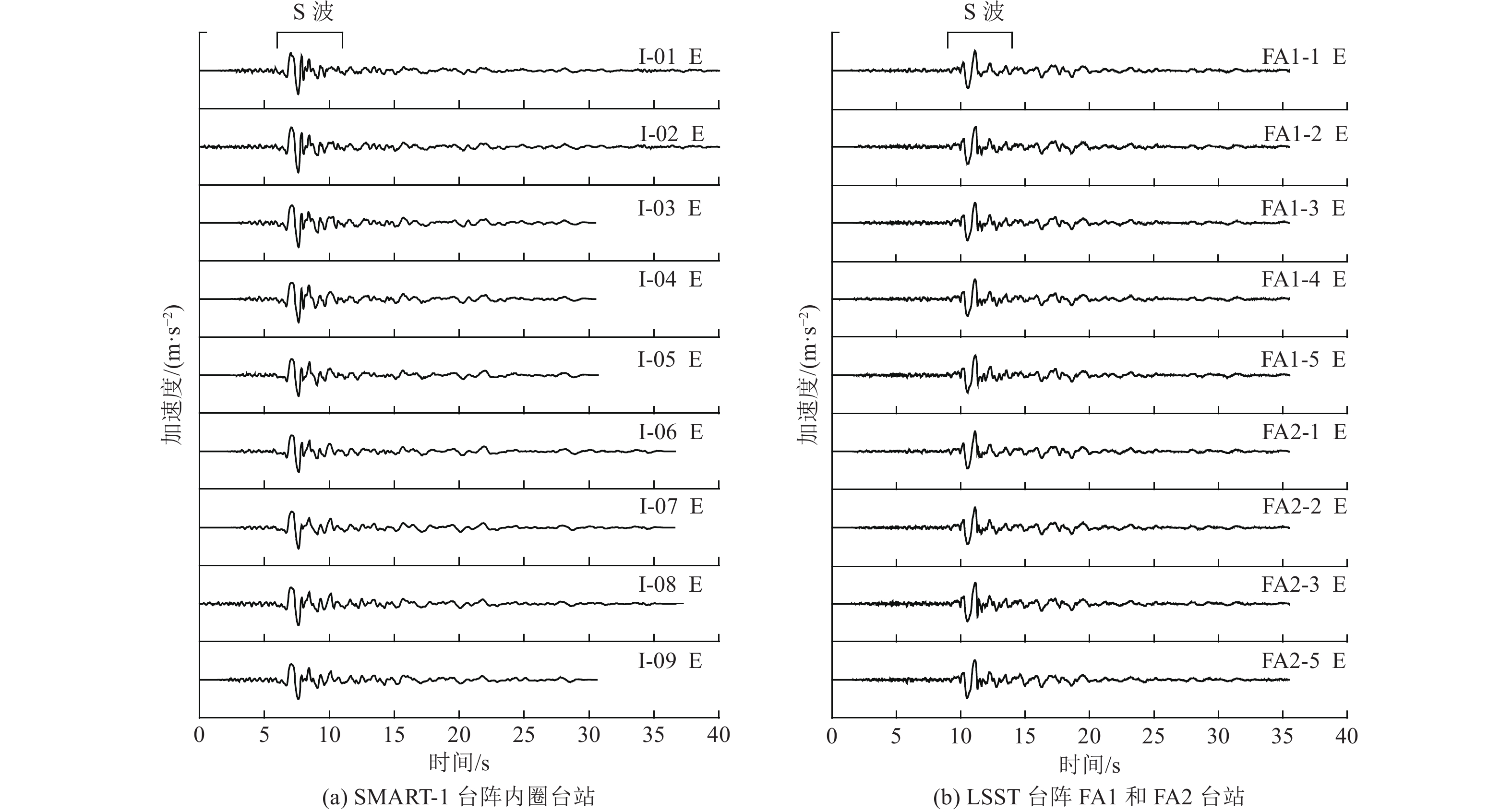
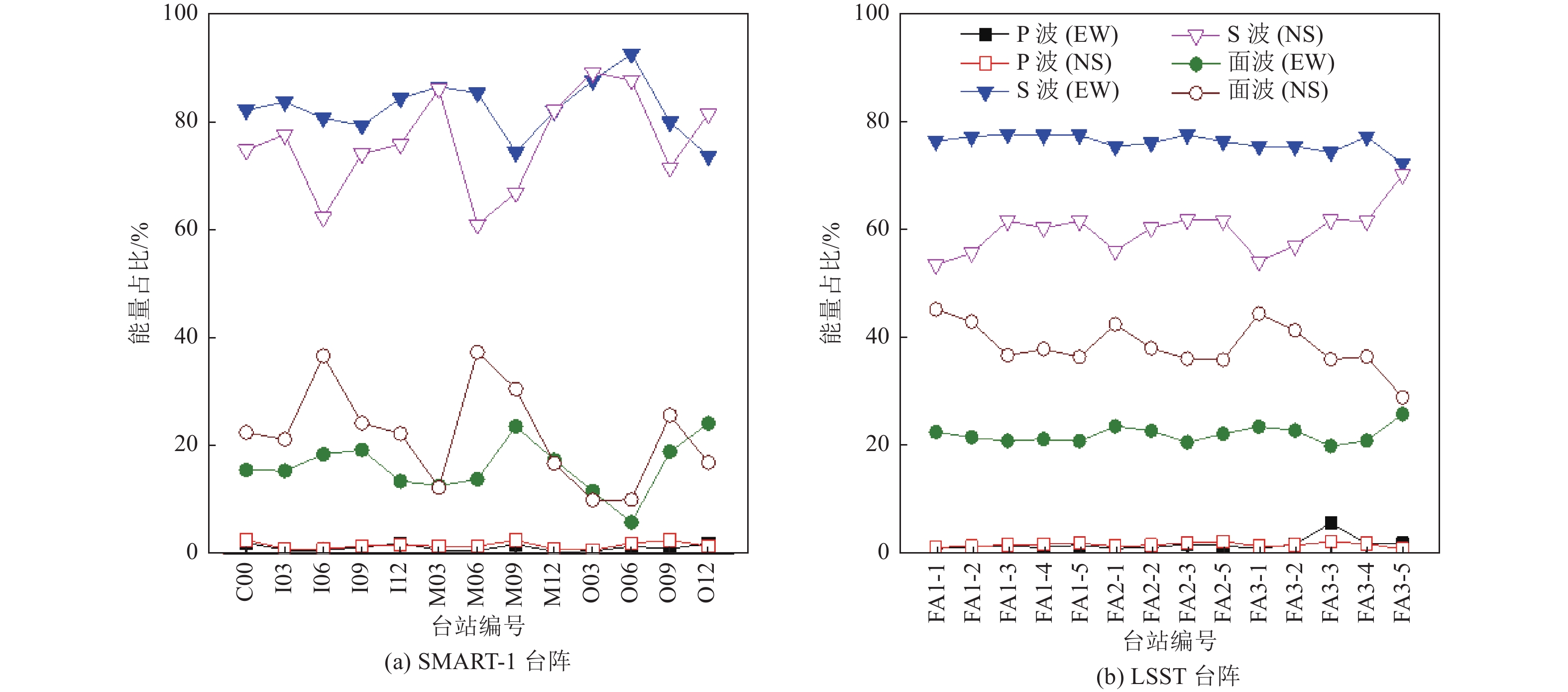
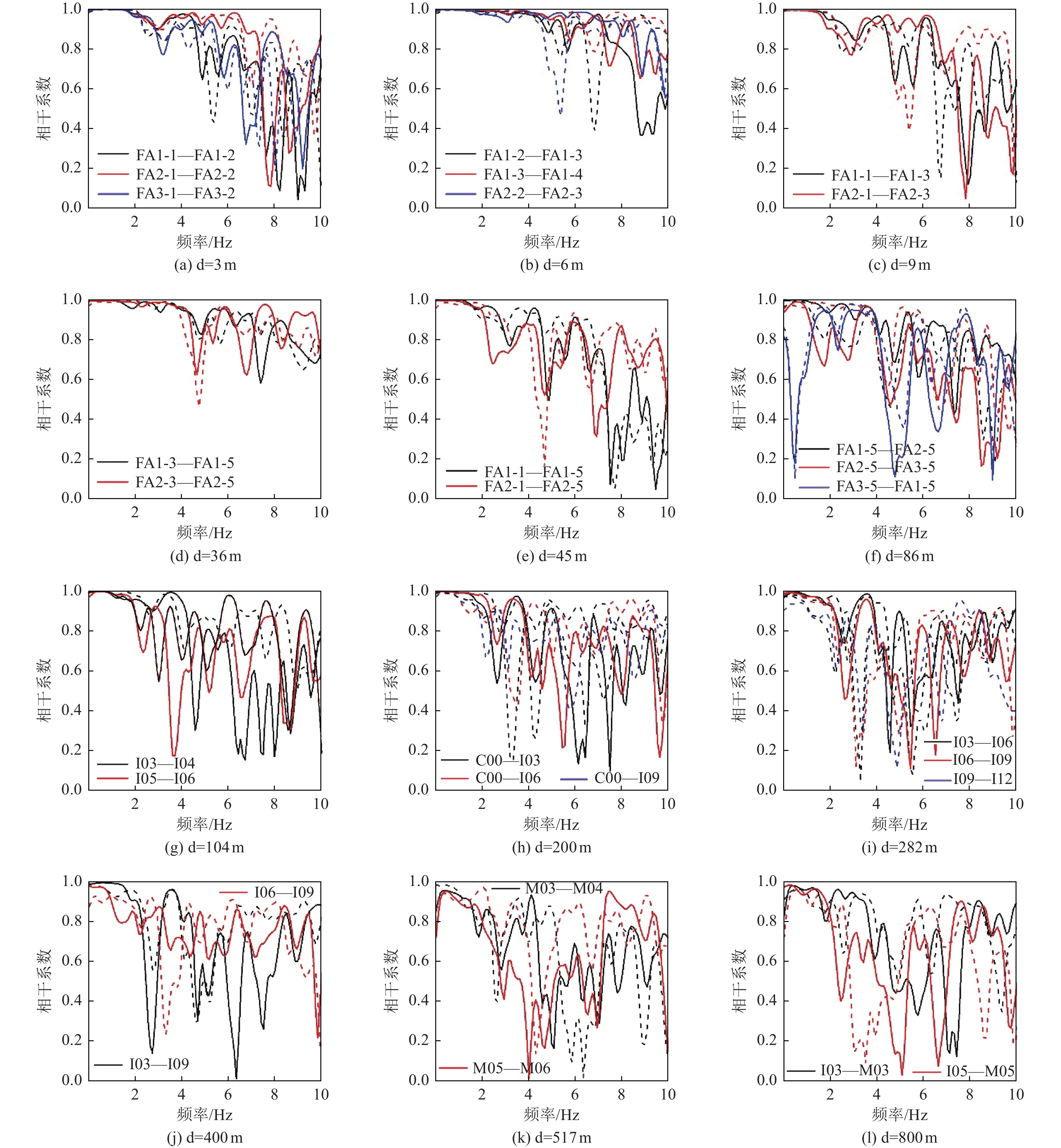
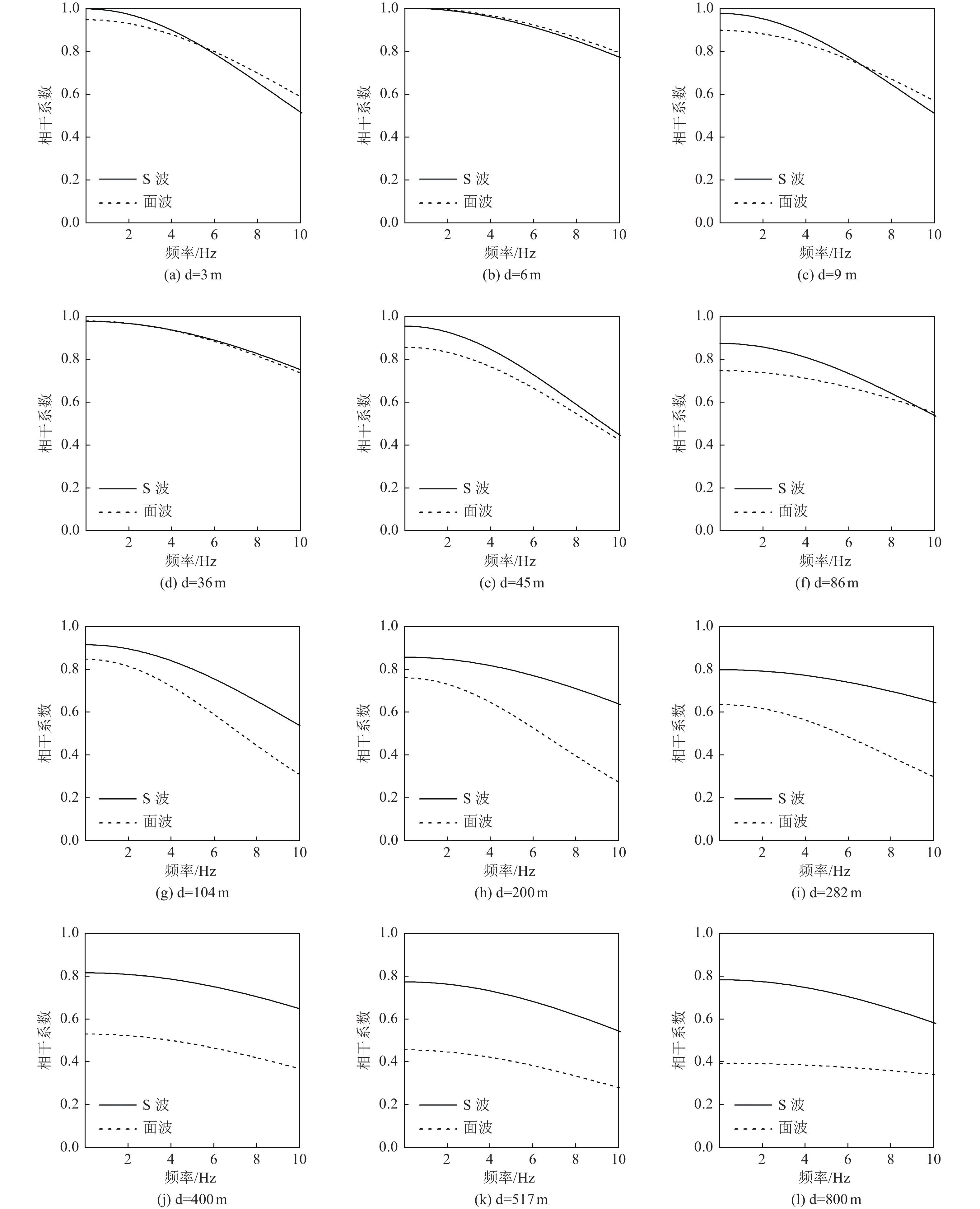
摘要: 本文选取台湾LSST、SMART-1台阵地震记录，分别计算不同间距S波和面波相干系数，采用Loh提出的相干函数模型对计算结果进行参数拟合。研究结果表明，当台站间距
$ d < \text{50}\;{\rm{m}} $ 时，面波和S波相干系数基本相同；当台站间距$d = \text{500}\;{\rm{m}}$ 时，面波相干系数小于S波相干系数，且随着台站间距的增大，二者的差别逐渐增大；当台站间距$ d > \text{500}\;{\rm{m}}$ 时，面波空间相干性几乎不存在，可不考虑。本文给出的面波相干函数模型参数可作为大型盆地中的长大结构抗震分析时合成地震动场的参考。Abstract: In this paper, seismic records of Taiwan LSST array and SMART-1 array were selected to calculate the S-wave and surface wave coherence coefficients at different station distances. And then the coherence function model proposed by Loh was used to fit the calculation results. After comparison and analysis, we found that when the distance d < 50 m, the coherency coefficients of surface wave and S-waves are basically the same; when the distance d = 50 m , the coherency coefficients of surface wave is smaller than that of S-wave, and as the distance increases, the differences gradually increase. When the distance d > 500 m, the spatial coherency of the surface wave hardly exists, so no further consideration is needed. Finally, the surface wave coherency model parameters were given in this paper, which can be used as a reference for the synthetic ground motion field in the seismic analysis for long and large structures in large basins.-
Key words:
- S-wave /
- Surface wave /
- Spatial coherency /
- SMART-1 array /
- LSST array
-
引言
据中国地震台网正式测定，当地时间2021年2月13日23时7分（北京时间2021年2月13日22时7分）在日本本州福岛东岸近海发生MS7.1地震，震源深度50 km，震中位于（37.745°N，141.749°E）（图1），震中5 km范围内平均海拔约−356 m。此次地震记录到的最大峰值加速度PGA出现在震中距约70 km处的MYGH010台站（图2），其NS向分量的PGA为1 450 cm/s2，明显高于相同震级的大陆浅地壳地震在70 km处的PGA强度。
图 2 最大峰值加速度出现的台站MYGH10各分量时程Figure 2. Time history of each component of station MYGH10 with maximum peak ground acceleration本次地震的震源深度较深且发生在海中，由于俯冲带地区地壳介质的特殊性，地震波能量衰减慢，在地下介质中传播较远，导致在近海岸处仍呈现出较强的地面震动现象。本文从地震应急和地震动评估角度，对本次地震峰值加速度的空间分布特征及加速度时程进行快速评估，并结合实际的地形、厚场地覆盖层等信息对部分台站地震动模拟结果进行修正，以期获得较可靠的高频地震动评估结果。本文将经验格林函数法作为地震动评估工具，选择与主震震中和震源深度相同的MS4.8小震作为格林函数（图1），快速合成此次MS7.1大震的高频地震动。
1. 研究方法与数据
1.1 经验格林函数法
Hartzell（1978）最早提出了经验格林函数法，利用大震的前震或余震记录作为格林函数合成大震。由于小震记录本身已包含了传播介质的影响，所以用小震记录合成的大震时程也考虑了传播介质的复杂性，并能克服计算理论格林函数的困难。Irikura等（1994，2011，2017）系统性地提出了利用经验格林函数法模拟未来地震动的方法，并结合多个震例验证了该方法的可靠性，总结了利用该方法模拟地震动的一般步骤。经众多学者的不断努力，经验格林函数法已发展为较完善和成熟的模拟强地震地面运动的方法，已被广大学者认可（Hartzell，1978；Kanamori，1979；Irikura，1983，1986；Boore，2003；罗奇峰，1989；Irikura等，1994，2011，2017；Kamae等，1998；Miyake等，2003；李宗超，2017；李宗超等，2016，2019 a，2019 b；Li等，2018，2021 a，2021 b，2022）。
经验格林函数法将大震震源看作由一系列子震震源构成，选择大小合适的余震或前震记录作为格林函数（Irikura，1986；Miyake等，2003），如图3所示，将小震等同于子震，按照一定的破裂方式，将这些经验格林函数叠加得到大震地震动时程（Irikura，1986；Miyake等，2003；李宗超等，2019 a，2019 b）。
图 3 经验格林函数法用到的有限断层震源模型Figure 3. Finite fault source model注：rij为第（i，j）个子断层到观测点的距离,r0为破裂初始点到观测点的距离;ξij为第（i，j）个子断层到初始破裂位置的距离，W和L分别为大震断层面的长度和宽度，w和l分别为小震断层面的长度和宽度1.2 地震数据与基本震源参数
本文所用的加速度记录全部来自于日本NIED强震台网（K-NET和KiK-net台网）的加速度记录，选用MS4.8余震作为格林函数，震中位置位于（37.6°N，141.63°E），与主震的初始破裂位置一致，保证了大、小地震传播路径的高度一致性。根据日本NIED强震台网信息，记录到本次MS7.1主震波形的日本境内台站有930多个，记录到M4.8地震的台站共122个（图1）。如果全部台站均模拟，工作量大，目前的计算程序未达到并行计算的能力，因此本文从日本福岛县境内靠近震中的陆上区域选择离散分布的18个台站作为研究对象，包括15个K-NET台站和3个KiK-net台站（图1）。本文对选择的格林函数进行了数据基线校正、去除波形的数据头和尾等初步处理。
本文所用的主要震源参数如表1所示，破裂面积、地震矩、破裂速度数据来自于李宗超（2017，2019）的研究，震源深度数据来自于日本NIED强震台网信息，剪切波速数据来自于Wang（2014）的研究，震源上升时间数据来自于Geller（1976）的研究。断层破裂面积和地震矩等参数根据李宗超（2017）更新后的震源参数经验关系式计算得到：
表 1 震源参数Table 1. Parameters of related source参数 震级 MS7.1 MS4.8 破裂面积/km2 6.29×103 2.76×102 地震矩/dyne·cm 1.54×1026 7.26×1023 震源深度/km 50.7 50.0 剪切波速/km·s−1 4.2 4.2 破裂速度/km·s−1 3.3 3.3 震源上升时间/s 3.04 3.04 $$ {\mathrm{lg}}{M}_{0}=1.057{M}_{{\rm{S}}}+11.787 $$ (1) $$ {\mathrm{lg}}S=0.542{\rm{lg}}{M}_{0}-0.6 $$ (2) 式中，MS为面波震级；M0为地震的地震矩；S为地震的破裂面积。
凹凸体参数如表2所示，凹凸体面积、凹凸体地震矩数据来自于Somerville等（1999）和李宗超（2017）的研究，划分子断层的数量N及大、小地震应力降比值C数据来自于Miyake等（2003）和李宗超（2017）的研究。凹凸体面积约占整个断层破裂面积的22%，凹凸体地震矩约占整个断层地震矩的44%，破裂速度取S波剪切波速的0.78倍（李宗超等，2019 a，2019 b）。凹凸体区域既是强震生成区，又是产生高频地震动的主要区域，其产生的地震动峰值加速度与整个地震产生的地震动峰值加速度的强度基本相当（Miyake等，2003），因此本文主要模拟凹凸体区域产生的地震动。计算过程中采用“布龙模型”，将地震断层面等效为圆盘模型（Brune，1970），将地震视为圆盘形断层面上剪切应力的突然释放。C、N计算如下（Kanamori等，1975；Kanamori，1979；李宗超，2017；李宗超等，2019 a，2019 b）：
表 2 凹凸体参数Table 2. Parameters of the asperity参数 数值 凹凸体面积/m2 1.38×109 凹凸体地震矩/dyne·cm 3.40×1025 大、小地震应力降比值C 5.45 划分子断层数量N 4.13 子断层长度dx/km 10.52 子断层宽度dw/km 5.26 $$ \Delta {\sigma }_{\mathrm{A}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{y}}=\frac{7{M}_{\mathrm{A}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{y}}}{16R{r}_{\mathrm{A}\mathrm{a}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{y}}^{2}} $$ (3) $$ \Delta {\sigma }_{\mathrm{s}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{l}}=\frac{7{M}_{\mathrm{s}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{l}}}{16{r}_{\mathrm{s}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{l}}^{3}} $$ (4) $$ C=\frac{\Delta {\sigma }_{\mathrm{A}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{y}}}{\Delta {\sigma }_{\mathrm{s}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{l}}} $$ (5) $$ N=\sqrt[\uproot{18}{\scriptstyle{3}}]{\frac{{M}_{\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}}}{C{M}_{\mathrm{s}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{l}}}} $$ (6) 式中，MLarge为主震的地震矩，MAsperity为凹凸体的地震矩，Msmall为小震的地震矩；R为主震的等效半径；rAsperity为凹凸体的等效半径，rsmall为小地震的等效半径；ΔσAsperity为凹凸体的应力降；Δσsmall为小震的应力降；C为大、小地震应力降的比值；N为划分子断层的数量。
震源上升时间计算如下（Geller，1976）：
$$ {\tau }^{*}=16{S}^{1/2}/(7{{\text{π}} }^{3/2}\beta ) $$ (7) 式中，S为主震的破裂面积，β为S波的剪切波速。本文计算得到的震源上升时间为3.04 s。
2. 地震动初步模拟结果
经初步模拟，得到了18个强震台站的模拟加速度时程，并与本次地震的观测值进行了初步对比分析，结果如图4、5所示。由图4、5可知，大部分台站地震动加速度时程初步模拟值与观测值拟合结果较好，包括11个K-NET台站和2个KiK-net台站，PGA和有效时程基本一致，有效时程为30～40 s。初步模拟结果表明经验格林函数法合成的地震动加速度时程可基本代表真实的地震动时程，同时也可验证表1中的震源参数基本准确。
图 4 初步模拟结果较好的部分台站地震动加速度时程Figure 4. Acceleration time history of some stations with good initial simulation results
图 5 初步模拟结果欠佳的5个台站地震动加速度时程Figure 5. Acceleration time history of 5 stations with poor initial simulation results部分台站地震动加速度时程模拟结果欠佳（图5），包括4个K-NET台站和1个KiK-net台站，模拟值的加速度幅值小于观测值的加速度幅值，有效持时较短。
将18个台站PGA空间分布特征对比如图6所示，由图6可知，观测值与模拟值的PGA空间分布在局部区域存在明显差异。
图 6 初步模拟后观测值与模拟值的PGA空间分布特征对比Figure 6. After the preliminary simulation, the spatial distribution characteristics of PGA between the observed valuesand the simulated values were compared3. 部分台站地震动结果的修正
由于大、小地震来自相同的台站，其传播路径、场地条件、震源位置具备较高的一致性，本文认为初期的参数（如地震矩、断层破裂尺度、震源深度、划分子断层的数量、凹凸体参数等）选取是合理的，且选取MS4.8小震作为格林函数是合适的。主震与小震震中在同一位置，本文选取的18个台站震中距均＞70 km，震源距均＞92 km，主震与小震传播路径较一致，因此地震波从初始破裂点到台站接收点的传播路径差异是可接受的。因此造成部分台站地震动模拟结果欠佳的原因可能为场地因素的影响，大震在部分台站处表现出了不同的非线性特性，而经验格林函数法无法考虑局部区域特殊地形及场地的影响，获得的结果仅为台站场址处的水平地震动场。对模拟结果欠佳的台站进行检查，结果表明存在特殊地形和场地条件，如FKS002、FKS017和FKS019台站地处两山脉间的峡谷地带（图1），MYG014台站靠近山脉，位于山脚处，因此地震波传至台站时有可能发生盆地的放大效应，增加了PGA强度。本文选取的MS4.8地震震源深度达50 km，由于地震较小，地震总能量有限，小震地震波传至FKS002、FKS017、FKS019、MYG014台站时，自身高频成分已大部分衰减，即使遇见盆地峡谷地形，也难以起到与主震相同的地震动放大效应，因此难以利用MS4.8地震在FKS002、FKS017、FKS019和MYG014台站的小震记录直接合成经盆地放大效应后的MS7.1地震在对应台站处的地震动。MYGH10台站虽在平原地带，无特殊地形影响，但该场址覆盖土层剪切波速较低，覆盖层厚度为34 m（表3），根据《建筑抗震设计规范》（GB 50011—2010）（中华人民共和国住房和城乡建设部等，2010），场地类别为Ⅱ类，因此，相对于基岩场地，主震的地震波在此处会受到较大的场地放大效应影响，PGA强度会增大。然而，对于小震的情况，由于震源深度较大且距MYGH10台站较远，所以小震受场地放大效应的影响较小。
表 3 MYGH10台站波速结构Table 3. The velocity structure of station MYGH10土层编号 厚度/m 深度/m P波速度
VP/m·s−1剪切波速VS/m·s−1 1 1 1 500 110 2 2 3 1 750 250 3 31 34 1 750 390 4 80 114 1 830 590 5 — — 1 920 770 对MS4.8地震在FKS002、FKS017、FKS019、MYG014、MYGH10等台站处的加速度时程幅值进行修正，将每个台站的加速度幅值乘以修正系数（表4），使其适当体现盆地放大效应或场地放大效应的影响，然后重新模拟修正后的地震动时程，如图7所示，部分台站地震动傅氏谱如图8所示，修正后的18个台站PGA空间分布特征如图9所示。结果表明，修正后合成的地震动时程、PGA强度空间分布特征与观测值的地震动时程、PGA强度空间分布特征的拟合质量得到提升，傅氏谱在1.0～20.0 Hz，尤其是3.0 Hz以上时，观测值与模拟值拟合结果更好，各台站地震动反应谱在较短周期拟合效果较好，验证了经验格林函数法在大震后快速产出地震动时程及PGA强度的可行性，这也为依托经验格林函数法评估已发生中小地震地区未来发生破坏性大震时可能出现的地震动强度特征奠定了基础。
表 4 台站加速度时程幅值修正系数Table 4. Correction coefficient of acceleration time history amplitude of each station台站编号 初始PGA（EW向）/
cm·s−2初始PGA（NS向）/
cm·s−2修正系数 修正后PGA（EW向）/
cm·s−2修正后PGA（NS向）/
cm·s−2FKS002 12.7 17.5 1.4 17.78 24.5 FKS017 3.9 3.5 3.5 13.65 12.3 FKS019 10.3 11.5 1.8 18.54 20.7 MYG014 5.7 6.3 1.5 8.55 9.5 MYGH10 20.1 29.5 2.1 42.21 61.9 
图 8 部分台站（1.0～20.0 Hz）观测值与模拟值的地震动傅氏谱对比Figure 8. The fourier spectra of some stations （1.0～20 Hz） are compared with the simulated values通过对本次地震的快速模拟评估，意识到特殊地形、场地可能对地震强度产生放大影响，而选取实际小震记录作为格林函数时难以直接考虑特殊场地、地形等因素的影响，因此需合理修正特殊位置的小震记录。本文针对评估结果欠佳的5个台站，将观测值地震动作为参照时程，初步采用试错法得到了特殊场地台站的小震记录修正系数（表4）。而评估未来设定震级地震动时程时无参照时程，因此需给出一定范围的修正系数，获得的地震动应为一定合理取值范围的结果。实际的特殊地形、场地对地震动放大作用的影响较复杂，但基于震后地震动快速产出可知，如果能给出大致的地震动放大效应取值范围，表征主要的地震动强度特征，即可满足震后应急产品的要求。另外，一般的盆地区域是人口较密集的区域，从安全角度考虑，建议在盆地区域内采用较高的修正系数。
在工程实际应用中，场地放大效应主要通过场地峰值加速度调整系数进行考虑，该系数受场地类别和输入地震动强度影响（吕红山等，2007；高孟潭等，2009；李小军，2013）。基于《中国地震动参数区划图》（GB 18306—2015）（中华人民共和国国家质量监督检验检疫总局等，2016）表E.1可得不同场地相对于Ⅱ类场地的地震动峰值加速度调整系数，其值为0.72～1.25，转换为不同场地相对于I1类场地，即硬基岩场地为1.0～1.8。而日本KiK-net台站所有类型场地的场地放大系数主要集中于2～8，占比为80.7%，PGA放大系数主要集中在2～4，占比为41.7%（王亮，2014）。
综合已有盆地放大效应及场地放大效应的研究成果（吕红山等，2007；胡进军等，2017；付长华，2012；王建龙等，2014；于彦彦，2016；李春果等，2020；张龙飞，2020），并结合本文5个台站的修正系数（表4）、《中国地震动参数区划图》（GB 18306—2015）（中华人民共和国国家质量监督检验检疫总局等，2016）、日本KiK-net台站统计的场地放大系数，认为利用经验格林函数法快速合成地震动时，将小震记录在盆地及覆盖层较厚处的地震动修正系数界定在1.0～3.0是有实际效果的，可满足小震合成大震的地震动强度要求。关于调整系数问题，本文结果是相对保守的。仅依靠当前5个台站的结果和有限的文献资料难以准确表达特殊地形及场地的地震动非线性特征，但本文给出的修正系数可在一定程度上优化地震动的快速模拟结果。当评估某地区不同设定震级的破坏性地震的地震动时，对于特殊地形及厚覆盖层区域的修正系数，除可参考较保守的1.0～3.0范围外，还可补充更多的当地已有地震地质资料及钻孔勘探资料，进而获得更精确的修正系数。场地或盆地放大效应的影响是复杂的问题，需进行大量补充研究，以给出相对准确的修正系数。
4. 结论和讨论
采用经验格林函数法快速合成日本福岛MS7.1地震，得出以下结论：
（1）因俯冲带地区地壳介质的特殊性，地震波衰减较慢，70 km外的地震动强度较大，表明MS7.1地震在较大的震源深度时，其影响范围将扩大较多，高频地震波辐射范围更广；
（2）经验格林函数法可利用震后的小震记录快速模拟主震的加速度时程及PGA空间分布特征，可用于震后地震动强度空间分布的快速产出；
（3）经验格林函数法合成的地震动是台站所处位置的地震动，包含各种场地类别，不单纯是基岩层面上的地震动；
（4）主震与小震在盆地等特殊地形及有较厚覆盖层处的地震动放大倍数不同，因此利用余震快速合成主震时，需在盆地等特殊地形和厚覆盖层处考虑小震的修正系数，本文建议修正系数取值为1.0～3.0。
（5）本研究验证了经验格林函数法评估某地破坏性地震的地震动特征的可行性，为地震区划、建筑物震害分析所用的地震动输入等奠定基础。
俯冲带地震震源深度较深，但该区域地震波衰减较慢，导致强地震动影响范围较广，在近海区域可能造成严重的危害。我国有较长的海岸线，部分省市靠近板块俯冲带区域，俯冲带区域发生的大震可能造成较大影响，本研究认为下一代地震区划图（第六代）应针对沿海区域重点考虑类似海域俯冲带大震的影响，尤其是大震长周期地震动与沿海深厚覆盖土层放大效应的双重影响。
-
图 1 SMART-1台阵和LSST台阵相对位置示意
Figure 1. Relative positions of SMART-1 array and LSST array
图 3 东西向加速度时程及S波时间窗
Figure 3. Acceleration traces of EW components and the S-wave time window we used
图 6 不同台站间距的面波相干系数
Figure 6. Coherency coefficients of surface wave for different distances
图 7 不同间距下S波和面波拟合相干系数对比
Figure 7. Comparison of the coherency coefficients of S-wave and surface wave for different distances
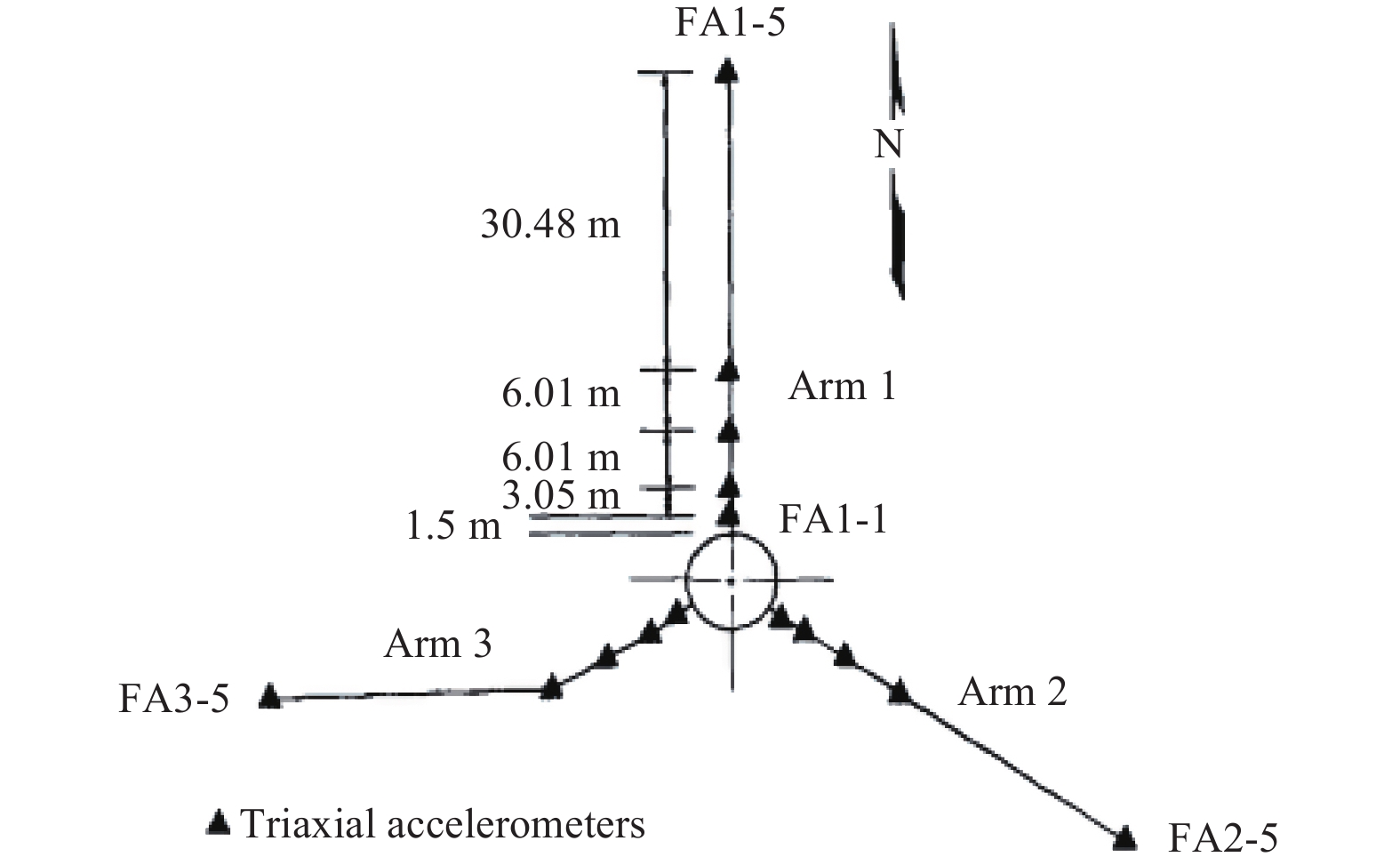
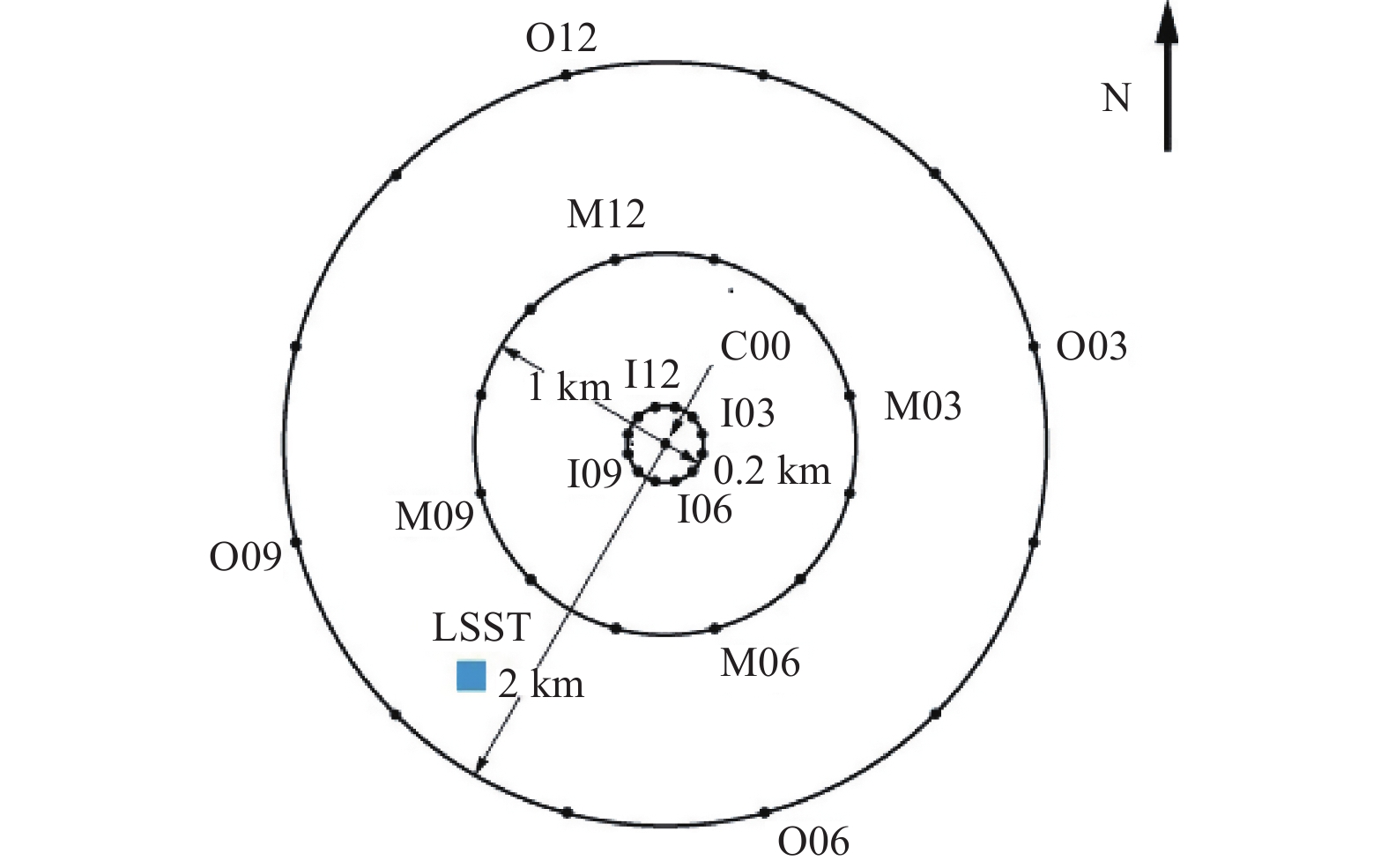
表 1 LSST台阵台站间距和相应的台站对
Table 1. Station spacing and station pairs of LSST array
台站间距d/m 台站对 3 FA1-1—FA1-2，FA2-1—FA2-2，FA3-1—FA3-2 6 FA1-2—FA1-3，FA1-3—FA1-4，FA2-2—FA2-3，
FA3-2—FA3-3，FA3-3—FA3- 49 FA1-1—FA1-3，FA2-1—FA2-3，FA3-1—FA3-3 36 FA1-3—FA1-5，FA2-3—FA2-5，FA3-3—FA3-5 45 FA1-1—FA1-5，FA2-1—FA2-5，FA3-1—FA3-5 86 FA1-5—FA2-5，FA2-5—FA3-5，FA3-5—FA1-5 
下载: 导出CSV
表 2 SMART-1台阵台站间距和相应的台站对
Table 2. Station spacing and station pairs of SMART-1 array
台站间距d/m 台站对 104 I03—I04，I04—I05，I05—I06，I06—I07 200 C00—I03，C00—I06，C00—I09，C00—I12 282 I03—I06，I06—I09，I09—I12 400 I01—I07，I03—I09，I06—I12 517 M03—M04，M05—M06 800 I03—M03，I05—M05，I06—M06
下载: 导出CSV
-
[1] 丁海平, 罗翼, 饶威波等, 2018. 截止频率的取值对地震动空间相干函数统计结果的影响. 地震学报, 40(5): 664—672Ding H. P. , Luo Y. , Rao W. B. , et al. , 2018. The influence of cut-off frequency on the statistical results of spatial coherency function of seismic ground motion. Acta Seismologica Sinica, 40(5): 664—672. (in Chinese) [2] 丁海平, 朱越, 李昕, 2020. 基于AR模型的相干函数有效频段范围的确定. 地震工程与工程振动, 40(1): 30—38Ding H. P. , Zhu Y. , Li X. , 2020. Determination of effective frequency range for coherency function based on autoregressive model. Earthquake Engineering and Engineering Dynamics, 40(1): 30—38. (in Chinese) [3] 李英民, 吴哲骞, 陈辉国, 2013. 地震动的空间变化特性分析与修正相干模型. 振动与冲击, 32(2): 164—170 doi: 10.3969/j.issn.1000-3835.2013.02.032Li Y. M. , Wu Z. Q. , Chen H. G. , 2013. Analysis and modeling for characteristics of spatially varying ground motion. Journal of Vibration and Shock, 32(2): 164—170. (in Chinese) doi: 10.3969/j.issn.1000-3835.2013.02.032 [4] 刘先明, 叶继红, 李爱群, 2004. 竖向地震动场的空间相干函数模型. 工程力学, 21(2): 140—144 doi: 10.3969/j.issn.1000-4750.2004.02.024Liu X. M. , Ye J. H. , Li A. Q. , 2004. Space coherency function model of vertical ground motion. Engineering Mechanics, 21(2): 140—144. (in Chinese) doi: 10.3969/j.issn.1000-4750.2004.02.024 [5] 马俊玲, 罗翼, 丁海平, 2018. 不同地震波波形对相干系数影响的对比分析. 自然灾害学报, 27(5): 20—26Ma J. L. , Luo Y. , Ding H. P. , 2018. Comparison of influence of different seismic wave types on coherence coefficient. Journal of Natural Disasters, 27(5): 20—26. (in Chinese) [6] Abrahamson N. A. , Bolt B. A. , Darragh R. B. , et al. , 1987. The SMART I accelerograph array (1980-1987): a review. Earthquake Spectra, 3(2): 263—287. doi: 10.1193/1.1585428 [7] Abrahamson N. A. , Schneider J. F. , Stepp J. C. , 1991. Empirical spatial coherency functions for application to soil-structure interaction analyses. Earthquake Spectra, 7(1): 1—27. doi: 10.1193/1.1585610 [8] Darragh R. B., 1988. Analysis of near-source waves: separation of wave types using strong motion array recordings. Earthquake Engineering Research Center, Report No. UCB/EERC-88/08, Berkeley: University of California. [9] Ding H. P. , Trifunac M. D. , Todorovska M. I. , et al. , 2015. Coherence of dispersed synthetic strong earthquake ground motion at small separation distances. Soil Dynamics and Earthquake Engineering, 70: 1—10. doi: 10.1016/j.soildyn.2014.11.010 [10] Hao H., 1989. Effects of spatial variation of ground motions on large multiply-supported structures. Report No. UCB/EERC-89/06, Berkeley: University of California. [11] Hao H. , 1993. Arch responses to correlated multiple excitations. Earthquake Engineering & Structural Dynamics, 22(5): 389—404. [12] Harichandran R. S. , Vanmarcke E. H. , 1986. Stochastic variation of earthquake ground motion in space and time. Journal of Engineering Mechanics, 112(2): 154—174. doi: 10.1061/(ASCE)0733-9399(1986)112:2(154) [13] Imtiaz A., 2015. Seismic wave field, spatial variability and coherency of ground motion over short distances: near source and alluvial valley effects. French: Université Grenoble Alpes. [14] Liao S. T., 2006. Physical characterization of seismic ground motion spatial variation and conditional simulation for performance-based design. Philadelphia: Drexel University. [15] Loh C. H. , Lin S. G. , 1990. Directionality and simulation in spatial variation of seismic waves. Engineering Structures, 12(2): 134—143. doi: 10.1016/0141-0296(90)90019-O [16] Riepl J. , Oliveira C. S. , Bard P. Y. , 1997. Spatial coherence of seismic wave fields across an alluvial valley (weak motion). Journal of Seismology, 1(3): 253—268. doi: 10.1023/A:1009725604616 [17] Schneider J. F., Stepp J. C., Abrahamson N. A. 1992. The spatial variation of earthquake ground motion and effects of local site condition. Proceedings, Tenth World Conference on Earthquake Engineering. A. A. Balkema, Rotterdam. 967—972 [18] Todorovska M. I. , Trifunac M. D. , Ding H. P. , et al. , 2015. Coherency of dispersed synthetic earthquake ground motion at small separation distances: dependence on site conditions. Soil Dynamics and Earthquake Engineering, 79: 253—264. doi: 10.1016/j.soildyn.2015.08.004 [19] Toksöz M. N. , Dainty A. M. , Charrette III E. E. , 1991. Spatial variation of ground motion due to lateral heterogeneity. Structural Safety, 10(1—3): 53—77. doi: 10.1016/0167-4730(91)90006-U [20] Zerva A. , Zhang O. , 1997. Correlation patterns in characteristics of spatially variable seismic ground motions. Earthquake Engineering & Structural Dynamics, 26(1): 19—39. [21] Zerva A. , 2009. Spatial variation of seismic ground motions. Boca Raton: CRC Press. [22] Zerva A. , Stephenson W. R. , 2011. Stochastic characteristics of seismic excitations at a non-uniform (rock and soil) site. Soil Dynamics and Earthquake Engineering, 31(9): 1261—1284. doi: 10.1016/j.soildyn.2011.05.006 -
下载:
点击查看大图
计量
- 文章访问数: 147
- HTML全文浏览量: 56
- PDF下载量: 13
- 被引次数: 0
