Study on Vibration Effect of Combined Heavy Tamping on Soft Soil Foundation in City
-
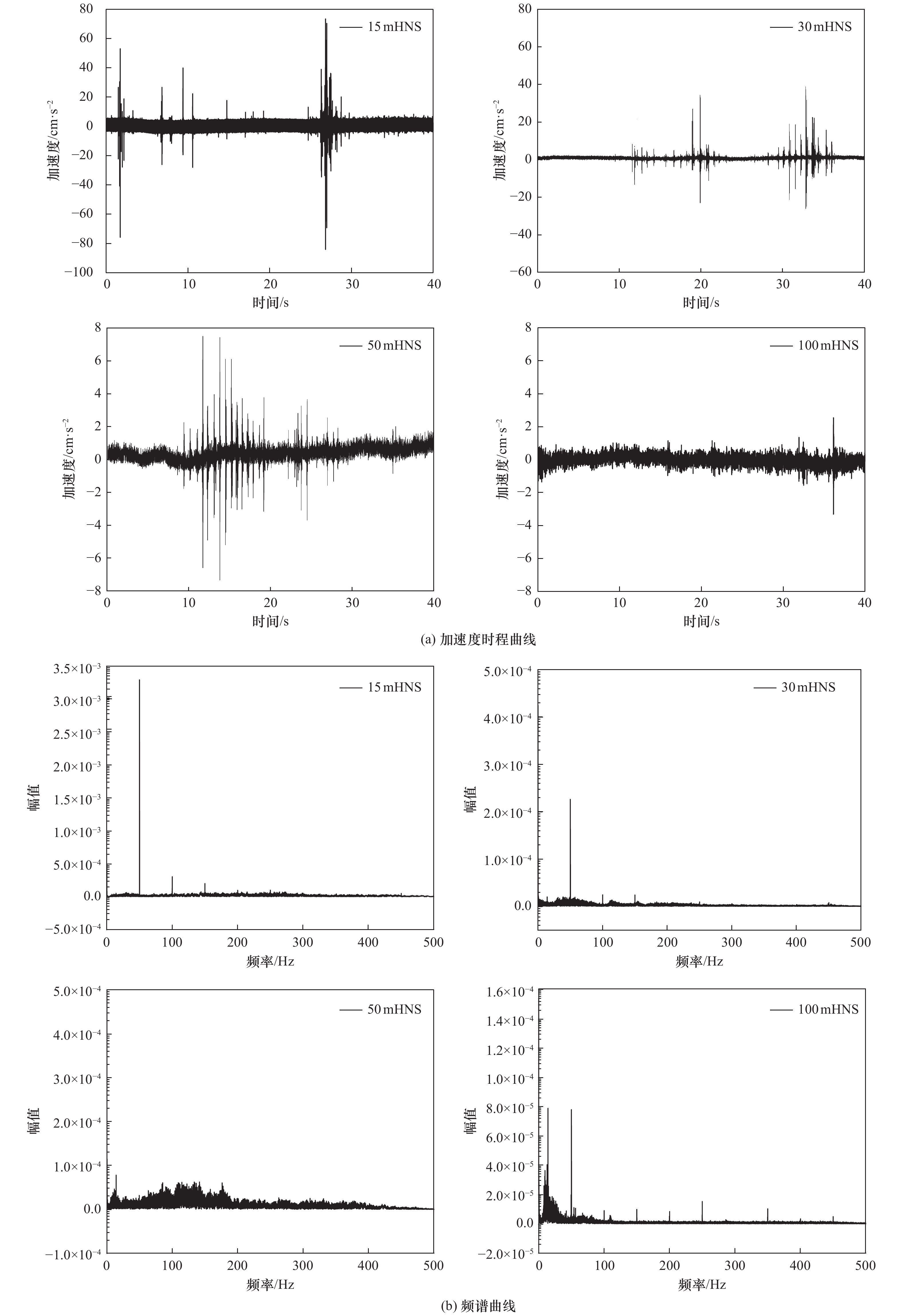
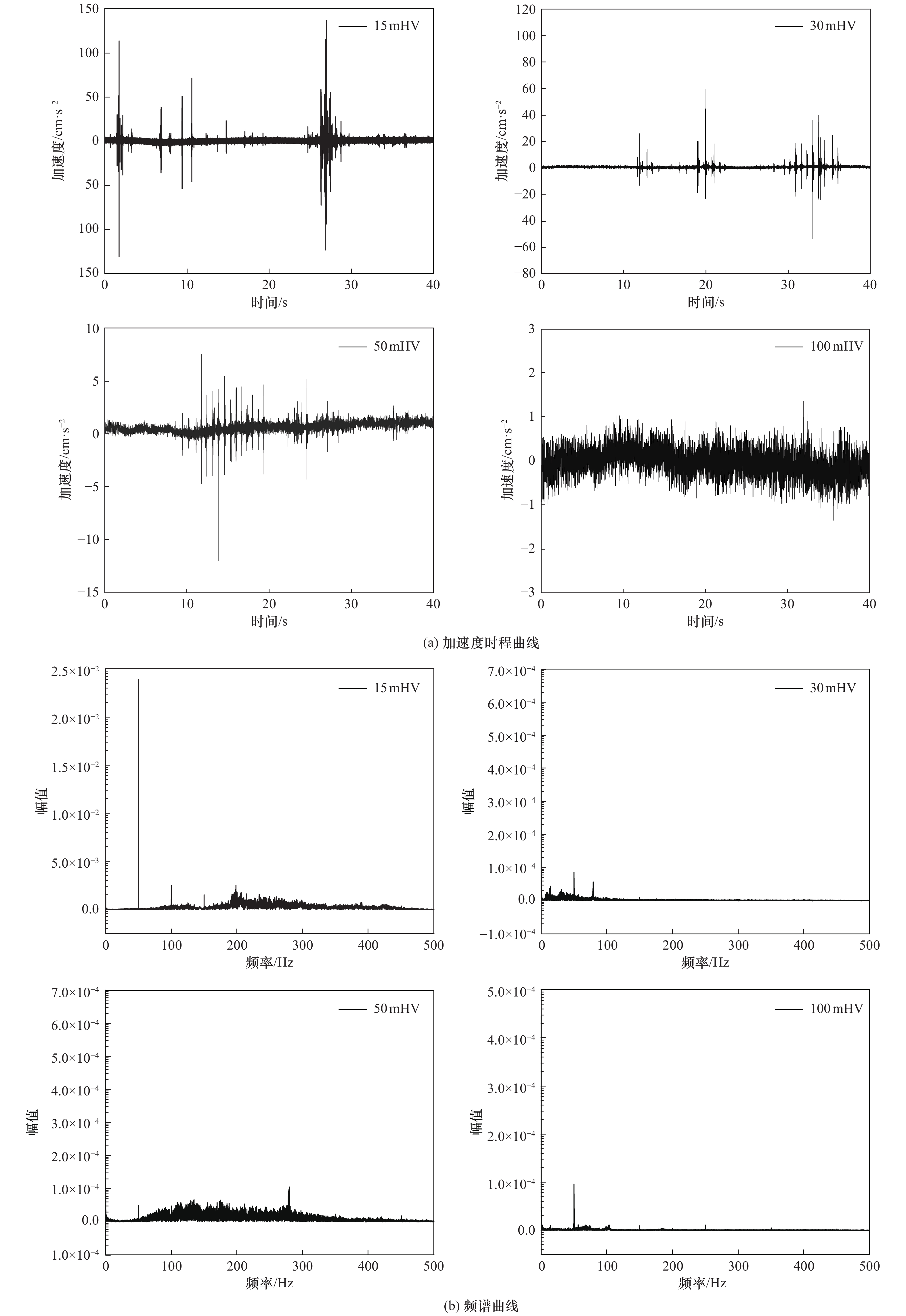
摘要: 为研究组合锤法强夯振动对周边场地环境的影响，对南昌市某软土地基进行现场原位试验。考虑距强夯点的距离、振动方向及锤击次数的影响，在各监测点分别布置水平东西、南北向和竖向振动传感器。结果表明：采用组合锤法进行地基强夯施工时，场地竖向振动是需重点监测的内容，振动响应随监测点与强夯点距离的增大而减小；距强夯点50 m范围处地面振动速度衰减至0.2 cm/s以下，可根据地面振动速度确定安全施工范围；地面加速度受锤击次数的影响较大，且水平向加速度对锤击次数的敏感性略高于竖向，锤击次数对地面水平向振动的影响不可忽略；基于试验数据和波源振动理论建立的振动加速度衰减模型综合考虑了距强夯点的距离、振动方向和修正系数（锤击次数的影响），经算例验证具有较强的适用性，可为同类场地采用组合锤法强夯施工提供参考。Abstract: In order to study the vibration effect of composite hammer method on the surrounding environment and its influencing factors, a soft soil foundation in Nanchang was tested. In the test, the influence of different distance, vibration direction and hammer times from the tamping point is considered, and the horizontal east-west, north-south and vertical vibration sensors are arranged at each measuring point respectively.The results show that the vertical vibration of the site is the key content to be monitored during the dynamic compaction of foundation by the combined hammer method, and the vibration response decreases with the increase of the distance between the monitoring point and the hammer point.The vibration velocity of the ground out the 50 m range attenuates to less than 0.2 cm/s, and the safe construction range can be determined according to the vibration velocity of the ground.The ground acceleration is greatly affected by the number of hammer blows (the maximum increase is 61.0%), and the sensitivity of horizontal acceleration to the number of hammer blows is slightly higher than that of vertical. The impact of the number of rammers on the horizontal vibration of the ground cannot be ignored.The attenuation model of vibration acceleration based on test data and wave source vibration theory takes into account the influence of distance, vibration direction and correction coefficient (the number of hammer strikes), which is proved to have strong applicability by calculation examples, and provides a certain reference for similar sites using combined hammer method.
-
图 2 监测点水平东西向加速度时程曲线与频谱曲线
Figure 2. Time history analysis curve and spectrum curve of horizontal east-west acceleration at different distances
图 3 监测点水平南北向加速度时程曲线与频谱曲线
Figure 3. Acceleration time history analysis curves of horizontal north-south direction at different distances
图 4 监测点竖向加速度时程曲线与频谱曲线
Figure 4. Acceleration time-history analysis curves and spectrum curves of vertical direction at different distances
图 5 监测点加速度峰值随距离衰减曲线
Figure 5. Attenuation curve of peak acceleration of monitoring points with distance
图 6 监测点竖向速度峰值随距离衰减曲线
Figure 6. Attenuation curve of peak vertical velocity of monitoring points with distance
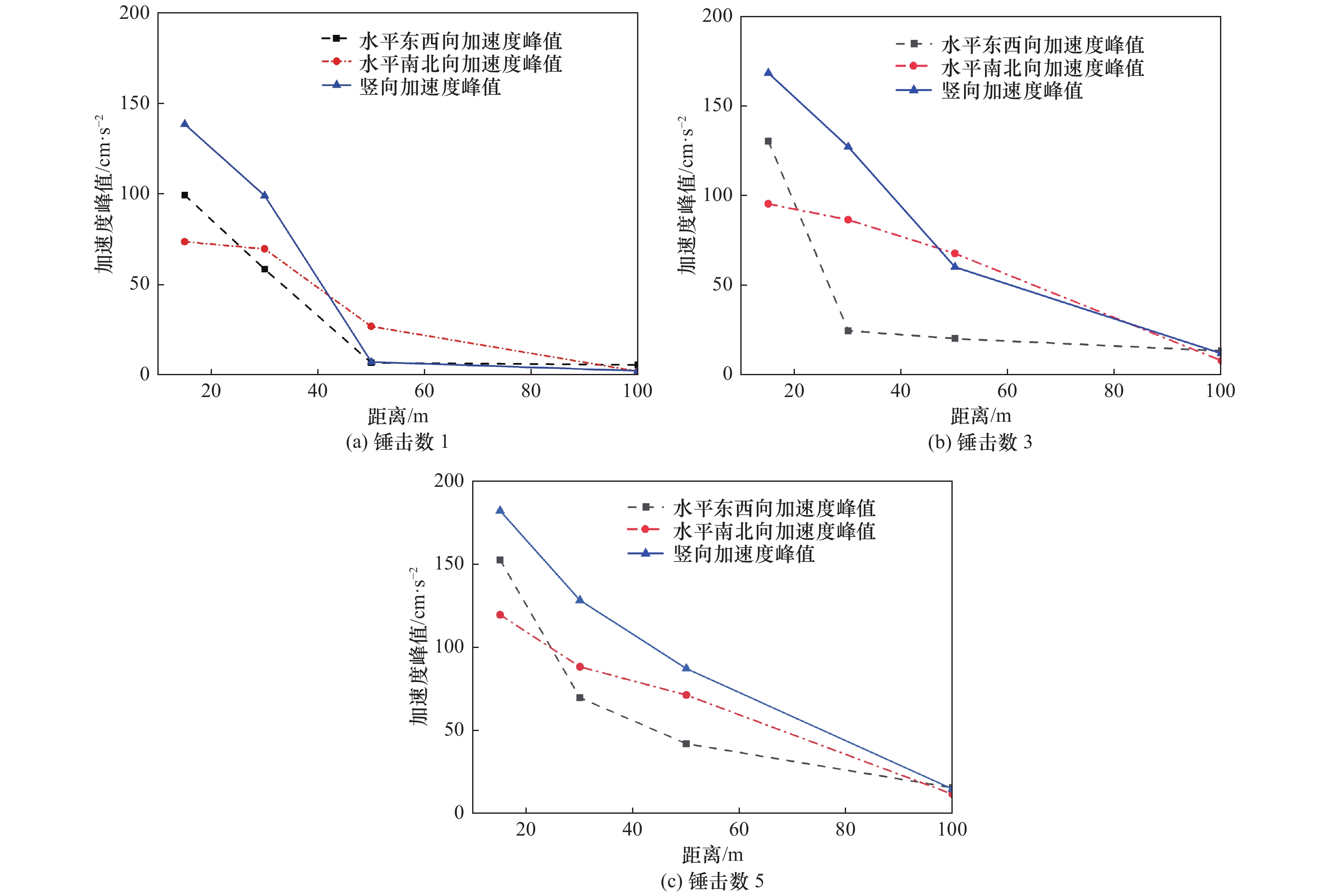
表 1 监测点加速度峰值与速度峰值
Table 1. Peak acceleration and peak velocity at monitoring points
监测点 水平东西向 水平南北向 竖向 加速度峰值/cm·s−2 速度峰值/cm·s−1 加速度峰值/cm·s−2 速度峰值/cm·s−1 加速度峰值/cm·s−2 速度峰值/cm·s−1 15 m 99.9 2.5 74.1 2.8 139.1 3.1 30 m 58.9 1.8 71.6 2.0 99.5 2.6 50 m 7.2 0.3 27.1 0.4 7.5 2.0 100 m 5.9（剔除异常点） 0.1 2.4 0.1 2.6 0.3 
下载: 导出CSV
表 2 衰减曲线回归分析结果
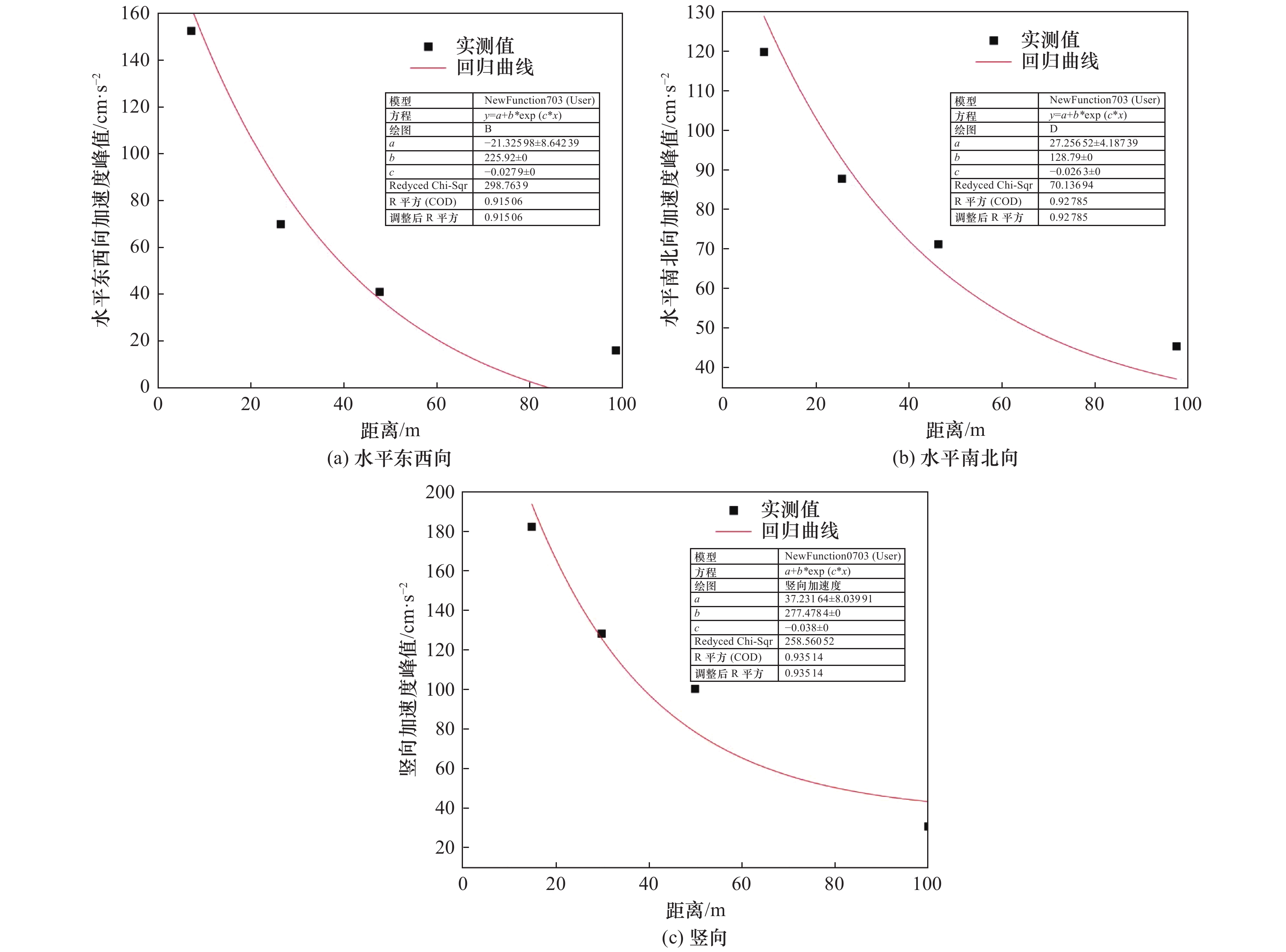
Table 2. Results of regression analysis of attenuation curveResults of regression analysis of attenuation curve
方向 加速度衰减公式 相关系数 水平东西向 ${A_x} = - 21.325 + 225.927\;5{ {\rm{e} }^{\left({ - 0.02\;9r/{r_{_0}}{\rm{} } } \right)} }$ 0.915 水平南北向 ${A_y} = 27.256 + 138.790\;3{ {\rm{e} }^{\left({ - 0.026\;3r/{r_{_0}}{\rm{} } } \right)} }$ 0.927 竖向 ${A_z} = 37.231 + 277.478\;4{ {\rm{e} }^{\left({ - 0.038\;0r/{r_{_0}} } \right)} }$ 0.935
下载: 导出CSV
-
[1] 韩俊艳, 万宁潭, 赵密等, 2020. 打桩荷载作用下自由场土体振动衰减规律研究. 震灾防御技术, 15(2): 274—284.Han J. Y., Wan N. T., Zhao M., et al., 2020. Research on vibration attenuation of free field soil under pile driving load. Technology for Earthquake Disaster Prevention, 15(2): 274—284. [2] Hwang J. H., Tu T. Y., 2006. Ground vibration due to dynamic compaction. Soil Dynamics and Earthquake Engineering, 26(5): 337—346. doi: 10.1016/j.soildyn.2005.12.004 [3] 李俊如, 高建光, 邵蔚等, 2002. 砂土中的强夯振动对周边环境的影响研究. 岩土力学, 23(S1): 198—200.Li J. R., Gao J. G., Shao W., et al., 2002. Research on influence of dynamic compaction vibration of sand-soil on surroundings. Rock and Soil Mechanics, 23(S1): 198—200. [4] 林伟斌, 周雷靖, 2018. 回填砂土地基上强夯振动影响及处理效果研究. 武汉大学学报(工学版), 51(S1): 174—177.Lin W. B., Zhou L. J., 2018. Research on vibration effect from dynamic compaction on backfilling sand-soil subgrade and its treatment result. Engineering Journal of Wuhan University, 51(S1): 174—177. [5] Pan J. L., Selby A. R., 2002. Simulation of dynamic compaction of loose granular soils. Advances in Engineering Software, 33(7—10): 631—640. [6] 尚军雷, 徐风, 王韶光, 2006. 施工振动对邻近建筑的危害. 工业建筑, 36(S1): 981—982.Shang J. L., Xu F., Wang S. G., 2006. The vibration damage to the adjacent buildings during construction. Industrial Construction, 36(S1): 981—982. [7] 时伟, 邵琪琳, 董炳寅等, 2019. 深厚粉细砂场地8000 kN·m能级强夯振动衰减规律研究. 西安建筑科技大学学报(自然科学版), 51(3): 309—314.Shi W., Shao Q. L., Dong B. Y., et al., 2019. Research on vibration decay law of 8 000 kN·m energy level dynamic compaction in deep silty sand site. Journal of Xi'an University of Architecture & Technology (Natural Science Edition), 51(3): 309—314. [8] 谭捍华, 孙进忠, 祁生文, 2001. 强夯振动衰减规律的研究. 工程勘察, (5): 11—14.Tan H. H., Sun J. Z., Qi S. W., 2001. On the bracing technique by using jet anchor for sandy gravel excavation engineering. Geotechnical Investigation & Surveying, (5): 11—14. [9] 王杰贤, 2001. 动力地基与基础. 北京: 科学出版社. [10] 王鹏程, 刘建坤, 冯瑞玲, 2015. 强夯振动主控因素研究. 地下空间与工程学报, 11(5): 1282—1288.Wang P. C. Liu J. K. Feng R. L., 2015. Research on the primary controlling factors of vibration of dynamic compaction. Chinese Journal of Underground Space and Engineering, 11(5): 1282—1288. [11] 王斯海, 陈海军, 王世坚, 2016. 不同土层结构场地强夯振动效应研究. 施工技术, 45(S1): 15—19.Wang S. H., Chen H. J., Wang S. X., 2016. Study on vibration effect by dynamic compaction in different site condition of soil layer. Construction Technology, 45(S1): 15—19. [12] 吴绵拔, 李俊如, 1992. 强夯对环境的振动影响研究. 土工基础, (2): 13—18.Wu M. B., Li J. R., 1992. Study of environmental effect of vibration caused by dynamic compaction. Soil Engineering and Foundation, (2): 13—18. [13] 夏瑞良, 龚小平, 沈小七, 2001. 强夯引起地面振动的衰减特征. 地震学刊, 21(2): 41—43, 66. doi: 10.3969/j.issn.1672-2132.2001.02.010Xia R. L., Gong X. P., Shen X. Q., 2001. Attenuation characteristics of the ground vibration caused by strong tamping. Journal of Seismology, 21(2): 41—43, 66. doi: 10.3969/j.issn.1672-2132.2001.02.010 [14] 杨明, 黄曙英, 2011. 强夯振动监测及评估方法在变电站工程中的应用. 武汉大学学报(工学版), 44(S1): 397—400.Yang M., Huang S. Y., 2011. Vibration monitoring and evaluation of dynamic compaction method in substation engineering. Engineering Journal of Wuhan University, 44(S1): 397—400. [15] 张宏博, 厉超, 宋修广等, 2015. 强夯加固粉土地基地面振动衰减规律研究. 地下空间与工程学报, 11(5): 1289—1295.Zhang H. B., Li C., Song X. G., et al., 2015. Study on ground vibration attenuation law of silt foundation treated with dynamic compaction. Chinese Journal of Underground Space and Engineering, 11(5): 1289—1295. [16] 张力闻, 2017. 强夯振动对挡土墙稳定性的影响研究. 北京: 中国地质大学（北京）.Zhang L. W., 2017. Study on the influence of dynamic compaction vibration on the stability of retaining wall. Beijing: China University of Geosciences (Beijing). [17] 张露露, 方勇, 2016. 强夯振动监测及安全距离预估. 施工技术, 45(13): 75—77. doi: 10.7672/sgjs2016130075Zhang L. L., Fang Y., 2016. Vibration monitoring and safety distance forecast of dynamic consolidation construction. Construction Technology, 45(13): 75—77. doi: 10.7672/sgjs2016130075 [18] 周洋, 阿拉塔, 郭迅等, 2018. 强夯振动衰减规律及其对建筑安全性的影响. 震灾防御技术, 13(4): 860—868. doi: 10.11899/zzfy20180413Zhou Y., A L. T., Guo X., et al., 2018. Investigation on vibration attenuation laws with dynamic compaction vibration and the effect on building safety. Technology for Earthquake Disaster Prevention, 13(4): 860—868. doi: 10.11899/zzfy20180413 [19] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会, 2015. GB 6722—2014 爆破安全规程. 北京: 中国标准出版社.General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of China, 2015. GB 6722—2014 Safety regulations for blasting. Beijing: China Standards Press (in Chinese). -
点击查看大图
计量
- 文章访问数: 183
- HTML全文浏览量: 49
- PDF下载量: 5
- 被引次数: 0
