Study on Nonlinear Statistical Characteristics of Surface/Downhole Response Spectrum Ratio and Influencing Factors
-
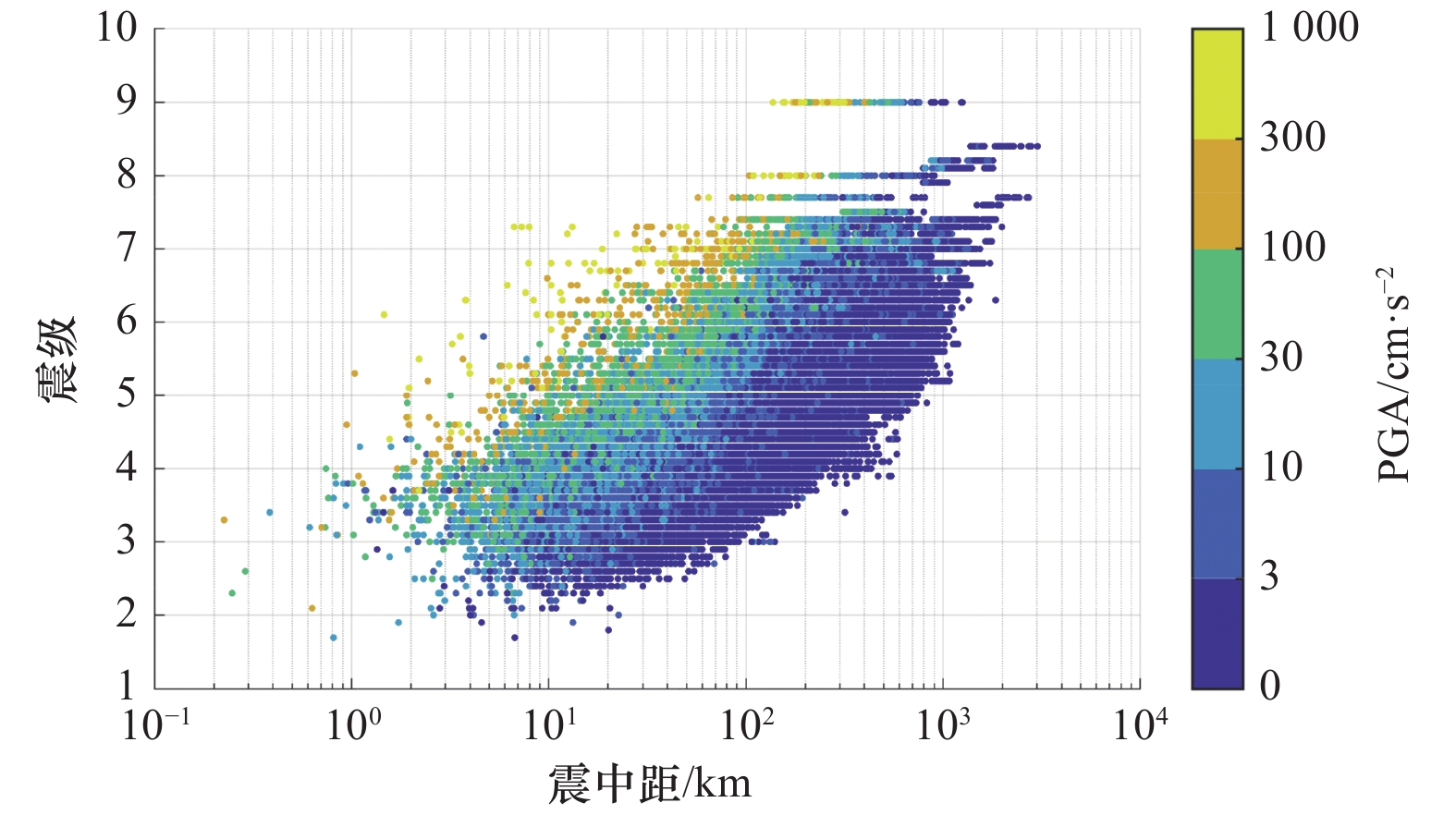
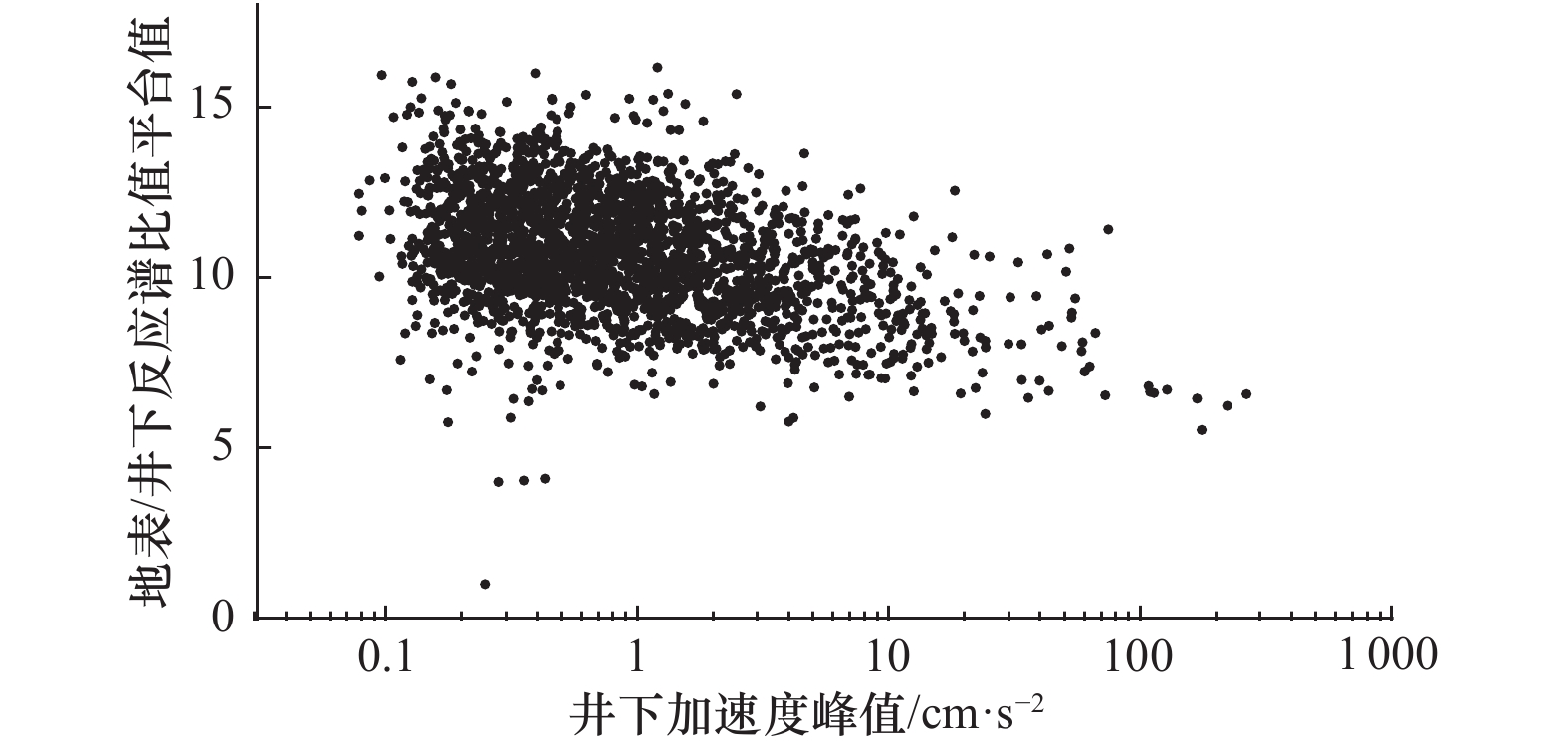
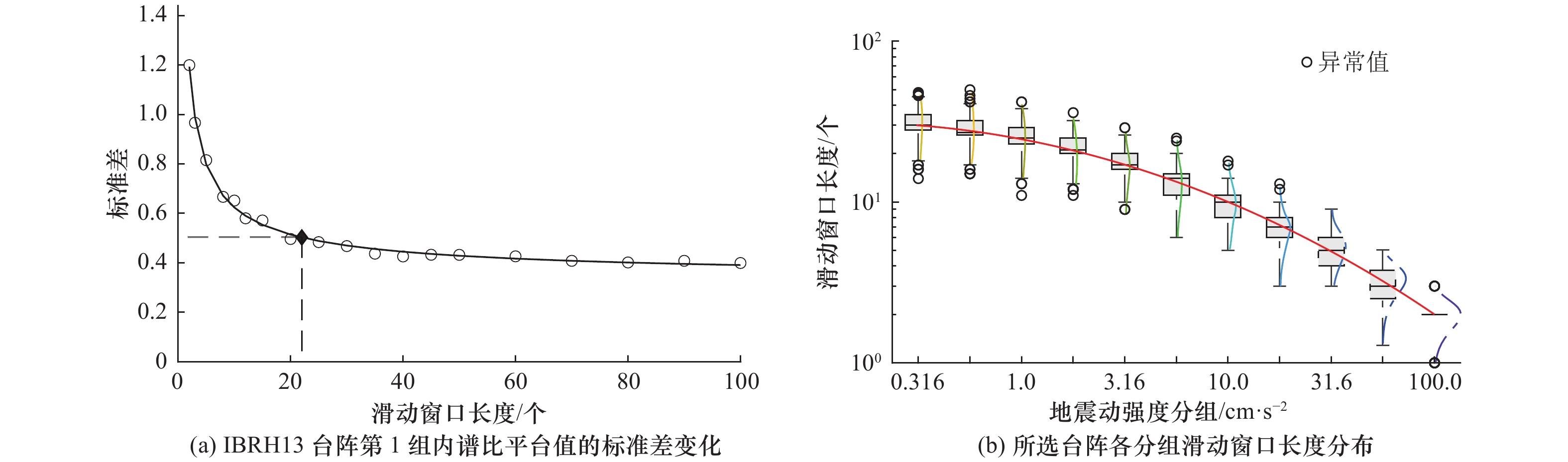
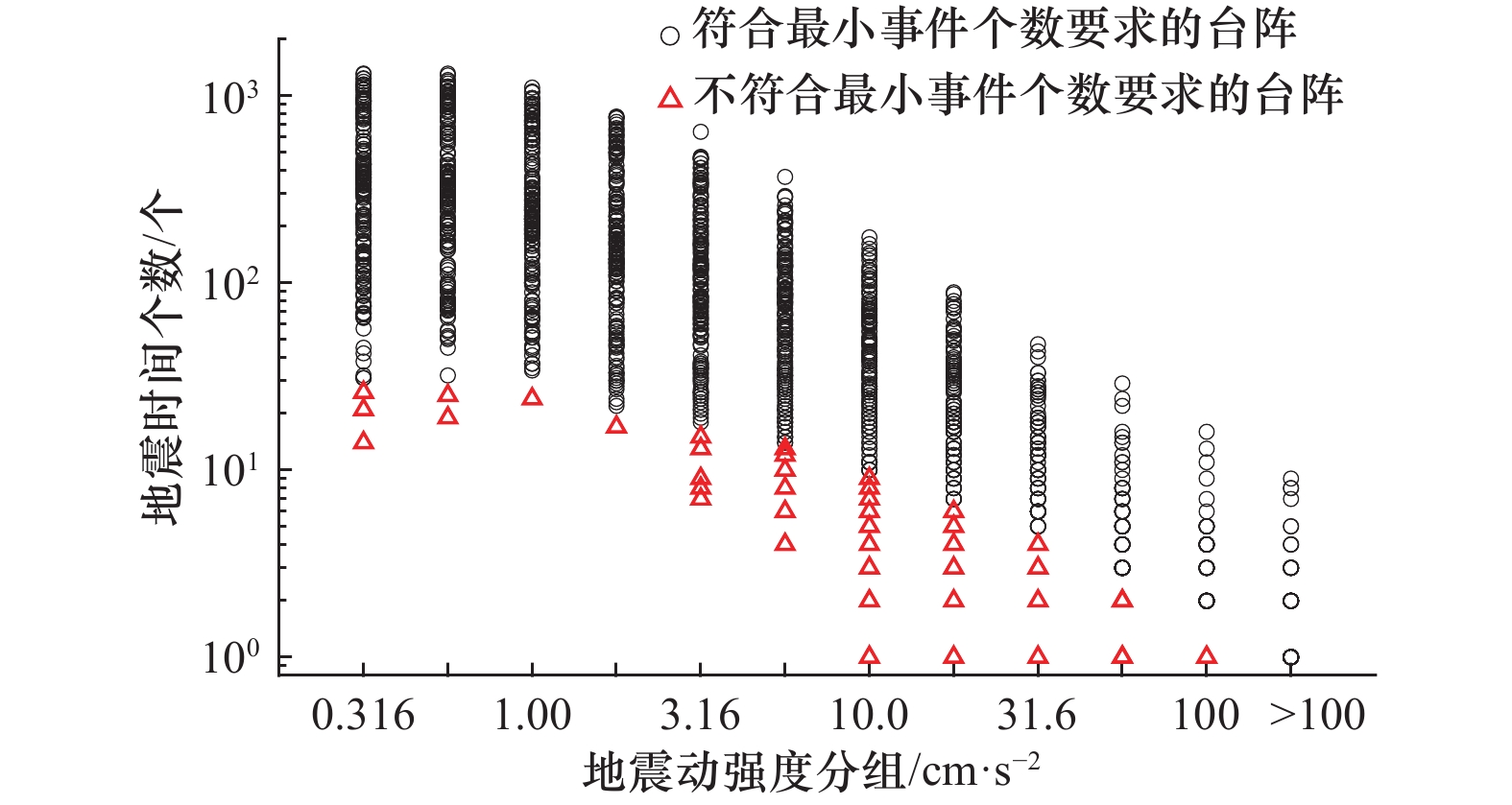
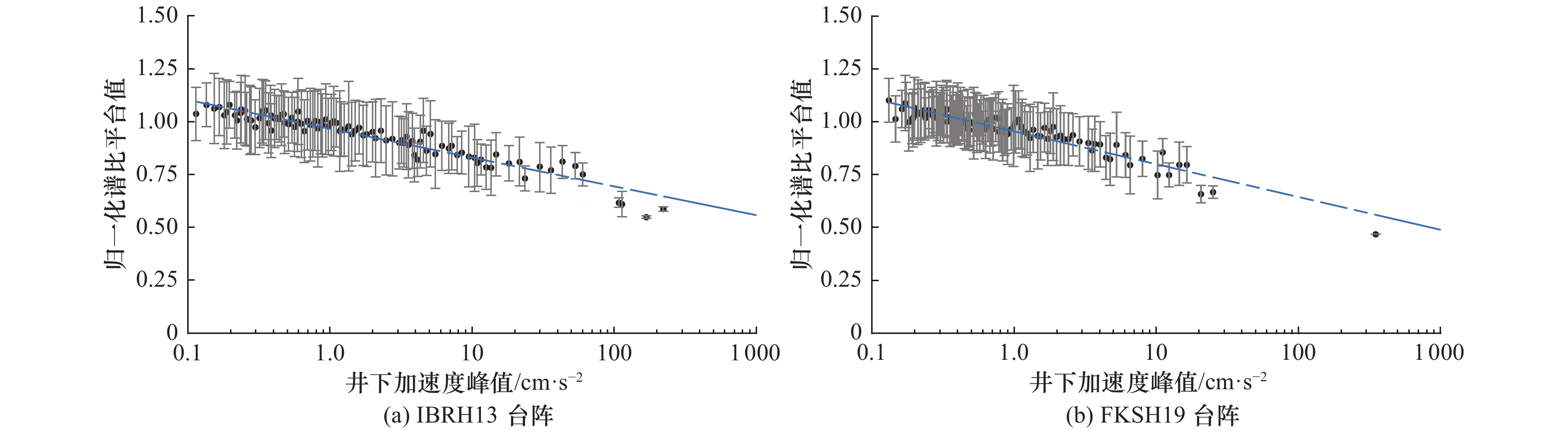
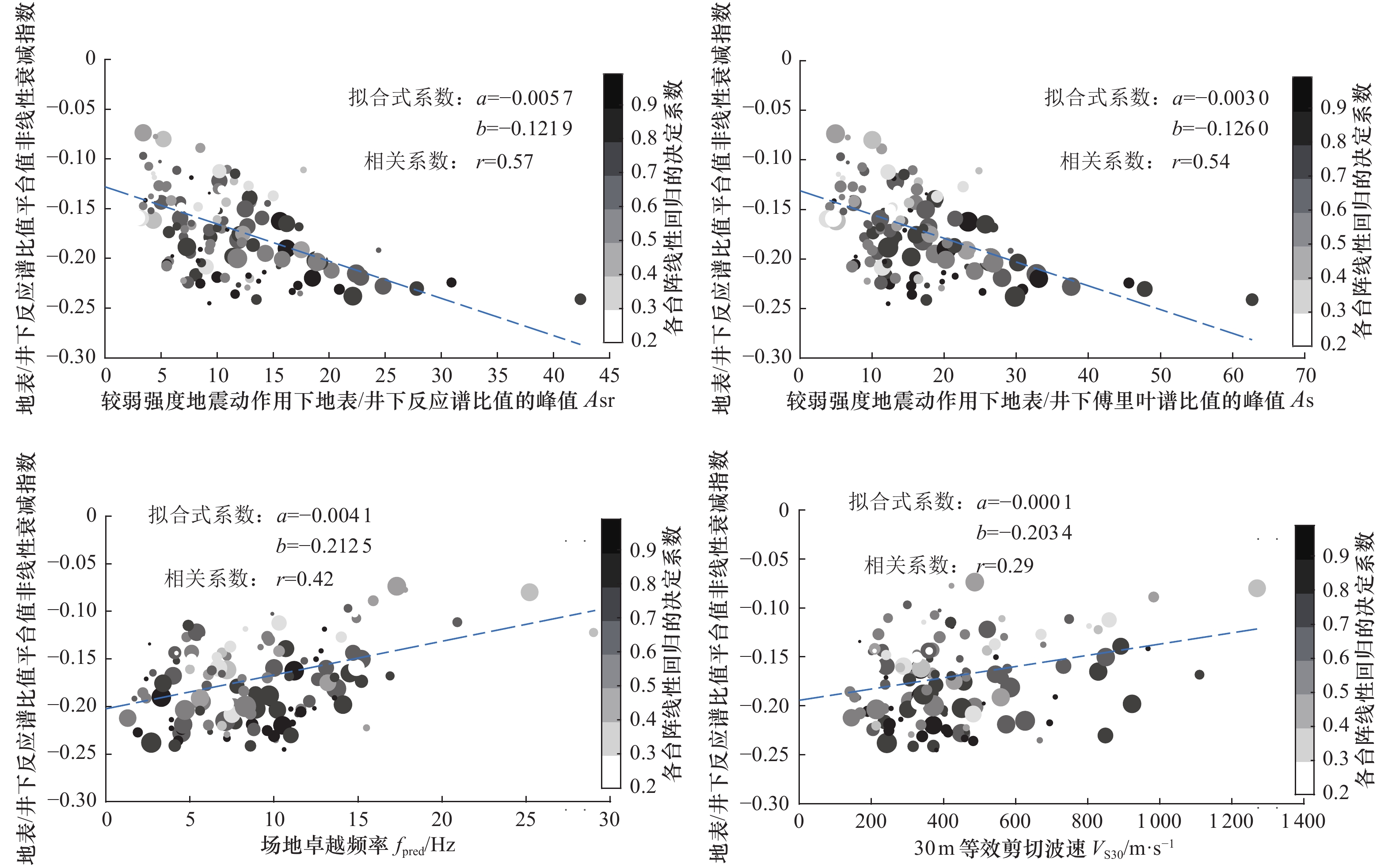
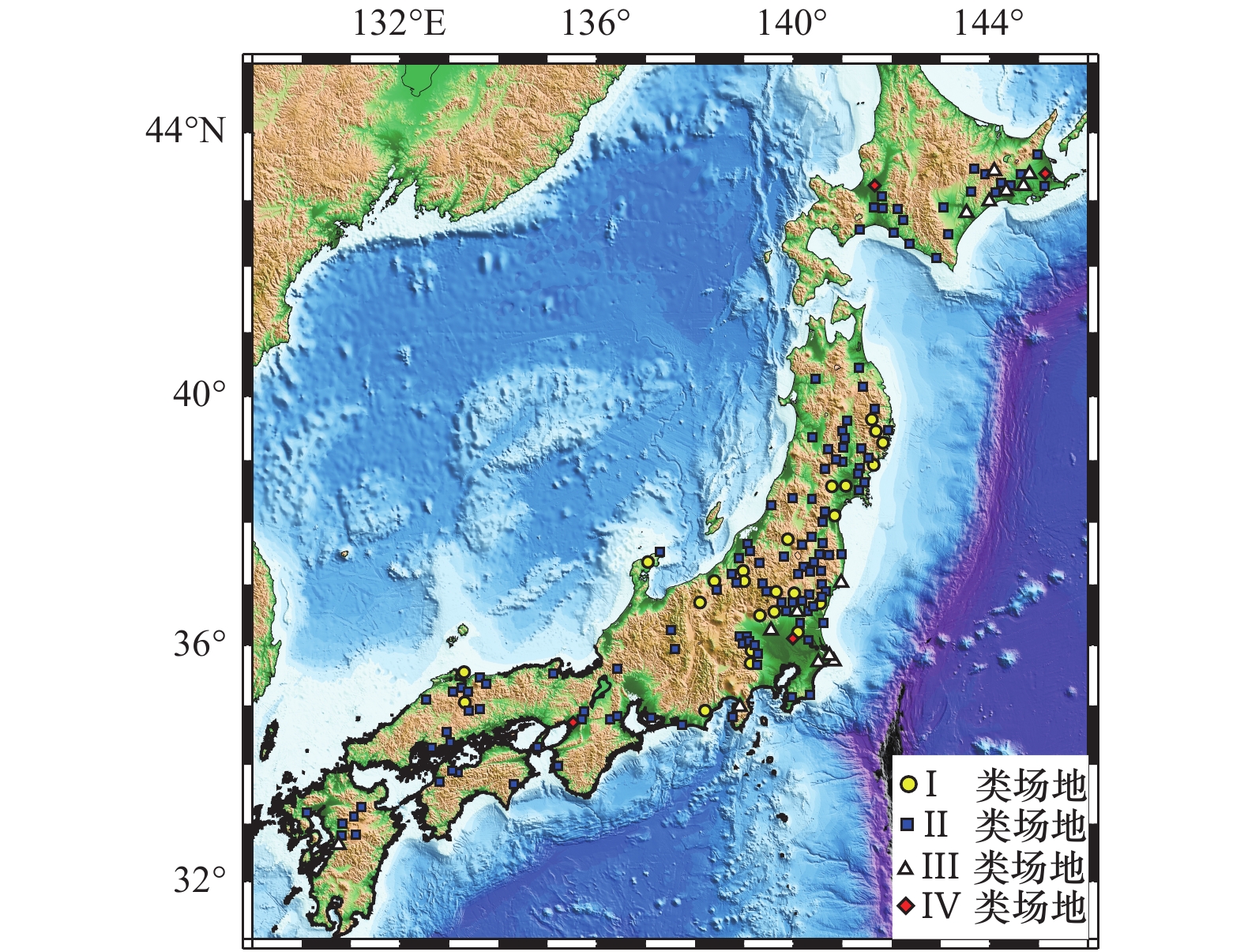
摘要: 浅地表软弱覆盖层对地震动的影响具有强非线性，但因观测记录样本量过小，难以通过参考谱比法等直接方法予以可靠分析。本文基于日本KiK-net台网136个竖向钻井台阵获取的141881组加速度记录的统计分析，研究了地表/井下反应谱比值随地震动强度变化的非线性变化规律与主要影响因素。利用变窗口尺度的滑动窗口平均法加强数据线性度，并确定了与地震动强度相关的台站最小记录样本量，统计结果表明地表/井下反应谱比值平台值随地震动强度变化的非线性衰减指数为−0.24～−0.08。利用套索（Lasso）算法统计回归发现，本研究12个场地特性表征参数中，30 m平均剪切波速（
$ {V}_{\mathrm{s}30} $ ）、场地卓越频率与地表/井下反应谱比值非线性衰减指数具有较好的正相关性；较弱强度地震动作用下地表/井下傅里叶谱比值峰值、地表/井下反应谱比值峰值与地表/井下反应谱比值非线性衰减指数具有较好的负相关性。Abstract: The influence of shallow soft overburden on ground motion is strongly nonlinear, but it is difficult to make reliable analysis by direct methods such as reference spectral ratio method because of the small sample size of observation records. In this study, based on the statistical analysis of 141881 sets of acceleration records obtained from 136 vertical borehole array in Japan’s KiK-net network, the nonlinear variation of surface/downhole response spectrum ratio and its main influencing factors of field motion intensity were studied. The sliding window average method with variable window scale was used to enhance the linearity of the data, and the minimum sample size related to the ground motion intensity was determined. The statistical results show that the nonlinear attenuation index of ground motion intensity variation is between −0.24 and −0.08 for the platform value of the surface/underground response spectrum ratio. According to Lasso regression statistics, the average shear wave velocity of 30 m ($ {V}_{S30} $ ) and site predominant frequency have a good positive correlation with the nonlinear attenuation index of surface/downhole response spectrum ratio among the 12 site characteristic parameters studied. However, the peak values of the surface/downhole fourier spectrum ratio and the surface/downhole response spectrum ratio are negatively correlated with the nonlinear attenuation index of the surface/downhole response spectrum ratio under the weak ground motion.-
Key words:
- Strong motion /
- Site effect /
- Response spectrum /
- Nonlinear /
- Vertical borehole arrays
-
1. 2019年中国地震概况
2019年中国共发生5.0级（含）以上地震32次（其中大陆发生20次，台湾地区及附近海域发生12次），其中5.0—5.9级地震27次，6.0—6.9级地震5次。最大地震为2019年4月18日台湾花莲县发生的6.7级地震（表 1）。
表 1 2019年中国5.0级（含）以上地震一览表Table 1. Catalogue of earthquakes (M≥5.0) in China in 2019序号 日期 北京时间 经度/度 纬度/度 震源深度/km 震级/M 震中位置 1 01月03日 08:48 104.86 28.20 15 5.3 四川宜宾市珙县 2 01月12日 12:32 75.59 39.57 10 5.1 新疆喀什地区疏附县 3 01月20日 22:28 87.77 30.09 10 5.0 西藏日喀则市谢通门县 4 01月30日 13:21 122.43 23.77 20 5.2 台湾花莲县海域 5 02月02日 05:54 83.34 46.73 16 5.2 新疆塔城地区塔城市 6 03月08日 10:32 121.34 22.46 11 5.3 台湾台东县海域 7 03月28日 05:36 90.89 38.28 9 5.0 青海海西州茫崖市 8 04月03日 09:52 120.87 22.95 12 5.7 台湾台东县 9 04月04日 09:56 120.85 22.99 10 5.1 台湾台东县 10 04月09日 23:13 121.61 23.96 10 5.0 台湾花莲县海域 11 04月18日 13:01 121.65 24.02 24 6.7 台湾花莲县海域 12 04月24日 04:15 94.61 28.40 10 6.3 西藏林芝市墨脱县 13 05月18日 06:24 124.75 45.30 10 5.1 吉林松原市宁江区 14 06月04日 17:46 121.75 22.82 9 5.8 台湾台东县海域 15 06月17日 22:55 104.9 28.34 16 6.0 四川宜宾市长宁县 16 06月17日 23:36 104.77 28.43 16 5.1 四川宜宾市珙县 17 06月18日 07:34 104.89 28.37 17 5.3 四川宜宾市长宁县 18 06月22日 22:29 104.77 28.43 10 5.4 四川宜宾市珙县 19 07月04日 10:17 104.74 28.41 8 5.6 四川宜宾市珙县 20 07月13日 08:57 128.26 29.15 230 6.0 东海海域 21 07月19日 17:22 92.89 27.67 10 5.6 西藏山南市错那县 22 08月08日 05:28 121.96 24.52 30 6.4 台湾宜兰县海域 23 08月18日 12:05 121.57 23.74 6 5.0 台湾花莲县 24 09月05日 21:58 116.16 14.77 20 5.2 南海海域 25 09月08日 06:42 104.79 29.55 10 5.4 四川内江市威远县 26 09月16日 20:48 100.35 38.60 11 5.0 甘肃张掖市甘州区 27 10月12日 22:55 110.51 22.18 10 5.2 广西玉林市北流市 28 10月17日 19:44 122.58 24.02 16 5.1 台湾花莲县海域 29 10月27日 13:29 78.82 41.21 11 5.0 新疆阿克苏地区乌什县 30 10月28日 01:56 102.69 35.10 10 5.7 甘肃甘南州夏河县 31 11月25日 09:18 106.65 22.89 10 5.2 广西百色市靖西市 32 12月18日 08:14 104.82 29.59 14 5.2 四川内江市资中县 2. 2019年中国大陆地震灾害情况
2019年，中国大陆共发生地震灾害事件15次（表 2），造成17人死亡，425人受伤，直接经济损失约91亿元。其中，灾害最为严重的地震为四川长宁6.0级地震，造成13人死亡，299人受伤，直接经济损失约56亿元，占全年地震造成直接经济损失的61.54%（四川省地震局，2019a）。中国大陆地区5级以上地震和成灾地震（含4.9级地震）分布图如图 1所示，其中造成人员死亡的地震划分为致灾严重地震，造成人员受伤和经济损失的地震划分为致灾较轻地震，未造成经济损失的地震划分为一般地震。
表 2 2019年大陆地区地震灾害损失一览表Table 2. Losses caused by earthquake disasters in Chinese mainland in 2019序号 日期 北京时间 震中位置 震级/M 人员伤亡 直接经济损失/万元 死亡或失踪/人 受伤/人 1 01月03日 08:48 四川宜宾市珙县 5.3 0 1 6000 2 02月24日 05:38 四川自贡市荣县 4.7 2 13 17700 02月25日 08:40 4.3 13:15 4.9 3 03月28日 05:36 青海海西州茫崖市 5.0 0 0 66700 4 04月24日 04:15 西藏林芝市墨脱县 6.3 — — — 5 05月18日 06:24 吉林松原市宁江区 5.1 0 0 5100 6 06月17日 22:55 四川宜宾市长宁县 6.0 13 299 561700 23:36 四川宜宾市珙县 5.1 7 07月21日 20:23 云南丽江市永胜县 4.9 0 0 8100 8 09月08日 06:42 四川内江市威远县 5.4 1 82 58200 9 09月16日 20:48 甘肃张掖市甘州区 5.0 0 0 4700 10 10月02日 20:04 贵州铜仁市沿河县 4.9 0 0 860 11 10月12日 22:55 广西玉林市北流市 5.2 0 0 1300 12 10月28日 01:56 甘肃甘南州夏河县 5.7 0 7 161900 13 11月25日 09:18 广西百色市靖西市 5.2 1 5 12200 14 12月18日 08:14 四川内江市资中县 5.2 0 18 4900 15 12月26日 18:36 湖北孝感市应城市 4.9 0 0 1500 合计 17 425 910860 注：数据来源应急管理部国家减灾中心，2020。其中，国家减灾中心对2月24日和2月25日地震造成的人员伤亡和经济损失情况只进行一次统计，因此看作一次地震灾害事件。 
图 1 2019年中国大陆地区5级以上地震和成灾地震（含4.9级地震）分布图Figure 1. Distribution of earthquake (M≥5.0) and disastrous earthquake (including M4.9) in Chinese mainland in 20193. 2019年中国地震灾害主要特点
2019年，地震造成中国大陆10个省（区、市）59.4万人次受灾，14万人次紧急转移安置，3900余间房屋倒塌，33.4万间房屋不同程度损坏（表 3）。同2000—2018年均值（不含2008年汶川地震巨灾数据）相比，主要灾情指标均减少五成以上，死亡（含失踪）人口、倒塌房屋数量减少九成以上。
表 3 2019年中国大陆各省份地震灾害损失一览表Table 3. Losses caused by earthquake disasters in provinces of Chinese mainland in 2019序号 省份 死亡或失踪/人 受伤/人 直接经济损失/万元 1 四川 16 413 648500 2 甘肃 0 7 166600 3 青海 0 0 66700 4 广西 1 5 12200 5 云南 0 0 8100 6 吉林 0 0 5100 7 湖北 0 0 1500 8 广东 0 0 1300 9 贵州 0 0 860 10 西藏 — — — 注：数据来源四川省地震局, 2019a, b, c, d, e；甘肃省地震局，2019；广西壮族自治区地震局，2019。 2019年我国大陆地区地震灾害主要呈现以下特点：
（1）我国大陆地区未发生重特大地震灾害事件，地震灾害损失明显偏轻。
（2）我国大陆地区有10个省份受灾，人员伤亡和经济损失主要集中在四川省。四川省死亡失踪人口、受伤人口、倒塌房屋均占全国地震总损失的9成以上，损坏房屋占8成以上，直接经济损失占7成以上。
（3）新疆、云南等传统地震灾害重灾区的灾情显著减轻。新疆地区共发生5级以上地震3次，但均未造成损失。云南未发生5级以上地震，未造成死亡失踪人口和房屋倒塌，灾情明显减轻。
（4）我国海域地区及台湾发生多次5级以上地震。台湾及海域地区发生5.0级以上地震12次，其中6.0级以上地震3次，最大地震为台湾花莲县海域6.7级地震，造成1人死亡，16人受伤。
4. 2019年中国大陆主要地震事件及震害特点
4.1 四川珙县5.3级地震
1月3日8时48分，四川省宜宾市珙县发生5.3级地震，震源深度15km。地震造成1人受伤，直接经济损失约0.6亿元。最高地震烈度为Ⅵ（6度），主要涉及珙县、兴文县。Ⅵ（6度）区面积为416km2，主要涉及珙县玉和苗族乡、底洞镇、上罗镇、下罗镇、仁义乡、沐淳镇、孝儿镇、曹营镇，兴文县毓秀苗族乡、周家镇、仙峰苗族乡、九丝城镇共12个乡镇。
本次地震灾害具有以下特点：
（1）地震震害特征主要表现为部分房屋建筑破坏程度存在一定差异性，当地抗震设防烈度为Ⅵ（6度），经过正规设计规范施工建造的具有抗震措施的框架结构房屋在本次地震中表现良好，受损较轻；而农村自建砖混结构房屋（无抗震加固措施）出现破坏较重现象；老旧砖木（包括用作厨房的偏房）和土木结构房屋破坏较重。
（2）地震中生命线系统工程结构遭受破坏程度较轻。地震造成个别道路边坡垮塌和路基沉降，有崩塌落石短暂阻碍交通。另外山坪塘、蓄水池、渠道等水利设施也受到轻微震损（四川省地震局，2019b）。
4.2 四川荣县4.7级、4.3级、4.9级地震
2月24日5时38分、2月25日8时40分、13时15分，四川省自贡市荣县分别发生4.7级、4.3级、4.9级地震，共造成2人死亡、13人受伤，直接经济损失约1.77亿元。此次最高地震烈度为Ⅵ（6度），Ⅵ（6度）区面积为268km2，其中自贡市荣县183km2，自贡市贡井区7km2，内江市威远县78km2。主要涉及自贡市荣县旭阳镇、双石镇、望佳镇、高山镇、东兴镇、墨林乡，自贡市贡井区章佳乡，内江市威远县镇西镇、庆卫镇、新场镇。荣县政府新闻办通报称，2月25日13时15分在四川自贡市荣县附近（北纬29.49度，东经104.49度）发生4.9级地震，荣县高山镇两名群众在街道行走过程中，遇二楼阳台护栏掉落砸伤致死（四川省地震局，2019c）。
本次地震灾害具有以下特点：
（1）由于当地抗震设防烈度为Ⅵ（6度），本次地震Ⅵ（6度）区房屋震害特征主要为：土木结构房屋大部分基本完好，少数出现屋瓦掉落、墙体开裂、墙体抹灰脱落，极少数出现倒塌；砖木结构房屋大部分基本完好，少数出现屋瓦掉落、墙体开裂，极少数出现墙体外闪、倒塌；砖混结构房屋大部分基本完好，少数出现墙体裂缝、吊顶脱落现象，女儿墙、阳台护墙倒塌；框架结构房屋无明显震害特征。
（2）经过正规设计，规范施工建造的具有抗震措施的框架结构房屋在本次地震中表现良好，无明显震害特征；农村自建砖混结构房屋（无抗震加固措施）受损较轻；老旧砖木和土木结构房屋破坏明显。
4.3 四川长宁6.0级地震
6月17日22时55分，四川省宜宾市长宁县发生6.0级地震，震源深度16km，此次地震造成13人死亡、299人受伤，直接经济损失约56.17亿元。最高地震烈度为Ⅷ（8度），Ⅵ（6度）区及以上面积为3058km2，主要涉及宜宾市长宁县、高县、珙县、兴文县、江安县、翠屏区6个区县。
本次地震灾害具有以下特点：
（1）地震造成部分房屋建筑和生命线工程破坏。造成灾区长宁县、珙县、江安县、高县、兴文县、翠屏区6个区县61个乡镇房屋不同程度受损。当地抗震设防烈度为Ⅵ（6度），灾区范围内房屋结构类型主要包括框架结构、砖混结构及砖木结构。框架结构和砖混结构房屋是灾区的主要建筑结构形式，具有抗震设防措施，抗震性能较好；砖木结构房屋抗震性能一般，在灾区分布较广，主要是作为厨房等偏房使用。在此次地震中，砖木房屋出现少数倒毁和大量严重破坏情况。
（2）地震中生命线系统工程结构破坏程度较重，交通、通信、电力、供排水等系统均有不同程度震损，特别是交通系统，出现多处山体滑坡、滚石、路基坍塌等，导致公路中断（四川省地震局，2019a）。
4.4 四川威远5.4级地震
9月8日6时42分，四川省内江市威远县发生5.4级地震，震源深度10km。此次地震造成1人死亡，82人受伤，直接经济损失约5.82亿元。最高地震烈度为Ⅵ（6度），Ⅵ（6度）区面积为680km2，共造成四川省内江市威远县、资中县、市中区、自贡市大安区4个区县受灾（四川省地震局，2019d）。
本次地震灾害具有以下特点：
（1）震害特征主要表现为部分房屋建筑和工程结构的破坏。当地抗震设防烈度为Ⅵ（6度），经过正规设计规范施工建造的具有抗震措施的框架结构房屋在本次地震中表现良好，受损较轻；而农村自建砖混结构房屋（无抗震加固措施）在灾区出现破坏较重的现象；老旧砖木和土木结构房屋破坏较严重。
（2）地震中生命线和行业系统的工程结构破坏程度较轻，地震造成个别道路边坡垮塌和路基沉降。另外山坪塘、蓄水池、渠道等水利设施也轻微震损。
4.5 甘肃夏河5.7级地震
10月28日1时56分，甘肃甘南州夏河县发生5.7级地震，震源深度10km。此次地震共造成7人受伤，约7300间房屋受损。地震最高烈度为Ⅶ（7度），Ⅵ（6度）区及以上面积约为1591km2，其中Ⅶ（7度）区面积为193平方千米，Ⅵ（6度）区面积为1398km2，共造成甘肃省甘南州夏河县、合作市2个县（市）受灾，直接经济损失约16.19亿元（甘肃省地震局，2019）。
本次地震灾害具有以下特点：
（1）属于中强地震，震感强烈，波及范围广。震区大部位于甘南高山草原，人员稀少，地震造成人员伤亡较轻，财产损失不大。
（2）发震断裂并未出露地表，地震地质灾害不发育，生命线工程未出现较大破坏。
（3）震区抗震设防烈度为Ⅶ（7度），但由于处于藏区，佛教寺庙分布较多，地震对寺庙破坏较为明显。
4.6 广西靖西5.2级地震
11月25日9时18分，广西靖西市发生5.2级地震，震源深度10km。此次地震共造成1人死亡，5人轻伤，无房屋倒塌。最高地震烈度为Ⅵ（6度），面积为118km2，共造成广西壮族自治区百色市靖西市、崇左市大新县2个县市的4个乡镇受灾，直接经济损失约1.22亿元（广西壮族自治区地震局，2019）。
本次地震灾害具有以下特点：
（1）地震震感强烈，造成1人死亡、5人轻伤，无房屋倒塌，Ⅵ（6度）区面积较小。
（2）灾区当地抗震设防烈度为Ⅵ（6度），房屋以砖混结构为主，旧砖房屋多为砖木结构，无土坯房。砖混结构多有圈梁加固，具有一定的抗震能力。
（3）此次地震引发多处山体崩塌、山石滚落等次生地质灾害。同时，砖混结构房屋出现小裂隙、小裂缝、掉灰、玻璃窗破坏等现象，有的水泥地面出现裂缝；砖结构房屋出现掉瓦、滑瓦等现象；未出现房屋较严重破坏或倒塌现象。
4.7 四川资中5.2级地震
12月18日8时14分在四川省内江市资中县发生5.2级地震，震源深度14km。此次地震共造成5人重伤、4人中度伤、9人轻伤。最高地震烈度为Ⅵ（6度），主要涉及到内江市资中县、威远县、市中区3个区县。Ⅵ（6度）区面积约为360km2，主要涉及内江市资中县陈家镇、公民镇、银山镇、宋家镇、双河镇5个镇，内江市威远县龙会镇、高石镇、严陵镇、东联镇、靖和镇5个镇，内江市市中区全安镇、朝阳镇、龚家镇、凤鸣镇4个镇，共计14个镇，直接经济损失约0.49亿元（四川省地震局，2019e）。
本次地震灾害具有以下特点：
（1）震区当地抗震设防烈度为Ⅵ（6度），经正规设计和规范施工建造的具有抗震加固措施的框架结构房屋，在本次地震中表现良好，受损较轻；而农村自建砖混结构房屋（无抗震加固措施）破坏较重；老旧砖木和土木结构房屋破坏较严重。另外，本次地震震中与2019年9月8日威远5.4级地震震中仅相距5km，烈度Ⅵ（6度）区范围基本与威远地震Ⅵ（6度）区影响范围重合，前后两次地震相隔时间较短，震害叠加现象明显，加之民房建筑质量普遍较差，造成了极个别老旧房屋的严重破坏。
（2）生命线和行业系统的工程结构破坏程度较轻。
（3）地震造成个别道路边坡垮塌和路基沉降，滚石掉落阻断公路。另外山坪塘、蓄水池、渠道等水利设施也受到轻微震损，震后震区部分地区出现短暂供电中断。
5. 1998年以来中国大陆自然灾害与地震灾害数据统计特点
1998年中国遭受长江全流域的洪水自然灾害，造成了严重的人员伤亡和经济财产损失（孙继昌等，2004）。民政部和国家减灾中心完整记录中国大陆自然灾害造成的人员伤亡和财产损失的详细数据。1998年以来，中国大陆自然灾害共造成人员死亡（含失踪）139162人，造成直接经济损失75560.6亿元（民政部救灾救济司备灾处等，2005；冯长根等，2007；国家减灾中心灾害信息部, 2008, 2009, 2010；民政部救灾司等，2011）。其中，地震灾害造成人员死亡（含失踪）91819人，占比达65.98%，造成的直接经济损10992.18亿元，占比达14.59%（中国地震局监测预报司，2001；中国地震局震灾应急救援司, 2010, 2015）。可见，自然灾害中地震灾害造成人员死亡（含失踪）的比例较高，大震巨灾造成的人员死亡（含失踪）更为突出（表 4）。
表 4 1998年以来中国大陆自然灾害和地震灾害伤亡及损失情况一览表Table 4. List of casualties and losses of natural disasters and earthquake disasters in Chinese mainland since 1998年份 自然灾害 地震灾害 地震灾害造成死亡失踪占比/% 地震灾害造成经济损失占比/% 死亡失踪人数/人 直接经济损失/亿元 死亡失踪人数/人 直接经济损失/亿元 2019 909 3270.9 17 91.09 1.87 2.78 2018 635 2644.6 0 31.21 0.00 1.18 2017 979 3018.7 37 217.38 3.78 7.20 2016 1706 5032.9 3 66.82 0.18 1.33 2015 967 2704.1 33 180.00 3.41 6.66 2014 1818 3373.8 736 355.64 40.48 10.54 2013 2284 5808.4 294 995.36 12.87 17.14 2012 1530 4185.5 86 82.88 5.62 1.98 2011 1126 3096.4 32 60.11 2.84 1.94 2010 7844 5339.9 2975 235.70 37.93 4.41 2009 1528 2523.7 3 27.38 0.20 1.08 2008 88928 13547.5 87150 8523.00 98.00 62.91 2007 2325 2363.0 3 18.99 0.13 0.80 2006 3186 2528.1 25 8.00 0.78 0.32 2005 2475 2042.1 15 17.88 0.61 0.88 2004 2250 1602.3 8 9.50 0.36 0.59 2003 2259 1884.2 319 46.60 14.12 2.47 2002 2384 1637.2 2 1.48 0.08 0.09 2001 2538 1942.2 9 14.80 0.35 0.76 2000 3014 2045.3 10 14.50 0.33 0.71 1999 2966 1962.4 3 4.59 0.10 0.23 1998 5511 3007.4 59 17.66 1.07 0.59 平均值 6325.55 3434.57 4173.59 499.64 10.23 5.75 平均值
（不含2008年）2392.10 2953.00 222.33 118.93 9.29 4.03 本文汇总1998年以来我国自然灾害所造成人员伤亡和直接经济损失的统计数据，研究地震造成的人员死亡（含失踪）和直接经济损失的变化趋势特点，剔除2008年汶川地震巨灾的数据对比来看，地震灾害造成人员死亡（含失踪）占全国自然灾害比近10%，2010年青海玉树7.1级地震和2014年云南鲁甸6.5级地震造成了严重的人员伤亡，使得当年地震造成人员死亡（含失踪）占全国自然灾害人员死亡（含失踪）比分别达37.93%和40.48%（郑通彦等, 2011, 2015a；冯蔚等，2016）。1998年以来，地震灾害造成直接经济损失占全国自然灾害直接经济损失比平均达4%以上，2013年四川庐山7.0级地震和甘肃岷县漳县6.6级地震，使得当年地震造成的直接经济损失占全国自然灾害直接经济损失比达17.14%（郑通彦等，2015b）。对比1998年以来地震灾害造成人员伤亡及损失情况占全部自然灾害比例变化（图 2），可以看出2010年以来地震造成的人员伤亡和经济损失在自然灾害中所占的比重较原来大幅增长，特别是多数年份直接经济损失所占比例超过或接近1998年以来的平均水平。整体表现为随着经济水平的不断发展，地震灾害造成的人员伤亡比重有所减少，而经济损失比重呈增加趋势。
图 2 1998年以来地震灾害造成人员伤亡及损失情况占全部自然灾害比例变化图Figure 2. Proportion of casualties and losses caused by earthquake disasters in all natural disasters since 19986. 结语
2019年我国大陆地区未发生特重大地震灾害事件，地震灾害损失明显偏轻。地震共造成10个省份（区、市）受灾，17人死亡失踪。多震区地震活动差异仍然明显，地震造成的人员伤亡和经济损失主要集中在四川省，而传统地震灾害严重的云南、新疆等地区灾情偏轻。部分弱震地区地震活跃，小震致灾致亡现象不容忽视。地震造成的灾害损失整体表现出随着经济水平的不断发展，人员伤亡比重有所减少，经济损失比重呈增加的趋势。
致谢: 本文涉及部分人员伤亡和经济损失的数据由应急管理部国家减灾中心、中国气象局国家气候中心、水利部信息中心、中国地质环境监测院和自然资源部海洋减灾中心等单位提供，在此表示感谢。同时感谢四川省地震局、吉林省地震局、甘肃省地震局、贵州省地震局和广西壮族自治区地震局提供的地震现场调查评估资料。 -
图 1 本研究选取台阵的空间分布与场地类别划分
Figure 1. The spatial distribution and site types of the selected array in this paper
图 2 本研究选取地震记录的震级、震中距和地面加速度峰值分布
Figure 2. The magnitude and epicentre distance along with the peak ground acceleration(PGA) of the selected recordings
图 3 地表/井下反应谱比值曲线与标定结果
Figure 3. The ratio of surface/downhole response spectrum shifted to the long period and the calibration results under different groups of input ground motion intensity
图 4 典型台阵（IBRH13）地表/井下反应谱比值平台值与地震动强度的相关性
Figure 4. The correlation between the surface/downhole response spectrum ratio and ground motion intensity of a typical array(IBRH13)
图 5 分组滑动平均法窗口长度选取方法与分布情况
Figure 5. The window length selection method and distribution of the grouping moving average method
图 6 所选台阵在各分组区间内的地震事件个数与台阵筛选
Figure 6. The number of seismic eventsand array selection of the selected array in each grouping interval
图 7 典型台阵归一化地表/井下反应谱比值平台值一元线性回归结果
Figure 7. Linear regression of the normalized surface/downhole response spectrum ratio platform value of a typical array
图 8 相关性前4的场地条件表征参数与地表/井下反应谱比值平台值非线性衰减指数的关系
Figure 8. Correlation of the first four site parameters and the nonlinear attenuation index of the surface/downhole response spectrum ratio platform value
表 1 不同地震动强度分组下的最小可信样本量
Table 1. Minimum reliable sample size for different ground motion intensity groups
组别 1 2 3 4 5 6 7 8 9 10 11 12 分组标准/cm·s−2 0.178～
0.5620.316～
1.0000.562～
1.7801.000～
3.1601.780～
5.6203.160～
10.0005.620～
17.80010.000～
31.60017.800～
56.20031.600～
100.00056.200～
177.800>100.000 n0平均值/个 30 27 25 21 17 14 10 7 5 3 2 1 
下载: 导出CSV
表 2 场地条件表征参数
Table 2. The site characterization parameters selected in this paper
参数 含义 定义 参考文献 $ {V}_{\rm{se}} $ 我国规范定义的等效剪切波速 ${V}_{\rm{se}}={d}_{0}/{\displaystyle\sum }_{i=1}^{n}\left({d}_{i}/{V}_{\mathrm{s}i}\right)$ 中华人民共和国住房和城乡建设部等，2010 $ {V}_{\mathrm{S}30} $ 美国规范定义的平均剪切波速 ${V}_{\mathrm{S}30}=30/{\displaystyle\sum }_{i=1}^{n}\left({d}_{i}/{V}_{\mathrm{s}i}\right)$ BSSC，2001（美国NEHRP规范） $ {B}_{30} $ 剪切波速剖面梯度 $ {\mathrm{log}}_{10}{V}_{\mathrm{s}}\left(z\right)={B}_{Z\mathrm{m}\mathrm{a}\mathrm{x}}{\mathrm{log}}_{10}\left(z\right)+{A}_{Z\mathrm{m}\mathrm{a}\mathrm{x}}\pm {\sigma }_{Z\mathrm{m}\mathrm{a}\mathrm{x}} $ Régnier等，2013 $ {Z}_{0.5} $ 0.5 km/s覆盖层厚度 剪切波速达0.5 km/s时的土层深度 中华人民共和国住房和城乡建设部等，2010 $ {Z}_{0.8} $ 0.8 km/s覆盖层厚度 剪切波速达0.8 km/s时的土层深度 Zhu等，2020 $ {Z}_{1.0} $ 1.0 km/s覆盖层厚度 剪切波速达1.0 km/s时的土层深度 Zhu等，2020 $ {V}_{\mathrm{s}\mathrm{a}\mathrm{v}} $ 整个土层沉积平均剪切波速 地表到$ {V}_{\mathrm{s}}>800 $ m/s的“地震基岩”
土层厚度内的走时平均剪切波速Pitilakis等，2013 $ {f}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}} $ 场地卓越频率 弱震平均傅里叶谱放大系数峰值对应的频率 Régnier等，2013 $ {f}_{\mathrm{s}} $ 场地基本频率 弱震HVSR曲线峰值对应的频率 陈国兴等，2020 $ {T}_{\mathrm{s}} $ 场地基本周期 $ {f}_{\mathrm{s}} $的倒数 陈国兴等，2020 $ {A}_{\mathrm{s}} $ 弱震平均傅里叶谱放大系数峰值 — Régnier等，2013 $ {A}_{\mathrm{s}\mathrm{r}} $ 弱震平均反应谱放大系数峰值 —
下载: 导出CSV
-
[1] 陈国兴, 谢君斐, 张克绪, 1995. 土的动模量和阻尼比的经验估计. 地震工程与工程振动, 15(1): 73-84.Chen G. X., Xie J. F., Zhang K. X., 1995. The empirical evaluation of soil moduli and damping ratio for dynamic analysis. Earthquake Engineering and Engineering Vibration, 15(1): 73-84. (in Chinese) [2] 陈国兴, 丁杰发, 方怡等, 2020. 场地类别分类方案研究. 岩土力学, 41(11): 3509-3522, 3582.Chen G. X., Ding J. F., Fang Y., et al., 2020. Investigation of seismic site classification scheme. Rock and Soil Mechanics, 41(11): 3509-3522, 3582. (in Chinese) [3] 杜修力, 路德春, 2011. 土动力学与岩土地震工程研究进展. 岩土力学, 32(S2): 10-20.Du X. L., Lu D. C., 2011. Advances in soil dynamics and geotechnical earthquake engineering. Rock and Soil Mechanics, 32(S2): 10-20. (in Chinese) [4] 刘红帅, 2009. 基于小生境遗传算法的设计地震动反应谱标定方法. 岩土工程学报, 31(6): 975-979. doi: 10.3321/j.issn:1000-4548.2009.06.025Liu H. S., 2009. Calibrating method for seismic response spectra based on niche genetic algorithm. Chinese Journal of Geotechnical Engineering, 31(6): 975-979. (in Chinese) doi: 10.3321/j.issn:1000-4548.2009.06.025 [5] 罗桂纯, 2016. 基于强震动观测的场地效应非线性特性研究. 国际地震动态, (1): 46-48. [6] 王海云, 谢礼立, 2010. 自贡市西山公园地形对地震动的影响. 地球物理学报, 53(7): 1631-1638. doi: 10.3969/j.issn.0001-5733.2010.07.014Wang H. Y., Xie L. L., 2010. Effects of topography on ground motion in the Xishan park, Zigong city. Chinese Journal of Geophysics, 53(7): 1631-1638. (in Chinese) doi: 10.3969/j.issn.0001-5733.2010.07.014 [7] 王玉石, 李小军, 兰日清等, 2016. 强震动作用下土体非线性动力特征研究发展与展望. 震灾防御技术, 11(3): 480-492. doi: 10.11899/zzfy20160305Wang Y. S., Li X. J., Lan R. Q., et al., 2016. Development and prospect of study on soil nonlinear dynamic characteristics under strong-motion. Technology for Earthquake Disaster Prevention, 11(3): 480-492. (in Chinese) doi: 10.11899/zzfy20160305 [8] 夏江, 陈清军, 2006. 基于遗传算法的设计地震反应谱标定方法. 力学季刊, 27(2): 317-322. doi: 10.3969/j.issn.0254-0053.2006.02.021Xia J., Chen Q. J., 2006. Calibrating method of seismic response spectrum based on genetic algorithm. Chinese Quarterly of Mechanics, 27(2): 317-322. (in Chinese) doi: 10.3969/j.issn.0254-0053.2006.02.021 [9] 叶鹏, 2013. 四川地区强震动台站的场地反应研究. 哈尔滨: 中国地震局工程力学研究所.Ye P., 2013. Study on site responses of strong motion stations in Sichuan area. Harbin: Institute of Engineering Mechanics, China Earthquake Administration. (in Chinese) [10] 袁晓铭, 孙锐, 孙静等, 2000. 常规土类动剪切模量比和阻尼比试验研究. 地震工程与工程振动, 20(4): 133-139. doi: 10.3969/j.issn.1000-1301.2000.04.020Yuan X. M., Sun R., Sun J., et al., 2000. Laboratory experimental study on dynamic shear modulus ratio and damping ratio of soils. Earthquake Engineering and Engineering Vibration, 20(4): 133-139. (in Chinese) doi: 10.3969/j.issn.1000-1301.2000.04.020 [11] 张立宝, 2018. 基于钻井台阵数据的场地非线性效应研究. 北京: 中国地震局地球物理研究所.Zhang L. B., 2018. Study on nonlinearity of site effects on ground motion based on vertical borehole array data. Beijing: Institute of Geophysics, China Earthquake Administration. (in Chinese) [12] 中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局, 2010. GB 50011—2010 建筑抗震设计规范（附条文说明）（2016年版）. 北京: 中国建筑工业出版社.Ministry of Housing and Urban-Rural Development of the People’s Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. 2010. GB 50011—2010 Code for seismic design of buildings. Beijing: China Architecture & Building Press. (in Chinese) [13] Aguirre J., Irikura K., 1997. Nonlinearity, liquefaction, and velocity variation of soft soil layers in Port Island, Kobe, during the Hyogo-ken Nanbu earthquake. Bulletin of the Seismological Society of America, 87(5): 1244-1258. [14] Aki K., 1993. Local site effects on weak and strong ground motion. Tectonophysics, 218(1-3): 93-111. doi: 10.1016/0040-1951(93)90262-I [15] Andrews D. J., 1986. Objective determination of source parameters and similarity of earthquakes of different size. In: Das S., Boatwright J., Scholz C. H., eds., Earthquake Source Mechanics. Washington: American Geophysical Union, 259—267. [16] Beresnev I. A., Field E. H., Van Den Abeele K., et al., 1998. Magnitude of nonlinear sediment response in Los Angeles basin during the 1994 Northridge, California, earthquake. Bulletin of the Seismological Society of America, 88(4): 1079-1084. [17] Bernardie S., Foerster E., Modaressi H., 2006. Non-linear site response simulations in Chang-Hwa region during the 1999 Chi–Chi earthquake, Taiwan. Soil Dynamics and Earthquake Engineering, 26(11): 1038-1048. doi: 10.1016/j.soildyn.2006.02.004 [18] Bonilla L. F., Steidl J. H., Gariel J. C., et al., 2002. Borehole response studies at the garner valley downhole array, Southern California. Bulletin of the Seismological Society of America, 92(8): 3165-3179. doi: 10.1785/0120010235 [19] Bonilla L. F., Tsuda K., Pulido N., et al., 2011. Nonlinear site response evidence of K-NET and KiK-net records from the 2011 off the Pacific coast of Tohoku Earthquake. Earth, Planets and Space, 63(7): 785-789. doi: 10.5047/eps.2011.06.012 [20] Borcherdt R. D., 1970. Effects of local geology on ground motion near San Francisco Bay. Bulletin of the Seismological Society of America, 60(1): 29-61. [21] Building Seismic Safety Council (BSSC), 2001. NEHRP recommended provisions for seismic regulations for new buildings and other structures, 2000 Edition. Washington, DC: Federal Emergency Management Agency. [22] Castro-Cruz D., Régnier J., Bertrand E., et al., 2020. A new parameter to empirically describe and predict the non-linear seismic response of sites derived from the analysis of Kik-Net database. Soil Dynamics and Earthquake Engineering, 128: 105833. doi: 10.1016/j.soildyn.2019.105833 [23] Darragh R. B., Shakal A. F., 1991. The site response of two rock and soil station pairs to strong and weak ground motion. Bulletin of the Seismological Society of America, 81(5): 1885-1899. [24] Field E. H., Johnson P. A., Beresnev I. A., et al., 1997. Nonlinear ground-motion amplification by sediments during the 1994 Northridge earthquake. Nature, 390(6660): 599-602. doi: 10.1038/37586 [25] Frankel A. D., Carver D. L., Williams R. A., 2002. Nonlinear and linear site response and basin effects in Seattle for the M 6.8 Nisqually, Washington, earthquake. Bulletin of the Seismological Society of America, 92(6): 2090-2109. doi: 10.1785/0120010254 [26] Hardin B. O., Drnevich V. P., 1972. Shear modulus and damping in soils: measurement and parameter effects. Journal of the Soil Mechanics and Foundations Division, 98(6): 603-624. doi: 10.1061/JSFEAQ.0001756 [27] Hartzell S., 1998. Variability in nonlinear sediment response during the 1994 Northridge, California, earthquake. Bulletin of the Seismological Society of America, 88(6): 1426-1437. [28] Héloïse C., Bard P. Y., Rodriguez-Marek A., 2012. Site effect assessment using KiK-net data: part 1. A simple correction procedure for surface/downhole spectral ratios. Bulletin of Earthquake Engineering, 10(2): 421-448. doi: 10.1007/s10518-011-9283-1 [29] Huang H. C., Shieh C. S., Chiu H. C., 2001. Linear and nonlinear behaviors of soft soil layers using Lotung downhole array in Taiwan. Terrestrial, Atmospheric and Oceanic Sciences, 12(3): 503-524. doi: 10.3319/TAO.2001.12.3.503(T) [30] Noguchi S., Sasatani T., 2008. Quantification of degree of nonlinear site response. In: The 14th World Conference on Earthquake Engineering. Beijing, China: WCEE. [31] Pavlenko O., Irikura K., 2002. Changes in shear moduli of liquefied and nonliquefied soils during the 1995 Kobe earthquake and its aftershocks at three vertical-array sites. Bulletin of the Seismological Society of America, 92(5): 1952-1969. doi: 10.1785/0120010143 [32] Pavlenko O. V., Wen K. L., 2008. Estimation of nonlinear soil behavior during the 1999 Chi-Chi, Taiwan, Earthquake. Pure and Applied Geophysics, 165(2): 373-407. doi: 10.1007/s00024-008-0309-9 [33] Pender M. J., 1997. Recent developments in earthquake geotechnical engineering. Bulletin of the New Zealand Society for Earthquake Engineering, 30(2): 167-173. doi: 10.5459/bnzsee.30.2.167-173 [34] Pitilakis K., Riga E., Anastasiadis A., 2013. New code site classification, amplification factors and normalized response spectra based on a worldwide ground-motion database. Bulletin of Earthquake Engineering, 11(4): 925-966. doi: 10.1007/s10518-013-9429-4 [35] Régnier J., Cadet H., Bonilla L. F., et al., 2013. Assessing nonlinear behavior of soils in seismic site response: statistical analysis on kik-net strong-motion data. Bulletin of the Seismological Society of America, 103(3): 1750-1770. doi: 10.1785/0120120240 [36] Régnier J., Cadet H., Bard P. Y., 2016. Empirical quantification of the impact of nonlinear soil behavior on site response. Bulletin of the Seismological Society of America, 106(4): 1710-1719. doi: 10.1785/0120150199 [37] Seed H. B., Idriss I. M., Kiefer F. W., 1969. Characteristics of rock motions during earthquakes. Journal of the Soil Mechanics and Foundations Division, 1969, 95(15): 1199-1218. [38] Steidl J. H., Tumarkin A. G., Archuleta R. J., 1996. What is a reference site?. Bulletin of the Seismological Society of America, 86(6): 1733-1748. [39] Tibshirani R., 2011. Regression shrinkage and selection via the lasso: a retrospective. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 73(3): 273-282. doi: 10.1111/j.1467-9868.2011.00771.x [40] Trifunac M. D., Todorovska M. I., 1996. Nonlinear soil response-1994 Northridge, California, earthquake. Journal of Geotechnical Engineering, 122(9): 725-735. doi: 10.1061/(ASCE)0733-9410(1996)122:9(725) [41] Tsuda K., Archuleta R. J., Koketsu K., 2006. Quantifying the spatial distribution of site response by use of the Yokohama high-density strong-motion network. Bulletin of the Seismological Society of America, 96(3): 926-942. doi: 10.1785/0120040212 [42] Wen K. L., Beresnev I. A., Yeh Y. T., 1994. Nonlinear soil amplification inferred from downhole strong seismic motion data. Geophysical Research Letters, 21(24): 2625-2628. doi: 10.1029/94GL02407 [43] Wen K. L., Lin C. M., Chiang H. J., et al., 2008. Effect of surface geology on ground motions: the case of station TAP056-Chutzuhu site. Terrestrial, Atmospheric and Oceanic Sciences, 19(5): 451-462. doi: 10.3319/TAO.2008.19.5.451(T) [44] Zhu C. B., Pilz M., Cotton F., 2020. Which is a better proxy, site period or depth to bedrock, in modelling linear site response in addition to the average shear-wave velocity?. Bulletin of Earthquake Engineering, 18(3): 797-820. doi: 10.1007/s10518-019-00738-6 -
下载:
点击查看大图
计量
- 文章访问数: 217
- HTML全文浏览量: 108
- PDF下载量: 9
- 被引次数: 0
