Analytical Solution to Transient Response of Arc-shaped Basin Incident by SH Wave
-
摘要: 地震波散射问题的解析解是研究局部场地、地形、盆地等不规则地层结构对地震动参数放大效应影响的重要理论工具。现有解析解大部分在频域内给出，无法直接用于研究不规则地层结构对地震动峰值、反应谱等参数的放大效应。本文基于平面SH波入射下圆弧状沉积盆地动力响应宽频带稳态解析解，通过Fourier变换，获取瞬态响应解析解。基于此，研究El Centro波入射下，沉积盆地对地震动峰值加速度、峰值速度、峰值位移及不同周期反应谱的放大效应。研究结果表明，盆地宽度和深度、沉积介质波速、入射波角度等对盆地放大效应具有显著影响，地震动反应谱谱比最大值超过2.0，且宽度达10 km的较大型盆地对长周期地震动参数具有显著放大效应，对于位于该类盆地的超高层建筑、大型储液罐、大跨度桥梁等长周期结构，应充分考虑盆地对抗震设防参数的影响。Abstract: Analytical solution to scattering problem of seismic waves is an important tool to study amplification effects induced by irregular surficial earth structures, such as local site, topography, and basin, on ground motion. However, most analytical solutions are presented in frequency domain, and cannot be applied directly to probe the amplification effects of such irregularities on the peaks and response spectra of ground motion. In this paper, based on the stationary broad-band analytical solution for the dynamic response of arc-shaped basin incident by SH wave, presented in this paper is the transient analytical solution for the out-plane dynamic response of arc-shaped basin is derived.. From the transient solutions, studied are the amplification effects of alluvial basin on peak ground acceleration, velocity, displacement, and spectral accelerations at different natural periods are studied. The results reveal that the width, depth, and shear velocity of alluvium significantly influence the amplification effects of basin on ground motion, and the maximum value of spectral ratio of ground-motion response spectrum exceeds 2.0. Furthermore, as to large basin with the width to 10 km, it imposes significant influence on long-period ground motion. Therefore, the aseismic design of long-period structures located in large basins, such as high-rise building, large-scale fluid reservoir, and long-span bridge, should take into account of the effects of basin on the design ground motion parameters.
-
Key words:
- Plane SH wave /
- Basin /
- Analytical solution /
- Response Spectrum /
- Long period
-
引言
众所周知，我国是地震频发的国家，地震可能造成高速铁路列车脱轨事故，为此，我国建立了相应的地震报警及紧急处置系统，力争在潜在破坏性地震到达之前发出报警，降低列车发生脱轨或倾覆的概率。目前广泛采用的地震报警参数主要为峰值加速度PGA，然而PGA主要体现地震波幅值，未考虑频谱及持时影响，对于无破坏性的高频小震可能产生误报现象。为避免这种干扰，郭恩栋等（2015）引入谱强度SI作为高速铁路地震报警参数，并给出相应的计算方法，SI从能量方面出发，考虑了幅值及频谱影响，忽略持时的影响，但相比PGA更合理。美国电力研究所EPRI（O'Hara 等，1991）在核电厂地震监测报警中引入累积绝对速度CAV作为报警参数，研究发现低频震动对CAV的贡献明显高于高频震动。我国三代核电站AP1000参考国外标准也引入了CAV作为地震报警参数（胡进军等，2013）。林宜娴（2002）提出CAV、PGA、PGV等参数可作为地震报警参数，其稳定性好，且确定性较高。Kostov（2005）根据欧洲几次强地震动数据，分析得出标准化累积绝对速度CAVSTD在预测地震动破坏能力方面明显优于PGA。伊斯坦布尔在地震预报警系统中利用累积绝对速度快速判别强地震动（Erdik等，2003）。Fahjan等（2011）在地震报警的触警算法中引入CAV，并提出新的用于报警系统的参数。黄俊等（2014）引入CAV作为报警参数，分析其在高速铁路报警中的适用性，研究发现CAV可有效排除破坏性小的高频小震对高速铁路列车地震报警的干扰。目前虽对CAV在地震报警中的应用有了深入研究，但在高速铁路列车地震报警中的研究较少，仅通过相关的地震波数据处理得出，未考虑车轨动力响应关系，且给出的计算参数为CAVSTD，为此，需探讨考虑车轨关系的基于相关起算阈值的CAV计算方法。
1. CAV相关参数
目前，地震工程界主要研究CAV、CAVSTD、CAV5。其中CAV于1988年由美国电力研究所（O'Hara等，1991）在核电厂报警中第2级判别标准中提出的，其概念为记录地震加速度数据的绝对值对记录时间进行积分，记为累积绝对速度CAV：
$${\rm{ CAV}} = \mathop \int \nolimits_0^{{{{t}}_{{\rm{max}}}}} \left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t$$ (1) 为提高CAV在核电厂报警中的准确度，EPRI在报告中引入标准化累积绝对速度CAVSTD，其可有效避免长持时记录的地震波尾部对应的幅值小且破坏性小的地震动对其数值的影响，其定义如下：将记录的加速度时程分成以1 s为时间间隔的N个小段，当1 s时间段内存在加速度绝对值≥0.025 g时，对该秒内加速度数值的绝对值进行积分，否则该秒内的积分值记为零，然后将整个记录时程进行相加求和，表达式为：
$$ {\rm{CA{V_{STD}}}} = \mathop \sum \limits_{{i=1}}^n \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\left| {{{a}}\left( {{t}} \right)} \right| < 0.025\;g}\\ {1,\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.025\;{{g}}} \end{array}} \right.$$ (2) Kramer等（2002）于2002年提出CAV5，用于场地液化判别，其概念为：将记录的加速度时程中对加速度数值的绝对值≥0.005 g进行积分求和，表达式为：
$${{\rm{ CAV}}_5} = \displaystyle\int \nolimits_0^\infty \left\langle {\rm{\chi }} \right\rangle \left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\left\langle {\rm{\chi }} \right\rangle = \left\{ {\begin{array}{*{20}{c}} {0\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.005\;g}\\ {1\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.005\;{{g}}} \end{array}} \right. $$ (3) 式中，a(t)为加速度时程，Wi为权重。
2. 改进的标准化累积绝对速度应用于高速铁路地震报警阈值中的计算方法
2.1 改进的标准化累积绝对速度起算阈值确定
本文引入31自由度的SY97477车辆模型（崔恩文，2014），结合车轨典型非线性接触关系，依据列车安全行驶的3项评判指标（脱轨系数、轮重减载率及横向力)，分析车体在轨道不平顺（我国高速铁路无砟轨道标准谱）与简谐波（仅考虑横向输入，与列车行驶方向垂直）共同激励下的动态响应，考虑95%的安全保证，引入2.55倍的动力放大系数（孙汉武等，2007），计算安全极限状态（超出3项指标任意1个限值）下不同车速对应的简谐波幅值随周期的变化关系，如图1所示。具体模型参数、车轨接触关系及评判标准可参考崔恩文（2014）的研究。
图 1 列车安全运行极限状态下不同车速对应的简谐波幅值随周期的变化关系Figure 1. The relationship between the amplitude of simple harmonic wave corresponding to different speeds and periods under the safe running limit state of the train由图1可知，车速一定时，即使幅值很小（<0.025 g）的低频简谐波也可能使列车脱轨，因此不能简单地套用标准化累积绝对速度CAVSTD计算公式，有必要研究改进的标准化累积绝对速度应用在高速铁路地震报警阈值中的计算方法。车速一定时，简谐波幅值随周期增加逐渐递减，最终趋于常数，且周期越大，不同车速对应的简谐波幅值之间的差值越小。车速为200 km/h时，当简谐波周期达2.2 s时，其幅值开始趋于常数，该常数约为0.008 g，本文规定此时的周期为简谐波幅值趋于常数对应的起始周期Tst，该常数记为Amin。不同车速下简谐波幅值趋于常数对应的起始周期及该常数的数值如表1所示。
表 1 不同车速下简谐波幅值趋于常数对应的起始周期及该常数的数值Table 1. The initial period of the simple harmonic wave amplitude tending to be constant at different speeds and the value of the constant项目 车速/（km·h−1） 200 250 300 350 400 起始周期Tst/s 2.2 2.3 2.1 2.0 1.7 Amin/g 0.008 0.004 0.004 0.004 0.004 由表1可知，车速为200 km/h与车速≥250 km/h时对应的Amin不同，车速≥250 km/h时Amin相同，但起始周期Tst随车速的增加呈递减趋势，说明车速越大，简谐波趋于常数所需的周期越小。
车速为200 km/h时，幅值低于0.008 g的简谐波对列车运行安全的影响可忽略不计。车速≥250 km/h时，幅值低于0.004 g的简谐波对列车运行安全的影响可忽略不计。由此可推算出改进的标准化累积绝对速度起算阈值，如表2所示。
表 2 不同车速下改进的标准化累积绝对速度起算阈值Table 2. Starting threshold of improved calculation of standardized cumulative absolute velocity at different speeds项目 车速/（km·h−1） 200 ≥250 改进的标准化累积绝对速度起算阈值/g 0.008 0.004 2.2 改进的标准化累积绝对速度应用在地震报警中的可行性分析
考虑改进的标准化累积绝对速度为累积过程的算法，其值对于加速度超过0.004 g或0.008 g的有限个数的高频小震会很小，因此，可较好地排除高速铁路沿线的高频小震，是较好的地震监测报警参数。
魏智祥（2015）分析了京武高速铁路线布置的强震仪监测到的列车运行时震动记录数据，发现列车运行产生的震动记录明显高于背景噪声，且发现东西、南北、垂直方向列车振动噪声幅值均≤0.002 g，由此可知本文设定的不同车速下改进的标准化累积绝对速度可有效排除列车振动的影响。
综上所述，本文给出改进的标准化累积绝对速度用于高速铁路地震报警是可行的。
2.3 改进的标准化累积绝对速度计算公式的确定
参照CAVSTD计算方法，本文给出车速为200 km/h时改进的标准化累积绝对速度CAV8计算公式如下：
$${{\rm{CAV}}_8} = \mathop \sum \limits_{i=1}^n \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.008\;g}\\ {1,\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.008\;{{g}}} \end{array}} \right.$$ (4) 当
$ a\left(t\right) $ $< 0.008\;g$ 时，${{W}}_{{i}}$ =0；当$\left|{a}\left({t}\right)\right|\geqslant 0.008\;g$ 时，${{W}}_{{i}}$ =1。本文给出的CAV8定义为：将加速度时程按1 s为时间间隔进行划分，如果在这1 s内加速度绝对值≥0.008 g，则对该秒内的加速度绝对值进行积分，否则忽略该秒内的积分值，然后将整个时程中每秒积分得到的数值进行累积求和。
车速为250 km/h时改进的标准化累积绝对速度CAV4计算公式如下：
$${ {\rm{CAV}}_4} = \mathop \sum \limits_{i=1}^{{n}} \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.004\;g}\\ {1,\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.004\;{{g}}} \end{array}} \right.$$ (5) 当
${a}\left({t}\right)$ $< 0.004\;g$ 时，${{W}}_{{i}}=0$ ；当$\left|{a}\left({t}\right)\right|\geqslant 0.004\;{g}$ 时，${{W}}_{{i}}$ =1。本文给出的CAV4定义为：将加速度时程按1 s为时间间隔进行划分，如果在这1 s内加速度绝对值≥0.004 g，则对该秒内的加速度绝对值进行积分，否则忽略该秒内的积分值，然后将整个时程中每秒积分得到的数值进行累积求和。
3. 高速铁路地震报警阈值确定
为确定基于改进的标准化累积绝对速度高速铁路地震报警阈值，本文从Peer数据库选取6条不同场地地震波（表3），对应的加速度反应谱如图2所示，对其进行归一化处理，分析加速度幅值与评判列车脱轨3项指标之间的关系，确定不同车速下影响行车安全的6条地震波加速度上限值，按照本文给出不同车速下改进的标准化累积绝对速度计算公式，给出6条地震波对应的改进的标准化累积绝对速度上限值，如表4所示。
表 3 地震波相关信息Table 3. Seismic wave information项目 地震波台站名称 Cape Mendocino TCU045 Capitola Hector EL Centro Imp. Co. Cent Poe Road 震级 7.01 7.62 6.93 7.13 6.54 6.54 峰值加速度/g 0.376 5 0.008 1 0.528 5 0.265 6 0.357 9 0.446 3 v30/（m·s−1） 567.78 704.64 288.62 726.00 192.05 316.64 加速度记录持时/s 36.0 45.0 39.9 45.3 40.0 22.3 表 4 不同车速下6条地震波加速度上限值与改进的标准化累积绝对速度上限值Table 4. The upper limit of acceleration amplitudes and upper limit improved calculation of standardized cumulative absolute velocity CAV of six seismic waves at different speeds地震波台站名称 车速200 km/h 车速250 km/h 车速300 km/h 车速350 km/h 车速400 km/h 加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-secCape Mendocino 0.074 0.17 0.070 0.17 0.055 0.13 0.040 0.09 0.039 0.09 TCU045 0.101 0.55 0.090 0.49 0.078 0.43 0.062 0.34 0.039 0.21 Capitola 0.109 0.34 0.078 0.25 0.062 0.20 0.054 0.17 0.039 0.11 Hector 0.101 0.27 0.070 0.19 0.062 0.17 0.054 0.14 0.047 0.12 EL Centro Imp. Co. Cent 0.078 0.16 0.070 0.18 0.054 0.13 0.039 0.08 0.027 0.05 Poe Road 0.074 0.19 0.054 0.14 0.043 0.11 0.039 0.10 0.035 0.08 由表4可知，车速相同时，即使地震波加速度相同，其对应的改进的标准化累积绝对速度不一定相同，如车速为200 km/h时，台站名称为Cape Mendocino与Poe Road的地震波加速度相同，但对应的改进的标准化累积绝对速度不同，且Cape Mendocino台站加速度记录持时较大，说明改进的标准化累积绝对速度与频谱紧密相关。车速≥250 km/h时，对于同一台站的地震波，峰值加速度越大其对应的改进的标准化累积绝对速度越大，如台站名称为Cape Mendocino的地震波，说明对于同一地震波而言，加速度影响累积绝对速度。根据改进的标准化累积绝对速度定义，加速度记录持时影响其数值。综上所述，改进的标准化累积绝对速度数值不仅与加速度幅值有关，还与频谱及加速度记录持时密切相关，可较好地反映地震动三要素。
选取6条地震波改进的标准化累积绝对速度最小值作为报警阈值，给出不同车速下基于改进的标准化累积绝对速度高速铁路地震报警阈值，如表5所示。由表5可知，改进的标准化累积绝对速度报警阈值与车速整体呈线性递减关系，中间车速对应的改进的标准化累积绝对速度可按线性插入计算。
表 5 不同车速下改进的标准化累积绝对速度高速铁路地震报警阈值Table 5. High-speed earthquake alarm threshold based on improved calculation of standardized cumulative absolute velocity thresholds at different vehicle speeds项目 车速/（km·h−1） 200 250 300 350 400 报警阈值/g-sec 0.16 0.14 0.11 0.08 0.05 4. 结论
（1）通过建立车轨模型，分析列车安全运行极限状态下简谐波幅值与周期的关系，得出不同车速下改进的标准化累积绝对速度起算阈值，并论证改进的标准化累积绝对速度在高速铁路地震报警中的可行性。
（2）参照标准化累积绝对速度CAVSTD计算公式，本文给出不同车速下改进的标准化累积绝对速度计算公式。
（3）根据本文给出的改进的标准化累积绝对速度计算公式，选取6条不同场地的地震波，分析列车在轨道不平顺及地震波共同激励下的动力响应，计算不同车速下改进的标准化累积绝对速度报警阈值，以供参考。
-
图 2 自由基岩、盆地中心点和边界点地震动加速度时程曲线
Figure 2. The time history curve of ground motion acceleration of free bedrock, central point and boundary point of basin
图 3 自由基岩、盆地中心点和边界点地震动速度时程曲线
Figure 3. The time history curve of ground motion velocity of free bedrock, central point and boundary point of basin
图 4 自由基岩、盆地中心点和边界点地震动位移时程曲线
Figure 4. The time history curve of ground motion displacement of free bedrock, central point and boundary point of basin
图 5 垂直入射下盆地地表地震动反应谱谱比曲线簇
Figure 5. The spectral ratio curve cluster of ground motion response spectrum under vertical incidence
图 6 不同入射角下地震动参数放大系数空间变化曲线
Figure 6. The spatial variational curve of ground motion parameters amplification factor at different incident angles
图 7 地震动峰值放大系数与盆地宽度关系曲线
Figure 7. The relationship curve between the peak amplification factor of ground motion and the width of basin
图 9 不同盆地宽度条件下深度对地震动放大系数的影响
Figure 9. The effect of depth on ground motion amplification factor under different basin widths
-
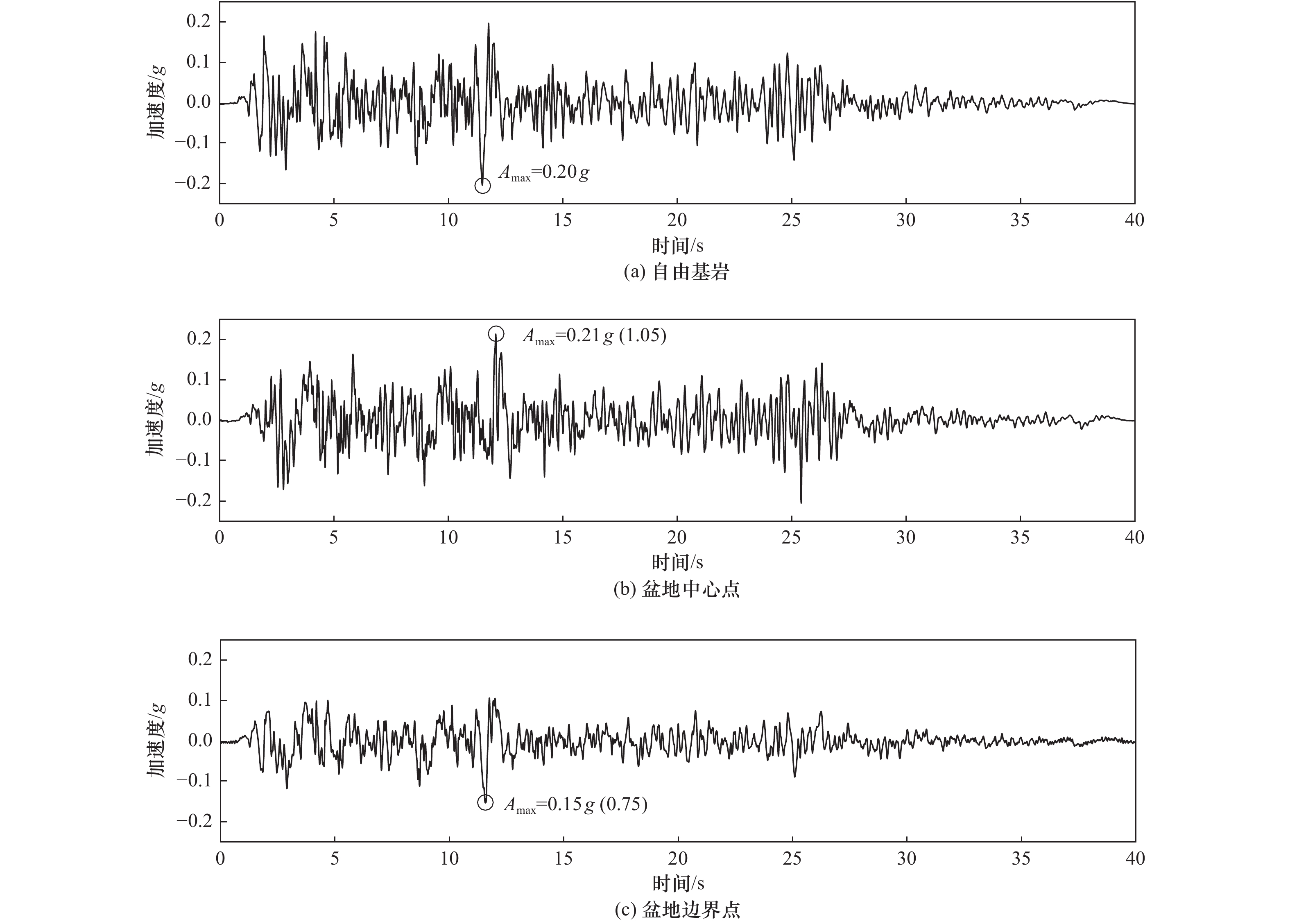
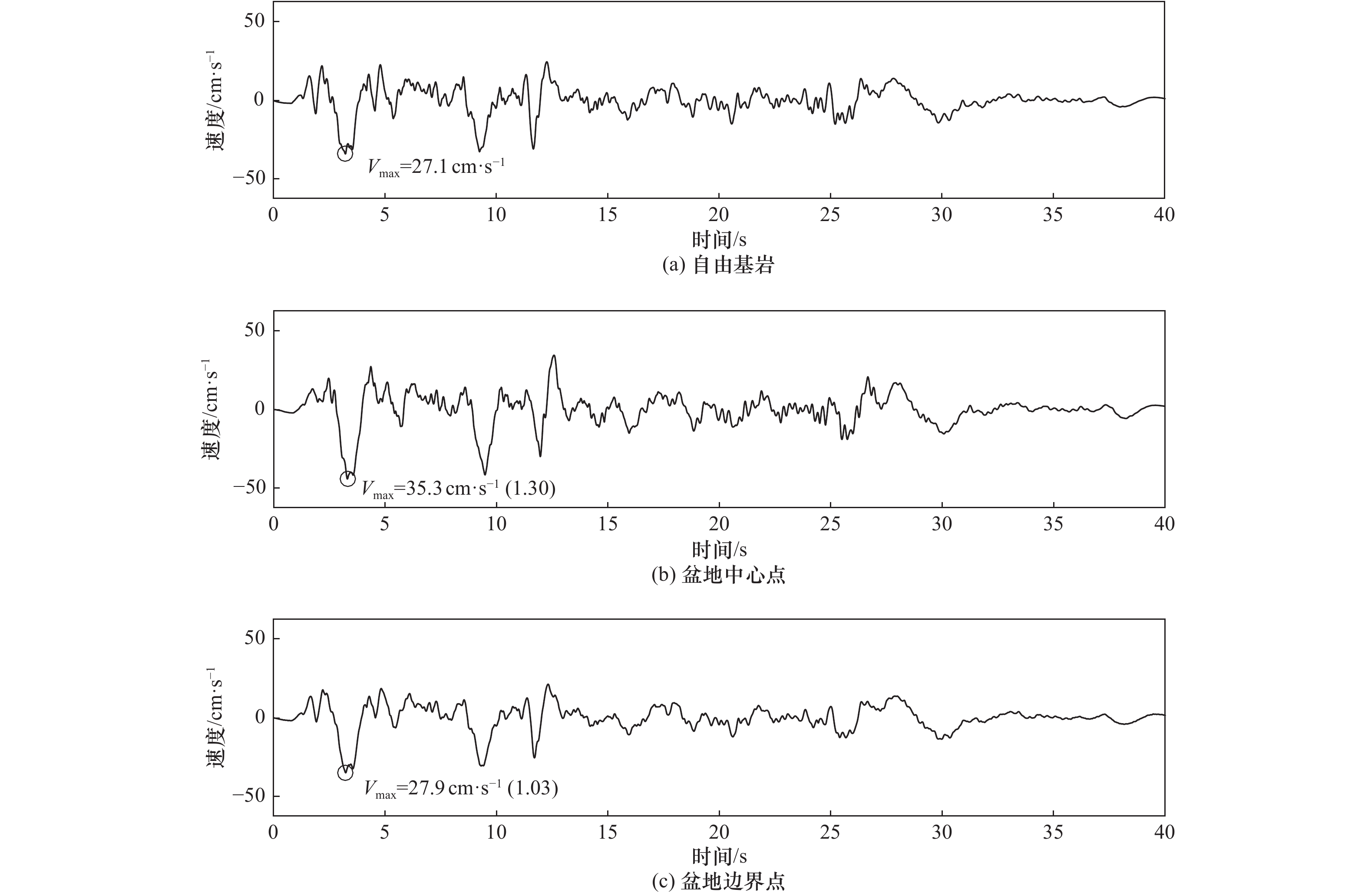
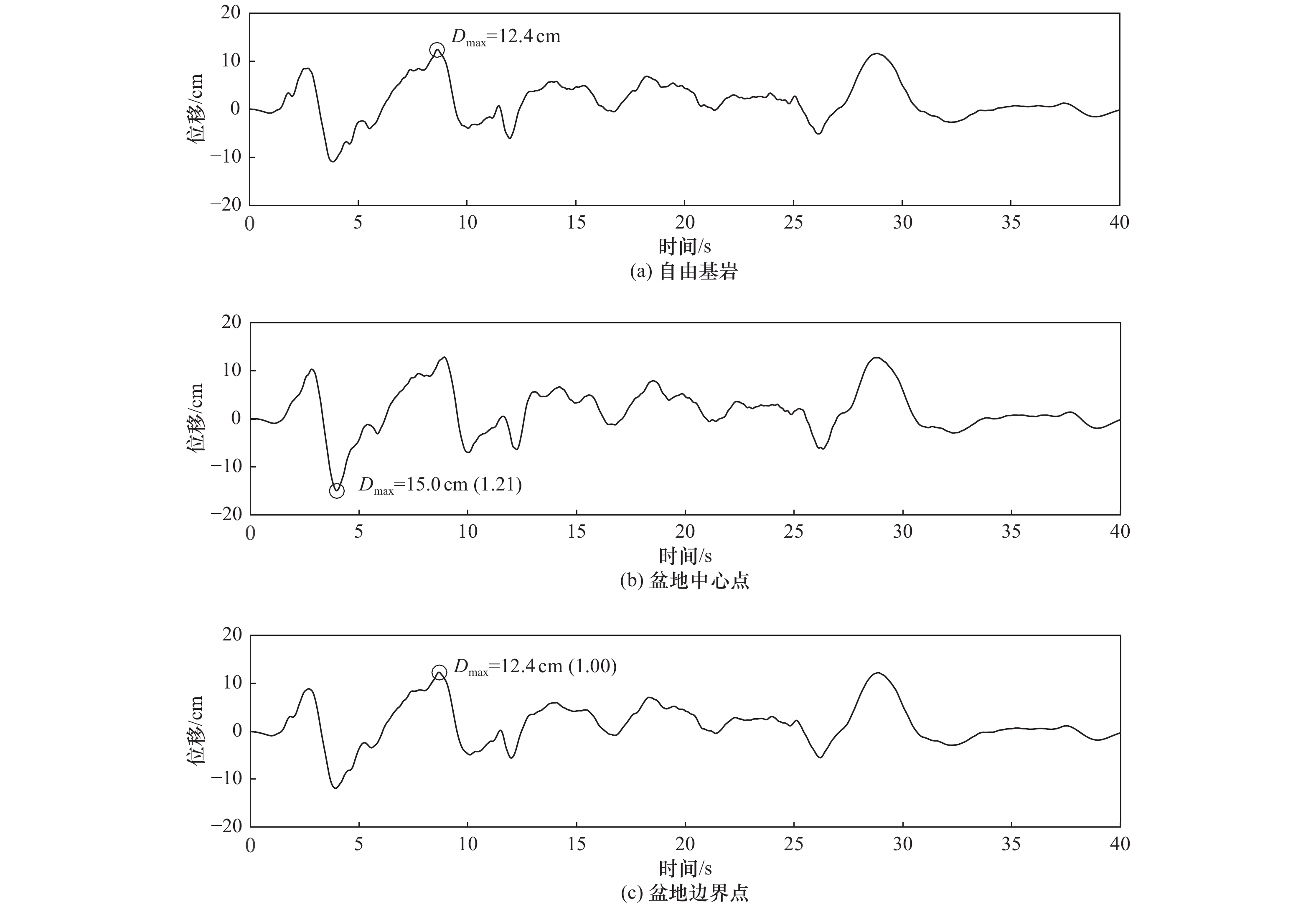
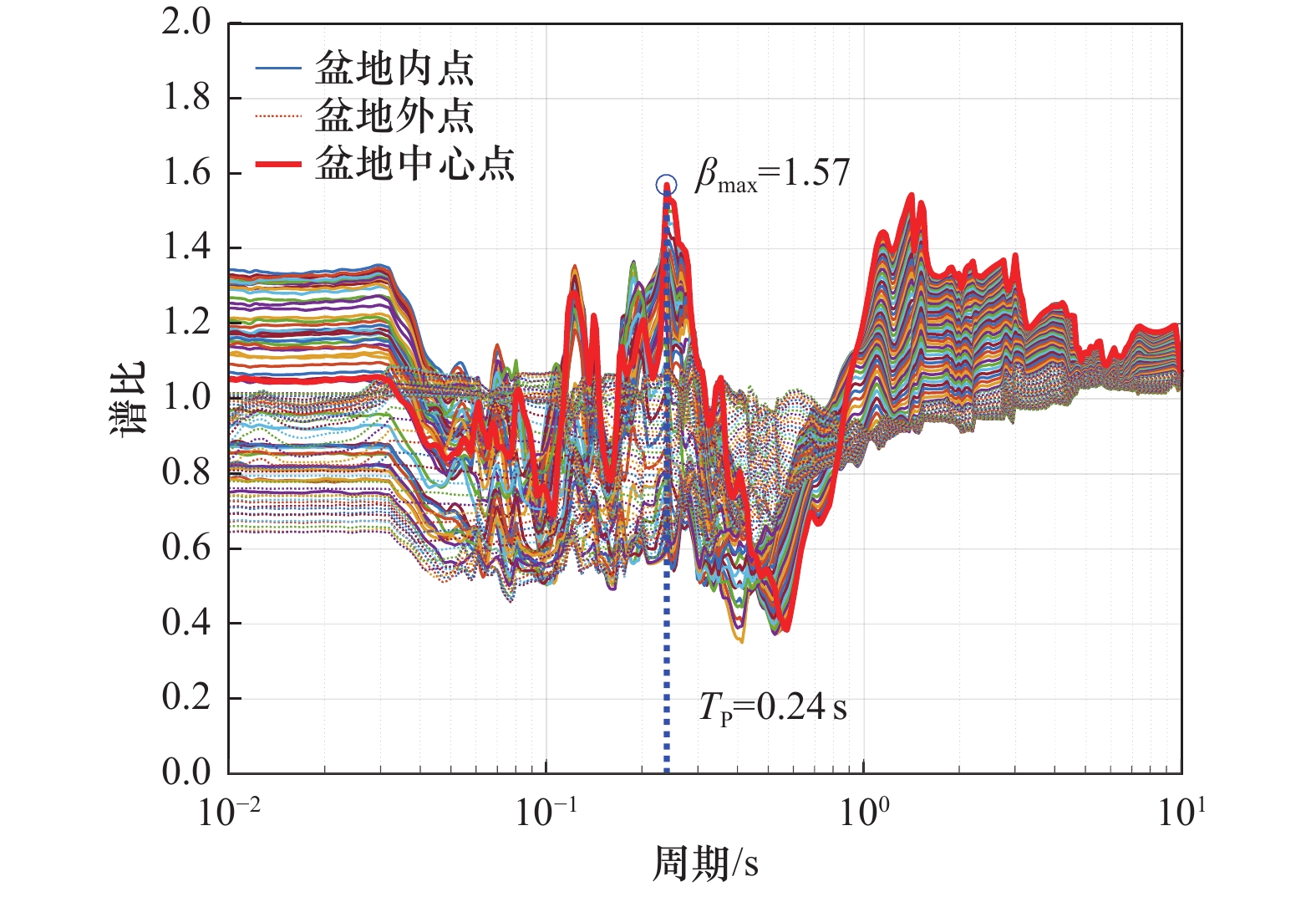
[1] 李伟华, 赵成刚, 2004. 饱和土沉积谷场地对平面SV波的散射问题的解析解. 地球物理学报, 47(5): 911—919. doi: 10.3321/j.issn:0001-5733.2004.05.025Li W. H., Zhao C. G., 2004. Scattering of plane SV waves by circular-arc alluvial valleys with saturated soil deposits. Chinese Journal of Geophysics, 47(5): 911—919. (in Chinese) doi: 10.3321/j.issn:0001-5733.2004.05.025 [2] 梁建文, 严林隽, 李军伟等, 2001. 圆弧形沉积河谷场地在平面P波入射下的响应. 岩土力学, 22(2): 138—143. doi: 10.3969/j.issn.1000-7598.2001.02.005Liang J. W., Yan L. J., Li J. W., et al., 2001. Response of circular-arc alluvial valleys under incident plane P waves. Rock and Soil Mechanics, 22(2): 138—143. (in Chinese) doi: 10.3969/j.issn.1000-7598.2001.02.005 [3] 梁建文, 严林隽, 秦东等, 2003. 圆弧形沉积河谷场地在平面SV波入射下的动力响应. 土木工程学报, 36(12): 74—82. doi: 10.3321/j.issn:1000-131X.2003.12.013Liang J. W., Yan L. J., Qin D., et al., 2003. Dynamic response of circular-arc sedimentary valley site under incident plane SV waves. China Civil Engineering Journal, 36(12): 74—82. (in Chinese) doi: 10.3321/j.issn:1000-131X.2003.12.013 [4] 梁建文, 张秋红, 李方杰, 2006. 浅圆沉积谷地对瑞雷波的散射—高频解. 地震学报, 28(2): 176—182. doi: 10.3321/j.issn:0253-3782.2006.02.008Liang J. W., Zhang Q. H., Li F. J., 2006. Scattering of Rayleigh waves by a shallow circular alluvial valley: high-frequency solution. Acta Seismologica Sinica, 28(2): 176—182. (in Chinese) doi: 10.3321/j.issn:0253-3782.2006.02.008 [5] 梁建文, 魏新磊, Lee V. W., 2009a. 圆弧形沉积谷地对平面SV波三维散射解析解. 岩土工程学报, 31(9): 1345—1353.Liang J. W., Wei X. L., Lee V. W., 2009a. 3D scattering of plane SV waves by a circular-arc alluvial valley. Chinese Journal of Geotechnical Engineering, 31(9): 1345—1353. (in Chinese) [6] 梁建文, 魏新磊, Lee V. W., 2009b. 圆弧形沉积谷地对Rayleigh波三维散射解析解. 天津大学学报, 42(1): 24—34.Liang J. W., Wei X. L., Lee V. W., 2009b. Analytical solution for 3D scattering of rayleigh waves by a circular-arc alluvial valley. Journal of Tianjin University, 42(1): 24—34. (in Chinese) [7] 梁建文, 魏新磊, Lee V. W., 2010. 圆弧形沉积谷地对平面P波的三维散射解析解. 岩土力学, 31(2): 461—470. doi: 10.3969/j.issn.1000-7598.2010.02.022Liang J. W., Wei X. L., Lee V. W., 2010. 3-D scattering of plane P waves by a circular-arc alluvial valley. Rock and Soil Mechanics, 31(2): 461—470. (in Chinese) doi: 10.3969/j.issn.1000-7598.2010.02.022 [8] 张郁山, 2010. 圆弧状沉积谷地在平面SH波入射下的动力响应. 岩土工程学报, 32(1): 1—6.Zhang Y. S., 2010. Dynamic response of arc-layered alluvial valley under incidence of plane SH waves. Chinese Journal of Geotechnical Engineering, 32(1): 1—6. (in Chinese) [9] Abramowitz M., Stegun I. A., 1972. Handbook of mathematical functions with formulas, graphs and mathematical tables. New York: Dover Publication. [10] Li W. H., Zhao C. G., Shi P. X., 2005. Scattering of plane P waves by circular-arc alluvial valleys with saturated soil deposits. Soil Dynamics and Earthquake Engineering, 25(12): 997—1014. doi: 10.1016/j.soildyn.2004.10.010 [11] Todorovska M. I., Lee V. W., 1991. Surface motion of shallow circular alluvial valleys for incident plane SH waves-analytical solution. Soil Dynamics and Earthquake Engineering, 10(4): 192—200. doi: 10.1016/0267-7261(91)90033-V [12] Trifunac M. D., 1971. Surface motion of a semi-cylindrical alluvial valley for incident plane SH waves. Bulletin of the Seismological Society of America, 61(6): 1755—1770. [13] Wong H. L., Trifunac M. D., 1974. Surface motion of a semi-elliptical alluvial valley for incident plane SH waves. Bulletin of the Seismological Society of America, 64(5): 1389—1408. [14] Yuan X. M., Liao Z. P., 1995. Scattering of plane SH waves by a cylindrical alluvial valley of circular-arc cross-section. Earthquake Engineering & Structural Dynamics, 24(10): 1303—1313. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 207
- HTML全文浏览量: 82
- PDF下载量: 7
- 被引次数: 0
