Analysis of Toppling Failure of Anti Toppling Rock Slope Based on Numerical Manifold Method
-
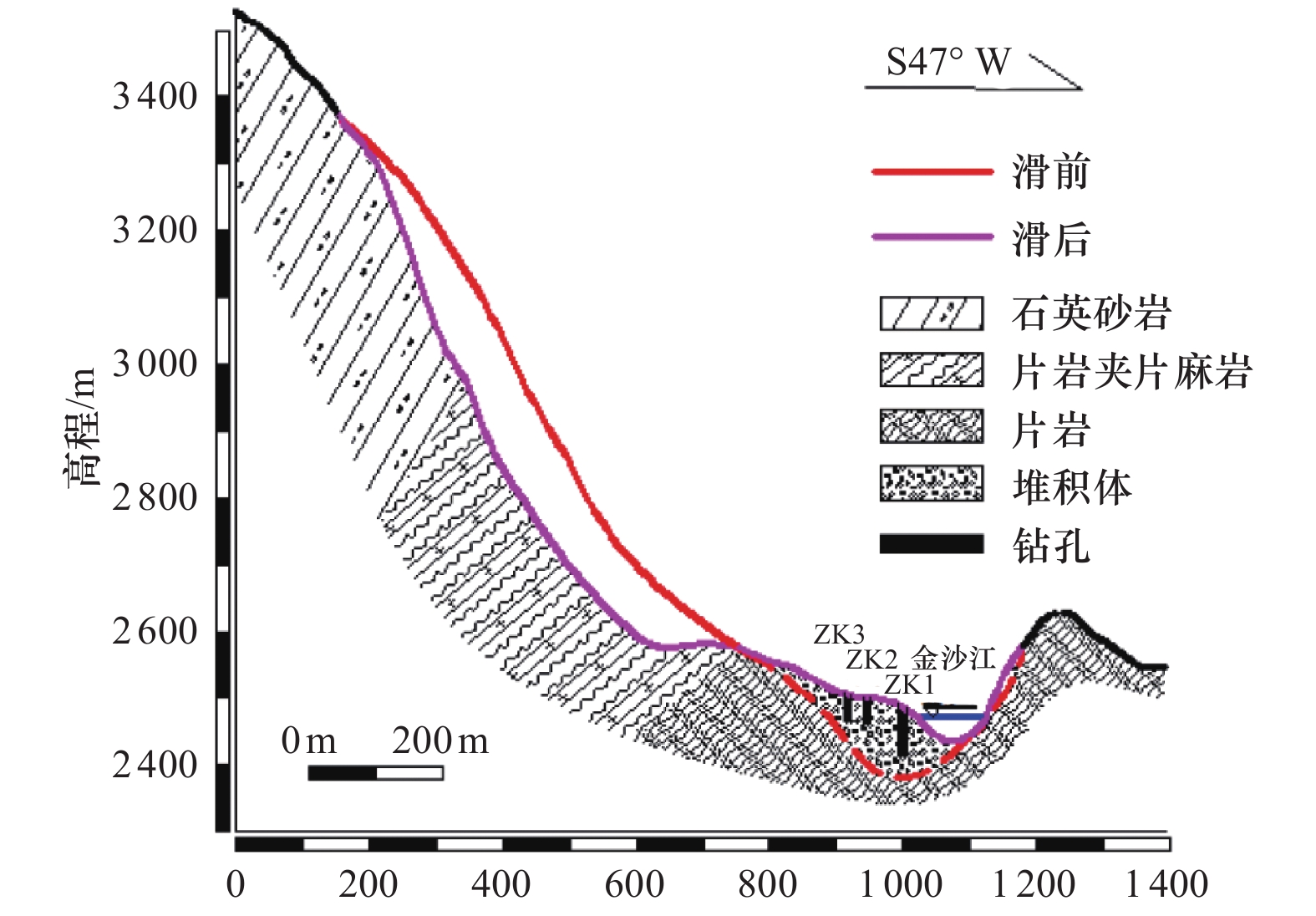
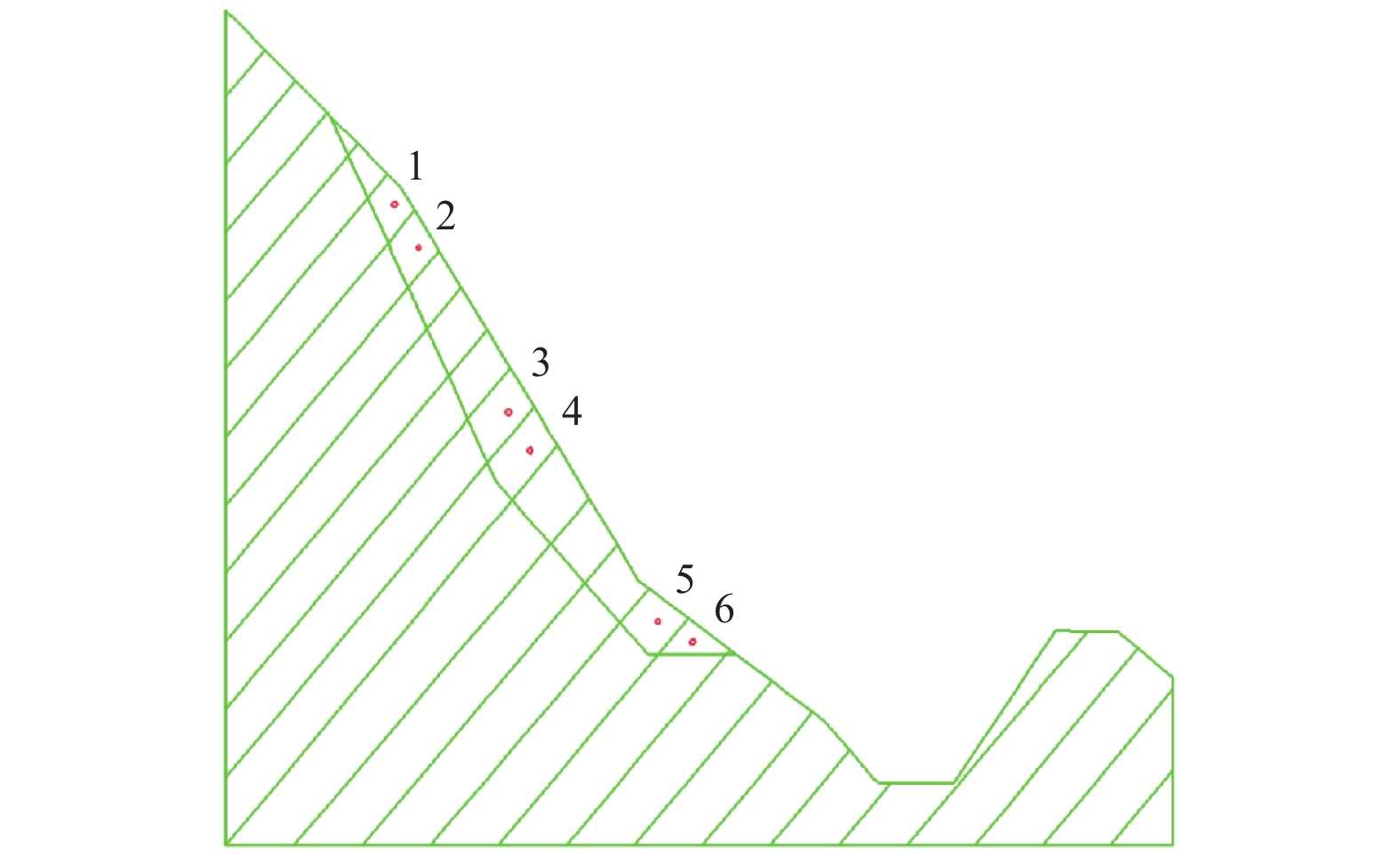
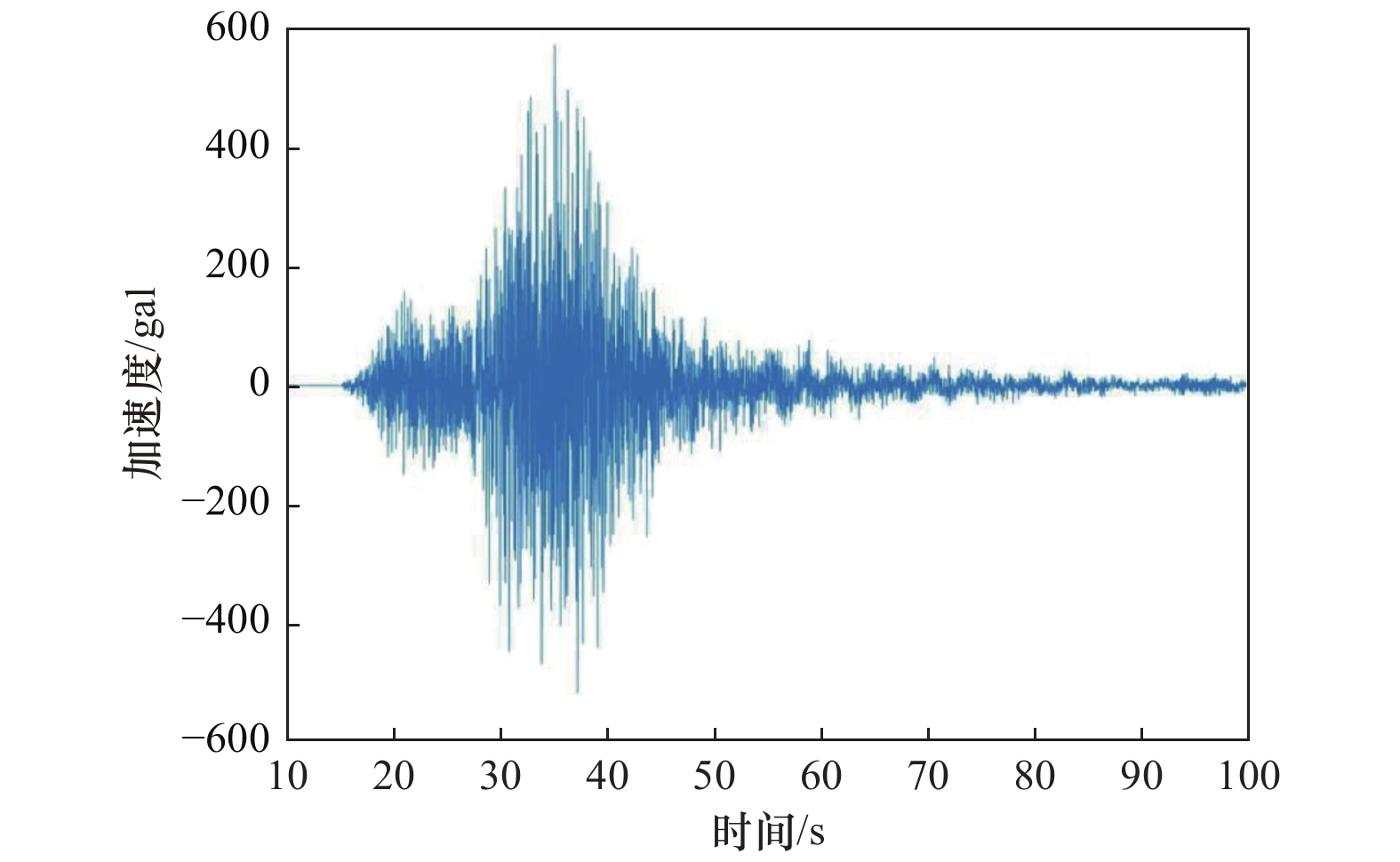
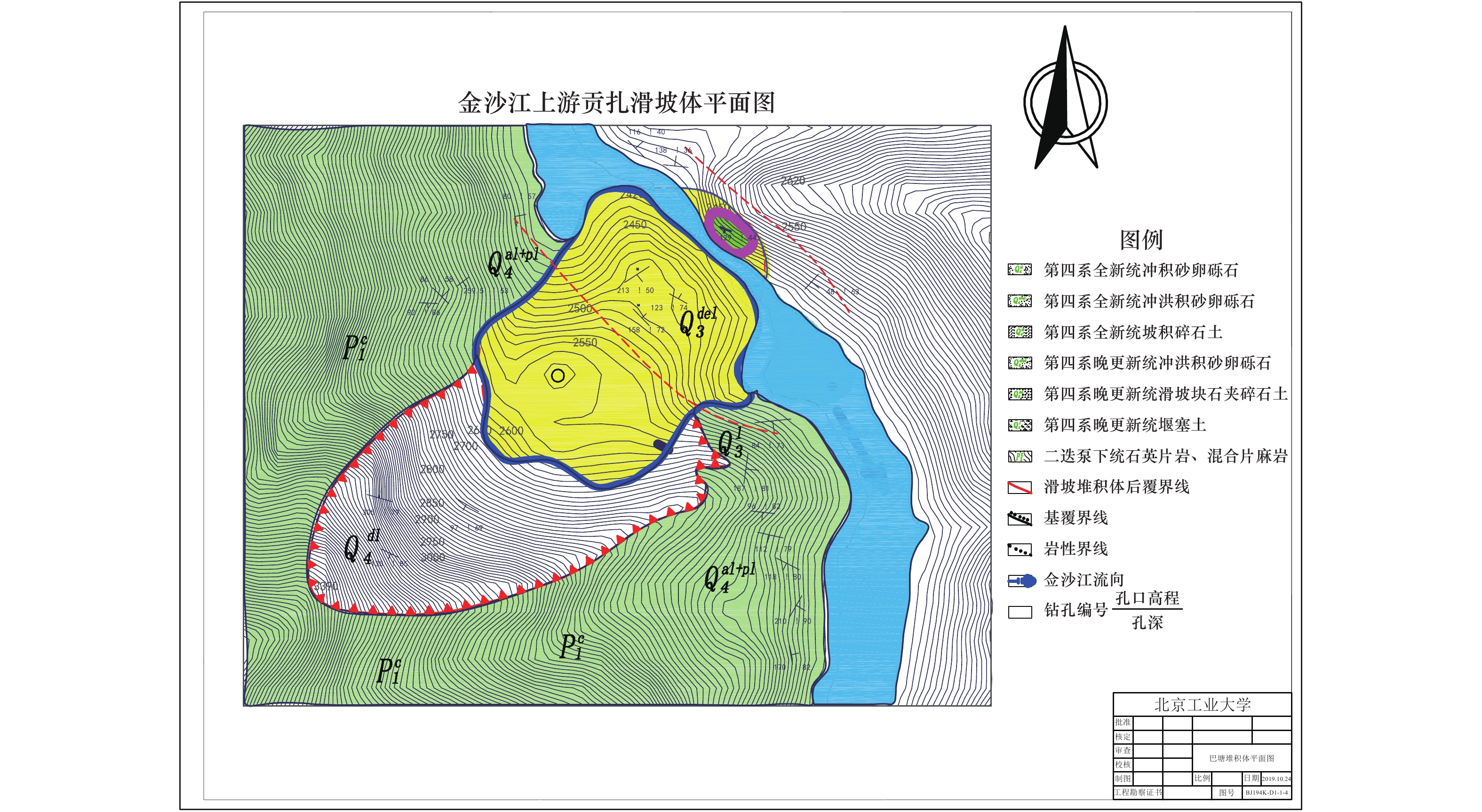
摘要: 边坡破坏是累积性过程，从变形到破坏的过程中会产生永久位移，如果永久位移过大，极有可能产生滑坡。因此根据不同工况下采集到的位移数据，分析地震作用下反倾层状岩质边坡在不同内摩擦角下的破坏特征。利用二维数值流形法（NMM），以青藏高原金沙江流域西藏昌都地区芒康县索多西乡贡扎倾倒滑坡为研究对象，依据实地考察数据及室内力学试验得到的物理力学参数，建立数值计算模型，模拟地震作用下反倾层状岩质边坡倾倒破坏过程，并在边坡上布置3组监测点获取位移数据。模拟结果表明：随着内摩擦角的增大，边坡坡体从开始破坏到新的平衡状态和达到最大位移所需的时间越短，同时，滑动块体最大水平位移逐渐减小；内摩擦角＜40°时，坡体在前15 s呈整体移动趋势，大部分岩块产生整体滑移，靠近坡顶处的岩块发生轻微转动，推动前面的岩块加速滑动，呈倾倒-滑移模式；内摩擦角＞40°时，靠近坡顶的岩块首先产生滑动，并转动驱使前面的岩块，推动坡脚处岩块产生滑动，最终上部岩块达到新的平衡，呈渐进式倾倒破坏，产生整体性破坏的可能性较小。Abstract: Slope failure is a cumulative process, and permanent displacement will be produced from deformation to failure process, if the value of permanent displacement is too large, it is very likely to produce landslide. Therefore, the displacement data generated by different friction angles under seismic load are used to analyze the failure characteristics of anti dip layered rock slope under different friction angles. Based on the two-dimensional numerical manifold method (NMM) proposed by Dr. Shi Genhua, the gongzha landslide in suoduoxi Township, Mangkang County, Changdu Prefecture, Tibet, is studied. According to the field investigation data and the required physical and mechanical parameters obtained from the indoor mechanical test, a numerical calculation model is established to simulate the toppling failure process of the anti inclined rock slope under the action of earthquake. In the process of simulation, three groups of monitoring points were arranged on the slope to obtain displacement data. The simulation results show that: with the increase of friction angle, the process of slope from failure to new equilibrium state and the time to reach the maximum displacement value are shorter. At the same time, the maximum horizontal displacement of the sliding block decreases gradually. When the friction angle is less than 40 degrees, the slope will move as a whole in the first 15 seconds, most of the rock blocks will slide as a whole, and the rock blocks near the top of the slope will rotate slightly to accelerate the sliding of the rock blocks in front, showing a toppling sliding mode; when the friction angle is more than 40 degrees, the rock blocks near the top of the slope will first slide and rotate to drive the rock blocks in front, and push the rock blocks at the foot of the slope to slide Finally, the upper rock mass reaches a new balance and presents progressive collapse failure, so the possibility of overall failure is small.
-
引言
中国大陆东部断裂系统是由一系列北东和北西走向断裂构成的共轭剪切破裂系统，其中北西向断裂处于破裂初期，活动性较强，多断续，集中成带分布并一定程度上控制着中强地震的发生（邵云惠，1980；李祖武，1983；冯希杰，1988；徐杰等，2003）。针对该组断裂的研究成果将对防震减灾产生重要意义。由于平原区NW向断裂都是隐伏断裂，所以对其具体位置尚需更深入的研究。通过测量断层气来探测隐伏断裂带已成为行之有效的方法之一，目前已在多条隐伏断裂探测工作中取得了良好的效果（汪成民等，1991；陈刚等，1995；苏鹤军等，2005；刘菁华等，2006；邵永新等，2007；姚道平等，2008；刘学领等，2011；冯军等，2011；张慧等，2013）。该方法将断裂视为天然地质体中连接深部与浅部的“通道”，大量深部气体如H2、Rn和Hg气等可经该通道向上逸出，导致以上气体浓度在断裂位置附近异常升高，利用该原理则可通过圈定断层气异常点位来探测断裂的空间位置。
研究区位于华北平原西部，区内第四系厚度达150—300m以上（河南省地质矿产局，1989）。新郑-太康断裂为一条北西向隐伏断裂（王志铄等，2017），由于缺乏系统的浅层地震勘探和钻孔资料，目前对其空间展布仍然存在争议。本次在利用石油勘探资料对新郑-太康断裂进行深部定位的基础上，在新郑地区布置2条与断层走向近垂直的地球化学测线，通过测量土壤中的H2浓度并分析H2分布特征，以确定该断裂的浅层位置。
1. 区域地震地质背景
太康隆起西接豫西隆起，东邻鲁西隆起，南北分别为周口坳陷和开封坳陷。该区是豫西隆起与鲁西隆起延伸、连接的过渡单元，其基底以元古代五指岭组花岗片麻岩、黑云母片麻岩为主，上覆震旦系坚硬的安山玢岩（河南石油勘探指挥部地质大队，1976），进入新生代以来该区整体下沉并伴随强烈的断裂活动（石油化工部物探局，1975）。南部周口坳陷是第三系及上古生界的沉积坳陷，基底埋深约3—6km，岩性以五指岭组片岩、嵩山组石英岩和登封杂岩为主（燃化部六四六厂研究所，1972）。其内部发育多条具有一定规模的北西向隐伏断裂（图 1），如登封-西华断裂（F4）和临颍-郸城断裂（F5），将周口坳陷切割为多个次级凹陷与凸起。
图 1 区域地震、地震构造与测线分布图（图（b）为图（a）红框区的放大图）Figure 1. Regional seismo-tectonic map and location of survey lines新郑-太康断裂（F1）起于新郑市北，向东经鄢陵，延伸至太康县以南，长147km，是太康隆起和周口坳陷的分界断裂（图 1）。最新的深部石油勘探资料表明该断裂整体倾向北，倾角较陡，在东段显示出正断特征，中段和西段表现为逆断层。新郑-太康断裂在浅部向上分叉，与北部次级断裂组合为负花状构造，具有明显的离散走滑特征，且新近纪以来活动明显，新近系底界断距可达150m（图 2，据河南油田勘探开发研究院内部资料）。
图 2 新郑-太康断裂东段TK-90-311地震偏移剖面（剖面位置见图 1（a））Figure 2. Seismic profile No.TK-90-311 across the eastern segment of Xinzheng-Taikang fault此外，周口坳陷内发生过多次5.0—6.0级地震，地震活动水平略高于太康隆起，区内最新的地震为2010年太康4.7级地震，震中位置见图 1（a），发震构造为新郑-太康断裂（孙杰等，2014）。
2. 探测实施与结果
2.1 探测仪器及测试方法
本次H2测试采用的仪器为德国德尔格公司生产的X-am 7000型多气体检测仪，传感器为电化学传感器，当气体扩散进入传感器后，在反应电极表面经过氧化或还原反应产生电流，并通过外电路流经2个电极，可通过外电路的负荷电阻测量气体浓度。该传感器可检测H2浓度上限为2000ppm，灵敏度为5ppm，测量误差±5%。该仪器稳定性和抗干扰能力均较强。
测线位置选择在新郑市解放路路侧和马庄村-前宫村的村间道路旁，测线位置见图 1（b），附近无污染源，地下水位稳定，埋深约10—15m。测量前，先对仪器进行校正，稳定后开始测量。测量时，先用锤将1.2m的钢钎打入土中成孔，拔出后立即将锥形麻花钻收集管拧入土中封孔，土壤气体通过锥形麻花钻收集管、胶皮管后进入测试仪器，由于H2比重小，逸出迅速。测量多次取峰值作为最终结果。
2.2 数据处理及断裂浅部定位
异常值的判定采用数值分析法，考虑到：① 测试区附近无污染源，空气中H2浓度背景值较低（2.113—5.998ppm）；② 松散的第四系覆盖较厚，H2逸出条件复杂多变；③ 该断裂东段（太康段）向上延伸并分叉形成花状构造，分支断裂数目多且规模不等（中国地震局地球物理勘探中心，2015），同时断裂两侧裂隙发育，气体的逸出通道彼此相连或将导致产生于次级断裂深部的H2沿逸出条件更好的主断裂逸出，即气体发生偏移，我们认为异常值下限定得过高会导致部分次级断裂信息的丢失，因此将平均值与1倍标准差之和、平均值与2倍标准差之和综合考虑来划分异常。
断层的活动性质、几何特征（Ciotoli等，2007）以及破碎带和断层的发育程度（King等，1996；Annunziatellis等，2008）在一定程度上决定了地下裂隙的产生、分布及闭合，进而通过改变地下通道的连通状况来影响气体由深至浅的迁移过程。断层气浓度曲线蕴含丰富的地质信息，以下将对2条测线分别进行讨论：
（1）解放路测线
该测线位于新郑市西北解放路路侧（图 1（b）），共39个测点，长2035m，平均测点间距50m，当H2浓度明显高时，加密到每25m一个测点。至测线两端，测点间距扩大至100m。
各测点H2浓度的平均值μ=214.6ppm，标准差σ=341.4ppm，我们将浓度高于μ+2σ的异常点定为A类异常，表示异常幅度大，异常形态明显，对应规模较大的断裂；将高于μ+σ的异常点定为B类异常，该类异常幅度稍小，对应规模稍小的次级断裂。该测线异常点位置及类型见表 1，解释后的断裂见图 3。H2浓度在310m处异常高（1901ppm），为A类异常，且明显高于两侧，反映气体的逸出条件向两侧逐渐变差，破碎带集中在一个较窄的范围，故判断该处发育近直立的走滑断裂（Ciotoli等，2007）；在760m与1035m处H2浓度接近（分别为789ppm和814.1ppm），为B类异常，在气体浓度曲线上表现出“双峰”态。由于新郑-太康断裂长期活动，带内充分发育断层泥等细粒物质导致断裂带渗透性降低，气体绕过渗透性低的断层带而从其两侧逸出，造成860—1010m间H2浓度低（340—360ppm）的现象，该处对应断裂带（King等，1996；Annunziatellis等，2008），其宽约150m。H2浓度在1035m处向北迅速下降，判断该断裂带倾向北。根据异常类型判断，该断裂带的规模、活动性不及南部的走滑断裂（张大其，1991；孟广魁等，1997；焦德成等，2012）。
表 1 解放路测线异常点位及类型Table 1. Location and type of anomalies from the Jiefang road survey line距测线起始点位置/m H2浓度/ppm 异常类型 断层倾向 310 1901 A 近直立 760 789 B N 1035 814.1 B N 
图 3 解放路测线H2测量结果与异常分析Figure 3. The H2 concentration curve of the Jiefang road survey line（a）测线异常点位与石油勘探资料解译的深部断点位置对比结果；（b）测线H2浓度曲线及解释平面上，将各异常点位置与断裂深部资料相比对可以发现，北部断裂带位置与断裂深部位置吻合较好。该测线H2浓度的高异常准确地反映了断裂的浅层位置（图 3）。
（2）马庄村-前宫村测线
该测线位于解放路测线的东南（图 1（b）），测线长2125m，共35个测点，点间距在测线两端为100m，高值附近加密到每25m一个点。各测点间H2浓度平均值μ为256.8ppm，标准差σ为302.7ppm。测线异常点位及类型见表 2，解释后的断裂见图 4。
表 2 马庄村-前宫村测线异常点位及类型Table 2. Location and types of anomalies from the Mazhuang-qiangong survey line距测线起始点距离/m H2浓度/ppm 异常类型 断层倾向 900 600 B S 1225 1250 A S 1475 1210 A S 
图 4 马庄村-前宫村测线H2测量结果与异常分析Figure 4. The H2 concentration curve of the Mazhuang-qiangong survey line（a）测线异常点位与深部石油勘探资料解译的断点位置对比结果；（b）测线H2浓度曲线及解释根据表 2，该测线共有2处A类异常：H2浓度在测线1225m和1475m处分别为1250ppm和1210ppm，在浓度曲线上表现出与解放路类似的“双峰”形态，1275—1425m之间H2浓度低（25—175ppm），对应断裂带宽约150m。自1175m处向南H2浓度逐渐下降，故判断该断裂带倾向南。900m附近存在一处B类异常，H2浓度为600ppm，对应活动性稍弱的次级断裂（图 4）。
断裂在该段的深部位置由TK-94-237.5测线和TK-94-244.5测线控制，可以看到H2浓度异常点位置与石油勘探资料确定的断裂深部位置吻合较好，前者较准确地反映了断裂的浅层位置。
对比解放路和马庄村-前宫村H2浓度曲线可知，2条H2浓度曲线解释出了相近的断裂组合，即北部存在宽约150m的断裂带，以及向南约325—450m处发育的单支断裂。不同之处在于断裂带的倾向：解放路H2浓度曲线显示断裂带北倾，而马庄村-前宫村H2浓度曲线显示断裂带倾向南，倾向的变化表明新郑-太康断裂具有明显的走滑特征（漆家福等，2003；宋明春等，2015）。
不仅如此，我们还发现如下现象：
就单一测线而言，解放路H2浓度曲线表明该处南部的断裂规模更大、活动性更强，而马庄村-前宫村H2浓度曲线则表明该处北部断裂带的规模更大、活动性更强；就H2浓度沿断裂走向的变化规律而言，由北西向南东，北部断裂带的H2浓度升高，而南部断裂的H2浓度降低。
3. 结论与讨论
通过圈定和分析解放路与马庄村-前宫村测线上H2浓度的异常点，与深部石油勘探资料相对比，获得的主要结论如下：
（1）2条测线出现的高水平H2点位与石油勘探资料确定的断裂深部位置吻合度较高，准确地反映了断裂的浅层位置。
（2）2条测线同步解释出一条走滑断裂，以及其北部发育的一条宽约150m、产状变化的断裂带，产状变化与其走滑性质有关。
值得注意的是，就气体浓度沿断裂走向的变化规律而言，由北西向南东，北部断裂带H2浓度升高，而南部断裂的H2浓度降低。在气体逸出条件相近的前提下，南、北2条断裂的活动性呈“此消彼长”的关系。考虑到2条测线相距约20km，我们认为这2条测线可能位于一组左旋左阶断裂的阶区部位。但由于受到测线密度的限制，该结论有待进一步证实。
此外，关于该区氢气来源的问题亦值得讨论。华北地台具有由结晶基底和沉积盖层组成的“双重结构”（翟明国，2011；朱日祥等，2012；滕吉文等，2014）：中条运动形成的结晶基底及上覆未经变质的中元古代以来的沉积盖层，盖层以碳酸盐岩和碎屑岩为主，而这些岩层中产生的H2微不足道（Ware等，1984）。目前已有大量实验表明，H2与CO2和CH4不同，其主要为无机过程的产物（Giardini等，1976；Ruff等，1980；Sugisaki等，1983）。构造应力作用下，破碎的矿物如石英（Hughes-Schrader等，1961；Wakita等，1980）、长石及硅酸盐矿物（Sugisaki，1980）表面的原子团与渗入裂隙中的水反应可以生成H2（Scharder机制，即Si+H2O→Si-OH+H2），含有黑云母的花岗岩可释放更多的H2（Sugisaki等，1983）。前已提及，太康隆起的沉积盖层下为震旦系火成岩、以花岗片麻岩及黑云母片麻岩为主的结晶基底，富含石英、黑云母等矿物，在动力破碎后通过反应释放出的大量H2，可能是本区土壤氢气的主要来源，由此可初步判断新郑-太康断裂至少为发育于上地壳的断裂，但由于缺乏更广泛、更精确的断层气及钻孔资料，该结论有待进一步研究和证实。
-
图 7 内摩擦角不同时边坡破坏特征
Figure 7. Failure characteristics of slope with different friction angles
表 1 岩石力学参数取值
Table 1. Rock mechanical parameters
岩层 密度/ g·m−3 体积模量/MPa 抗拉强度/MPa 剪切模量/MPa 黏聚力/MPa 内摩擦角/° 石英片岩 2.86 1677 9.44 2500 17.23 47.39 片麻岩 1.78 1225 1.11 1 838 2.02 41.57 
下载: 导出CSV
-
[1] 代仲海, 胡再强, 尹小涛等, 2018. 工程荷载作用下缓倾角反倾似层状岩质边坡变形稳定性分析. 岩土力学, 39(S1): 412—418.Dai Z. H., Hu Z. Q., Yin X. T., et al., 2018. Deformation stability analysis of gentle reverse inclined layer-like rock slope under engineering load. Rock and Soil Mechanics, 39(S1): 412—418. (in Chinese) [2] 韩贝传, 王思敬, 1999. 边坡倾倒变形的形成机制与影响因素分析. 工程地质学报, 7(3): 213—217. doi: 10.3969/j.issn.1004-9665.1999.03.004Han B. C., Wang S. J., 1999. Mechanism for toppling deformation of slope and analysis of influencing factors on it. Journal of Engineering Geology, 7(3): 213—217. (in Chinese) doi: 10.3969/j.issn.1004-9665.1999.03.004 [3] 黄润秋, 2007. 20世纪以来中国的大型滑坡及其发生机制. 岩石力学与工程学报, 26(3): 433—454. doi: 10.3321/j.issn:1000-6915.2007.03.001Huang R. Q., 2007. Large-scale landslides and their sliding mechanisms in China since the 20th century. Chinese Journal of Rock Mechanics and Engineering, 26(3): 433—454. (in Chinese) doi: 10.3321/j.issn:1000-6915.2007.03.001 [4] 李明霞, 董联杰, 2015. 层状反倾边坡变形特征及影响因素分析. 计算力学学报, 32(6): 831—837. doi: 10.7511/jslx201506019Li M. X., Dong L. J., 2015. Analysis on influential factors and deformation characteristics of toppling slope. Chinese Journal of Computational Mechanics, 32(6): 831—837. (in Chinese) doi: 10.7511/jslx201506019 [5] 刘云鹏, 邓辉, 黄润秋等, 2012. 反倾软硬互层岩体边坡地震响应的数值模拟研究. 水文地质工程地质, 39(3): 30—37.Liu Y. P., Deng H., Huang R. Q., et al., 2012. Numerical simulation of seismic response of anti-dumping rock slope interbedded by hard and soft layers. Hydrogeology and Engineering Geology, 39(3): 30—37. (in Chinese) [6] 裴觉民, 1997. 数值流形方法与非连续变形分析. 岩石力学与工程学报, 16(3): 80—93.Pei J. M., 1997. Numerical manifold method and discontinuous deformation analysis. Chinese Journal of Rock Mechanics and Engineering, 16(3): 80—93. (in Chinese) [7] 陶志刚, 张海江, 尹利洁等, 2017. 基于FDEM的戒台寺古滑体开裂破坏过程数值模拟. 水文地质工程地质, 44(3): 105—112.Tao Z. G., Zhang H. J., Yin L. J., et al., 2017. Numerical modeling of cracking for the Jietai temple ancient landslide with the combined finite-discrete element method. Hydrogeology and Engineering Geology, 44(3): 105—112. (in Chinese) [8] 王霄, 陈志坚, 徐进鹏等, 2018. 似层状岩质边坡倾倒变形破坏过程数值模拟. 水文地质工程地质, 45(1): 137—143.Wang X., Chen Z. J., Xu J. P., et al., 2018. Numerical simulation of deformation and failure process of a toppling-sliding rock slope with a quasi-lamellar structure. Hydrogeology and Engineering Geology, 45(1): 137—143. (in Chinese) [9] 王宇, 李晓, 王梦瑶等, 2013. 反倾岩质边坡变形破坏的节理有限元模拟计算. 岩石力学与工程学报, 32(S2): 3945—3953.Wang Y., Li X., Wang M. Y., et al., 2013. Failure mechanism of topping rock slope using jointed finite element simulation method. Chinese Journal of Rock Mechanics and Engineering, 32(S2): 3945—3953. (in Chinese) [10] 王章琼, 晏鄂川, 尹晓萌等, 2014. 层状反倾岩质边坡崩塌机理研究: 以湖北鹤峰红莲池铁矿边坡为例. 中南大学学报(自然科学版), 45(7): 2295—2302.Wang Z. Q., Yan E. C., Yin X. M., et al., 2014. Study on collapse mechanism of anti inclined rock slope: A case study of Honglianchi Iron Mine slope in Hefeng, Hubei province. Journal of Central South University (Science and Technology), 45(7): 2295—2302. (in Chinese) [11] Goodman R. E., Bray J. W., 1976. Toppling of rock slopes. In: Proceedings of the Specialty Conference on Rock Engineering for Foundations and Slopes. Boulder: American Society of Civil Engineering, 201－234. -
下载:
点击查看大图
计量
- 文章访问数: 191
- HTML全文浏览量: 55
- PDF下载量: 1
- 被引次数: 0
