Study on Restoring Force Model of High-strength Concrete Columns Reinforced with Multiple Composite Central Reinforcements
-
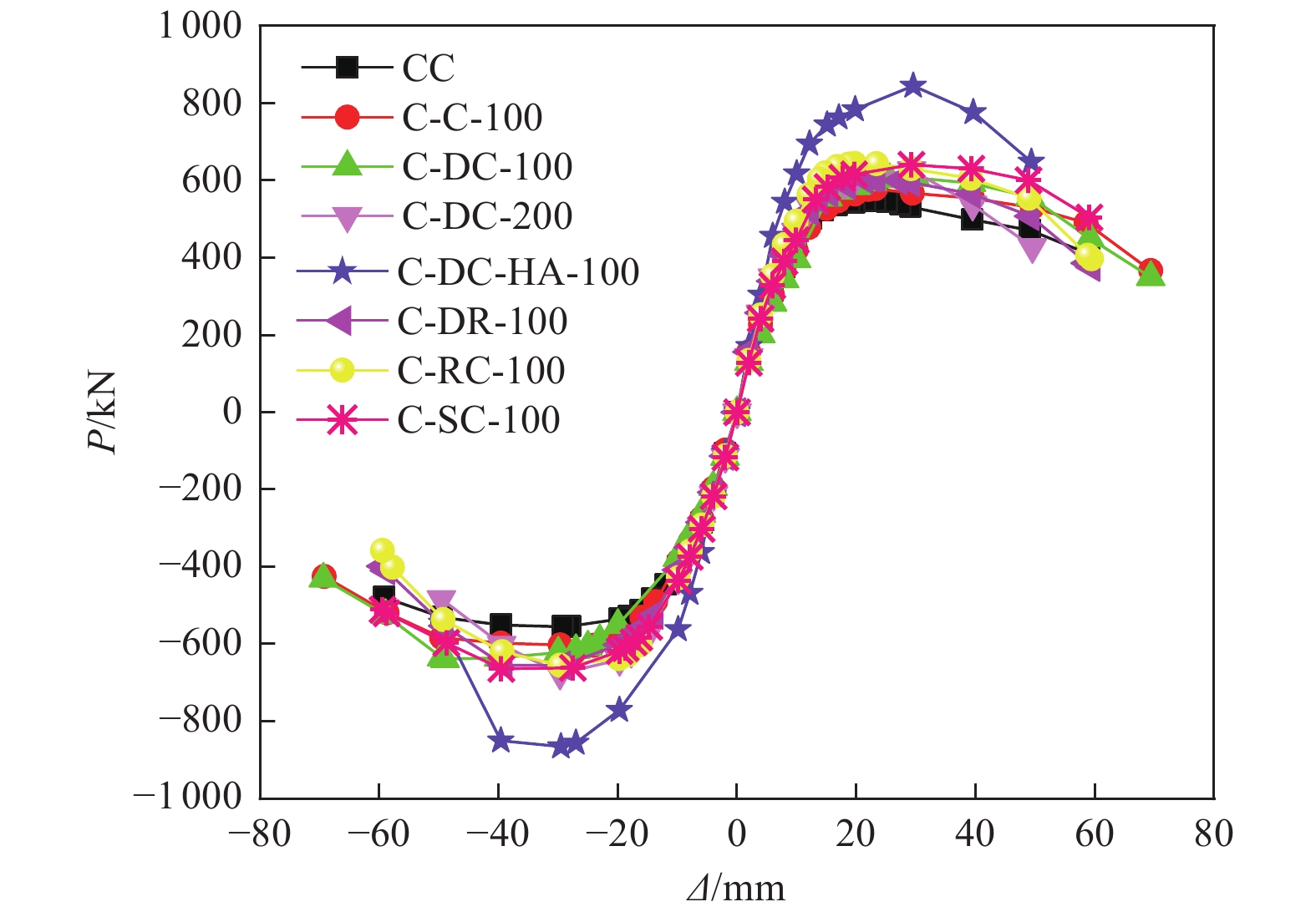
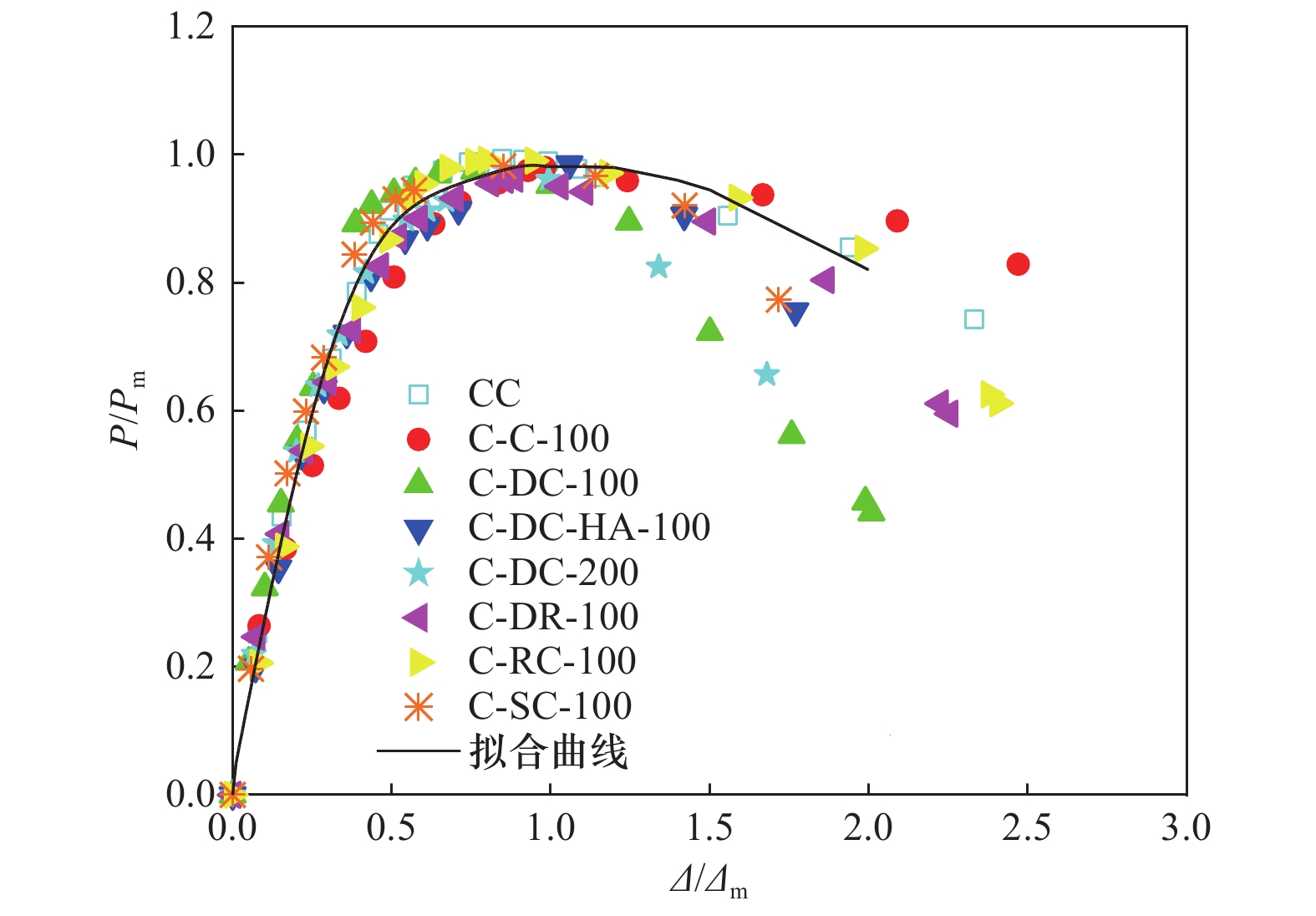
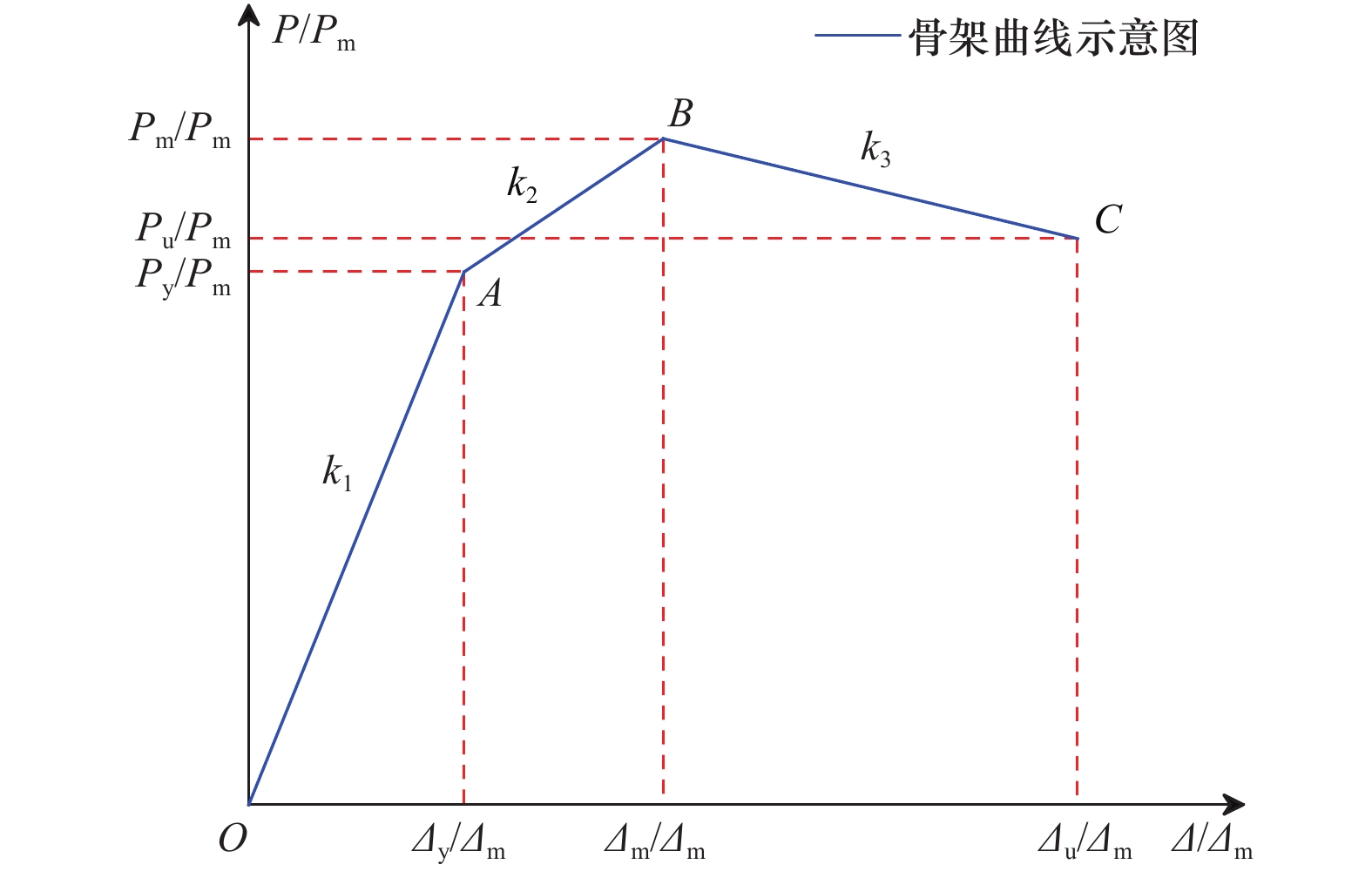
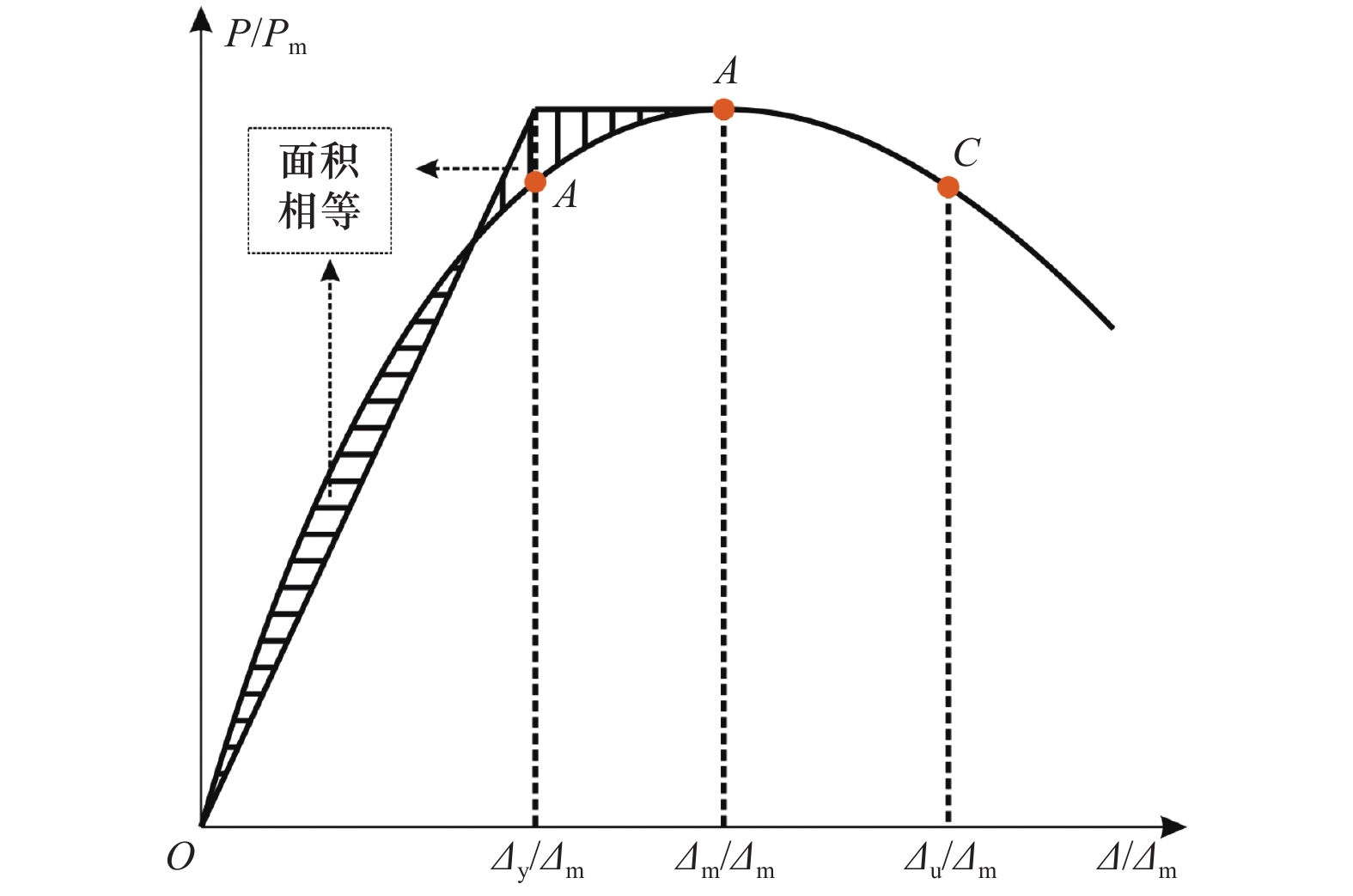
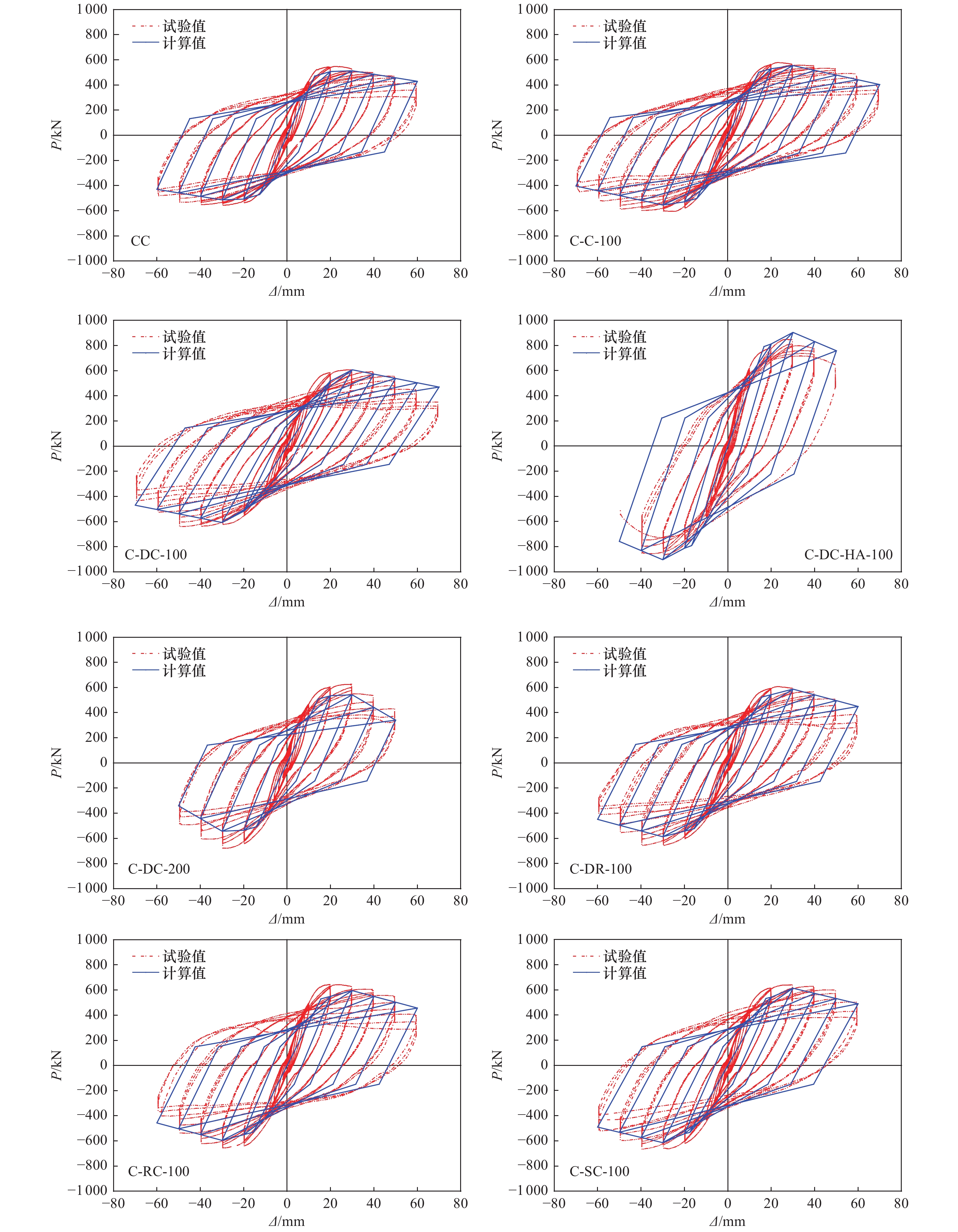
摘要: 基于8根高强混凝土多重复合芯柱在低周往复荷载作用下的试验结果，考虑轴压比、箍筋间距、配箍率等因素，提出骨架曲线特征点理论计算模型。同时，考虑加载历程对芯柱性能退化的影响，根据试验拟合结果引入刚度退化模型，以反映各试件滞回曲线卸载刚度退化规律，给出恢复力模型滞回规则，并将滞回曲线模拟值与试验值进行对比。结果表明：骨架曲线特征点计算方法具有较高精度，计算骨架曲线与试验测量骨架曲线吻合良好，可为高强混凝土多重复合芯柱非线性地震反应分析和工程设计提供参考。Abstract: Based on the quasi-static cyclic tests of eight high-strength concrete columns reinforced with multiple composite central reinforcements, a theoretical calculation model was presented to predict the characteristic points of skeleton curves for the columns considering influencing factors such as the axial compression ratio, stirrup spacing, and stirrup ratio. In addition, a restoring force model was introduced considering the degradation of unloading stiffness based on the fitted results of cyclic loading test data. The results show that the proposed model can accurately predict the characteristic points for these columns. The simulated hysteretic behaviors based on the restoring force model had good agreement with those from experimental results. Therefore, the proposed restoring force model can be applied for the nonlinear dynamic analysis of structures with such kinds of multiple reinforcement high-concrete columns.
-
Key words:
- Core column /
- Stirrup form /
- Skeleton curve /
- Seismic behavior /
- Restoring force model
-
引言
众所周知，我国是地震频发的国家，地震可能造成高速铁路列车脱轨事故，为此，我国建立了相应的地震报警及紧急处置系统，力争在潜在破坏性地震到达之前发出报警，降低列车发生脱轨或倾覆的概率。目前广泛采用的地震报警参数主要为峰值加速度PGA，然而PGA主要体现地震波幅值，未考虑频谱及持时影响，对于无破坏性的高频小震可能产生误报现象。为避免这种干扰，郭恩栋等（2015）引入谱强度SI作为高速铁路地震报警参数，并给出相应的计算方法，SI从能量方面出发，考虑了幅值及频谱影响，忽略持时的影响，但相比PGA更合理。美国电力研究所EPRI（O'Hara 等，1991）在核电厂地震监测报警中引入累积绝对速度CAV作为报警参数，研究发现低频震动对CAV的贡献明显高于高频震动。我国三代核电站AP1000参考国外标准也引入了CAV作为地震报警参数（胡进军等，2013）。林宜娴（2002）提出CAV、PGA、PGV等参数可作为地震报警参数，其稳定性好，且确定性较高。Kostov（2005）根据欧洲几次强地震动数据，分析得出标准化累积绝对速度CAVSTD在预测地震动破坏能力方面明显优于PGA。伊斯坦布尔在地震预报警系统中利用累积绝对速度快速判别强地震动（Erdik等，2003）。Fahjan等（2011）在地震报警的触警算法中引入CAV，并提出新的用于报警系统的参数。黄俊等（2014）引入CAV作为报警参数，分析其在高速铁路报警中的适用性，研究发现CAV可有效排除破坏性小的高频小震对高速铁路列车地震报警的干扰。目前虽对CAV在地震报警中的应用有了深入研究，但在高速铁路列车地震报警中的研究较少，仅通过相关的地震波数据处理得出，未考虑车轨动力响应关系，且给出的计算参数为CAVSTD，为此，需探讨考虑车轨关系的基于相关起算阈值的CAV计算方法。
1. CAV相关参数
目前，地震工程界主要研究CAV、CAVSTD、CAV5。其中CAV于1988年由美国电力研究所（O'Hara等，1991）在核电厂报警中第2级判别标准中提出的，其概念为记录地震加速度数据的绝对值对记录时间进行积分，记为累积绝对速度CAV：
$${\rm{ CAV}} = \mathop \int \nolimits_0^{{{{t}}_{{\rm{max}}}}} \left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t$$ (1) 为提高CAV在核电厂报警中的准确度，EPRI在报告中引入标准化累积绝对速度CAVSTD，其可有效避免长持时记录的地震波尾部对应的幅值小且破坏性小的地震动对其数值的影响，其定义如下：将记录的加速度时程分成以1 s为时间间隔的N个小段，当1 s时间段内存在加速度绝对值≥0.025 g时，对该秒内加速度数值的绝对值进行积分，否则该秒内的积分值记为零，然后将整个记录时程进行相加求和，表达式为：
$$ {\rm{CA{V_{STD}}}} = \mathop \sum \limits_{{i=1}}^n \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\left| {{{a}}\left( {{t}} \right)} \right| < 0.025\;g}\\ {1,\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.025\;{{g}}} \end{array}} \right.$$ (2) Kramer等（2002）于2002年提出CAV5，用于场地液化判别，其概念为：将记录的加速度时程中对加速度数值的绝对值≥0.005 g进行积分求和，表达式为：
$${{\rm{ CAV}}_5} = \displaystyle\int \nolimits_0^\infty \left\langle {\rm{\chi }} \right\rangle \left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\left\langle {\rm{\chi }} \right\rangle = \left\{ {\begin{array}{*{20}{c}} {0\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.005\;g}\\ {1\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.005\;{{g}}} \end{array}} \right. $$ (3) 式中，a(t)为加速度时程，Wi为权重。
2. 改进的标准化累积绝对速度应用于高速铁路地震报警阈值中的计算方法
2.1 改进的标准化累积绝对速度起算阈值确定
本文引入31自由度的SY97477车辆模型（崔恩文，2014），结合车轨典型非线性接触关系，依据列车安全行驶的3项评判指标（脱轨系数、轮重减载率及横向力)，分析车体在轨道不平顺（我国高速铁路无砟轨道标准谱）与简谐波（仅考虑横向输入，与列车行驶方向垂直）共同激励下的动态响应，考虑95%的安全保证，引入2.55倍的动力放大系数（孙汉武等，2007），计算安全极限状态（超出3项指标任意1个限值）下不同车速对应的简谐波幅值随周期的变化关系，如图1所示。具体模型参数、车轨接触关系及评判标准可参考崔恩文（2014）的研究。
图 1 列车安全运行极限状态下不同车速对应的简谐波幅值随周期的变化关系Figure 1. The relationship between the amplitude of simple harmonic wave corresponding to different speeds and periods under the safe running limit state of the train由图1可知，车速一定时，即使幅值很小（<0.025 g）的低频简谐波也可能使列车脱轨，因此不能简单地套用标准化累积绝对速度CAVSTD计算公式，有必要研究改进的标准化累积绝对速度应用在高速铁路地震报警阈值中的计算方法。车速一定时，简谐波幅值随周期增加逐渐递减，最终趋于常数，且周期越大，不同车速对应的简谐波幅值之间的差值越小。车速为200 km/h时，当简谐波周期达2.2 s时，其幅值开始趋于常数，该常数约为0.008 g，本文规定此时的周期为简谐波幅值趋于常数对应的起始周期Tst，该常数记为Amin。不同车速下简谐波幅值趋于常数对应的起始周期及该常数的数值如表1所示。
表 1 不同车速下简谐波幅值趋于常数对应的起始周期及该常数的数值Table 1. The initial period of the simple harmonic wave amplitude tending to be constant at different speeds and the value of the constant项目 车速/（km·h−1） 200 250 300 350 400 起始周期Tst/s 2.2 2.3 2.1 2.0 1.7 Amin/g 0.008 0.004 0.004 0.004 0.004 由表1可知，车速为200 km/h与车速≥250 km/h时对应的Amin不同，车速≥250 km/h时Amin相同，但起始周期Tst随车速的增加呈递减趋势，说明车速越大，简谐波趋于常数所需的周期越小。
车速为200 km/h时，幅值低于0.008 g的简谐波对列车运行安全的影响可忽略不计。车速≥250 km/h时，幅值低于0.004 g的简谐波对列车运行安全的影响可忽略不计。由此可推算出改进的标准化累积绝对速度起算阈值，如表2所示。
表 2 不同车速下改进的标准化累积绝对速度起算阈值Table 2. Starting threshold of improved calculation of standardized cumulative absolute velocity at different speeds项目 车速/（km·h−1） 200 ≥250 改进的标准化累积绝对速度起算阈值/g 0.008 0.004 2.2 改进的标准化累积绝对速度应用在地震报警中的可行性分析
考虑改进的标准化累积绝对速度为累积过程的算法，其值对于加速度超过0.004 g或0.008 g的有限个数的高频小震会很小，因此，可较好地排除高速铁路沿线的高频小震，是较好的地震监测报警参数。
魏智祥（2015）分析了京武高速铁路线布置的强震仪监测到的列车运行时震动记录数据，发现列车运行产生的震动记录明显高于背景噪声，且发现东西、南北、垂直方向列车振动噪声幅值均≤0.002 g，由此可知本文设定的不同车速下改进的标准化累积绝对速度可有效排除列车振动的影响。
综上所述，本文给出改进的标准化累积绝对速度用于高速铁路地震报警是可行的。
2.3 改进的标准化累积绝对速度计算公式的确定
参照CAVSTD计算方法，本文给出车速为200 km/h时改进的标准化累积绝对速度CAV8计算公式如下：
$${{\rm{CAV}}_8} = \mathop \sum \limits_{i=1}^n \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.008\;g}\\ {1,\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.008\;{{g}}} \end{array}} \right.$$ (4) 当
$ a\left(t\right) $ $< 0.008\;g$ 时，${{W}}_{{i}}$ =0；当$\left|{a}\left({t}\right)\right|\geqslant 0.008\;g$ 时，${{W}}_{{i}}$ =1。本文给出的CAV8定义为：将加速度时程按1 s为时间间隔进行划分，如果在这1 s内加速度绝对值≥0.008 g，则对该秒内的加速度绝对值进行积分，否则忽略该秒内的积分值，然后将整个时程中每秒积分得到的数值进行累积求和。
车速为250 km/h时改进的标准化累积绝对速度CAV4计算公式如下：
$${ {\rm{CAV}}_4} = \mathop \sum \limits_{i=1}^{{n}} \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.004\;g}\\ {1,\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.004\;{{g}}} \end{array}} \right.$$ (5) 当
${a}\left({t}\right)$ $< 0.004\;g$ 时，${{W}}_{{i}}=0$ ；当$\left|{a}\left({t}\right)\right|\geqslant 0.004\;{g}$ 时，${{W}}_{{i}}$ =1。本文给出的CAV4定义为：将加速度时程按1 s为时间间隔进行划分，如果在这1 s内加速度绝对值≥0.004 g，则对该秒内的加速度绝对值进行积分，否则忽略该秒内的积分值，然后将整个时程中每秒积分得到的数值进行累积求和。
3. 高速铁路地震报警阈值确定
为确定基于改进的标准化累积绝对速度高速铁路地震报警阈值，本文从Peer数据库选取6条不同场地地震波（表3），对应的加速度反应谱如图2所示，对其进行归一化处理，分析加速度幅值与评判列车脱轨3项指标之间的关系，确定不同车速下影响行车安全的6条地震波加速度上限值，按照本文给出不同车速下改进的标准化累积绝对速度计算公式，给出6条地震波对应的改进的标准化累积绝对速度上限值，如表4所示。
表 3 地震波相关信息Table 3. Seismic wave information项目 地震波台站名称 Cape Mendocino TCU045 Capitola Hector EL Centro Imp. Co. Cent Poe Road 震级 7.01 7.62 6.93 7.13 6.54 6.54 峰值加速度/g 0.376 5 0.008 1 0.528 5 0.265 6 0.357 9 0.446 3 v30/（m·s−1） 567.78 704.64 288.62 726.00 192.05 316.64 加速度记录持时/s 36.0 45.0 39.9 45.3 40.0 22.3 表 4 不同车速下6条地震波加速度上限值与改进的标准化累积绝对速度上限值Table 4. The upper limit of acceleration amplitudes and upper limit improved calculation of standardized cumulative absolute velocity CAV of six seismic waves at different speeds地震波台站名称 车速200 km/h 车速250 km/h 车速300 km/h 车速350 km/h 车速400 km/h 加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-secCape Mendocino 0.074 0.17 0.070 0.17 0.055 0.13 0.040 0.09 0.039 0.09 TCU045 0.101 0.55 0.090 0.49 0.078 0.43 0.062 0.34 0.039 0.21 Capitola 0.109 0.34 0.078 0.25 0.062 0.20 0.054 0.17 0.039 0.11 Hector 0.101 0.27 0.070 0.19 0.062 0.17 0.054 0.14 0.047 0.12 EL Centro Imp. Co. Cent 0.078 0.16 0.070 0.18 0.054 0.13 0.039 0.08 0.027 0.05 Poe Road 0.074 0.19 0.054 0.14 0.043 0.11 0.039 0.10 0.035 0.08 由表4可知，车速相同时，即使地震波加速度相同，其对应的改进的标准化累积绝对速度不一定相同，如车速为200 km/h时，台站名称为Cape Mendocino与Poe Road的地震波加速度相同，但对应的改进的标准化累积绝对速度不同，且Cape Mendocino台站加速度记录持时较大，说明改进的标准化累积绝对速度与频谱紧密相关。车速≥250 km/h时，对于同一台站的地震波，峰值加速度越大其对应的改进的标准化累积绝对速度越大，如台站名称为Cape Mendocino的地震波，说明对于同一地震波而言，加速度影响累积绝对速度。根据改进的标准化累积绝对速度定义，加速度记录持时影响其数值。综上所述，改进的标准化累积绝对速度数值不仅与加速度幅值有关，还与频谱及加速度记录持时密切相关，可较好地反映地震动三要素。
选取6条地震波改进的标准化累积绝对速度最小值作为报警阈值，给出不同车速下基于改进的标准化累积绝对速度高速铁路地震报警阈值，如表5所示。由表5可知，改进的标准化累积绝对速度报警阈值与车速整体呈线性递减关系，中间车速对应的改进的标准化累积绝对速度可按线性插入计算。
表 5 不同车速下改进的标准化累积绝对速度高速铁路地震报警阈值Table 5. High-speed earthquake alarm threshold based on improved calculation of standardized cumulative absolute velocity thresholds at different vehicle speeds项目 车速/（km·h−1） 200 250 300 350 400 报警阈值/g-sec 0.16 0.14 0.11 0.08 0.05 4. 结论
（1）通过建立车轨模型，分析列车安全运行极限状态下简谐波幅值与周期的关系，得出不同车速下改进的标准化累积绝对速度起算阈值，并论证改进的标准化累积绝对速度在高速铁路地震报警中的可行性。
（2）参照标准化累积绝对速度CAVSTD计算公式，本文给出不同车速下改进的标准化累积绝对速度计算公式。
（3）根据本文给出的改进的标准化累积绝对速度计算公式，选取6条不同场地的地震波，分析列车在轨道不平顺及地震波共同激励下的动力响应，计算不同车速下改进的标准化累积绝对速度报警阈值，以供参考。
-
图 11 试验骨架曲线与计算骨架曲线比较
Figure 11. Comparison of skeleton curves from test and simulation results
图 14 试验滞回曲线与计算滞回曲线比较
Figure 14. Comparison between test and calculation results of hysteretic curves
表 1 试件主要参数
Table 1. Main parameters of specimens
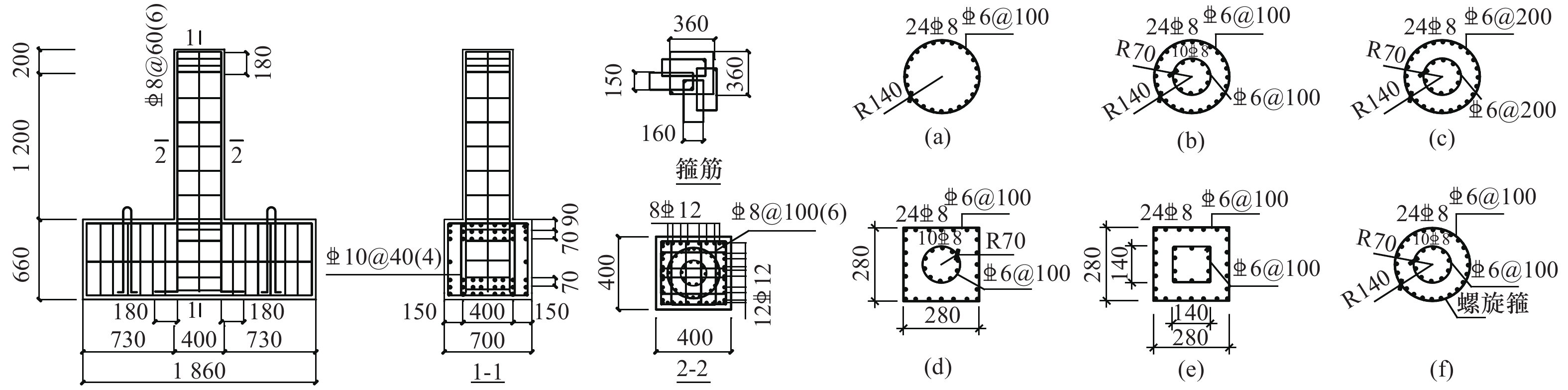
试件编号 外芯 内芯 内芯箍筋间距s/mm 纵筋配筋率ρl/% 体积配箍率ρw/% 轴力Nt/kN 试验轴压比n 柱高H/mm CC — — 100 2.83 1.68 1 270 0.19 1 200 C-C-100 圆形 — 100 3.58 1.87 1 270 0.19 1 200 C-DC-100 圆形 圆形 100 3.90 1.96 1 270 0.19 1 200 C-DC-HA-100 圆形 圆形 100 3.90 1.96 3 180 0.48 1 200 C-DC-200 圆形 圆形 200 3.90 0.98 1 270 0.19 1 200 C-RC-100 方形 圆形 100 3.90 2.02 1 270 0.19 1 200 C-DR-100 方形 方形 100 3.90 2.04 1 270 0.19 1 200 C-SC-100 螺旋 圆形 100 3.90 2.03 1 270 0.19 1 200 注：试件编号“C-DC-HA-100”中“C”表示芯柱试件，“DC”表示内芯和外芯均采用圆形箍筋形式的芯柱，“HA”表示高轴压比试件，“100”表示箍筋间距为100 mm，“RC”表示外芯和内芯分别为方形和圆形箍筋形式的芯柱；“DR”表示外芯和内芯均采用方形箍筋形式的芯柱；“SC”表示外芯和内芯分别为螺旋型和圆形箍筋形式的芯柱。 
下载: 导出CSV
表 2 侧向约束系数和约束混凝土强度
Table 2. Confinement factors and strength of confined concrete
试件名称 ${f'_{{\rm{el,s}}}}$ ${f'_{{\rm{el,d}}}}$ ${f'_{{\rm{el,h}}}}$ ${K_{\rm{s}}}$ ${K_{\rm{d}}}$ ${K_{\rm{h}}}$ ${f'_{{\rm{co}}}}$ ${f'_{{\rm{ccs}}}}$ ${f'_{{\rm{ccd}}}}$ ${f'_{{\rm{cch}}}}$ CC 2.03 — — 1.29 — — 43.4 56.1 — — C-C-100 2.03 2.66 — 1.29 1.37 — 43.4 56.1 59.6 — C-DC-100 2.03 2.66 3.46 1.29 1.37 1.47 43.4 56.1 59.6 63.7 C-DC-HA-100 2.03 2.66 3.46 1.29 1.37 1.47 43.4 56.1 59.6 63.7 C-DC-200 2.03 2.23 2.31 1.29 1.32 1.33 43.4 56.1 57.2 57.7 C-RC-100 2.03 2.38 3.19 1.29 1.34 1.44 43.4 56.1 58.1 62.3 C-DR-100 2.03 2.38 2.88 1.29 1.34 1.40 43.4 56.1 58.1 60.7 C-SC-100 2.03 2.78 3.58 1.29 1.39 1.48 43.4 56.1 60.2 64.3 注：${K_{\rm{s}}}$、${K_{\rm{d}}}$、${K_{\rm{h}}}$分别对应低约束区、中约束区、高约束区侧向约束因子；${f'_{{\rm{ccs}}}}$、${f'_{{\rm{ccd}}}}$、${f'_{{\rm{cch}}}}$分别对应低约束区、中约束区、高约束区混凝土峰值应力
下载: 导出CSV
表 3 计算结果与试验结果对比
Table 3. Comparison between calculated and measured results
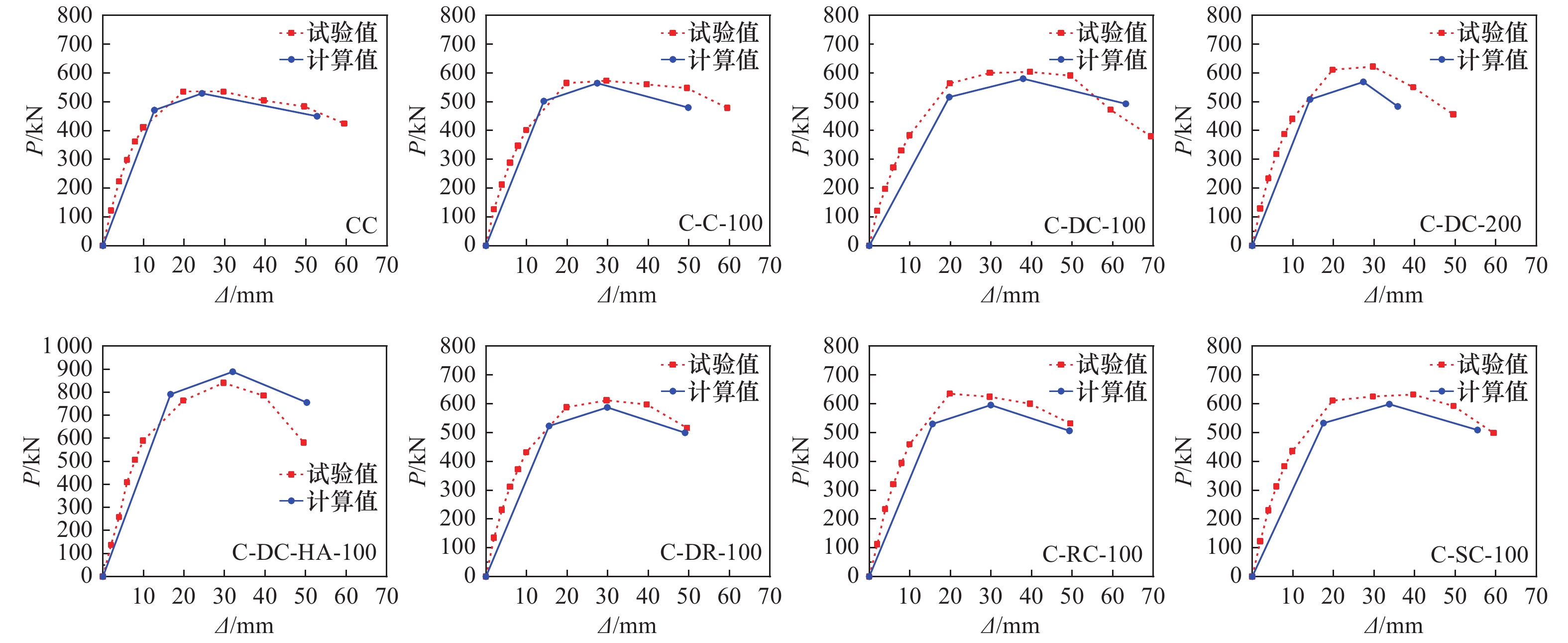
试件名称 屈服荷载Py/kN 屈服位移Δy/mm 峰值荷载Pm/kN 峰值位移Δm/mm 极限荷载Pu/kN 极限位移Δu/mm 位移延性系数μ CC 试验值 484.8 13.0 551.0 25.3 468.3 55.4 4.3 计算值 470.8 12.7 529.0 24.4 449.7 52.7 4.1 C-C-100 试验值 517.5 14.8 591.1 23.7 502.5 58.8 4.0 计算值 502.2 14.3 564.3 27.4 479.6 49.9 3.5 C-DC-100 试验值 554.1 17.7 622.6 39.5 529.2 55.2 3.1 计算值 516.1 19.7 579.9 37.9 492.9 63.2 3.2 C-DC-HA-100 试验值 743.4 16.0 857.4 27.9 728.8 43.5 2.7 计算值 791.2 16.7 889.0 32.0 755.7 50.3 3.0 C-DC-200 试验值 576.2 11.1 651.5 29.5 553.7 40.9 3.7 计算值 507.9 14.2 568.8 27.4 483.5 35.8 2.5 C-RC-100 试验值 581.2 14.1 649.4 24.7 552.0 48.2 3.4 计算值 530.0 15.6 595.5 29.9 506.2 49.3 3.2 C-DR-100 试验值 553.2 15.1 631.2 26.4 536.6 48.2 3.2 计算值 522.9 15.6 587.5 29.9 499.4 49.0 3.1 C-SC-100 试验值 578.7 15.5 652.2 34.4 554.4 53.9 3.5 计算值 532.8 17.6 598.6 33.8 508.8 55.5 3.2
下载: 导出CSV
-
[1] 董三升, 赵均海, 雷自学等, 2012. 高强混凝土加芯柱恢复力特性研究. 中国公路学报, 25(4): 90—96. doi: 10.3969/j.issn.1001-7372.2012.04.015Dong S. S., Zhao J. H., Lei Z. X., et al., 2012. Research on the restoring force of high-strength concrete columns with central reinforcement. China Journal of Highway and Transport, 25(4): 90—96. doi: 10.3969/j.issn.1001-7372.2012.04.015 [2] 范重, 钱稼茹, 吴学敏, 2001. 核心配筋柱抗震性能试验研究. 建筑结构学报, 22(1): 14—19. doi: 10.3321/j.issn:1000-6869.2001.01.003Fan Z., Qian J. R., Wu X. M., 2001. Experimental study on seismic behavior of concrete columns with central reinforcement. Journal of Building Structures, 22(1): 14—19. doi: 10.3321/j.issn:1000-6869.2001.01.003 [3] 冯鹏, 强翰林, 叶列平, 2017. 材料、构件、结构的“屈服点”定义与讨论. 工程力学, 34(3): 36—46. doi: 10.6052/j.issn.1000-4750.2016.03.0192Feng P., Qiang H. L., Ye L. P., 2017. Discussion and definition on yield points of materials, members and structures. Engineering Mechanics, 34(3): 36—46. doi: 10.6052/j.issn.1000-4750.2016.03.0192 [4] 郭子雄, 吕西林, 2004a. 高轴压比框架柱恢复力模型试验研究. 土木工程学报, 37(5): 32—38.Guo Z. X., Lü X. L., 2004a. Experimental study on the hysteretic model of RC columns with high axial compressive ratio. China Civil Engineering Journal, 37(5): 32—38. [5] 郭子雄, 杨勇, 2004b. 恢复力模型研究现状及存在问题. 世界地震工程, 20(4): 47—51.Guo Z. X., Yang Y., 2004b. State-of-the-art of restoring force models for RC structures. World Earthquake Engineering, 20(4): 47—51. [6] 黄永安, 2019. 外方内双螺旋箍筋约束混凝土柱轴压承载力计算方法. 铁道标准设计, 63(3): 130—137.Huang Y. A., 2019. Calculation method of axial compressive bearing capacity of concrete columns confined by double helix stirrups and rectangular stirrups. Railway Standard Design, 63(3): 130—137. [7] 黄永安, 张超凡, 2019. 外方内双圆箍筋约束高强混凝土柱抗震性能试验研究. 工业建筑, 49(6): 87—93.Huang Y. A., Zhang C. F., 2019. Experimental research on the seismic behavior of high-strength concrete columns confined by double circular stirrups and rectangular stirrups. Industrial Construction, 49(6): 87—93. [8] 姜磊, 郑春梅, 冯丽娜, 2020. 恢复力模型中求突变折点的一种新方法. 地震工程与工程振动, 40(2): 171—176.Jiang L., Zheng C. M., Feng L. N., 2020. A new method for dealing with the stiffness critical point in restoring force models. Earthquake Engineering and Engineering Dynamics, 40(2): 171—176. [9] 雷自学, 董三升, 郭军庆等, 2010. 高强混凝土加芯柱抗震性能试验研究. 建筑结构学报, 31(12): 83—91.Lei Z. X., Dong S. S., Guo J. Q., et al., 2010. Test study on seismic performance of high-strength concrete columns with central reinforcement. Journal of Building Structures, 31(12): 83—91. [10] 李升才, 张诚紫, 2014. 高轴压比下密置焊接环式高强复合箍筋约束高强混凝土柱恢复力模型研究. 地震工程与工程振动, 34(6): 188—197.Li S. C., Zhang C. Z., 2014. Study on restoring force model for high strength concrete columns confined by butt-welded closed composite high strength stirrups with high axial compression ratios. Earthquake Engineering and Engineering Dynamics, 34(6): 188—197. [11] 李正良, 冯宏, 陈永庆, 2010. HSRC框架柱的恢复力特性. 西南交通大学学报, 45(6): 888—892. doi: 10.3969/j.issn.0258-2724.2010.06.011Li Z. L., Feng H., Chen Y. Q., 2010. Characteristics of restoring force of high strength reinforced concrete frame columns. Journal of Southwest Jiaotong University, 45(6): 888—892. doi: 10.3969/j.issn.0258-2724.2010.06.011 [12] 齐岳, 郑文忠, 2010. 核心高强混凝土柱荷载-位移恢复力模型. 哈尔滨工业大学学报, 42(4): 531—535. doi: 10.11918/j.issn.0367-6234.2010.04.006Qi Y., Zheng W. Z., 2010. Restoring-force model of load versus displacement for concrete columns with high strength core. Journal of Harbin Institute of Technology, 42(4): 531—535. doi: 10.11918/j.issn.0367-6234.2010.04.006 [13] 邢国华, 王浩楠, 黄永安等, 2020. 高强混凝土多重复合芯柱抗震性能试验研究. 土木工程学报, 53(4): 50—60.Xing G. H., Wang H. N., Huang Y. A., et al., 2020. Experimental study on seismic behavior of high-strength concrete columns reinforced with multiple composite central reinforcement. China Civil Engineering Journal, 53(4): 50—60. [14] 阎石, 肖潇, 阚立新等, 2005. 高强钢筋高强混凝土柱恢复力模型. 沈阳建筑大学学报(自然科学版), 21(2): 81—85.Yan S., Xiao X., Kan L. X., et al., 2005. Resilience model of high-strength reinforcement and high-strength concrete columns. Journal of Shenyang Jianzhu University (Natural Science), 21(2): 81—85. [15] 张微敬, 张兵, 李振宝等, 2013. 强约束大尺寸钢筋混凝土柱抗震性能试验研究. 工程力学, 30(12): 236—241. doi: 10.6052/j.issn.1000-4750.2013.02.0123Zhang W. J., Zhang B., Li Z. B., et al., 2013. Experimental study on seismic performance of large scale reinforced concrete columns with strong confinement. Engineering Mechanics, 30(12): 236—241. doi: 10.6052/j.issn.1000-4750.2013.02.0123 [16] 张艳青, 贡金鑫, 韩石, 2017. 钢筋混凝土杆件恢复力模型综述(Ⅰ). 建筑结构, 47(9): 65—70.Zhang Y. Q., Gong J. X., Han S., 2017. Reviews of restoring force model for reinforced concrete members (I). Building Structure, 47(9): 65—70. [17] 张艳青, 贡金鑫, 韩石, 2018. 钢筋混凝土杆件恢复力模型综述(Ⅱ). 建筑结构, 48(18): 53—58.Zhang Y. Q., Gong Ji. X., Han S., 2018. Research advances in hysteretic model of reinforced concrete members (Ⅱ). Building Structure, 48(18): 53—58. [18] Belarbi A., Hsu T. T. C., 1994. Constitutive laws of concrete in tension and reinforcing bars stiffened by concrete. ACI Structural Journal, 91(4): 465—474. [19] Dhakal R. P., Maekawa K., 2002. Reinforcement stability and fracture of cover concrete in reinforced concrete members. Journal of Structural Engineering, 128(10): 1253—1262. doi: 10.1061/(ASCE)0733-9445(2002)128:10(1253) [20] Lehman D. E., 2000. Seismic performance of well-confined concrete bridge columns. Berkeley: University of California. [21] Mander J. B., Priestley M. J. N., Park R., 1988. Theoretical stress-strain model for confined concrete. Journal of Structural Engineering, 114(8): 1804—1826. doi: 10.1061/(ASCE)0733-9445(1988)114:8(1804) [22] Park R., 1988. Ductility evaluation from laboratory and analytical testing. In: Proceedings of the 9th World Conference on Earthquake Engineering. Kyoto: IAEE. [23] Priestley M. J. N., Park R., 1987. Strength and ductility of concrete bridge columns under seismic loading. ACI Structural Journal, 84(1): 61—76. [24] Sezen H., Setzler E. J., 2008. Reinforcement slip in reinforced concrete columns. ACI Structural Journal, 105(3): 280—289. [25] Yin S. Y. L., Wang J. C., Wang P. H., 2012. Development of multi-spiral confinements in rectangular columns for construction automation. Journal of the Chinese Institute of Engineers, 35(3): 309—320. doi: 10.1080/02533839.2012.655528 -
下载:
点击查看大图
计量
- 文章访问数: 148
- HTML全文浏览量: 56
- PDF下载量: 4
- 被引次数: 0
