Predict House Area By GM (1, 1) ModelA Case Study of Urumqi
-
摘要: 房屋面积数据是地震灾害损失评估的重要参数，也是地震应急数据库基础数据。数据库要求每年及时更新，但数据更新周期较长，达不到更新要求。本研究主要从乌鲁木齐统计年鉴中提取2001—2018年房屋基础数据，建立乌鲁木齐住宅建筑总面积及人均住宅面积数据增长模型，利用GM（1,1）预测模型和多元线性回归模型预测未来2年乌鲁木齐住宅建筑总面积和人均住宅面积。本研究得到的住宅建筑总面积及人均住宅面积数据可作为应急数据库中相关基础数据更新的补充手段，也可作为未来几年震害预测的参考基础数据。Abstract: Building area is an important parameter of seismic loss assessment and the basic data of earthquake emergency database. The database is required to be updated in time every year, but the statistical data is delayed and the cycle is long, which cannot meet the requirements. We extracted the basic housing data from 2001 to 2018 in Urumqi Statistical Yearbook, then we established the data growth model of total residential building area and per capita residential area in Urumqi. Finally the data of total residential building area and per capita residential area in Urumqi in the next two years were provided by using GM (1, 1) prediction model and multiple linear regression model. The data of total residential building area and per capita residential area obtained in our study can be used as a supplementary means to update the relevant basic data in the emergency database, or as a reference for seismic loss prediction in the next few years.
-
引言
近年来，随着中国城镇化进程的加快，高层建筑数量逐年增加，其中剪力墙结构凭借其整体性能好、刚度大、在水平作用下侧向变形小的优势，逐渐成为中国城镇的主要结构类型。中国80%的城镇位于Ⅶ度地震设防区，一旦发生破坏性地震，将造成巨大的经济损失和人员伤亡。为了评估现有高层钢筋混凝土结构的抗震能力，世界地震工程界进行了大量的研究，其中增量动力分析法是1种有效的分析方法。
增量动力分析方法（Incremental Dynamic Analysis，IDA）考虑了结构抗震能力和需求的不确定性和随机性因素，能较合理地评估不同性能水准下结构抗震能力。并且，通过IDA法可以分析结构从弹性到弹塑性、逐渐损伤直至破坏倒塌的全过程，进而可进一步研究控制结构破坏程度的条件和寻找防止结构倒塌的有效措施（吕西林等，2012）。
2000年，美国开创性地在FEMA-350（Federal Emergency Management Agency，2000）中引入了IDA的概念，以此作为未来新建建筑结构抗震设计的标准。Vamvatsikos等（2002）在前人的研究的基础上，总结并提出了增量动力分析方法，创造性地提出了hunt & fill点跟踪算法，为实际工程中增量动力分析方法的应用创造了先例。21世纪初以来，该方法已经被广泛用于结构抗震性能评估。
对于一般框架结构而言，影响其抗震能力的主要因素有柱轴压比、梁柱配筋率、梁剪跨比等，而对于高层剪力墙结构来说，由于主要承重构件的变化导致影响其抗震能力的主要因素为抗震设防等级、剪力墙轴压比、剪力墙厚度、结构高度、剪力墙配筋率等，其中在结构高度以及设防等级对剪力墙结构抗震能力的影响方面研究甚少。因此，本文在增量动力分析的基础上，讨论了抗震设防等级和高度对剪力墙结构抗震能力的影响，以期为研究工程结构的地震破坏和损失提供一定依据。
1. IDA分析方法的基本理论
1.1 IDA分析方法的定义
增量动力分析方法将1个或多个地震动记录输入到结构模型中，然后对地震动参数（如PGV、PGA等）按照一定的规则进行调幅。通过这种方式，获得了1组不同强度的地震动记录，继而在这组记录的激励下，可以得到该结构的弹塑性分析结果。根据分析结果，可得到地震动强度指标IM（Intensity Measures）和结构损伤指标DM（Damage Measures）之间的关系曲线，即IDA曲线。通过该曲线，可以研究不同强度地震作用下结构损伤的全过程及相关失效概率。
1.2 IDA分析方法的步骤
对结构进行IDA分析的主要流程和步骤为（卜一等，2009；汪梦甫等，2010）：
（1）严格按照抗震设计规范建立弹塑性模型；
（2）按照一定的规则选取有代表性的地震动记录（至少10条）；
（3）将选取的地震动记录按照既定的调幅方法进行调幅并输入到结构中进行计算分析；
（4）将得到的IM、DM点连接成线，即为结构的IDA曲线。
1.3 地震动记录的选取
考虑到断层距、结构周期以及场地类型等因素的影响，谢礼立等（2003）基于地震动潜在破坏势提出了最不利地震动的概念，并且综合考虑中国规范中有关场地类型的划分以及地震动强度等级的相关规定，给出了确定最不利地震动的方法和对应于不同类型的场地和结构的最不利地震动记录，从中选取了10条地震动作为地震动输入记录，如表 1所示。
表 1 最不利设计地震动详细信息Table 1. The detailed information of the most unfavorable design ground vibration编号 震级 年份 地点 断层距/km PGA/g F2 6.69 1994 北岭 54.45 0.154 F3 6.61 1971 圣费尔南多 22.63 0.32 F4 5.01 1979 帝王谷#10 12.96 0.054 F5 7.36 1952 克恩县 38.89 0.18 F7 6.95 1940 埃尔森特罗 6.09 0.281 F10 6.36 1983 科林加 29.48 0.274 F11 6.53 1979 帝王谷#6 1.35 0.449 F12 6.19 1966 帕克菲尔德 12.9 0.272 N1 6.7 1988 澜沧 17.6 0.207 N4 7.8 1976 宁河 67 0.15 在表 1的地震动记录中，Ⅰ类场地的有F2、N1；Ⅱ类场地的有F3、F4、F5；Ⅲ类场地的有F7、F12；Ⅳ类场地的有F10、F11、N4。
远场地震动记录的断层距大于20km，根据表 1中的信息可知属于远场地震动记录的有F2、F3、F5、F10，其余的均为近场地震动记录，由此可见选取的地震动记录充分考虑了断层距、场地类型等因素的影响。
2. 典型剪力墙结构IDA分析
2.1 典型剪力墙结构结构设计
为了使结构分析结果具有普遍意义，有必要选择典型的结构，因此本文选择了剪力墙结构比较普遍的住宅楼，如图 1所示。
选取的工程为上海金桥地铁保障房，钢筋混凝土剪力墙结构体系，该建筑结构地上31层，总高度86.8m，层高2.8m，高宽比为5.36，安全等级为二级，丙类建筑，Ⅶ度设防，基本地震加速度值为0.10g，设计地震分组为第1组，Ⅳ类场地，特征周期为0.9s。
为达到研究目的，本文以图 1为模板，严格按照中国规范规定分别建立了Ⅵ、Ⅶ、Ⅷ度3种不同抗震设防，15层、20层、25层、30层4种不同房屋高度的12个模型（中华人民共和国住房和城乡建设部，2010；中华人民共和国建设部，2010；中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局，2010；中华人民共和国住房和城乡建设部，2012），以此来研究不同抗震设防等级以及不同结构高度对建筑结构抗震能力的影响。
2.2 增量动力分析
本文选择Etabs进行结构的弹塑性分析。梁、柱采用三维框架单元模拟，剪力墙和楼板采用三维壳体单元模拟，为了反映混凝土材料在地震荷载作用下非线性阶段刚度退化的影响，其恢复力模型采用Takeda模型，而基于钢筋材料的特性，恢复力模型则采用考虑包辛格效应的Kinematic模型，强屈比取值为1.2，极限塑性应变取0.025。在进行弹塑性分析时采用显式积分法。
逐一对所选择的地震动进行调幅，调幅后的PGA分别为0.005g、0.205g、0.455g、0.755g、1.105g和1.505g，地震动强度按X、Y向1:0.85输入，并按照文献（韩建平等，2007）的判断准则确定继续调幅或是终止分析。进而，可得到结构性能参数（最大层间位移角θmax）与地震动强度（地面峰值加速度PGA）之间的关系曲线，即IDA曲线。图 2绘出了12个不同模型的IDA曲线，图中3条IDA曲线分别为50%、16%、84%分位的IDA曲线。从图中可以看出，16%、84%分位的IDA曲线与结构的均值曲线，即50%分位的IDA曲线偏差并不大。
2.3 结构破坏等级与性能指标
工程结构的破坏可分为5个等级：基本完好，轻微破坏，中等破坏，严重破坏，倒塌。本文使用最大层间位移角作为损伤量化指标，结合邓明科等（2008）及韩淼等（2011）关于高层钢筋混凝土剪力墙结构破坏状态的划分原则，给出本文不同破坏状态水平下的量化指标限值，如表 2所示。
表 2 量化指标限值Table 2. Limits of the quantitative indicators破坏等级 基本完好 轻微破坏 中等破坏 严重破坏 倒塌 最大层间位移角θmax ＜1/950 1/950—1/500 1/500—1/175 1/175—1/90 ＞1/90 2.4 各性态点的确定
根据上述破坏状态定义原则，对各模型的IDA曲线进行分析，为了得到一般性结论，选用50%分位曲线为研究对象，通过线性插值确定各个破坏状态下结构所能经受的地震强度指标值，具体数据见表 3。
表 3 结构各破坏状态对应的能力值（50%分位曲线）Table 3. The corresponding ability value of each failure state of the structure模型 轻微破坏 中等破坏 严重破坏 倒塌 θmax PGA/g θmax PGA/g θmax PGA/g θmax PGA/g Ⅵ度15层 0.00105 0.1222 0.002 0.2402 0.00571 0.7437 0.01111 1.242 Ⅵ度20层 0.1195 0.2331 0.7289 1.218 Ⅵ度25层 0.1174 0.2274 0.718 1.1753 Ⅵ度30层 0.114 0.2191 0.7029 1.1328 Ⅶ度15层 0.1483 0.2981 0.8138 1.3803 Ⅶ度20层 0.1417 0.2857 0.8006 1.3413 Ⅶ度25层 0.1348 0.2713 0.7858 1.3014 Ⅶ度30层 0.1297 0.2592 0.7725 1.2784 Ⅷ度15层 0.173 0.3647 0.9619 1.6712 Ⅷ度20层 0.1654 0.3507 0.9449 1.6077 Ⅷ度25层 0.1524 0.3284 0.9342 1.5273 Ⅷ度30层 0.1505 0.3206 0.9223 1.4911 2.5 抗震设防等级对剪力墙结构抗震能力的影响
根据表 3的数据，可以定量地分析出结构随抗震设防等级的提高在各个性能点处抗震能力提高的程度，为了更直观的表现，将以上数据绘制在图 3中。
图 3 各破坏性能点随抗震设防等级变化的规律Figure 3. The regular graph of the failed performance point varying with the earthquake resistance level由图 3可知，无论结构高度如何，随着抗震设防等级的增加，各破坏状态点处的地震指标（PGA）都相应的增加，虽然轻微破坏和中等破坏所对应的PGA值有所增加，但是增加的幅度较小，而严重破坏和倒塌所对应的PGA值却大幅度增加。由此可见，相同地震动强度下，不同抗震设防等级的结构发生轻微破坏、中等破坏的概率变化并不大，但是抗震设防等级越低，发生严重破坏和倒塌的概率越大。
2.6 结构高度对剪力墙结构抗震能力的影响
根据表 3的数据，还可定量地分析出结构随高度的增加在各个性能点处抗震能力降低的程度，为了更直观地表现，将以上数据绘制在图 4中。
图 4 各破坏性能点随结构高度变化的规律Figure 4. The regular graph of the failed performance point varying with the structure height将结构层数信息用高度来表示，见表 4。
表 4 结构层数所对应高度Table 4. The height value corresponding to the number of structural layers结构层数 15 20 25 30 结构高度/m 41.2 55.2 69.2 83.2 由表 4和图 4可以看出，Ⅵ、Ⅶ和Ⅷ度设防的结构，随着结构高度的增加，各破坏状态点处的地震指标PGA值都相应的降低，虽然轻微破坏、中等破坏和严重破坏所对应的PGA值有所降低，但是降低的幅度较小，而倒塌性能点所对应的PGA值却大幅度降低。由此可见，相同地震动强度下，不同结构高度的结构发生轻微破坏、中等破坏和严重破坏的概率变化并不大，但是结构高度的增加，会导致发生倒塌的概率显著增加。
3. 结语
本文以Ⅵ、Ⅶ和Ⅷ度3种不同抗震设防等级和15层、20层、25层、30层4种不同结构高度共计12个剪力墙结构模型为基本算例，通过IDA对比分析，对不同抗震设防等级和不同结构高度的剪力墙结构的抗震性能进行了评估，总结出以下结论：
（1）在对比分析不同抗震设防等级下剪力墙结构模型时发现，随着结构抗震设防等级的增加，结构的抗震能力随之增强，虽然在较小最大层间位移角处抗震设防等级的增加，并未导致PGA显著提高，但随着最大层间位移角的增大，抗震设防等级的提高所带来的抗震能力会有显著的提高。即抗震设防等级越高，结构在刚度、强度及延性等方面的表现越好，在遭受同等强度的地震动作用下结构也就越难发生轻微破坏、中等破坏和严重破坏。抗震设防等级的增大对增强结构抗震能力的效果很明显。
（2）在对比分析不同结构高度下剪力墙结构模型时发现，随着结构高度的增加，结构的抗震能力随之降低，结构高度对抗震能力的影响并没有抗震设防等级对结构抗震能力的影响明显。但随着最大层间位移角的增加，较高的房屋其地震危险性还是比较大的。
-
图 3 乌鲁木齐市住宅建筑总面积预测曲线图
Figure 3. Predictive Fitting curve of total area of residential buildings in Urumqi
表 1 乌鲁木齐市住宅建筑总面积和人均住宅面积
Table 1. Total area of residential buildings and per capita residential area in Urumqi
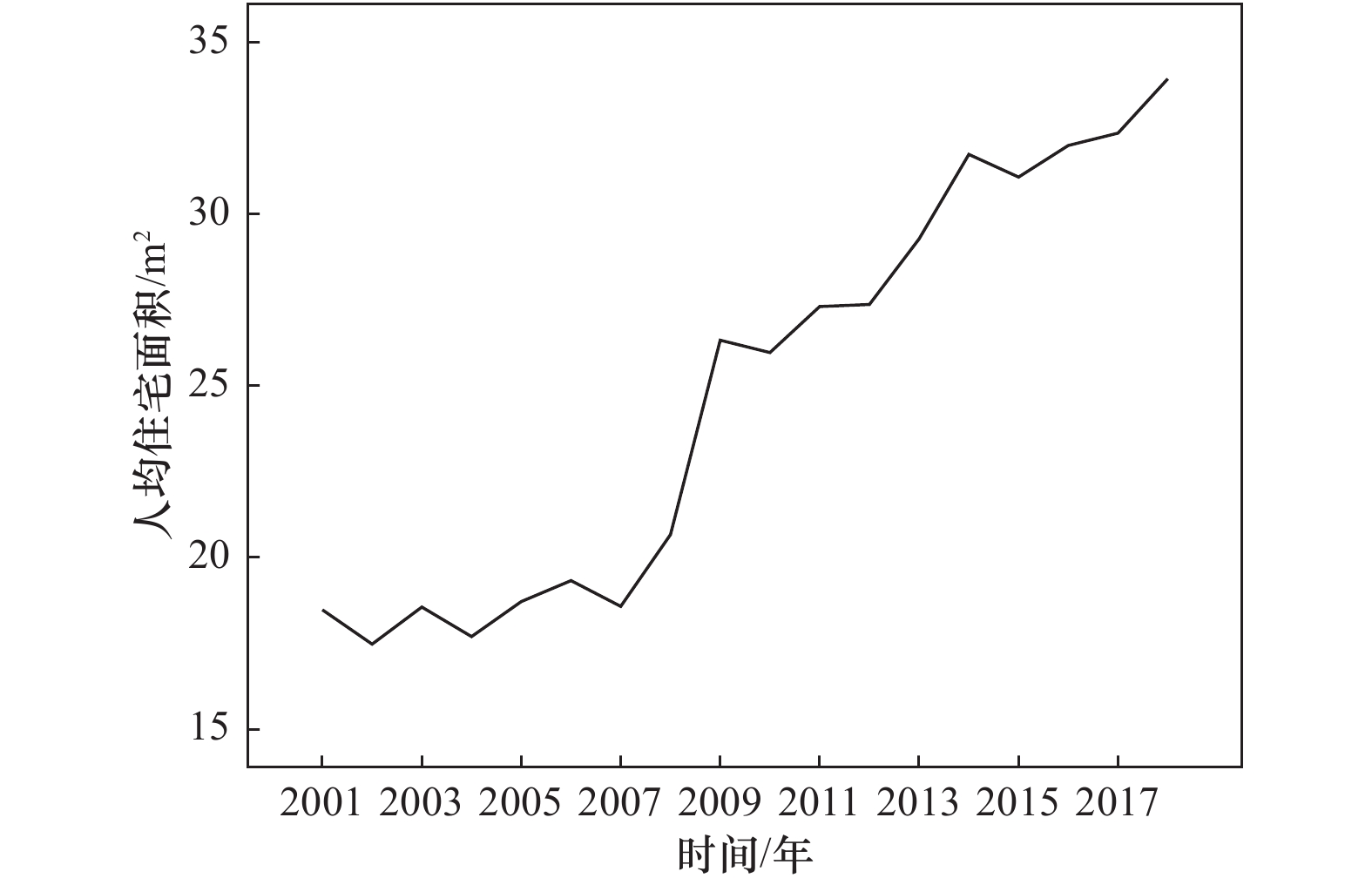
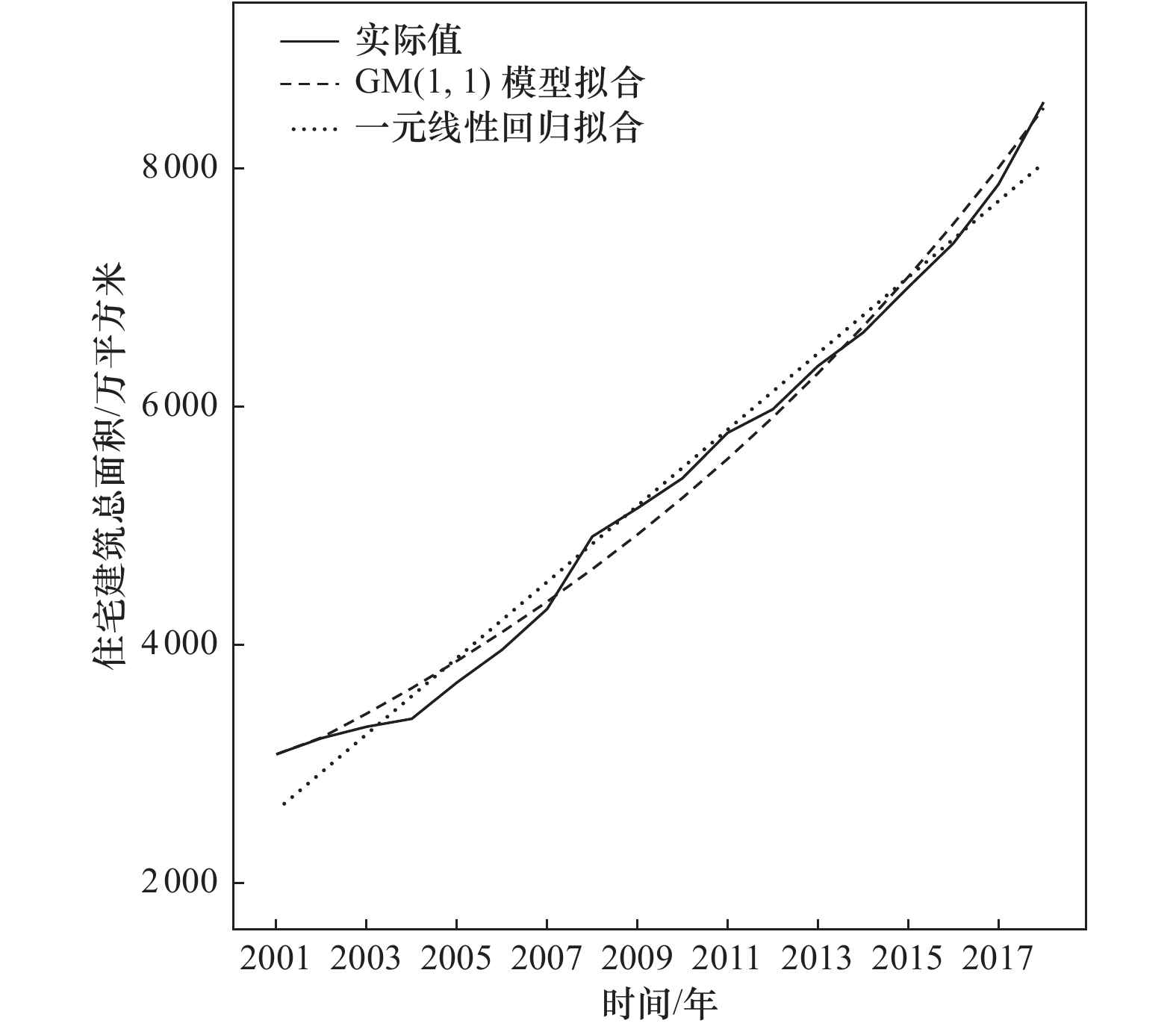
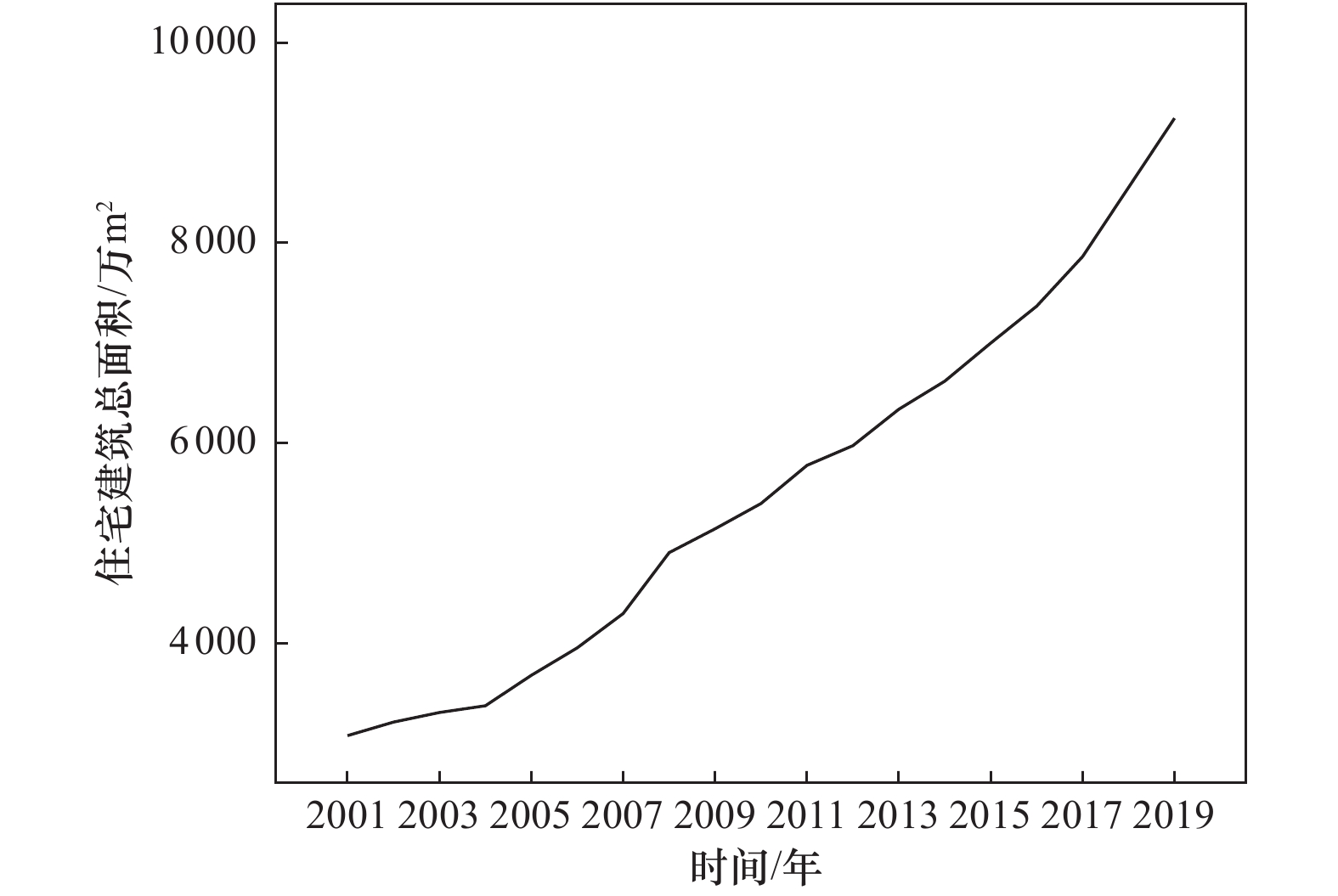
年份 总面积/104m2 人均面积/m2 年份 总面积/104m2 人均面积/m2 2001 3081.00 18.48 2010 5398.93 25.97 2002 3216.00 17.48 2011 5779.95 27.31 2003 3312.00 18.56 2012 5976.64 27.37 2004 3379.00 17.70 2013 6340.26 29.28 2005 3683.31 18.72 2014 6620.65 31.74 2006 3957.60 19.33 2015 7001.20 31.08 2007 4300.37 18.58 2016 7369.64 32.00 2008 4908.29 20.67 2017 7865.22 32.36 2009 5146.32 26.33 2018 8555.64 33.94 
下载: 导出CSV
表 2 灰色系统GM（1,1）模型乌鲁木齐市住宅建筑总面积拟合
Table 2. Predictive fitting of total area of residential buildings in Urumqi using grey system GM(1,1) model
年份 实际值/104m2 预测值/104m2 相对误差 年份 实际值/104m2 预测值/104m2 相对误差 2001 3081.00 3081 0.00 2010 5398.93 5234 0.03 2002 3216.00 3221 0.00 2011 5779.95 5561 0.04 2003 3312.00 3422 0.03 2012 5976.64 5909 0.01 2004 3379.00 3636 0.08 2013 6340.26 6279 0.01 2005 3683.31 3864 0.05 2014 6620.65 6672 0.01 2006 3957.60 4106 0.04 2015 7001.20 7089 0.01 2007 4300.37 4362 0.01 2016 7369.64 7533 0.02 2008 4908.29 4635 0.06 2017 7865.22 8004 0.02 2009 5146.32 4925 0.04 2018 8555.64 8505 0.01
下载: 导出CSV
表 3 乌鲁木齐住宅建筑总面积GM（1,1）模型参数
Table 3. Parameters a and b of GM(1,1) model of total area of residential buildings in Urumqi
系数 数值 a −0.0607 b 2936.9
下载: 导出CSV
表 4 精度检验等级参照表
Table 4. Precision inspection level reference table
精度等级指标 相对误差 一级 0.01 二级 0.05 三级 0.10
下载: 导出CSV
表 5 乌鲁木齐住宅建筑总面积一元线性回归参数
Table 5. Univariate linear regression parameter values of total area of residential buildings and per capita residential area in Urumqi
a 系数b 有关指数R2 显著性概率Sig 常数项 斜率 统计量F 系数 319.674 −637058.012 0.983 0.000 −30.144 30.396 923.909
下载: 导出CSV
表 6 一元线性回归模型拟合得到的乌鲁木齐住宅建筑总面积
Table 6. Predictive fitting of total area of residential buildings in Urumqi by univariate linear regression
年份 实际值/104m2 预测值/104m2 相对误差 年份 实际值/104m2 预测值/104m2 相对误差 2001 3081.00 2609.66 0.15 2010 5398.93 5486.73 0.00 2002 3216.00 2929.34 0.09 2011 5779.95 5806.40 0.02 2003 3312.00 3249.01 0.02 2012 5976.64 6126.08 0.00 2004 3379.00 3568.68 0.06 2013 6340.26 6445.75 0.03 2005 3683.31 3888.36 0.06 2014 6620.65 6765.42 0.02 2006 3957.60 4208.03 0.06 2015 7001.20 7085.10 0.01 2007 4300.37 4527.71 0.06 2016 7369.64 7404.77 0.00 2008 4908.29 4847.38 0.05 2017 7865.22 7724.45 0.02 2009 5146.32 5167.05 0.01 2018 8555.64 8044.12 0.06
下载: 导出CSV
表 7 2001—2018年乌鲁木齐人均住宅面积影响因素原始数据
Table 7. Raw data of influencing factors of per capita residential area in Urumqi from 2001 to 2018
年份 人均住宅面积/m2 人均GDP/万元 居民人均可支配收入/元 常住人口/万人 住宅竣工面积/104m2 2001 18.48 1.8331 7897.0 166.71 388.35 2002 17.48 1.7780 8652.0 172.37 389.71 2003 18.56 1.9899 9087.0 178.63 376.44 2004 17.70 2.2820 8948.2 183.74 231.68 2005 18.72 2.5507 9605.0 190.50 267.93 2006 19.33 2.8261 10432.0 198.00 270.08 2007 18.58 3.1140 11373.0 263.42 404.33 2008 20.67 3.7133 12328.0 273.24 427.76 2009 26.33 3.8249 13075.0 284.32 387.32 2010 25.97 4.4917 14402.0 311.03 309.85 2011 27.31 5.2649 16141.0 321.21 287.39 2012 27.37 5.9576 18385.0 335.00 613.24 2013 29.28 6.4695 21304.0 346.00 442.24 2014 31.74 7.0428 26890.0 353.00 812.59 2015 31.08 7.4340 31604.0 355.00 591.62 2016 32.00 6.9865 34190.0 351.96 295.07 2017 32.36 7.7756 37028.0 350.40 378.87 2018 33.94 8.7196 40101.0 350.58 365.24
下载: 导出CSV
表 8 系数
Table 8. Coefficient
项目 非标准化系数 标准系数 斜率 显著性概率Sig 系数b 标准误差 常量b0 10.123 2.702 — 3.746 0.002 人均GDP 1.525 0.020 0.283 1.774 0.2610 常住人口 0.023 1.544 0.133 0.483 0.8637 人均可支配收入 0.746 1.191 0.584 1.281 0.2230 住宅竣工面积 0.000 0.003 −0.008 −0.116 0.9090
下载: 导出CSV
表 9 各模型对乌鲁木齐人均住宅面积拟合值（m2）
Table 9. Predictive fitting of per capita residential area in Urumqi of each model（Unit:m²）
年份 实际值 多元线性回归模型 GM(1,1)模型 一元线性回归模型 理论值 绝对误差 理论值 绝对误差 理论值 绝对误差 2001 18.48 17.34 0.06 18.48 0.00 15.31 0.17 2002 17.48 17.44 0.00 17.11 0.02 16.41 0.06 2003 18.56 17.94 0.03 17.90 0.04 17.50 0.06 2004 17.70 18.50 0.05 18.74 0.06 18.59 0.05 2005 18.72 19.11 0.02 19.61 0.05 19.68 0.05 2006 19.33 19.77 0.02 20.52 0.06 20.77 0.07 2007 18.58 21.78 0.17 21.48 0.16 21.87 0.18 2008 20.67 22.99 0.11 22.47 0.09 22.96 0.11 2009 26.33 23.47 0.11 23.52 0.11 24.05 0.09 2010 25.97 25.20 0.03 24.61 0.05 25.14 0.03 2011 27.31 26.74 0.02 25.76 0.06 26.23 0.04 2012 27.37 28.28 0.03 26.96 0.02 27.33 0.00 2013 29.28 29.54 0.01 28.21 0.04 28.42 0.03 2014 31.74 30.99 0.02 29.53 0.07 29.51 0.07 2015 31.08 31.98 0.03 30.90 0.01 30.60 0.02 2016 32.00 31.42 0.02 32.34 0.01 31.69 0.01 2017 32.36 32.80 0.01 33.84 0.05 32.79 0.01 2018 33.94 34.48 0.02 35.42 0.04 33.88 0.00
下载: 导出CSV
表 10 不同模型误差分布比例
Table 10. Error distribution ratio of each model
模型 误差分级 一级 二级 三级 GM（1,1）模型 17% 61% 89% 一元线性回归模型 22% 56% 83% 多元线性回归模型 17% 78% 83%
下载: 导出CSV
表 11 2019—2020年乌鲁木齐人均住宅面积影响因素预测值
Table 11. The result of total area of per capita residential area in Urumqi from 2019 to 2020
年份 人均GDP/万元 居民人均可支配收入/元 常住人口/万人 2019 10.1917 44550 341.12 2020 11.1629 50070 351.34
下载: 导出CSV
表 12 2019—2020年乌鲁木齐住宅建筑总面积和人均住宅面积预测结果
Table 12. The result of total area of residential buildings and per capita residential area in Urumqi from 2019 to 2020
项目 年份 2019 2020 乌鲁木齐住宅建筑总面积/104m2 9037 9602 乌鲁木齐人均住宅面积/104m2 36.83 38.96
下载: 导出CSV
-
[1] 常想德, 孙静, 谭明等, 2017. 2016年新疆呼图壁6.2级地震房屋震害及成因浅析. 震灾防御技术, 12(1): 1—13. doi: 10.11899/zzfy20170101Chang X. D., Sun J., Tan M., et al., 2017. Study on earthquake damages by the 2016 Hutubi MS 6.2 earthquake. Technology for Earthquake Disaster Prevention, 12(1): 1—13. (in Chinese) doi: 10.11899/zzfy20170101 [2] 陈志敏, 2008. 乌鲁木齐统计年鉴. 北京: 中国统计出版社.Chen Z. M., 2008. Urumqi statistical yearbook. Beijing: China Statistics Press. (in Chinese) [3] 陈志敏, 2009. 乌鲁木齐统计年鉴. 北京: 中国统计出版社.Chen Z. M., 2009. Urumqi statistical yearbook. Beijing: China Statistics Press. (in Chinese) [4] 陈志敏, 2010. 乌鲁木齐统计年鉴. 北京: 中国统计出版社.Chen Z. M., 2010. Urumqi statistical yearbook. Beijing: China Statistics Press. (in Chinese) [5] 邓聚龙, 1990. 灰色系统理论教程. 武汉: 华中理工大学出版社. [6] 何少林, 李佐唐, 张苏平等, 2007. 甘肃省地震应急指挥技术系统设计与实现. 地震地磁观测与研究, 28(5): 71—79. doi: 10.3969/j.issn.1003-3246.2007.05.015He S. L., Li Z. T., Zhang S. P., et al., 2007. Design and implement of technical system for earthquake emergency direction in Gansu Province. Seismological and Geomagnetic Observation and Research, 28(5): 71—79. (in Chinese) doi: 10.3969/j.issn.1003-3246.2007.05.015 [7] 黄国森, 2012. 乌鲁木齐统计年鉴. 北京: 中国统计出版社.Huang G. S., 2012. Urumqi statistical yearbook. Beijing: China Statistics Press. (in Chinese) [8] 黄国森, 2013. 乌鲁木齐统计年鉴. 北京: 中国统计出版社.Huang G. S., 2013. Urumqi statistical yearbook. Beijing: China Statistics Press. (in Chinese) [9] 黄国森, 2014. 乌鲁木齐统计年鉴. 北京: 中国统计出版社.Huang G. S., 2014. Urumqi statistical yearbook. Beijing: China Statistics Press. (in Chinese) [10] 姜立新, 吴天安, 刘在涛等, 2004. 地震现场应急指挥技术系统的结构与设计. 地震, 24(3): 35—41. doi: 10.3969/j.issn.1000-3274.2004.03.006Jiang L. X., Wu T. A., Liu Z. T., et al., 2004. Structure and design of emergency command system in earthquake site. Earthquake, 24(3): 35—41. (in Chinese) doi: 10.3969/j.issn.1000-3274.2004.03.006 [11] 李凯, 张涛, 2018. 基于组合插值的GM(1,1)模型背景值的改进. 计算机应用研究, 35(10): 2994—2999. doi: 10.3969/j.issn.1001-3695.2018.10.026Li K., Zhang T., 2018. Optimization of background value in GM (1,1) model based on combination interpolation. Application Research of Computers, 35(10): 2994—2999. (in Chinese) doi: 10.3969/j.issn.1001-3695.2018.10.026 [12] 刘颂, 江立敏, 1999. GM(1,1)模型在上海市区人均居住面积预测中的应用. 住宅科技, (8): 3—5. [13] 刘伟, 陈浮, 1999. GM(1,1)模型在南京市人均居住面积预测和关联分析中的应用. 城市问题, (1): 15—18.Liu W., Chen F., 1999. Application of GM (1,1) model in the prediction and correlation analysis of per capita living area in Nanjing. Urban Problems, (1): 15—18. (in Chinese) [14] 卢永坤, 代博洋, 庞卫东等, 2011. 云南地区房屋建筑面积的统计和调查结果. 地震研究, 34(4): 533—537. doi: 10.3969/j.issn.1000-0666.2011.04.021Lu Y. K., Dai B. Y., Pang W. D., et al., 2011. Statistical and investigative result of buildings in Yunnan. Journal of Seismological Research, 34(4): 533—537. (in Chinese) doi: 10.3969/j.issn.1000-0666.2011.04.021 [15] 马建, 常想德, 黄帅堂等, 2020. 无人机摄影技术在精河地震房屋震害定量评估中的应用. 震灾防御技术, 15(1): 208—215. doi: 10.11899/zzfy20200121Ma J., Chang X. D., Huang S. T., et al., 2020. Application of UAV photography technology in quantitative assessment of building damage of the Jinghe Earthquake. Technology for Earthquake Disaster Prevention, 15(1): 208—215. (in Chinese) doi: 10.11899/zzfy20200121 [16] 潘世锦, 2015. 乌鲁木齐统计年鉴. 北京: 中国统计出版社.Pan S. J., 2015. Urumqi statistical yearbook. Beijing: China Statistics Press. (in Chinese) [17] 潘世锦, 2016. 乌鲁木齐统计年鉴. 北京: 中国统计出版社.Pan S. J., 2016. Urumqi statistical yearbook. Beijing: China Statistics Press. (in Chinese) [18] 潘世锦, 2017. 乌鲁木齐统计年鉴. 北京: 中国统计出版社.Pan S. J., 2017. Urumqi statistical yearbook. Beijing: China Statistics Press. (in Chinese) [19] 潘世锦, 2018. 乌鲁木齐统计年鉴. 北京: 中国统计出版社.Pan S. J., 2018. Urumqi statistical yearbook. Beijing: China Statistics Press. (in Chinese) [20] 潘世锦, 2019. 乌鲁木齐统计年鉴. 北京: 中国统计出版社.Pan S. J., 2019. Urumqi statistical yearbook. Beijing: China Statistics Press. (in Chinese) [21] 彭振斌, 张闯, 彭文祥等, 2017. GM(1,1)模型背景值构造的不同方法与应用. 东北大学学报(自然科学版), 38(6): 869—873. doi: 10.12068/j.issn.1005-3026.2017.06.022Peng Z. B., Zhang C., Peng W. X., et al., 2017. Different structure methods and application of background value in GM (1,1) model. Journal of Northeastern University (Natural Science), 38(6): 869—873. (in Chinese) doi: 10.12068/j.issn.1005-3026.2017.06.022 [22] 沈艳, 尹金姗, 韩帅等, 2019. 基于数值积分公式的GM(1,1)模型优化研究. 计算机工程与应用, 55(24): 41—45. doi: 10.3778/j.issn.1002-8331.1812-0390Shen Y., Yin J. S., Han S., et al., 2019. Research and its optimization of GM (1,1) model based on numerical integration formula. Computer Engineering and Applications, 55(24): 41—45. (in Chinese) doi: 10.3778/j.issn.1002-8331.1812-0390 [23] 王伟, 2011. 乌鲁木齐统计年鉴. 北京: 中国统计出版社.Wang W., 2011. Urumqi statistical yearbook. Beijing: China Statistics Press. (in Chinese) [24] 王宇, 敬莉, 2016. 基于灰色GM(1, 1)模型和一元线性回归的人口发展趋势预测——以新疆南疆三地州为例. 西部学刊, (7): 54—59. [25] 谢江丽, 李帅, 姚远, 2019. 地震应急数据库中人口数据预测——以乌鲁木齐市为例. 中国地震, 35(2): 389—398. doi: 10.3969/j.issn.1001-4683.2019.02.018Xie J. L., Li S., Yao Y., 2019. Prediction of population data in earthquake emergency database - a case study of Urumqi. Earthquake Research in China, 35(2): 389—398. (in Chinese) doi: 10.3969/j.issn.1001-4683.2019.02.018 [26] 叶淳, 吴翔华, 黄雨婴, 2020. 城镇人均住房建筑面积预测研究——以江苏省为例. 中国房地产, (18): 73—79. [27] 曾亮, 2019. 基于振荡序列的灰色GM(1,1|sin)幂模型及其应用. 浙江大学学报(理学版), 46(6): 697—704.Zeng L., 2019. Grey GM (1,1|sin) power model based on oscillation sequences and its application. Journal of Zhejiang University (Science Edition), 46(6): 697—704. (in Chinese) [28] 赵卓峰, 杨宗润, 2017. 基于残差修正GM(1,1)模型的车流量预测. 计算机科学, 44(4): 96—99, 130. doi: 10.11896/j.issn.1002-137X.2017.04.021Zhao Z. F., Yang Z. R., 2017. Traffic flow forecast based on residual modification GM (1,1) model. Computer Science, 44(4): 96—99, 130. (in Chinese) doi: 10.11896/j.issn.1002-137X.2017.04.021 [29] 郑坚, 陈斌, 2018. 基于时间权重序列的GM(1,1)初始条件优化模型. 控制与决策, 33(3): 529—534.Zheng J., Chen B., 2018. Initial condition optimization of GM (1,1) model based on time weighted sequence. Control and Decision, 33(3): 529—534. (in Chinese) [30] 朱明, 王志荣, 梁华等, 2017. 基于GM(1,1)的残差修正模型的电梯故障率预测. 安全与环境学报, 17(5): 1701—1704.Zhu M., Wang Z. R., Liang H., et al., 2017. Prediction of the elevator failure rate based on the residual error correcting model of GM (1,1). Journal of Safety and environment, 17(5): 1701—1704. (in Chinese) -
下载:
点击查看大图
计量
- 文章访问数: 228
- HTML全文浏览量: 85
- PDF下载量: 13
- 被引次数: 0
