Based on the Infinite Element Boundary Analysis, the Study of the Effect of Continuous Barrier on the Environmental Vibration of High-speed Railway
-
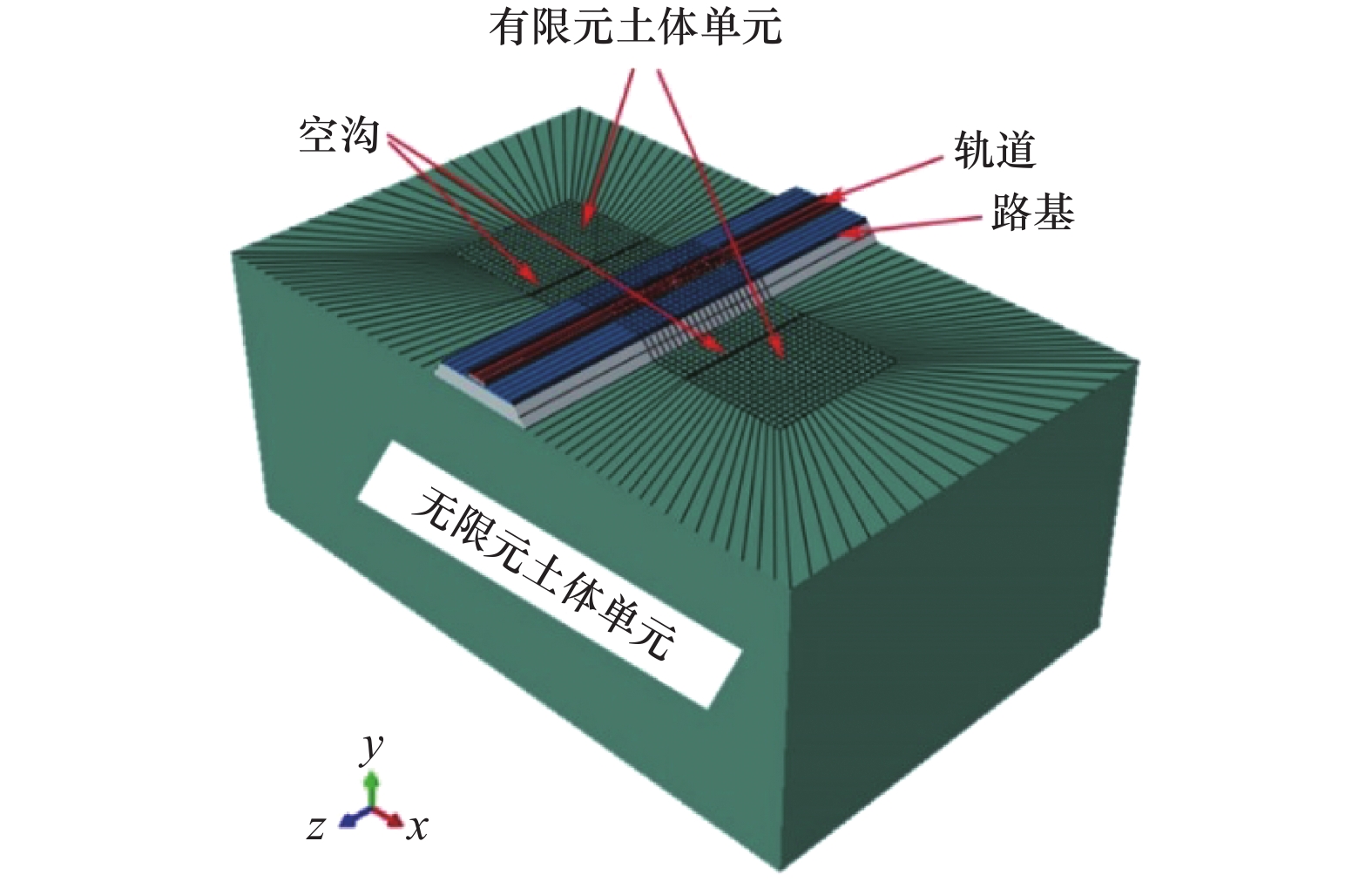
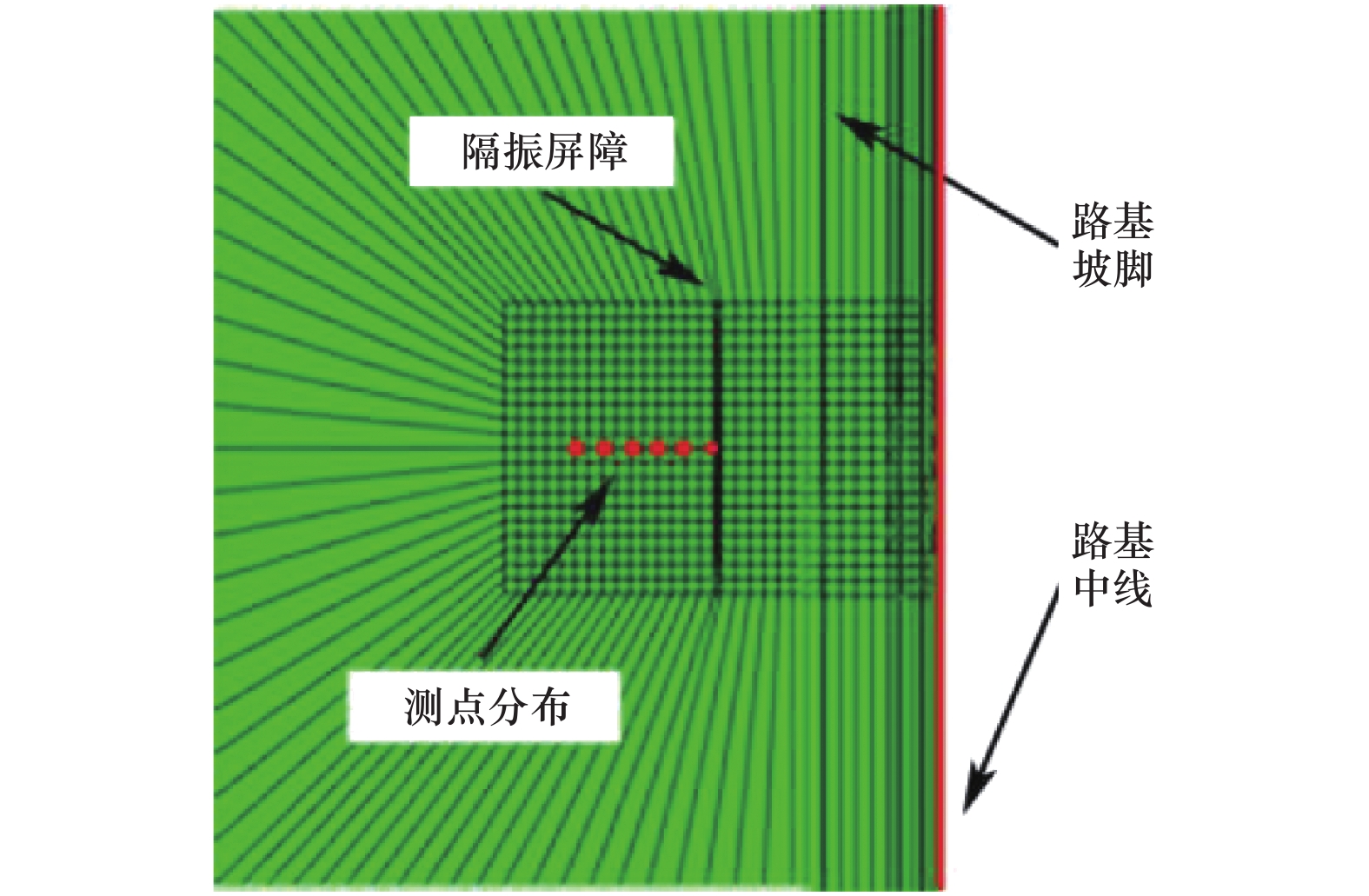
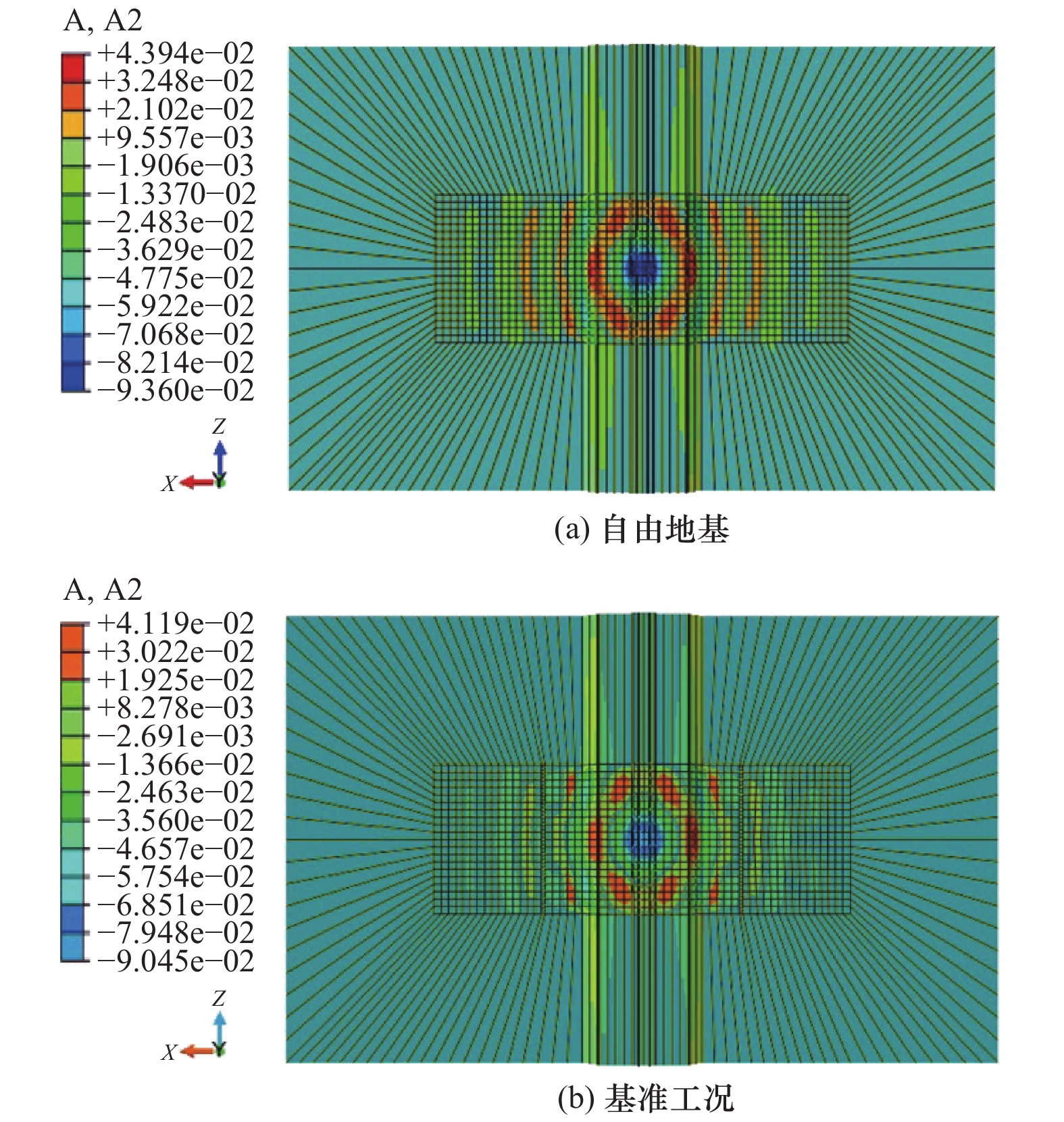
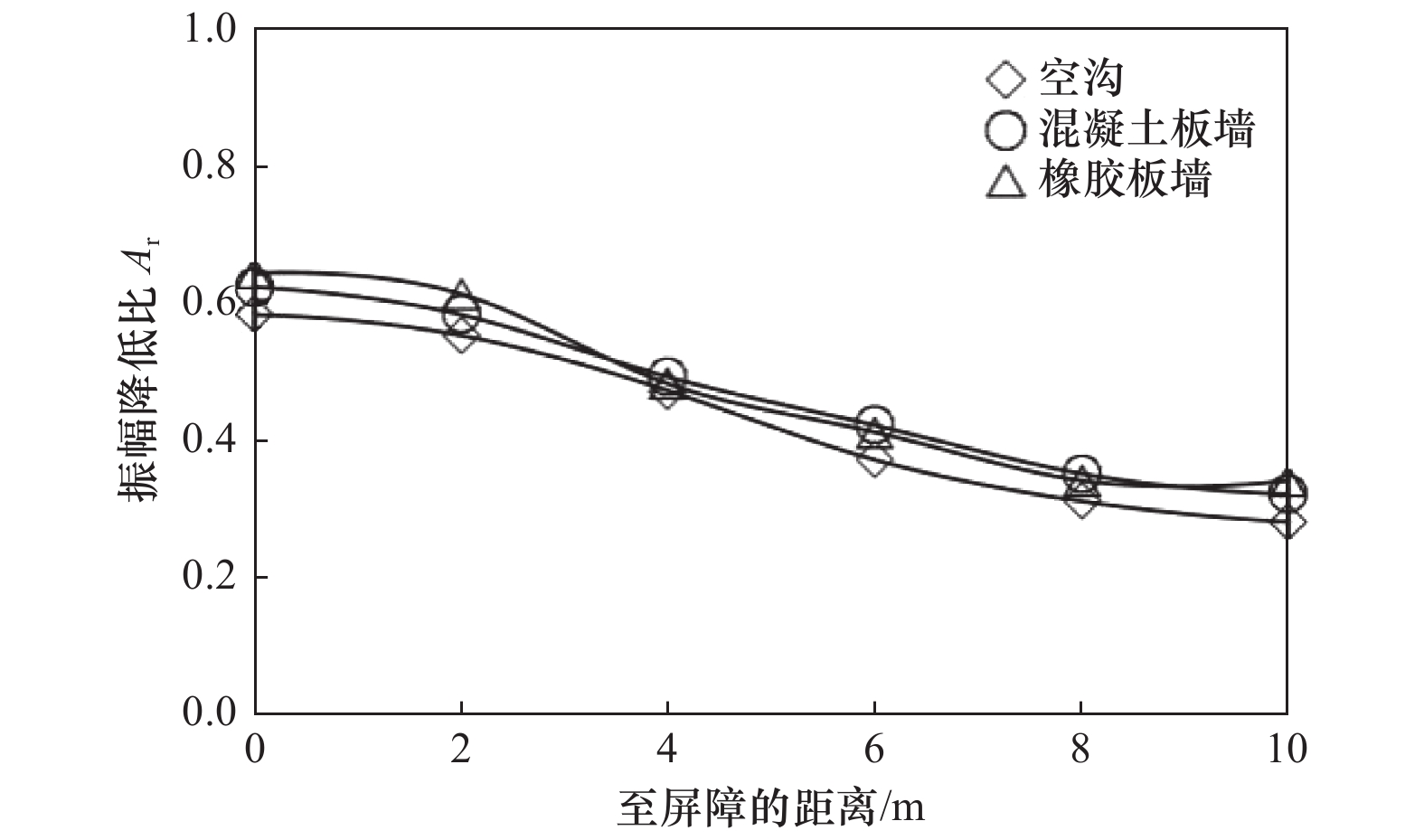
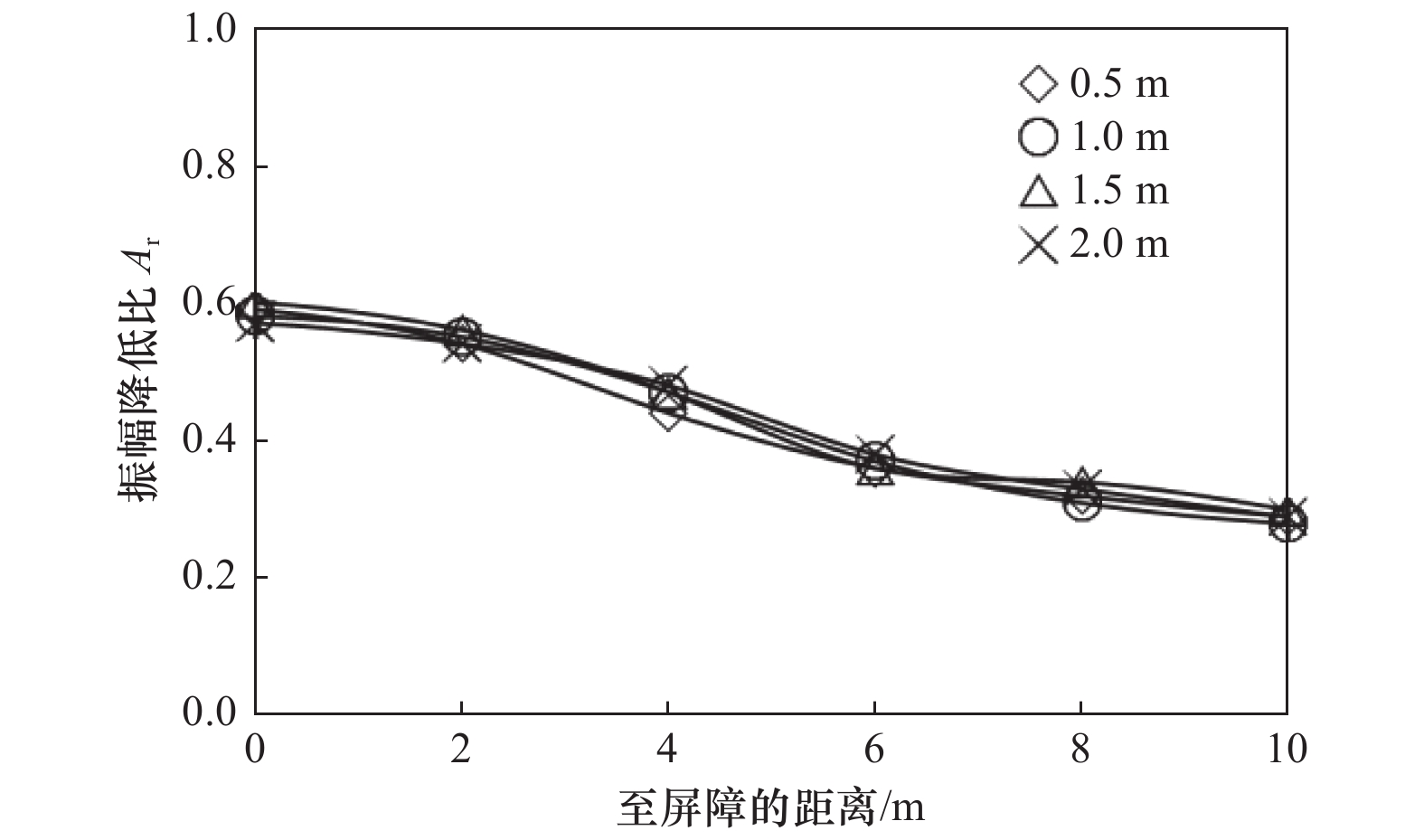
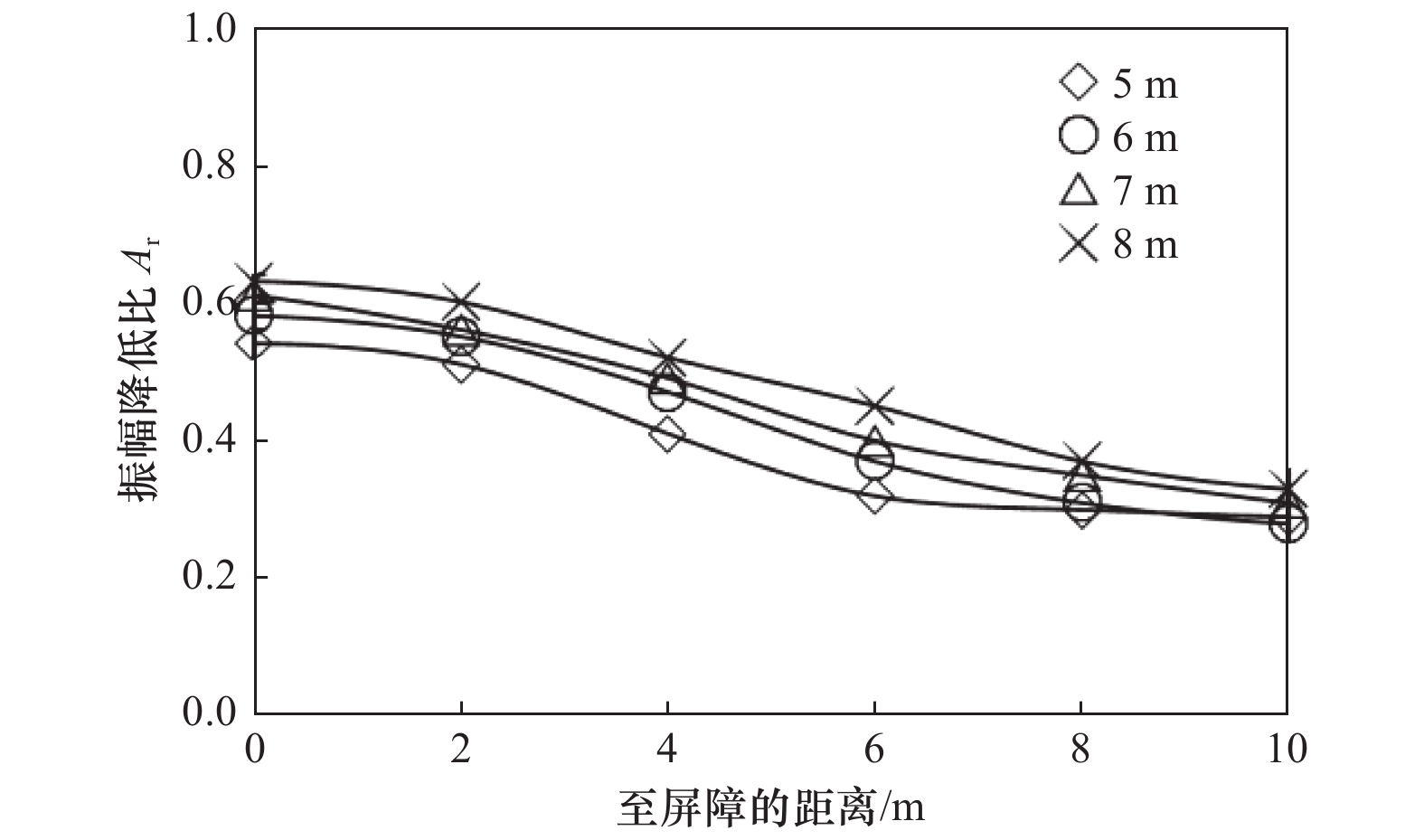
摘要: 为探究高速铁路两侧隔振屏障隔振效果，采用有限元与无限元边界结合的方式进行分析，研究不同连续型隔振屏障及布置形式对隔振效果的影响。通过现场试验与同尺寸、同属性有限元模型对比试验，验证有限元模型合理性。计算结果表明：不同连续型隔振屏障中，空沟隔振效果最优，空沟隔振措施适合高速列车隔振；隔振屏障宽度为0.6～2.5倍波长时，其对隔振效果的影响较小，随着宽度的改变，隔振效果变化幅度较小；隔振屏障深度为3.8～15.2倍波长时，其对隔振效果的影响较明显，随着深度的增加，隔振效果增强；屏障位置对隔振效果的影响较大，建议屏障应靠近路基布置；连续型隔振屏障对高频的隔振效果优于低频。Abstract: In order to explore the vibration isolation effect of the vibration isolation barriers on both sides of high-speed railway, the finite element method combined with infinite element boundary was used to calculate and analyze the influence of different continuous vibration isolation barriers and their layout on the vibration isolation effect. Firstly, the validity of the finite element part was verified by setting experiment and finite element model of the same size and same attribute. The verified results were valid. The results show that the best vibration isolation effect of the gully is obtained by comparing all kinds of continuous vibration isolation barriers, and the gully is suitable for high-speed trains. The width within the range of 0.6～2.5 times of the wavelength has little influence on the vibration isolation effect. With the change of width, the vibration isolation effect changes only slightly. The vibration isolation effect is obviously affected when the depth of the vibration barrier varies from 3.8 to 15.2 wavelength. With the increase of depth, the vibration isolation effect is enhanced. The position of the barrier has great influence on the vibration isolation effect. It is suggested that the barrier should be close to the roadbed. Continuous barrier has better vibration isolation effect at high frequency than at low frequency.
-
Key words:
- High speed railway /
- Continuous barrier /
- Vibration isolation /
- ABAQUS
-
引言
1995年阪神地震中大开地铁车站的严重倒塌破坏在世界范围内引起了地震研究学者们对地下结构抗震问题的广泛关注。在地下结构地震反应特征和抗震设计方法等问题的研究过程中，逐渐形成了一系列实用抗震设计方法（刘晶波等，2010a；许成顺，2017）。其中，反应位移法与反应加速度法凭借理论明确、操作简便等优点，在实际工程设计中得到广泛应用，已被《城市轨道交通结构抗震设计规范》（GB 50909—2014）（中华人民共和国住房和城乡建设部，2014）和《地下结构抗震设计标准》（GB/T 51336—2018）（中华人民共和国住房和城乡建设部，2018）采纳。
反应加速度法通过将顶、底板相对位移最大时刻的自由场水平加速度施加于土-结模型上，计算地下结构变形与内力。与反应位移法相比，主要优势为：反应加速度法建立的土-结构模型可较准确地反映土-结构间相互作用，无须计算地基弹簧刚度系数，大大提高了计算效率与精度；反应位移法受限于地基弹簧与地震作用的施加方式，决定了其主要适用于矩形断面，而反应加速度法施加的地震作用为体积力，且模型采用土-结构整体模型，决定了其可适用于复杂断面地下结构的地震反应计算。总的来说，反应加速度法优于反应位移法（刘晶波等，2013；李新星等，2014）。
反应加速度法的应用关键在于地震输入荷载的确定。为简化计算过程，反应加速度法假设输入荷载为地震作用下自由场的反应加速度，然而，该假设忽略了结构的存在对自由场反应加速度的影响。基于此，刘如山等（2007）从一维自由土层反应的剪应力入手，首先对一维自由土层反应剪应力沿竖直方向进行微分，然后将其作为水平体荷载离散到有限元节点上，以此作为加载方法；董正方等（2014）运用柔度系数法中的结构变形和自由场变形之间的相互作用系数，修正了自由场地震反应加速度，近似考虑了结构的存在对反应加速度法的影响；Liu等（2018）通过理论解析方式推导了自由场模型与土-结模型之间场地反应加速度的关系，结果表明可通过2种模型场地相对位移修正场地反应加速度法；徐琨鹏等（2019）对比了反应加速度法和仅在土体施加加速度的简化方法，发现2种方法对侧边距取值不敏感；禹海涛等（2020）通过动力时程分析，提出地下结构附近存在动力响应增强区和衰减区，利用动力响应调整系数提高了反应加速度法的计算精度。
为考虑结构的存在对反应加速度法中地震输入荷载的影响，本文提出将土-结构模型转换为自由场模型的等效方式，采用等效后的土层参数进行自由场反应加速度计算，以此近似地反映结构的存在对地震输入荷载的影响，进而改进反应加速度法中地震输入荷载的计算过程。采用有限元软件ABAQUS对大开车站地震反应进行数值模拟分析，验证等效方式的有效性，并探讨等效模型宽度取值范围对结果的影响，初步给出等效模型宽度范围。
1. 反应加速度法
采用改进前反应加速度法对地下结构横断面进行抗震分析时，计算模型为图1所示的土-结构整体模型。一般地，土体采用二维平面应变单元模拟，结构采用梁单元模拟。将模型底边固定，模型两侧设置水平滑移边界。通过将地下结构顶、底板位置处土层相对位移最大时刻的各土层水平加速度或有效惯性加速度施加于土-结构整体模型上，获得地下结构变形与内力等反应。
反应加速度法主要计算步骤如下：
（1）一维土层地震反应分析。采用等效线性化程序EERA或SHAKE91对一维土层进行地震反应分析，记录结构顶、底板位置处土层最大相对位移时刻，各土层加速度及等效剪切模量Gi。《城市轨道交通结构抗震设计规范》建议，土层简单时地震输入荷载直接采用自由场水平加速度，土层复杂时地震输入荷载采用土层有效惯性加速度。
（2）建立土-结构模型。《城市轨道交通结构抗震设计规范》建议模型底面可取设计地震作用基准面，顶面取地表面，侧面边界到结构的距离宜取结构水平有效宽度的2～3倍，本文针对模型宽度对计算结果的影响展开进一步讨论。
（3）施加等效地震作用。将土层水平加速度或有效惯性加速度按各土层单元的位置施加于土-结构模型中的各土层上，结构部分按所在土层深度位置作用相应的加速度。
从反应加速度法计算模型和计算步骤可看出，该方法地震输入荷载采用的是自由场反应加速度，未考虑结构的存在对自由场加速度反应的影响，尤其是当地下结构刚度和周围土体刚度相差较大时，结构的存在可能会在较大程度上影响周围土体的地震反应。此外，在动力学理论方面，该方法忽略了阻尼因素的影响，仅是某种程度的近似，当土层反应仅有一阶振型发育时，该方法精度尚可，当遇到复杂土层时误差将增大。
2. 改进反应加速度法研究
2.1 等效思路
为考虑结构的存在对反应加速度法中地震输入荷载的影响，对反应加速度法中的加速度求解方法进行改进。首先，按结构周围土体的分层将土-结构模型中的结构与土体等效为自由场，计算等效自由场的土层参数；然后，采用等效线性化程序EERA将等效自由场土层参数进行处理，得到土层等效剪切模量，并计算等效自由场各土层反应加速度，如图2所示。
将图2所示土-结构模型等效为自由场模型时需进行结构等效和土层等效，其中Ki为等效后土体的刚度；K1i为结构的刚度；K2i为等效前土体的刚度。对于地下结构横断面，其顶、底板在断面水平方向上连续，侧墙、中柱在断面水平方向上间断，而土层为分层结构，在断面水平方向上连续。为便于土体与结构进行等效，将断面水平方向上间断的侧墙与中柱等效为连续结构，形成图3（a）所示的分层结构形式。在此基础上，按结构周围土层的划分，将分层结构与分层土体按照相对位置等效为分层的自由场，如图3（b）所示。
上述2个等效过程均包含等质量等效计算和等侧向刚度等效计算。自由场在地震作用下的反应加速度主要受场地质量分布与刚度分布的影响，等质量等效计算假设等效前后土-结构模型与自由场模型中各土层质量保持不变：
$$ {\rho _i}{V_i} = {\rho _{1i}}{V_{1i}} + {\rho _{2i}}{V_{2i}} $$ (1) 式中，
${\rho _i}$ 为等效后第i层土体密度；${V_i}$ 为采用土-结构模型总宽度计算的第i层土体体积；${\rho _{1i}}$ 为第i层土体对应的结构部分的密度；${V_{1i}}$ 为第i层土体中包含的结构体积；${\rho _{2i}}$ 为第i层土体密度；${V_{2i}}$ 为减去结构体积的第i层土体体积。等侧向刚度等效计算中，假设等效前后各土层侧向刚度保持不变，各土层与结构为短柱，进行侧向刚度的串并联叠加：
$$ {G_i}{b_i} = {G_{1i}}{b_{1i}} + {G_{2i}}{b_{2i}} $$ (2) 式中，
${G_i}$ 为等效后第i层土体剪切模量；${b_i}$ 为采用土-结构模型总宽度；${G_{1i}}$ 为结构剪切模量；${b_{1i}}$ 为第i层土体中结构的宽度；${G_{2i}}$ 为第i层土体剪切模量；${b_{2i}}$ 为减去结构宽度的第i层土体宽度。2.2 等效模型宽度的选取
为便于区分，将改进前反应加速度法称为反应加速度法-1（以下简称“RAM-1”），将改进后反应加速度法称为反应加速度法-2（以下简称“RAM-2”）。
采用图4所示土-结构模型边界至结构侧边的距离B表示模型宽度。在RAM-2计算过程中，反应加速度法拟静力计算时涉及土-结构模型宽度（以下简称“模型宽度-F”）、等效土-结构模型宽度（以下简称“模型宽度-B”）的选取。由前文可知，模型宽度-B不同，将直接改变等效自由场土层参数，影响等效自由场场地反应，从而影响反应加速度法计算结果。因此，本文针对不同模型宽度-B对反应加速度法计算结果的影响进行了探讨。
3. 实例分析
3.1 计算模型与参数选取
为验证等效方式的有效性，以大开车站为研究对象，进行了RAM-1、RAM-2与动力时程方法计算。结构断面尺寸如图5所示，结构埋深4.8 m，周围土层参数如表1所示（矢的照夫等，1996）。结构中柱沿车站纵向按3.5 m等间距分布，将其按一定原则等效为连续墙体，等效后中柱弹性模量为8.57 GPa，密度为714 kg/m3。顶、底板与侧墙弹性模量为30 GPa，密度为2 500 kg/m3。土-结构整体分析模型如图6所示，车站结构采用梁单元模拟，土体采用平面应变单元模拟。土体底边界固定，两侧边界设置水平滚轴边界。假设土体与结构之间接触良好，且不产生相对滑移，数值计算时土体与结构之间采用绑定约束。
表 1 土层参数表Table 1. Physical properties of soils分层 土质 厚度/m 密度/(t·m−3) 剪切波速/(m·s−1) 泊松比 1 填土 1 1.9 140 0.333 2 砂土 4.1 1.9 140 0.488 3 砂土 3.2 1.9 170 0.493 4 黏土 3.1 1.9 190 0.494 5 黏土 5.8 1.9 240 0.490 6 砂土 22 2.0 330 0.487 由于缺少大开车站周围土体动力参数，本文采用典型砂土和黏土剪切模量比、阻尼比与剪应变关系曲线（杜修力等，2018），如图7所示。考虑到地震动特性对地下结构地震反应的影响，基岩输入地震动选用Kobe地震动与El Centro地震动，地震动加速度时程曲线如图8所示，将加速度幅值调整为0.1、0.2、0.3 g。
验证等效思路有效性时，RAM-1与RAM-2模型宽度-F均取3倍结构宽度，RAM-2模型宽度-B取3倍结构宽度。动力时程分析共6种计算工况，反应加速度法共12种计算工况（包括RAM-1、RAM-2各6种计算工况）。
在探讨不同模型宽度-B对RAM-2计算结果的影响时，RAM-1与RAM-2模型宽度-F仍取为3倍结构宽度，RAM-2模型宽度-B分别取为1、2、3、4、5、7倍结构宽度。在0.1 g幅值的Kobe地震动作用下进行动力时程计算、RAM-1计算与不同模型宽度-B的RAM-2计算。
3.2 结果与分析
刘晶波等（2010b）和杜修力等（2017）指出地下结构中柱为抗震关键构件，在此基础上，计算不同地震作用下中柱与顶、底板位置处的相对位移、中柱底部弯矩、中柱底部剪力和侧墙底部弯矩，结果如表2所示，表中括号内为相应的误差。
表 2 不同地震作用下结构内力与变形Table 2. Internal force and deformation of structure under different earthquake load地震动 幅值 计算方法 顶、底板相对位移/mm 中柱底部弯矩/
[(kN·m)·m−1]中柱底部剪力/
(kN·m−1)侧墙底部弯矩/
[(kN·m)·m−1]Kobe 0.1 g 动力时程分析法 5.77 36.12 11.09 358.40 RAM-1 5.56(3.66%) 34.06(5.70%) 10.48(5.50%) 341.50(4.72%) RAM-2 5.71(1.04%) 35.00(3.10%) 10.78(2.80%) 351.20(2.01%) 0.2 g 动力时程分析法 16.93 102.70 30.88 887.30 RAM-1 16.17(4.47%) 99.31(3.30%) 30.80(0.26%) 879.50(0.88%) RAM-2 16.44(2.86%) 102.00(0.68%) 30.51(1.20%) 877.00(1.16%) 0.3 g 动力时程分析法 31.15 187.50 55.97 1476.00 RAM-1 30.30(2.76%) 181.70(3.09%) 54.43(2.75%) 1447.00(1.96%) RAM-2 30.94(0.67%) 185.50(1.07%) 55.44(0.95%) 1474.00(0.14%) EL Centro 0.1 g 动力时程分析法 14.12 86.02 26.09 771.40 RAM-1 13.41(5.02%) 81.68(5.05%) 25.04(4.02%) 741.00(3.94%) RAM-2 13.61(3.62%) 83.07(3.43%) 25.59(1.92%) 755.90(2.01%) 0.2 g 动力时程分析法 26.73 160.40 47.59 1288.00 RAM-1 25.36(5.15%) 151.70(5.42%) 45.47(4.45%) 1241.00(3.65%) RAM-2 26.12(2.30%) 156.30(2.56%) 46.82(1.62%) 1278.00(0.78%) 0.3 g 动力时程分析法 38.75 231.60 68.07 1755.00 RAM-1 35.48(8.44%) 210.60(9.07%) 62.24(8.56%) 1628.00(7.24%) RAM-2 37.51(3.22%) 222.10(4.10%) 65.35(4.00%) 1704.00(2.91%) 由表2可知，以动力时程为基准，不同工况下RAM-1计算的结构变形与内力最大误差为9%，不同工况下RAM-2计算的结构变形与内力最大误差为4.1%，等效方式将反应加速度法的计算误差由10%以内缩小至5%以内，提高了反应加速度法计算精度，表明了等效方式的有效性；RAM-2在不同幅值Kobe地震动作用下计算的结构变形与内力最大误差为3.1%，在不同幅值El Centro地震动作用下计算的结构变形与内力最大误差为4.1%，最大误差随地震动强度的改变未明显变化，说明该方法的计算结果较稳定。
以动力时程为基准计算的结构变形与内力、不同模型宽度-B 下 RAM-2 计算的结构变形与内力如表3所示，表中括号内为相应的误差。由表3、图9可知，与动力时程分析法相比，随着模型宽度-B的减小，RAM-2计算结果逐渐增加，逐渐接近动力时程计算结果，甚至大于动力时程计算结果；而RAM-1最大计算误差为5.7%，模型宽度-B为7、5、4、3倍结构宽度时，RAM-2最大计算误差分别为6.15%、4.51%、4.1%、3.1%，表明当模型宽度取值较大时，改进反应加速度法计算误差呈增大趋势，这是由于模型宽度越大，等效后的自由场模型更接近原始自由场模型，此时等效模型无法充分反映结构的存在造成的影响。结合表2所示不同工况下RAM-1计算的结构变形与内力最大误差为9%，不同工况下模型宽度-B为3倍结构宽度时，RAM-2最大计算误差为4.1%，若以计算误差减小50%为衡量标准，建议模型宽度-B取为1～3倍结构宽度。
表 3 不同模型宽度-B下结构内力与变形Table 3. Internal force and deformation of structure with different model width计算方法 模型宽度-B/
结构宽度顶、底板相对
位移/mm中柱底部弯矩/
[(kN·m)·m−1]中柱底部剪力/
(kN·m−1)侧墙底部弯矩/
[(kN·m)·m−1]动力时程分析法 — 5.77 36.12 11.09 358.40 RAM-1 — 5.56(3.66%) 34.06(5.70%) 10.48(5.50%) 341.50(4.72%) RAM-2 1 5.98(3.67%) 36.67(1.52%) 11.31(1.98%) 368.80(2.90%) 2 5.78(0.16%) 35.42(1.94%) 10.92(1.53%) 355.50(0.81%) 3 5.71(1.04%) 35.00(3.10%) 10.78(2.80%) 351.20(2.01%) 4 5.65(2.05%) 34.64(4.10%) 10.68(3.70%) 347.70(2.99%) 5 5.63(2.49%) 34.49(4.51%) 10.64(4.06%) 346.20(3.40%) 7 5.53(4.16%) 33.90(6.15%) 10.46(5.68%) 340.20(5.08%) 4. 结论
本文采用有限元分析软件ABAQUS对大开车站进行不同工况下的动力时程分析和改进前后反应加速度法分析，验证了等效方式对反应加速度法的有效性。在验证等效思路有效的基础上，进行了不同等效模型宽度的改进反应加速度法计算，初步给出了等效模型宽度的选取范围。
（1）在未改变RAM-1理论基础的前提下，对关键参数——地震输入荷载进行了修正。与动力时程分析法相比，修正后的反应加速度法使不同工况下的最大计算误差由10%以内缩小至5%以内，提高了反应加速度法计算精度。
（2）与动力时程分析结果相比，修正后的反应加速度法在不同工况下的最大计算误差未明显改变，说明修正结果具有稳定性。
（3）对不同等效模型宽度对反应加速度法计算结果的影响进行分析，根据结果建议等效模型边界至结构侧边的距离取为1～3倍结构宽度。
-
图 11 不同振源距的Ar曲线
Figure 11. Ar curves of different distances from test point to the foot of roadbed slope
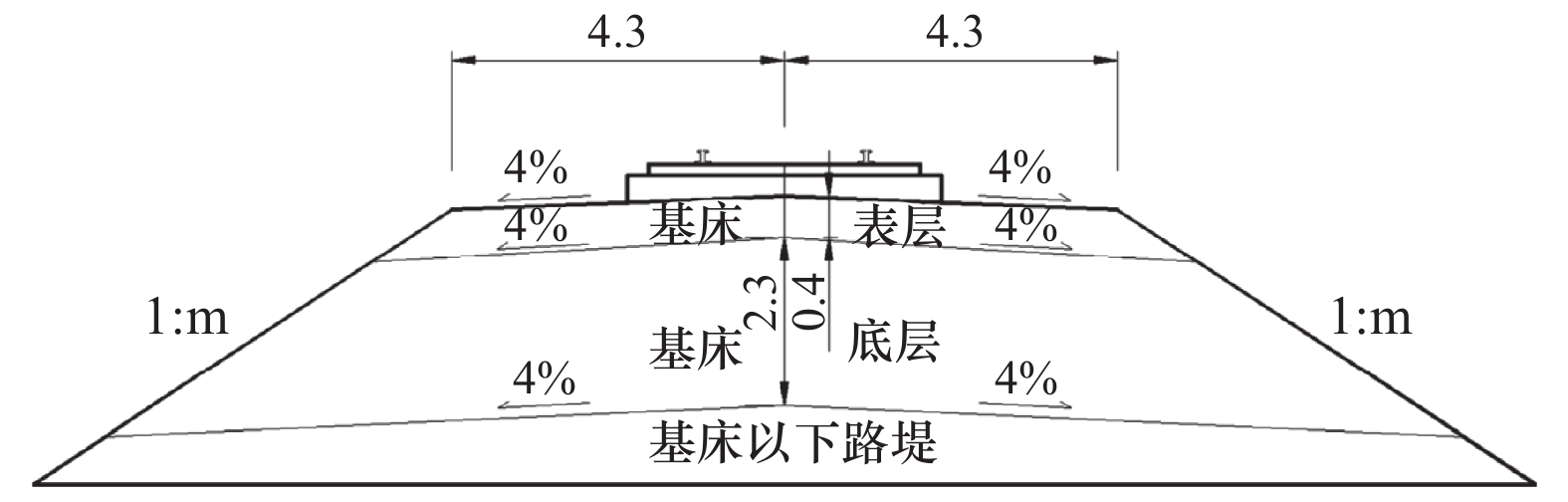
表 1 路基与屏障材料参数
Table 1. Material parameters of subgrade
类型 密度/kg·m−3 弹性模量/Pa 泊松比 路基表层 2 000 1.80×108 0.250 路基底层 1 950 1.10×108 0.250 地基土 1 900 2.00×107 0.300 轨道板 2500 3.50×1010 0.167 钢轨 7800 2.10×1011 0.300 支承层 2500 2.70×1010 0.167 混凝土板墙 2400 3.00×1010 0.200 橡胶板墙 1200 7.80×106 0.470 
下载: 导出CSV
表 2 工况水平组合表
Table 2. Table of combination of parameter levels
水平 类型A 宽度B/m 深度C/m 振源距D/m 激振频率E/Hz 1 空沟 0.5 3.0 5.0 20 2 混凝土板墙 1.0 6.0 6.0 60 3 橡胶板墙 1.5 9.0 7.0 130 4 — 2.0 12.0 8.0 —
下载: 导出CSV
-
[1] 巴振宁, 梁建文, 张艳菊, 2016. 三维层状黏弹性半空间中球面SH、P和SV波源自由场. 地球物理学报, 59(2): 606—623. doi: 10.6038/cjg20160218Ba Z. N., Liang J. W., Zhang Y. J., 2016. Free-field responses of spherical SH-, P-and SV-wave sources in a layered visco-elastic half space. Chinese Journal of Geophysics, 59(2): 606—623. (in Chinese) doi: 10.6038/cjg20160218 [2] 巴振宁, 刘冰松, 张龙等, 2018. 环境振动下德和园大戏楼动力响应分析. 建筑结构, 48(S1): 414—420.Ba Z. N., Liu B. S., Zhang L., et al., 2018. Dynamic response analysis of the Grand Theater in the Garden of Virtuous Harmony under the environmental vibration. Building Structure, 48(S1): 414—420. (in Chinese) [3] 陈行, 晏启祥, 黄希, 2017. 列车振动荷载作用下高速铁路近距地铁平行隧道的动力响应特性分析. 铁道标准设计, 61(6): 116—119, 130.Chen H., Yan Q. X., Huang X., 2017. Research on dynamic response of high-speed train vibration in parallel tunnel close to metro. Railway Standard Design, 61(6): 116—119, 130. (in Chinese) [4] 陈昆, 贾霄, 刘彬等, 2014. 高速铁路空沟隔振措施隔振效果的有限元分析. 地震工程学报, 36(3): 575—579. doi: 10.3969/j.issn.1000-0844.2014.03.0575Chen K., Jia X., Liu B., et al., 2014. Finite element analysis of reducing the high-speed railway vibration effect on the environment using open trenches. China Earthquake Engineering Journal, 36(3): 575—579. (in Chinese) doi: 10.3969/j.issn.1000-0844.2014.03.0575 [5] 丁智, 张霄, 吴敏慧等, 2019. 双线地铁运营隔振沟屏障性能研究. 地震工程学报, 41(1): 9—15. doi: 10.3969/j.issn.1000-0844.2019.01.009Ding Z., Zhang X., Wu M. H., et al., 2019. Vibration isolation effect of isolation trenches during double-line subway operation. China Earthquake Engineering Journal, 41(1): 9—15. (in Chinese) doi: 10.3969/j.issn.1000-0844.2019.01.009 [6] 关歆莹, 刘超, 2011. 地下铁道的振动及其控制措施的研究. 震灾防御技术, 6(1): 77—84. doi: 10.3969/j.issn.1673-5722.2011.01.008Guan X. Y., Liu C., 2011. The study on the vibration of metro and its control measures. Technology for Earthquake Disaster Prevention, 6(1): 77—84. (in Chinese) doi: 10.3969/j.issn.1673-5722.2011.01.008 [7] 国家铁路局, 2015. TB 10621-2014 高速铁路设计规范. 北京: 中国铁道出版社.National Railway Administration of the People’s Republic of China, 2015. TB 10621—2014 Code for design of high speed railway. Beijing: China Railway Publishing House. (in Chinese) [8] 蒋英礼, 赵伯明, 胡晓勇, 2009. 软土地铁车站中柱在强震作用下的响应研究. 防灾减灾工程学报, 29(4): 405—410.Jiang Y. L., Zhao B. M., Hu X. Y., 2009. Study on response of Centre column of metro station in soft soils to strong earthquake. Journal of Disaster Prevention and Mitigation Engineering, 29(4): 405—410. (in Chinese) [9] 刘厚毅, 周游, 钟康明等, 2018. 场地条件对高速铁路地基土振动影响的研究. 震灾防御技术, 13(4): 893—902. doi: 10.11899/zzfy20180416Liu H. Y., Zhou Y., Zhong K. M., et al., 2018. Variation characteristics of foundation soil vibration caused by high speed train with depth under different site conditions. Technology for Earthquake Disaster Prevention, 13(4): 893—902. (in Chinese) doi: 10.11899/zzfy20180416 [10] 刘晶磊, 赵晓玉, 张瑞恒等, 2019. 混凝土排桩深度优化及隔振效果研究. 安全与环境工程, 26(6): 202—208.Liu J. L., Zhao X. Y., Zhang R. H., et al., 2019. Research on depth optimization and vibration isolation effect of concrete row piles. Safety and Environmental Engineering, 26(6): 202—208. (in Chinese) [11] 刘晶磊, 赵倩, 梅名彰等, 2020. 轨道交通荷载下桩板结构主动隔振效果研究. 地震工程学报, 42(1): 7—14. doi: 10.3969/j.issn.1000-0844.2020.01.007Liu J. L., Zhao Q., Mei M. Z., et al., 2020. Active vibration isolation effect of the pile-plank structures under rail traffic loads. China Earthquake Engineering Journal, 42(1): 7—14. (in Chinese) doi: 10.3969/j.issn.1000-0844.2020.01.007 [12] 孙立强, 李嘉, 刘彬等, 2015. 空沟、碎石填充沟和排桩隔振效果试验研究. 地震工程学报, 37(2): 342—348. doi: 10.3969/j.issn.1000-0844.2015.02.0342Sun L. Q., Li J., Liu B., et al., 2015. Experimental study on vibration-isolation effects of open trench, gravel-filled trench, and piles in a row. China Earthquake Engineering Journal, 37(2): 342—348. (in Chinese) doi: 10.3969/j.issn.1000-0844.2015.02.0342 [13] 肖木洋, 2017. 轨道交通地震监测及预警系统现状分析. 地震工程学报, 39(S1): 189—194.Xiao M. Y., 2017. Status analysis of earthquake monitoring and warning system for rail transit. China Earthquake Engineering Journal, 39(S1): 189—194. (in Chinese) [14] 肖世伟, 雷长顺, 郭超等, 2011. 高速铁路空沟隔振数值分析. 铁道工程学报, (8): 23—29. doi: 10.3969/j.issn.1006-2106.2011.08.005Xiao S. W., Lei C. S., Guo C., et al., 2011. Numerical analysis of vibration reduction of open trench for high-speed railway. Journal of Railway Engineering Society, (8): 23—29. (in Chinese) doi: 10.3969/j.issn.1006-2106.2011.08.005 [15] 徐平, 2017. 空沟对平面纵波隔离效果的理论解答. 振动与冲击, 36(5): 67—71, 101.Xu P., 2017. Theoretical analysis for isolation effect of an open trench on plane longitudinal waves. Journal of Vibration and Shock, 36(5): 67—71, 101. (in Chinese) [16] Adam M., Von Estorff O., 2005. Reduction of train-induced building vibrations by using open and filled trenches. Computers & Structures, 83(1): 11—24. [17] Andersen L., Nielsen S. R. K., 2005. Reduction of ground vibration by means of barriers or soil improvement along a railway track. Soil Dynamics and Earthquake Engineering, 25(7—10): 701—716. doi: 10.1016/j.soildyn.2005.04.007 [18] Ganji V., Gucunski N., Maher A., 1997. Detection of underground obstacles by SASW method－numerical aspects. Journal of Geotechnical and Geoenvironmental Engineering, 123(3): 212—219. doi: 10.1061/(ASCE)1090-0241(1997)123:3(212) [19] Haupt W. A., 1978. Surface waves in nonhomogeneous half-space. In: Prange B, ed., Dynamical Methods in Soil and Rock Mechanics. Rotterdam: Balkema, 335—367. [20] Ju S. H., Lin H. T., 2006. Reduction of vibrations due to foundation slabs. Journal of Geotechnical and Geoenvironmental Engineering, 132(4): 511—520. doi: 10.1061/(ASCE)1090-0241(2006)132:4(511) [21] Persson, K., Persson P., Sandberg G., 2016. Numerical study of reduction in ground vibrations by using barriers. Engineering Structures, 115: 18—27. doi: 10.1016/j.engstruct.2016.02.025 [22] Woods R. D., 1968. Screening of surface waves in soils. Journal of the Soil Mechanics and Foundations Division, 94(4): 951—979. doi: 10.1061/JSFEAQ.0001180 [23] Zhu H. Y., Wang J. W., Cai C. B., et al., 2017. Development of a vibration attenuation track at low frequencies for urban rail transit. Computer‐Aided Civil and infrastructure Engineering, 32(9): 713—726. doi: 10.1111/mice.12285 期刊类型引用(0)
其他类型引用(1)
-
下载:
点击查看大图
计量
- 文章访问数: 200
- HTML全文浏览量: 24
- PDF下载量: 0
- 被引次数: 1
