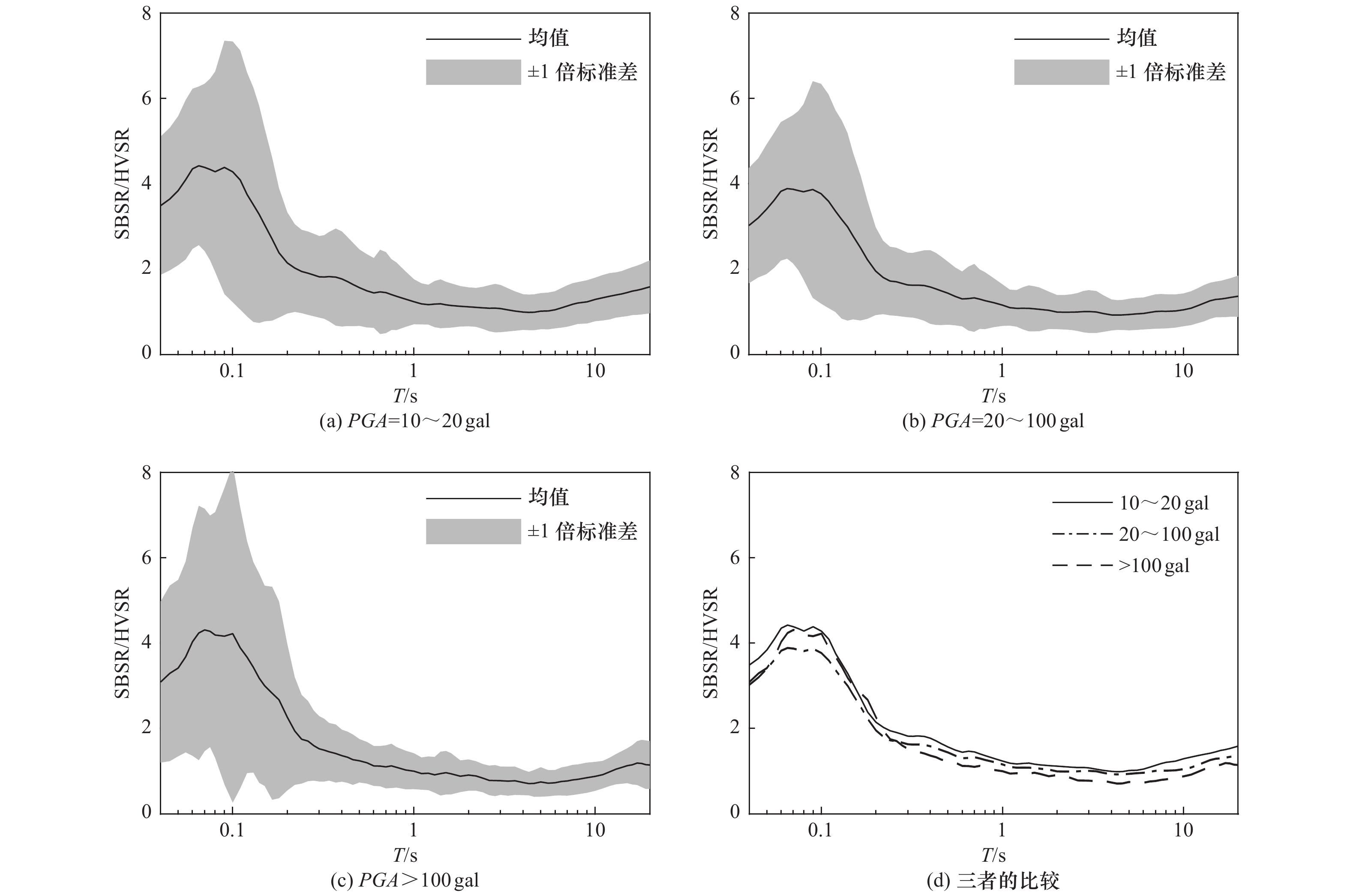
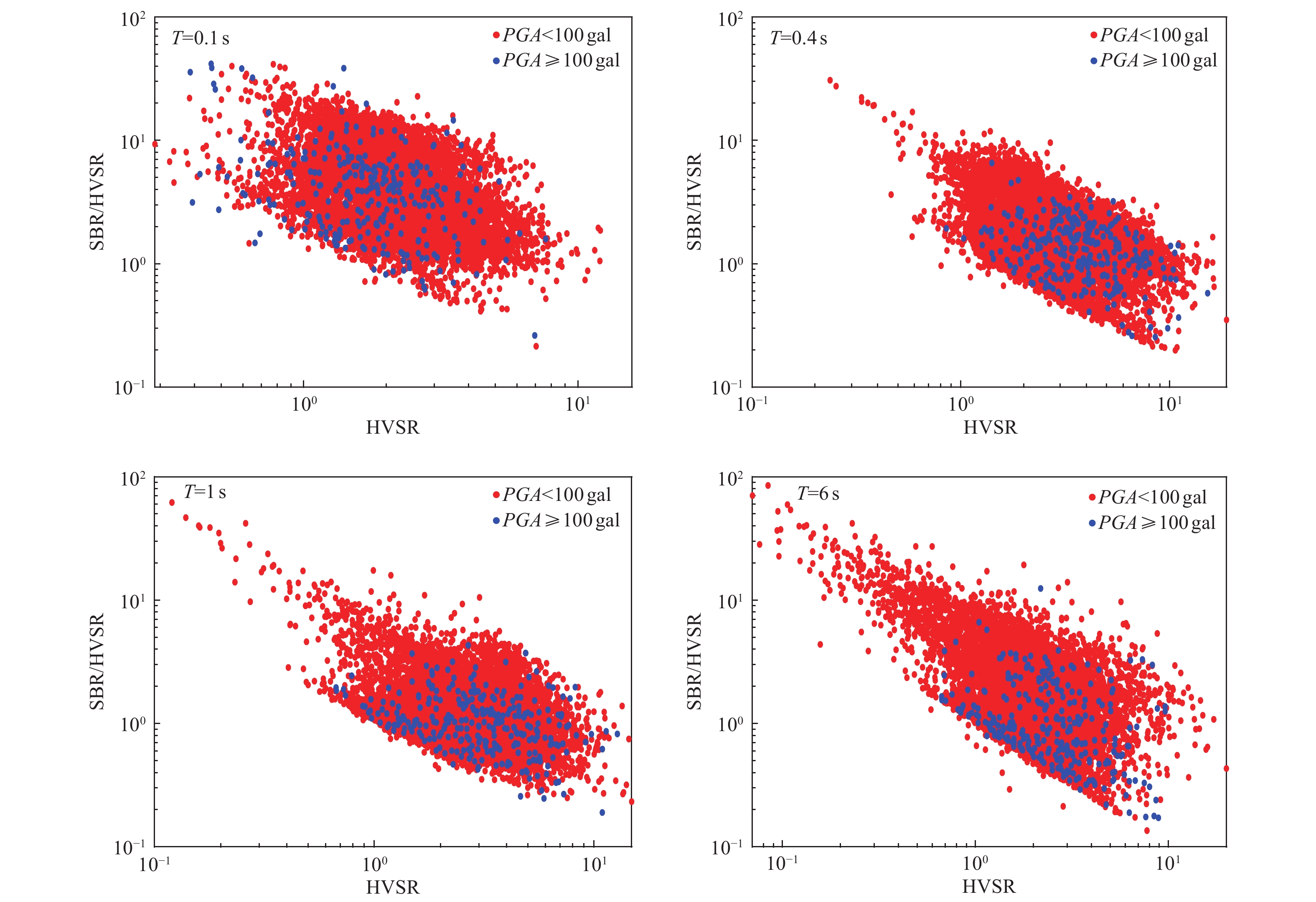
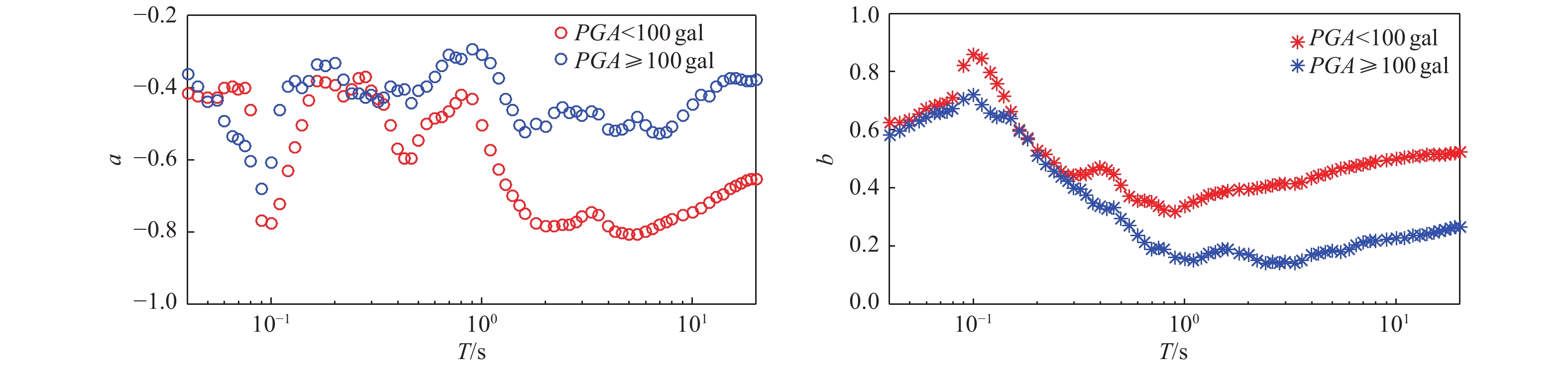
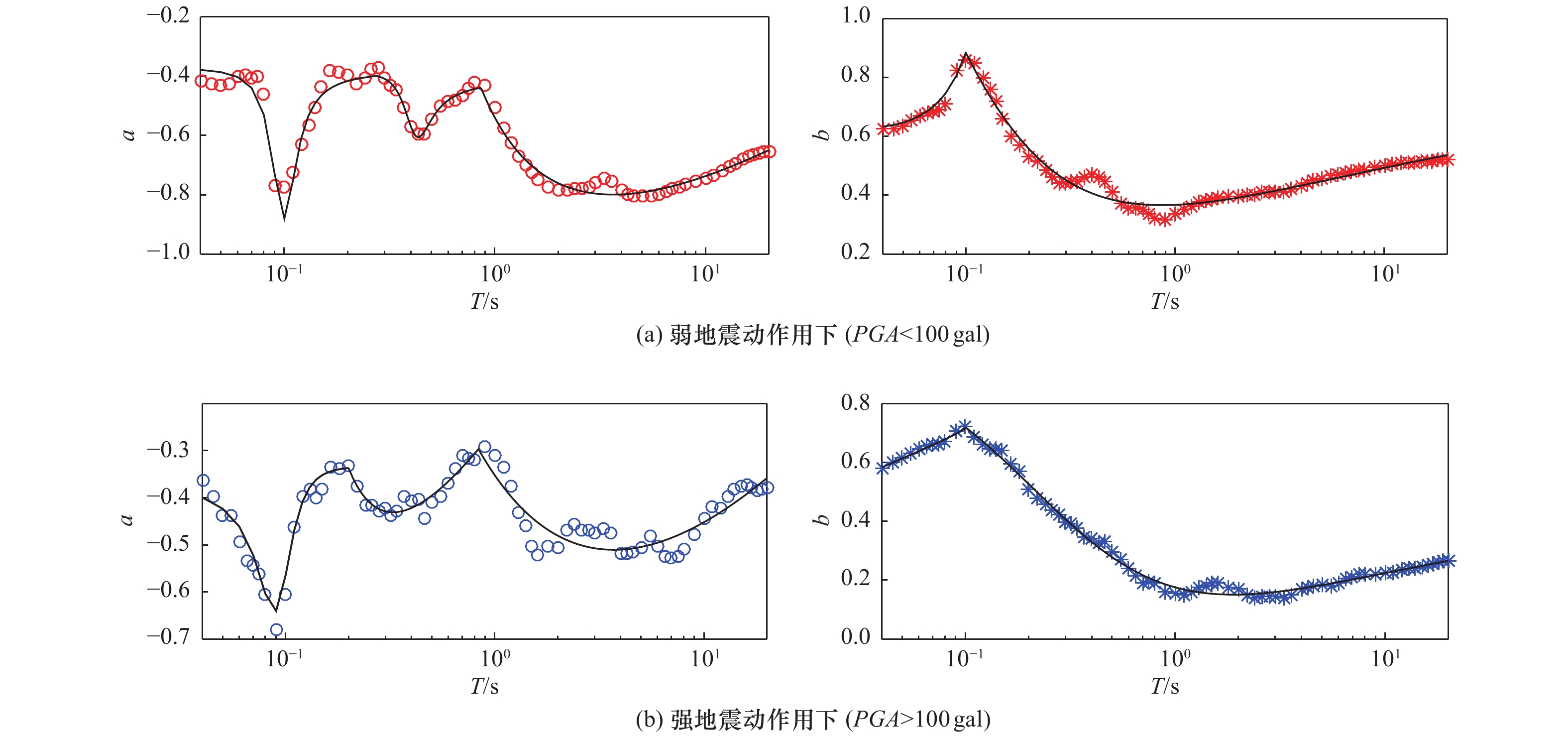
Difference Between Horizontal-to-Vertical Spectral Ratio and Surface-to-Bedrock Spectral ratio of Strong-Motion and Modified Horizontal-to-Vertical Spectral Ratio Method
-
摘要: 局部场地条件是决定场地地震动强度和频谱的重要因素，基于强震动和脉动记录的统计分析，获取表征场地条件影响的特征参数已成为确定工程场地设计地震动的较经济和实用方法，特别是对于大范围或难以开展现场勘测的工程场地。利用日本KiK-net台网强震动记录计算分析了台站场地地震动水平/竖向谱比（HVSR）与地表/基底谱比（SBSR）的差异，揭示SBSR/HVSR与HVSR呈对数线性分布的统计特征，并给出其定量关系，据此提出表征场地对地震动影响的修正水平/竖向谱比法。修正水平/竖向谱比法具有仅需地表观测记录的优势，并进一步考虑了场地竖向地震效应对水平/竖向谱比法精度的影响，更能合理地表征场地对地震动的影响。Abstract: During an earthquake, local site conditions are an important factor in determining the intensity and spectrum of ground motion. Statistical analysis to obtain characteristic parameters to characterize the influence of site conditions based on strong-motion and microtremor has become a more economical and practical method to determine the design ground motion of engineering sites, especially for a large survey area or an engineering site that are difficult to carry out site survey. The differences between the surface-to-bedrock spectral ratio (HVSR) and the horizontal-to-vertical spectral ratio (SBSR) of the strong-motion station sites were analyzed by using the strong-motion records from the Japanese KiK-net network, the statistical characteristics of log linear relation between SBSR/HVSR and HVSR was revealed, and a quantitative relationship between them was obtained, and then a modified horizontal-to-vertical spectral ratio method was proposed to characterize the influence of site conditions on ground-motion. This modified method has the advantage that the HVSR method only needs surface records, and further considers the influence of the vertical seismic effect on the accuracy of the HVSR method. The modified HVSR method can more reasonably characterize the influence of site conditions on ground-motion.
-
引言
北京时间2019年2月2日5时54分，新疆塔城地区塔城市(46.73°N，83.34°E)发生MS5.2地震，震源深度16km，震中距塔城市区27km、距额敏县城32km、距裕民县城64km、距托里县城90km、距克拉玛依市区172km、距和布克赛尔县城181km、距乌合尔区194km。塔城市、托里县、额敏县、博乐市、精河县、温泉县、和布克赛尔县、兵团第五师83团、奎屯市、乌苏市、霍尔果斯市、阿勒泰市、福海市、兵团北屯市、克拉玛依市、伊宁市等地震感强烈。地震造成震中附近房屋发生不同程度破坏，其中以无抗震能力的土木结构房屋破坏最为严重。
地震频度高、震源浅、分布广、灾害重是本次地震灾害的主要特征，随着经济、社会的不断发展，各级政府对乡村地区房屋抗震意识不断提高，在城镇地区推行多种有针对性的房屋改造工程。2004年新疆开始正式实施城乡抗震安居工程(张勇，2006)，2011年开始按“高起点规划、高水平建设、高效益配套”要求建设每户不低于80m2，户型实用、耐用、设施齐全，反映地域特色和文化内涵的安居富民房(谭明等，2014；常想德，2017a，2017b)。安居富民工程的实施推广使新疆农、牧区房屋抗震性能迅速提高，此类房屋在新疆境内多次破坏性地震中均未出现破坏，其抗震性能得到检验。相反，未经正规抗震设计的老旧、自建房屋破坏和倒塌比例非常高，所以推广安居富民工程对减少地震带来的损失具有至关重要的意义(姚远等, 2015, 2016；阿里木江·亚力昆等，2018；温和平等，2017)。
本文在分析塔城市MS5.2地震震区烈度分布及场地条件的基础上，归纳总结房屋结构、震害特征，并通过分析等震线分布、活动构造特征及深部构造，探讨本次地震可能的发震构造。
1. 地震烈度及场地条件
1.1 地震烈度
新疆维吾尔自治区地震局地震现场工作队按照《地震现场工作第3部分：调查规范》(GB/T 18208.3—2011)(中华人民共和国国家质量监督检验检疫总局等，2011)、《中国地震烈度表》(GB/T 17742—2008)(中华人民共和国国家质量监督检验检疫总局等，2008)对震区7个乡(镇、场)共33个调查点开展烈度调查，确定Ⅵ度点13个、Ⅴ度点20个，依据烈度调查情况，确定了本次地震极震区烈度为Ⅵ度，Ⅵ度区西起喀拉哈巴克乡以东，东至恰夏镇东北地区，等震线呈近EW走向，与该地区活动断裂走向近一致，等震线长轴半径约9.7km，短轴半径约6.8km，总面积206.77km2，主要涉及塔城市恰夏镇、恰合吉牧场及喀拉哈巴克乡(图 1)。
图 1 塔城地震烈度、调查点及震区场地条件分布Figure 1. The seismic intensity, survey point distribution and site conditions map of the Tacheng earthquake1.2 震区场地条件
震区位于塔城坳陷带内，地貌主要由震中东部锡伯图河冲积扇与西部阿不都拉河冲积扇组成的山前冲、洪积扇群组成。总体地势北高南低，东西向地势为冲积扇轴部向冲积扇两侧或冲积扇结合部倾斜，盆地地形平坦、开阔，坡度平缓。震区地层岩性具典型的二元结构，由上部粉土与下部厚层卵砾石组成，局部地区上部粉土层较厚，地貌现多为农田。
新构造运动以来，随着西准噶尔山地及塔尔巴哈台山和巴尔鲁克山的不一致隆升，造成山体倾斜，山势由西向东呈阶梯状下降。同时，河流下切造成河谷内形成多级高度不同的阶地，如达尔布特河发育高度不同的多级河流阶地，喀浪古尔河与阿布都拉河等在山口地带发育2~3级河流阶地。这反映出震区现代构造运动具有间歇性和差异性的特点，各级阶地拔河高度大致反映了晚第四纪以来的抬升幅度。另外，在山体隆升的同时，塔城盆地发生相对沉降，沉降幅度由南北山前地带向盆地中央逐渐增大，在盆地内部沉积了较厚的第四纪堆积物，厚度可达258m。本次地震震中位于山前冲洪积平原上，该地貌单元内场地条件单一，为Ⅱ类场地(图 1)。
2. 震区房屋结构类型及震害特征
2.1 震区房屋结构类型
本次地震涉及的房屋结构类型主要包括土木结构、砖木结构、砖混结构、框架结构和安居富民房。
(1) 土木结构。震区土木结构房屋多数为20世纪八九十年代建造的“干打垒”房屋，墙体由黏性土夯打密实而成。部分房屋基础和底部为砖砌体墙体，并砌筑土坯墙(土坯墙与砖墙间未进行有效、可靠连接)，部分房屋墙体勒脚为后期填充式单砖砌筑，还有部分房屋将木梁房顶上面改造成彩钢板房顶。该类房屋在灾区乡村占比较大，承重墙体多为土坯墙和夯土墙，建筑材料强度低，是典型的脆性结构，无任何抗震措施，屋面与墙体之间缺乏有效连接，房屋整体性很差，在水平地震作用下，整个屋面易产生推力，破坏承重外墙(葛鸣等，2012；王永亮等，2014)，从而出现墙体倒塌或屋顶坍塌现象。本次地震后，恰夏镇禾斯阔甫尔村和喀拉哈巴克乡阿热散村“干打垒”房屋由于地基不稳，加之风雨侵蚀，使后墙外闪，纵横墙间出现裂缝(图 2(a)、2(b))。此外，震区土木结构房屋多因年久失修，震前已普遍存在细小裂缝，本次地震使旧裂缝加宽，部分房屋旧裂缝加宽现象相对明显(图 2(c)、2(d))；还有一些房屋墙皮发生脱落、纵横墙连接处出现竖向裂缝、门(窗)洞角出现斜裂缝(图 2(e))，恰夏镇靠近震中方向的西山墙与纵墙裂缝较多，单坡屋顶类的房屋滴水侧南纵墙与横墙间裂缝较多(图 2(f))。
图 2 土木结构房屋受损情况Figure 2. Damage of soil-wood by the earthquake(a)禾斯阔甫尔村“干打垒”房屋中等程度破坏，后墙外闪，出现纵横墙间裂缝；(b)阿热散村老旧土木结构房屋后纵墙外闪；(c)、(d)阿热散村土木结构房屋已有裂缝加宽；(e)农二队土木结构房屋门洞角裂缝加宽、墙皮脱落；(f)科克塔尔村“干打垒”房屋出现纵横墙间裂缝(2) 砖木结构。震区该类房屋较少，主要为年代较久的居民自建房、政府、学校，房屋墙体为黏土砖砌筑，无圈梁及构造柱等抗震措施，多为硬山搁檩形式，与墙体间无可靠连接措施。震区附近砖木结构房屋虽抗震性能差，但本次震害不明显，多数为基本完好，少数出现旧裂缝加宽现象，如喀拉哈巴克乡巴斯博孜达克东村一户2002年修建的120m2砖木结构房屋，因地基不稳造成房屋后纵墙裂缝，2008年曾进行抗震加固，但本次地震仍使旧裂缝加宽(图 3(a))。
图 3 其他结构房屋受损情况Figure 3. Damage of other houses by the earquake(a)巴斯博孜达克东村老旧砖木结构房屋裂缝加宽；(b)农二队砖混结构房屋墙体裂缝加宽；(c)农二队砖混结构房屋预制板顶连接处出现裂缝；(d)滑雪场砖混结构房屋门洞角出现斜裂缝；(e)恰夏镇中心学校小学教学楼框架结构轻微破坏，填充墙墙体门洞角出现斜裂缝；(f)恰夏镇中心学校小学教学楼框架结构轻微破坏，廊洞部出现横向裂缝(3) 砖混结构。该类房屋主要分为预制板楼顶和现浇楼顶两类，主要为建成一段时间的居民自建房、乡(镇)政府办公用房、干部周转房、学校、幼儿园等，此类房屋一般进行了抗震设防，设置了圈梁、构造柱等抗震措施，且施工质量较好，建设时依据的抗震设计规范版本虽不同，但抗震性能相对较好。震区调查结果显示该类房屋多数基本完好，个别出现轻微破坏，主要震害现象为墙体斜裂缝、门(窗)洞角斜裂缝、预制板间连接处开裂、吊顶脱落等，如恰合吉牧场农二队和滑雪场砖混结构房屋预制板顶连接处出现裂缝(图 3(b))，门洞角出现斜裂缝(图 3(c))。单层砖混结构民居房屋多为未经抗震设防的自建房，材料强度和砌体整体强度较低，部分房屋建造年代久远，施工质量差，缺乏抗震措施，抗震性能较差(图 3(d))。
(4) 框架结构。该类房屋是由钢筋混凝土梁、柱等构件组成承重体系的房屋，主要为乡(镇)政府办公楼、学校幼儿园教学楼等，具有平面布置灵活、可任意分割房间、易满足生产工艺和使用要求、自重轻、能有效减小地震作用等优点。设计合理的框架结构房屋抗震性能一般较好，具有良好的延性。震区调查结果显示该类房屋框架主体结构未遭受破坏，多数为完好无损。恰夏镇中心学校小学教学楼轻微破坏，填充墙墙体门洞角出现斜裂缝(图 3(e))和廊洞部横向裂缝(图 3(f))，这可能因为填充墙多采用空心砖或混凝土砌块，使填充墙侧向刚度大于框架侧向刚度，框架结构属于柔性结构，框架柱变形大于填充墙，变形不协调，从而导致填充墙产生轻微裂缝(谭明等，2014；孙静等，2014)。
(5) 安居富民房。该类房屋多在原宅基地上新建，部分为集中成片建设。为确保安居富民房达到抗震要求，各级政府和相关部门采取了一系列管理和技术措施，并为建房户提供指导和服务。震区安居富民房主要以砖混结构为主，随着建设任务的完成，砖木结构和砖混结构房屋占比迅速扩大，将成为主要结构类型。该类房屋抗震措施满足设防要求，抗震性能良好，在本次地震中未发生明显破坏(图 4(a)、4(b))。
2.2 地震灾害特征分析
(1) 本次地震震中烈度为Ⅵ度，根据烈度调查，初步认为本次地震发震构造为塔城盆地北缘塔克台断裂向盆地扩展形成的一条隐伏断层，房屋震害较重的调查点以近东西向展布。本次地震Ⅵ度区受山前断裂和场地条件的影响明显，Ⅵ度区影响范围大体呈东西向条带状分布。
(2) 本次地震Ⅵ度区涉及恰夏镇、恰合吉牧场、喀拉哈巴克乡，现场调查发现本次地震未造成人员伤亡，也未造成大面积房屋结构性破坏，仅造成少数老旧土木结构房屋破坏、个别砖混结构房屋和框架结构房屋轻微破坏，损失和影响范围较小。
(3) 安居富民房具有良好的结构抗震措施和合理的基础防护措施，抵御了本次地震灾害，震区此类房屋抗震性能良好，未出现破坏。
(4) 恰合吉牧场场部距微观震中仅2km，但未造成大面积房屋破坏，居民房屋抗震能力较强，且老旧房屋占比较小，这是地震灾害少的原因。
3. 震区发震构造分析
3.1 地震构造背景
塔城盆地位于天山和阿尔泰山之间，在大地构造上位于哈萨克斯坦—准噶尔板块内(罗福忠等，2015)，是在古生代褶皱基底上发育的新生代山间盆地。盆地东西长约160km，南北宽约90km，总面积约8300km2(冯乾文，2009)。盆地由北部的塔尔巴哈台山、南部的巴尔鲁克山以及东部的乌尔喀什尔山(谢米斯台山)环抱而成(图 5(a))，在空间上呈不规则方形，主体走向为NE—SW向。布格重力异常及剩余重力异常、二维地震及电法反演资料均显示，塔城盆地南北向具有“两拗夹一隆”构造格局(吕铁良等，2015)。盆地构造格局总体上被NE—近EW向塔克台断裂、冬别列克断裂控制。
本次地震震中位于塔尔巴哈台山以南的塔城盆地内，盆地内活动断裂不发育，距震中最近的一条区域性活动断裂带为塔城盆地北缘的塔克台断裂，该断裂东部沿和布克赛尔盆地北缘延伸，向西穿过西准噶尔山地经塔城盆地北缘延伸至哈萨克斯坦境内，全长约438km。断裂走向近EW向，延伸至哈萨克斯坦境内转为NW向，主断面北倾，具有逆断层性质。由于境外塔克台断裂几何展布情况不明，本文未展示境外部分。根据断裂几何学展布特征，将该断裂初步划分为东、西两段，东段从布克赛尔盆地北至塔城盆地东北端，全长约163km，走向近EW向；西段从塔城盆地东北端至哈萨克斯坦境内(图 5(a))，全长约275km，走向近EW向，后又转为NW向。
断裂在阿布都拉河一带分为两条，即北支断裂与南支断裂，构成塔尔巴哈台山与塔城盆地的界线。北支断裂在塔城市北喀浪古尔河渠首，断裂在地貌上，呈近EW向的断裂谷地，断裂断错水系西岸，断面北倾，倾角约68°，沿断面发育较厚的红色断层泥。该断裂分布在泥盆系基岩区内，断层两侧泥盆系产状不一致，北盘地层北倾，倾斜相对较缓，而南盘地层南倾，倾斜陡立。断层两侧地层受挤压较破碎，破碎带宽约30m。
南支断裂构成塔城盆地西北边界，分布在山前地带，在塔城市北喀浪古尔河山口处河西岸可见断裂断错了Ⅱ、Ⅲ级河流阶地，并形成清晰的断层陡坎。河流阶地基座为泥盆系，上覆阶地砾石层与黄土层。但在Ⅰ级阶地上，阶地面平坦，未发现断裂断错Ⅰ级阶地形成明显的断层陡坎(图 6(a))。在阿布都拉河河口一带，断裂构成山地与盆地的界线，并分布老断崖(图 6(b))。
3.2 发震构造分析
从图像上看，塔城MS5.2地震等震线长轴走向与断层走向近一致，震中位于塔克台断裂下盘，主断裂发震的可能性相对较小，收集塔城盆地近南北向地震剖面，如图 5所示，剖面显示塔城盆地及邻区发育除塔克台两条活动断裂外，盆地内还发育多条隐伏断层，这些断层均向北倾，在地表呈高角度逆断层性质，推测本次地震发震构造为塔克台断裂不断向盆地方向迁移、扩展形成的一条隐伏断裂(图 7)。由于本次地震震级较小，地震产生的能量不足以使地表发生破裂，所以目前发震断裂仍隐伏于地下，初步认为该地震发震构造仍为塔城盆地北缘塔克台断裂，但需在以后的工作中进一步寻找相关的地质地貌证据。
4. 讨论与建议
(1) 本次地震引起损失的主要原因包括：震区存在大量老旧、自建土木结构和砖木结构房屋，多未经正规设计，地基处理不规范，震前已产生不同程度的纵横墙间裂缝、门(窗)洞角斜裂缝，本次地震使房屋破坏更严重，部分房屋墙体外闪，已不具备居住条件；砖混结构房屋由于采取了一定抗震措施，主要震害为墙体斜裂缝、预制板顶连接处开裂、门(窗)洞角斜裂缝等；除个别近几年修建的办公楼和幼儿园框架结构房屋出现填充墙墙体斜裂缝、填充墙与主体结构裂缝外，其他框架结构房屋完好无损；安居富民房在本次地震中经受住了考验，抗震性能良好，未发生明显破坏。
(2) 根据本次地震现场野外调查工作，结合地震等震线分布情况，初步判定本次地震发震构造为塔克台断裂向盆地方向迁移形成的一条隐伏断裂。
(3) 通过现场调查发现，因常年未经历破坏性地震，震区群众防震减灾意识不强，政府部门应积极引导群众持续推进安居富民工程。同时，新建房屋须结合震区房屋震害特点，选址应避开不利地带，做好地基处理。
致谢: 本文房屋调查及地震地质灾害等相关资料由新疆塔域MS5.2地震现场工作队提供，特此感谢应急队全体工作人员的辛勤工作，同时感谢审稿专家对本文提出的建设性修改意见及建议。 -
图 1 同一台站不同PGA分档地震动记录HVSR、SBSR及SBSR/HVSR平均值
Figure 1. The average value of SBSR, HVSR and SBSR/HVSR for strong-motion records with different PGA ranges at the same station
图 4 a和b随T变化分布
Figure 4. Variation of statistical values of parameters a and b with period T
图 5 a和b模型拟合曲线
Figure 5. Regression curves of parameters a and b under different intensities of ground motion
表 1 选取台站及相关信息
Table 1. Selected stations and related information in this study
编号 台站代码 纬度N/° 经度E /° 钻井度/m VS,30/m·s−1 美国分类场地类别 日本分类场地类别 1 AKTH02 39.6634 140.5721 100 620.404 C SCⅠ 2 AKTH13 39.9819 140.4072 100 535.723 C SCⅠ 3 AOMH05 40.8564 141.1033 312 238.302 D SCⅢ 4 AOMH13 40.5794 141.4451 150 154.274 E SCⅣ 5 AOMH16 40.4624 141.0923 150 225.750 D SCⅣ 6 AOMH17 40.4624 141.3374 114 378.362 C SCⅡ 7 FKSH11 37.2006 140.3386 115 239.826 D SCⅢ 8 FKSH14 37.0264 140.9702 147 236.561 D SCⅣ 9 FKSH20 37.4911 140.9871 109 350.000 D SCⅣ 10 HDKH01 42.7031 142.2296 100 368.252 C SCⅡ 11 HDKH04 42.5126 142.0381 220 235.026 D SCⅣ 12 IBRH10 36.1112 139.9889 900 144.138 E SCⅣ 13 IBRH13 36.7955 140.5750 100 335.369 D SCⅡ 14 IBRH17 36.0864 140.3140 510 300.774 D SCⅣ 15 IBUH01 42.8739 141.8191 101 306.785 D SCⅣ 16 IWTH02 39.8250 141.3826 102 389.567 C SCⅡ 17 IWTH06 40.2611 141.1709 100 431.655 C SCⅡ 18 IWTH08 40.2686 141.7831 100 304.521 D SCⅢ 19 IWTH24 39.1979 141.0118 150 486.412 C SCⅣ 20 IWTH27 39.0307 141.532 100 670.313 C SCⅠ 21 KMMH01 33.1090 130.695 100 574.631 C SCⅠ 22 KSRH06 43.2200 144.4285 237 326.193 D SCⅣ 23 KSRH07 43.1359 144.3274 222 204.104 D SCⅣ 24 KSRH10 43.2084 145.1168 255 212.875 D SCⅣ 25 MYGH13 38.6990 141.4180 100 570.591 C SCⅠ 26 NIGH11 37.1728 138.7440 205 375.000 C SCⅣ 27 NMRH04 43.3978 145.1224 216 168.103 E SCⅣ 28 SMNH12 35.1634 132.8558 101 590.200 C SCⅠ 29 TCGH12 36.6959 139.9842 120 343.678 D SCⅣ 30 TKCH08 42.4865 143.1520 100 353.208 D SCⅣ 
下载: 导出CSV
表 2 不同峰值加速度分组的地震动记录数量
Table 2. The number of strong-motion records in different PGA groups
场地类型 台站代码 PGA/gal 10～20 20～100 100～200 200～300 >300 C AKTH02 74 54 2 0 0 AKTH13 122 79 9 0 0 AOMH17 299 106 9 4 0 HDKH01 127 60 3 0 4 IWTH02 876 667 42 11 14 IWTH06 181 85 6 0 0 IWTH24 185 112 10 3 2 IWTH27 1079 504 31 8 8 KMMH01 99 39 6 2 0 MYGH13 675 311 13 1 2 NIGH11 146 110 9 3 3 SMNH12 52 52 6 4 0 D AOMH05 417 207 15 3 0 AOMH16 428 171 9 2 0 FKSH11 622 285 12 2 3 FKSH14 635 283 18 2 2 FKSH20 393 238 21 0 2 HDKH04 119 56 4 1 2 IBRH13 1175 732 79 23 33 IBRH17 796 424 21 2 3 IBUH01 317 136 10 3 4 IWTH08 423 182 13 0 2 KSRH06 349 155 3 1 8 KSRH07 286 149 8 1 4 KSRH10 273 174 11 3 5 TCGH12 680 338 6 0 2 TKCH08 197 117 10 0 1 E AOMH13 213 86 7 0 0 IBRH10 522 248 16 2 0 NMRH04 328 150 8 0 2
下载: 导出CSV
表 3 a和b模型系数取值
Table 3. Coefficient values of relation of parameters a and b with period T
参数 PGA/gal 周期T/s 回归系数 p1 p2 p3 q1 q2 q3 R a <100 [0.04，0.27] −0.376 −0.762 −0.391 1 2.014 1.019 0.902 [0.27，0.86] −0.404 −0.318 −0.067 1 0.768 0.154 0.957 [0.86，20.00] 0.538 −1.404 −0.354 0 1.000 0.656 0.952 ≥100 [0.04，0.20] −0.348 −0.707 −0.365 1 2.066 1.077 0.958 [0.20，0.84] 0.813 0.361 −0.277 0 1.000 1.090 0.874 [0.84，20.00] 0.879 −1.510 −0.634 0 1.000 1.799 0.789 b <100 [0.04，0.10] −0.250 −0.118 −0.072 0 1.000 0.763 0.962 [0.10，20.00] 1.124 1.103 1.114 1 2.745 3.032 0.966 ≥100 [0.04，0.10] 0.309 1.307 0.964 0 1.000 0.951 0.985 [0.10，20.00] 0.670 −0.117 0.282 1 1.120 1.607 0.992
下载: 导出CSV
-
[1] 郭明珠, 赵芳, 赵凤仙, 2013. 场地地震动局部地形效应研究进展. 震灾防御技术, 8(3): 311-318. doi: 10.3969/j.issn.1673-5722.2013.03.010Guo M. Z., Zhao F., Zhao F. X., 2013. A review of the effect of small-scale surface topography on ground motions. Technology for Earthquake Disaster Prevention, 8(3): 311-388. (in Chinese) doi: 10.3969/j.issn.1673-5722.2013.03.010 [2] 黄雅虹, 吕悦军, 彭艳菊, 2009. 国内外不同抗震设计规范中场地分类方法的内在关系研究. 震灾防御技术, 4(1): 80-90. doi: 10.3969/j.issn.1673-5722.2009.01.008Huang Y. H., Lu Y. J., Peng Y. J., 2009. Study on the relations of site classification methods in seismic design standards between china and abroad. Technology for Earthquake Disaster Prevention, 4(1): 80-90. (in Chinese) doi: 10.3969/j.issn.1673-5722.2009.01.008 [3] 李小军, 1992. 场地土层对地震地面运动影响的分析方法. 世界地震工程, 8(2): 49-60. [4] 李小军, 彭青, 2001. 不同类别场地地震动参数的计算分析. 地震工程与工程振动, 21(1): 29-36. doi: 10.3969/j.issn.1000-1301.2001.01.005Li X. J., Pen Q., 2001. Calculation and analysis of earthquake ground motion parameters for different site categories. Earthquake Engineering and Engineering Vibration, 21(1): 29-36. (in Chinese) doi: 10.3969/j.issn.1000-1301.2001.01.005 [5] 李小军, 2013. 地震动参数区划图场地条件影响调整. 岩土工程学报, 35(S2): 21-29.LI X. J., 2013. Adjustment of seismic ground motion parameters considering site effects in seismic zonation map. Chinese Journal of Geotechnical Engineering, 35(S2): 21-29. (in Chinese) [6] 吕悦军, 彭艳菊, 兰景岩等, 2008. 场地条件对地震动参数影响的关键问题. 震灾防御技术, 3(2): l26-l35. doi: 10.3969/j.issn.1673-5722.2008.02.003Lu Y. J., Peng Y. J., Lan J. Y., et al., 2008. Some key problems about site effects on seismic ground motion parameters. Technology for Earthquake Disaster Prevention, 3(2): 126-135. (in Chinese) doi: 10.3969/j.issn.1673-5722.2008.02.003 [7] 荣棉水, 李小军, 王振明等, 2016. HVSR方法用于地震作用下场地效应分析的适用性研究. 地球物理学报, 59(8): 2878-2891. doi: 10.6038/cjg20160814Rong M. S., Li X. J., Wang Z. M., et al., 2016. Applicability of HVSR in analysis of site-effects caused by earthquakes. Chinese Journal of Geophysics, 59(8): 2878-2891. (in Chinese) doi: 10.6038/cjg20160814 [8] 中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局, 2010. GB 50011—2010 建筑抗震设计规范(2016年版). 北京: 中国建筑工业出版社.Ministry of Housing and Urban-Rural Development of the People’s Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, 2010. GB 50011—2010 Code for seismic design of buildings (2016 Edition). Beijing: China Architecture and Building Press. (in Chinese) [9] Baise L. G., 2000. Investigations in site response from ground motion observations in vertical arrays. Berkeley: University of California. [10] Borcherdt R. D., 1970. Effects of local geology on ground motion near San Francisco Bay. Bulletin of the Seismological Society of America, 60(1): 29-61. [11] Borcherdt R. D., Gibbs J. F., 1976. Effects of local geological conditions in the San Francisco Bay region on ground motions and the intensities of the 1906 earthquake. Bulletin of the Seismological Society of America, 66(2): 467-500. [12] Building Seismic Safety Council, 2004. 2003 Edition NEHPR recommended provisions for seismic regulations for new buildings and other structures (FEMA 450), Part 1(Provisions). Washington D C: Building Seismic Safety Council, National Institute of Building Sciences, 19-45. [13] Chen Q. F., Liu L. B., Wang W. J., et al., 2009. Site effects on earthquake ground motion based on microtremor measurements for metropolitan Beijing. Chinese Science Bulletin, 54(2): 280-287. [14] Fukushima Y., Bonilla L. F., Scotti O., et al., 2007. Site classification using horizontal-to-vertical response spectral ratios and its impact when deriving empirical ground-motion prediction equations. Journal of Earthquake Engineering, 11(5): 712-724. doi: 10.1080/13632460701457116 [15] Hwang H. H. M., Lin H. J., Huo J. R., 1997. Site coefficients for design of buildings in eastern United States. Soil Dynamics and Earthquake Engineering, 16(1): 29-40. doi: 10.1016/S0267-7261(96)00031-0 [16] Kawase H., Sánchez-Sesma F. J., Matsushima S., 2011. The optimal use of horizontal-to-vertical spectral ratios of earthquake motions for velocity inversions based on diffuse-field theory for plane waves. Bulletin of the Seismological Society of America, 101(5): 2001-2004. doi: 10.1785/0120100263 [17] Konno K., Ohmachi T., 1998. Ground-motion characteristics estimated from spectral ratio between horizontal and vertical components of microtremor. Bulletin of the Seismological Society of America, 88(1): 228-241. [18] Lee C. T., Cheng C. T., Liao C. W., et al., 2001. Site classification of Taiwan free-field strong-motion stations. Bulletin of the Seismological Society of America, 91(5): 1283-1297. [19] Lermo J., Chávez-García F. J., 1993. Site effect evaluation using spectral ratios with only one station. Bulletin of the Seismological Society of America, 83(5): 1574-1594. [20] Li X. J., Jing B. B., Liu C., et al., 2019. Site classification method based on geomorphological and geological characteristics and its application in China. Bulletin of the Seismological Society of America, 109(5): 1843-1854. doi: 10.1785/0120190058 [21] Liu H. X., 2002. The great Tangshan earthquake of 1976. California: Earthquake Engineering Research Laboratory, California Institute of Technology, 171-338. [22] Nagashima F., Matsushima S., Kawase H., et al., 2014. Application of horizontal‐to‐vertical spectral ratios of earthquake ground motions to identify subsurface structures at and around the K‐NET site in Tohoku, Japan. Bulletin of the Seismological Society of America, 104(5): 2288-2302. doi: 10.1785/0120130219 [23] Nakamura Y., 1989. A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface. Quarterly Report of the Railway Technical Research Institute, 30(1): 25-33. [24] Pitilakis K., Riga E., Anastasiadis A., 2013. New code site classification, amplification factors and normalized response spectra based on a worldwide ground-motion database. Bulletin of Earthquake Engineering, 11(4): 925-966. doi: 10.1007/s10518-013-9429-4 [25] Régnier J., Cadet H., Bonilla L. F., et al., 2013. Assessing nonlinear behavior of soils in seismic site response: statistical analysis on KiK-net strong-motion data. Bulletin of the Seismological Society of America, 103(3): 1750-1770. doi: 10.1785/0120120240 [26] Seed H. B., Ugas C., Lysmer J., 1976a. Site-dependent spectra for earthquake-resistant design. Bulletin of the Seismological Society of America, 66(1): 221-243. [27] Seed H. B., Murarka R., Lysmer J., et al., 1976b. Relationships of maximum acceleration, maximum velocity, distance from source, and local site conditions for moderately strong earthquakes. Bulletin of the Seismological Society of America, 66(4): 1323-1342. [28] Seed H. B., Romo M. P., Sun J. I., et al., 1988. The Mexico earthquake of September 19, 1985-relationships between soil conditions and earthquake ground motions. Earthquake Spectra, 4(4): 687-729. doi: 10.1193/1.1585498 [29] Wen K. L., Beresnev I. A., Yeh Y. T., 1994. Nonlinear soil amplification inferred from downhole strong seismic motion data. Geophysical Research Letters, 21(24): 2625-2628. doi: 10.1029/94GL02407 [30] Wen K. L., Beresnev I. A., Yeh Y. T., 1995. Investigation of non-linear site amplification at two downhole strong ground motion arrays in Taiwan. Earthquake Engineering & Structural Dynamics, 24(3): 313-324. [31] Wen R. Z., Ren Y. F., Zhou Z. H., et al., 2010. Preliminary site classification of free-field strong motion stations based on Wenchuan earthquake records. Earthquake Science, 23(1): 101-110. doi: 10.1007/s11589-009-0048-8 [32] Wood H. O., 1908. Distribution of apparent intensity in San Francisco. In: The California Earthquake of April 18, 1906, Report of the State Earthquake Investigation Commission. Washington DC: Carnegie Institution of Washington. [33] Yamazaki F., Ansary M. A., 1997. Horizontal-to-vertical spectrum ratio of earthquake ground motion for site characterization. Earthquake Engineering & Structural Dynamics, 26(7): 671-689. [34] Zhang X. L., Peng X. B., Li X. J., et al., 2020. Seismic effects of a small sedimentary basin in the eastern Tibetan plateau based on numerical simulation and ground motion records from aftershocks of the 2008 Mw7.9 Wenchuan, China earthquake. Journal of Asian Earth Sciences, 192: 104257. doi: 10.1016/j.jseaes.2020.104257 [35] Zhao J. X., Irikura K., Zhang J., et al., 2006. An empirical site-classification method for strong-motion stations in Japan using H/V response spectral ratio. Bulletin of the Seismological Society of America, 96(3): 914-925. doi: 10.1785/0120050124 -
下载:
点击查看大图
计量
- 文章访问数: 344
- HTML全文浏览量: 38
- PDF下载量: 58
- 被引次数: 0
