Study on Seismic Hazard Assessment Algorithm Considering Seismogenic Sources of Subduction Zones and Its Application on Chinese Marine Territory
-
摘要:
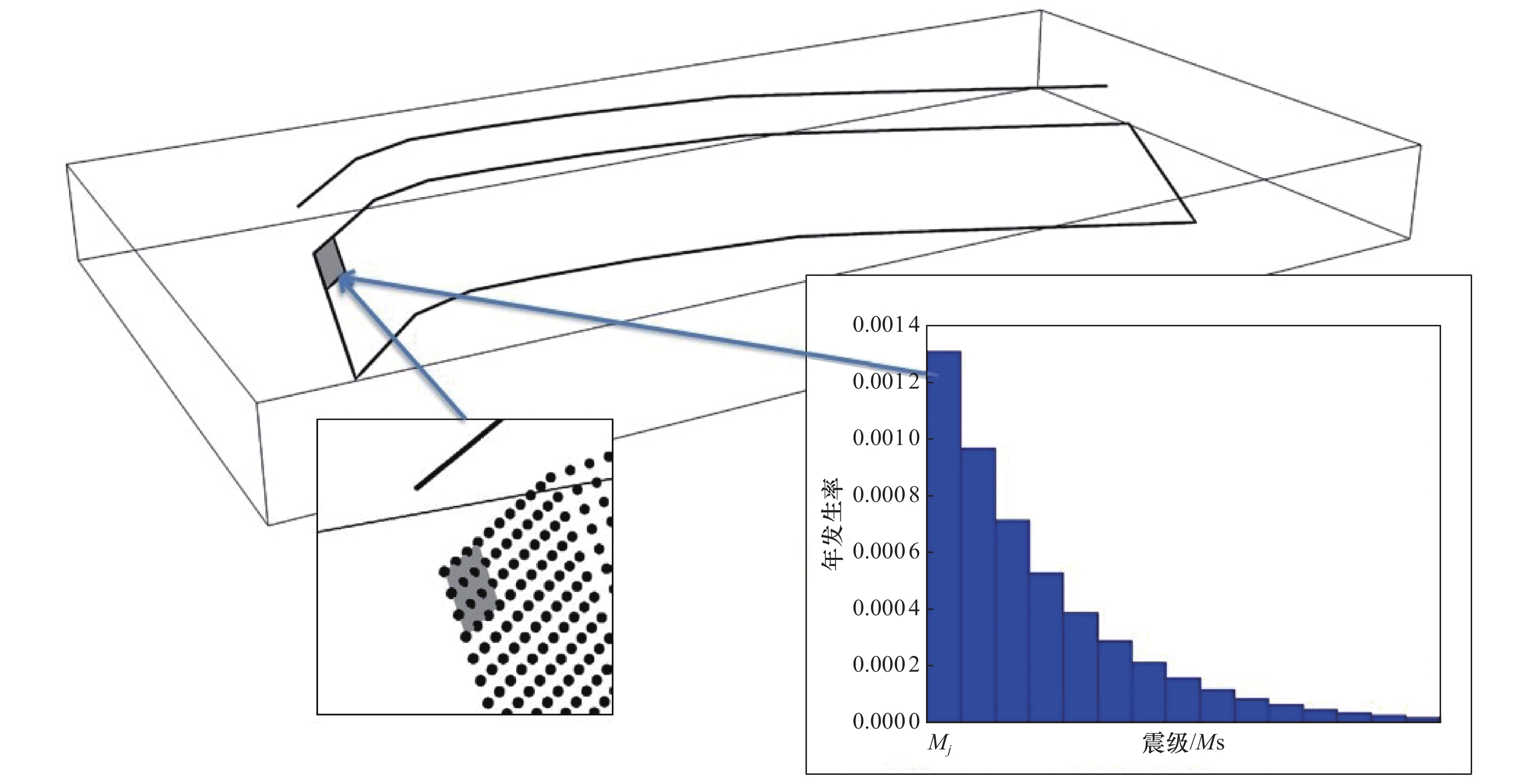
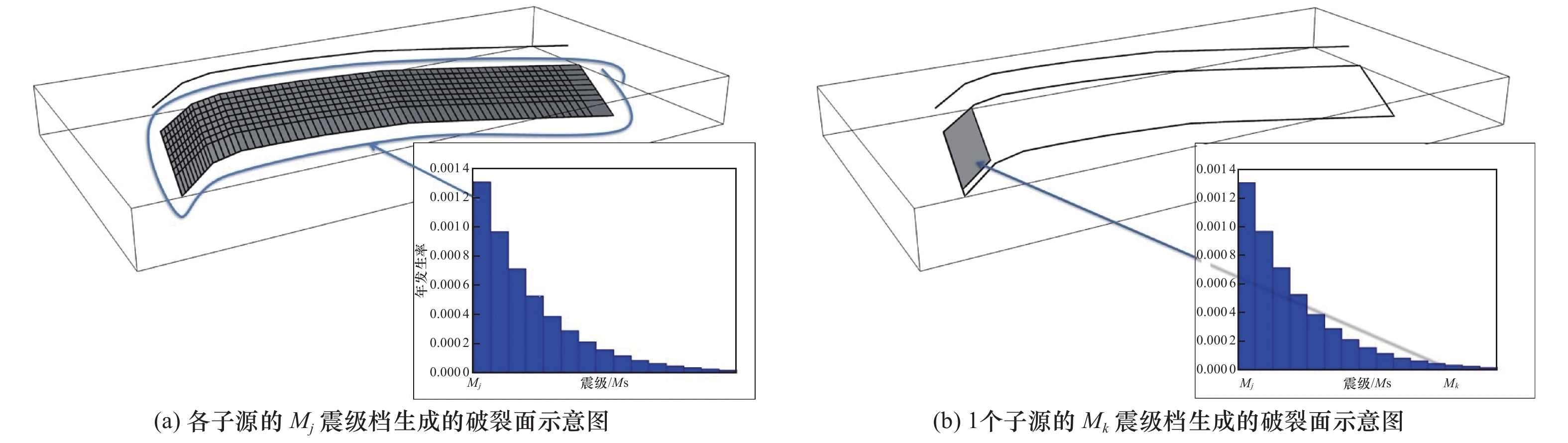
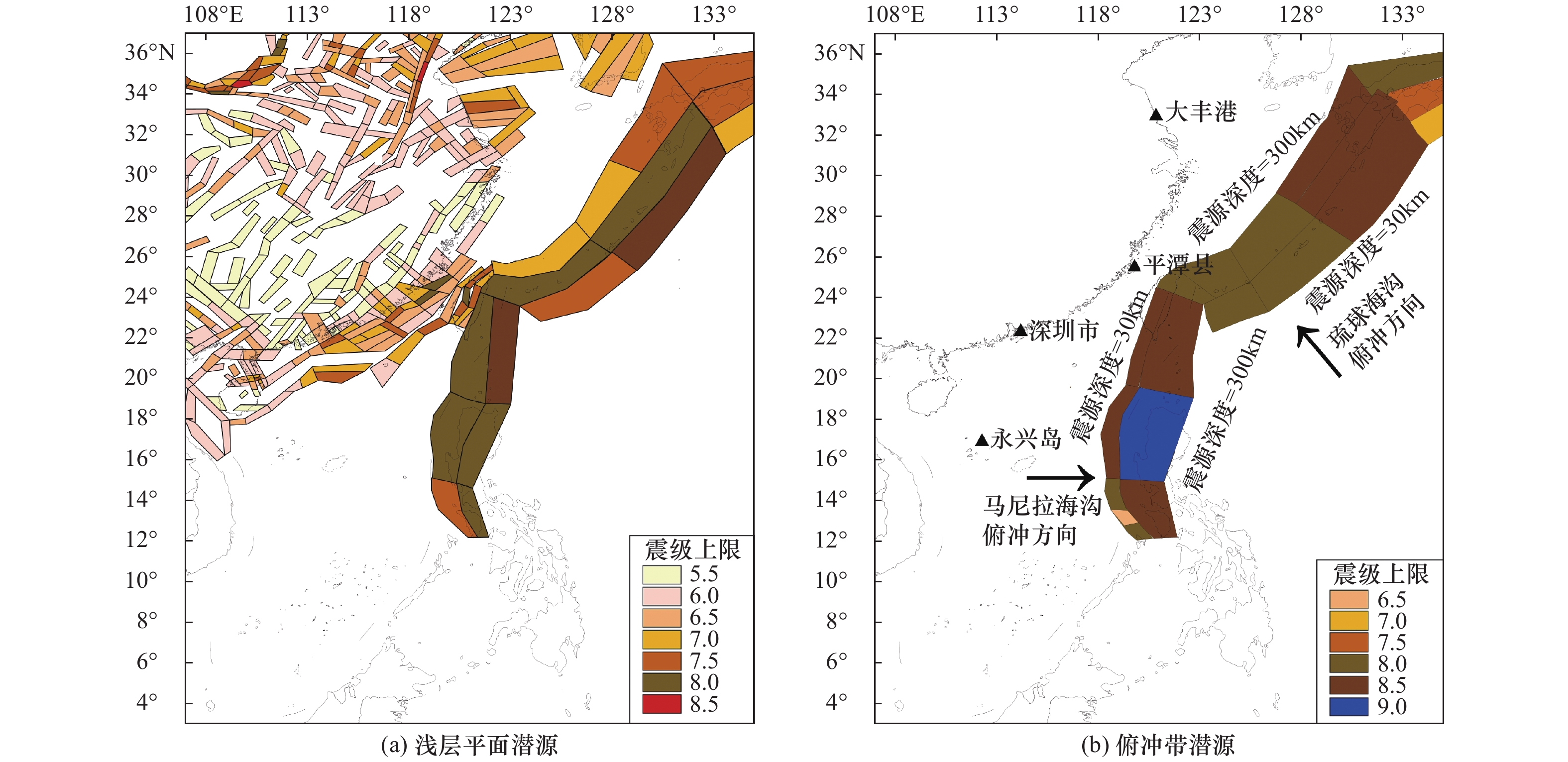
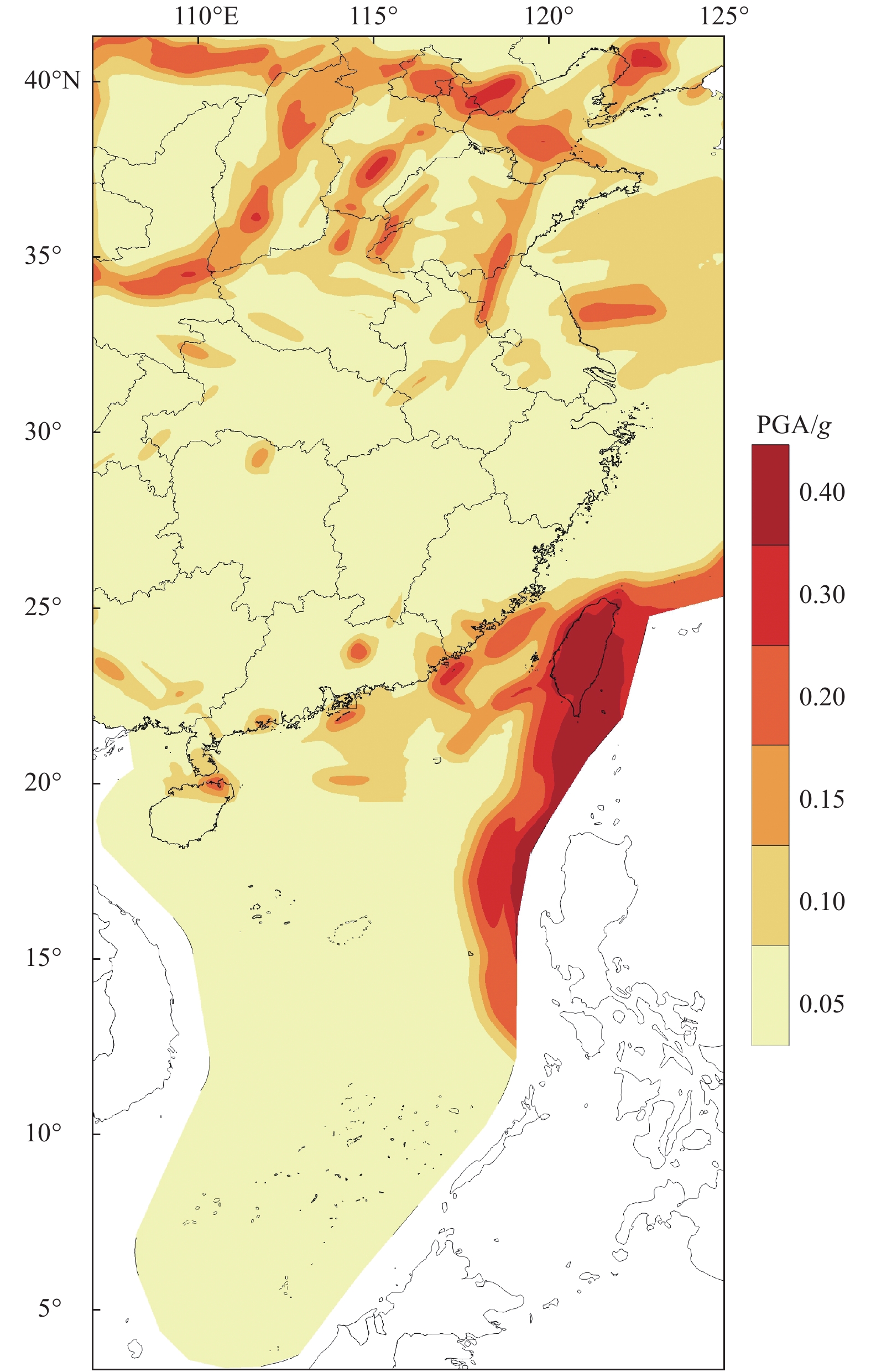
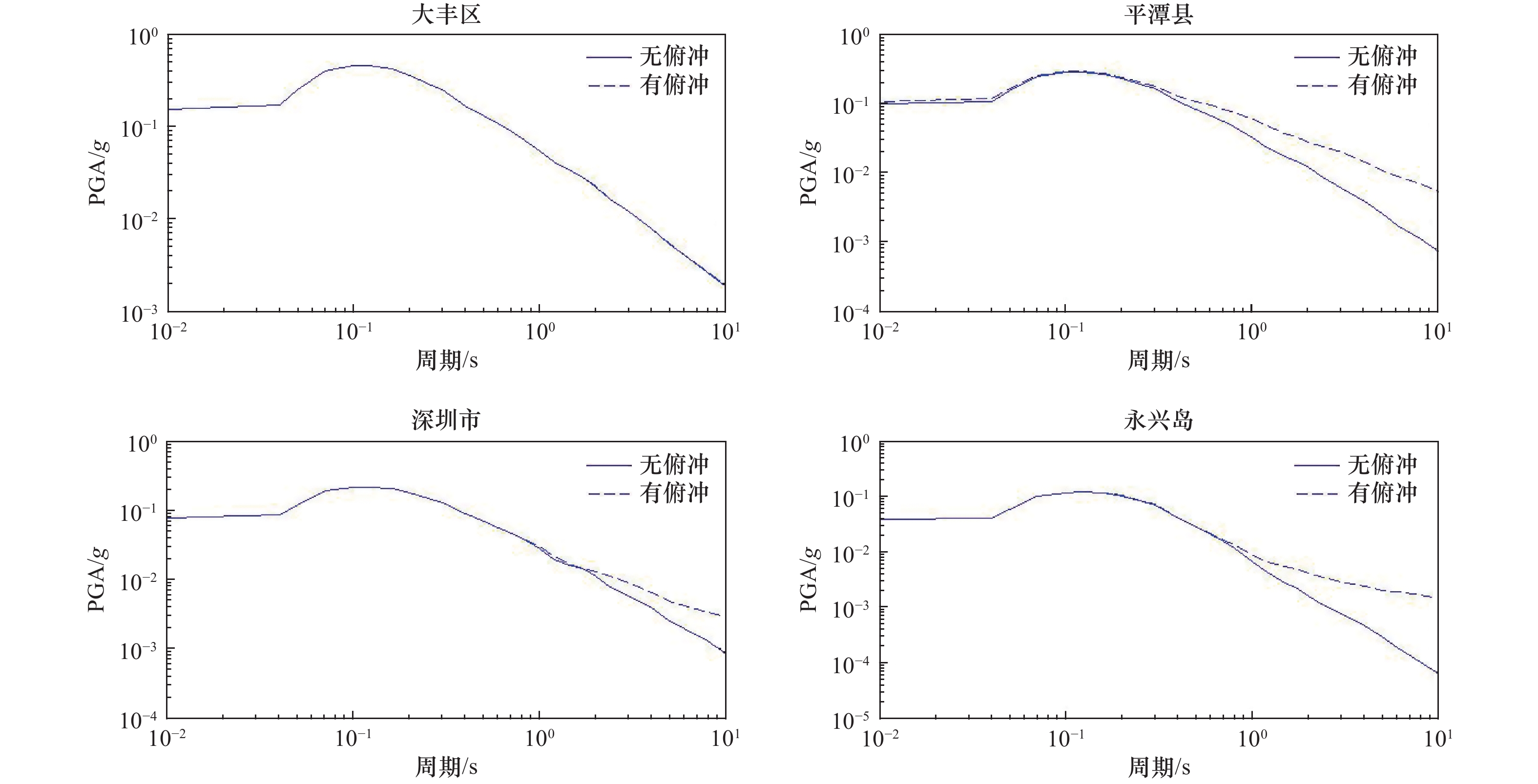
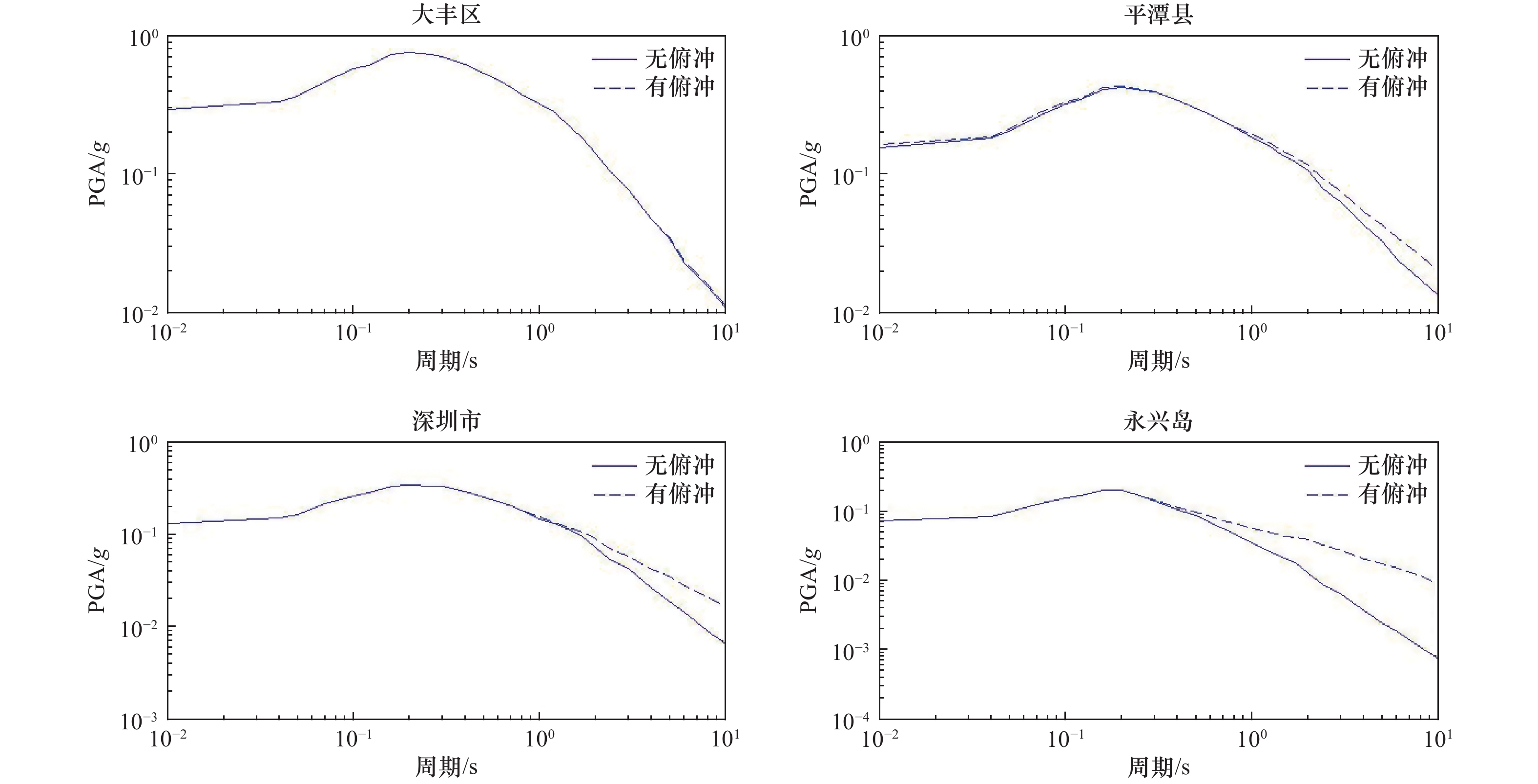
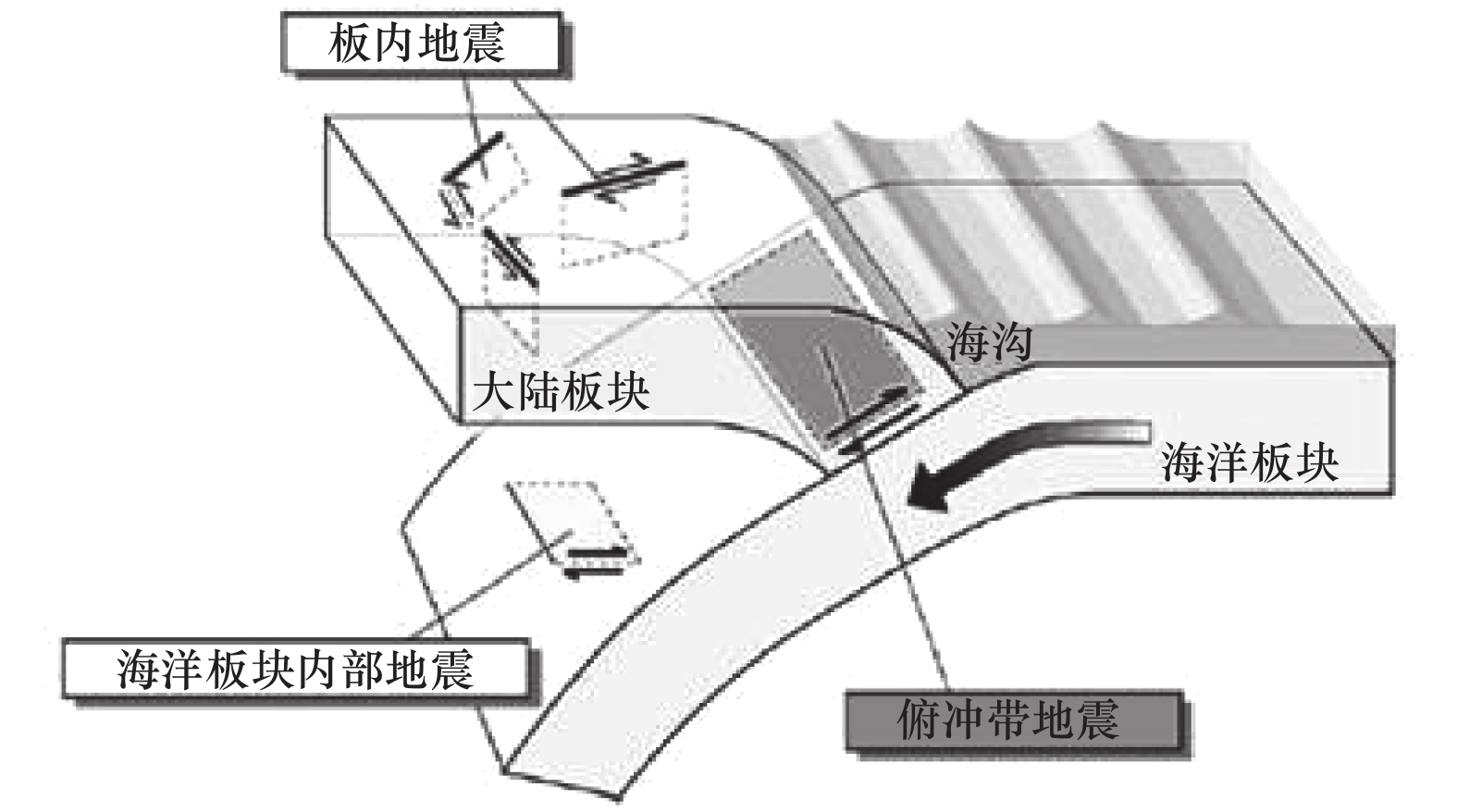
本文研究了俯冲带潜在震源区离散化方法及考虑俯冲带高震级地震震源破裂面和震源深度的场点地震动计算方法，推导了俯冲带潜在震源区地震危险性计算公式，并使用中国海域及邻区地震危险性模型进行地震危险性试算。结果表明，本文建立的考虑俯冲带潜在震源区的地震危险性算法能够实现场点地震危险性计算时对俯冲带高震级地震震源破裂面和震源深度的考虑。
Abstract:This paper studies the discretization method of the seismogenic sources of the subduction zone and the ground motion calculation method considering the source rupture surface and focal depth of the high-magnitude earthquakes in the subduction zone. The calculation formula for the seismic hazard of the seismogenic sources of the subduction zone is derived, and the preliminary seismic hazard calculation for Chinese marine territory is tested. The main conclusions are: the seismic hazard algorithm established in this paper considering the seismogenic sources of the subduction zone can realize the consideration of the source rupture surface and focal depth of the high-magnitude earthquake in the subduction zone in the seismic hazard calculation of the site.
-
Key words:
- Seismic hazard /
- Seismic hazard mapping /
- Marine earthquake /
- Subduction zone /
- 3D seismogenic sources
-
引言
1995年阪神地震中大开地铁车站的严重倒塌破坏在世界范围内引起了地震研究学者们对地下结构抗震问题的广泛关注。在地下结构地震反应特征和抗震设计方法等问题的研究过程中，逐渐形成了一系列实用抗震设计方法（刘晶波等，2010a；许成顺，2017）。其中，反应位移法与反应加速度法凭借理论明确、操作简便等优点，在实际工程设计中得到广泛应用，已被《城市轨道交通结构抗震设计规范》（GB 50909—2014）（中华人民共和国住房和城乡建设部，2014）和《地下结构抗震设计标准》（GB/T 51336—2018）（中华人民共和国住房和城乡建设部，2018）采纳。
反应加速度法通过将顶、底板相对位移最大时刻的自由场水平加速度施加于土-结模型上，计算地下结构变形与内力。与反应位移法相比，主要优势为：反应加速度法建立的土-结构模型可较准确地反映土-结构间相互作用，无须计算地基弹簧刚度系数，大大提高了计算效率与精度；反应位移法受限于地基弹簧与地震作用的施加方式，决定了其主要适用于矩形断面，而反应加速度法施加的地震作用为体积力，且模型采用土-结构整体模型，决定了其可适用于复杂断面地下结构的地震反应计算。总的来说，反应加速度法优于反应位移法（刘晶波等，2013；李新星等，2014）。
反应加速度法的应用关键在于地震输入荷载的确定。为简化计算过程，反应加速度法假设输入荷载为地震作用下自由场的反应加速度，然而，该假设忽略了结构的存在对自由场反应加速度的影响。基于此，刘如山等（2007）从一维自由土层反应的剪应力入手，首先对一维自由土层反应剪应力沿竖直方向进行微分，然后将其作为水平体荷载离散到有限元节点上，以此作为加载方法；董正方等（2014）运用柔度系数法中的结构变形和自由场变形之间的相互作用系数，修正了自由场地震反应加速度，近似考虑了结构的存在对反应加速度法的影响；Liu等（2018）通过理论解析方式推导了自由场模型与土-结模型之间场地反应加速度的关系，结果表明可通过2种模型场地相对位移修正场地反应加速度法；徐琨鹏等（2019）对比了反应加速度法和仅在土体施加加速度的简化方法，发现2种方法对侧边距取值不敏感；禹海涛等（2020）通过动力时程分析，提出地下结构附近存在动力响应增强区和衰减区，利用动力响应调整系数提高了反应加速度法的计算精度。
为考虑结构的存在对反应加速度法中地震输入荷载的影响，本文提出将土-结构模型转换为自由场模型的等效方式，采用等效后的土层参数进行自由场反应加速度计算，以此近似地反映结构的存在对地震输入荷载的影响，进而改进反应加速度法中地震输入荷载的计算过程。采用有限元软件ABAQUS对大开车站地震反应进行数值模拟分析，验证等效方式的有效性，并探讨等效模型宽度取值范围对结果的影响，初步给出等效模型宽度范围。
1. 反应加速度法
采用改进前反应加速度法对地下结构横断面进行抗震分析时，计算模型为图1所示的土-结构整体模型。一般地，土体采用二维平面应变单元模拟，结构采用梁单元模拟。将模型底边固定，模型两侧设置水平滑移边界。通过将地下结构顶、底板位置处土层相对位移最大时刻的各土层水平加速度或有效惯性加速度施加于土-结构整体模型上，获得地下结构变形与内力等反应。
反应加速度法主要计算步骤如下：
（1）一维土层地震反应分析。采用等效线性化程序EERA或SHAKE91对一维土层进行地震反应分析，记录结构顶、底板位置处土层最大相对位移时刻，各土层加速度及等效剪切模量Gi。《城市轨道交通结构抗震设计规范》建议，土层简单时地震输入荷载直接采用自由场水平加速度，土层复杂时地震输入荷载采用土层有效惯性加速度。
（2）建立土-结构模型。《城市轨道交通结构抗震设计规范》建议模型底面可取设计地震作用基准面，顶面取地表面，侧面边界到结构的距离宜取结构水平有效宽度的2～3倍，本文针对模型宽度对计算结果的影响展开进一步讨论。
（3）施加等效地震作用。将土层水平加速度或有效惯性加速度按各土层单元的位置施加于土-结构模型中的各土层上，结构部分按所在土层深度位置作用相应的加速度。
从反应加速度法计算模型和计算步骤可看出，该方法地震输入荷载采用的是自由场反应加速度，未考虑结构的存在对自由场加速度反应的影响，尤其是当地下结构刚度和周围土体刚度相差较大时，结构的存在可能会在较大程度上影响周围土体的地震反应。此外，在动力学理论方面，该方法忽略了阻尼因素的影响，仅是某种程度的近似，当土层反应仅有一阶振型发育时，该方法精度尚可，当遇到复杂土层时误差将增大。
2. 改进反应加速度法研究
2.1 等效思路
为考虑结构的存在对反应加速度法中地震输入荷载的影响，对反应加速度法中的加速度求解方法进行改进。首先，按结构周围土体的分层将土-结构模型中的结构与土体等效为自由场，计算等效自由场的土层参数；然后，采用等效线性化程序EERA将等效自由场土层参数进行处理，得到土层等效剪切模量，并计算等效自由场各土层反应加速度，如图2所示。
将图2所示土-结构模型等效为自由场模型时需进行结构等效和土层等效，其中Ki为等效后土体的刚度；K1i为结构的刚度；K2i为等效前土体的刚度。对于地下结构横断面，其顶、底板在断面水平方向上连续，侧墙、中柱在断面水平方向上间断，而土层为分层结构，在断面水平方向上连续。为便于土体与结构进行等效，将断面水平方向上间断的侧墙与中柱等效为连续结构，形成图3（a）所示的分层结构形式。在此基础上，按结构周围土层的划分，将分层结构与分层土体按照相对位置等效为分层的自由场，如图3（b）所示。
上述2个等效过程均包含等质量等效计算和等侧向刚度等效计算。自由场在地震作用下的反应加速度主要受场地质量分布与刚度分布的影响，等质量等效计算假设等效前后土-结构模型与自由场模型中各土层质量保持不变：
$$ {\rho _i}{V_i} = {\rho _{1i}}{V_{1i}} + {\rho _{2i}}{V_{2i}} $$ (1) 式中，
${\rho _i}$ 为等效后第i层土体密度；${V_i}$ 为采用土-结构模型总宽度计算的第i层土体体积；${\rho _{1i}}$ 为第i层土体对应的结构部分的密度；${V_{1i}}$ 为第i层土体中包含的结构体积；${\rho _{2i}}$ 为第i层土体密度；${V_{2i}}$ 为减去结构体积的第i层土体体积。等侧向刚度等效计算中，假设等效前后各土层侧向刚度保持不变，各土层与结构为短柱，进行侧向刚度的串并联叠加：
$$ {G_i}{b_i} = {G_{1i}}{b_{1i}} + {G_{2i}}{b_{2i}} $$ (2) 式中，
${G_i}$ 为等效后第i层土体剪切模量；${b_i}$ 为采用土-结构模型总宽度；${G_{1i}}$ 为结构剪切模量；${b_{1i}}$ 为第i层土体中结构的宽度；${G_{2i}}$ 为第i层土体剪切模量；${b_{2i}}$ 为减去结构宽度的第i层土体宽度。2.2 等效模型宽度的选取
为便于区分，将改进前反应加速度法称为反应加速度法-1（以下简称“RAM-1”），将改进后反应加速度法称为反应加速度法-2（以下简称“RAM-2”）。
采用图4所示土-结构模型边界至结构侧边的距离B表示模型宽度。在RAM-2计算过程中，反应加速度法拟静力计算时涉及土-结构模型宽度（以下简称“模型宽度-F”）、等效土-结构模型宽度（以下简称“模型宽度-B”）的选取。由前文可知，模型宽度-B不同，将直接改变等效自由场土层参数，影响等效自由场场地反应，从而影响反应加速度法计算结果。因此，本文针对不同模型宽度-B对反应加速度法计算结果的影响进行了探讨。
3. 实例分析
3.1 计算模型与参数选取
为验证等效方式的有效性，以大开车站为研究对象，进行了RAM-1、RAM-2与动力时程方法计算。结构断面尺寸如图5所示，结构埋深4.8 m，周围土层参数如表1所示（矢的照夫等，1996）。结构中柱沿车站纵向按3.5 m等间距分布，将其按一定原则等效为连续墙体，等效后中柱弹性模量为8.57 GPa，密度为714 kg/m3。顶、底板与侧墙弹性模量为30 GPa，密度为2 500 kg/m3。土-结构整体分析模型如图6所示，车站结构采用梁单元模拟，土体采用平面应变单元模拟。土体底边界固定，两侧边界设置水平滚轴边界。假设土体与结构之间接触良好，且不产生相对滑移，数值计算时土体与结构之间采用绑定约束。
表 1 土层参数表Table 1. Physical properties of soils分层 土质 厚度/m 密度/(t·m−3) 剪切波速/(m·s−1) 泊松比 1 填土 1 1.9 140 0.333 2 砂土 4.1 1.9 140 0.488 3 砂土 3.2 1.9 170 0.493 4 黏土 3.1 1.9 190 0.494 5 黏土 5.8 1.9 240 0.490 6 砂土 22 2.0 330 0.487 由于缺少大开车站周围土体动力参数，本文采用典型砂土和黏土剪切模量比、阻尼比与剪应变关系曲线（杜修力等，2018），如图7所示。考虑到地震动特性对地下结构地震反应的影响，基岩输入地震动选用Kobe地震动与El Centro地震动，地震动加速度时程曲线如图8所示，将加速度幅值调整为0.1、0.2、0.3 g。
验证等效思路有效性时，RAM-1与RAM-2模型宽度-F均取3倍结构宽度，RAM-2模型宽度-B取3倍结构宽度。动力时程分析共6种计算工况，反应加速度法共12种计算工况（包括RAM-1、RAM-2各6种计算工况）。
在探讨不同模型宽度-B对RAM-2计算结果的影响时，RAM-1与RAM-2模型宽度-F仍取为3倍结构宽度，RAM-2模型宽度-B分别取为1、2、3、4、5、7倍结构宽度。在0.1 g幅值的Kobe地震动作用下进行动力时程计算、RAM-1计算与不同模型宽度-B的RAM-2计算。
3.2 结果与分析
刘晶波等（2010b）和杜修力等（2017）指出地下结构中柱为抗震关键构件，在此基础上，计算不同地震作用下中柱与顶、底板位置处的相对位移、中柱底部弯矩、中柱底部剪力和侧墙底部弯矩，结果如表2所示，表中括号内为相应的误差。
表 2 不同地震作用下结构内力与变形Table 2. Internal force and deformation of structure under different earthquake load地震动 幅值 计算方法 顶、底板相对位移/mm 中柱底部弯矩/
[(kN·m)·m−1]中柱底部剪力/
(kN·m−1)侧墙底部弯矩/
[(kN·m)·m−1]Kobe 0.1 g 动力时程分析法 5.77 36.12 11.09 358.40 RAM-1 5.56(3.66%) 34.06(5.70%) 10.48(5.50%) 341.50(4.72%) RAM-2 5.71(1.04%) 35.00(3.10%) 10.78(2.80%) 351.20(2.01%) 0.2 g 动力时程分析法 16.93 102.70 30.88 887.30 RAM-1 16.17(4.47%) 99.31(3.30%) 30.80(0.26%) 879.50(0.88%) RAM-2 16.44(2.86%) 102.00(0.68%) 30.51(1.20%) 877.00(1.16%) 0.3 g 动力时程分析法 31.15 187.50 55.97 1476.00 RAM-1 30.30(2.76%) 181.70(3.09%) 54.43(2.75%) 1447.00(1.96%) RAM-2 30.94(0.67%) 185.50(1.07%) 55.44(0.95%) 1474.00(0.14%) EL Centro 0.1 g 动力时程分析法 14.12 86.02 26.09 771.40 RAM-1 13.41(5.02%) 81.68(5.05%) 25.04(4.02%) 741.00(3.94%) RAM-2 13.61(3.62%) 83.07(3.43%) 25.59(1.92%) 755.90(2.01%) 0.2 g 动力时程分析法 26.73 160.40 47.59 1288.00 RAM-1 25.36(5.15%) 151.70(5.42%) 45.47(4.45%) 1241.00(3.65%) RAM-2 26.12(2.30%) 156.30(2.56%) 46.82(1.62%) 1278.00(0.78%) 0.3 g 动力时程分析法 38.75 231.60 68.07 1755.00 RAM-1 35.48(8.44%) 210.60(9.07%) 62.24(8.56%) 1628.00(7.24%) RAM-2 37.51(3.22%) 222.10(4.10%) 65.35(4.00%) 1704.00(2.91%) 由表2可知，以动力时程为基准，不同工况下RAM-1计算的结构变形与内力最大误差为9%，不同工况下RAM-2计算的结构变形与内力最大误差为4.1%，等效方式将反应加速度法的计算误差由10%以内缩小至5%以内，提高了反应加速度法计算精度，表明了等效方式的有效性；RAM-2在不同幅值Kobe地震动作用下计算的结构变形与内力最大误差为3.1%，在不同幅值El Centro地震动作用下计算的结构变形与内力最大误差为4.1%，最大误差随地震动强度的改变未明显变化，说明该方法的计算结果较稳定。
以动力时程为基准计算的结构变形与内力、不同模型宽度-B 下 RAM-2 计算的结构变形与内力如表3所示，表中括号内为相应的误差。由表3、图9可知，与动力时程分析法相比，随着模型宽度-B的减小，RAM-2计算结果逐渐增加，逐渐接近动力时程计算结果，甚至大于动力时程计算结果；而RAM-1最大计算误差为5.7%，模型宽度-B为7、5、4、3倍结构宽度时，RAM-2最大计算误差分别为6.15%、4.51%、4.1%、3.1%，表明当模型宽度取值较大时，改进反应加速度法计算误差呈增大趋势，这是由于模型宽度越大，等效后的自由场模型更接近原始自由场模型，此时等效模型无法充分反映结构的存在造成的影响。结合表2所示不同工况下RAM-1计算的结构变形与内力最大误差为9%，不同工况下模型宽度-B为3倍结构宽度时，RAM-2最大计算误差为4.1%，若以计算误差减小50%为衡量标准，建议模型宽度-B取为1～3倍结构宽度。
表 3 不同模型宽度-B下结构内力与变形Table 3. Internal force and deformation of structure with different model width计算方法 模型宽度-B/
结构宽度顶、底板相对
位移/mm中柱底部弯矩/
[(kN·m)·m−1]中柱底部剪力/
(kN·m−1)侧墙底部弯矩/
[(kN·m)·m−1]动力时程分析法 — 5.77 36.12 11.09 358.40 RAM-1 — 5.56(3.66%) 34.06(5.70%) 10.48(5.50%) 341.50(4.72%) RAM-2 1 5.98(3.67%) 36.67(1.52%) 11.31(1.98%) 368.80(2.90%) 2 5.78(0.16%) 35.42(1.94%) 10.92(1.53%) 355.50(0.81%) 3 5.71(1.04%) 35.00(3.10%) 10.78(2.80%) 351.20(2.01%) 4 5.65(2.05%) 34.64(4.10%) 10.68(3.70%) 347.70(2.99%) 5 5.63(2.49%) 34.49(4.51%) 10.64(4.06%) 346.20(3.40%) 7 5.53(4.16%) 33.90(6.15%) 10.46(5.68%) 340.20(5.08%) 4. 结论
本文采用有限元分析软件ABAQUS对大开车站进行不同工况下的动力时程分析和改进前后反应加速度法分析，验证了等效方式对反应加速度法的有效性。在验证等效思路有效的基础上，进行了不同等效模型宽度的改进反应加速度法计算，初步给出了等效模型宽度的选取范围。
（1）在未改变RAM-1理论基础的前提下，对关键参数——地震输入荷载进行了修正。与动力时程分析法相比，修正后的反应加速度法使不同工况下的最大计算误差由10%以内缩小至5%以内，提高了反应加速度法计算精度。
（2）与动力时程分析结果相比，修正后的反应加速度法在不同工况下的最大计算误差未明显改变，说明修正结果具有稳定性。
（3）对不同等效模型宽度对反应加速度法计算结果的影响进行分析，根据结果建议等效模型边界至结构侧边的距离取为1～3倍结构宽度。
-
图 3 俯冲带潜源1个子源的Mj级地震产生的破裂面空间范围示意图
Figure 3. Spatial range of a rupture surface by a magnitude Mj earthquake on a subduction zone
图 4 各子源生成破裂面原理示意图
Figure 4. Theory of rupture surfaces generating for each sub-sources of a source
图 5 中国海域及邻区潜在震源区划分图
Figure 5. Seismogenic sources in Chinese oceanic area and surrounding areas
图 6 中国海域及邻区50年超越概率10%的PGA分布图
Figure 6. Map of PGA with 10% probability of exceedance in 50 years for Chinese oceanic area and surrounding areas
图 7 4个场点考虑和不考虑俯冲带潜在震源区的50年超越概率10%的地震动反应谱
Figure 7. Earthquake response spectrum with 10% probability of exceedance in 50 years considering and without subduction sources for the 4 sites
-
邓起东, 张裕明, 环文林等, 1980. 中国地震烈度区划图编制的原则和方法. 地震学报, 2(1): 90—110.Deng Q. D., Zhang Y. M., Huan W. L., et al., 1980. Principles and methods of composing the seismic zoning map of China. Acta Seismologica Sinica, 2(1): 90—110. (in Chinese) 地震调查研究推进本部地震委员会, 2018. 全国地震动预测地图2018年版. 东京: 地震调查研究推进本部事务局. 高孟潭, 2003. 新的国家地震区划图. 地震学报, 25(6): 630—636. doi: 10.3321/j.issn:0253-3782.2003.06.009Gao M. T., 2003. New national seismic zoning map of China. Acta Seismologica Sinica, 25(6): 630—636. (in Chinese) doi: 10.3321/j.issn:0253-3782.2003.06.009 李善邦, 1957. 中国地震区域划分圖及其說明Ⅰ. 总的說明. 地球物理学报, 6(2): 127—158.Li S. B., 1957. The map of seismicity of China. Chinese Journal of Geophysics, 6(2): 127—158. (in Chinese) 李小军, 胡进军, 陈苏等, 2020. 海域地震动传播规律及场地影响模型研究报告, 16—28. 北京: 中国地震局地球物理研究所. 吕悦军, 冉洪流, 徐伟进等, 2020. 海域地震活动性模型及其评价方法研究报告, 23—31. 北京: 应急管理部国家自然灾害防治研究院. 潘华, 高孟潭, 谢富仁, 2013. 新版地震区划图地震活动性模型与参数确定. 震灾防御技术, 8(1): 11—23. doi: 10.3969/j.issn.1673-5722.2013.01.002Pan H., Gao M. T., Xie F. R., 2013. The earthquake activity model and seismicity parameters in the new seismic hazard map of China. Technology for Earthquake Disaster Prevention, 8(1): 11—23. (in Chinese) doi: 10.3969/j.issn.1673-5722.2013.01.002 任治坤, 高战武, 李正芳等, 2020. 海域活动构造框架和地震构造模型研究报告, 18-24. 北京: 中国地震局地质研究所. 陶夏新, 1992. 我国新的地震区划编图和中国地震烈度区划图(1990). 自然灾害学报, 1(1): 99—109.Tao X. X., 1992. On the new national seismic zonation and the seismic intensity zoning map of China (1990). Journal of Natural Disasters, 1(1): 99—109. (in Chinese) 肖亮, 2019. 海域地震动预测方程模型研究报告, 8-12. 北京: 中国地震局地球物理研究所. 肖亮, 2020. 海域地震动传播规律及场地影响模型研究报告, 1—13. 北京: 中国地震局地球物理研究所. 俞言祥, 李山有, 肖亮, 2013. 为新区划图编制所建立的地震动衰减关系. 震灾防御技术, 8(1): 24—33. doi: 10.3969/j.issn.1673-5722.2013.01.003Yu Y. X., Li S. Y., Xiao L., 2013. Development of ground motion attenuation relations for the new seismic hazard map of China. Technology for Earthquake Disaster Prevention, 8(1): 24—33. (in Chinese) doi: 10.3969/j.issn.1673-5722.2013.01.003 中国地震烈度区划图编委会, 1992. 中国地震烈度区划图(1990)及其说明. 中国地震, 8(4): 1—11.The Compiling Committee of Seismic Zoning Map in China, 1992. Seismic intensity zoning map of China (1990) and its explanations. Earthquake Research in China, 8(4): 1—11. (in Chinese) 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会, 2016. GB 18306—2015 中国地震动参数区划图. 北京: 中国标准出版社.General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration, 2016. GB 18306-2015 Seismic ground motion parameters zonation map of China. Beijing: Standards Press of China. (in Chinese) 周本刚, 陈国星, 高战武, 等, 2013. 新地震区划图潜在震源区划分的主要技术特色. 震灾防御技术, 8(2): 113—124. doi: 10.3969/j.issn.1673-5722.2013.02.001Zhou B. G., Chen G. X., Gao Z. W., et al., 2013. The technical highlights in identifying the potential seismic sources for the update of national seismic zoning map of China. Technology for Earthquake Disaster Prevention, 8(2): 113—124. (in Chinese) doi: 10.3969/j.issn.1673-5722.2013.02.001 Cheng J., Rong Y. F., Magistrale H., et al., 2017. An mw-based historical earthquake catalog for mainland China. Bulletin of the Seismological Society of America, 107(5): 2490—2500. doi: 10.1785/0120170102 Cornell C. A., 1968. Engineering seismic risk analysis. Bulletin of the Seismological Society of America, 58(5): 1583—1606. Danciu L., Şeşetyan K., Demircioglu M., et al., 2018. The 2014 earthquake model of the middle east: seismogenic sources. Bulletin of Earthquake Engineering, 16(8): 3465—3496. doi: 10.1007/s10518-017-0096-8 Giardini D., Wössner J., Danciu L., 2014. Mapping Europe’s seismic hazard. EOS, Transactions, American Geophysical Union, 95(29): 261—262. Gutenberg B., Richter C. F., 1944. Frequency of earthquakes in California. Bulletin of the Seismological Society of America, 34(4): 185—188. McGuire R. K., 1995. Probabilistic seismic hazard analysis and design earthquakes: closing the loop. Bulletin of the Seismological Society of America, 85(5): 1275—1284. Petersen M. D., Moschetti M. P., Powers P. M., et al., 2015. The 2014 United States national seismic hazard model. Earthquake Spectra, 31(1S): S1—S30. Wells D. L., Coppersmith K. J., 1994. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bulletin of the Seismological Society of America, 84(4): 974—1002. Woessner J., Laurentiu D., Giardini D., et al., 2015. The 2013 European seismic hazard model: key components and results. Bulletin of Earthquake Engineering, 13(12): 3553—3596. doi: 10.1007/s10518-015-9795-1 期刊类型引用(0)
其他类型引用(1)
-
下载:
下载:
点击查看大图
计量
- 文章访问数: 94
- HTML全文浏览量: 40
- PDF下载量: 8
- 被引次数: 1
