Characteristics and Activity of the Northern Segment of the Littoral Fault Zone at Northern Jiansu Region
-
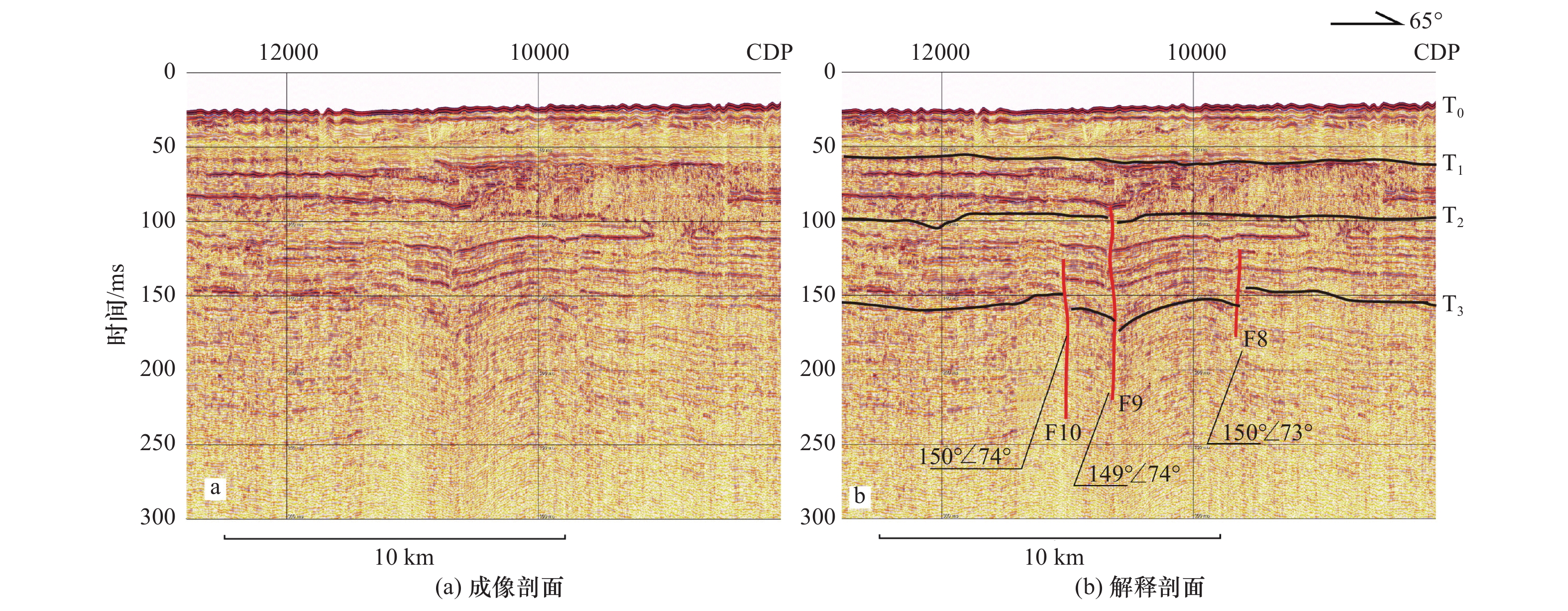
摘要:
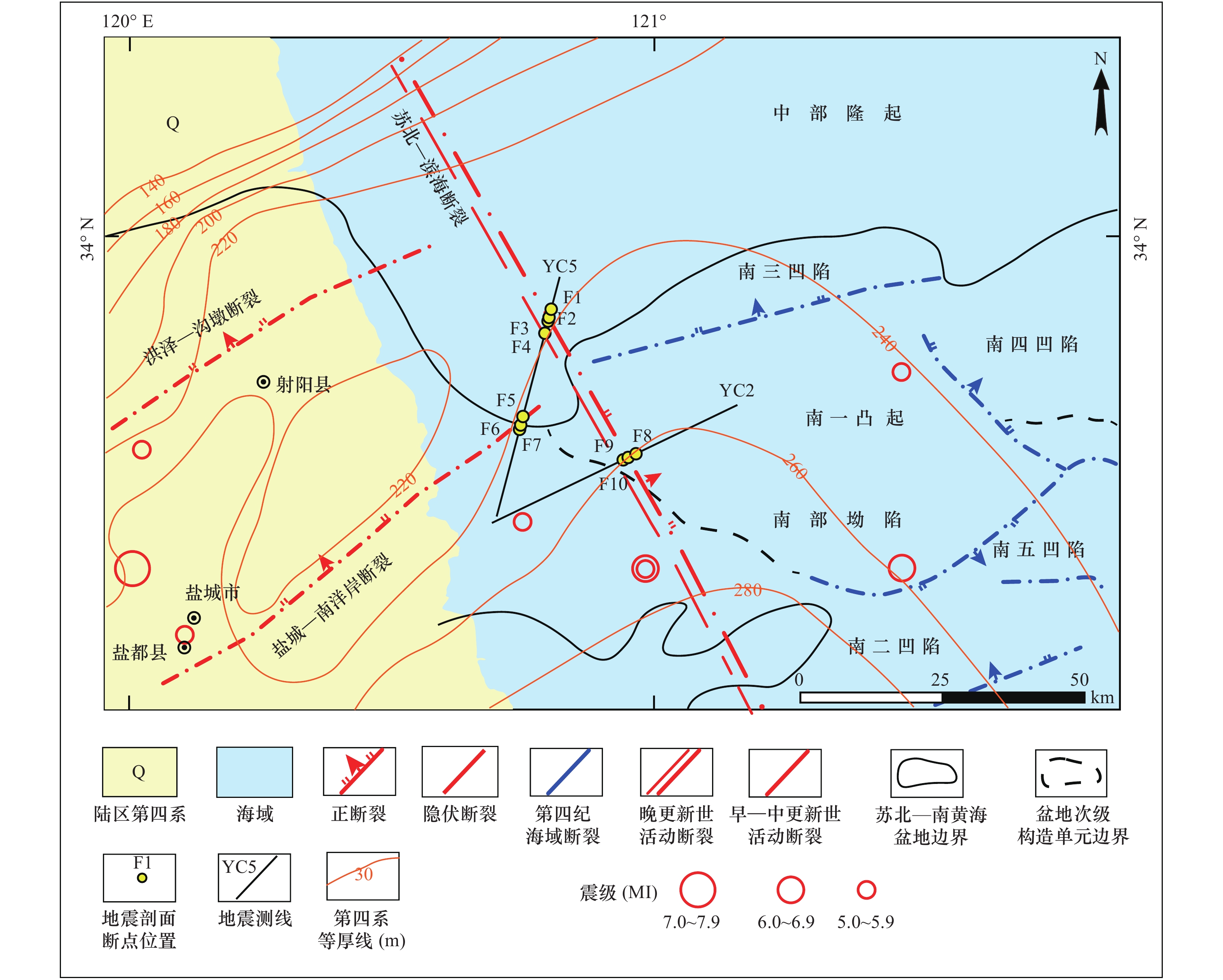
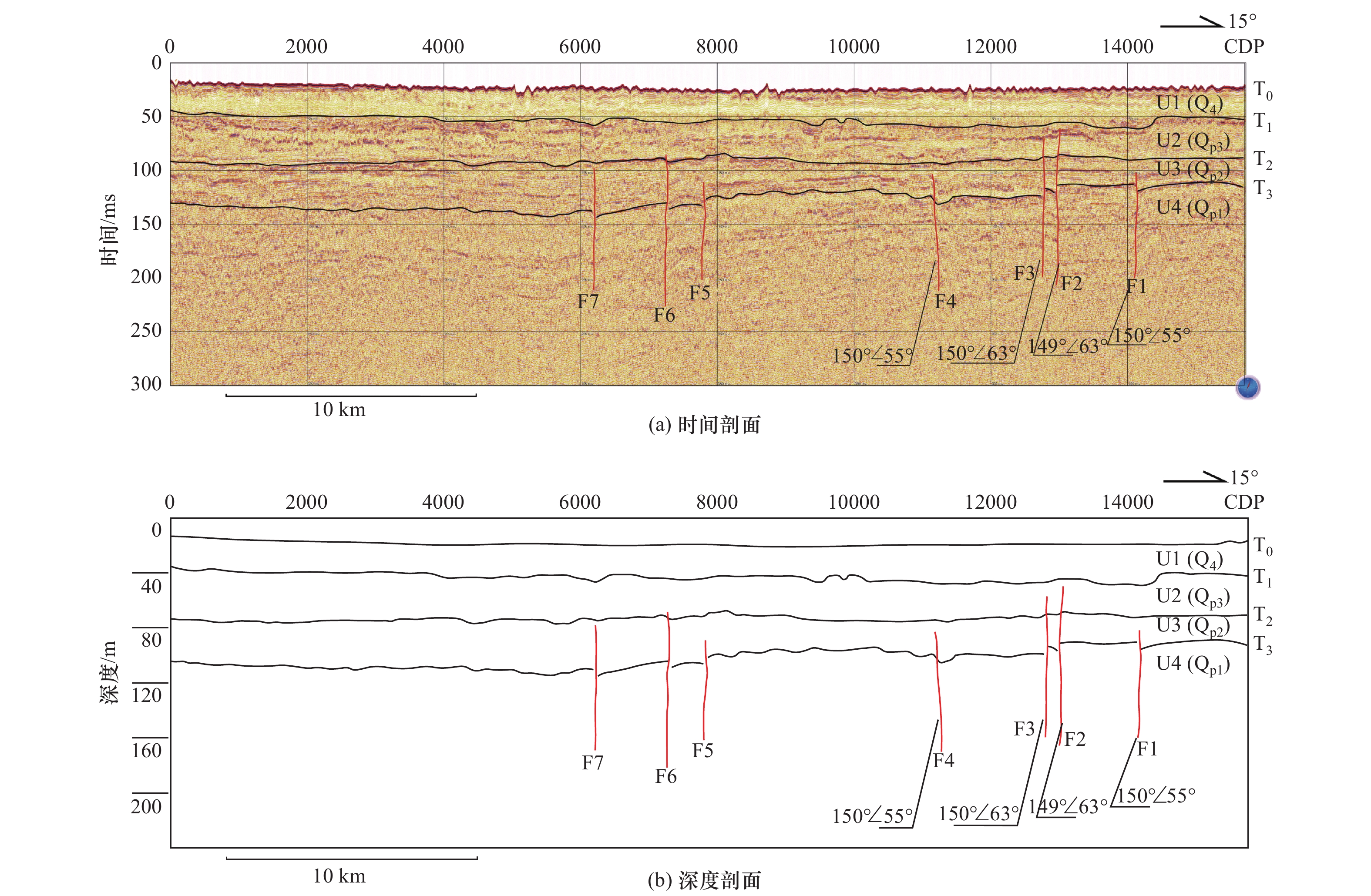
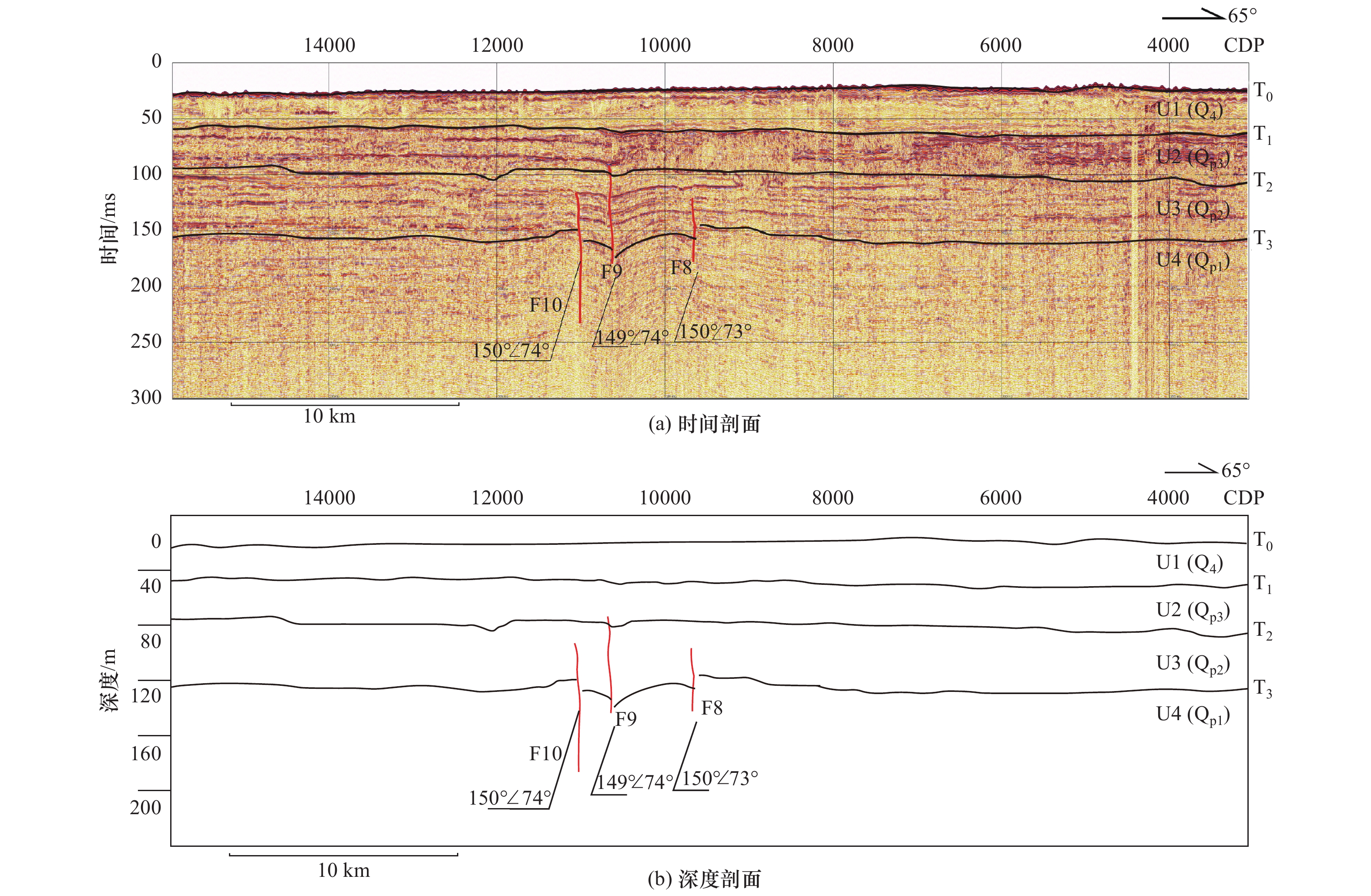
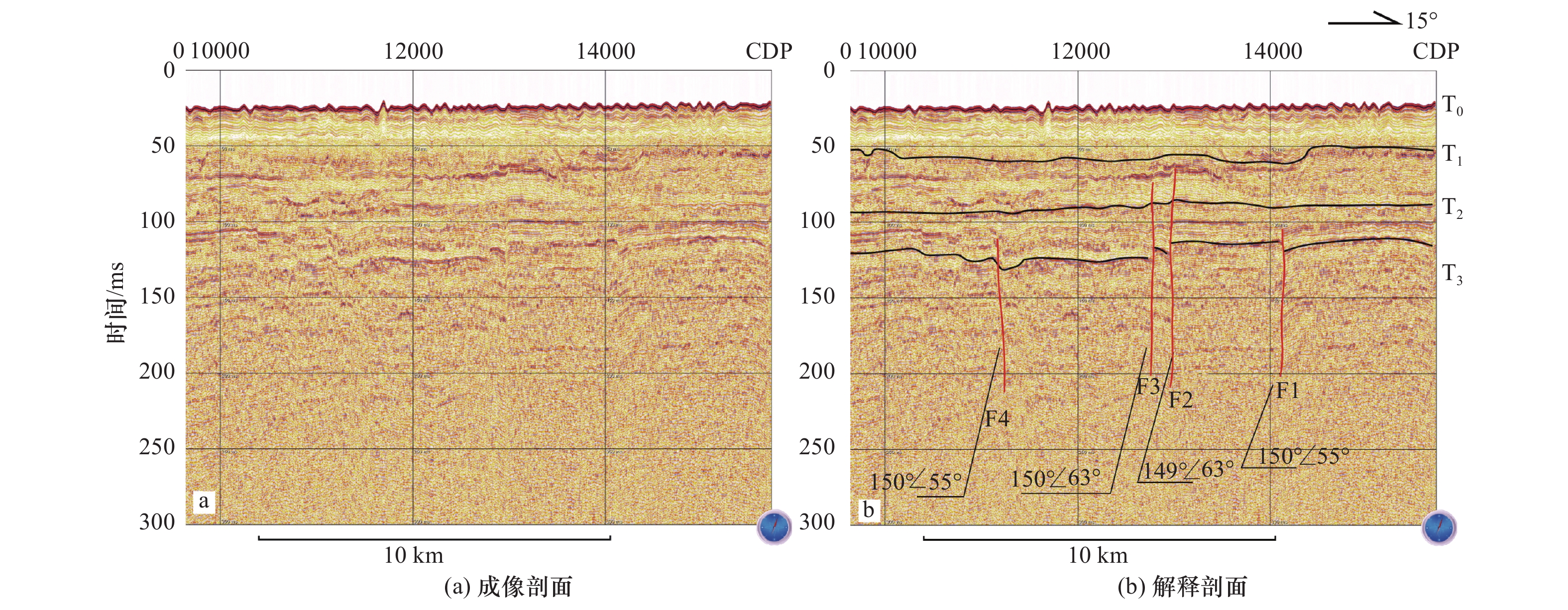
苏北—滨海断裂在江苏以北的存在与活动性长期以来存在争议。本研究通过小多道地震探测技术，对苏北—滨海断裂北段及附近海域进行探测，识别出4个反射界面，将研究区第四纪地层划分为4个地震层序，分别对应全新世、晚更新世、中更新世和早更新世4个地质时期。对照区域地质构造，对地震剖面断点进行分析，认为断点F1、F2、F3、F4、F8、F9、F10对应为苏北—滨海断裂，断裂错动的最新地层为晚更新世，因此推断苏北—滨海断裂为晚更新世活动断裂。
Abstract:The activity of the northern segment of littoral fault zone at northern Jiangsu is still unclear and in debate. In this study, we carried out small mini-multichannel seismic survey across the northern segment of the littoral fault zone and around the adjacent sea area. There are four reflection interfaces were identified from the seismic reflection profiles. The Quaternary stratigraphy in the study area was divided into four seismic sequences corresponding to four geological periods, as Holocene, Late Pleistocene, Middle Pleistocene and Early Pleistocene. According to the regional geological structure, the fracture points F1, F2, F3, F4 and F8, F9 and F10 correspond to the northern littoral fault zone in the study are, and the latest strata of fault movements are in the Late Pleistocene. Therefore, it can be inferred that the northern segment of the littoral fault zone is of Late Pleistocene activity at Northern Jiangsu region.
-
Key words:
- Mini-multichannel seismic survey /
- Littoral fault zone /
- Fault activity
-
引言
近年来，随着世界经济的发展，中国近海结构的研究得到了快速发展，如跨海桥梁、海上风电、人工岛和石油平台等。然而，中国福建、广东沿海和中国台湾等地区的近海结构面临着地震作用的威胁。在地震作用下，桥梁与周围水体的相互作用会对桥墩产生动水压力。地震作用下水体与结构的动力相互作用会对结构产生附加动水压力，其不仅会改变结构的动力特性，还会对水中结构的动力反应产生较大影响(Liaw等，1974；Han等，1996；黄信等，2011a；江辉等，2014)。因此，充分认识和研究地震激励下近海结构的动水压力，对于近海结构的抗震设计具有重要意义。
在实际近海工程中存在各种截面形式的墩柱结构，如圆形和椭圆形等。目前，国内外学者对圆柱结构地震动水压力的研究已取得大量的研究成果。Liaw等(1974)基于辐射波浪理论推导了圆柱结构的动水压力公式，结果表明，对于细长结构可以忽略水体压缩性的影响；表面波仅在低频时对动水压力的影响比较明显。忽略水体压缩性和表面波时，该动水压力可视为部分水体质量与结构加速度的乘积，这部分水体称为“附加质量”。Williams(1986)采用边界积分方法研究了地震作用下水中圆柱结构的动力反应。Tanaka等(1988)分析了水平地震作用下弹性圆柱体动水压力的附加质量系数和阻尼系数。Han等(1996)提出了计算水中圆柱结构自振频率的简化公式。赖伟等(2004)提出了一种圆形桥墩上地震动水压力的半解析半数值方法。黄信等(2011b, 2012)讨论了水体压缩性、表面波和水底吸收边界对圆形桥墩地震动水压力的影响。杜修力等(2012)、Du等(2014)提出了可压缩水体条件下圆柱结构地震动水压力的时域算法和时域简化公式。Goyal等(1989)、Li等(2013)和Jiang等(2017)提出了圆柱形桥墩上地震动水压力的附加质量简化计算公式。另外，Liao(1985)研究了水中多个圆柱结构的动力相互作用；Sun等(1991)研究了轴对称结构的地震动水压力；Avilés等(2001)讨论了海底吸收条件对轴对称结构地震动水压力的影响；Wei等(2015)提出了水中轴对称结构的地震设计和分析的简化方法。
上述分析表明，地震作用下圆柱结构与水体的动力相互作用问题已取得了可供实际应用的研究成果，但对椭圆柱体结构动水压力方面仍鲜有研究。本文基于椭圆坐标系，根据线性辐射波浪理论，利用分离变量法推导了椭圆柱体结构动水压力的解析解，并采用有限元方法建立了地震作用下水体与椭圆柱体结构动力相互作用的简化分析方法。
1. 椭圆形柱体动水压力求解
地震作用下椭圆柱体结构与水体动力相互作用的分析模型如图 1所示，a和b分别表示椭圆外径的半长轴和半短轴，a1和b1分别表示椭圆内径的半长轴和半短轴，h为水深，H为柱体高度。直角坐标系下，z轴沿柱体轴线向上，坐标原点位于柱体底部；地基为刚性，地面运动加速度为$\ddot{u}$g。水体假定为无旋、无粘、可压缩的小扰动流体，并忽略表面重力波的影响。
图 1 椭圆柱体与水体相互作用分析模型Figure 1. Analytical model of the interactiin of elliptic cylinder and water1.1 控制方程和边界条件
由于柱体截面呈椭圆形，故在椭圆坐标系下求解椭圆柱体的地震动水压力。椭圆坐标系如图 2所示。直角坐标系与椭圆坐标系直接的变化关系为：
$$ x=\mu \cos h\xi \cos \eta $$ (1) $$ y=\mu \text{sin}h\xi \text{sin}\eta $$ (2) 式中，$\mu =\sqrt{{{a}^{2}}-{{b}^{2}}}$，$\xi $和η分别为椭圆坐标系的径向和环向坐标，取值范围分别为$0\le \xi <\infty $和$ 0\le \eta < 2\text{ }\pi\text{ }$。其中，椭圆柱体表面的环向坐标为：
$$ {{\xi }_{0}}=\text{ta}{{\text{n}}^{-1}}(b/a) $$ (3) 在椭圆柱坐标系下，以动水压力p表示的流体控制方程为(Bhatta，2005)：
$$ \frac{2}{{{\mu }^{2}}(\text{cos}h2\xi-\text{cos}2\eta)}\left(\frac{{{\partial }^{2}}p}{\partial {{\xi }^{2}}}+\frac{{{\partial }^{2}}p}{\partial {{\eta }^{2}}} \right)+\frac{{{\partial }^{2}}p}{\partial {{z}^{2}}}=0 $$ (4) 水体底部、静水表面和无穷远边界条件为：
$$ \frac{\partial p}{\partial z}\left| _{z=0} \right.=0 $$ (5) $$ p\left| _{z=h} \right.=0 $$ (6) $$ p\left| _{\xi \to \infty } \right.=0 $$ (7) 地震动沿长轴方向时，η=0和η=0.5π面的对称边界条件为：
$$ \frac{\partial p}{\partial \eta }\left| _{\eta =0} \right.=0 $$ (8a) $$ p\left| _{\eta =0.5\pi } \right.=0 $$ (8b) 地震动沿短轴方向时，η=0和η=0.5π面的对称边界条件为：
$$ \frac{\partial p}{\partial \eta }\left| _{\eta =0.5\pi } \right.=0 $$ (9a) $$ p\left| _{\eta =0} \right.=0 $$ (9b) 地震动沿长轴和短轴方向时，水体与结构交界面边界条件分别为：
$$ \frac{\partial p}{\partial \xi }\left| _{\xi ={{\xi }_{0}}} \right.=-\rho \ddot{u}b\text{cos}\eta $$ (10) $$ \frac{\partial p}{\partial \xi }\left| _{\xi ={{\xi }_{0}}} \right.=-\rho \ddot{u}a\text{sin}\eta $$ (11) 式中，ρ表示水体密度，$\ddot{u}$表示结构的加速度。
1.2 分离变量求解
在椭圆柱坐标系下，$p(\xi, \eta, z)$可分离变量为：
$$ p=R(\xi)G(\eta)Z(z) $$ (12) 将式(12)代入式(4)整理得到3个解耦的方程：
$$ {Z}''+\lambda _{j}^{2}Z=0 $$ (13) $$ {G}''+({{a}_{0}}+2q\text{cos}2\eta)G=0 $$ (14) $$ {R}''-({{a}_{0}}+2q\text{cos}h2\xi)R=0 $$ (15) 式中，${{\lambda }_{j}}$和${{a}_{0}}$是分离变量常数，$q={{\mu }^{2}}\lambda _{j}^{2}/4$为一无量纲参数。
由方程(13)和边界条件式(5)、(6)可得：
$$ Z={{d}_{j}}\text{cos}{{\lambda }_{j}}z $$ (16) 式中，dj为待定系数，${{\lambda }_{j}}=(2j-1)\text{ }\pi\text{ }/2h$，j=1，2，…。通过正交归一化可得${{d}_{j}}=\sqrt{2/h}$。
方程(14)为修正的角向马蒂厄方程(熊天信，2014)，其解为第一类角向马蒂厄函数$c{{e}_{n}}(\eta, -q)$和$s{{e}_{n}}(\eta, -q)$，即：
$$ c{{e}_{2n}}(\eta, -q)={{(-1)}^{n}}\sum\limits_{k=0}^{\infty }{{{(-1)}^{k}}A_{2k}^{(2n)}}\text{cos}2k\eta $$ (17a) $$ c{{e}_{2n+1}}(\eta, -q)={{(-1)}^{n}}\sum\limits_{k=0}^{\infty }{{{(-1)}^{k}}B_{2k+1}^{(2n+1)}}\text{cos}(2k+1)\eta $$ (17b) $$ s{{e}_{2n+2}}(\eta, -q)={{(-1)}^{n}}\sum\limits_{k=0}^{\infty }{{{(-1)}^{k}}B_{2k+2}^{(2n+2)}}\text{sin}(2k+2)\eta $$ (17c) $$ s{{e}_{2n+1}}(\eta, -q)={{(-1)}^{n}}\sum\limits_{k=0}^{\infty }{{{(-1)}^{k}}A_{2k+1}^{(2n+1)}}\text{sin}(2k+1)\eta $$ (17d) 函数$c{{e}_{n}}(\eta, q)$和$s{{e}_{n}}(\eta, q)$的归一化正交关系为：
$$ \begin{array}{l} \int_0^{2\pi } {c{e_m}(\eta ,q)c{e_n}(\eta ,q){\rm{d}}\eta } = \left\{ \begin{array}{l} \pi ,m = n\\ 0,m \ne n \end{array} \right.\\ \int_0^{2\pi } {s{e_m}(\eta ,q)s{e_n}(\eta ,q){\rm{d}}\eta } = \left\{ \begin{array}{l} \pi ,m = n\\ 0,m \ne n \end{array} \right. \end{array} $$ (18) $$ \begin{array}{l} \int_0^{2{\rm{\pi }}} {c{e_n}(\eta ,q){\rm{cos}}k\eta {\rm{d}}\eta = {\rm{\pi }}A_k^{(n)}} \\ \int_0^{2{\rm{\pi }}} {s{e_n}(\eta ,q){\rm{sin}}k\eta {\rm{d}}\eta = {\rm{\pi }}B_k^{(n)}} \end{array} $$ (19) 方程(15)为修正的径向马蒂厄方程(熊天信，2014)。整数阶径向马蒂厄方程的完全解为：
$$ R=\left\{ \begin{align} & \sum\limits_{n=0}^{\infty }{C_{n}^{1}I{{e}_{n}}}(\xi, -q)+C_{n}^{2}K{{e}_{n}}(\xi, -q) \\ & \sum\limits_{n=0}^{\infty }{C_{n+1}^{3}I{{o}_{n+1}}}(\xi, -q)+C_{n+1}^{4}K{{o}_{n+1}}(\xi, -q) \\ \end{align} \right. $$ (20) 式中，$C_{n}^{1}$、$C_{n}^{2}$、$C_{n}^{3}$和$C_{n}^{4}$是任意常数；函数$I{{e}_{n}}(\xi, -q)$和$I{{o}_{n}}(\xi, -q)$称为第一类变形贝塞尔型径向马蒂厄函数，是单调递增函数；函数$K{{e}_{n}}(\xi, -q)$和$K{{o}_{n}}(\xi, -q)$称为第二类变形贝塞尔型径向马蒂厄函数，是单调递减函数。
1.3 柱体的动水压力
当地震动沿长轴方向时，根据边界条件式(5)—(8)和(10)，并利用式(18)的正交性可得式(12)的解为：
$$ p=-\rho b\sum\limits_{j=1}^{\infty }{{{u}_{j}}\frac{B_{1}^{(1)}K{{e}_{1}}(\xi, -q)}{K{{e}_{1}}^{\prime }({{\xi }_{0}}, -q)}c{{e}_{1}}(\eta, -q)Z} $$ (21) 式中，${{u}_{j}}=\int_{0}^{h}{{\ddot{u}}}Z\text{d}z$，$K{{e}_{1}}^{\prime }(\xi, -q)$为函数$K{{e}_{1}}(\xi, -q)$的一阶导数。
当地震动沿短轴方向时，根据边界条件式(5)—(7)、(9)和(11)，并利用式(18)的正交性可得式(12)的解为：
$$ p=-\rho a\sum\limits_{j=1}^{\infty }{{{u}_{j}}\frac{B_{1}^{(1)}K{{o}_{1}}(\xi, -q)}{K{{o}_{1}}^{\prime }({{\xi }_{0}}, -q)}s{{e}_{1}}(\eta, -q)Z} $$ (22) 式中，$K{{o}_{1}}^{\prime }(\xi, -q)$为函数$K{{o}_{1}}(\xi, -q)$的一阶导数。
地震作用沿长轴方向时，椭圆截面柱体表面单位高度上的动水力为：
$$ {{f}_{x}}(z)=-\int_{0}^{2\pi }{p({{\xi }_{0}}, \eta, z)}b\text{cos}\eta \text{d}\eta $$ (23) 将式(21)代入式(23)整理得：
$$ {{f}_{x}}(z)=-\rho \text{ }\pi\text{ }{{b}^{2}}\sum\limits_{j=1}^{\infty }{{{u}_{j}}{{S}_{xj}}}Z $$ (24a) $$ {{S}_{xj}}=-\frac{{{[B_{1}^{(1)}]}^{2}}K{{e}_{1}}({{\xi }_{0}}, -q)}{K{{e}_{1}}^{\prime }({{\xi }_{0}}, -q)} $$ (24b) 地震作用沿短轴方向时，椭圆截面柱体表面单位高度上的动水力为：
$$ {{f}_{y}}(z)=-\int_{0}^{2\pi }{p({{\xi }_{0}}, \eta, z)}a\text{sin}\eta \text{d}\eta $$ (25) 将式(22)代入式(25)整理得：
$$ {{f}_{y}}(z)=-\rho \text{ }\pi\text{ }{{a}^{2}}\sum\limits_{j=1}^{\infty }{{{u}_{j}}{{S}_{yj}}}Z $$ (26a) $$ {{S}_{yj}}=-\frac{{{[A_{1}^{(1)}]}^{2}}K{{o}_{1}}({{\xi }_{0}}, -q)}{K{{o}_{1}}^{\prime }({{\xi }_{0}}, -q)} $$ (26b) 1.4 方法验证
首先，通过圆形桥墩动水力的解析解(Li等，2013)验证本文提出的椭圆形截面柱体动水压力的解析解。假定结构为刚性，将单位高度动水力沿高度积分，可得到椭圆形柱体的均布附加质量系数为：
$$ {{C}_{M}}=-\frac{1}{h{{m}_{0}}{{{\ddot{u}}}_{g}}}\int_{0}^{h}{f(z)\text{dz}} $$ (27) 式中，${{m}_{0}}$为单位高度水体的附加质量，沿长轴方向时${{m}_{0}}=\rho \text{ }\pi\text{ }{{b}^{2}}$，沿短轴方向时${{m}_{0}}=\rho \text{ }\pi\text{ }{{a}^{2}}$。图 3为本文圆柱体附加质量系数的解与圆柱解析解的对比。由图 3可以看出，本文解与圆柱解析解很好地吻合。
图 3 圆柱解析解与本文解的对比Figure 3. The proposed solution compared with the analytical solution for circular cylinders and this paper进一步通过Wang等(2019)提出的数值方法验证本文提出的椭圆形截面柱体动水压力的解析解，该方法实质上是用垂向特征函数展开，将三维辐射问题简化为二维问题；然后用外域特征函数展开解与结构截面附近内域有限元联合求解。图 4为本文椭圆柱体附加质量系数的解与数值解的对比，椭圆柱的长轴和短轴尺寸分别为a=20m、b=10m。由图 4可以看出，本文的解与椭圆柱数值解很好地吻合。
图 4 椭圆柱数值解与本文解的对比Figure 4. The proposed solution compared with the numerical solution for elliptical cylinders and this paper2. 水中椭圆柱体结构的地震反应求解
采用有限元方法将柔性柱体结构离散为梁单元，则地震作用下水中椭圆柱体的动力方程为(王勖成，2003)：
$$ {\bf{M}}{{{\bf{\ddot{u}}}}_{s}}(t)\text{+}{\bf{C}}{{{\bf{\dot{u}}}}_{s}}(t)+{\bf{K}}{{{\bf{u}}}_{s}}(t)=-{\bf{M}}{{{\bf{\ddot{u}}}}_{g}}(t)+{\bf{F}} $$ (28) 式中，M、C和K分别为结构质量、阻尼和刚度矩阵；${{\bf{u}}_{\rm{s}}}$为结构柔性位移列向量；F为地震动水力列向量。将地震动水力式(24)或(26)进行有限元离散，则F可以表示为
$$ {\bf{F}}\text{=}-{{{\bf{M}}}_{p}}[{{{\bf{\ddot{u}}}}_{g}}(t)+{{{\bf{\ddot{u}}}}_{s}}(t)] $$ (29) $$ {{{\bf{M}}}_{p}}\text{=}{\bf{W}}\left[\sum\limits_{j=1}^{\infty }{{{m}_{0}}S_{j}^{{}}{\bf{Z}}_{{}}^{\text{T}}{\bf{Z}}} \right]\bf{W} $$ (30) $$ {\bf{W}}\text{=}\int_{0}^{h}{{{{\bf{N}}}^{\text{T}}}{\bf{N}}\text{d}}z $$ (31) 式中，Mp为附加质量矩阵，N为形函数列向量；Sj如式(24b)或(26b)。
将式(29)代入式(28)整理得：
$$ ({\bf{M}}+{{{\bf{M}}}_{\text{p}}}){{{\bf{\ddot{u}}}}_{\text{s}}}+{\bf{C}}{{{\bf{\dot{u}}}}_{\text{s}}}+{\bf{K}}{{{\bf{u}}}_{\text{s}}}=-({\bf{M}}+{{{\bf{M}}}_{\text{p}}}){{{{\bf{\ddot{u}}}}}_{\text{g}}} $$ (32) 式(32)可通过数值积分方法Newmark-β方法求解(刘晶波等，2005)。需要指出的是，附加质量矩阵Mp是满阵的，难以在商业有限元中实现。本文将附加质量矩阵Mp的每一行元素进行集中化形成1个集中的附加质量矩阵Mg，即：
$$ {{\bf{M}}_{\text{p}}}=\left[\begin{array}{*{35}{l}} {{m}_{1, 1}} & {{m}_{1, 2}} & \cdots & {{m}_{1, L-1}} & {{m}_{1, L}} \\ {{m}_{2, 1}} & {{m}_{2, 2}} & \cdots & {{m}_{2, L-1}} & {{m}_{2, L}} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {{m}_{L-1, 1}} & {{m}_{L-1, 2}} & \cdots & {{m}_{L-1, L-1}} & {{m}_{L-1, L}} \\ {{m}_{L, 1}} & {{m}_{L, 2}} & \cdots & {{m}_{L, L-1}} & {{m}_{L, L}} \\ \end{array} \right] $$ (33) $$ {{\bf{M}}_{\text{g}}}=\left[\begin{array}{*{35}{l}} {{m}_{1}} & 0 & 0 & 0 & 0 \\ 0 & {{m}_{2}} & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & {{m}_{L-1}} & 0 \\ 0 & 0 & \cdots & 0 & {{m}_{L}} \\ \end{array} \right] $$ (34) 式中，${{m}_{i, j}}\text{=}{{m}_{j, i}}$，${{m}_{i}}={{m}_{i, 1}}+{{m}_{i, 2}}+\cdots \cdots +{{m}_{i, L-1}}+{{m}_{i, L}}$，L表示柱体结构水下的节点数目。
通过柔性椭圆柱体验证提出的集中附加质量矩阵的精度。图 5为地面运动位移，脉冲持时0.2s，频谱覆盖了地震作用频段。椭圆柱体尺寸为H=80m、a=40m、b=20m、a1=30m、b1=15m；密度和弹性模量分别为2500kg/m3和30GPa；水深h=80m；梁单元长8m；不考虑阻尼作用。图 6为地面运动沿长轴方向时，采用精确附加质量模型和集中附加质量模型计算得到的结构顶部位移时程。由图可见，采用集中附加质量方法计算的位移反应的周期偏大，即结构柔性运动引起的水体附加质量偏大。
图 5 地面位移时程和傅里叶谱Figure 5. The time history of displacement of the ground motion and its Fourier spectrum
图 6 参考解和集中附加质量模型位移时程的对比Figure 6. The comparison of time history of displacement of the cylinder obtained by reference solution and lumped added mass method因此，本文进一步提出修正的集中附加质量方法，即将式(32)修正为如下形式：
$$ ({\bf{M}}+\alpha {{{\bf{M}}}_{\text{g}}}){{{\bf{\ddot{u}}}}_{\text{s}}}+{\bf{C}}{{{\bf{\dot{u}}}}_{\text{s}}}+{\bf{K}}{{{\bf{u}}}_{\text{s}}}=-({\bf{M}}+{{{\bf{M}}}_{\text{g}}}){{{\bf{\ddot{u}}}}_{\text{g}}} $$ (35) 式中，$\alpha \le 1$为集中附加质量矩阵修正系数。图 7为集中附加质量矩阵修正系数随无量纲参数宽深比(l)和长短轴比(δ)的变化；无量纲参数宽深比(l)和长短轴比(δ)的定义如公式(36)和(37)所示：
$$ l=\frac{D}{h} $$ (36) $$ \delta =\frac{a}{b} $$ (37) 式中，地震方向沿x轴时$D=2a$，地震方向沿y轴时$D=2b$。
图 8 参考解和修正集中附加质量模型的位移时程比较Figure 8. The comparison of time history of displacement of the cylinder obtained by reference solution and modified-lumped added mass method图 8为地面运动沿长轴方向时，采用满阵附加质量模型和修正集中附加质量模型计算得到的结构顶部位移时程，满阵附加质量模型解为参考解。由图可见，采用修正集中附加质量方法计算的位移反应与参考解很好地吻合。
3. 椭圆形柱体均布附加质量简化公式
式(34)所示的集中附加质量矩阵与通过刚性结构动水力解析公式计算得到的附加质量是一致的。需要指出的是，动水力附加质量解析公式的数学表达复杂，难以在工程中进行应用。因此，提出附加质量的简化计算公式。假定附加质量沿高度均匀分布，相应的附加质量系数定义如式(27)所示。将式(24a)或(26a)代入式(27)整理得：
$$ {{C}_{M}}=\sum\limits_{j=1}^{\infty }{\frac{8{{S}_{j}}}{{{(2j-1)}^{2}}{{\text{ }\pi\text{ }}^{2}}}} $$ (38) 式中，$S_{j}^{{}}$的定义见式(24b)或(26b)。需要指出的是，简化公式是在$0.2\le l\le 2$和$0.2\le \delta \le 5$的范围内拟合得到的。
通过曲线拟合，圆形柱体均布附加质量系数的简化公式为：
$$ {{C}_{M1}}=0.6{{\text{e}}^{-0.93l}}+0.403{{\text{e}}^{-0.156l}} $$ (39) 当地震动沿长轴方向时，通过曲线拟合得到椭圆形柱体沿长轴方向的均布附加质量系数的简化公式为：
$$ {{C}_{Mx}}/{{C}_{M1}}={{p}_{11}}{{\delta }^{2}}+{{p}_{12}}\delta +{{p}_{13}} $$ (40) $$ {{p}_{11}}=0.00367{{l}^{1.554}}+0.0221 $$ (41a) $$ {{p}_{12}}=-0.185{{l}^{0.507}}-0.041 $$ (41b) $$ {{p}_{13}}=0.157{{l}^{0.505}}+1.037 $$ (41c) 当地震动沿短轴方向时，通过曲线拟合，得到椭圆形柱体沿短轴方向的均布附加质量系数的简化公式为：
$$ {{C}_{My}}/{{C}_{M1}}={{p}_{21}}{{\delta }^{{{p}_{22}}}}+{{p}_{23}} $$ (42) $$ {{p}_{21}}=-0.277{{\text{e}}^{-0.0186l}}+0.293{{\text{e}}^{-1.102l}} $$ (43a) $$ {{p}_{22}}=-0.008{{l}^{2}}+0.186l-1.056 $$ (43b) $$ {{p}_{23}}=1.295{{{\rm{e}}}^{-0.0106l}}-0.31{{{\rm{e}}}^{-1.052l}} $$ (43c) 图 9为椭圆柱体附加质量系数的解析解与简化公式的对比，图 10则为简化公式的误差，可以看出简化公式与解析解吻合较好。
图 9 附加质量系数解析解和简化公式的对比Figure 9. The comparison of coefficient of the added mass obtained by analytical solution and simplified formula
图 10 附加质量系数简化公式的误差Figure 10. The error of the simplified formula for the added mass coefficient4. 结语
(1) 基于椭圆坐标系，采用分离变量法将拉普拉斯方程转换为马蒂厄方程。通过求解马蒂厄方程，提出了椭圆柱体结构地震动水压力的解析解。
(2) 建立了地震作用下椭圆柱体结构与水体相互作用的动力有限元方程，结构的动水力通过附加质量矩阵施加，该矩阵是满阵的。
(3) 为便于椭圆柱体结构附加质量矩阵在商业有限元中实现，提出了集中附加质量矩阵的方法，该方法中柔性运动引起的附加质量为集中附加质量矩阵和修正系数的乘积。
(4) 基于刚性柱体结构动水力的解析解，通过曲线拟合的方法建立了椭圆柱体结构动水力的均布附加质量简化公式，公式中的系数仅与无量纲参数宽深比和长短轴比相关。
-
图 1 江苏—南黄海地区地震构造
Figure 1. The main faults distribution in Jiangsu—South Yellow Sea region
图 2 苏北—滨海断裂及邻区构造简图
Figure 2. Simplified geological map of the littoral fault zone and its adjacent region
表 1 地层单元地质时代划分
Table 1. Seismic unit age and era division table
地层时代 地层单元 年龄范围/（ka BP） 全新世 U1 13～0 晚更新世 U2 128～13 中更新世 U3 700～128 早更新世 U4 >750 
下载: 导出CSV
表 2 剖面识别断点
Table 2. List of profile recognition breakpoints
推测断裂 序号 所在测线 断点编号 纬度 经度 视倾角/(°) 上断点深度/m 苏北—滨海断裂 1 YC2 F8 33°39′17.283″N 120°58′13.413″E 42.50 96.2 2 YC2 F9 33°38′46.832″N 120°57′0.061″E 44.87 73.6 3 YC2 F10 33°38′37.990″N 120°56′34.094″E 43.84 98.4 4 YC5 F4 33°48′31.201″N 120°47′6.311″E 37.20 91.1 5 YC5 F3 33°50′57.200″N 120°47′53.492″E 46.54 52.1 6 YC5 F2 33°51′15.778″N 120°47′59.501″E 45.80 48.6 7 YC5 F1 33°53′05.222″N 120°48′34.727″E 36.30 92.7 盐城—南洋岸断裂 8 YC5 F7 33°41′34.151″N 120°44′45.578″E 39.45 92.4 9 YC5 F6 33°42′45.906″N 120°45′14.179″E 58.31 66.7 10 YC5 F5 33°43′30.144″N 120°45′29.170″E 49.26 72.5
下载: 导出CSV
-
陈新, 毛正毅, 汪福田, 1991. 南黄海地质及地震. 地震地质, (3): 205-212.Chen X., Mao Z. Y., Wang F. T., 1991. The geology and seismicity of the southern Huanghai (Yellow) sea. Seismology and Geology, (3): 205-212. (in Chinese) 崔敏, 张功成, 王鹏等, 2017. 苏北-南黄海盆地NW向断层特征及形成机制. 中国矿业大学学报, 46(6): 1332-1339.Cui M., Zhang G. C., Wang P., et al., 2017. Characteristics and genetic mechanism of NW faults in North Jiangsu and South Yellow Sea basin. Journal of China University of Mining & Technology, 46(6): 1332-1339. (in Chinese) 邓起东, 晁洪太, 闵伟等, 2002. 海域活动断裂探测和古地震研究. 中国地震, 18(3): 311-315. doi: 10.3969/j.issn.1001-4683.2002.03.012Deng Q. D., Chao H. T., Min W., et al., 2002. Marine active fault exploration and Paleoearthquake research. Earthquake Research in China, 18(3): 311-315. (in Chinese) doi: 10.3969/j.issn.1001-4683.2002.03.012 高中和, 吴少武, 2000. 苏北滨海大断裂活动性评价及其构造意义. 见: 中国地震学会第八次学术大会. 长春: 中国地震学会. 黄耘, 李清河, 张元生等, 2008. 江苏及邻区地震重新定位和构造特征分析. 地球物理学报, 51(1): 175-185. doi: 10.3321/j.issn:0001-5733.2008.01.022Huang Y., Li Q. H., Zhang Y. S., et al., 2008. Relocation of earthquakes in Jiangsu and neighboring areas, China and analysis of structural features. Chinese Journal of Geophysics, 51(1): 175-185. (in Chinese) doi: 10.3321/j.issn:0001-5733.2008.01.022 李小军, 陈苏, 任治坤等, 2020. 海域地震区划关键技术研究项目及研究进展. 地震科学进展, 50(1): 2-19. doi: 10.3969/j.issn.2096-7780.2020.01.001Li X. J., Chen S., Ren Z. K., et al., 2020. Project plan and research progress on key technologies of seismic zoning in sea areas. Progress in Earthquake Sciences, 50(1): 2-19. (in Chinese) doi: 10.3969/j.issn.2096-7780.2020.01.001 李旭东, 刘绍文, 王丽, 2018. 江苏-南黄海地区地震活动时空分布特征及其孕震构造分析. 高校地质学报, 24(4): 551-562.Li X. D., Liu S. W., Wang L., 2018. Spatiotemporal pattern of earthquake activities and Seismotectonics in Jiangsu and Adjacent Southern Yellow Sea Area. Geological Journal of China Universities, 24(4): 551-562. (in Chinese) 练铭祥, 薛冰, 杨盛良, 2001. 苏北新生代盆地断陷和坳陷的形成机理. 石油实验地质, 23(3): 256-260. doi: 10.3969/j.issn.1001-6112.2001.03.002Lian M. X., Xue B., Yang S. L., 2001. Formation mechanism of depressions and rifts in the Cenozoic Basin of North Jiangsu Province. Petroleum Geology & Experiment, 23(3): 256-260. (in Chinese) doi: 10.3969/j.issn.1001-6112.2001.03.002 刘东鹰, 2010. 苏北-南黄海盆地的构造演化分析. 石油天然气学报, 32(6): 27-31. doi: 10.3969/j.issn.1000-9752.2010.06.006Liu D. Y., 2010. Analysis on structural evolution of Northern Jiangsu-South Yellow Sea Basin. Journal of Oil and Gas Technology, 32(6): 27-31. (in Chinese) doi: 10.3969/j.issn.1000-9752.2010.06.006 陶倩倩, 2009. 南黄海西部陆架埋藏古三角洲研究. 青岛: 中国海洋大学.Tao Q. Q., 2009. The study of Paloe deltas in Western shelf of the South Yellow Sea. Qingdao: Ocean University of China. (in Chinese) 田建明, 徐徐, 谢华章等, 2004. 江苏及南黄海地区历史地震类型分布特征. 地震学报, 26(4): 432-439. doi: 10.3321/j.issn:0253-3782.2004.04.013Tian J. M., Xu X., Xie H. Z., et al., 2004. Distribution characteristics of historical earthquake classes in Jiangsu Province and South Huanghai Sea Region. Acta Seismologica Sinica, 26(4): 432-439. (in Chinese) doi: 10.3321/j.issn:0253-3782.2004.04.013 万鹏, 陈亮, 2016. 古沉积环境研究在海上风电工程勘察中的应用. 勘察科学技术, (S1): 16-18, 41. 王斌, 梁雪萍, 周健, 2008. 江苏及其周边地区断裂活动性与地震关系的分析. 高原地震, 20(1): 38-43. doi: 10.3969/j.issn.1005-586X.2008.01.007Wang B., Liang X. P., Zhou J., 2008. Analysis on relationship between fault Activity and Earthquakes in Jiangsu province and its adjacent areas. Plateau Earthquake Research, 20(1): 38-43. (in Chinese) doi: 10.3969/j.issn.1005-586X.2008.01.007 王恩惠, 张广伟, 谢卓娟等, 2020. 盐城地区小震精定位及构造意义. 地球物理学进展, 35(2): 461-466. doi: 10.6038/pg2020DD0037Wang E. H., Zhang G. W., Xie Z. J., et al., 2020. Precise relocation of small earthquakes in the Yancheng area and associated tectonic implications. Progress in Geophysics, 35(2): 461-466. (in Chinese) doi: 10.6038/pg2020DD0037 吴德城, 朱晓青, 王庆良等, 2020. 南黄海西北部与深大断裂相关的活动断层特征. 海洋地质前沿, 36(2): 12-18.Wu D. C., Zhu X. Q., Wang Q. L., et al., 2020. Characteristics of active faults related to deep faults in the northwestern part of the South Yellow Sea. Marine Geology Frontiers, 36(2): 12-18. (in Chinese) 邢磊, 2012. 海洋小多道地震高精度探测关键技术研究. 青岛: 中国海洋大学.Xing L., 2012. Study of the key technologies of high-precision marine multichannel seismic survey. Qingdao: Ocean University of China. (in Chinese) 许兵, 李兴唐, 王德民等, 1984. 苏南核电站区域地壳稳定性评价. 水文地质工程地质, (6): 1-4, 9. 杨继超, 2014. 南黄海盆地中部第四纪地震层序和地层学. 青岛: 中国海洋大学.Yang J. C., 2014. Quaternary seismic sequence and stratigraphy in the central South Yellow Sea Basin. Qingdao: Ocean University of China. (in Chinese) 杨琦, 陈红宇, 2003. 苏北-南黄海盆地构造演化. 石油实验地质, 25(S1): 562-565.Yang Q., Chen H. Y., 2003. Tectonic evolution of the North Jiangsu-South Yellow Sea Basin. Petroleum Geology & Experiment, 25(S1): 562-565. (in Chinese) 袁迎如, 1988. 南黄海西南部的活动断裂. 海洋科学, (2): 8-12. 赵成彬, 刘保金, 姬计法, 2011. 活动断裂探测的高分辨率地震数据采集技术. 震灾防御技术, 6(1): 18-25. doi: 10.3969/j.issn.1673-5722.2011.01.002Zhao C. B., Liu B. J., Ji J. F., 2011. The acquisition technique of high-resolution seismic data for prospecting of active faults. Technology for Earthquake Disaster Prevention, 6(1): 18-25. (in Chinese) doi: 10.3969/j.issn.1673-5722.2011.01.002 赵月霞, 2003. 南黄海第四纪高分辨率地震地层学研究. 青岛: 中国海洋大学.Zhao Y. X., 2003. Quaternary seismic stratigraphic interpretation of high-resolution seismic profiles of the South Yellow Sea. Qingdao: Ocean University of China. (in Chinese) -
下载:
点击查看大图
计量
- 文章访问数: 173
- HTML全文浏览量: 36
- PDF下载量: 14
- 被引次数: 0
