Application Research of Genetic Neural Network in Seismic Intensity Evaluation
-
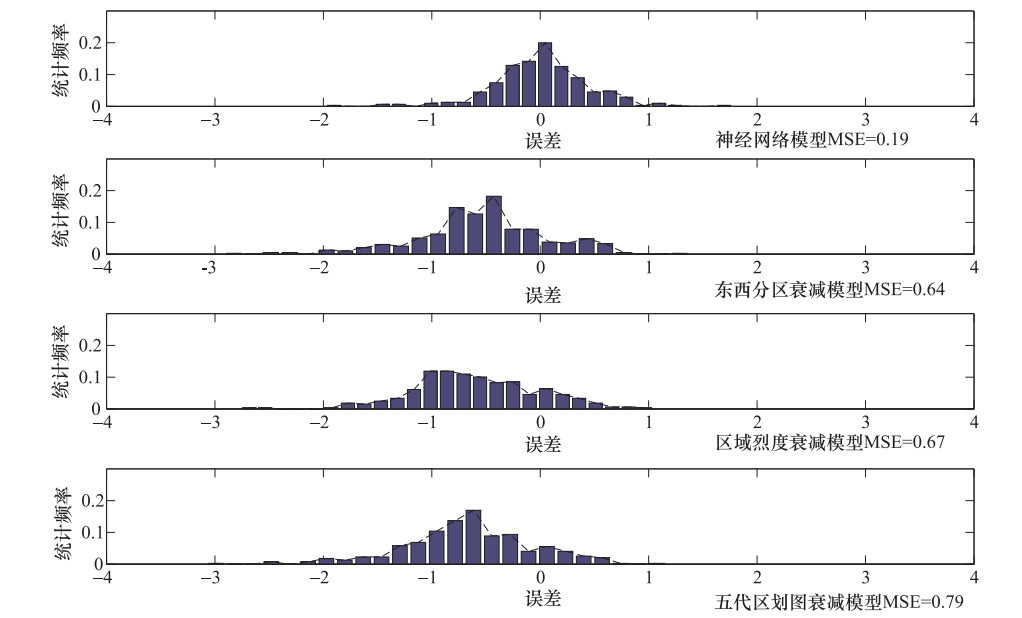
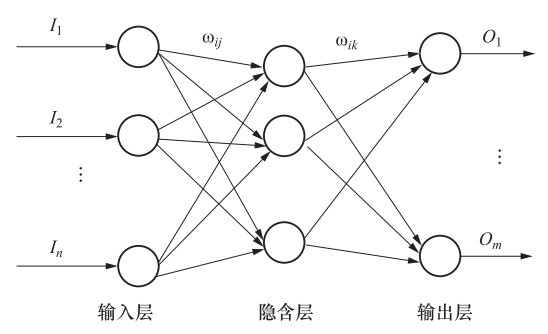
摘要: 准确判定极震区烈度是震后应急工作高效开展的重要基础。收集1966—2017年发生在中国大陆地区MS 5.0以上有详细烈度记录的地震事件322例，选取与极震区烈度有关的7个因子进行主成分分析，将提取的主成分确定为BP神经网络的输入，极震区烈度为输出，在遗传算法优化的基础上，构建用于极震区烈度预测的BP神经网络模型。结果显示，与传统模型相比，神经网络模型在预测误差分布、精度和预测结果正确率等方面都具有明显的优越性。Abstract: Accurate and rapid determination of seismic intensity in meizoseismal area is an important basis for efficient post-earthquake emergency work. In this paper, 322 earthquake events of MS 5.0 or more occurred in the mainland of China are collected. Seven factors related to the intensity of the epicenter are selected and principal component analysis is carried out. The extracted principal component is determined as the input of BP neural network when the intensity of the epicenter is the output of the network. Based on the optimization of genetic algorithm, a model for intensity prediction in epicentral area is constructed. Finally, the new model is compared with three traditional ones, and the results show that the neural network model constructed in this paper has obvious advantages in prediction error distribution, accuracy, as well as correctness of prediction.
-
引言
我国渤海海域的油气资源较为丰富，大部分油气资源集中在浅海大陆架上，占我国石油年产量的1/3（薛永安等，2020），渤海海域布设了大量导管架海洋平台用于开采海上油气资源。渤海浅海海域丰富的油气资源与该地区频繁的地质构造运动密切相关，如郯庐断裂带晚期强烈地质活动形成了大量构造圈闭储藏油气（万桂梅等，2009），但这也导致地震等灾害的发生。历史上，渤海海域共发生有记录的7级以上地震4次，6级以上地震2次，地震海啸1次（王健，2007）。虽然渤海海域纬度较高，但近年来时有台风发生，如2014年的“麦德姆”台风，2019年的“利奇马”台风，2020年的“巴威”台风。导管架平台的设计使用年限一般都会达到15年以上，存在部分超期服役的导管架平台，如果地震和台风同时或先后发生，必然会对平台造成损坏，甚至会造成严重的次生灾害。作为渤海浅海海域海洋平台的主要结构形式，生产中的导管架平台如果发生破坏，当地自然环境必然遭受严重破坏，产生重大安全事故。因此，对地震-台风耦合作用下的导管架平台进行相应的动力响应分析具有重要意义。
国内外学者针对海洋平台的动力响应进行了一系列研究。张光发等（2011）用解析方法分析导管架下水系统三维运动得到的数学模型优化了导管架下水参数的计算；吴家鸣等（2009）对桁架式近海构筑物进行数值分析，结果表明结构物对波浪的响应主要取决于其自身尺寸与波浪环境参数；刘育丰等（2012）对渤海区域海洋平台抗震设防经验进行总结，对不同地震危险性分区给出了设防参数；孙久洋等（2020）对比增量动力法和耐震时程法对强震作用下的导管架进行分析后，认为耐震时程分析法的计算效率更高；董汝博等（2010）基于流固耦合理论对海洋储油罐平台地震反应进行数值模拟，并与简化模型进行对比，结果表明采用流固耦合的方法更加精确；Wu等（2018）通过在海洋平台上加装非线性磁力调制阻尼器进行振动台实验，发现调制阻尼器在宽频段内的抑制作用十分显著且能解决平台在大震下延迟响应等问题；张大勇等（2015）对钻井平台进行冰激动力响应分析，并对冰振安全评估提出了建议；Sharma等（2019）通过在导管架平台上设置调质阻尼器，分析其在地震和冰荷载作用下的动力响应，结果表明设置调质阻尼器能够有效减小平台层的位移；朱本瑞（2014）进行大型导管架平台风洞实验，得到了平台周围风场变化规律；左华楠（2017）分析了导管架平台在恶劣风浪条件下的动力响应，给出了其在不同水深和上浪高度下的响应规律及甲板的应力变化情况。目前，针对地震-台风耦合作用下海洋平台动力响应分析的研究仍有待丰富。
针对导管架平台这类重要工程，在地震、台风等自然灾害作用下的灾害风险评估、隐患排查和安全评估具有一定实际意义。本文针对地震-台风耦合作用下导管架平台的安全评估，开展如下研究：
（1）通过Morison方程及Stokes五阶波理论将波浪力、台风拖曳力施加至结构上，建立运动方程；
（2）基于Abaqus建立地震-台风耦合作用下的导管架平台数值分析模型；
（3）对模型进行模态分析和非线性时程响应计算，对数值模拟后得到的应力、顶层位移角等结果进行分析，并与美国石油学会（American petroleum institute, API）的相关规范和《海上平台状态评定指南》（GD 04—2005）（中国船级社，2005）中所要求的响应参数进行对比，评估导管架平台在地震-台风耦合作用下的安全性能。
1. 地震-台风耦合环境下荷载施加基本理论
1.1 波浪力施加
对于流体中的刚架或桁架等构件直径较波浪波长小的结构，可通过Morison方程求得结构所受的波浪力，波浪力主要包括拖曳力和惯性力。流体的拖曳力与稳态流的速度和特定波浪形式有关，惯性力与波浪的加速度有关。
流体在杆件轴向正交方向的拖曳力为：
$$ {{\boldsymbol{F}}_{\text{D}}}{\text{ = }}\frac{{\text{1}}}{{\text{2}}}\rho {C_{\text{D}}}D\Delta {{\boldsymbol{v}}_{\text{n}}}{\left( {\Delta {{\boldsymbol{v}}_{\text{n}}} \cdot \Delta {{\boldsymbol{v}}_{\text{n}}}} \right)^{\frac{1}{2}}} $$ (1) 流体质点的相对速度沿杆件轴向正交方向分量为：
$$ \Delta {{\boldsymbol{v}}_{\text{n}}} = \Delta {\boldsymbol{v}}{{ - }}\Delta {{\boldsymbol{v}}_{\text{t}}} $$ (2) 流体质点相对速度沿杆件轴向分量为：
$$ \Delta {{\boldsymbol{v}}_{\text{t}}} = \left( {\Delta {\boldsymbol{v}} \cdot {\boldsymbol{t}}} \right){\boldsymbol{t}} $$ (3) 流体质点相对速度为：
$$ \Delta {\boldsymbol{v}} = {{\boldsymbol{v}}_{\text{f}}} - {\alpha _{\text{R}}}{{\boldsymbol{v}}_{\text{p}}} $$ (4) 式中，
$ {{\boldsymbol{v}}_{\text{f}}} $ 为流体质点速度；$ {{\boldsymbol{v}}_{\text{p}}} $ 为导管架结构质点速度；$ {\alpha _{\text{R}}} $ 为结构速度常数；$ {\boldsymbol{t}} $ 为沿着单元轴向的单位向量；$ \rho $ 为流体密度；CD为拖曳系数；D为杆件外径。由于流体惯性引起的单位长度上的惯性力为：
$$ {{\boldsymbol{F}}_{\text{I}}}{\text{ = }}\rho \frac{{{\text{π}} {D^2}}}{4}\left[ {{C_{\text{M}}}{{\boldsymbol{a}}_{{\text{fn}}}} - {C_{\text{A}}}{{\boldsymbol{a}}_{{\text{pn}}}}} \right] $$ (5) 式中，CM为流体惯性系数；CA为附加质量系数；
$ {{\boldsymbol{a}}_{{\text{fn}}}} $ 为流体在杆件轴向正交方向上的加速度；$ {{\boldsymbol{a}}_{{\text{pn}}}} $ 为流体在杆件轴向正交方向上的加速度。1.2 台风荷载的施加
台风与波浪类似，也会对结构产生拖曳力，但流体对结构的拖曳力仅在液面以下产生，而台风对结构的拖曳力在液面以上结构部分产生，且这部分结构上的风速要符合假设的风速廓线，本文采用指数律风速廓线模式。该部分拖曳力以静力的形式施加在结构上。
指数律风速廓线为：
$$ u = u_{\left( t \right)}^0{\left( {\frac{z}{{{z_0}}}} \right)^\alpha } $$ (6) 风作用在结构上的拖曳力为：
$$ F = \left( {\rho /2} \right){u^2}{C_{\text{S}}}A $$ (7) 式中，u为风速；
$ u_{\left( t \right)}^0 $ 为$ {z_0} $ 处根据时间变化的风速；$ z $ 为海面上任一位置距海面的距离，$ z = 0 $ 时为海面；$ {z_0} $ 为某一已知风速位置距海面的距离；α为地面粗糙度指数；ρ为空气密度；CS为形状系数；A为结构的受力面积。1.3 运动方程建立
考虑地震-台风耦合作用下的结构运动方程（何晓宇等，2007）：
$$ \left[\boldsymbol M \right]\left\{ {\ddot {\boldsymbol{x}}} \right\} + \left[ \boldsymbol C \right]\left\{ {\dot {\boldsymbol{x}}} \right\} + \left[ \boldsymbol K \right]\left\{ x \right\} = - \left[ \boldsymbol M \right]\left\{ {{{\ddot {\boldsymbol{x}}}_{\text{g}}}} \right\}{\text{ + }}\left\{ {{{\boldsymbol{f}}_{\text{H}}}} \right\} $$ (8) 式中，
$ \left[ \boldsymbol M \right] $ 为结构质量矩阵；$ \left[ \boldsymbol C \right] $ 为结构阻尼矩阵；$ \left[ \boldsymbol K \right] $ 为结构刚度矩阵；$ \left\{ {\ddot {\boldsymbol{x}}} \right\} $ 为结构加速度向量；$ \left\{ {\dot {\boldsymbol{x}}} \right\} $ 为结构速度向量；$ \left\{ \boldsymbol x \right\} $ 为结构位移向量；$ \left\{ {{{\ddot {\boldsymbol{x}}}_{\text{g}}}} \right\} $ 为地震动加速度向量；$ \left\{ {{{\boldsymbol{f}}_{\text{H}}}} \right\} $ 为考虑了台风、波浪的环境荷载向量。环境荷载向量为：
$$ \left\{ {{{\boldsymbol{f}}_{\text{H}}}} \right\} = \left\{ {{{\boldsymbol{F}}_{\text{D}}}} \right\} + \left\{ {{{\boldsymbol{W}}_{\text{D}}}} \right\} + \left\{ {{{\boldsymbol{F}}_{\text{I}}}} \right\} $$ (9) 式中，
$ \left\{ {{{\boldsymbol{F}}_{\text{D}}}} \right\} $ 为流体引起的拖曳力向量；$ \left\{ {{{\boldsymbol{W}}_{\text{D}}}} \right\} $ 为台风引起的拖曳力向量；$ \left\{ {{{\boldsymbol{F}}_{\text{I}}}} \right\} $ 为流体引起的惯性力向量。运动方程建立后，采用ABAQUS中的动力显式分析方法，求解运动方程。
2. 有限元模型建立
2.1 环境及导管架参数
本文选取渤海海域某导管架海洋平台进行分析（图1）。平台采用四腿导管架型式，导管架顶标高5.0 m，底标高−13.4 m，工作点标高6.6 m。主导管采用Φ1350×24钢管，成矩形布置。在标高−4.0 m、−11.9 m之间设竖向斜拉筋。平台甲板共2层，上层平台梁顶标高12.0 m，平台主尺寸为18.5 m×19.0 m；下层平台梁顶标高10.0 m，平台尺寸为7.6 m×7.3 m。
潮位选择该海区不规则半日潮校核高水位3.08 m。对于地震-台风耦合作用的环境，由于波高较大，波面高度和水质点速度采用Stokes五阶波理论，波浪波高选择校核高水位最大可能波高8.0 m，波浪周期为8.6 s，浪向NE，台风风向为强风向NW。根据《海港水文规范》（JTS 145-2-2013）（中华人民共和国交通运输部，2013）的要求，本文流体拖曳力系数取1.2，惯性系数取2.0，地面粗糙度指数根据《建筑结构荷载规范》（GB 50009—2012）（中华人民共和国住房和城乡建设部等，2012）的要求，近海海面取0.12。风荷荷载的形状系数根据American Petroleum Institute（2014）取0.5。
2.2 导管架平台有限元模型
本文采用ABAQUS/AQUA模块进行动力响应分析。AQUA是ABAQUS中专门应用于海洋工程的分析模块，可用于水下结构或部分水下结构上的稳态流、波浪和风荷载计算。波浪和风的参数通过AQUA模块进行录入，拖曳力和惯性力通过子程序进行施加。下部导管架用B31单元进行模拟，上部甲板用S4R单元进行模拟。考虑到甲板上布设有设施和设备，通过质量点来进行模拟。在海床面以下的桩，采用固定约束进行模拟。本模型共包含5314个梁单元，1576个壳单元。导管架平台模型如图2所示。
导管架平台材料选择Q345钢，密度为7 850 kg/m3，弹性模量为206 GPa，泊松比为0.28，屈服应力为345 MPa，考虑材料的塑性变形，塑性阶段的应力-应变关系如图3所示，具体实验数据如表1所示（谢海波等, 2004）。
表 1 Q345钢应力-塑性应变参数Table 1. Stress-plastic strain parameters of Q345应力/MPa 塑性应变 276.00 0 300.48 1.4e-5 320.16 5.5e-5 333.96 1.24e-4 342.24 2.21e-4 345.00 3.45e-4 345.00 0.01338 2.3 模态分析
对导管架平台进行模态分析，前8阶振型的自振频率如表2所示，由表可知前3阶的自振频率较后面振型自振频率小的多。前3阶振型如图4所示，第1振型为y方向弯曲振型，第2振型为x方向弯曲振型，第3振型为扭转振型。
表 2 前8阶自振频率Table 2. The first 8 order natural frequencies振型编号 自振频率/Hz 1 2.8018 2 2.8753 3 2.9002 4 3.3711 5 3.4598 6 6.1433 7 6.1440 8 7.0278 根据《建筑结构荷载规范》（GB 50009—2012），参考高耸结构的基本自振周期经验公式，钢结构取下式经验系数中的较大值：
$$ T{\text{ = }}\left( {{\text{0}}{{.007\sim0}}{\text{.013}}} \right)H $$ (10) 式中，H为结构高度。
本文海洋平台属于钢结构，故取经验系数为0.013，结构高度为25.4 m，按式（10）计算自振周期为0.33 s，即自振频率为3.03 Hz，与模态分析得到的结构自振频率较为接近，说明本文采用的导管架平台建模方法合理可靠。
2.4 动力响应分析
2.4.1 地震动选取
本文选取2008年美国Chino Hills海底地震动CH08，震级Mw5.4，截取包含最大响应的20s地震动时程，并对地震动时程进行滤波、调幅，得到0.10 g、0.15 g、0.20 g和0.40 g共4种地震动强度，其中0.20 g和0.40 g分别为设防地震动强度和罕遇地震动强度，通过基底进行输入。该地震动x、y方向加速度时程如图5所示。对地震动进行频谱分析，得到其加速度傅里叶谱（图6），可见所选地震动的卓越频率与导管架平台的基本频率较为接近，符合最不利设计地震动要求（翟长海等，2005）。
2.4.2 波浪可视化
为使台风作用下的大浪在数值模型中可视化，进而更直观的观察地震-台风耦合作用下导管架平台的响应，本文在海面上建立了一个20 m×50 m的平面，用表面单元进行划分，来模拟波浪的变化。不同时间下波浪的形态如图7所示。
2.4.3 地震-台风耦合工况
近年来，受台风影响的渤海海域风速如表3所示。本文选取2种风速，第1种为近年来渤海海域出现的台风中风速最大的“利奇马”台风，其在山东登陆时风速为23 m/s；第2种为该导管架设计说明书中重现期为50年的3秒钟阵风风速，风速为33.6 m/s。地震动强度选择0.1 g、0.15 g、0.2 g和0.4 g。本文共考虑10种组合工况用于地震-台风耦合作用下的动力响应计算，如表4所示。
表 3 渤海海域风速Table 3. Wind speed of Bohai sea台风名称 风速/m·s−1 布拉万（2012） 20.8 利奇马（2019） 23 巴威（2020） 17.2 表 4 工况表Table 4. Table of working conditions地震动强度/g 风速/m·s−1 23 33.6 0 0.1 工况1 工况2 — 0.15 工况3 工况4 — 0.2 工况5 工况6 — 0.4 工况7 工况8 工况9 0 — 工况10 — 2.4.4 耦合作用下的动力响应
根据《海上平台状态评定指南》（GD 04—2005）结构动力分析评价中的强度要求，参考American Petroleum Institute（2014）相关规定，构件许用应力按下式进行计算：
$$ {F_{\text{t}}} = 0.6{F_{\text{y}}} $$ (11) 式中，Fy为构件屈服应力。
对于Q345钢，按上式计算得到其一般条件下构件许用应力为207 MPa。同时，API规范规定，对于极端环境条件下的构件应力校核，许用应力可相较于一般条件下构件应力校核提升70%，即允许少数构件出现屈服，而没有明显的破坏发生。
10种工况计算得到的最大应力如图8所示，除工况8外，其余9种工况的最大应力位置相同（图10），而工况8最大应力位置在C、D间的桩腿上（图11）。工况8～10的应力云图如图12所示，可以发现在地震-台风耦合作用下的导管架平台最大应力明显高于地震或台风单独作用下的最大应力，此时导管架帽下的立柱应力水平过高，接近屈服。
由于钢管构件上的应力相对较大，本文对80个钢管构件进行统计，以207 MPa为评估指标，得到在20 s的作用时间内不同工况下超过该指标的构件个数，如图9所示。其中，工况2、4、6、7超指标构件集中在导管架帽的4根立柱处，即图11所示E高度处的4根立柱；工况8超指标构件除导管架帽的4根立柱处外，还集中在图11所示C、D高度之间钢管构件处；工况9超指标构件集中在图11所示C、D高度之间；工况10超指标构件集中在导管架帽的2根立柱处。
图 9 各工况下超指标构件数量Figure 9. The number of over-indexed components under each working condition对比工况1～6 ，当风速为23 m/s时，导管架平台的应力水平较低，不存在超指标构件；当风速提高至33.6 m/s时，导管架平台的应力水平显著提高，超指标构件占比也随着地震动强度增加而提升，0.10 g时占总构件数的6.25%，0.15 g时占总构件数的10%，0.20 g时占总构件数的12.5%。
工况7、8为罕遇地震-台风耦合作用下的极端环境条件。工况7没有构件出现屈服，有5个构件超过评估指标，占总构件数的6.25%；工况8有16个构件应力超过评估指标，占总构件数的20%，其中有1个构件接近材料的屈服强度。相较于地震动强度为0.10 g、0.15 g和0.20 g的情况，在罕遇地震动强度下，风速的增大导致最大应力的增幅相对减弱。
对比工况2、4、6、8发现，在相同的风速条件下，导管架平台应力水平有所上升，但相较同一地震动强度下风速增大，应力水平增幅相对较小。
对比工况8、9、10发现，地震-台风耦合作用下超指标构件个数明显高于地震或台风单独作用下的超指标构件个数。
综上所述，地震-台风耦合作用对导管架平台的安全性能有较大影响，尤其在台风风速较快的情况下，必须考虑耦合作用的影响。
本文参考毛晨曦等（2018）对于通信铁塔的损伤标准，对导管架平台损伤状态进行评估。选取导管架平台顶点相对于基底的位移角（Relatively Displacement Angle, RDA）峰值作为评定导管架平台损伤状态的指标，即RDA为导管架平台顶相对于基底的最大位移与平台总高的比值，按下式进行计算：
$$ {\text{RDA = }}{\Delta _{\max }}/H $$ (12) 将导管架平台顶所能达到的最大顶层位移角，即极限位移角，用
$ {\text{RD}}{{\text{A}}_{{\text{ult}}}} $ 表示；屈服位移角用$ {\text{RD}}{{\text{A}}_{{\text{ye}}}} $ 表示；0.5倍的$ {\text{RD}}{{\text{A}}_{{\text{ye}}}} $ 用$ {\text{RD}}{{\text{A}}_{{\text{ud}}}} $ 表示，采用表5对导管架平台损伤状态进行定义。表 5 导管架平台损伤状态Table 5. Definition of damage state of jacket platform$ {\rm{RDA}} \leqslant {\rm{RD}}{{{A}}_{{\rm{ud}}}} $ $ {\rm{RD}}{{{A}}_{{\rm{ud}}}}{{ < \rm RDA}} \leqslant {\rm{RD}}{\rm{{A}}_{{\rm{ye}}}} $ $ {\rm{RD}}{{\rm{A}}_{{\rm{ye}}}}{{ < \rm RDA}} \leqslant {\rm{RD}}{{\rm{A}}_{{\rm{ult}}}} $ $ {\rm{RDA > RD}}{{\rm{A}}_{{\rm{ult}}}} $ 基本完好 轻微破坏 严重破坏 毁坏 为确定导管架平台的屈服位移角和极限位移角，对平台施加侧向倒三角形荷载，进行静力推覆分析。导管架平台的Pushover曲线如图13所示。
依据导管架平台损伤状态定义，由静力推覆分析得到各损伤状态限值，判断5种工况作用下损伤状态如表6所示。
表 6 各工况下导管架平台损伤状态Table 6. Damage state of jacket platform under each working condition工况 1 2 4 6 8 损伤状态 基本完好 轻微破坏 轻微破坏 轻微破坏 严重破坏 考虑到超指标构件主要集中在高度D、F之间和高度B、D之间，本文将选取的80个钢管构件进一步细分，分为28个上部导管架帽构件和52个下部导管架构件，对工况1、2、4、6和8进行统计，结果如表7所示。结果表明，当导管架平台处于基本完好时，没有构件超过指标限值；当处于轻微破坏时，导管架帽构件超过指标限值的比例小于1/4，导管架构件超过指标限值的比例小于1/20；当处于严重破坏时，导管架帽超过指标限值的比例小于1/4，导管架构件超过指标限值的比例小于1/5（表8）。
表 7 超指标构件数量统计Table 7. Statistics on the number of super-index components工况 导管架帽构件 导管架构件 超指标构件 1 0 0 0 2 5 0 5 4 8 0 8 6 8 2 10 8 8 8 16 表 8 不同损伤状态下超指标构件占比Table 8. Proportion of super-index components under different damage states损伤状态 超指标导管架帽构件比例 超指标导管架构件比例 基本完好 ≤0 ≤0 轻微破坏 ≤1/4 ≤1/20 严重破坏 ≤1/4 ≤1/5 3. 结论
针对近海导管架海洋平台在地震-台风耦合作用下的响应分析结果，可得到以下结论：
（1）地震-台风耦合作用下的导管架平台安全性能明显小于地震或台风单独作用下的安全性能，尤其是在台风风速较快的情况下，平台损伤较为严重。
（2）绝大多数工况下的最大应力均出现在同一构件处，在导管架平台设计时应对结构薄弱环节做适当加强，防止因局部构件的破坏导致整体结构倒塌。
（3）通过研究给出了导管架平台损伤状态的定量描述，为灾害风险评估和现场抢修工作提供了参考依据。
-
表 1 各成分贡献率及累积贡献率
Table 1. Contribution rate and cumulating contribution rate of each component
成分 特征值 贡献率/% 累积贡献率/% Q1 2.0680 29.5430 29.54 Q2 1.3824 19.7490 49.29 Q3 0.9396 13.4230 62.72 Q4 0.8565 12.2350 74.95 Q5 0.7146 10.2090 85.15 Q6 0.6861 9.8021 94.96 Q7 0.3528 5.0398 100.00 
下载: 导出CSV
表 2 选取的6个主成分因子载荷系数
Table 2. Lood factor of six principal components selected
指标 Q1 Q2 Q3 Q4 Q5 Q6 χ1 0.16412 0.41910 -0.75764 0.17834 0.41099 -0.13618 χ2 -0.00751 0.59456 0.44545 -0.31087 0.45350 0.36166 χ3 0.60009 -0.00592 0.09782 -0.17487 0.10146 -0.11982 χ4 0.37214 -0.15226 0.19900 0.76209 0.16748 0.42389 χ5 0.40596 0.30893 -0.21196 -0.17952 -0.68365 0.40464 χ6 -0.54154 0.10111 -0.21863 0.14641 -0.08768 0.52548 χ7 0.12785 -0.58478 -0.29267 -0.45445 0.33469 0.46558
下载: 导出CSV
表 3 极震区烈度神经网络仿真结果
Table 3. Neural network simulation of maximum intensity
地震名称 发震时间 极震区烈度/度 实际调查结果 神经网络仿真结果 新疆塔什库尔干5.5级 2017/05/11 7 7 内蒙古阿拉善左旗5.0级 2017/06/03 6 6 四川九寨沟7.0级 2017/08/08 9 9 新疆精河6.6级 2017/08/09 8 8 陕西宁强5.3级 2017/09/12 6 6 四川省青川县5.4级 2017/09/30 6 6 西藏米林6.9级 2017/11/18 8 8 重庆武隆5.0级 2017/11/23 6 6 吉林松原5.7级 2018/05/28 7 6 新疆伽师5.5级 2018/09/04 7 7
下载: 导出CSV
表 4 四种模型的预测结果
Table 4. Prediction results of four models
项目/% 神经网络模型 东西分区烈度衰减模型 区域烈度衰减模型 五代区划图烈度衰减模型 准确率 80 66 61 62 大于实际值 11 19 22 24 小于实际值 9 15 17 14
下载: 导出CSV
-
陈鲲, 俞言祥, 高孟潭, 2010. 考虑场地效应的ShakeMap系统研究. 中国地震, 26(1): 92—102. doi: 10.3969/j.issn.1001-4683.2010.01.009 胡旺, 张建, 陈维锋等, 2018. 基于神经网络的烈度衰减融合模型研究. 电子科技大学学报, 47(2): 224—229. doi: 10.3969/j.issn.1001-0548.2018.02.010 雷建成, 高孟潭, 俞言祥, 2006. 西南地区近代地震的震中烈度与有感半径的统计研究. 震灾防御技术, 1(2): 137—145. doi: 10.3969/j.issn.1673-5722.2006.02.007 雷建成, 高孟潭, 俞言祥, 2007. 四川及邻区地震动衰减关系. 地震学报, 29(5): 500—511. doi: 10.3321/j.issn:0253-3782.2007.05.007 刘军, 吕红山, 温和平等, 2014. 稳健回归模型在地震烈度衰减关系中的应用. 地震工程学报, 36(1): 114—119. doi: 10.3969/j.issn.1000-0844.2014.01.0114 马骏驰, 窦远明, 苏经宇等, 2005. 东南沿海地区震级与震中烈度的统计关系. 世界地震工程, 21(4): 119—122. doi: 10.3969/j.issn.1007-6069.2005.04.020 聂高众, 徐敬海, 2018. 基于震源深度的极震区烈度评估模型. 地震地质, 40(3): 611—621. doi: 10.3969/j.issn.0253-4967.2018.03.008 钱枫林, 崔健, 2013. BP神经网络模型在应急需求预测中的应用——以地震伤亡人数预测为. 中国安全科学学报, 23(4): 20—25. https://www.cnki.com.cn/Article/CJFDTOTAL-ZAQK201304005.htm 韶丹, 孙哲, 田勤虎, 2018a. 联合钻孔资料及地形数据估算宝鸡地区VS30. 地震地磁观测与研究, 39(1): 117—122. https://www.cnki.com.cn/Article/CJFDTOTAL-DZGJ201801020.htm 韶丹, 孙哲, 田勤虎等, 2018b. 中国大陆历史地震烈度统计. 地震地磁观测与研究, 39(4): 135—140. https://www.cnki.com.cn/Article/CJFDTOTAL-DZGJ201804017.htm 王鹤, 刘梦琳, 席振铢等, 2018. 基于遗传神经网络的大地电磁反演. 地球物理学报, 61(4): 1563—1575. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201804030.htm 汪素云, 俞言祥, 高阿甲等, 2000. 中国分区地震动衰减关系的确定. 中国地震, 16(2): 99—106. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGZD200002000.htm 王晓军, 文毅, 鲁权等, 2012. 陕西分区烈度衰减关系研究. 灾害学, 27(4): 98—102, 113. https://www.cnki.com.cn/Article/CJFDTOTAL-ZHXU201204023.htm 肖恭伟, 欧吉坤, 刘国林等, 2018. 基于改进的BP神经网络构建区域精密对流层延迟模型. 地球物理学报, 61(8): 3139—3148. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201808004.htm 许卫晓, 杨伟松, 孙景江等, 2016. 震中烈度与震级和震源深度经验关系的统计回归分析. 自然灾害学报, 25(2): 139—145. https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZH201602016.htm 赵士达, 张楠, 张斯文等, 2016. 基于LM-BP神经网络的地震直接经济损失快速评估方法研究. 地震研究, 39(3): 500—506. https://www.cnki.com.cn/Article/CJFDTOTAL-DZYJ201603020.htm 周中红, 何少林, 陈文凯等, 2011. 甘肃地区地震烈度影响场计算模型参数的改进研究与应用. 震灾防御技术, 6(2): 180—189. http://zzfy.eq-j.cn/zzfyjs/ch/reader/view_abstract.aspx?flag=1&file_no=20110210&journal_id=zzfyjs 朱林, 姜立新, 杨天青, 2015. BP神经网络模型在地震应急人员伤亡评估中的应用. 自然灾害学报, 24(6): 33—41. https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZH201506004.htm Allen T. I., Wald D. J., 2007. Topographic slope as a proxy for seismic site-conditions (VS30) and amplification around the globe. Open-File Report 2007-1357, Reston, Virginia: U.S. Geological Survey. Wald D. J., Quitoriano V., Heaton T. H., et al., 1999. Trinet "ShakeMaps": rapid generation of peak ground motion and intensity maps for earthquakes in southern California. Earthquake Spectra, 15(3): 537—556. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=EASPEF000015000003000537000001&idtype=cvips&gifs=Yes -
下载:
点击查看大图
计量
- 文章访问数: 175
- HTML全文浏览量: 31
- PDF下载量: 4
- 被引次数: 0
