Comparative Study on Mode Analysis of Different Finite Element Mode of the High Temperature Gas-cooled Reactor Nuclear Power Plant Structure
-
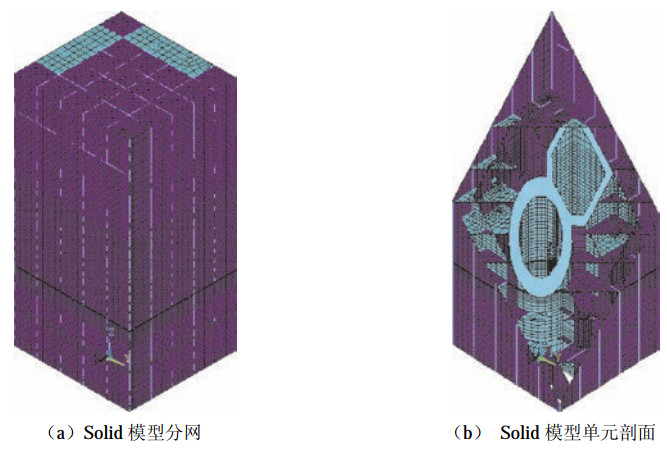
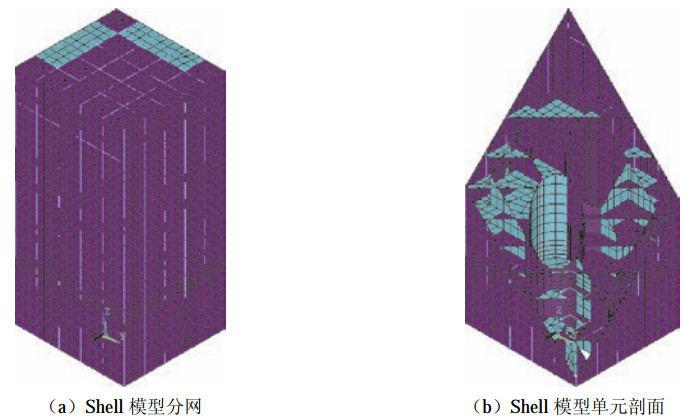
摘要: 建立有限元模型是核电厂建筑结构模态分析的重要前提。本文以某高温气冷堆核电厂建筑结构为原型，在分析方法相同的前提下，建立2种不同模型（Solid模型和Shell模型），并对这2种模型进行模态分析。重点分析、对比2种模型的自振频率和振型图，计算分析表明：Solid模型与Shell模型相比，计算得到的结构自振频率值较高，但两者的差异很小，前30阶自振频率相对误差小于3.4%；2种模型的计算结构振型基本一致。研究结果可为核电厂抗震性能分析和设计提供参考。Abstract: The establishment of finite element model is the key premise and important step of nuclear power plant building structure modal analysis. In this paper, a high temperature gas cooled reactor nuclear power plant building structure is regarded as a prototype. Building two different models, solid model and shell model, under the same analysis method, modal analysis of these two models is carried out. The natural frequency and mode shapes of the two models are analyzed and compared. The calculation and analysis show that:compared with shell model, the calculated natural frequencies of solid model are higher, but the difference between them is very small, and the relative error of the first 30 natural frequencies is less than 3.4%; the calculated structural vibration modes of the two models are basically the same. Research results can provide reference for seismic performance analysis and design of nuclear power plant.
-
图 1 高温气冷堆核电厂结构平面示意图
Figure 1. Structural plan of the high temperature gas-cooled reactor nuclear power plant
图 4 Solid模型在x、y方向上的1、2、3阶振型图
Figure 4. First, second and third order mode shapes of the Solid model in x and y directions
图 5 Shell模型在x、y方向上的1、2、3阶振型图
Figure 5. First, second and third order mode shapes of the Shell model in x and y directions
图 6 Solid模型和Shell模型扭转振型图
Figure 6. Torsional mode shapes of the Solid model and Shell model
表 1 2种模型的自振频率对比
Table 1. Comparison of natural frequencies of the two models
阶数 频率/Hz Solid Shell R 1 3.9598 3.8975 1.60% 2 5.0568 4.9366 2.43% 3 5.2341 5.1234 2.16% 4 6.7163 6.6561 0.90% 5 7.3261 7.2158 1.53% 6 7.3548 7.3548 1.27% 7 7.6120 7.4814 1.75% 8 7.7172 7.5667 1.99% 9 8.3577 8.2456 1.36% 10 8.6534 8.5334 1.41% 11 8.7922 8.6758 1.34% 12 9.8357 9.5777 2.69% 13 10.224 10.093 1.30% 14 10.849 10.682 1.56% 15 11.242 10.991 2.28% 16 11.354 11.085 2.43% 17 11.722 11.579 1.23% 18 12.001 11.606 3.40% 19 12.518 12.347 1.38% 20 12.800 12.673 1.00% 21 14.606 14.385 1.54% 22 15.490 15.366 0.81% 23 15.738 15.672 0.42% 24 16.601 16.401 1.22% 25 17.306 17.061 1.44% 26 17.421 17.320 0.58% 27 17.486 17.400 0.49% 28 17.872 17.827 0.25% 29 18.691 18.410 1.53% 30 18.855 18.792 0.34% 
下载: 导出CSV
-
傅志方, 华宏星, 2000.模态分析理论与应用.上海:上海交通大学出版社. 贺秋梅, 李小军, 张江伟等, 2014.某高温气冷堆核电厂结构地震反应分析.震灾防御技术, 9(1): 454-461. http://zzfy.eq-j.cn/zzfyjs/ch/reader/view_abstract.aspx?flag=1&file_no=20140312&journal_id=zzfyjs 贺秋梅, 李小军, 李亚琦等, 2015.地震动速度脉冲对高温气冷堆核电厂地震反应的影响.爆炸与冲击, 35(6): 799-806. https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ201506007.htm 王勖成, 邵敏, 1997.有限单元法基本原理和数值方法.北京:清华大学出版社. 周伯昌, 2007.不同地震环境下核电厂建筑结构地震反应特性分析.北京:中国地震局地球物理研究所. 周伯昌, 李小军, 李亚琦, 2008.我国核电厂厂址特定地震动特征分析.中国地震, 24(1): 55-60. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGZD200801007.htm -
点击查看大图
计量
- 文章访问数: 97
- HTML全文浏览量: 4
- PDF下载量: 6
- 被引次数: 0
