Influence of Constitutive Model and Simplified Model on Pit Deformation
-
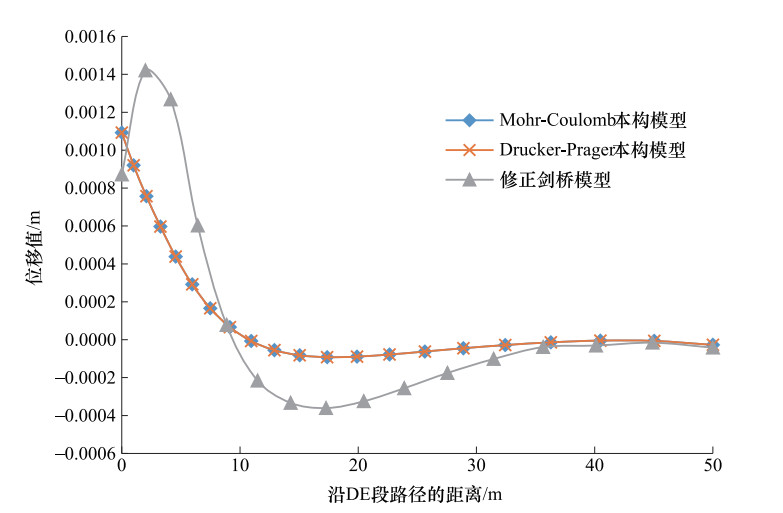
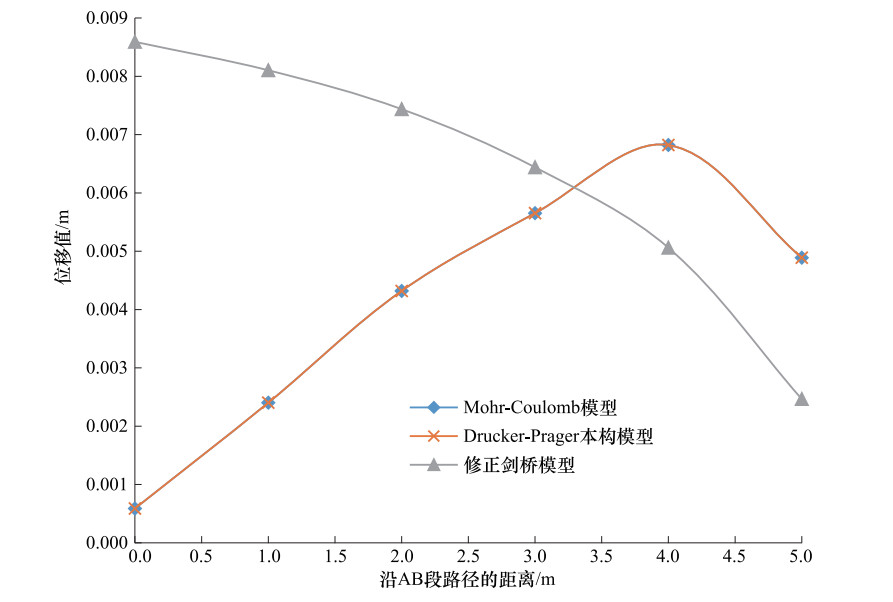
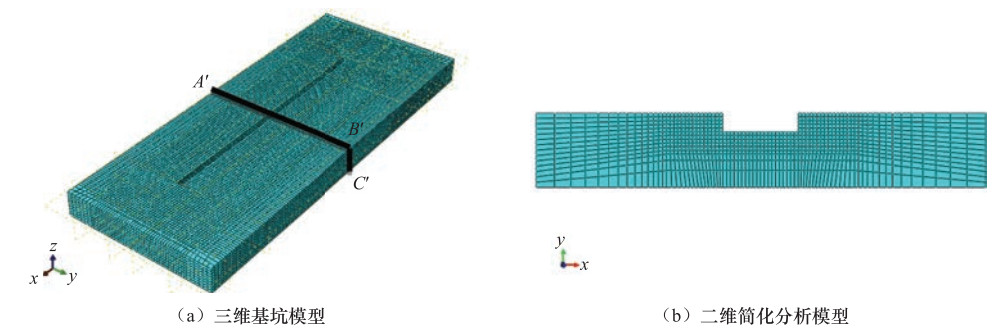
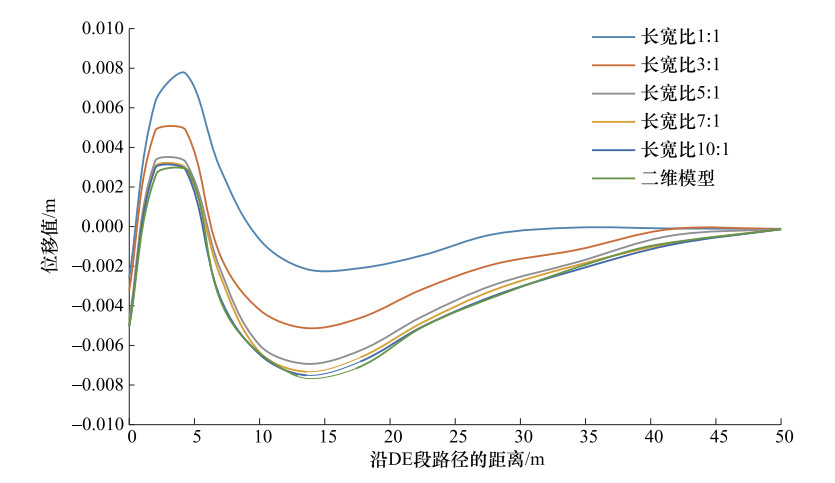
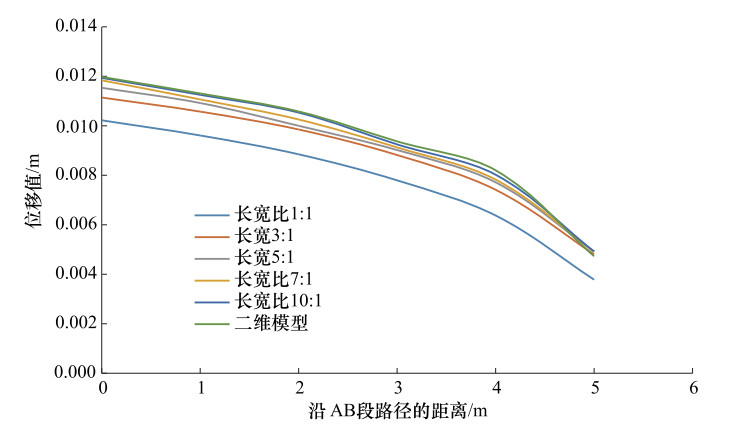
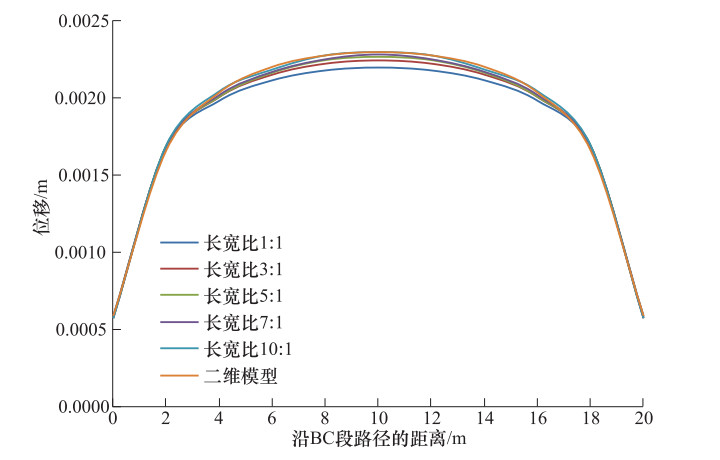
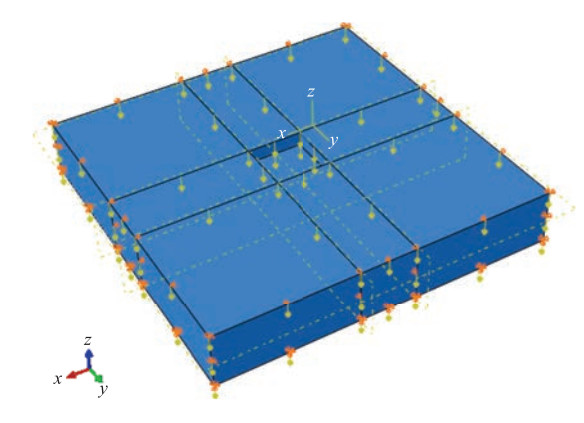
摘要: 基于大型商用专用软件的数值模拟方法已成为基坑开挖稳定性分析的重要手段之一,但对变形的分析研究较少。通过分析基坑开挖引起的地表沉降变形、基坑侧壁水平位移及坑底隆起变形,研究ABAQUS软件内置土体本构模型及二维简化分析模型对基坑开挖数值模拟结果的影响,并给出基坑开挖三维模型简化成二维模型的适用条件,为基于ABAQUS软件的基坑开挖稳定性分析及变形数值模拟提供参考。Abstract: In recent years, with the rapid development of computer technology, the numerical simulation methods based on large-scale commercial professional software have become an important method for stability analysis of foundation pit excavations. Among them, the finite element commercial software represented by ABAQUS was widely used in the stability analysis of foundation pit. However, the relevant analysis results show that the influencing factors of the numerical simulation results of the deformation caused by the excavation of the foundation pit were not only determined by the properties of the soil medium and the form of support, etc., but also affected by the soil constitutive and the analytical models.Through the analysis of the surface settlement deformation, the lateral displacement of the foundation pit and the heave deformation of the pit bottom caused by pit excavations, and has discussed the influence of ABAQUS built-in constitutive model and two-dimensional simplified analysis model on the numerical simulation results of foundation pit excavation was discussed. Also, the applicable conditions for simplifying the three-dimensional model of foundation pit excavation to two-dimensional model have been given, in order to provides reference for numerical simulation of foundation pit excavation stability analysis based on ABAQUS.
-
Key words:
- Constitutive model /
- Two dimensional model /
- Numerical simulation /
- Deformation analysis
-
-
费康, 张建伟, 2013.ABAQUS在岩土工程中的应用.北京: 中国水利水电出版社. 管俊峰, 胡晓智, 李庆斌等, 2017.边界效应与尺寸效应模型的本质区别及相关设计应用.水利学报, 48(8):955—967. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=slxb201708008 蒋明镜, 朱方园, 刘芳, 2012.两种常用本构模型在基坑开挖数值模拟中的适用性.河海大学学报(自然科学版), 40(5):568—575. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hhdxxb201205017 李广信, 2004.高等土力学.北京:清华大学出版社. 李平, 杨挺, 王义等, 2010.基坑工程隆起变形研究综述.河海大学学报(自然科学版), 38(2):196—201. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hhdxxb201002015 秦会来, 张甲峰, 郭院成等, 2012. ABAQUS在计算基坑开挖变形中的应用研究.岩土工程学报, 34(S1):82—86. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=7946264 徐中华, 王卫东, 2010.敏感环境下基坑数值分析中土体本构模型的选择.岩土力学, 31(1):258—264, 326. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ytlx201001044 Grande L., 1998. Some aspects on sheet pile wall analysis. Soil-structure interaction, International Conference on Soil Structure Interaction in Urban Civil Engineering, Darmstadt: 193—211. Hashash Y. M. A., Fu Q. W., Buthouich J., 2010. Generalized strain probing of constitutive models. International Journal for Numerical and Analytical Methods in Geomechanics, 28(15): 1503—1519. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1002/nag.397 Potts D. M., Axelsson K., Grande L., et al., 2002. Guidelines for the use of advanced numerical analysis. London: Thomas Telford. Potts D. M., Zdravkovicl L., 2001. Finite element analysis in geotechnical engineering. London: Thomas Telford. -



 下载:
下载: