Research on Vibration Attenuation of Free Field Soil under Pile Driving Load
-
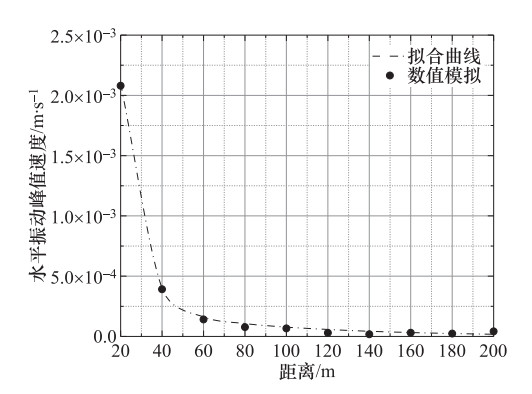
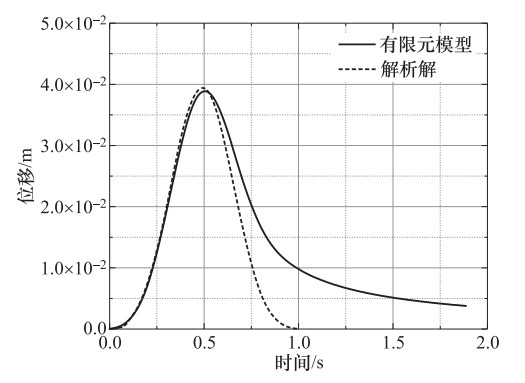
摘要: 为研究打桩荷载作用下自由场土体振动衰减规律，建立了考虑桩-土相互作用的二维有限元数值模型，并通过Lamb问题解析解验证了数值模型的有效性。通过分析打桩深度、土体阻尼比、打桩荷载等级和土质条件等因素的影响，研究了土体表面振动特性及振动衰减规律。参数分析表明，打桩深度对微振动的影响较小，在距振源一定距离处的土体表面振动响应基本保持一致；土体阻尼比对土体表面振动的影响显著，阻尼比越小，土体表面振动响应越剧烈；不同场地软硬条件影响微振动的限制距离，在一定距离范围内，土质越软，土体表面振动响应越显著，防振距离越长。基于参数分析结果，对峰值速度衰减曲线进行拟合，拟合公式计算结果与模拟结果较吻合，可为振动敏感建筑场地的选择提供参考。Abstract: In order to study the propagation and attenuation law of pile driving vibration load in free field soil, a two-dimensional finite element numerical model considering pile-soil interaction is established, and the validity of the numerical model is verified by analytical solution of Lamb problem. By analyzing the influence of factors such as pile depth, soil damping ratio, pile load level, and soil condition, the characteristics of soil surface vibration and the law of vibration attenuation are studied. The parameter analysis shows that the impact of pile driving depth on microvibration is small, and the vibration response of the soil surface is basically the same at a certain distance from the vibration source; The soil damping ratio has a significant effect on the soil surface vibration, with the decrease of the damping ratio, the vibration response of the soil surface becomes more severe; different soil conditions affect the limit distance of the microvibration, within a certain distance, the softer the soil quality, the more significant the vibration response of the soil surface, and the longer the vibration-proof distance.Based on the above-mentioned parameter analysis results, the peak velocity attenuation curve is fitted, and the settlement result of the fitting formula is in good agreement with the simulation result, which can provide a reference for the selection of vibration-sensitive building sites.
-
Key words:
- Soil characteristics /
- Dynamic Response /
- Vibration load /
- Finite element analysis
-
引言
随着我国交通基础建设的持续深入发展，穿越黏滑断层的隧道不断涌现，如在建的雅康高速二郎山隧道穿越保凰活动断裂，成兰铁路诸隧道穿越龙门山活动断裂等。在2008年汶川地震中，都映高速部分隧道，其所穿越的黏滑断层在强震诱发下发生黏滑错动，造成错动段隧道结构和围岩严重破坏，甚至出现了隧道整体垮塌的严重震害（图 1），这对灾后救援和灾后重建工作造成了严重影响（四川省交通厅公路规划勘察设计研究院，2008；于海英等，2008）。如何提高断层黏滑错动时隧道结构的安全性和稳定性是亟待研究和解决的关键技术问题之一。
图 1 龙溪隧道黏滑断层段隧道整体垮塌Figure 1. Collapse of stick-slip fracture section in Longxi tunnel目前，黏滑断层隧道的减错措施主要有二衬设置减错缝和初支与二衬之间设置减错层2种。设置减错缝可减小隧道结构的纵向刚度，提高了隧道结构适应断层黏滑错动所产生相对变位的性能；设置减错层可减小隧道结构的横向刚度，消减了传递至二衬结构的强制位移。
国内外专家、学者对穿越黏滑断层隧道的减错技术做了部分研究，主要有：穿越活动断层隧道震害特征及震害机理（高孟潭等，2008；崔光耀等，2013a；何川等，2014）；断层错动下围岩与隧道结构的位移和应力变化（赵伯明等，2009；李玉江等，2013）；不同倾角、错距下断层黏滑错动对山岭隧道洞身结构的受力特性（熊炜等，2010；蒋建平等，2011；刘学增等，2014；张理平等，2017）；设置不同减错缝的减错效果（崔光耀等，2013b；李学峰等，2014；信春雷等，2015）；设置不同减错层的减错效果（崔光耀等，2013c）等。以上研究在穿越黏滑断层隧道断层错动机制，设置减错缝不同间距、减错层不同厚度减错效果方面做了部分工作，但均未对穿越黏滑断层隧道设置减错缝不同缝宽、减错层不同刚度的减错效果进行研究。本文依托都汶高速友谊隧道F1黏滑断层段，对黏滑断层隧道设置不同缝宽减错缝、不同刚度减错层的减错效果进行研究，以期能够促进穿越黏滑断层隧道减错技术的发展。
1. 研究情况
1.1 友谊隧道F1黏滑断层段工程概况
1.1.1 工程地质
隧址区位于纸厂沟与小桃沟之间的山体内，受断层和岩性影响，节理裂隙较发育，岩体较破碎。
F1黏滑断层为挤压性逆断层，隧道洞身穿F1黏滑断层而过，走向北东，倾向北西，倾角60°，破碎带宽度0.5—2.0m，断层破碎带主要由糜棱岩、碎块岩组成，Ⅴ级围岩。上下盘岩体均为Ⅴ级围岩。
1.1.2 支护结构设计
隧道支护结构为复合式衬砌，跨度×高度＝9.4m×8.0m；隧道初支采用C25喷射混凝土，厚度25cm，二衬采用C25模筑混凝土，厚度40cm。
1.2 计算情况
1.2.1 计算模型
以友谊隧道F1黏滑断层段为研究背景，利用FLAC3D有限差分数值模拟软件建立计算模型，隧道埋深为40m，隧底围岩厚40m，左右两侧宽度取5倍隧道跨度，约60m，纵向开挖长度100m。本次计算采用brick单元，其中围岩单元47550个，衬砌单元6820个。计算时围岩按弹塑性材料考虑，衬砌则按弹性材料考虑。减错缝采用12m设缝间距（崔光耀等，2013b），减错层厚度采用10cm（崔光耀等，2013c）。通过在上盘围岩施加位移荷载来模拟断层错动，位移荷载通过施加速度来实现，错距10cm。
1.2.2 计算参数
施工中减错缝主要采用止水带进行连接，减错层一般采用橡胶板（王帅帅等，2016），围岩根据勘测资料选取Ⅴ级围岩。计算模型物理力学参数如表 1所示。
表 1 计算模型参数Table 1. Parameters of calculation model参数 重度/kN·m-3 弹性模量/MPa 泊松比 黏聚力/MPa 内摩擦角/° 围岩 20 15000 0.40 0.10 24 C25喷射混凝土 22 23000 0.20 C25模注混凝土 25 28000 0.20 减错缝 6 10 0.45 减错层 10 0—2000 0.45 1.2.3 计算工况
本文主要研究减错缝不同缝宽、减错层不同刚度对减错效果的影响规律，计算工况如表 2所示。
表 2 计算工况Table 2. Calculation condition工况 计算内容 备注 1 无减错措施 2 施设减错缝 缝宽分别为：5cm、10cm、15cm、20cm 3 施设减错层 弹模分别为：2.5MPa、5MPa、10MPa、20MPa、50MPa、100MPa、200MPa、500MPa、1000MPa、2000MPa 1.2.4 监测布置
计算模型上盘设4个监测断面、下盘设3个监测断面，每个监测断面设置8个监测点，监测布置如图 2所示。
2. 减错缝宽度对减错效果的影响分析
2.1 结构内力
提取各工况错动完成时的各监测断面计算数据，以缝宽10cm为例进行内力分析。轴力、弯矩的计算按照公式（1）、（2）计算（中华人民共和国交通部，2004）。监测断面最大轴力值见表 3，监测断面最大弯矩值见表 4。
表 3 监测断面最大轴力（单位：kN）Table 3. Maximum axial force of monitoring section (unit: kN)工况 距断层距离/m -22 -10 -2 2 10 22 34 无减错措施 -6468 -9754 -14884 -13376 -13341 -9551 -3702 缝宽10cm -5917 -9133 -14857 -13395 -12558 -8646 -3153 注：距断层距离正值为上盘，负值为下盘，其它同理。 表 4 监测断面最大弯矩（单位：kN·m）Table 4. Maximum bending moment of monitoring section (unit: kN·m)工况 距断层距离/m -22 -10 -2 2 10 22 34 无减错措施 -60.2 -142.1 -217.6 -185.0 -121.9 -45.1 -126.7 缝宽10cm -61.3 -140.2 276.1 -200.5 -127.7 48.5 -116.6 轴力、弯矩计算公式为：
$$ N=\frac{1}{2}E({\varepsilon _内}+{\varepsilon _外})bh $$ (1) $$ M=\frac{1}{{12}}E({\varepsilon _内}-{\varepsilon _外})b{h^2} $$ (2) 式中，b为截面宽度（m），取1m；h为截面厚度（m）；E为弹性模量（MPa）；${\varepsilon _内}$、${\varepsilon _外}$为结构内、外侧应变；N为结构轴力（N）；M为弯矩（N·m）；后同。
由表 3可知，施设减错缝与无减错措施工况监测断面最大轴力值均呈现压应力状态，且沿隧道纵向分布趋势相似，最大值均出现在下盘靠近断层的断面，其中无减错措施工况值为-14884kN，施设减错缝工况值为-14857kN；随着监测断面与断层的距离增大，监测断面最大轴力呈下降趋势。由各监测断面最大轴力整体分析可知，施设减错缝工况监测断面最大轴力略小于无减错措施工况。
由表 4可知，无减错措施工况监测断面最大弯矩均表现为外侧受拉，施设减错缝改变了隧道结构受力，出现内侧受拉部位；监测断面最大弯矩值均出现在下盘靠近断层的断面，其中不设减错缝工况值为-217.6kN·m，施设减错缝工况值为276.1kN·m。由各监测断面最大弯矩整体分析可知，施设减错缝工况监测断面最大弯矩略大于无减错措施工况。
轴力、弯矩指标主要用于结构设计，单一分析轴力、弯矩不能综合体现结构的力学性能。隧道支护的结构安全性可由安全系数（综合考虑了轴力、弯矩等指标）体现。
2.2 结构安全系数
提取各工况错动完成时的内力计算数据进行安全系数分析，安全系数K按照公式（3）、（4）计算（中华人民共和国交通部，2004）。以缝宽10cm进行安全系数分析，监测断面最小安全系数见表 5。
$$ KN \le \varphi \alpha{R_{\rm{a}}}bh $$ (3) $$ KN \le \varphi \frac{{1.75{R_1}bh}}{{6{e_0}/h - 1}} $$ (4) 表 5 监测断面最小安全系数Table 5. Minimum safety factor of monitoring section工况 距断层距离/m -22 -10 -2 2 10 22 34 无减错措施 1.933 1.282 0.840 0.935 0.937 1.309 3.377 缝宽10cm 2.112 1.326 0.841 0.933 0.995 1.446 3.964 式中，Ra为混凝土抗压极限强度（MPa）；Rl为混凝土抗拉极限强度（MPa）；φ为构件纵向弯曲系数；α为轴向力偏心影响系数；e0为轴向力对截面的偏心距（m）。
由表 5可知，施设减错缝与无减错措施工况监测断面最小安全系数沿隧道纵向分布趋势相似，最小值均出现在下盘靠近断层监测断面，其中无减错措施工况安全系数最小值为0.840，施设减错缝工况安全系数最小值为0.841；随着监测断面与断层距离的增大，监测断面最小安全系数呈增大趋势，上盘安全系数整体较下盘小。由各监测断面最小安全系数整体分析可知，施设减错缝工况监测断面最小安全系数略大于无减错措施工况。
2.3 减错效果
根据安全系数分析各工况减错效果，减错效果可按式（5）进行计算，各工况减错效果如图 3所示。
$$ \lambda= \frac{{{K_1}-{K_0}}}{{{K_0}}} \times 100\% $$ (5) 式中：λ为减错效果；K0为无减错措施工况监测断面最小安全系数；K1为施设减错缝工况监测断面最小安全系数。
由图 3可知，各工况减错效果沿隧道纵向分布趋势相似，随着监测断面与断层的距离增大，上下盘减错效果整体呈上升趋势，且上盘减错效果较下盘整体更好，其中上盘减错效果最大为24.50%，下盘减错效果最大为9.26%。随着减错缝宽度的增加，隧道上盘减错效果变好，下盘缝宽10—15cm时减错效果最好，主要由于断层黏滑错动对上盘的影响远大于下盘。减错缝宽度的增加适应了断层黏滑错动造成的上盘强制位移，断层黏滑错动的能量得到一定程度的释放，从而提高了上盘隧道的结构安全性，可以设想，对于隧道上盘部分存在最优减错缝宽度；减错缝宽度的增加虽然适应了断层黏滑错动造成的下盘强制位移，但由于抵御断层黏滑错动对下盘影响所需减错缝缝宽为10—15cm，当缝宽增加到20cm时，下盘隧道整体刚度的下降对下盘隧道的结构安全性造成了不利影响，致使减错效果下降。
3. 减错层弹性模量对减错效果的影响分析
3.1 结构内力
提取各工况错动完成时各监测断面的计算数据，以减错层弹性模量为2.5MPa为例进行内力分析。监测断面最大轴力值见表 6，监测断面最大弯矩值见表 7。
表 6 监测断面最大轴力（单位：kN）Table 6. Maximum axial force of monitoring section (unit: kN)工况 距断层距离/m -21 -11 -2 2 11 21 32 无减错措施 -6515 -10663 -17049 -14062 -12114 -7572 -3777 减错层弹模（2.5MPa） -5557 -7014 -8375 -8981 -8490 -6154 -3788 表 7 监测断面最大弯矩（单位：kN·m）Table 7. Maximum bending moment of monitoring section (unit: kN·m)工况 距断层距离/m -21 -11 -2 2 11 21 32 无减错措施 -78.5 -155.9 -218 -187.2 -100.3 -46.8 -35.9 减错层弹模（2.5MPa） -173.4 -269 -254.1 -217.1 -108.0 -59.3 -42.7 由表 6可知，施设减错层与无减错措施工况监测断面最大轴力值均呈现压应力状态，且沿隧道纵向分布趋势相似，最大值均出现在上下盘靠近断层的断面，其中无减错措施工况值为-17049kN，施设减错层工况值为-8981kN；随着监测断面与断层距离的增大，监测断面最大轴力呈下降趋势。由各监测断面最大轴力整体分析可知，施设减错层工况监测断面最大轴力小于无减错措施工况。
由表 7可知，施设减错层与无减错措施工况监测断面最大弯矩值均表现为外侧受拉；无减错措施工况监测断面最大弯矩值出现在下盘靠近断层的断面，其值为-218kN·m，施设减错层监测断面最大弯矩值出现在下盘距离断层11m处，其值为-269kN·m。由各监测断面最大弯矩整体分析可知，施设减错层工况监测断面最大弯矩大于无减错措施工况。
3.2 结构安全系数
提取各工况错动完成时各监测断面的计算数据，以减错层弹性模量为2.5MPa为例进行安全系数分析，监测断面最小安全系数见表 8。
表 8 监测断面最小安全系数Table 8. Minimum safety factor of monitoring section工况 距断层距离/m -21 -11 -2 2 11 21 32 无减错措施 1.919 1.172 0.733 0.889 1.032 1.651 3.310 减错层弹模（2.5MPa） 2.455 1.798 1.505 1.583 1.592 2.031 3.399 由表 8可知，施设减错层与无减错措施工况监测断面最小安全系数沿隧道纵向分布趋势相似，最小值均出现在下盘靠近断层监测的断面，其中无减错措施工况最小安全系数最小值为0.733，施设减错层工况最小安全系数最小值为1.505；随着监测断面与断层距离的增大，监测断面最小安全系数呈增大趋势，上盘安全系数整体较下盘小。由各监测断面最小安全系数整体分析可知，施设减错层工况监测断面最小安全系数大于无减错措施工况。
3.3 减错效果
根据安全系数分析各工况减错效果，减错效果计算方法同式（5），各工况减错效果如图 4所示。
由图 4可知，各工况减错效果沿隧道纵向分布趋势相似，随着监测断面与断层距离的增大，上下盘减错效果整体呈下降趋势，且下盘减错效果较上盘整体略好，其中下盘减错效果最大为105.32%，上盘减错效果最大为78.07%；当减错层弹性模量增加到一定程度（约100MPa），减错效果趋于稳定。
4. 结论
（1）断层黏滑错动对隧道上盘的影响远大于下盘，上盘部分是黏滑断层隧道减错设防设计的重点段落。
（2）减错缝对上盘部分隧道结构的减错效果优于下盘，其中上盘减错效果最大为24.50%，下盘减错效果最大为9.26%；减错层对下盘部分隧道结构的减错效果略优于上盘，其中下盘减错效果最大为105.32%，上盘减错效果最大为78.07%。
（3）随着减错缝宽度的增加，隧道上盘减错效果变好，下盘缝宽10—15cm减错效果最好，主要是由于断层黏滑错动对上盘的影响远大于下盘。减错缝宽度的增加适应了断层黏滑错动造成的上盘强制位移，断层黏滑错动的能量得到一定程度的释放，从而提高了上盘隧道的结构安全性，可以设想，对于隧道上盘部分存在最优减错缝宽度；减错缝宽度的增加虽然适应了断层黏滑错动造成的下盘强制位移，由于抵御断层黏滑错动对下盘影响所需减错缝缝宽为10—15cm，当缝宽增加到20cm时，下盘隧道整体刚度的下降对下盘隧道的结构安全性造成了不利影响，致使减错效果下降。
（4）随着减错层弹性模量的增加，隧道上下盘减错效果降低；当减错层弹性模量增加到一定程度（约100MPa），减错效果趋于稳定。
-
图 1 数值解与解析解对比
Figure 1. Comparison between the numerical solution and the analytical solution
图 6 不同阻尼比下振动响应峰值曲线
Figure 6. Peak response curves of vibration under different damping ratios
表 1 材料参数
Table 1. Material parameters
工况 材料 密度/kg·m-3 弹性模量/MPa 泊松比 工况1 黏土1(0—200m) 2000 30 0.35 工况2 黏土2(0—200m) 2100 60 0.35 工况3 黏土1(0—100m) 2000 30 0.35 黏土2(100—200m) 2100 60 0.35 工况4 黏土1(0—100m) 2100 60 0.35 黏土2(100—200m) 2000 30 0.35 桩 2500 2×103 0.20 
下载: 导出CSV
表 2 工况1水平振动速度衰减公式系数取值
Table 2. The coefficient of velocity attenuation formula of horizontal vibration in working condition 1
影响系数 ξ=0.05 ξ=0.15 ξ=0.25 2000kN 4000kN 6000kN 2000kN 4000kN 6000kN 2000kN 4000kN 6000kN a 0.0124 0.0248 0.0371 0.0019 0.0038 0.0057 0.0017 0.0035 0.0052 b -0.0987 -0.0987 -0.0987 -0.0809 -0.0809 -0.0809 -0.0790 -0.0790 -0.0790 c 3.08×10-4 6.17×10-4 6.17×10-4 6.17×10-4 1.57×10-5 2.35×10-5 4.61×10-5 9.22×10-5 1.38×10-4 d -0.0182 -0.0182 -0.0182 -0.0148 -0.0148 -0.0148 -0.0148 -0.0148 -0.0148
下载: 导出CSV
表 3 工况2水平振动速度衰减公式系数取值
Table 3. The coefficient of velocity attenuation formula of horizontal vibration in working condition 2
影响系数 ξ=0.05 ξ=0.15 ξ=0.25 2000kN 4000kN 6000kN 2000kN 4000kN 6000kN 2000kN 4000kN 6000kN a 0.0161 0.0321 0.0482 0.0022 0.0044 0.0066 0.0019 0.0038 0.0056 b -0.1083 -0.1083 -0.1083 -0.0782 -0.0782 -0.0782 -0.0828 -0.0828 -0.0828 c 3.38×10-4 6.75×10-4 0.001 1.24×10-4 2.47×10-4 3.71×10-4 5.60×10-5 1.12×10-4 1.68×10-4 d -0.0148 -0.0148 -0.0148 -0.0148 -0.0148 -0.0148 -0.0148 -0.0148 -0.0148
下载: 导出CSV
表 4 工况1竖向振动速度衰减公式系数取值
Table 4. The coefficient of the attenuation formula of vertical vibration velocity in working condition 1
影响系数 ξ=0.05 ξ=0.15 ξ=0.25 2000kN 4000kN 6000kN 2000kN 4000kN 6000kN 2000kN 4000kN 6000kN a 0.0118 0.0237 0.0355 0.0016 0.0033 0.0049 0.0027 0.0055 0.0082 b -0.0851 -0.0851 -0.0851 -0.1120 -0.1120 -0.1120 -0.1151 -0.1151 -0.1151 c 2.60×10-4 5.20×10-4 7.80×10-4 1.55×10-4 3.09×10-4 4.64×10-4 1.77×10-4 3.53×10-4 5.30×10-4 d -0.0182 -0.0182 -0.0182 -0.0182 -0.0182 -0.0182 -0.0182 -0.0182 -0.0182
下载: 导出CSV
表 5 工况2竖向振动速度衰减公式系数取值
Table 5. The coefficient of the attenuation formula of vertical vibration velocity in working condition 2
影响系数 ξ=0.05 ξ=0.15 ξ=0.25 2000kN 4000kN 6000kN 2000kN 4000kN 6000kN 2000kN 4000kN 6000kN a 0.0119 0.0237 0.0356 0.0108 0.0216 0.0324 0.0028 0.0055 0.0083 b -0.0857 -0.0857 -0.0857 -0.1544 -0.1544 -0.1544 -0.1132 -0.1132 -0.1132 c 3.21×10-4 6.41×10-4 9.62×10-4 2.91×10-4 5.82×10-4 8.73×10-4 1.64×10-4 3.29×10-4 4.93×10-4 d -0.0182 -0.0182 -0.0182 -0.0182 -0.0182 -0.0182 -0.0182 -0.0182 -0.0182
下载: 导出CSV
-
陈龙珠, 陈胜立, 梁发云, 2002.饱和地基竖向振动的衰减特性.上海交通大学学报, 36(3):376—381. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=shjtdxxb200203022 杜修力, 赵密, 王进廷, 2006.近场波动模拟的人工应力边界条件.力学学报, 38(1):49—56. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=lxxb200601007 韩云山, 董彦莉, 王元龙等, 2015.不同夯击方式下地表土体振动衰减规律研究.中北大学学报(自然科学版), 36(4):475—480, 487. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hbgxyxb201504015 李润, 简文彬, 康荣涛, 2011.强夯加固填土地基振动衰减规律研究.岩土工程学报, 33(S1):246—250. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=7508279 廖振鹏, 2002.工程波动理论导论.北京:科学出版社. 刘晶波, 王振宇, 杜修力等, 2005.波动问题中的三维时域粘弹性人工边界.工程力学, 22(6):46—51. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gclx200506008 刘毓氚, 刘一鸣, 2012.桩基础对邻近场地冲击荷载的响应分析.岩土力学, 33(9):2796—2802. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ytlx201209037 马蒙, 刘维宁, 王文斌, 2013.轨道交通地表振动局部放大现象成因分析.工程力学, 30(4):275—280, 309. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gclx201304040 陶连金, 张波, 王文沛等, 2011.冲击作用下地层振动衰减规律的现场试验研究.地震工程与工程振动, 31(4):33—39. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dzgcygczd201104005 滕忻利, 2008.强夯引发的环境振动效应分析与评价.北京: 北京交通大学. 王雨林, 刘勇健, 2005.基于波动理论的PHC桩桩锤选择研究.广东土木与建筑, (11):12—15, 25. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gdtmyjz200511005 向国威, 叶冠林, 王建华, 2012.冲击振动在砂土中传播的模型试验研究.上海交通大学学报, 46(1):136—141. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=shjtdxxb201201028 中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局, 2015.GB 51076—2015电子工业防微振工程技术规范.北京: 中国计划出版社, 2015. Deeks A. J., Randolph M. F., 1994. Axisymmetric time-domain transmitting boundaries. Journal of Engineering Mechanics, 120(1): 25—42. doi: 10.1061/(ASCE)0733-9399(1994)120:1(25) Ekanayake S. D., Liyanapathirana D. S., Leo C. J., 2013. Influence zone around a closed-ended pile during vibratory driving. Soil Dynamics and Earthquake Engineering, 53: 26—36. doi: 10.1016/j.soildyn.2013.06.005 Henke S., 2010. Influence of pile installation on adjacent structures. International Journal for Numerical and Analytical Methods in Geomechanics, 34(11): 1191—1210. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1002/nag.859 Kausel E., 2006. Fundamental solutions in elastodynamics: A compendium.Cambridge:Cambridge University Press. Lamb H., 1904. On the propagation of tremors over the surface of an elastic solid. Philosophical Transactions of the Royal Society of London, 203(359-371): 1—42. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=J-STAGE_2074456 Lysmer J., Kuhlemeyer A. M., 1969. Finite dynamic model for infinite media. Journal of the Engineering Mechanics Division, 95(4): 759—877. http://ci.nii.ac.jp/naid/10018723298 Masoumi H. R., Degrande G., Lombaert G., 2007. Prediction of free field vibrations due to pile driving using a dynamic soil–structure interaction formulation. Soil Dynamics and Earthquake Engineering, 27(2): 126—143. doi: 10.1016/j.soildyn.2006.05.005 Thandavamoorthy T. S., 2004. Piling in fine and medium sand-A case study of ground and pile vibration. Soil Dynamics and Earthquake Engineering, 24(4): 295—304. doi: 10.1016/j.soildyn.2003.12.005 -
下载:
点击查看大图
计量
- 文章访问数: 177
- HTML全文浏览量: 52
- PDF下载量: 8
- 被引次数: 0
