Review of Physical Vulnerability Assessment of Building Based on Indicator Method
-
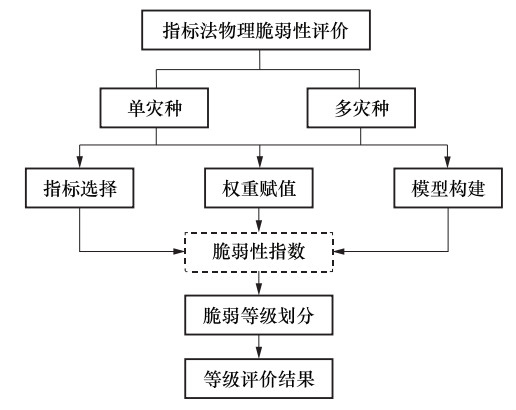
摘要: 承灾体脆弱性评估是科学进行灾害风险评估和预测的基础，房屋建筑作为面大量广的承灾体，众多学者对建筑物理脆弱性指标模型进行了研究。基于单灾种和多灾种2个维度，针对指标模型构建的各环节，全面梳理了几种典型单灾种物理脆弱性指标体系和评估模型构建情况，发现指标选取理论依据不明确，模型构建主观性较强，不能准确表征建筑特点与抗灾能力间的内在联系。系统总结了多灾种指标体系和耦合物理脆弱性指标模型研究现状，发现多灾种之间及其对承灾体影响的复杂耦合效应在现有指标模型中未得到充分体现。研究结果表明，明晰指标依据、优化模型构建是提升单灾种物理脆弱性评估准确性的关键；改进脆弱性耦合模型、拓展综合脆弱性评估方法是健全多灾种脆弱性评估研究的核心。Abstract: Vulnerability assessment of disaster bearing bodies is the basis of disaster risk assessment and prediction. Building is a kind of disaster bearing body vast in number and wide in scale, the research of physical vulnerability index model of buildings has attracted the interest of many researchers. The construction process of indicator-based method was introduced from the two dimensions of single-hazard and multi-hazard. The physical vulnerability index system and the index model construction of several typical single-hazard are comprehensively sorted out, and it is recognized that the scientific basis of model construction is not clear and the model construction is highly subjective which cannot accurately represent the internal relationship between the building characteristics and the ability to resist disasters. The research status of the physical vulnerability coupling index model for the triggering effect of multi-hazards was summarized, and it is found that coupling effects and their impacts on disaster bearing body are not fully reflected in the existing model. The research shows that optimizing index model and elaborating basis of indicators are the key to improve the effectiveness of single-hazard physical vulnerability assessment. Perfecting indicator system, improving coupled vulnerability model and developing the comprehensive vulnerability assessment method are the core of the research on multi-hazard vulnerability assessment.
-
Key words:
- Physical vulnerability /
- Index model /
- Single-hazard /
- Multi-hazard /
- Coupling effect /
- Comprehensive vulnerability
-
引言
古登堡和里希特在1941年美国地质学会会刊中提出全球的地震活动服从经验关系lgN=a-bM(式中M表示震级，N表示震级≥M的地震次数，a、b是常数)。一般认为a值代表地区的地震活动总体水平(Rundle，1989)；b值代表地震活动的大小地震数量的比例，是地震活动研究中的重要参量。研究表明，b值具有明确的物理意义，与地壳的介质特性、应力状态和不均匀性有关，能反映所研究区域的地质构造特征(王熠熙等，2015；谢卓娟等，2015)以及地震的震源特征(Schorlemmer等，2005；Gulia等，2010；刘静伟等，2016；张广伟，2016)。因此，b值广泛应用于地震危险性分析和地震预测研究之中。在地震危险性分析中，b值和地震年发生率共同用于确定地震活动的水平(胡聿贤，1999)，其取值对地震危险性分析结果的影响较大(鄢家全等，1996；黄玮琼等，1998；谢卓娟等，2013)；而在地震预测研究中，b值作为基本的地震活动性参数，成为地震预测的常用指标参数(韩渭宾，2003；沈建文等，2007)。
通常根据实际地震资料统计得到b值。目前，常用的b值估算方法是最大似然估计法(Aki，1965)和最小二乘法等，这些方法不仅对实际资料的完整性和精度有一定要求，同时也需要足够的地震资料。在实际工作中，对于历史地震资料短缺或地震活动水平低的地区，在计算b时常常将现代小震资料与历史地震资料联合使用，以弥补地震资料样本量的不足(黄玮琼等，1989；鄢家全等，1996；胡聿贤，1999；潘华等，2006)。统计b值对地震资料样本量需求的定量研究，国内尚无专门的研究报道。在国外，Nava等(2017)利用蒙特卡罗模拟地震目录进行抽样估计，研究最大似然法计算b值时对样本量的需求，得出计算b值时样本量和精度之间的相互关联关系，但没有应用实际地震目录进行分析。国内仅有少部分学者的研究涉及相关内容，如韩晓明等(2016)研究河套地震带b值时空变化特征的文章中，探讨了地震前后b值的变化规律，分别使用最小二乘法和最大似然法对b值时间和空间进行了扫描计算，在最小二乘法计算中，设定每次计算的窗长内包含的样本数目不少于100，而最大似然法的扫描窗内包含的样本数目不少于20；刘方斌等(2017)在鲁西南聊考断裂带地震危险性评价与活动性分布的研究中，利用最大似然法和最小二乘法估算b值并进行了对比研究，但是没有给出样本量的具体数目，且没有用分震级段的方法进行b值估算。
本文采用Utsu(1965)提出的最大似然法和最小二乘法，利用模拟地震目录和实际地震目录，定量分析最小二乘法和最大似然法计算b值时分别对地震资料样本量的需求。
1. 资料概况
1.1 模拟地震目录
蒙特卡罗法是以抽样和随机数的产生为基础的随机性方法，也称为随机抽样法、计算机随机模拟法等。蒙特卡罗方法的基本原理是通过数字模拟试验，得到所要求解的出现某种事件的概率作为问题的近似解。其基本思想是：为了求解数学、物理、工程技术以及管理等方面的问题，首先建立概率模型或随机过程，使用相应的参数，得到某些问题(如概率分布或数学期望等问题)的解；然后通过对模型或过程的观察或抽样试验来计算所求参数的统计特征，并用算术平均值作为所求解的近似值。因此，只要尽可能完整地表示地震震源模型，即获得某一区域内地震事件的发生时间和空间上的分布规律，那么就可以直接利用蒙特卡罗方法产生合成地震序列。
蒙特卡罗方法的基本依据是随机模拟次数足够多的情况下，事件发生的频率可以反映事件发生的概率。当模拟次数有限时，计算结果和真实值之间必然存在误差，这种误差随着模拟次数的增加而减少。
蒙特卡罗模拟中随机变量的简单子样(X1，X2，X3，……，XN)是独立分布的，即每次模拟中事件发生的次数与其它任意1次中事件发生的次数N无关，那么随机变量就是服从泊松分布的，当随机变量X的期望值趋向于无穷时，泊松分布趋近于正态分布。
本文利用蒙特卡罗方法模拟地震目录(张建中, 1974a, 1974b；任雪梅等，2011)，研究不同样本量下计算方法对b值的影响。
首先，构造概率分布模型：
$$ F(M) = \int_{{M_0}}^M {f(M){\rm{d}}M} $$ (1) 其中，f(M)为震级的概率密度函数，表示为：
$$ f(M) = \frac{{\beta {{\rm{e}}^{ - \beta M}}}}{{{{\rm{e}}^{ - \beta {M_0}}} - {{\rm{e}}^{ - \beta {M_{\rm{u}}}}}}} $$ (2) 其次，将公式(2)带入公式(1)，得到关于模拟震级M的函数：
$$ F(M)({{\rm{e}}^{ - \beta {M_0}}} - {{\rm{e}}^{ - \beta {M_{\rm{u}}}}}) = {{\rm{e}}^{ - \beta {M_0}}} - {{\rm{e}}^{ - \beta M}} $$ (3) $$ {{\rm{e}}^{ - \beta M}} = {{\rm{e}}^{ - \beta {M_0}}} - F(M)({{\rm{e}}^{ - \beta {M_0}}} - {{\rm{e}}^{ - \beta {M_{\rm{u}}}}}) $$ (4) $$ M = - \frac{1}{\beta }{\rm{ln(}}{{\rm{e}}^{ - \beta {M_0}}} - F(M)({{\rm{e}}^{ - \beta {M_0}}} - {{\rm{e}}^{ - \beta {M_{\rm{u}}}}})) $$ (5) 式中，$ \beta = b{\rm{ln}}(10)$，M0为计算所用截止的震级，Mu为震级上限。
设定b=1、M0=2.0、Mu=8.0，利用MATLAB随机数程序模拟生成不同样本量的地震目录，样本数分别为5000、4500、4000、3500、3000、2500、2000、1750、1500、1250、1000、750、500、250、100、80、60、40、20、10，每个目录模拟10000组。由于实际大地震非常稀缺，所以震级上限的限制对计算结果没有显著影响。
1.2 汾渭地震带实际地震目录
本研究使用的实际地震资料来自中国地震台网中心的地震数据库。研究表明地震资料的完整性对地震活动分析非常重要(Wiemer等，2000；Rotondi等，2002)。经统计分析(焦远碧等，1990；黄伟琼等, 1994a, 1994b；周公威等，2007；谢卓娟等，2012a；徐伟进等，2014)，1970年以来汾渭地震带M 2.0以上的地震资料基本完整，故本研究选取1970年1月—2010年12月，M≥2.0的8184次地震资料进行研究分析，其中M 2.0—2.9地震7044次、M 3.0—3.9地震964次、M 4.0—4.9地震148次、M 5.0—5.9地震25次、M 6.0—6.9地震3次，所用的地震目录均已删除前震、余震。汾渭地震带4.7级以上地震的震中分布见图 1。
图 1 汾渭地震带范围及震中分布Figure 1. The distribution of earthquakes in the Fen-Wei seismic tectonic zone2. 模拟地震目录的结果分析
利用最小二乘法和最大似然法对模拟的地震目录进行定量研究分析，比较2种方法在不同的样本量下计算得到的平均b值以及样本量的大小对计算结果的影响。
文中使用的最大似然法为Utsu(1965)提出的公式：
$$ b = \frac{{\lg {\rm{e}}}}{{\bar M - {\rm{(}}M{\rm{0}} - \Delta M/2)}} $$ (6) 其中，$ \bar M$是平均震级；$\Delta M $=0.1，用来对实际地震记录进行校正。当实际地震的震级记录精度为$\Delta M $、计算所用截止的震级为M0时，其实际代表($M{\rm{0}} - \Delta M/2 $)≤M0 < ($ M{\rm{0}} + \Delta M/2$)的地震。为了使拟合的地震目录尽量贴近实际情况，文中模拟的地震目录震级是连续变化的，将震级归并到各自$\Delta M $中，再用最大似然法拟合b值。
最小二乘法使用累积震级-频度关系($\lg N = a - bM $)计算b值，采用0.5作为震级间隔，即震级分档为0.5级。
采用上述最大似然法和最小二乘法计算，分别得到平均b值随样本量的变化，如图 2、3所示。
图 2 不同样本量下最大似然法计算得到的平均b值拟合图Figure 2. The fitting curve of mean b values calculated by maximum likelihood method under different sample sizes
图 3 不同样本量下最小二乘法计算得到的平均b值拟合图Figure 3. The fitting curve of mean b values calculated by least squares method under different sample sizes由图 2、3可知，当样本量大于300时，最大似然法计算的平均b值能取得符合预期的数值；样本量大于1000时，最小二乘法计算的平均b值趋于稳定，向理论值收敛。
采用Nava等(2017)提出的方法，分析不同样本量下的b值平均值和设定值之间的差异。设定样本组数Nr=10000，模拟不同容量的样本N来计算b值，并统计得出合理设定值的概率。表 1、2分别是2种方法在b=1时，不同样本量下的b值计算值、标准差及其正确估值概率，其中，b1表示设定b=1条件下得到的b值平均计算值，精度$\Delta b $=0.025；Pr-表示过低估计的概率(Pr- < 0.975)；Pr表示准确估计的概率(0.975≤Pr≤1.025)；Pr+表示过高估计的概率(Pr+ > 1.025)；$ \sigma $表示标准差。
表 1 最大似然法模拟结果Table 1. Simulation results by the maximum likelihood methodN b1 Pr- Pr Pr+ σ 10 1.221 0.46 0.14 0.40 0.42 20 1.211 0.46 0.25 0.29 0.38 50 1.145 0.44 0.30 0.16 0.16 100 1.061 0.53 0.37 0 0.13 200 1.039 0.52 0.48 0 0.11 400 1.036 0.47 0.53 0 0.09 500 1.025 0.45 0.55 0 0.08 1000 1.003 0.30 0.70 0 0.08 表 2 最小二乘法模拟结果Table 2. Simulation results by the least squares methodN b1 Pr- Pr Pr+ σ 10 0.870 0.79 0.08 0.13 0.52 20 0.895 0.76 0.07 0.17 0.48 50 0.918 0.68 0.27 0.05 0.42 100 0.941 0.64 0.28 0.08 0.37 200 0.942 0.46 0.48 0.06 0.32 400 0.955 0.48 0.52 0 0.28 500 0.982 0.45 0.50 0.05 0.16 1000 0.996 0.20 0.80 0 0.12 表 1、2表明，样本量低于200、b=1.00、精度$\Delta b $=0.025时，得到正确估算值的概率较低(小于0.5)，因此要求样本量至少大于200。
当设定b=1时，不同样本下得到的b值分布直方图见图 4。由图可知，当样本量≥200时，最大似然法计算的b值很好地向设定值收敛；样本量≥500时，最小二乘法计算的b值有较好的收敛效果。从估值概率来看，取得的b值一般都偏低。
图 4 不同样本量的b值分布直方图Figure 4. The histogram of the b value calculated under different sample sizes根据上述分析，2种方法虽然都能得到符合预期的数值，但最小二乘法计算的平均b值通常比最大似然法的小，而标准差比最大似然法的大；样本量小于1000时，利用最小二乘法得到的平均b值精确度较低；样本量大于1000时，2种计算方法得出的结果差别不大。进一步分析认为，虽然2种方法都需要一定的样本量，且样本量越大、得到的结果越准确，但最大似然法对样本量的要求要比最小二乘法低，样本量大于200时，计算得到的平均b值与设定值一致性较好；样本量大于1000时，基本等于设定值。
3. 实际地震目录的计算结果分析
根据汾渭地震带地震资料的完整性和可靠性研究，自1970年以来，台站记录得到的M≥2.0地震目录基本完整，故本研究以汾渭地震带1970年1月—2010年12月的地震记录为计算样本，研究实际地震目录样本量对b值计算的影响。表 3给出该地震带不同震级档的地震数目，并计算出不同震级档的年平均发生率(黄玮琼等，1989；潘华等，2006；吴兆营等2005；谢卓娟等，2012b)。
表 3 汾渭地震带地震分档统计和年平均发生率Table 3. The annual average incidence of different magnitude-class in Fen-Wei seismic zone震级档M 地震个数 年平均发生率 2.0—2.4 5038 119.95 2.5—2.9 2006 47.76 3.0—3.4 734 17.48 3.5—3.9 230 5.61 4.0—4.4 110 2.62 4.5—4.9 91 2.17 5.0—5.4 15 0.36 5.5—5.9 10 0.23 6.0—8.5 3 0.07 注：年平均发生率指震级≥M的年均地震数，代表地震活动水平。 根据表 3中统计的各震级档的地震个数和年平均发生率，利用最小二乘法和最大似然法计算得到的b值分别为0.75和0.75335。
为研究实际地震目录下b值计算对样本量的要求，采用任雪梅(2011)的抽样原则，对汾渭地震带的地震目录进行均匀抽样分析，每次抽样完将样本放回进行下一次抽样，得到样本量分别为10、50、100、200、300、500、700、1000、5000的地震目录，每个目录重复抽样10000次。同样，采用2种方法分别计算不同样本量下的平均b值(表 4)，并分析不同样本量下的b值变化。
表 4 汾渭地震带b值拟合情况(1500—2010年)Table 4. The b value fitting of earthquakes from 1500—2010 in the Fen-Wei seismic zone样本量 均匀抽样计算b值 最小二乘法 最大似然法 10 0.60 0.897 50 0.62 0.923 100 0.63 0.816 200 0.63 0.728 300 0.65 0.767 500 0.69 0.752 700 0.70 0.756 1000 0.72 0.746 2000 0.74 0.751 5000 0.75 0.753 由表 4可以看出，2种计算方法得到b值随着样本量的增加逐渐接近真实b值；当样本量大于200时，最大似然法能够得出相对稳定可靠的b值；当样本量大于500时，最小二乘法才能得到相对稳定可靠的b值。因此，对实际的地震目录，最小二乘法对样本量的要求也比较高，且受地震目录完整性的影响较大。
4. 结论
通过上述研究和对比分析，得到以下认识：
(1) 利用最大似然法计算b值时，样本量至少要在200以上；对于最小二乘法，样本量要求不少于1000；一般来说，计算的b值都低于设定值。
(2) 最小二乘法利用震级-频度的线性关系来拟合计算b值，样本量不足会影响其线性关系。因此，最小二乘法受样本量影响较大，样本量小于1000时，b值的计算值与设定值相差较大，数值也不稳定。
(3) 最大似然法方便快捷，受样本量影响小，计算出的b值相对稳定，但误差估计值偏大，其利用平均震级计算，只与地震个数有关，受数据质量的影响较小；最小二乘法受样本量影响较大，在样本量充足的情况下计算的b值比较准确，而在样本量不足时b值波动较大，误差也随着样本量的减少而增加。在实际应用中，以地震目录充足为前提，研究不同区域的b值优先选用最小二乘法；而研究某区域b值时间上的变化时，采用最大似然法估算的b值相对稳定，更能体现b值长期变化的趋势。
(4) 从误差和计算量来看，最大似然法比最小二乘法要小，但随着样本量的增加，2种方法计算结果的差异越来越小。但由于半对数坐标下不同震级档数据权重的不对等性，国外已极少使用最小二乘法。
-
表 1 脆弱性等级划分标准
Table 1. Classification rule of vulnerability level
等级划分 脆弱性指数划分 涉及灾种 划分特点 来源 低、中、高 [0—0.33]、[0.34—0.66]、[0.67—1.00] 洪水 等间隔划分脆弱性指数，无脆弱等级描述 Yankson等（2017） 轻微破坏、中等破坏、大量破坏、完全毁坏 [0.1—0.3]、[0.4—0.6]、[0.7—0.8]、[0.9—1.0] 泥石流 按照破坏等级分配脆弱性指数，破坏等级与HAZUS地震方法中定义的破坏状态相似 Kang等（2016） 基本完好、轻微破坏、中等破坏、严重破坏、完全破坏 [0.1—0.2]、[0.2—0.4]、[0.4—0.6]、[0.6—0.8]、[0.8—1.0] 滑坡 等间隔划分脆弱性指数，根据专家调查确定破坏等级 guillard-gonalves等（2016） 极低、低、中、高、极高 [0—0.2]、[0.2—0.4]、[0.4—0.6]、[0.6—0.8]、[0.8—1.0] 多灾种 等间隔划分脆弱性指数，脆弱等级描述结合已有研究及专家意见 卢颖等（2017） 
下载: 导出CSV
表 2 泥石流物理脆弱性评估方法
Table 2. Assessment method of physical vulnerability of debris flow
作者 研究区域 指标体系 模型方法 评估特点 Jean-Claude等（2014） 秘鲁南部阿雷基帕46个城市街区的约1000座建筑物 建筑物类型、建筑物材料、楼层数、维护状态、屋顶类型、位置和角度、基岩类型、冲积阶地的存在、坡度 主成分分析法（PCA） 指标选择较详细，分析方法降低了主观性，消除评估指标间的相关性影响。模型还适用于其他城市泥石流脆弱性研究，可应用性较强 Papathoma-Köhle等（2003） 意大利南蒂罗尔马尔泰地区51座建筑物 建筑物材料、维护状态、楼层数、周围街道树木朝向 专家判断法 指标选择上较宽泛，分析方法人为色彩较浓，但将指标法与脆弱性曲线结合，对于改进物理脆弱性评估方法具有重要作用 Ding等（2012） 云南省昆明市东川区小江流域 结构类型、建设年代、楼层数、住房面积 SOM神经网络法 由于研究目的为风险评估，物理脆弱性评估因子选择较简单，缺乏对灾害作用下环境特征指标的综合考虑 庞金彪（2017） 岷江上游山区各县乡 建筑物功能、建筑物结构、建筑物材料、建筑物面积、建筑物到最近泥石流沟的距离 SOM神经网络法 选择了建筑物功能指标，但建筑物功能、建筑物材料、建筑物结构间存在相关性，其对脆弱性的影响还需进一步探讨。SOM模型在数据分类中主观干扰小，聚类结果合理
下载: 导出CSV
表 3 滑坡物理脆弱性评估模型
Table 3. Physical vulnerability assessment model of landslide
作者 模型类型 指标体系 脆弱性模型 Papathoma- Köhle等（2007） 定性模型 建筑物材料（a）、楼层数（b）、周围环境（c）、滑坡面是否开窗（d）、是否存在潜在滑坡危险（e） $V = 5a + 4b + 3c + 2d + e$
式中，$V$为物理脆弱性，$a-e$为各指标得分Uzielli等（2008） 定量模型 结构类型${\xi _{{\rm{STY}}}}$、维护状态${\xi _{{\rm{SMN}}}}$ $ V=I·S$ $S = 1 - (1 - {\xi _{{\rm{STY}}}})(1 - {\xi _{{\rm{SMN}}}})$
式中，V为物理脆弱性，I为滑坡强度，S为建筑物易感性，${\xi _{{\rm{STY}}}}$为结构类型指标得分，${\xi _{{\rm{SMN}}}}$为维护状态指标得分Li等（2010） 定量模型 建筑物材料${\xi _{{\rm{SFD}}}}$、建筑物高度${\xi _{{\rm{STY}}}}$、建造年代${\xi _{{\rm{Smn}}}}$、基础深度${\xi _{{\rm{Sht}}}}$ $ V=f(I·R)$ $ R=\sqrt[4]{{\xi }_{\rm{SFD}}·{\xi }_{\rm{STY}}·{\xi }_{\rm{Smn}}·{\xi }_{\rm{Sht}}}$
式中，V为物理脆弱性，I为滑坡强度，R为建筑物抵抗力；${\xi _{{\rm{SFD}}}}$、${\xi _{{\rm{STY}}}}$、${\xi _{{\rm{Smn}}}}$、${\xi _{{\rm{Sht}}}}$为各指标得分Silva等（2014） 定量模型 结构类型CT、建筑物材料CM、楼屋面板材料FRS、楼层数NF、维护状态CS $ PV=LM·(1-BR)$
$BR = 0.3CT + 0.3CM + 0.2FRS + 0.1NF + 0.1CS$
式中，PV为物理脆弱性，LM为滑坡强度，BR为建筑物抵抗能力
下载: 导出CSV
表 4 洪水物理脆弱性评估模型
Table 4. Physical vulnerability assessment model of flood
作者 研究目标 指标体系 权重方法 评估特点 Fernandez等（2016） 社会、经济、环境、物理脆弱性 建筑物密度、楼层数、建造年代、结构类型 主成分分析法（PCA） 分析方法提高了指标选择和数量灵活性，但指标选取上略显粗糙 Müller等（2011） 社会、物理脆弱性 建筑物材料、建筑物位置、植被覆盖比例、排水设施 专家判断 进行了指标权重敏感性分析，结果表明指标对权重值的变化不敏感，指标选取具有合理性 Uwakwe（2015） 物理脆弱性 墙体材料、建筑物高度、楼层数、建造年代、保存状况 专家判断 指标权重赋值时对不同领域专家分值进行了综合，其中建筑物高度被认为是影响洪水脆弱性最重要的因素 Yankson等（2017） 物理、社会、环境脆弱性 房屋类型、房屋材料（地板、屋顶、外墙材料）、排水设施、建筑物位置（高程、坡度、到海岸线的距离） 专家判断 指标选取上用高程、坡度、海岸线距离作为量化评估因子，改善了定性评估的不确定性 Krellenberg等（2017） 社会、环境、物理脆弱性 建造质量、结构类型、是否有防护墙、屋顶类型、植被覆盖程度 专家判断 屋顶类型指标选取不合理，因其与洪水脆弱性的相关性较低。研究认为结构类型、植被覆盖程度是影响脆弱性的主要驱动因素 Romanescu等（2016） 物理、人口脆弱性 建筑物距河道的距离、水利工程存在与否、建筑物材料、建筑物质量、建筑物用途 专家判断 建筑物距河道的距离指标被赋予了更高的权重，作为影响脆弱性的主要原因
下载: 导出CSV
-
陈国华, 邹梦婷, 黄孔星等, 2019.化工园区多灾种耦合脆弱性方法探究与前沿综述.化工进展, 38(5):2527—2535. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hgjz201905055 葛全胜, 邹铭, 郑景云, 2008.中国自然灾害风险综合评估初步研究.北京:科学出版社. 辜智慧, 王娟, 葛怡等, 2015.基于PTVA修正模型的建筑单体台风脆弱性评估方法.中国安全科学学报, 25(11):99—105. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgaqkxxb201511017 哈斯, 张继权, 佟斯琴等, 2016.灾害链研究进展与展望.灾害学, 31(2):131—138. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zhx201602027 季安康, 2017.震区砌体结构房屋抗震能力评价体系研究.哈尔滨: 东北林业大学. 李莉, 王晓婷, 王辉, 2010.脆弱性内涵、评价与研究趋势综述.中国渔业经济, 28(3):161—169. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgyyjj201003027 李琳, 王俊杰.2018.四川省城市地震灾害脆弱性综合评价研究.震灾防御技术, 13(4):968—977. http://zzfy.eq-j.cn/zzfyjs/ch/reader/view_abstract.aspx?file_no=20180424&flag=1 刘爱华, 2013.城市灾害链动力学演变模型与灾害链风险评估方法的研究.长沙: 中南大学. 刘爱华, 吴超, 2015.基于复杂网络的灾害链风险评估方法的研究.系统工程理论与实践, 35(2):466—472. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xtgcllysj201502022 刘希林, 莫多闻, 2002.泥石流易损度评价.地理研究, 21(5):569—577. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dlyj200205005 刘珍, 文彦君, 薛界兰等, 2018.宝鸡农村地区地震灾害房屋脆弱性空间变化.华北地震科学, 36(4):25—32. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hbdzkx201804004 卢颖, 侯云玥, 郭良杰等, 2015.沿海城市多灾种耦合危险性评估的初步研究——以福建泉州为例.灾害学, 30(1):211—216. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zhx201501037 卢颖, 王洁鑫, 姜学鹏等, 2017.基于PTVA模型的房屋多灾种耦合物理脆弱性评估.中国安全科学学报, 27(8):1—6. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgaqkxxb201708001 罗军华, 林孝松, 牟凤云等, 2018.山区公路暴雨-洪水灾害链贝叶斯网络建模推理.中国安全科学学报, 28(12):1—6. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgaqkxxb201812001 明晓东, 徐伟, 刘宝印等, 2013.多灾种风险评估研究进展.灾害学, 28(1):126—132, 145. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zhx201301027 潘毅, 李玲娇, 姚蕴艺等, 2016.砖石结构古建筑震后破坏状态评估方法.西南交通大学学报, 51(4):704—713. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xnjtdxxb201604015 庞金彪, 2017.岷江上游泥石流胁迫下山区建筑物易损性评价.绵阳: 西南科技大学. 石先武, 国志兴, 张尧等, 2016.风暴潮灾害脆弱性研究综述.地理科学进展, 35(7):889—897. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dlkxjz201607010 史培军, 2002.三论灾害研究的理论与实践.自然灾害学报, 21(3):1—9. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zrzhxb200203001 史培军, 1996.再论灾害研究的理论与实践.自然灾害学报, 1(4):6—17. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199600705870 史培军, 吕丽莉, 汪明等, 2014.灾害系统:灾害群、灾害链、灾害遭遇.自然灾害学报, 23(6):1—12. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zrzhxb201406001 薛晔, 刘耀龙, 张涛涛, 2013.耦合灾害风险的形成机理研究.自然灾害学报, 22(2):44—50. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zrzhxb201302007 张学玲, 余文波, 蔡海生等, 2018.区域生态环境脆弱性评价方法研究综述.生态学报, 38(16):5970—5981. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=stxb201816035 周扬, 李宁, 吴文祥, 2014.自然灾害社会脆弱性研究进展.灾害学, 29(2):128—135. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zhx201403030 周瑶, 王静爱, 2012.自然灾害脆弱性曲线研究进展.地球科学进展, 27(4):435—442. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dqkxjz201204009 Alwang J., Siegel P. B. Jorgensen S. L., 2001. Vulnerability: A view from different disciplines. Social Protection and Labor Policy and Technical Notes. Balica S., Wright N. G., 2010. Reducing the complexity of the flood vulnerability index. Environmental Hazards-human and Policy Dimensions, 9(4): 321—339. doi: 10.3763/ehaz.2010.0043 Birkmann J., 2006. Indicators and criteria. Measuring vulnerability to natural hazards: Towards disaster resilient societies. Chen H. X., Zhang S., Peng M., et al., 2015. A physically-based multi-hazard risk assessment platform for regional rainfall-induced slope failures and debris flows. Engineering Geology, 203: 15—29. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=c153bad1f6eb864a4730e9d0e3d48e02 Dall'Osso F., Dominey-Howes D., Tarbotton C., et al., 2016. Revision and improvement of the PTVA-3 model for assessing tsunami building vulnerability using "international expert judgment": Introducing the PTVA-4 model. Natural Hazards, 83(2): 1229—1256. doi: 10.1007/s11069-016-2387-9 Dall'Osso F., Gonella M., Giovanni G. et al., 2009. A revised(PTVA)model for assessing the Vulnerability of buildings to Tsunami damage. Natural Hazards and Earth System Sciences, 9(5): 1557—1565. doi: 10.5194/nhess-9-1557-2009 Dall'Osso F., Maramai A., Graziani L., et al., 2010. Applying and validating the PTVA-3 model at the Aeolian Islands, Italy: Assessment of the vulnerability of buildings to tsunami. Natural Hazards and Earth System Sciences, 10(7): 1547—1562. doi: 10.5194/nhess-10-1547-2010 Ding M. T., Wei F. Q., Hu K. H., 2012. Property insurance against debris-flow disasters based on risk assessment and the principal-agent theory. Natural Hazards, 60(3): 801—817. doi: 10.1007/s11069-011-9897-2 Dombrowsky W. R., 1995. Again and again: Is a disaster what we call a 'Disaster'? International Journal of Mass Emergencies and Disasters, 13(3): 241—254. http://www.mendeley.com/catalog/again-again-disaster-we-call-disaster/ Dominey-Howes D., Papathoma-Kohle M., 2007. Validating a tsunami vulnerability assessment model (the PTVA model) using field data from the 2004 Indian Ocean Tsunami. Natural Hazards, 40(1): 113—136. doi: 10.1007/s11069-006-0007-9 Fernandez P., Mourato S., Moreira M., et al., 2016. A new approach for computing a flood vulnerability index using cluster analysis. Physics and Chemistry of the Earth, Parts A/B/C, 94: 47—55. doi: 10.1016/j.pce.2016.04.003 Ferreira T. M., Vicente R., Mendes da Silva J. A. R., et al., 2013. Seismic vulnerability assessment of historical urban centres: case study of the old city centre in Seixal, Portugal. Bulletin of Earthquake Engineering, 11(5): 1753—1773. doi: 10.1007/s10518-013-9447-2 Formisano A., Chieffo N., Marius M., et al., 2017. Seismic vulnerability and damage of a historical center in the district of Caserta (Italy). 3rd International Conference on Protection of Historical Constructions. Gent Franch K. A., Giuliano Morbelli G. M., Astroza Inostroza M. A., et al., 2008. A seismic vulnerability index for confined masonry shear wall buildings and a relationship with the damage. Engineering Structures, 30(10): 2605—2612. doi: 10.1016/j.engstruct.2008.02.005 Gill J. C., Malamud B. D., 2016. Hazard interactions and interaction networks (cascades) within multi-hazard methodologies. Earth System Dynamics, 7(3): 659—679. doi: 10.5194/esd-7-659-2016 Godfrey A., Ciurean R. L., Westen C. J., et al., 2015. Assessing vulnerability of buildings to hydro-meteorological hazards using an expert based approach-An application in Nehoiu Valley, Romania. International Journal of Disaster Risk Reduction, 13: 229—241. doi: 10.1016/j.ijdrr.2015.06.001 Guillard-Gonalves C., Zêzere J. L., Pereira S. S., et al., 2016. Assessment of physical vulnerability of buildings and analysis of landslide risk at the municipal scale-application to the Loures municipality, Portugal. Natural Hazards and Earth System Sciences Discussions, 16(2): 311—331. doi: 10.5194/nhess-16-311-2016 Inter American Development Bank (IDB), 2011. Indicators for disaster risk and risk management: Program for Latin-America and the Caribbean: Bahamas. Idb Publications. International Strategy for Disaster Reduction, 2004. Living with risk: A global review of disaster reduction initiatives Geneva: United Nations. Izquierdo T., Fritis E., Abad M., 2018. Analysis and validation of the PTVA tsunami building vulnerability model using the 2015 Chile post-tsunami damage data in Coquimbo and La Serena cities. Natural Hazards and Earth System Sciences, 18(6): 1703—1716. doi: 10.5194/nhess-18-1703-2018 Jean-Claude T., Ettinger S., Guitton M., et al., 2014. Assessing physical vulnerability in large cities exposed to flash floods and debris flows: The case of Arequipa (Peru). Natural Hazards, 73(3): 1771—1815. doi: 10.1007/s11069-014-1172-x Kang H., Kim Y., 2016. The physical vulnerability of different types of building structure to debris flow events. Natural Hazards, 80(3): 1475—1493. doi: 10.1007/s11069-015-2032-z Kappes M., Keiler M., Glade T., 2010. From single-to multi-hazard risk analyses: A concept addressing emerging challenges. Mountain Risks: Bridging Science to Society. Kappes M., Papathoma-Köhle M., Keiler M., 2012. Assessing physical vulnerability for multi-hazards using an indicator-based methodology. Applied Geography, 32(2): 577—590. doi: 10.1016/j.apgeog.2011.07.002 Krellenberg K., Welz J., 2017. Assessing urban vulnerability in the context of flood and heat hazard: Pathways and challenges for indicator-based analysis. Social Indicators Research, 132(2): 709—731. doi: 10.1007/s11205-016-1324-3 Li Z. H., Nadim F., Huang H. W., et al., 2010. Quantitative vulnerability estimation for scenario-based landslide hazards.Landslides, 7(2): 125—134. doi: 10.1007/s10346-009-0190-3 Marzocchi W., Garcia-Aristizabal A., Gasparini P., et al., 2012. Basic principles of multi-risk assessment: A case study in Italy. Natural Hazards, 62(2): 551—573. doi: 10.1007/s11069-012-0092-x Marzocchi W., Mastellone M., Di Ruocco A., et al., 2009. Principles of multi-risk assessment: interactions amongst natural and man-induced risks. European Commission. Maskrey A., 1989. Disaster mitigation: a community based approach. Oxford, England: Oxford England Oxfam. Müller A., Reiter J., Weiland U., 2011. Assessment of urban vulnerability towards floods using an indicator-based approach-a case study for Santiago de Chile. Natural Hazards and Earth System Sciences Discussions. 11(8): 2107—2123. doi: 10.5194/nhess-11-2107-2011 Nardo M., Saisana M., Saltelli A., et al., 2008. Handbook on constructing composite indicators: Methodology and user guide. Oecd Statistics Working Papers, 73(2): 1111. http://www.researchgate.net/publication/263538041_Handbook_on_Constructing_Composite_Indicators_Methodology_and_User_Guide Gasparini P., Garcia-Aristizabal A., 2014. Seismic risk assessment, cascading effects. Encyclopedia of Earthquake Engineering. Springer-Verlag Berlin Heidelberg. Papathoma-Köhle M., 2016. Vulnerability curves vs. vulnerability indicators: Application of an indicator-based methodology for debris-flow hazards. Natural Hazards and Earth System Sciences, 16(8): 1771—1790. doi: 10.5194/nhess-16-1771-2016 Papathoma-Köhle M., Dominey-Howes D., Zong Y., et al., 2003. Assessing tsunami vulnerability, an example from Herakleio, Crete. Natural Hazards and Earth System Sciences, 3(5): 377—389. doi: 10.5194/nhess-3-377-2003 Papathoma-Köhle M., Gems B., Sturm M., Fuchs S., et al., 2017. Matrices, curves and indicators: A review of approaches to assess physical vulnerability to debris flows. Earth-Science Reviews, 171: 272—288. doi: 10.1016/j.earscirev.2017.06.007 Papathoma-Köhle M., Neuhä; user B., Ratzinger K., et al., 2007. Elements at risk as a framework for assessing the vulnerability of communities to landslides. Natural Hazards and Earth System Sciences, 7(6): 765—779. doi: 10.5194/nhess-7-765-2007 Perles Roselló M. J., Cantarero Prados F., 2010. Problems and challenges in analyzing multiple territorial risks. Methodological proposals for multi-hazard mapping. Boletın de la Asociación de Geógrafos Espanoles, 52: 399—404. http://www.researchgate.net/publication/288556258_Problems_and_challenges_in_analyzing_multiple_territorial_risks_Methodological_proposals_for_multi-hazard_mapping Romanescu G., Chelariu O. E., Ionut M., et al., 2016. Flood vulnerability assessment in the mountain–plateau transition zone. Case study for Marginea village (Romania).Journal of Flood Risk Management, 11(S1): S502—S513. doi: 10.1111/jfr3.12249 Santos A., Tavares A. O., Emidio A., 2014. Comparative tsunami vulnerability assessment of an urban area: An analysis of Setúbal city, Portugal.Applied Geography, 55: 19—29. doi: 10.1016/j.apgeog.2014.08.009 Silva M., Pereira S. S., 2014. Assessment of physical vulnerability and potential losses of buildings due to shallow slides. Natural Hazards, 72(2): 1029—1050. doi: 10.1007/s11069-014-1052-4 Uwakwe A. C., 2015. Assesment of physical vulnerability to flood in Saint Lucia: Case studies: Castries old central business district and dennery village. Enschede, Netherlands: University of Twente Faculty of Geo-Information and Earth Observation (ITC). Uzielli M., Nadim F., Lacasse S., et al., 2008. A conceptual framework for quantitative estimation of physical vulnerability to landslides. Engineering Geology, 102(3): 251—256. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=e14b158e454420e47ef7c5623bd85575 Voulgaris G., Murayama Y., 2014. Tsunami vulnerability assessment in the Southern Boso Peninsula, Japan. International Journal of Disaster Risk Reduction, 10: 190—200. doi: 10.1016/j.ijdrr.2014.08.001 Westgate K., 1978. UNDRO-disaster prevention and mitigation-compendium of current knowledge-united-nations. Disasters, 2(2-3): 176—178. http://www.safetylit.org/citations/index.php?fuseaction=citations.viewdetails&citationIds[]=citjournalarticle_35885_4 Xu C., Xu X. W., Dai F. C., et al., 2012. Comparison of different models for susceptibility mapping of earthquake triggered landslides related with the 2008 Wenchuan earthquake in China. Computers & Geosciences, 46: 317—329. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=f697d8239be9baa741270e0821c2e018 Xu L. F., Meng X. W., Xu X. G., 2014. Natural hazard chain research in China: A review. Natural Hazards, 70(2):1631—1659. doi: 10.1007/s11069-013-0881-x Xu M. Z., Wang Z. Y., Qi L. J., et al., 2012. Disaster chains initiated by the Wenchuan earthquake. Environmental Earth Sciences, 65(4): 975—985. doi: 10.1007/s12665-011-0905-3 Yankson P. W. K., Owusu A. B., Owusu G., et al., 2017. Assessment of coastal communities' vulnerability to floods using indicator-based approach: A case study of Greater Accra Metropolitan Area, Ghana.Natural Hazards, 89(2): 661—689. doi: 10.1007/s11069-017-2985-1 Zuccaro G., De Gregorio D., Leone M. F., 2018. Theoretical model for cascading effects analyses. International Journal of Disaster Risk Reduction, 30: 199—215. doi: 10.1016/j.ijdrr.2018.04.019 期刊类型引用(5)
1. 徐宗学 ，卢兴超 ，施奇妙 . 城市暴雨洪涝灾害特征与风险评估研究进展. 水利水电科技进展. 2025(01): 1-9+46 . 
百度学术2. 黄晶，王子勍，戴强，王慧敏. 考虑人群活动的城市场所洪涝灾害风险动态评估——以深圳市为例. 地理科学. 2024(04): 711-720 . 百度学术3. 褚传丰，王伟，石雨欣，张洪云，黄莉. 粤港澳大湾区复合灾害承灾体脆弱性评估. 三峡大学学报(自然科学版). 2024(04): 60-67 . 百度学术4. 王辉，李优，李瑚均，陈辉华，程建华，张建设. 土木工程建造系统脆弱性研究综述. 铁道科学与工程学报. 2024(07): 2932-2943 . 百度学术5. 岳建伟，任国友. 农村社区风险评估体系的建立和应用. 安全. 2022(04): 29-35 . 百度学术其他类型引用(2)
-
下载:
点击查看大图
计量
- 文章访问数: 594
- HTML全文浏览量: 92
- PDF下载量: 66
- 被引次数: 7
