Analysis of the Influence of Uniform Excitation and Multi-point Excitation on the Seismic Response of Suspension Bridge
-
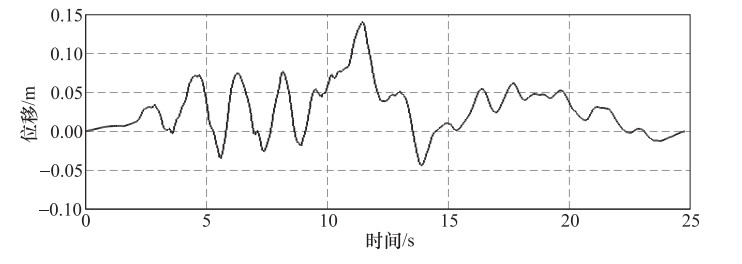
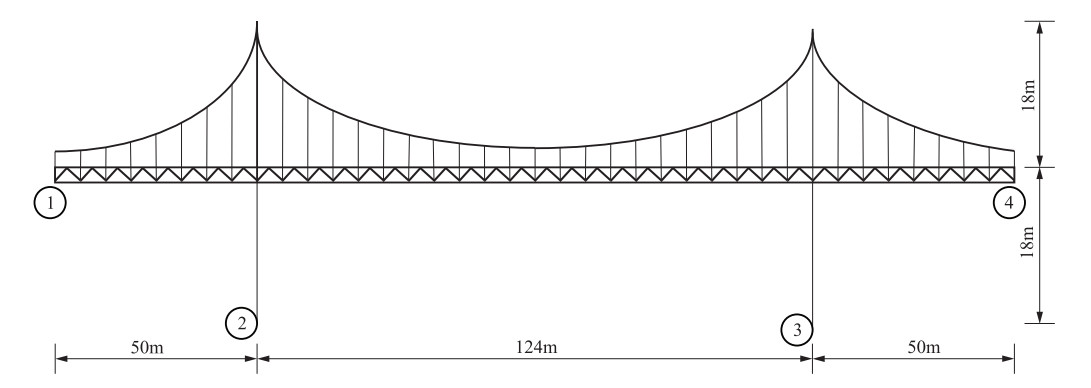
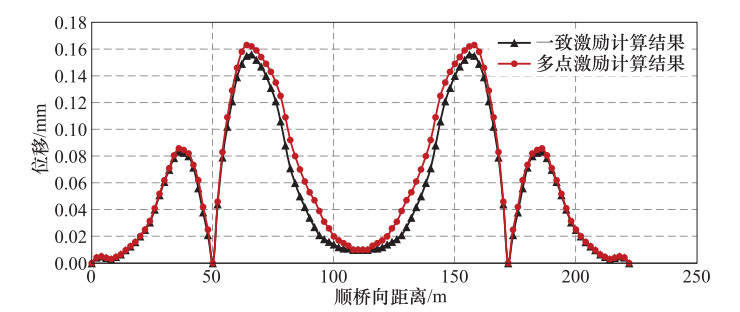
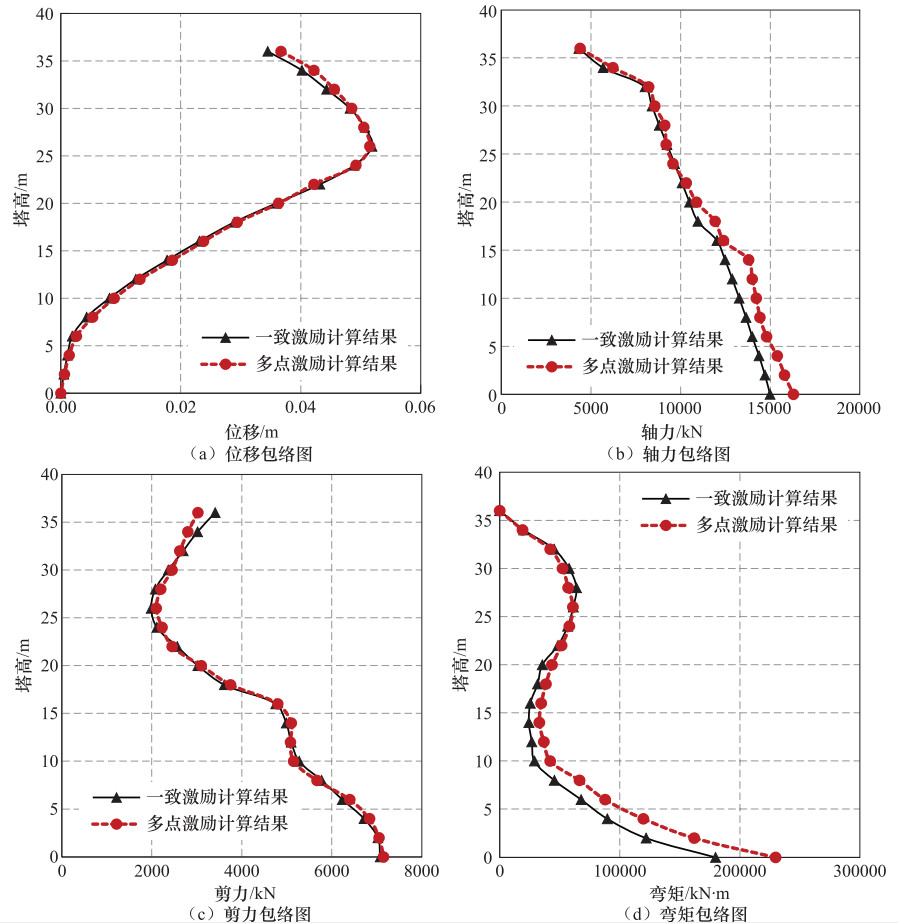
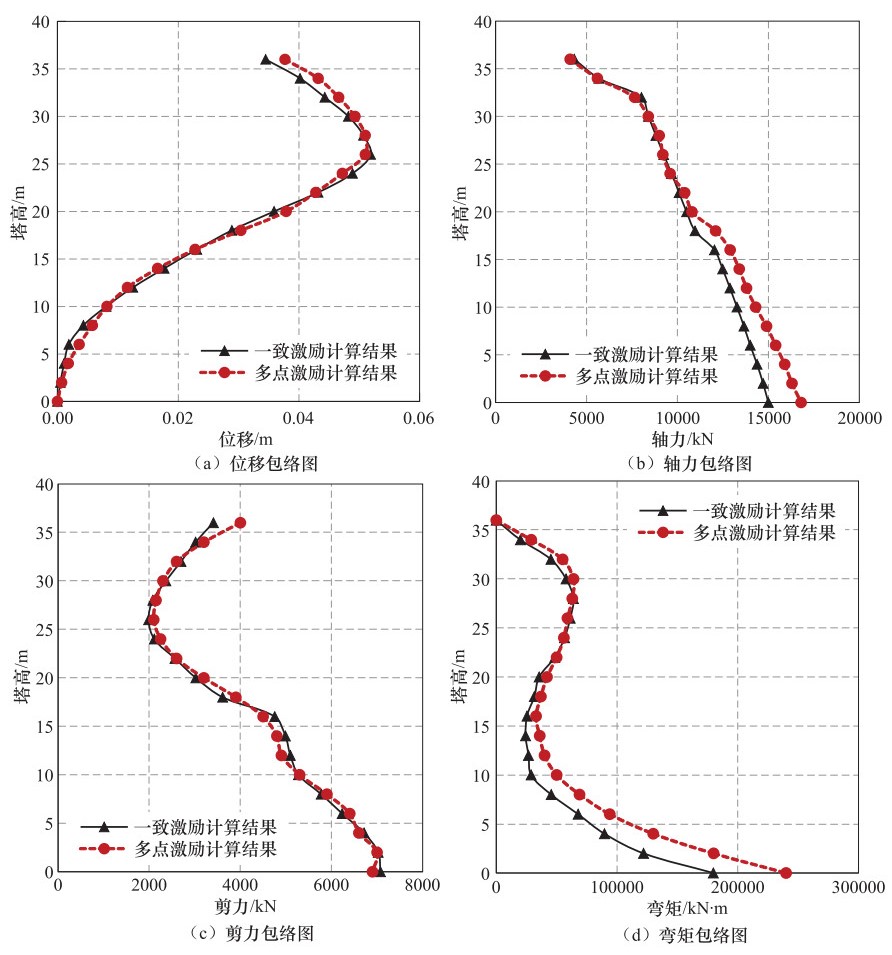
摘要: 利用大型通用有限元软件ANSYS的APDL参数化语言，建立某悬索桥结构三维有限元模型，通过加速度时程积分曲线，获得相应的位移时程曲线，在桥台及桥墩处施加位移时程荷载，分析桥梁结构多点激励地震响应，并分析一致激励与多点激励下桥梁关键位置位移、内力差异，研究不同激励方式的影响。Abstract: Using the APDL parametric language of the general finite element software ANSYS, a three-dimensional finite element model of the structure of a suspension bridge was established. Through the integration of acceleration time history, the corresponding displacement time history is derived. With the input of displacement time history on the bridge abutment and bridge pier, the seismic response of bridge structure under multi-support excitation is analysized, and the internal force and deformation is compared with those derived under uniform excitation. The influence of different excitation on bridge is concluded.
-
Key words:
- Suspension bridge /
- Multiple-support excitation /
- Seismic response
-
图 1 输入Kobe波加速度时程曲线（顺桥向）
Figure 1. The input Kobe wave of acceleration time history curve (Along the bridge)
图 2 Kobe波位移时程曲线（顺桥向）
Figure 2. The input Kobe wave of displacement time history curve (Along the bridge)
图 3 桥梁结构立面图及荷载激励点布置
Figure 3. The elevation and load excitation point layout of the bridge
图 5 主梁顺桥向最大位移包络图
Figure 5. Envelope diagram of maximum displacement of main beam along bridge direction
图 6 南桥塔纵向位移、轴力、剪力及弯矩包络图
Figure 6. The envelope of displacement, axial force, shearing force and bending moment of the occurrence bridge tower longitudinal
图 7 北桥塔纵向位移、轴力、剪力及弯矩包络图
Figure 7. The envelope of displacement, axial force, shearing force and bending moment of the north bridge tower longitudinal
表 1 桥梁结构材料物理参数
Table 1. The material physical parameters of bridge structure
构件 材料 弹性模量/Pa 泊松比 密度/kg·m-3 主缆 钢丝绳 21.0×1010 0.167 7850 吊索 钢丝绳 21.0×1010 0.167 7850 加劲桁架、纵梁 C30混凝土 3.0×1010 0.300 2500 桥塔、桥面板 C20混凝土 2.8×1010 0.300 2500 
下载: 导出CSV
表 2 输入位移时程延迟时间（s）
Table 2. The delay time of input displacement time history (s)
支座编号 ① ② ③ ④ 时间间隔 0.000 0.050 0.174 0.224
下载: 导出CSV
-
范立础, 胡世德, 叶爱君, 2001.大跨度桥梁抗震设计.北京:人民交通出版社. 江洋, 2010.大跨建筑结构多点输入地震响应计算与抗震设计方法研究.北京: 清华大学. 景鹏旭, 李丽, 2017.湖北秭归千将坪滑坡微破裂过程震动分析.地震工程学报, 39(5):951—956. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xbdzxb201705021 黎璟, 杨华平, 钱永久等, 2019.非一致激励下大跨度铁路斜拉桥地震响应规律.铁道建筑, 59(6):14—16, 32. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=tdjz201906004 李光军, 2012.大跨度悬索桥地震反应分析.哈尔滨: 中国地震局工程力学研究所. 李国豪, 2003.桥梁结构稳定与振动.北京:中国铁道出版社. 李丽, 景鹏旭, 徐沁, 2018a.基于多点地震动输入条件下的土质边坡地震反应分析.防灾减灾工程学报, 38(2):352—358, 384. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dzxk201802020 李丽, 李吉, 景鹏旭等, 2018b.钢管混凝土柱的非线性变形及受力性能研究.建筑结构, 48(S2):571—574. http://www.cnki.com.cn/Article/CJFDTotal-JCJG2018S2115.htm 刘春城, 张哲, 石磊, 2004.多支承激励下自锚式悬索桥空间地震反应分析.哈尔滨工业大学学报, 11(36):1568—1570. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hebgydxxb200411040 刘润舟, 2008.交通系统震后连通性研究.哈尔滨: 中国地震局工程力学研究所. 刘旭政, 王鹏, 2018.行波效应对长跨连续刚构桥地震响应的影响.华东交通大学学报, 35(1):20—26. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hdjtdxxb201801004 梅泽洪, 李小军, 王玉石等, 2017.考虑场地效应的非一致激励下桥梁地震响应特点分析.震灾防御技术, 12(3):646—654. http://zzfy.eq-j.cn/zzfyjs/ch/reader/view_abstract.aspx?file_no=20170320&flag=1 钱炜, 2007.柔性悬索桥静力分析及抗震性能研究.合肥: 合肥工业大学. 苏成, 陈海斌, 2008.多点激励下大跨度桥梁的地震反应.华南理工大学学报(自然科学版), 36(11):101—107. http://www.cqvip.com/Main/Detail.aspx?id=29122224 铁道部大桥工程局桥梁科学研究所, 1996.悬索桥.北京:科学技术文献出版社. 王蕾, 赵成刚, 王智峰, 2006.考虑地形影响和多点激励的大跨高墩桥地震响应分析.土木工程学报, (1):50—53, 59. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=tmgcxb200601010 王再荣, 孙利民, 程纬, 2016.超大跨斜拉桥地震行波效应分析.同济大学学报(自然科学版), 44(10):1471—1481. http://d.wanfangdata.com.cn/Periodical/tjdxxb201610001 许基厚, 王学伟, 祝兵等, 2019.非对称单侧混合梁斜拉桥多点激励地震响应分析.地震工程学报, 41(5):1207—1214. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xbdzxb201905014 严琨, 王立新, 姜慧, 2017.伸缩缝刚度对大跨度悬索桥动力特性的影响.震灾防御技术, 12(3):667—676. http://zzfy.eq-j.cn/zzfyjs/ch/reader/view_abstract.aspx?file_no=20170322&flag=1 张沧海, 2011.大跨度桥梁多点多向激励地震反应分析.哈尔滨: 中国地震局工程力学研究所. 张凡, 颜晓伟, 李帅等, 2016.考虑波速影响的斜拉桥非一致激励地震响应研究.建筑科学与工程学报, 33(4):60—68. Fleming J. F., Egeseli E.A., 1980. Dynamic behavior of a cable-stayed bridge. Earthquake Engineering and Structure Dynamic, 8(1):1—16. doi: 10.1002/eqe.4290080102 Leger P., Ide I. M., Paultre P., 1990. Multiple-support seismic analysis of large structures. Computers & Structures, 36(6): 1153—1158. http://www.sciencedirect.com/science/article/pii/004579499090224P -
点击查看大图
计量
- 文章访问数: 385
- HTML全文浏览量: 41
- PDF下载量: 15
- 被引次数: 0
