Focal Mechanism Solution for Jiashi Ms5.5 Earthquake Sequence on September 4, 2018 and the Characteristics of Stress Field in the Source Area
-
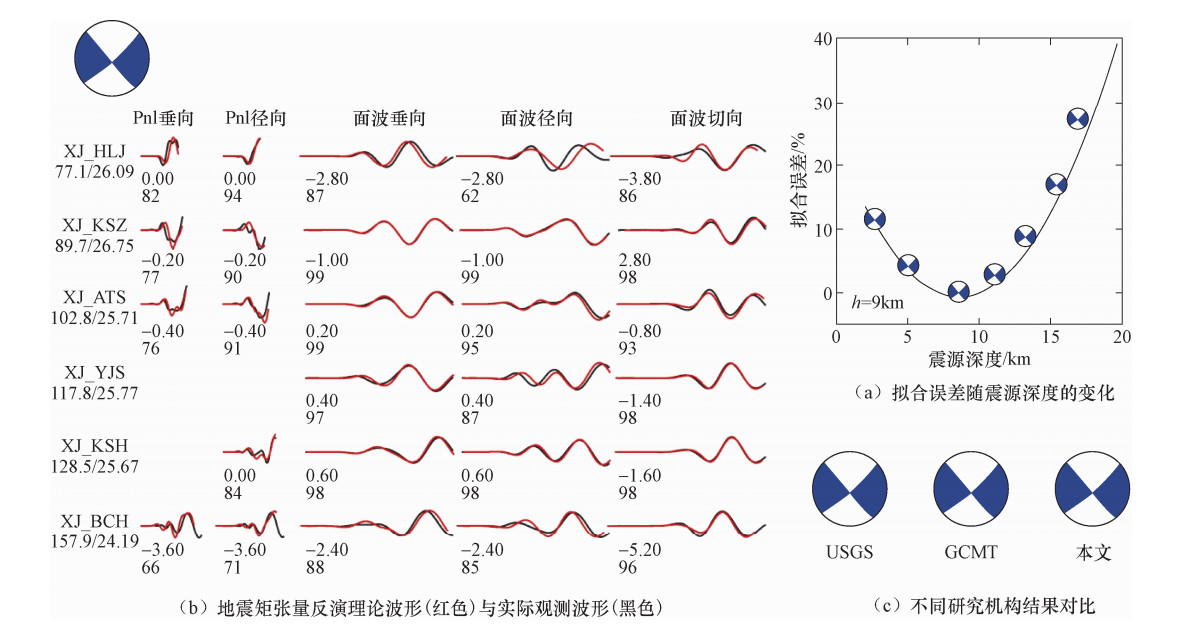
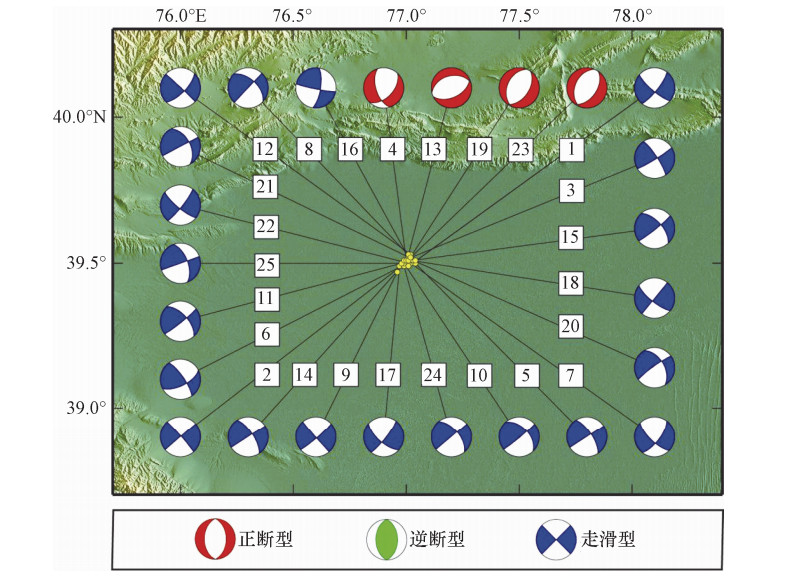
摘要: 本文采用新疆测震台网数字波形记录，利用CAP和P、S波初动和振幅比方法计算2018年9月4日伽师5.5级地震序列中MS≥2.5地震的震源机制解，结合地震烈度等震线和双差重定位后的地震序列空间展布等特征分析了此次地震的发震构造，反演了震源处应力场。结果表明，伽师5.5级地震呈NE向的节面I为发震断层面，属于左旋走滑断层，震源深度为9km，发震构造可能为浅部超基底断裂；地震序列中有21次为走滑型，4次为正断型，说明绝大多数序列的破裂方式与主震相近，表明余震应力场主要受主震震源应力场控制；P轴方位在NNE向有明显的优势分布且倾伏角较小，T轴方位在NWW向有明显的优势分布且倾伏角较小，说明震源处主要以NNE向水平挤压和NWW向水平拉张作用为主；此次伽师5.5级地震序列表现的浅部应力场与已有研究得出的震源区深部应力场基本一致，应力形因子R的最优解为0.17，说明震源处近NE向中间主应力σ2有一定挤压成分。Abstract: Based on the digital waveforms record of Xinjiang seismic network,the CAP and P-wave,S-wave initial motion and amplitude ratio methods were used to calculate the focal mechanism solution of the MS≥2.5 earthquake sequence of Jiashi Ms5.5 earthquake on September 4,2018. The seismogenic structure of this earthquake was analyzed based on the seismic intensity isoseismic lines and the spatial distribution of the earthquake sequence after double differential relocation,and the stress field in the source area was inverted. The results show that the nodal plane I is the seismogenic fault,which is northeast trend and nearly upright left-lateral strike slip fault. The focal depth of main shock is about 9km. It is preliminarily inferred that the seismogenic structure may be superficial ultra crystalline basement fault. The 21 earthquake sequences are strike-slip and 4 earthquake sequences are normal faults. The rupture pattern of most earthquake sequences is similar to that of the main shock,indicating that the aftershock stress field is mainly controlled by the main shock source area stress field. P axis is near north-northeast,and the inclination angle is small. T axis is near northwest-west,and the inclination angle is small. It indicates that the stress field of source area is mainly under action of north-northeast horizontal compression and the northwest-west horizontal tensional. The shallow stress field shown in Jiashi 5.5 earthquake sequences is basically the same as the deep stress field obtained from previous research. The stress shape ratio is 0.17,and it shows that there is a certain compression of σ2.
-
Key words:
- Jiashi MS5.5 earthquake /
- Focal mechanism solution /
- Stress field /
- CAP /
- First motion /
- Amplitude ratio /
- Double difference location
-
引言
近年来，频繁的地震灾害造成了巨大的人员伤亡和经济损失，选择可靠的加固方法对既有混凝土结构进行加固与维护变得尤为重要。随着经济和技术的发展，高性能材料大量涌现。纤维增强复合材料（Fiber Reinforced Polymer，简称FRP）以其轻质、高强、耐腐蚀、施工方便等优点，在混凝土结构加固中得到越来越广泛的应用（Hollaway等，2008；Teng等，2002；Xiao等，2009）。聚对苯二甲酸乙二醇酯纤维增强复合材料（Polyethylene Terephthalate Fiber Reinforced Polymer，简称PET FRP）和聚萘二甲酸乙二醇酯纤维增强复合材料（Polyethylene Naphthalene Fiber Reinforced Polymer，简称PEN FRP）以其断裂应变较大（ >5%）的特点，弥补了传统FRP断裂应变较小（1.5～3%）的不足。与传统FRP相比，高延性FRP由回收废弃塑料制成，价格相对低廉，且符合绿色环保发展理念（Han等，2020）。由于高延性特点，高延性FRP加固柱可避免发生脆性破坏。因此，在混凝土结构抗震加固中，高延性FRP成为传统碳纤维增强复合材料（Carbon Fiber Reinforced Polymer，简称CFRP）的可替代方案。
随着建筑材料科学的发展，结构跨度、高度及形式越来越多样化，混凝土结构主体各部分和构件尺寸逐渐增大。然而，FRP约束混凝土柱轴压力学性能研究多基于小尺寸试件，对FRP约束混凝土大尺寸柱破坏机理和力学性能的研究较少（蔡静，2015；龙跃凌等，2010；邓宗才等，2019；Dai等，2011；Han等，2020；Ozbakkaloglu等，2013；Saleem等，2016；Wang等，2008；Zeng等，2018）。因此，需进一步对FRP约束混凝土大尺寸柱进行研究。为此，本文对8个PET FRP约束混凝土圆柱（直径300、400 mm试件各4个）和8个PEN FRP约束混凝土方柱（边长300、400 mm试件各4个）进行试验研究和理论分析，以期为实际工程提供理论依据。
1. 试验概况
1.1 试件设计
本文以构件截面形状及FRP层数为参数，试件长细比均为2，截面尺寸如图1所示，编号及参数如表1所示。试件编号中“C”表示圆柱，“S”表示方柱，“PET”表示PET FRP，“PEN”表示PEN FRP，“300”表示试件直径或边长为300 mm，“400”表示试件直径或边长为400 mm，“2”表示FRP为2层，“3”表示FRP为3层，“4”表示FRP为4层，“a，b”表示2个完全相同的试件。
表 1 试件编号及参数Table 1. Details of specimens试件编号 直径或边长/mm 高度/mm 角半径/mm 材料类型 FRP层数/层 C-PET-300-2-a,b 300 600 — PET FRP 2 C-PET-300-3-a,b 300 600 — PET FRP 3 C-PET-400-2-a,b 400 800 — PET FRP 2 C-PET-400-4-a,b 400 800 — PET FRP 4
S-PEN-300-2-a,b
300
600
60
PEN FRP
2
S-PEN-300-3-a,b
300
600
60
PEN FRP
3
S-PEN-400-2-a,b
400
800
80
PEN FRP
2
S-PEN-400-4-a,b
400
800
80
PEN FRP
41.2 材料性能
1.2.1 混凝土
所有试件均使用当地制造商提供的同批预拌混凝土进行浇筑。试块按标准养护28 d后，根据ASTM标准（ASTM C469，2002），在北京工业大学结构实验室进行抗压强度试验，测得素混凝土标准圆柱平均抗压强度
$ f_{{\rm{co}}}' $ 为33.3 MPa，本文将未约束混凝土的峰值应变εco取0.225%，该值由下式计算得到（Popovics，1973）：$$ {\varepsilon _{{\rm{co}}}} = 9.37 \times {10^{ - 4}}\sqrt[{4}]{{f_{{\rm{co}}}^\prime }} $$ (1) 1.2.2 CFRP及胶体力学性能
CFRP由北京卡本工程技术研究所有限公司生产，PET FRP和PEN FRP从日本Maeda Kosen公司购买，胶体由上海三悠树脂有限公司生产。CFRP、PET FRP和PEN FRP名义厚度分别为0.111、0.841、1.272 mm，抗拉强度分别为3972、740、790 MPa，伸长率分别为1.77 %、8.3 %、5.8 %。CFRP弹性模量为245.5 GPa，PET FRP和PEN FRP第1阶段弹性模量分别为17.9、27.0 GPa，第2阶段弹性模量分别为8.3、12.0 GPa。
按照ASTM标准（ASTM D3039M，2008），对PET FRP和PEN FRP进行平板拉伸试验，如图2、3所示。PET FRP和PEN FRP拉伸应力-应变曲线分别如图4、5所示，可知曲线表现出近似双折线的应力-应变关系。
1.3 试件制作
试件制作步骤如下：（1）准备模具，将模具固定在模板上，并做好模具底部防水工作；（2）浇筑混凝土；（3）养护成型，拆模；（4）湿铺法包裹纤维布，纤维布搭接长度为试件周长的1/2，防止接口处因黏结不牢影响构件加固效果；（5）各试件上、下端分别采用60、100 mm宽CFRP进行加固，防止加载过程中出现端部破坏现象。
1.4 量测方案
采用YAM-72000J型电液伺服试验机进行加载，选择位移控制加载方式，加载速率为0.6 mm/min。为避免FRP突然断裂损坏试验机器，圆柱试件在外包PET FRP环向应变最大值达3.5 %时终止试验，方柱试件在外包PEN FRP环向应变最大值达2.2 %时终止试验。各试件使用3对LVDT位移传感器进行轴向位移测量，其中1对用于测量试件整体轴向变形，另外2对均匀放置在接近试件四角位置的位移架上，用于测量试件中部区域范围内的轴向变形，如图6所示，所有试验数据均由采集仪记录。
试件环向应变均采用长度为20 mm的电阻式应变片进行测量，应变片（编号SG1～SG10）布置如图7所示。
2. 试验结果与分析
2.1 主要试验结果
基于同批压爆的小尺寸试件得到的经验及试验过程中遇到的情况，调整得到终止试验时的PET FRP与PEN FRP环向应变最大值。总之，在保证实验室安全的前提下，尽量使试件加载时间更久，试验曲线更长。试验结束后的试件如图8所示，主要试验结果如表2、3所示。表2、3中fcu ′ 为试件极限应力，取试验终止时的应力；εcu表示试件极限轴向应变；εh,rup表示试件环向断裂应变；εh,c表示方柱试件2个角上环向断裂应变的平均值；εh,s表示方柱试件3个面上环向断裂应变的平均值；在混凝土中，压应力和压应变符号为正；在FRP中，拉伸应力和拉伸应变符号为正；应力表示轴向荷载与截面面积的比值；应变表示测区竖向位移与卡距的比值。
表 2 圆柱主要试验结果Table 2. Key results of circular column tests试件编号 fcu ′ /MPa εcu/% εh,rup/% 最大环向应变对应的应变片编号 C-PET-300-2-a 37.2 1.79 3.38 SG1 C-PET-300-2-b 39.2 2.28 3.86 SG5 C-PET-300-3-a
49.6
3.51
4.16
SG1C-PET-300-3-b 50.4 3.41 4.24 SG4 C-PET-400-2-a 35.9 1.67 3.38 SG1 C-PET-400-2-b 36.2 1.75 3.23 SG2 C-PET-400-4-a 45.2 2.19 3.28 SG5 C-PET-400-4-b 45.0 2.24 3.36 SG1 表 3 方柱主要试验结果Table 3. Key results of square column tests试件编号 fcu ′ /MPa εcu/% εh,c/% εh,s/% 最大环向应变对应的应变片编号 S-PEN-300-2-a 37.6 2.34 1.46 2.19 SG9 S-PEN-300-2-b 38.4 2.28 1.75 2.34 SG1 S-PEN-300-3-a 54.8 3.14 1.77 2.84 SG1 S-PEN-300-3-b 53.3 3.42 1.37 2.73 SG1 S-PEN-400-2-a 35.5 1.66 1.60 2.01 SG9 S-PEN-400-2-b 35.5 1.79 2.40 2.38 SG5 S-PEN-400-4-a 47.9 2.64 1.50 2.43 SG9 S-PEN-400-4-b 49.0 2.39 0.90 2.18 SG1 2.2 混凝土柱轴向应力-应变曲线
试件轴向应力-应变曲线如图9所示，其中侧向应变εl显示在坐标原点左边，轴向应变εc显示在坐标原点右边。由图9可知，FRP可显著提高混凝土柱极限抗压强度和延性。
2.3 环向应变分布
对于FRP约束混凝土柱，FRP提供的横向约束为被动约束，仅在核心混凝土膨胀时横向约束才会增加。部分方柱试件环向应变分布如图10所示，其中，SG3、SG7对应角，SG10对应重叠区。由于方柱4个角部位出现应力集中，所以方柱沿周长方向受力不均匀。由图10可知，同一高度区域，面中部环向应变大于角部环向应变。
高延性FRP约束混凝土柱轴向应变和环向面应变、角应变之间的关系如图11所示。与传统FRP相比，高延性FRP约束混凝土柱由于断裂应变大的特性表现出较大的轴向和环向变形。对于圆柱，应变取为PET FRP圆周方向上叠合区之外的5个应变点的平均值；对于方柱，面上应变取为PEN FRP周长方向叠合区之外的3个平面内测点的平均值，角部应变取为2个角部测点的平均值。
3. 模型适用性研究
3.1 基于刚度的高延性FRP设计模型
Bai等（2019）刚度设计模型认为高延性FRP约束混凝土柱的应力-应变曲线由3部分组成：第1部分为抛物线段，第2、3部分为直线段。直线段具有不同的轴向刚度。
对于高延性FRP强约束混凝土柱
$\left( {{E_2} \geqslant 0} \right) $ ：$$ {\sigma _{\rm{c}}} = \left\{ {\begin{array}{*{20}{l}} {{E_{\rm{c}}}{\varepsilon _{\rm{c}}} - \dfrac{{{{\left( {{E_{\rm{c}}} - {E_2}} \right)}^2}}}{{4{{f}_{{\rm{co}}}'}}}{\varepsilon _{\text{c}}^2} \quad,{\text{ 0}} \leqslant {\varepsilon _{\rm{c}}} \leqslant {\varepsilon _{\rm{t}}}} \\ \begin{gathered} {{f}_{{\rm{co}}}'} + {E_2}{\varepsilon _{\rm{c}}} \quad\quad\quad\quad \;\;\;\;,{\text{ }}{\varepsilon _{\rm{t}}} \leqslant {\varepsilon _{\rm{c}}} \leqslant \varepsilon _{\rm{t}}^* \hfill \\ \sigma _{\rm{t}}^* + E_2^*({\varepsilon _{\rm{c}}}{{ - }}\varepsilon _{\rm{t}}^*) {\text{ }} \quad\quad\;\;\,,\,\, \varepsilon _{\rm{t}}^* \leqslant {\varepsilon _{\rm{c}}} \leqslant {\varepsilon _{\rm{cu}}} \hfill \\ \end{gathered} \end{array}} \right.{\text{ }} $$ (2) 式中，σc为FRP约束混凝土轴向应力；εc为FRP约束混凝土轴向应变；Ec为未约束混凝土初始弹性模量；E2为第2部分直线段斜率；
$E_2^* $ 为第3部分直线段斜率；$\varepsilon _{\rm{t}} $ 为第1部分抛物线段与第2部分直线段连接处的轴向应变；$\sigma_{\rm{t}}^* $ 和$\varepsilon _{\rm{t}}^* $ 分别为第2、3部分直线段连接处的轴向应力和轴向应变。同样地，对于高延性FRP弱约束混凝土柱
$\left( {{E_2} < 0} \right) $ ：$$ {\sigma _{\rm{c}}} = \left\{ {\begin{array}{*{20}{l}} {{E_{\rm{c}}}{\varepsilon _{\rm{c}}} - \dfrac{{E_{\rm{c}}^2}}{{4{{f}_{{\rm{co}}}'}}}\varepsilon _{\rm{c}}^2 \quad\quad\;,\;{\text{0}} \leqslant {\varepsilon _{\rm{c}}} \leqslant {\varepsilon _{\rm{t}}}} \\ \begin{gathered} {{f}_{{\rm{co}}}'} + {E_2}{\varepsilon _{\rm{c}}}{\text{ }} \quad\quad\quad\;\;,\; {\varepsilon _{\rm{t}}} \leqslant {\varepsilon _{\rm{c}}} \leqslant \varepsilon _{\rm{t}}^* \hfill \\ \sigma _{\rm{t}}^* + E_2^*({\varepsilon _{\rm{c}}}{{ - }}\varepsilon _{\rm{t}}^*{\text{) }} \quad\;\,,\; \varepsilon _{\rm{t}}^* \leqslant {\varepsilon _{\rm{c}}} \leqslant {\varepsilon _{\rm{cu}}} \hfill \\ \end{gathered} \end{array}} \right.{\text{ }}{\text{ }} $$ (3) FRP对混凝土的约束应力σl为：
$$ {\sigma _{\rm{l}}} = \frac{{{E_{{\rm{FRP}}}}{t_{{\rm{FRP}}}}{\varepsilon _{\rm{h}}}}}{R} $$ (4) 式中，EFRP和tFRP分别为FRP弹性模量和厚度；εh为混凝土柱轴压测试中FRP环向应变；R为混凝土圆柱半径。
约束刚度定义为约束刚度比（2EFRPtFRP/D，D为圆柱直径）与未约束混凝土强度
$f_{{\rm{co}}}' $ 的比值：$$ \rho = \frac{{2{E_{{\rm{FRP}}}}{t_{{\rm{FRP}}}}}}{{D{{f}_{{\rm{co}}}'}}} $$ (5) εco由下式给出：
$$ {\varepsilon _{{\rm{co}}}} = \frac{{2{{f}_{{\rm{co}}}'}}}{{{E_{\rm{i}}}}} $$ (6) 式中，Ei为未约束混凝土初始弹性模量，取值与Ec同。
新的膨胀模型为：
$$ \frac{{{\varepsilon _{\rm{c}}}}}{{{\varepsilon _{{\rm{co}}}}}} = \left( {1.0 + 8.0\frac{{{\sigma _{\rm{l}}}}}{{{{f}_{{\rm{co}}}'}}}} \right) \cdot \left[ {0.97{\text{0}}{{\left( {\frac{{ - {\varepsilon _{\rm{l}}}}}{{{\varepsilon _{{\rm{co}}}}}}} \right)}^{0.43{\text{1}}}} + 0.06{\text{7}}\left( {\frac{{ - {\varepsilon _{\rm{l}}}}}{{{\varepsilon _{{\rm{co}}}}}}} \right)} \right] $$ (7) 式中，εl为FRP约束混凝土侧向应变。
通过回归分析建立以下方程：
$$ \dfrac{{{E_2}}}{{{{f}_{{\rm{co}}}'}}} = - 259.8{\rho ^{ - 0.5}} + 108.5 $$ (8) $$ \frac{{E_2^*}}{{{{f}_{{\rm{co}}}'}}} = - 57.7{({\rho ^*})^{ - 0.5}} + 38.1 $$ (9) 式中，ρ为第2部分直线段约束刚度；ρ*为第3部分直线段约束刚度。
εt表达式如下：
$$ {\varepsilon _{\rm{t}}} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{2{{f}_{{\rm{co}}}'}}}{{{E_{\rm{c}}} - {E_2}}}}&{\left( {{E_2} \geqslant 0} \right)} \\ {\dfrac{{2{{f}_{{\rm{co}}}'}\left( {{E_{\rm{c}}} - {E_2}} \right)}}{{E_c^2}}}&{\left( {{E_2} < 0} \right)} \end{array}} \right. $$ (10) 第1部分抛物线段与第2部分直线段连接处的轴向应力σt表达式如下：
$$ {\sigma _{\rm{t}}} = \left\{ {\begin{array}{*{20}{l}} {{{f}_{{\rm{co}}}'} + {E_2}{\varepsilon _{\rm{t}}}}&{\left( {{E_2} \geqslant 0} \right)} \\ {{E_{\rm{c}}}{\varepsilon _{\rm{t}}} - \dfrac{{E_{\rm{c}}^2}}{{4{{f}_{{\rm{co}}}'}}}\varepsilon _{\rm{t}}^2}&{\left( {{{\rm{E}}_2} < 0} \right)} \end{array}} \right. $$ (11) 3.2 Pimanmas等模型
Pimanmas等（2019）模型由3部组成，即应力-应变曲线达峰值前的上升段、强度软化区的下降段、应力达最低点后的上升段。本文仅给出决定该模型曲线形状的主要公式。
（1）应力-应变曲线达峰值前的上升段
此阶段表达式如下：
$$ {f_{\rm{c}}} = {E_{\rm{c}}}{\varepsilon _{\rm{c}}}\left[ {1 - \frac{1}{n}{{\left( {\frac{{{\varepsilon _{\rm{c}}}}}{{{\varepsilon _{{\rm{c}}1}}}}} \right)}^{n - 1}}} \right]{\text{ ， }} 0 <\varepsilon_{{\rm{c}}}<\varepsilon_{{\rm{c}}1} $$ (12) $$ n = \frac{{{E_{\rm{c}}}{\varepsilon _{{\rm{c}}1}}}}{{{E_{\rm{c}}}{\varepsilon _{{\rm{c}}1}} - {f_{{\rm{c}}1}}}} $$ (13) $$ \frac{{{f_{{\rm{c}}1}}}}{{{{f}_{{\rm{co}}}'}}} = 1 + 0.48{\left( {\frac{{{f_{{\rm{la}}}}}}{{{{f}_{{\rm{co}}}'}}}} \right)^{0.5}} $$ (14) $$ \frac{{{\varepsilon _{{\rm{c}}1}}}}{{{\varepsilon _{{\rm{co}}}}}} = 1 + 80{\varepsilon _{{\rm{fu}}}}\left( {\frac{{{f_{{\rm{la}}}}}}{{{{f}_{{\rm{co}}}'}}}} \right) $$ (15) 式中，εc1为峰值应变；fc1为峰值应力；n为系数；fla为FRP实际的最大环向约束应力；εfu为平板拉伸试验测得的FRP极限拉伸断裂应变平均值。
（2）应力-应变曲线强度软化区的下降段
此阶段第1部分表达式如下：
$$ {f_{\rm{c}}} = \frac{{K{f_{{\rm{c}}1}}\left( {\dfrac{{{\varepsilon _{\rm{c}}}}}{{{\varepsilon _{{\rm{c}}1}}}}} \right)}}{{1 + A\left( {\dfrac{{{\varepsilon _{\rm{c}}}}}{{{\varepsilon _{{\rm{c}}1}}}}} \right) + B{{\left( {\dfrac{{{\varepsilon _{\rm{c}}}}}{{{\varepsilon _{{\rm{c}}1}}}}} \right)}^2} + C{{\left( {\dfrac{{{\varepsilon _{\rm{c}}}}}{{{\varepsilon _{{\rm{c}}1}}}}} \right)}^3}}}{\text{，}} \varepsilon_{\mathrm{c1}}<\varepsilon_{{\rm{c}}}<\varepsilon_{\mathrm{cs}} $$ (16) $$ A=C+K-2 $$ (17) $$ B=1-2 C $$ (18) $$ C=K \frac{\left(K_{\sigma}-1\right)}{\left(K_{\varepsilon }-1\right)^{2}}-\frac{1}{K_{\varepsilon}} $$ (19) $$ K=\frac{E_{{\rm{c}}}}{E_{{\rm{sec}}}} $$ (20) $$ E_{{\rm{sec}}}=\frac{f_{{\rm{c}}1}}{\varepsilon _{{\rm{c}} 1}} $$ (21) $$ K_{\varepsilon }=\frac{\varepsilon_{{\rm{c s}}}}{\varepsilon_{{\rm{c}} 1}} $$ (22) $$ \frac{{{\varepsilon _{{\rm{cs}}}}}}{{{\varepsilon _{{\rm{co}}}}}} = 5.47 + 84.6{\varepsilon _{{\rm{fu}}}}\left( {\frac{{{f_{{\rm{la}}}}}}{{{{f}_{{\rm{co}}}'}}}} \right) $$ (23) $$ K_{\sigma }=\frac{f_{{\rm{c}} 1}}{f_{{\rm{cs}}}} $$ (24) $$ \frac{{{f_{{\rm{cs}}}}}}{{{{f}_{{\rm{co}}}'}}} = 0.53 + 1.65\left( {\frac{{{f_{{\rm{la}}}}}}{{{{f}_{{\rm{co}}}'}}}} \right) $$ (25) 式中，K为刚度比，取无约束混凝土的初始弹性模量（Ec）与割线模量（Esec）的比值；Kε为应变比，取峰值后下降段斜率最大点（拐点）的应变（εcs）与峰值应变（εc1）的比值；Kσ为应力比，取峰值应力（fc1）与峰值后下降段斜率最大点的应力（fcs）的比值。
此阶段第2部分表达式如下：
$$ f_{{\rm{c}}}=f_{{\rm{cs}}}-E_{{\rm{s}}}\left(\varepsilon_{{\rm{c}} 2}-\varepsilon_{{\rm{cs}}}\right) {\text{，}} \varepsilon_{{\rm{cs}}} < \varepsilon_{{\rm{c}}}< \varepsilon_{{\rm{c}} 2} $$ (26) $$ {E_{\rm{s}}} = \frac{{{f_{{\rm{cs}}}} - {f_{{\rm{c2}}}}}}{{{\varepsilon _{{\rm{c2}}}} - {\varepsilon _{{\rm{cs}}}}}} $$ (27) $$ \frac{{{f_{{\rm{c2}}}}}}{{{{f}_{{\rm{co}}}'}}} = 0.448 + 1.83\left( {\frac{{{f_{{\rm{la}}}}}}{{{{f}_{{\rm{co}}}'}}}} \right) $$ (28) $$ \frac{{{\varepsilon _{{\rm{c}}2}}}}{{{\varepsilon _{{\rm{co}}}}}} = 1 + 45.91{\varepsilon _{{\rm{fu}}}}{\left( {\frac{{{f_{{\rm{la}}}}}}{{{{f}_{{\rm{co}}}'}}}} \right)^{ - 0.5}} $$ (29) 式中，Es为峰值后下降段斜率最大点（拐点）应力（fcs）与曲线最低点应力（fc2）之间的割线模量；εc2为下降段最低点应变。
（3）应力-应变曲线应力达最低点后的上升段
此阶段表达式如下：
$$ {f_{\rm{c}}} = {f_{{\rm{c}}2}} + {E_{\rm{a}}}\left( {{\varepsilon _{{\rm{cu}}}} - {\varepsilon _{{\rm{c}}2}}} \right) {\text{，}} \varepsilon_{{\rm{c}}2} < \varepsilon_{{\rm{c}}}< \varepsilon_{{\rm{c u}}} $$ (30) $$ {E_{\rm{a}}} = \frac{{f_{{\rm{cu}}}' - {f_{{\rm{c}}2}}}}{{{\varepsilon _{{\rm{cu}}}} - {\varepsilon _{{\rm{c}}2}}}} $$ (31) $$ \frac{{{{f}_{{\rm{c}}{\text{u}}}'}}}{{{{f}_{{\rm{co}}}'}}} = 0.56 + 3.33\left( {\frac{{{f_{{\rm{la}}}}}}{{{{f}_{{\rm{co}}}'}}}} \right) $$ (32) $$ \frac{{{\varepsilon _{{\rm{cu}}}}}}{{{\varepsilon _{{\rm{co}}}}}} = 1 + 537{\varepsilon _{{\rm{fu}}}}{\left( {\frac{{{f_{{\rm{la}}}}}}{{{{f}_{{\rm{co}}}'}}}} \right)^{0.25}}{\left( {0.5 + \frac{{2r}}{b}} \right)^{ - 1.1}} $$ (33) 式中，Ea为极限轴向应力（
$f_{{\rm{cu}}}'$ ）与最低点应力（fc2）之间的割线模量；$f_{{\rm{cu}}}'$ 为极限轴向应力。模型预测结果与试验结果的对比如图12所示。由图12可知，Bai等（2019）刚度设计模型和Pimanmas等（2019）模型可合理预测试验曲线，模型准确性较高；Bai等（2019）刚度设计模型预测曲线略低于试验曲线，略低估了试件极限应力，因此该模型可用于大尺寸圆柱保守设计；Pimanmas等（2019）模型预测曲线略低于试验曲线，略高估了试件极限应力和极限应变，这是由于该模型中实际环向断裂应变是由平板拉伸试验测得的FRP极限拉伸断裂应变平均值乘有效因子得到的。
4. 结论
（1）高延性FRP约束大尺寸混凝土柱应力-应变曲线由3个不同的部分组成，第1部分上升段与无侧限混凝土相似，峰值强度略高于无侧限强度。第2部分过渡区趋势受约束刚度的影响较大，约束刚度较低的试件具有应变软化行为，而约束刚度较大的试件倾向于表现出应变硬化行为。第3部分曲线开始再次上升，直至FRP被拉断，试件破坏。
（2）相同尺寸的试件，随着高延性FRP层数（厚度）的增加，高延性FRP包裹柱的承载力提高，延性更好。
（3）由于方柱沿周长方向受力不均匀，在同一轴向变形、高度区域处，PEN FRP约束混凝土方柱面上中部环向应变较角部环向应变大，且面上中间区域环向应变增加值大于角区域。
（4）采用现有的高延性FRP约束混凝土本构模型，对高延性FRP约束圆柱、方柱进行了评估。结果表明，Bai等（2019）刚度设计模型和Pimanmas等（2019）模型预测结果与试验结果较吻合，该模型可为实际工程应用提供相对合理的预测。
-
图 3 震相走时曲线和序列重定位后的地震序列空间分布
Figure 3. Travel time curves of seismic phases and spatial distribution of seismic sequences after relocation
图 4 伽师5.5级地震序列震源深度分布直方图
Figure 4. Histogram of focal depth of Jiashi MS5.5 earthquake sequences
图 5 伽师5.5级地震和早期24次MS≥2.5地震序列震源机制解
Figure 5. Focal mechanism solutions of Jiashi MS5.5 earthquake and the early 24 MS≥2.5 earthquake sequences
图 6 伽师5.5级地震和早期24次MS≥2.5地震序列震源机制解参数统计
Figure 6. The normalized frequency statistics of Jiashi MS5.5 earthqueake and the early 24 MS≥2.5 earthquake sequence
图 7 伽师5.5级地震震源处应力反演结果球面投影图
注：图中红色表示σ1，绿色表示σ2，蓝色表示σ3，黑色十字表示最优解，彩色点表示95%的置信区间
Figure 7. Spherical projection of source stress field of Jiashi MS5.5 earthquake
表 1 伽师5.5级地震和早期24次MS≥2.5地震序列震源机制解
Table 1. Focal mechanism solutions of Jiashi MS5.5 earthquake and the early 24 MS≥2.5 earthquake sequences
序号 发震时刻 震中/(°) 震级MS 节面Ⅰ/(°) 节面Ⅱ/(°) P轴 T轴 B轴 方法 东经 北纬 走向 倾角 滑动角 走向 倾角 滑动角 方位 倾伏角 方位 倾伏角 方位 倾伏角 1 2018-09-04
05:51:4477.01 39.49 4.7 38 78 -13 130 77 -167 354 17 84 1 176 72 CAP 2 2018-09-04
05:52:5577.01 39.51 5.5 49 90 3 319 87 -180 183 2 274 2 49 87 CAP 3 2018-09-04
06:48:2676.99 39.51 3.3 9 58 85 327 80 175 192 3 283 9 83 80 Snoke 4 2018-09-04
06:52:5877.00 39.51 3.3 43 51 -42 163 58 -132 17 54 282 4 189 35 Snoke 5 2018-09-04
07:10:1577.04 39.50 2.6 57 90 20 327 70 180 190 14 284 14 57 70 Snoke 6 2018-09-04
07:20:3877.03 39.51 3.2 63 64 16 326 75 153 16 7 282 28 120 60 Snoke 7 2018-09-04
08:25:2477.02 39.50 3.8 37 70 -20 134 71 -158 355 28 265 1 173 62 CAP 8 2018-09-04
09:31:3577.02 39.52 2.7 43 90 35 313 55 180 173 23 274 23 43 55 Snoke 9 2018-09-04
10:51:2476.96 39.47 4.6 49 84 -2 139 88 -174 4 6 274 3 158 84 CAP 10 2018-09-04
11:26:1776.99 39.50 3.1 50 86 39 318 50 175 177 24 282 29 54 50 Snoke 11 2018-09-04
15:11:5476.98 39.50 3.0 51 85 29 318 60 174 181 16 278 24 60 60 Snoke 12 2018-09-04
16:12:2077.02 39.53 2.6 44 70 2 314 88 160 1 12 267 15 129 70 Snoke 13 2018-09-04
21:11:4477.01 39.53 3.2 255 40 -82 65 50 -96 295 82 160 5 70 5 Snoke 14 2018-09-04
21:57:5776.98 39.49 3.4 57 90 20 327 70 180 190 14 284 14 57 70 Snoke 15 2018-09-05
01:10:4177.03 39.51 2.6 51 85 29 318 60 174 181 16 278 24 60 60 Snoke 16 2018-09-05
01:52:5077.01 39.52 3.0 101 85 19 9 70 174 233 10 326 17 115 70 Snoke 17 2018-09-05
02:44:0876.97 39.49 3.6 38 81 -23 131 67 -170 352 22 87 9 197 65 CAP 18 2018-09-05
11:15:2177.02 39.51 3.7 39 90 -15 129 75 180 353 10 85 10 219 75 CAP 19 2018-09-07
02:05:4277.01 39.51 2.6 34 50 -83 204 40 -97 344 82 119 5 209 5 Snoke 20 2018-09-07
02:42:4577.03 39.51 3.3 234 83 -39 329 50 -171 184 31 288 21 46 50 Snoke 21 2018-09-07
04:06:4277.04 39.51 3.1 62 90 40 332 50 180 190 27 295 27 62 50 Snoke 22 2018-09-07
09:01:2377.01 39.50 3.0 38 82 -13 130 77 -172 353 14 84 4 189 75 Snoke 23 2018-09-07
17:14:5677.02 39.52 2.5 34 50 -83 204 40 -97 344 83 119 5 209 5 Snoke 24 2018-09-08
21:49:2876.99 39.49 2.6 50 90 30 320 60 180 180 20 279 20 50 60 Snoke 25 2018-09-20
13:24:0576.98 39.50 3.0 70 90 30 340 60 180 200 20 299 20 70 60 Snoke 
下载: 导出CSV
表 2 伽师5.5级地震震源处应力反演结果
Table 2. Source stress field of Jiashi MS5.5 earthquake
σ1 σ2 σ3 应力形因子 应力结构 方位/(°) 倾角/(°) 方位/(°) 倾角/(°) 方位/(°) 倾角/(°) R -163
-320— -21824
-63—8640
12—20164
-23—88-69
-80— -609
1—200.17
0.01—0.45走滑 注：表中数值范围为各参数95%置信度的不确定性范围
下载: 导出CSV
-
刁桂苓, 王海涛, 高国英等, 2005.伽师强震系列应力场的转向过程.地球物理学报, 48(5):1062-1068. doi: 10.3321/j.issn:0001-5733.2005.05.012 高国英, 聂晓红, 夏爱国, 2004.2003年伽师6.8级地震序列特征和震源机制的初步研究.中国地震, 20(2):179-186. doi: 10.3969/j.issn.1001-4683.2004.02.008 高国英, 王海涛, 温和平等, 2001.帕米尔东北侧中强地震前应力场动态变化特征分析.西北地震学报, 23(4):389-394. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xbdzxb200104012 李艳永, 王成虎, 杨佳佳, 2018.呼图壁地区震源机制解及构造应力场特征分析.大地测量与地球动力学, 38(12):1246-1250. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dkxbydz201812007 刘启元, 陈九辉, 李顺成等, 2000.新疆伽师强震群区三维地壳上地幔S波速度结构及其地震成因的探讨.地球物理学报, 43(3):356-365, 433. doi: 10.3321/j.issn:0001-5733.2000.03.009 龙海英, 高国英, 聂晓红, 2007.1997-1998年伽师强震群震源区应力场特征.西北地震学报, 29(2):145-149. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xbdzxb200702010 单新建, 何玉梅, 朱燕等, 2002.伽师强震群震源破裂特征的初步分析.地球物理学报, 45(3):416-425. doi: 10.3321/j.issn:0001-5733.2002.03.013 苏廼秦, 2003.新疆伽师强震群强震主破裂面走向初探.西北地震学报, 25(3):269-274. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xbdzxb200303014 屠泓为, 万秀红, 高歌等, 2008.1977年至2006年新疆伽师地震断层性质及应力场变化原因初探.地球物理学进展, 23(4):1038-1044. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dqwlxjz200804007 万永革, 2008.美国Landers地震和Hector Mine地震前震源机制与主震机制一致现象的研究.中国地震, 24(3):216-225. doi: 10.3969/j.issn.1001-4683.2008.03.003 万永革, 2019.同一地震多个震源机制中心解的确定.地球物理学报, 62(12):4718-4728. doi: 10.6038/cjg2019M0553 王晓楠, 唐方头, 邵翠茹, 2018.南迦巴瓦构造结周边地区主要断裂现今运动特征.震灾防御技术, 13(2):267-275. http://zzfy.eq-j.cn/zzfyjs/ch/reader/view_abstract.aspx?flag=1&file_no=20180202&journal_id=zzfyjs 王筱荣, 孙甲宁, 王季达, 2005.1997-2004年伽师地区6级地震序列特征研究.内陆地震, 19(1):44-52. doi: 10.3969/j.issn.1001-8956.2005.01.007 徐朝繁, 段永红, 田晓峰等, 2007.新疆伽师强震群区基底界面结构特征.地震学报, 29(5):477-482. doi: 10.3321/j.issn:0253-3782.2007.05.004 张志斌, 金花, 朱皓清, 2019a.2018年9月4日伽师MS 5.5地震与97年及03年伽师强震属于同一发震构造吗?.地球物理学进展, 34(6):2232-2238. 张志斌, 冉慧敏, 金花, 2019b.2016年12月8日新疆呼图壁MS6.2地震发震构造初步研究.地震工程学报, 41(4):962-969. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xbdzxb201904020 赵翠萍, 陈章立, 郑斯华等, 2008.伽师震源区中等强度地震矩张量反演及其应力场特征.地球物理学报, 51(3):782-792. doi: 10.3321/j.issn:0001-5733.2008.03.019 周仕勇, 许忠淮, 陈晓非, 2001.伽师强震群震源特征及震源机制力学成因分析.地球物理学报, 44(3):654-662. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dqwlxb200105009 周仕勇, 许忠淮, 韩京等, 1999.主地震定位法分析以及1997年新疆伽师强震群高精度定位.地震学报, 21(3):258-265. doi: 10.3321/j.issn:0253-3782.1999.03.005 Efron B. R., Tibshirani, 1986. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat. Sci, 1(1):54-75. http://doi.ieeecomputersociety.org/resolve?ref_id=doi:10.1214/ss/1177013815&rfr_id=trans/tk/2010/04/ttk2010040565.htm Hardebeck J. L., Michael A. J., 2006. Damped regional-scale stress inversions:Methodology and examples for southern California and the Coalinga aftershock sequence. Journal of Geophysical Research:Solid Earth, 111 (B11):B11310. Kagan Y. Y., 1991.3-D rotation of double-couple earthquake source.Geophys J Int, 106 (3):709-716. doi: 10.1111/j.1365-246X.1991.tb06343.x Kagan Y. Y., 2003. Accuracy of modern global earthquake catalogs. Phys Earth planet Inter, 135 (2-3):173-209. doi: 10.1016/S0031-9201(02)00214-5 Kagan Y. Y., Jackson D. D., 2000. Probabilistic forecasting of earthquakes. Geophys J Int, l43 (2):438-453. doi: 10.1046/j.1365-246X.2000.01267.x Martínez-Garzón P., Kwiatek G., Ickrath M., et al., 2014. MSATSI:A MATLAB package for stress inversion, combining solid classic methodology, a new simplified user handling, and a visualization tool. Seismological Research Letters, 85 (4):896-904. doi: 10.1785/0220130189 Snoke J. A., Munsey J. W., Teague A. G., et al., 1984. A program for focal mechanism determination by combined use of polarity and SV-P amplitude ratio data. Earthquake Notes, 55 (3):15. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1111/j.1528-1167.2006.00001_8.x Waldhauser F., Ellsworth W. L., 2000. A double difference earthquake location algorithm:Method and application to the Northern Hayward Faul, Califomia. Bul1. Seism. Soc. Am, 90 (6):1353-1368. doi: 10.1785/0120000006 Zhao L. S., Helmberger D. V., 1994. Source estimation from broadband regional seismograms.Bull Seismol Soc Amer, 84 (1):91-104. Zhu L. P., Helmberger D. V., 1996. Advancement in source estimation techniques using broadband regional seismograms. Bull Seismol Soc Amer, 86 (5):1634-l641. 期刊类型引用(0)
其他类型引用(1)
-
下载:
点击查看大图
计量
- 文章访问数: 199
- HTML全文浏览量: 28
- PDF下载量: 1
- 被引次数: 1
