Relationship between Shear Wave Velocity and Soil Depth of Typical Soil Layers in Hangzhou Area
-
摘要: 基于杭州市丰富的场地钻孔剪切波速资料，采用3种常见的剪切波速与埋深回归分析模型，分析杭州地区5类常规土在场地分类和场地未分类情况下的最优拟合公式和预测范围，并对推荐模型进行可靠性验证，对常规粉质粘土和粉砂进行地区差异性分析。研究结果表明：本文推荐的剪切波速与埋深关系公式具有良好的可靠性；地区、岩土类型和预测深度均对剪切波速与埋深关系模型的可靠性产生显著影响，故应用时应优先选用本地区统计模型，如若未有，则需根据已有资料，对选用模型进行岩土类型和适应预测深度范围验证，以保证所选模型的可靠性；受地区、岩土类型和预测深度的影响，考虑场地分类并不一定提高统计模型的预测精度，在实际工程应用中具有不确定性。Abstract: Based on abundant of shear wave velocity from lots of boreholes in Hangzhou, three common regression models were used to analyze the relationship between shear wave velocity and soil buried depth. In the case of site classification and unclassification, this paper analyzed the optimal fitting formulas and prediction range of five types of soils in Hangzhou. In this paper, the reliability of all recommended models were verified, and the regional differences of conventional silty clay and silt were analyzed. The research results show that the regression equations of shear wave velocity and buried depth recommended in this paper has good reliability. Regions, geotechnical types and predicted depths have significant effects on the reliability of the relationship between shear wave velocity and soil buried depth. Therefore, to ensure the reliability of the selected models, local statistical models should be put in the first place, otherwise, it is necessary to verify the geotechnical types and the prediction depth of the selected models. Influenced by regions, geotechnical types and prediction depths, considering site classification does not necessarily improve the prediction accuracy of statistical models, which has uncertainty in practical engineering applications.
-
Key words:
- Shear wave velocity /
- Buried depth /
- Site classification /
- Regression analysis
-
引言
地震动高频衰减在工程地震领域有着重要的应用，常被用于震源、地震动模拟和衰减关系研究等工作中。kappa值是描述地震动高频衰减参数之一，多位学者对其进行了研究，如Sun等（2013）选用汶川地震52个主震加速度数据，得到kappa值变化范围，认为kappa值与震源和传播路径有关。Anderson等（1984，1986，1991）发现在美国加州地区强震数据中，kappa值与震中距表现出正相关关系。李文倩（2014）基于华北地区近2000条数据，利用Anderson等（1984）的方法得到kappa值，认为kappa值与震级和震源深度无关，但离散性较大；朱百慧（2016）采用Anderson等（1984）经典计算方法、固定应力降计算方法及宽带反演计算方法，以日本东北地区为研究区域，利用K-NET和KiK-net强震记录，对kappa值与传播途径、震级及局部场地特征的关系进行分析，发现kappa值与震中距具有一定线性关系，随着震中距的增大kappa值呈增长趋势，kappa值与震级的线性关系不明显，随着VS30的增大kappa值呈对数下降趋势。
鄂尔多斯块体是古克拉通块体，其内部结构稳定，但其外部地震频发，尤其是鄂尔多斯块体西缘地区，该区域属于亚洲东部“大三角”地震构造区东边缘（高祥林等，2010），“大三角”地震构造沿华南、鄂尔多斯西边缘向北延伸至贝加尔湖附近，曾被称为中蒙大陆中轴构造带，研究该区域具有深远意义。鄂尔多斯西缘地区由内蒙古强震动台网、宁夏强震动台网属地监控，该区域共有14个强震动台站，台站积累了真实可靠的地震数据，为研究提供了数据支撑。
本文以鄂尔多斯西缘地区（34°N—42°N，103°E—109°E）14个固定强震台站（包括8个内蒙古强震台站和6个宁夏强震台站）2007—2020年116条强震记录（1≤MS≤8）为研究对象，利用Anderson等（1984）提出的经典算法，通过MATLAB软件计算kappa0值，讨论kappa值与震中距、kappa0值与VS20、VS30的关系。
1. 研究区域台站分布与地质构造特征
鄂尔多斯西缘地区地质条件复杂，北部临河断陷盆地西南方向与潮水—吉兰泰断陷盆地相连。南部有银川地堑、干盐池盆地，东部鄂尔多斯盆地是古老的克拉通地块，地块相对稳定。西北部地区为阿拉善块体，近年中小震频发。区域内有河套平原和宁夏平原，均为第四纪泥沙沉积覆盖的冲击平原。
临河断陷盆地自早第三纪晚期开始发育，新生界沉积厚度最大达10000 m以上，第四纪以来断陷活动依然保持了第三纪晚期的活动特征，周边山地继续抬升，断陷继承性沉降，第四纪厚度2400 m。吉兰泰盆地最初发育于早白垩纪，但晚白垩纪-早第三纪古新世时期抬生为陆地，始新世又重新开始发育，直到现在。该断陷盆地内新生界厚度约2 000 m，其中第四纪最大厚度约400 m，沉降中心靠近巴彦乌拉山东麓断裂。银川地堑是由喜马拉雅造山运动时期构造活跃的贺兰山褶皱带与鄂尔多斯盆地相对上升形成的，其为本区域最大的拉张型活动盆地，北起石嘴山，南至青铜峡，长160 km，最宽55 km，地堑形成于渐新世，其后持续下陷，沉积了巨厚的新生代地层，总厚度达7000 m，其中古近纪最大厚度3600 m，新近系最大厚度2500 m，第四纪最大厚度>1609 m。干盐池盆地为青藏高原东北边界海原断裂带内最大的拉分盆地，沉积物粒度呈向上逐渐变细的趋势，湖泊沉积为主，干盐池盆地主要受南—西华山与唐家坡—干盐池断层的控制，最深处可能>550 m。第四纪以来，构造运动主要以大面积的周期节奏性震荡上升为主，在西吉县形成了剥蚀构造山地、构造剥蚀红岩丘陵，剥蚀堆积黄土丘陵，侵蚀堆积河谷平原。西吉县大面积被第四纪覆盖。河套平原是冲击平原，河套地区北部、南部断层证明该区域存在断层下陷，黄河流经低洼地区带来泥沙淤积，形成河套平原。宁夏平原也是冲击平原，由于贺兰山与鄂尔多斯高原的抬升，宁夏平原断裂下陷形成地堑带，后由于黄河携带大量泥沙堆积形成宁夏平原，可知宁夏平原是由地壳运动、断裂下陷、河流流水搬运堆积而成。
2. 计算分析
2.1 数据选取
研究数据来自于内蒙古自治区地震局和宁夏自治区地震局提供的地震记录数据、钻孔资料、剪切波速测试资料、地质条件资料等，研究区域地震台站信息如表1所示，台站分布及地质构造如图1所示。
表 1 研究区域地震台站信息Table 1. The research area seismic station information序号 台站名称 经度 纬度 记录器型号 场地类型 1 巴彦浩特 105.7°E 38.8°N ETNA 土层 2 巴彦木仁 106.7°E 39.9°N ETNA 土层 3 宝丰 106.3°E 39.0°N MR-2002 土层 4 磴口 106.9°E 40.3°N ETNA 土层 5 干盐池 105.3°E 36.6°N MR-2002 土层 6 公地 106.8°E 40.6°N ETNA 土层 7 吉兰泰 105.7°E 39.7°N ETNA 土层 8 临河 107.6°E 40.8°N ETNA 土层 9 灵武 106.3°E 38.1°N MR-2002 土层 10 前进农场 106.4°E 38.8°N MR-2002 土层 11 青铜峡 106.0°E 38.0°N MR-2002 基岩 12 沙海 106.9°E 40.9°N ETNA 土层 13 乌海 106.8°E 39.4°N ETNA 土层 14 西吉 105.4°E 35.5°N MR-2002 土层 
图 1 台站分布及地质构造Figure 1. The distribution of seismograph station and geologic structure2.2 计算方法
加速度反应谱法由Anderson等（1984）提出，是目前工程地震学领域中使用最广泛的方法，本文采用该方法计算kappa值，开展区域高频衰减特性研究。频率高于特定频率fE的单对数坐标系加速度傅立叶谱幅值衰减规律可表示为：
$$ {{A}}\left( {{f}} \right)={{{A}}_0}\cdot{\rm{exp}}\left( { - {{{\text{π}} kf}}} \right),\;f > {f_{\rm{E}}} $$ (1) 式中，A0为依赖于震源特征和传播距离的因子，k为谱衰减参数，f为地震动频率，fE为谱幅值对数值近似直线下降的起始点。
一般来说，当频率达fE后，谱幅值随着频率的增加呈指数下降。在线性-对数坐标系（即单对数坐标系）下，高频衰减参数k可用最简单的线性关系式近似得到：
$$ {{k}}= - {\rm{\lambda }}/{\rm{{\text{π}} }} $$ (2) $$ {\rm{\lambda }}=\frac{{\ln \left( {{A_2}\left( f \right)} \right) - \ln \left( {{A_1}\left( f \right)} \right)}}{{{f_2} - {f_1}}}=\frac{{\ln \left( {\varDelta a} \right)}}{{\varDelta f}} $$ (3) kappa值计算截止点为傅立叶谱与噪声谱重合的点或幅值平行起始点，利用最小二乘法进行线性拟合，得到的斜率即为kappa值（图2）。
图 2 Anderson等（1984）经典计算方法计算的kappa值Figure 2. Anderson&Hough's the classical method calculates k为计算和确定kappa值与震中距R的关系，利用最小二乘法得到线性回归方程：
$$ {{K=}}{{{K}}_{{0}}}{+}{{{K}}_{\rm{R}}}\cdot{{R}}\left( {{s}} \right) $$ (4) $$ {{\bar{{K}}}_{\rm{0}}}{\rm{=[kappa0}}\left( {{\rm{N - S}}} \right){\rm{+kappa0}}\left( {{\rm{E - W}}} \right){\rm{]/2}} $$ (5) 式中，R(s)为震中距，K0和KR为常数量，K0为由台站附近近地表地下地质构造引起的高频衰减参数值，KR为与区域相关的衰减参数值（Anderson等，1984）kappa（N-S）和kappa（E-W）分别为kappa南北向和东西向分量，
$ {{\bar{\rm{K}}}_{\rm{0}}}$ 表示强震台南北向、东西向kappa0均值。2.3 数据处理
利用MATLAB语言编辑计算处理全部程序，包括kappa值、kappa值与震中距关系、kappa0值、kappa0值与VS20、VS30关系计算程序。
（1）通过编程实现对强震观测记录数据的处理，包括基线调整、采用0.1～20 Hz的带通滤波（白立新等，2019）、数据初筛及人工复筛等工作（崔建文等，2007；万永革，2012）。
（2）分析单个台站多次地震事件，利用计算机程序获得每次地震每个分量的kappa值，进而利用每个分量的kappa值结合震中距，采用最小二乘法进行拟合，得到kappa值与震中距的线性回归方程（陶正如等，2015）。
（3）分别求出116条强震记录kappa0（N-S）与kappa0（E-W）值与震中距的回归方程，并计算拟合优度R2。计算kappa0（N-S）、kappa0（E-W）、
$ {{\bar{{K}}}_{\rm{0}}}$ 值，对$ {{\bar{{K}}}_{\rm{0}}}$ 值与VS20、VS30进行拟合，得到拟合关系曲线。2.3.1 kappa值与震中距的关系
kappa值与震中距的关系计算结果如表2、图3所示，由表2、图3可知，kappa值与震中距存在线性回归关系；kappa值在鄂尔多斯西缘大部分地区拟合优度值相对较高，为0.6～0.9，而西吉台站地区南北向、东西向拟合优度值分别为0.47、0.49，可能是由于台站记录地震数据较少、仪器噪声过高等原因导致kappa值相对离散，拟合优度较低。
表 2 kappa值与震中距拟合结果Table 2. The relationship between kappa and epicentral distance台站名称 方向 回归方程 K0/s 拟合优度值/R2 $ {{\bar{{K}}}_{\rm{0}}}$/s VS20/m·s−1 VS30/m·s−1 巴彦浩特 N-S kappa=0.000 3R+0.0264 0.0264 0.9803 0.02530 343.05 370.2 E-W kappa=0.000 3R+0.0242 0.0242 0.9854 巴彦木仁 N-S kappa=0.000 2R+0.0363 0.0363 0.8691 0.03485 353.4 389.4 E-W kappa=0.000 2R+0.0334 0.0334 0.9280 宝丰 N-S kappa=0.000 1R+0.0687 0.0687 0.6055 0.06560 180.4 222.1 E-W kappa=0.000 1R+0.0625 0.0625 0.7876 磴口 N-S kappa=0.000 1R+0.0605 0.0605 0.8971 0.05845 231.7 261.7 E-W kappa=0.000 1R+0.0564 0.0564 0.9425 干盐池 N-S kappa=0.000 1R+0.0531 0.0531 0.7542 0.05245 317.4 357.3 E-W kappa=0.000 1R+0.0518 0.0518 0.7194 公地 N-S kappa=0.000 2R+0.0541 0.0541 0.9790 0.05450 222.7 251.2 E-W kappa=0.000 2R+0.0549 0.0549 0.9730 吉兰泰 N-S kappa=0.000 2R+0.0526 0.0526 0.8812 0.05525 327.7 335.8 E-W kappa=0.000 2R+0.0579 0.0579 0.7826 临河 N-S kappa=0.000 1R+0.0530 0.0530 0.9977 0.05175 232.3 249.7 E-W kappa=0.000 1R+0.0505 0.0505 0.9960 灵武 N-S kappa=0.000 3R+0.0449 0.0449 0.9996 0.04415 292.6 325.1 E-W kappa=0.000 3R+0.0434 0.0434 0.9957 前进农场 N-S kappa=0.000 3R+0.0637 0.0637 0.7536 0.06555 209.5 248.9 E-W kappa=0.000 3R+0.0674 0.0674 0.6815 青铜峡 N-S kappa=0.000 1R+0.0428 0.0428 0.4987 0.04315 219.0 260.0 E-W kappa=0.000 1R+0.0435 0.0435 0.6287 沙海 N-S kappa=0.000 2R+0.0489 0.0489 0.9743 0.04870 188.3 216.5 E-W kappa=0.000 2R+0.0485 0.0485 0.9710 乌海 N-S kappa=0.000 5R+0.0155 0.0155 0.7320 0.01545 352.7 390.5 E-W kappa=0.000 5R+0.0154 0.0154 0.6702 西吉 N-S kappa=0.000 1R+0.0429 0.0429 0.4713 0.04240 195.1 228.7 E-W kappa=0.000 1R+0.0419 0.0419 0.4909 
图 3 鄂尔多斯西缘地区14个台站kappa值与震中距拟合关系Figure 3. The fitting relationship between kappa and epicentral distance of 14 stations in the western margin of Erdos region2.3.2 计算结果不确定性分析
通过大量计算得到研究区域116条地震记录地震动峰值加速度PGA及震中距，震级与震中距关系分布如图4所示，震级与峰值加速度PGA关系分布如图5所示。由图4、5可知，震级为Ms2.0～Ms8.0，震中距为0～1200 km，峰值加速度PGA为0～180 cm/s2，多数集中在0～60 cm/s2。
图 5 震级与峰值加速度PGA关系分布图Figure 5. Distribution of earthquake magnitude and PGA(peak acceleration value）由于研究区域地震较少，覆盖层较厚，台站有效记录地震数据不足，且kappa值与震中距拟合关系受远震（汶川地震等）影响，故拟合结果存在一定不确定性。针对此问题，剔除了震中距500 km以上的地震。部分台站拟合结果偏差较大，以巴彦木仁、磴口台站为例进行分析，结果如表3、图6所示。由表3、图6可知，剔除汶川地震等远震后，拟合优度值明显下降，巴彦木仁台南北向拟合优度值由0.86911降至0.6186，东西向拟合优度值由0.9280降至0.7081；磴口台南北向拟合优度值由0.8971降至0.2447，东西向拟合优度值由0.9425降至0.6064。综上所述，kappa值与震中距线性拟合受远震的影响较大，因此计算kappa值时应尽量考虑震中距为500 km以内的地震数据。
表 3 巴彦木仁、磴口台站kappa值与震中距拟合结果Table 3. Fitting results of kappa value and epicenter distance at Bayanmuren and Dengkou station台站名称 方向 回归方程 K0/s 拟合优度值/R2 巴彦木仁 N-S kappa=0.000 3R+0.0275 0.0275 0.6186 E-W kappa=0.000 3R+0.0266 0.0266 0.7081 磴口 NS kappa=0.000 1R+0.0650 0.0650 0.2447 EW kappa=0.000 1R+0.0562 0.0562 0.6064 
图 6 巴彦木仁、磴口台站kappa值与震中距拟合关系Figure 6. Fitting relationship between kappa and epicenter distance at Banyanmuren and Dengkou station2.3.3 kappa0值与剪切波速关系
研究区域有14个强震动台站，内蒙古强震动台网8个台站分别为：巴彦木仁台、巴彦浩特台、磴口台、公地台、吉兰泰台、临河台、沙海台、乌海台，宁夏强震动台网6个台站分别为：宝丰台、干盐池台、灵武台、前进农场台、青铜峡台、西吉台。计算得到研究区域内14个台站的kappa0值，结合合站提供的钻孔资料，得到剪切波速VS20、VS30值，进而得出台站kappa0值与剪切波速VS20拟合关系式为：
$$ {\rm{kappa}}0 = - 0.035\;89 \times {\rm{ln}}\;{V_{{\rm{S}}20}} + 0.245\;8,\;{{{R}}^2} = 0.392\;9 $$ (6) kappa0值与剪切波速VS30拟合关系式为：
$$ {\rm{kappa}}0 = - 0.042\;38 \times {\rm{ln}}\;{V_{{\rm{S}}30}} + 0.286\;8,\;{{{R}}^2} = 0.414\;4 $$ (7) kappa0值与剪切波速VS20、VS30拟合关系曲线如图7所示。由式（6）、式（7）、图7可知，kappa0值与剪切波速VS20、VS30存在对数关系，拟合优度值约为0.4，拟合效果不理想，结合朱百慧（2016)的研究成果，笔者认为kappa0值随着VS20、VS30的增大逐渐减至0（Ktenidou等，2013）。
图 7 kappa0值与剪切波速VS20、VS30拟合关系曲线Figure 7. The fitting relationship between kappa0 and shear-wave（VS20、VS30）velocity3. 结论
本文利用Anderson等（1984）提出的经典方法，通过计算得出以下结论：
（1）鄂尔多斯块体西缘地区强震台站kappa值与震中距呈线性相关，且拟合优度值较高；
（2）kappa0值为0.01545～0.06560 s；
（3）kappa0值与VS20、VS30呈指数相关关系，离散性较大，拟合优度值约为0.4；
（4）随着VS20、VS30的增大，kappa0值逐渐减至0。
（5）本研究采用的地震数据较少，分析得到的kappa值与震中距线性拟合受远震的影响较大，因此计算kappa值时应尽量考虑震中距500 km以内的地震数据。
致谢 本文在撰写过程中得到中国地震局工程力学研究所研究员陶正如、新疆地震局工程师李文倩、广东地震局高级工程师吴华灯、云南地震局研究员崔建文、防灾学院教授万永革、宁夏地震局高级工程师吕俊强及工程师李鸿廷的悉心帮助，在此向他们表示衷心感谢，同时感谢评审专家提出的宝贵意见。
-
图 2 296个钻孔资料中5类常规土剪切波速与埋深散点图
Figure 2. Scatter diagram of shear wave velocity and buried depth of five types of conventional soils in 296 borehole data
图 3 不同场地分类情况下粉质粘土剪切波速与埋深散点图
Figure 3. Scatter diagrams of shear wave velocity and buried depth of silty clay under different site classifications
图 4 不同场地分类情况下淤泥质粉质粘土剪切波速与埋深散点图
Figure 4. Scatter diagram of shear wave velocity and buried depth of mucky silty clay under different site classifications
图 5 不同场地分类情况下粉砂剪切波速与埋深散点图
Figure 5. Scatter diagram of shear wave velocity and buried depth of silty sand under different site classifications
图 6 不同场地分类情况下砂质粉土剪切波速与埋深散点图
Figure 6. Scatter diagram of shear wave velocity and buried depth of sandy silt under different site classifications
图 7 不同场地分类情况下粘质粉土剪切波速与埋深散点图
Figure 7. Scatter diagram of shear wave velocity and buried depth of clayey silt under different site classifications
图 8 不同场地分类情况下5类土拟合优度
Figure 8. Goodness of fitting of five types of soils under different site classification
图 9 Ⅲ类场地实测剪切波速与预测值的对比分析图
Figure 9. Comparative analysis of measured shear wave velocity and predicted value of site Ⅲ
图 10 粉质粘土下本文模型与其他模型剪切波速对比分析图
Figure 10. Comparative analysis of shear wave velocity of the model proposed in this paper and other models of silty clay
图 11 粉砂下本文模型与其他模型剪切波速对比分析图
Figure 11. Comparative analysis of shear wave velocity of the model proposed in this paper and other models of silty sand
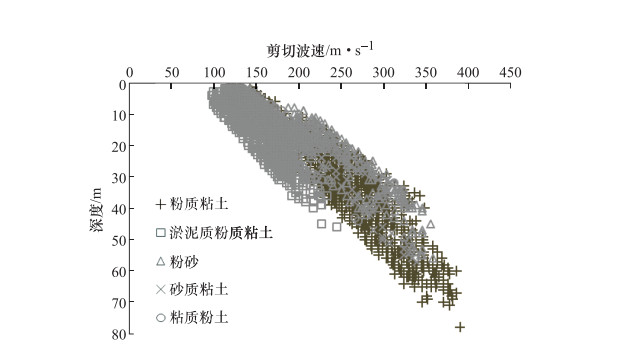
表 1 研究区不同土类剪切波速的分布范围
Table 1. Distribution ranges of shear wave velocity of different soils in study area
岩性 粉质粘土 淤泥质粉质粘土 粉砂 砂质粉土 粘质粉土 场地类别 总计 Ⅱ Ⅲ 总计 Ⅱ Ⅲ 总计 Ⅱ Ⅲ 总计 Ⅱ Ⅲ 总计 Ⅱ Ⅲ 测试点数 1915 324 1591 902 31 871 383 17 366 904 88 816 330 69 261 最小值/m·s-1 115 115 117 98 102 98 134 134 139 112 122 112 112 116 112 最大值/m·s-1 390 348 390 245 215 245 357 303 357 339 310 339 321 321 270 平均值/m·s-1 249.4 203.4 258.8 153.9 139.5 154.4 227.5 255.0 226.2 163.1 202.4 158.9 154.2 165.0 151.3 标准差/m·s-1 59.0 62.9 53.6 29.1 30.9 28.9 54.5 42.7 54.7 37.0 56.5 31.5 32.8 45.8 27.8 测试深度/m 2—78 2—44 2—78 2—46 4—24 2—46 1—56 1—30 5—56 1—57 1—34 1—57 2—44 2—36 2—44 
下载: 导出CSV
表 2 不同场地分类情况下5类土拟合优度
Table 2. Goodness of fitting of five types of soil under different site classification
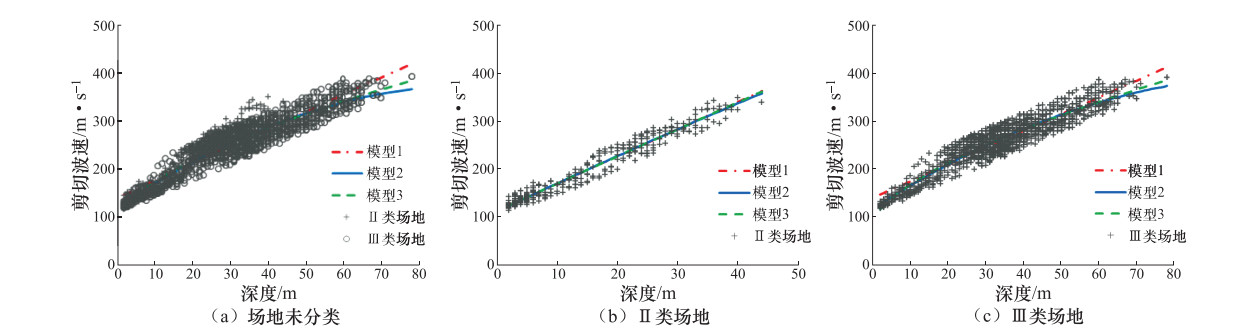
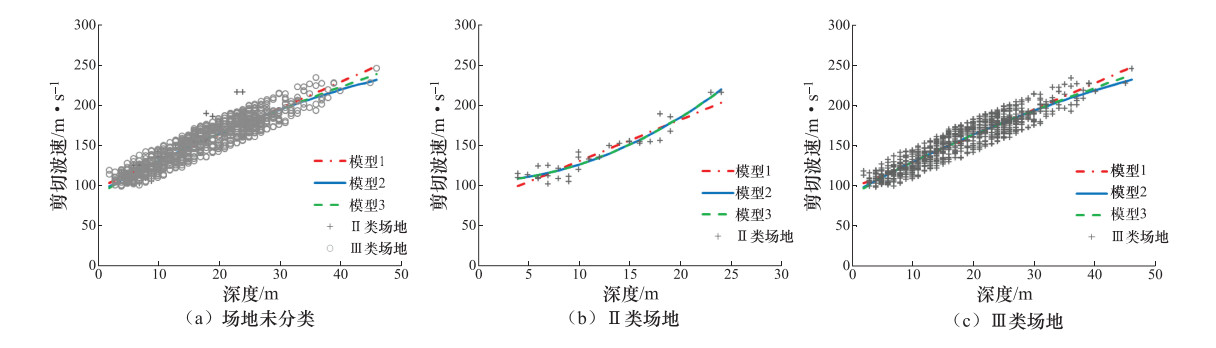
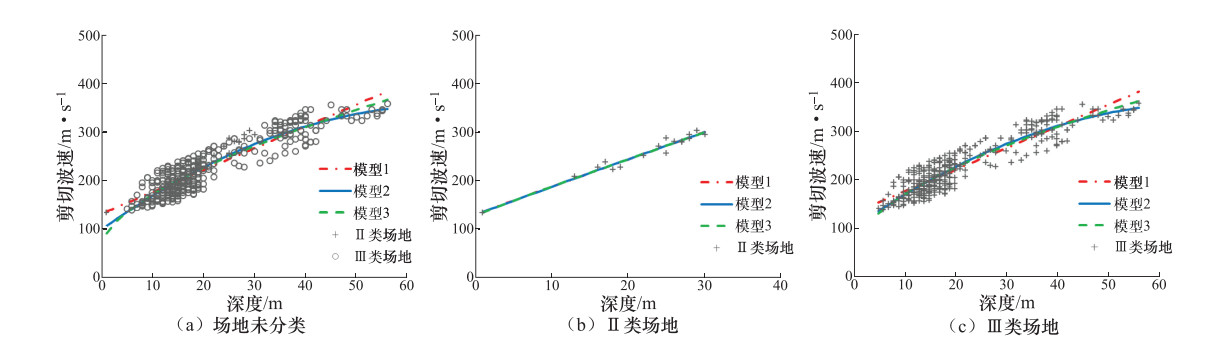
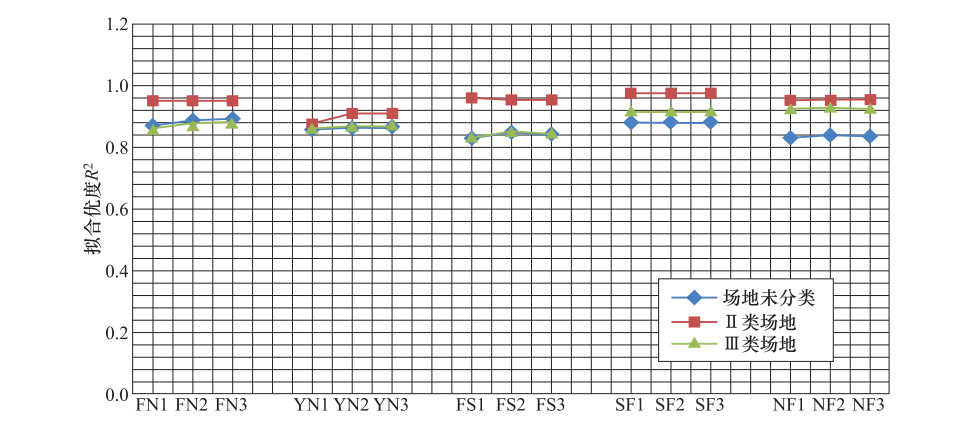
岩土类型 工况 R2 场地未分类 Ⅱ类场地 Ⅲ类场地 粉质粘土 FN1 0.86870 0.95298 0.86330 FN2 0.88890 0.95301 0.87860 FN3 0.89140 0.95284 0.88130 淤泥质粉质粘土 YN1 0.86130 0.87627 0.86470 YN2 0.86560 0.90946 0.86850 YN3 0.86460 0.90960 0.86770 粉砂 FS1 0.83000 0.95942 0.83480 FS2 0.84820 0.95659 0.84980 FS3 0.84140 0.95670 0.84540 砂质粉土 SF1 0.88030 0.97654 0.91490 SF2 0.88110 0.97672 0.91530 SF3 0.88020 0.97725 0.91550 粘质粉土 NF1 0.83070 0.95183 0.92820 NF2 0.83860 0.95568 0.92910 NF3 0.83520 0.95554 0.92810
下载: 导出CSV
表 3 各场地类型下不同岩土类型的推荐模型
Table 3. Recommended models for different geotechnical types under different site types
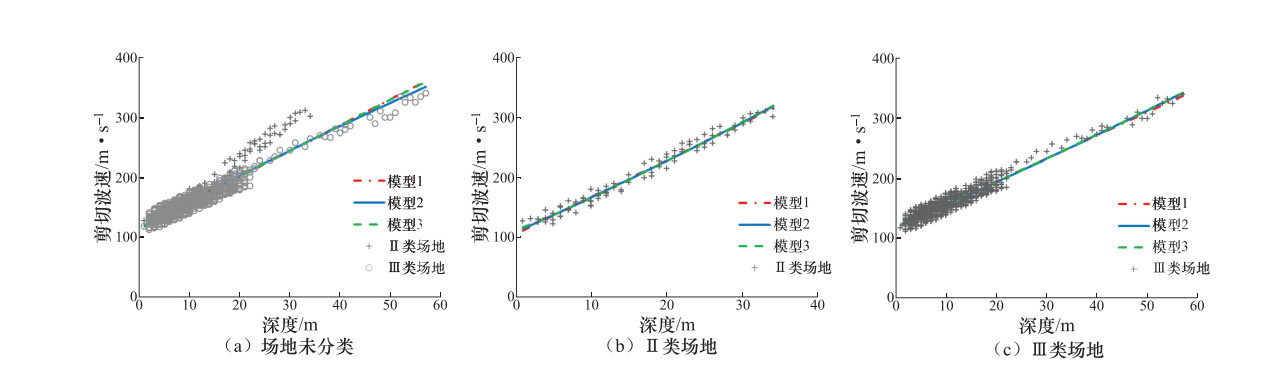
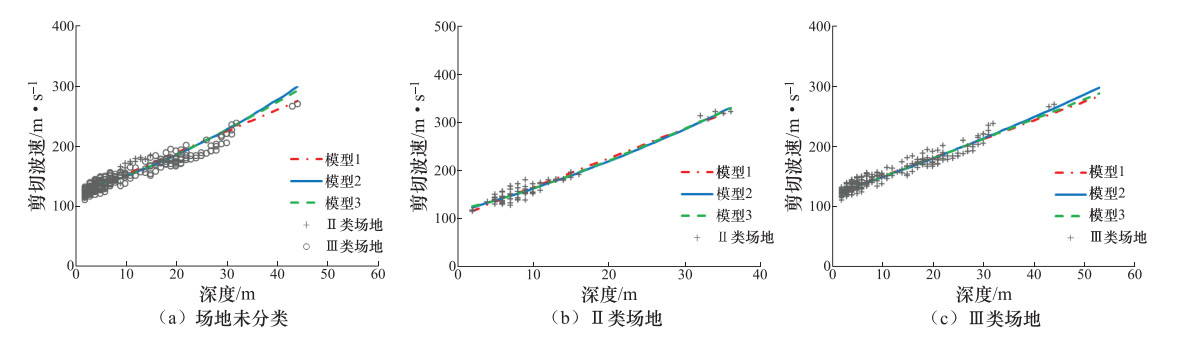
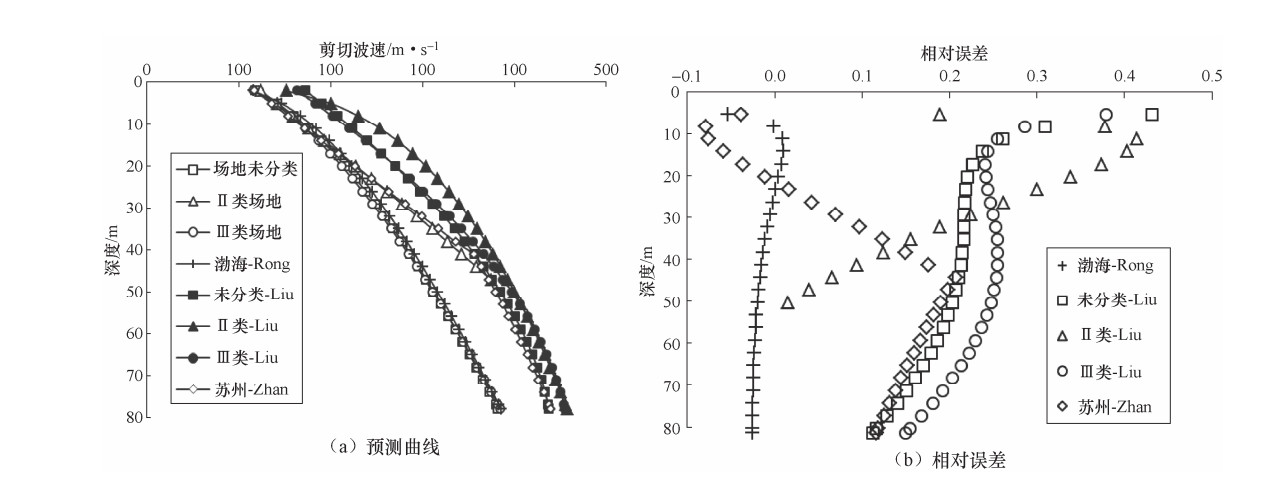
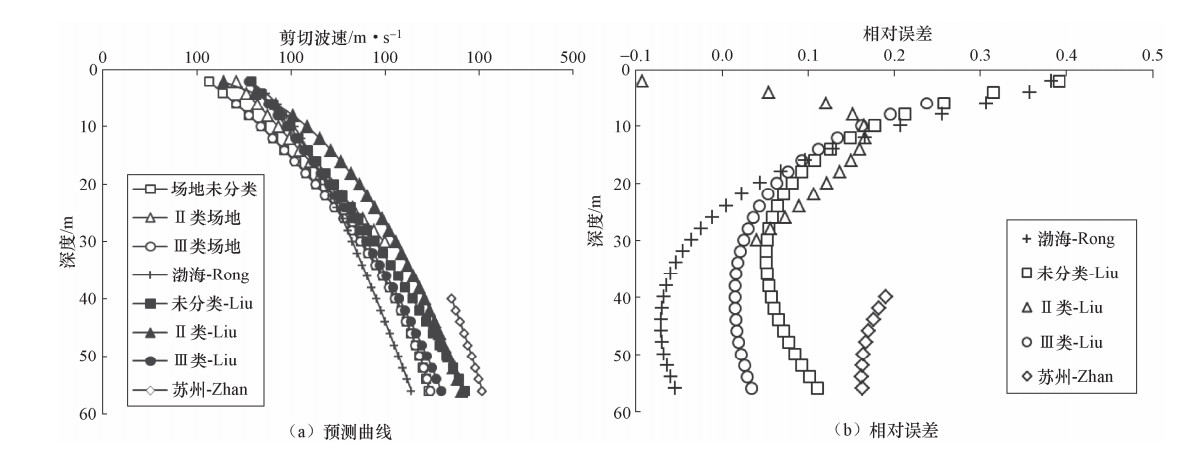
岩土类型 场地类别 推荐模型 回归方程 残差标准差 R2 适应范围/m 粉质粘土 Ⅱ类 模型2 ${v_s} = 112.4398 + 5.9058H - 0.0077{H^2}$ 13.58 0.9530 2—44 Ⅲ类 模型3 ${v_s} = 86.5602 + 18.7249{H^{0.6352}}$ 18.45 0.8813 2—78 场地未分类 模型3 ${v_s} = 85.5503 + 21.3380{H^{0.6041}}$ 19.44 0.8914 2—78 淤泥质粉质粘土 Ⅱ类 模型2 ${v_s} = 104.8362 + 0.2524{H^{1.9230}}$ 8.83 0.9096 4—24 Ⅲ类 模型2 ${v_s} = 90.5189 + 4.1075H - 0.0227{H^2}$ 10.46 0.8685 2—46 场地未分类 模型2 ${v_s} = 89.9598 + 4.1857H - 0.0245{H^2}$ 10.65 0.8656 2—46 粉砂 Ⅱ类 模型1 ${v_s} = 130.5509 + 5.6417H$ 8.08 0.9594 1—30 Ⅲ类 模型2 ${v_s} = 100.2213 + 7.3496H - 0.0521{H^2}$ 18.79 0.8498 5—56 场地未分类 模型2 ${v_s} = 98.7936 + 7.5598H - 0.0558{H^2}$ 21.19 0.8482 1—56 砂质粉土 Ⅱ类 模型3 ${v_s} = 112.9768 + 4.1008{H^{1.1103}}$ 8.37 0.9773 1—34 Ⅲ类 模型3 ${v_s} = 120.9837 + 3.0980{H^{1.0546}}$ 18.45 0.9155 1—57 场地未分类 模型2 ${v_s} = 113.5888 + 4.5896H - 0.0079{H^2}$ 12.73 0.8811 1—57 粘质粉土 Ⅱ类 模型2 ${v_s} = 115.3530 + 4.2818H + 0.0461{H^2}$ 9.42 0.9551 2—36 Ⅲ类 模型2 ${v_s} = 121.1832 + 2.7579H + 0.0110{H^2}$ 7.39 0.9291 2—44 场地未分类 模型2 ${v_s} = 123.4666 + 2.4199H - 0.0354{H^2}$ 13.14 0.8386 2—44
下载: 导出CSV
表 4 Ⅱ类场地实测剪切波速与预测值的对比分析
Table 4. Comparative analysis of measured shear wave velocity and predicted value of site Ⅱ
岩土类型 钻孔编号 深度
/m实测剪切波速
/m·s-1Ⅱ类场地预测值
/m·s-1相对误差
/%场地未分类预测值
/m·s-1相对误差
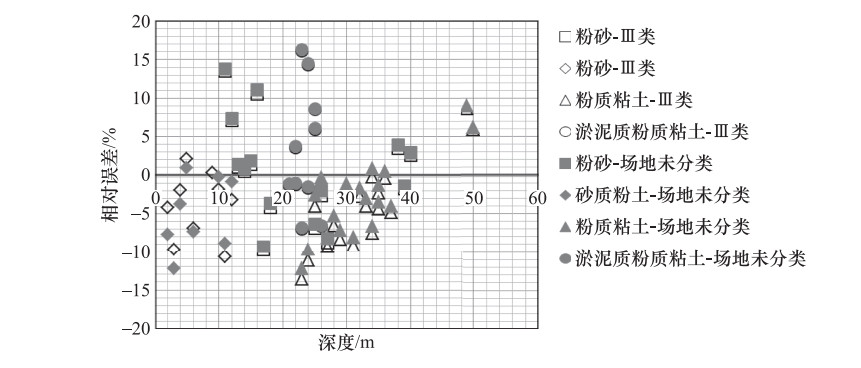
/%粉质粘土 JZ1 3 130 130 0.07 127 -2.32 JZ1 5 143 142 -0.84 142 -0.72 JZ-Ⅳ 8 152 159 4.76 160 5.58 JZ-Ⅳ 24 222 250 12.68 231 4.09 JZ-Ⅳ 27 263 267 1.44 242 -8.06 粉砂 JZ1 29 278 278 -0.06 249 -10.54 JZ1 24 233 266 14.14 248 6.48 JZ1 26 286 277 -3.06 258 -9.92 淤泥质粉质粘土 JZ-Ⅳ 16 154 157 1.97 151 -2.17 JZ-Ⅳ 17 145 163 12.75 154 6.23 JZ-Ⅳ 19 159 177 11.62 161 1.03
下载: 导出CSV
-
期刊类型引用(3)
1. 朱兰鑫，陈彦钧，王文伯，曹瑜珈，黄慧敏，张丁凡，李正斌. 高精度光纤旋转地震仪研制与应用. 地球物理学报. 2024(12): 4594-4610 . 
百度学术2. 郭高源，李维，张壹，王赟，曹瑜珈，张丁凡. 广州市区浅层横波速度六分量地震探测试验. 工程地球物理学报. 2023(03): 411-420 . 百度学术3. 李维，郭高源，王赟，张丁凡，曹瑜珈，吴志芳，张宝剑，钱荣毅. 两种可控震源的浅层地震六分量波场特征. 工程地球物理学报. 2022(05): 716-728 . 百度学术其他类型引用(1)
-
下载:
点击查看大图
计量
- 文章访问数: 257
- HTML全文浏览量: 68
- PDF下载量: 10
- 被引次数: 4
