Dynamic Response Law and Stability Analysis of Loess Multi-stage High Fill Slope under Horizontal Seismic Action
-
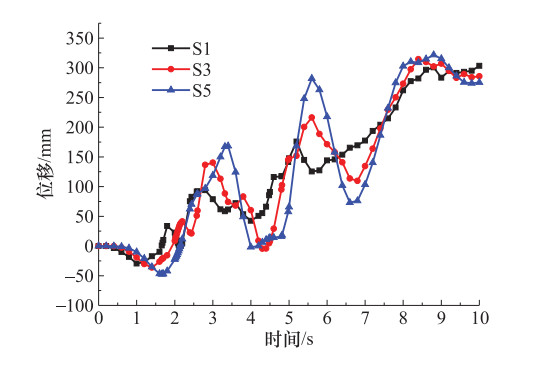
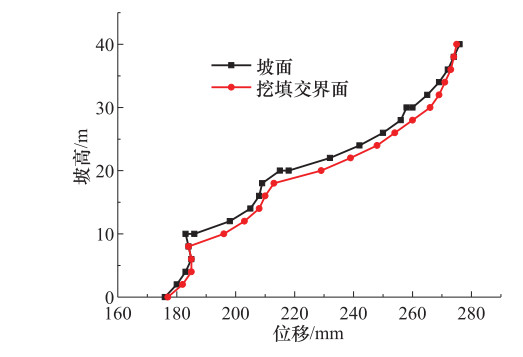
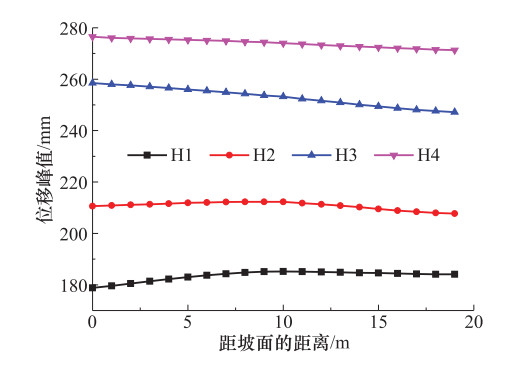
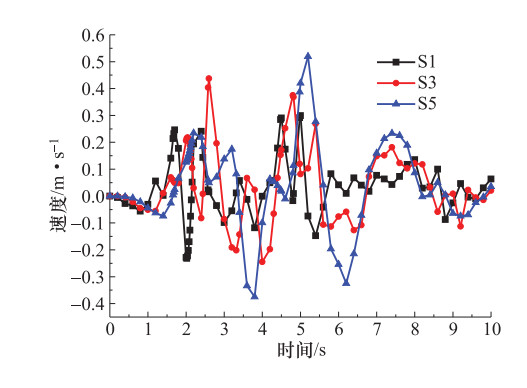
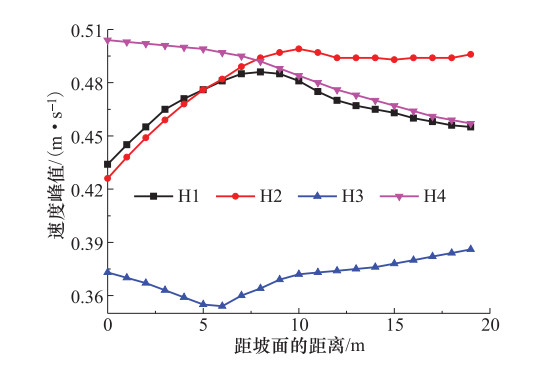
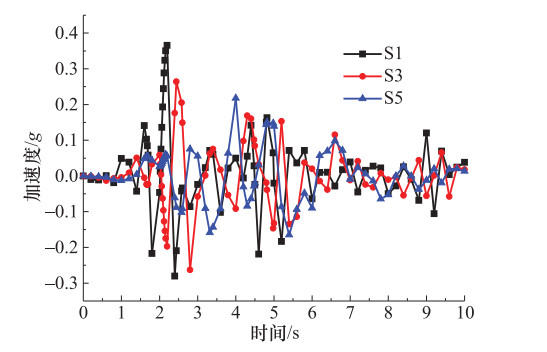
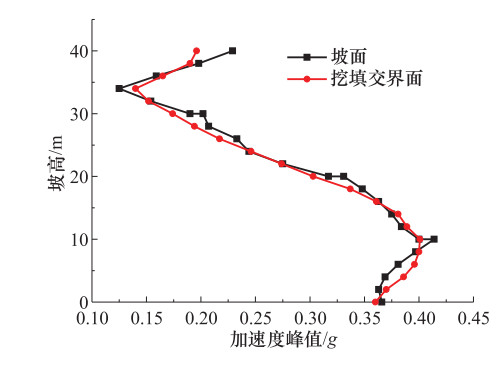
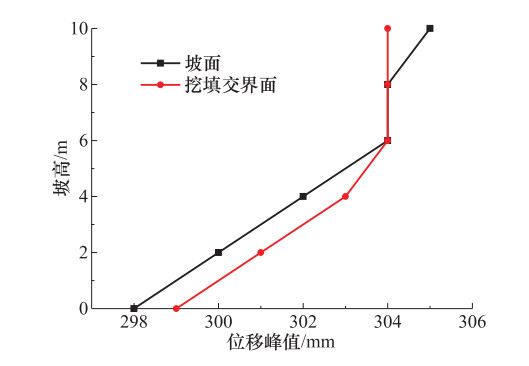
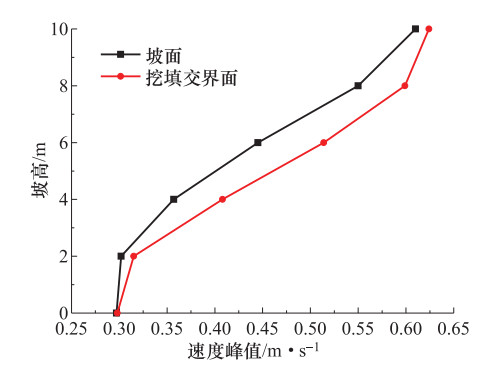
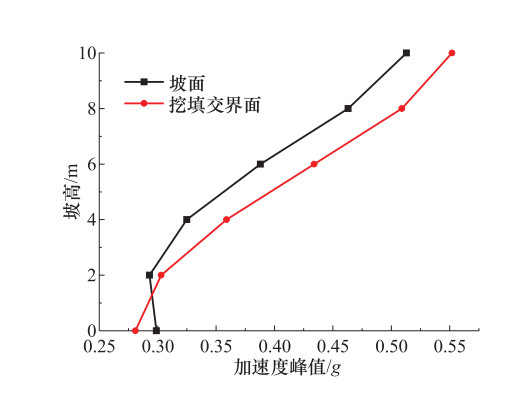
摘要: 为研究水平地震作用下黄土多级高填方边坡动力响应规律及稳定性，本文以某高填方边坡工程为背景，利用GeoStudio2012有限元分析软件建立模型进行分析，并对比分析多级高填方边坡与单级填方边坡动力响应结果。计算结果表明，边坡坡面和挖填交界面上动力响应规律表现为：位移幅值基本随着高程的增加而增加；速度幅值随着高程的增加先增大后减小再增大；加速度幅值随着高程的增加有减小趋势；多级高填方边坡动力响应规律与单级填方边坡动力响应规律不同，单级填方边坡位移幅值、速度幅值、加速度幅值均随着高程的增加递增；地震波在坡体内传播时，随着高程的增加具有滞后性。边坡稳定性随着地震加速度峰值的增大有所下降，相比静力作用，水平地震作用下边坡稳定性下降明显。本文相关研究可为西北地区黄土高填方边坡工程抗震提供一定理论依据。Abstract: In order to study the dynamic response law and stability of loess multi-stage high fill slope under horizontal seismic action, this paper takes a high fill slope project as the research background, uses Geo-Studio2012 finite element analysis software to establish a model for analysis, and compares the dynamic response results of multi-stage high fill slope and single-stage fill slope. The calculation results show that, the displacement amplitude of slope surface and excavation-filling interface basically increases with the increase of elevation, the velocity amplitude increases first and then decreases and then increases with the increase of elevation, and the acceleration amplitude has a decreasing trend with the increase of elevation. The dynamic response law of high fill slope is different from that of single-stage fill slope. The displacement amplitude, velocity amplitude and acceleration amplitude of single-slope fill slope increase with the increases of elevation. The seismic wave has hysteresis with the increase of elevation when it propagates in the slope. The slope stability decreases with the increase of the seismic acceleration peak value, and the slope stability decreases significantly under horizontal seismic action. The research can provide a theoretical basis for seismic protection of loess high fill slope engineering in Northwest China.
-
Key words:
- Loess /
- Multi-stage high fill slope /
- Horizontal seismic /
- Dynamic response /
- Stability
-
图 13 单级填方边坡模型及监测点布置
Figure 13. Single-stage fill slope model and layout of monitoring points
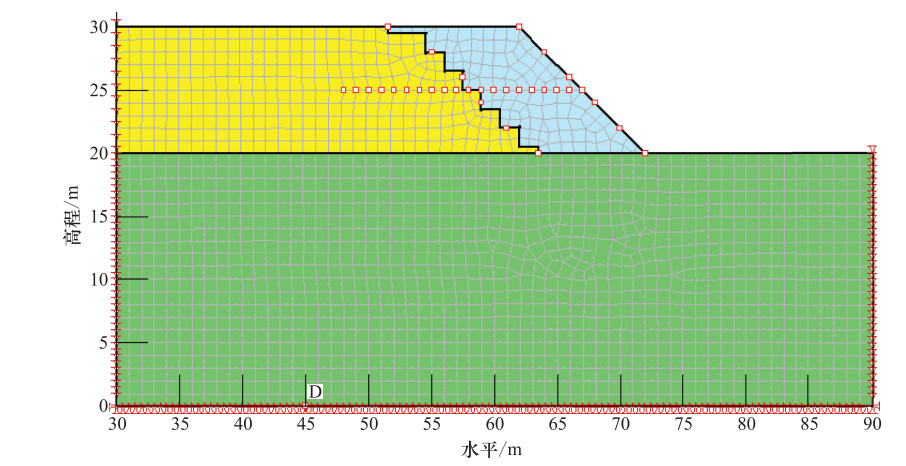
表 1 土体物理力学参数
Table 1. Physical mechanical parameters of soil
土层序号 土层名称 初始动剪切模量
Gmax/MPa重度γ
/kN·m-3动黏聚力
cd/kPa动内摩擦角ϕd
/°泊松比v 阻尼比 ① 填料 6.0 17.5 20 22 0.35 0.20 ② 黄土状粉土 3.0 17.0 16 20 0.38 0.12 ③ 卵石 23.9 22.0 0 35 0.20 0.05 
下载: 导出CSV
-
-
点击查看大图
图(16) / 表(1)
计量
- 文章访问数: 195
- HTML全文浏览量: 46
- PDF下载量: 5
- 被引次数: 0
