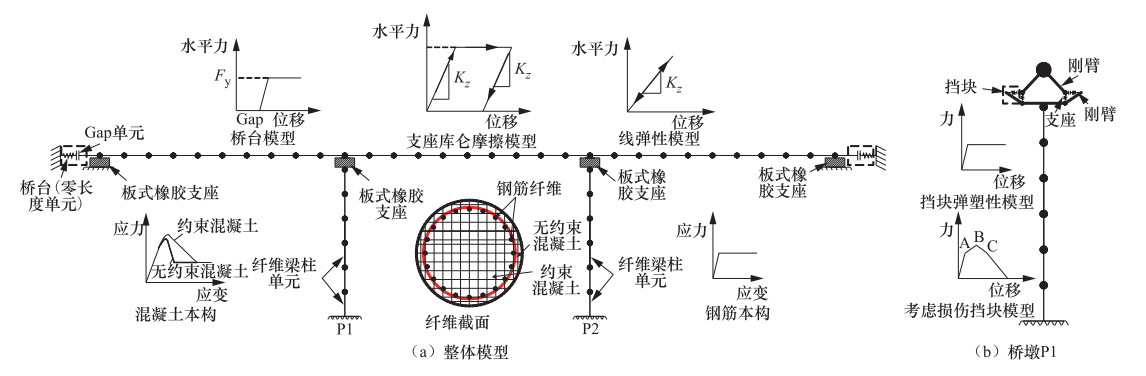
Seismic Vulnerability Analysis of Small and Medium Span Girder Bridges Considering the Sliding of Bearing and Shear Key Damage
-
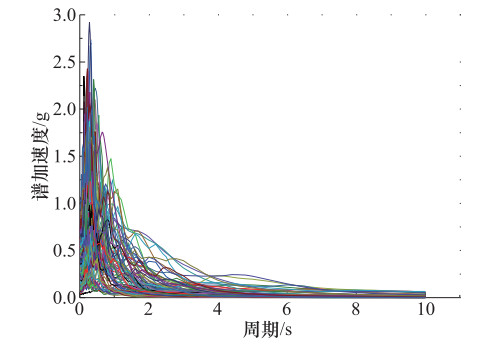
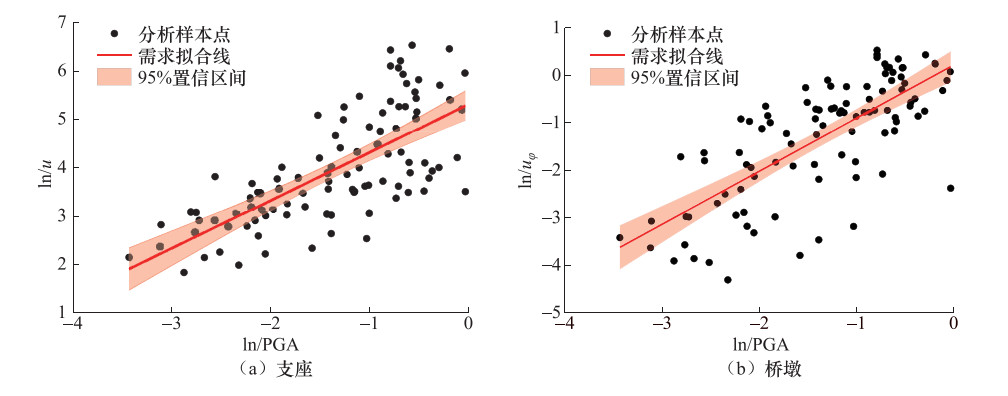
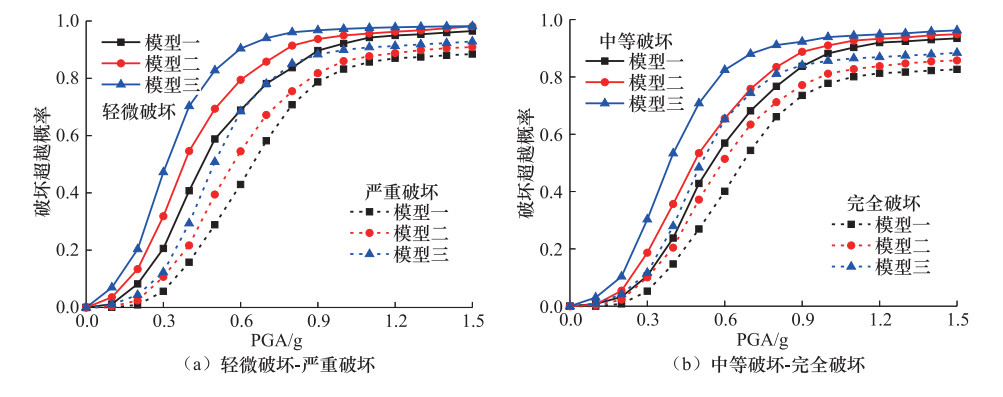
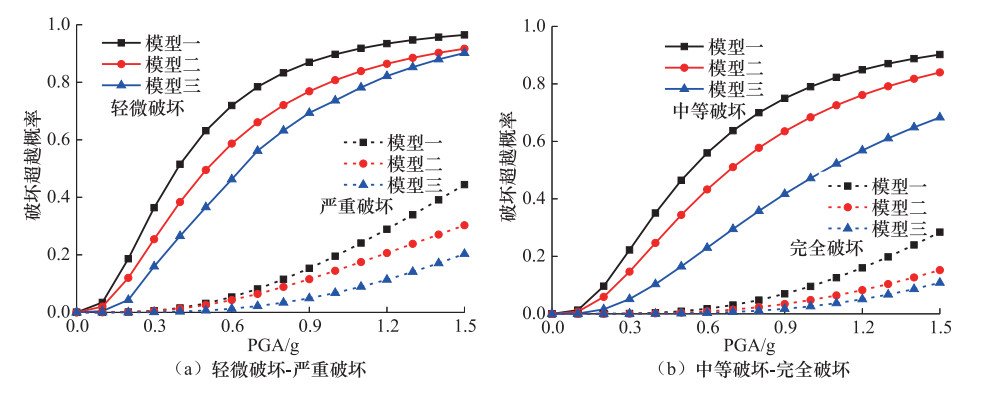
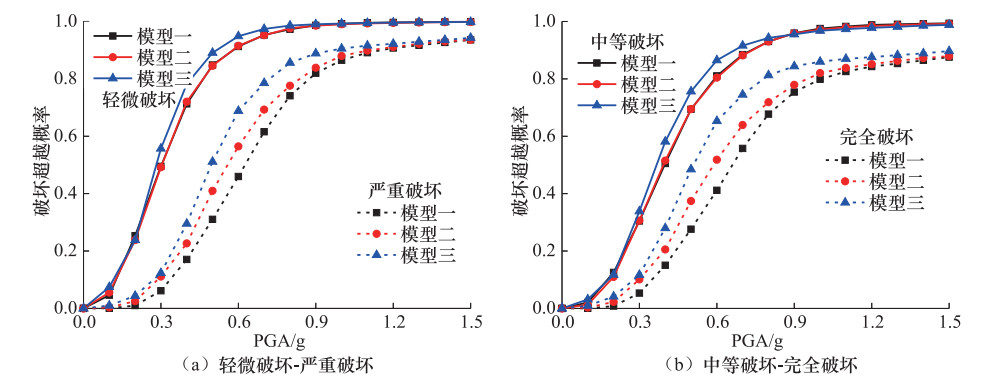
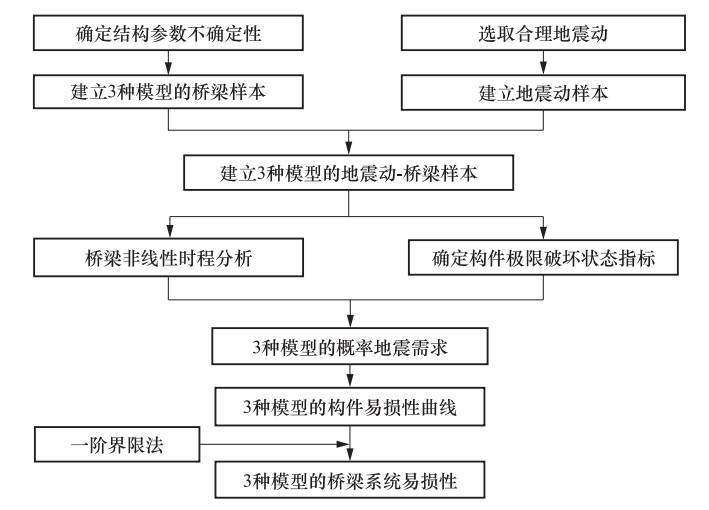
摘要: 从板式橡胶支座及混凝土挡块抗震设计角度，以一座典型的3跨预应力混凝土连续梁桥为例，结合概率地震需求分析及桥墩、支座等抗震关键构件极限破坏状态，建立不同支座及挡块分析模型的中小跨径梁桥地震易损性曲线，研究考虑支座滑移效应及挡块破坏的中小跨径梁桥的易损性特征。研究结果表明：不考虑橡胶支座的滑移效应及混凝土挡块破坏，桥墩地震破坏概率明显增大，且会低估支座破坏概率；桥梁系统易损性受支座破坏状态的影响显著，需设置合理的限位装置；在中小跨径梁桥地震易损性分析中，考虑支座的滑移效应及混凝土挡块的破坏十分必要。Abstract: From the perspective of seismic designs of plate type elastomeric pad bearings and concrete shear key,a typical three-span prestressed concrete continuous girder bridge was taken as a case study. Combined with the probabilistic seismic demand analysis and the limit failure states of critical members such as piers and bearings,this study developed the vulnerability curves of the bridges with different models of bearings and shear keys and studies the Vulnerability characteristics of the small and medium-span bridge considering the slip effect of the bearing and the shear key damage. The results show that the seismic damage probability of the pier is obviously increased without considering the slip effect of bearings and the shear key damage,and the probability of the bearing damage is underestimated; the system vulnerability is significantly affected by the damage of bearings,and a reasonable limit device is needed for the bearing; the sliding effect of bearings and shear key damages should be considered in the seismic vulnerability analysis of small and medium span girder bridges.
-
引言
凸起地形是常见的复杂地形之一，对地震波的传播有很大影响，会造成局部范围内震害的明显差异。国内外震后调查均发现山体上的结构震害显著（胡聿贤等，1980；孙平善等，1991；袁一凡等，2012；Çelebi，1987；Athanasopoulos等，1999；Paolucci，2002；Çelebi等，2010），强震仪也常记录到凸起地形顶部出现的异常高峰值加速度，如1971年圣费尔南多6.4级地震在靠近Pacoima大坝的尖锐三角形凸起的顶部PGA为1.25 g（Trifunac等，1971），1994年北岭地震在Tarzana山地的PGA达1.78 g（Spudich等，1996），2008年我国四川汶川特大地震中自贡西山公园从山脚到山顶的7个基岩场地的PGA基本呈现出逐渐增大的趋势（唐晖等，2012）。
为研究凸起地形的地震动特性，已有学者采用多种解析方法和数值方法研究了不同入射波、波长、入射角、倾斜角等因素对凸起地形放大效应的影响（刘晶波，1996；杜永军等，2005；Kamalian等，2006；梁建文等，2006；郝明辉等，2018；Dai等，2019；Kumar等，2021）。在这些研究中，多采用单个凸起模型，对于多个凸起地形对地震波放大效应的影响研究较少（郝明辉等，2015；巴振宁等，2018；刘中宪等，2018），而对层状半空间及层状半空间相邻凸起地形的地震响应研究更少（梁建文等，2008；巴振宁等，2015，2017）。
本文利用ANSYS有限元软件与多次透射公式MTF（Multi-transmitting Formula）相结合方法（廖振鹏，2002），计算层状半空间单个半圆形凸起地形和相邻圆半圆形凸起地形对入射SV波的地震响应。为避免采用不同的地震波入射下呈现的地表地震动峰值分布存在差异（周国良等，2012；盛志强等，2013；丁海平等，2017），本文对频域结果进行分析，通过对不同入射波频率、入射角度和半圆形凸起间距等条件下凸起地形地表谱放大系数
$ \beta $ 的比较，讨论层状半空间相邻半圆形凸起地形地震响应的相互影响。1. 计算方法
由人工边界和地表包围的区域结构-地基系统如图1所示，运动方程如下：
图 1 结构-地基系统动力反应分析示意Figure 1. Schematic diagram of dynamic response analysis of structure-foundation system$$ {\boldsymbol{M}}\ddot {\boldsymbol{u}} + {\boldsymbol{C}}\dot {\boldsymbol{u}} + {\boldsymbol{Ku}} = {\boldsymbol{P}} $$ (1) 式中，M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；P为外力矢量。
在地震波作用下，本文所讨论的波动问题有2个问题需要解决好，一是边界问题，二是地震波的输入问题，且这2个问题是相关联的。本文的人工边界采用MTF边界（廖振鹏，2002）。设某入射波以人工波速
$C_{{\rm{a}}}$ 沿x轴从左侧射向人工边界点0（图2），点j在p时刻的位移表达式为：
图 2 人工边界附近节点（一维波动模型）Figure 2. Node number near artificial boundary（One-dimensional wave model）$${u}_{j}^{p}=u(p\Delta t{\text{，}}j\Delta x) $$ (2) 式中，j和p为整数；
$ \Delta t $ 为时间步距；$ \Delta x $ 为空间步距。若$ \Delta t=\Delta x/C_{{\rm{a}}} $ ，则$ {u}_{0}^{p+1} $ 可直接用与人工边界垂直方向上的内部节点位移$ {u}_{j}^{p+1-j} $ 确定：$$ u_0^{p + 1} = \sum\limits_{j = 1}^N {{{( - 1)}^{j + 1}}C_j^Nu_j^{p + 1 - j}} $$ (3) 式中二项式系数为：
$$ {C}_{j}^{N}=\frac{N!}{\left(N-j\right)!j!} $$ (4) 由于MTF模拟的是外行波，即散射波
$ {u}_{\mathrm{s}} $ 表达式为：$$ {u_{\rm{s}}} = u - {u_{\rm{r}}} $$ (5) 式中，
$ {u}_{\mathrm{s}} $ 为散射波位移，u为全波场位移，$ {u}_{\mathrm{r}} $ 为参考波场的位移（对底边界，参考波场可直接取输入场，对侧边界，则通常取为自由场）。令式（3）中
${u_0} = {u_{{\rm{s}},0}}$ ，将式（5）代入式（3）中，有：$$ u_{{\rm{s}},\;0}^{p + 1} = \sum\limits_{j = 1}^N {{{( - 1)}^{j + 1}}C_j^Nu_j^{p + 1 - j} - \sum\limits_{j = 1}^N {{{( - 1)}^{j + 1}}C_j^Nu_{{\rm{r}},\;j}^{p + 1 - j}} } $$ (6) 假定输入地震波为位移，则输入面为人工边界节点所在位置，人工边界点的全波场位移为：
$$ u_0^{p + 1} = u_{{\rm{s}},\;0}^{p + 1} + u_{{\rm{r}},\;0}^{p + 1} = \sum\limits_{j = 1}^N {{{( - 1)}^{j + 1}}C_j^Nu_j^{p + 1 - j} - \sum\limits_{j = 1}^N {{{( - 1)}^{j + 1}}C_j^Nu_{{\rm{r}},\;j}^{p + 1 - j}} } + u_{{\rm{r}},\;0}^{p + 1} $$ (7) 式（7）中的
$ {u}_{0}^{p+1} $ 即为结构-地基系统在地震作用下的边界点位移反应。将式（1）改写成：
$$ \left[ \begin{gathered} {M_{ii}}\;\;{M_{ib}} \\ {M_{bi}}\;\;{M_{bb}} \\ \end{gathered} \right]\;\left\{ \begin{gathered} {{\ddot u}_i} \\ {{\ddot u}_b} \\ \end{gathered} \right\} + \left[ \begin{gathered} {C_{ii}}\;\;{C_{ib}} \\ {C_{bi}}\;\;{C_{bb}} \\ \end{gathered} \right]\;\left\{ \begin{gathered} {{\dot u}_i} \\ {{\dot u}_b} \\ \end{gathered} \right\} + \left[ \begin{gathered} {K_{ii}}\;\;{K_{ib}} \\ {K_{bi}}\;\;{K_{bb}} \\ \end{gathered} \right]\;\left\{ \begin{gathered} {u_i} \\ {u_b} \\ \end{gathered} \right\} = \left\{ \begin{gathered} {p_i} \\ {p_b} \\ \end{gathered} \right\} $$ (8) 式中，i表示内节点（包括自由表面节点），b表示边界节点。
对于散射问题，式（8）的右侧荷载项为0，则式（8）成为已知边界点
$ {u}_{b} $ 的位移求解内节点位移问题。对于波源问题，式（8）的右侧$ {p}_{b} $ 为0，则式（8）成为已知边界点$ {u}_{b} $ 的位移和$ {p}_{i} $ 求解内节点位移问题。通过选择合适的数值积分格式，可对式（8）进行求解。2. 方法验证
为验证本文计算方法的正确性，采用与Kamalian等（2006）研究相同的凸起模型作为算例（图3），以垂直入射脉冲波
$ (\theta =0°) $ 的计算结果与文献进行对比。模型尺寸为$ 400\;\mathrm{m}\times 200\;\mathrm{m} $ ，介质密度$ \rho =1\;500\; \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} $ ，泊松比$ \mu =1/3 $ ，剪切波速$ {C}_{\mathrm{s}}=500\;\mathrm{m}/\mathrm{s} $ ，半圆形凸起半径$ a=50\;\mathrm{m} $ 。选取上述模型地表的73个观测点（编号为0～72）水平方向和竖直方向位移时程，并进行傅里叶变换，计算与入射波位移傅里叶幅值谱的比值，得到地表各点谱放大系数
$ \beta $ 。本文计算结果与Kamalian等（2006）结果的对比如图4所示，二者结果吻合较好，说明本文的计算方法是可行的。
图 4 本文计算结果与文献（Kamalian等，2006）Figure 4. Comparison of results from this paper and reference（Kamalian et al.，2006）3. 输入波形与计算模型
假定模型底部入射SV波，脉冲波采用δ函数的有限差分近似（刘晶波等，2005）：
$$ U(t) = 16\left[ {G(t) - 4G\left(t - \frac{1}{4}\right) + 6G\left(t - \frac{1}{2}\right) - 4G\left(t - \frac{3}{4}\right) + G(t - 1)} \right] $$ (9) 式中，
$ G\left(t\right)={\left(\tau \right)}^{3}H\left(\tau \right)，\tau =\dfrac{t}{T} $ ，T为脉冲持时，$ H\left(\tau \right) $ 为Heaviside函数。波形如图5（a）所示，对应的傅里叶谱如图5（b）所示，由图5可知截止频率
$ {f}_{\mathrm{c}\mathrm{u}\mathrm{t}}=40\;\mathrm{H}\mathrm{z} $ 。进行有限元数值模拟时，网格尺寸一般需满足在1个有意义的波长内包含6～10个单元网格，本文取：$$ \Delta x \leqslant \frac{\lambda }{{10}} = \frac{{{C_{\rm{s}}}}}{{10{f_{{\text{cut}}}}}} $$ (10) 式中，
$ \lambda $ 为入射波波长；$ {f}_{\mathrm{c}\mathrm{u}\mathrm{t}} $ 为入射波的截止频率。解析方法给出的场地地震响应一般是基于无量纲频率的谱比（或称谱放大系数），其中无量纲频率定义为：
$$ \eta = \frac{{2a}}{{{\lambda _{\rm{s}}}}} = \frac{{\omega a}}{{{\text{π}} {C_{\rm{s}}}}} = 2f\frac{a}{{{C_{\rm{s}}}}} $$ (11) 式中，
$ a $ 为凸起地形半宽；$ {\lambda }_{\mathrm{s}} $ 为土层介质中剪切波波长；$ \omega $ 为圆频率。无量纲频率
$ \eta $ 由凸起地形宽度与土层介质中剪切波波长之比决定，$ \eta $ 值越大，入射波波长越小，对应的频率$ f $ 越高。由于在图5脉冲波作用下得到的是实际频率的地震动放大效应，需转换为无量纲频率下的结果。根据计算模型中凸起半宽与土介质特性，由式（11）可得无量纲频率与实际频率的对应关系，如表1所示。
表 1 无量纲频率对应的实际频率Table 1. Actual frequency corresponding to the dimensionless frequency$ \eta $ 0.25 0.5 0.75 1 2 4 $ f $/Hz 1.25 2.5 3.75 5 10 20 4. 算例与分析
本文计算模型为层状半空间相邻2个凸起半圆地形模型，模型长度为600 m，高度为200 m，其中土层高度为75 m，基岩高度为125 m，如图6所示。模型中土层剪切波速为500 m/s，密度为1 500 kg/m3，泊松比为1/3；基岩剪切波速为800 m/s，密度为2 100 kg/m3，泊松比为1/3。半圆形凸起模型半宽a=50 m，有限元计算网格大小为1.25 m。
图 6 计算模型示意（相邻2个凸起半圆地形）Figure 6. Schematic diagram of calculation model- two adjacent cylindrical hills为便于描述，模型A的坐标原点设在左侧凸起的中点，用于分析右侧凸起对左侧凸起的影响；模型B的坐标原点设在右侧凸起的中点，用于分析左侧凸起对右侧凸起的影响；共考虑3种不同的凸起间距，分别为a、2a和3a。另外，将模型A中去掉右侧凸起或模型B中去掉左侧凸起的模型称为单个凸起模型，类似图3。
根据2个假定计算模型的计算结果，分析入射波频率、入射角度及凸起间距等因素对相邻凸起模型SV波放大效应的影响。同时，与对应的均匀半空间相邻凸起地形模型的对应结果进行对比分析，此时取基岩参数与土层参数相同，剪切波速均为500 m/s，密度均为1 500 kg/m3，泊松比均为1/3。
4.1 右侧凸起对左侧凸起的影响
采用本文提出的有限元模拟方法，首先得到了SV波分别以0°、15°、30°入射层状半空间单个半圆形模型及相邻2个半圆形模型的左侧凸起（图6（a））地表各点位移时程；然后对场地地表各点位移时程进行傅里叶变换，得到频域响应的傅里叶谱；最后计算与入射脉冲波的傅里叶谱的比值，即谱放大系数
$ \beta $ ，本文给出了无量纲频率为0.25、0.5、0.75、1、2、4时的谱放大系数$ \beta $ 结果，如图7～图9所示。
图 7 不同凸起间距下左侧凸起地表位移谱放大系数（模型A，$ \theta $ =0°）Figure 7. Spectral amplification of surface observation points of left hill with different hill distance （Model A,$ \theta $ =0°）
图 8 不同凸起间距下左侧凸起地表位移谱放大系数（模型A，$ \theta $ =15°）Figure 8. Spectral amplification of surface observation points of left hill with different hill distance （Model A,$ \theta $ =15°）
图 9 不同凸起间距下左侧凸起地表位移谱放大系数（模型A，$ \theta $ =30°）Figure 9. Spectral amplification of surface observation points of left hill with different hill distance （Model A,$ \theta $ =30°）由图7～图9可知，右侧凸起对左侧凸起的影响较大，特别是在
$ \left|x/a\right| $ ≤1.0范围内，谱放大系数差异是由右侧凸起造成的。不同无量纲频率、入射角度、凸起间距下，谱放大系数不同，如当$ \eta $ =0.75、$ \mathrm{\theta } $ =0°、$ \left|x/a\right| $ =−0.8时，单个凸起的谱放大系数$ \beta $ =1.51（均匀半空间单个凸起地形模型的谱放大系数β1=1.31），而凸起间距为a时的谱放大系数$ \beta $ =2.86（均匀半空间相应的相邻凸起地形模型的普放大系数β2=1.86），由于右侧凸起的存在，谱放大系数$ \beta $ 增大了0.89倍；当$ \eta $ =0.5、$ \mathrm{\theta } $ =30°、$ \left|x/a\right| $ =0时，单个凸起的谱放大系数$ \beta $ =3.05（β1=2.41），而凸起间距为3a时的谱放大系数$ \beta $ =3.79（β2=1.62），谱放大系数$ \beta $ 增大了0.24倍。由于右侧凸起的存在，$ \left|x/a\right| $ ≤1.0范围内的谱放大系数$ \beta $ 减小，如当$ \eta $ =0.25、$ \mathrm{\theta } $ =30°、$ \left|x/a\right|=0 $ 时，单个凸起的谱放大系数$ \beta $ =10.99（β1=7.65），凸起间距为2a时的谱放大系数$ \beta $ =9.59（β2=9.04），谱放大系数$ \beta $ 减小了0.13倍；当$ \eta $ =0.5、$ \mathrm{\theta } $ =0°、x/a=0时，单个凸起的谱放大系数$ \beta $ =2.50（β1=2.24），凸起间距为2a时的谱放大系数$ \beta $ =2.33（β2=1.62），谱放大系数$ \beta $ 减小了0.07倍。根据图7～图9的谱放大系数
$ \beta $ 值难以得到入射波频率、入射角度及凸起间距等因素对左侧凸起表面各点频谱放大的影响规律。但当$ \eta $ <1.0时，对于不同的入射波频率、入射角度和凸起间距，分别在$ \left|x/a\right| $ ≤1.0和$ \left|x/a\right| $ ≥1.0范围内，谱放大系数$ \beta $ 变化较有规律性，$ \beta $ 曲线较光滑；而当$ \eta $ >1.0时，随着入射角度的增大，谱放大系数$ \beta $ 变化规律较杂乱。4.2 左侧凸起对右侧凸起的影响
无量纲频率分别为0.25、0.5、0.75、1、2、4时左侧凸起对右侧凸起表面和邻近点地震响应的影响如图10～图12所示。
图 10 不同凸起间距下右侧凸起地表位移谱放大系数（模型B，$ \theta $ =0°）Figure 10. Spectral amplification of surface observation points of right hill with different hill distance （Model B,$ \theta $ =0°）
图 11 不同凸起间距下右侧凸起地表位移谱放大系数（模型B，$ \theta $ =15°）Figure 11. Spectral amplification of surface observation points of right hill with different hill distance （Model B,$ \theta $ =15°）
图 12 不同凸起间距下右侧凸起地表位移谱放大系数（模型B，$ \theta $ =30°）Figure 12. Spectral amplification of surface observation points of right hill with different hill distance （Model B,$ \theta $ =30°）由图10～图12可知，左侧凸起对右侧凸起的影响较大，不同无量纲频率、入射角度、凸起间距对谱放大系数
$ \beta $ 的影响不同，如当$ \eta $ =0.5、$ \mathrm{\theta } $ =15°、$ \left|x/a\right| $ =0时，水平方向单个凸起的谱放大系数$ \beta $ =2.69（均匀半空间单个凸起地形模型的谱放大系数β1=2.30），凸起间距为a时的谱放大系数$ \beta $ =3.64（均匀半空间相应的相邻凸起地形模型的谱放大系数β2=2.97），由于左侧凸起的存在，谱放大系数$ \beta $ 值增大了0.35倍；当$ \eta $ =0.75、$ \mathrm{\theta } $ =15°、$ \left|x/a\right| $ =0时，水平方向单个凸起的谱放大系数$ \beta $ =1.31（β 1=1.22），凸起间距为3a时的谱放大系数$ \beta $ =1.99（β2=1.88），谱放大系数$ \beta $ 值增大了0.52倍；当$ \eta $ =0.75、$ \mathrm{\theta } $ =30°、$ \left|x/a\right| $ =0时，单个凸起的谱放大系数$ \beta $ =2.05（β1=1.74），凸起间距为a时的谱放大系数$ \beta $ =5.15（β2=2.73），谱放大系数$ \beta $ 值增大了1.51倍。同时也存在谱放大系数
$ \beta $ 值减小的情况，如当$ \eta $ =1、$ \mathrm{\theta } $ =0°、$ \left|x/a\right| $ =−0.5时，单个凸起的谱放大系数$ \beta $ =3.66（β1=1.61），凸起间距为a时的谱放大系数$ \beta $ =3.47（β2=1.69），由于左侧凸起的存在，谱放大系数$ \beta $ 值减小了0.05倍；当$ \eta $ =0.25、$ \mathrm{\theta } $ =15°、$ \left|x/a\right| $ =0.5时，单个凸起的谱放大系数$ \beta $ =9.44（β1=4.00），凸起间距为a时的谱放大系数$ \beta $ =8.44（β2=3.15），谱放大系数$ \beta $ 值减小了0.11倍。同样，根据图10～图12中的谱放大系数
$ \beta $ 值难以得到入射波频率、入射角度及凸起间距等因素对右侧凸起表面各点频谱放大的影响规律。4.3 与均匀半空间相邻半圆形凸起地形结果比较
无量纲频率分别为0.25、0.5和1.0，入射角分别为0°、15°和30°，凸起间距为a时，左侧凸起半圆和右侧凸起半圆的地表位移谱放大系数如图13、图14所示。对单个凸起模型结果（图13、图14中黑色实线和黑色虚线）进行比较，可以发现当频率、入射角度较小时，层状半空间地表位移谱放大系数明显大于均匀半空间地表位移谱放大系数，不同地表位置放大程度不同；随着频率、入射角度的增大，在
$ \left|x/a\right| $ ≥1.0范围内，存在层状半空间地表位移谱放大系数小于均匀半空间地表位移谱放大系数的情况，如图13中$ \eta $ = 1.0、$ \mathrm{\theta } $ =30°的情形，相邻2个凸起半圆模型（红实线和红虚线）也有类似情况出现，如图14中$ \eta $ = 1.0、$ \mathrm{\theta } $ =30°的情形。
图 13 左侧凸起地表位移谱放大系数比较（L = a） Figure 13. Comparison of the surface spectral amplification of the left hill （L=a ）
图 14 右侧凸起地表位移谱放大系数比较（L = a） Figure 14. Comparison of the surface spectral amplification of the right hill （L=a ）5. 结论
本文采用有限元数值方法计算了层状半空间相邻半圆形凸起地形对入射SV波的放大效应，分析了不同入射波频率、入射角度和凸起间距等对层状半空间相邻2个半圆形凸起间相互作用的影响，得出以下结论：
（1）对于不同的入射波频率和入射角度，不同凸起间距对相邻半圆形凸起地表位移谱放大系数的影响无规律性，但当无量纲频率较小时，如为0.25时，凸起间距对谱放大系数的影响明显大于其他频率；此外，凸起间距越小，右侧凸起对左侧凸起的影响越大，这主要是受右侧凸起产生的反射波影响，左侧凸起对右侧凸起的影响还需考虑入射角度。
（2）当无量纲频率>1.0时，对于相同的入射波频率和入射角度，不同凸起间距下的地表位移谱放大系数差别较小，且无量纲频率越大，凸起间距对谱放大系数的影响越小。无量纲临界频率为
$ 1.0 $ ，其与土层剪切波速和凸起地形宽度有关。因此研究凸起地形的影响时，需考虑输入地震波的频谱成分，当输入地震波波长大于凸起地形宽度（输入波频率大于临界频率）时，相邻凸起地形的影响可不予考虑。（3）与SV波入射下半空间凸起半圆地形模型的地震响应相比，无论是单个凸起模型还是相邻2个半圆形凸起模型，在
$ \left|x/a\right| $ ≤1.0范围内，层状半空间地表位移谱放大系数明显大于均匀半空间地表位移谱放大系数；在$ \left|x/a\right| $ ≥1.0范围内，出现了层状半空间地表位移谱放大系数小于均匀半空间地表位移谱放大系数的情况。因此，进行复杂场地对地震波传播影响研究时，需综合考虑地表地形条件和地下波速结构。 -
表 1 梁桥不确定参数及其概率分布
Table 1. Uncertainty parameters and distribution types of girder bridges
参数 分布类型 均值 变异系数 钢筋屈服强度/MPa 对数正态分布 381.65 0.074 混凝土抗压强度/MPa 正态分布 28.03 0.172 滑动支座摩擦系数 正态分布 0.06 0.5 支座剪切模量/MPa 正态分布 1.18 0.14 阻尼比 正态分布 0.05 0.2 上部结构质量/（kg·m3） 正态分布 2600 0.1 
下载: 导出CSV
表 2 构件极限破坏状态及其限值
Table 2. Damage states and limit values of components
破坏状态 桥墩曲率延性比$\mu {}_\varphi $ 支座水平位移u/mm 轻微破坏 1≤$\mu {}_\varphi $ < 1.41 76≤u < 114 中等破坏 1.41≤$\mu {}_\varphi $ < 5.28 114≤u < 152 严重破坏 5.28≤$\mu {}_\varphi $ < 8.28 152≤u < 190 完全破坏 8.28≤$\mu {}_\varphi $ 190≤u
下载: 导出CSV
-
李宏男, 成虎, 王东升, 2018.桥梁结构地震易损性研究进展述评.工程力学, 35(9):1-16. http://d.old.wanfangdata.com.cn/Periodical/gclx201809001 李建中, 汤虎, 管仲国, 2015.中小跨径板式橡胶支座梁桥新型隔震系统.中国公路学报, 28(3):35-43. doi: 10.3969/j.issn.1001-7372.2015.03.005 李立峰, 吴文朋, 黄佳梅等, 2012.地震作用下中等跨径RC连续梁桥系统易损性研究.土木工程学报, 45(10):152-160. http://www.cqvip.com/QK/90342X/201210/43564774.html 宋帅, 2017.考虑构件相关性的桥梁系统地震易损性分析方法研究.成都: 西南交通大学. http://cdmd.cnki.com.cn/Article/CDMD-10613-1017298616.htm 汤虎, 李建中, 邵长宇, 2016.中小跨径板式橡胶支座梁桥横向抗震性能.中国公路学报, 29(3):55-65. doi: 10.3969/j.issn.1001-7372.2016.03.008 王凯睿, 徐秀丽, 李雪红等, 2017.考虑板式支座滑动效应的桥梁振动台试验研究.振动与冲击, 36(12):68-74. http://d.old.wanfangdata.com.cn/Periodical/zdycj201712012 王克海, 李冲, 李茜等, 2014.考虑支座摩擦滑移的中小跨径桥梁抗震设计方法.工程力学, 31(6):85-92. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gclx201406011 吴刚, 王全录, 王克海等, 2018.考虑支座及挡块力学性能退化的桥梁横向地震响应分析.振动与冲击, 37(2):189-196. http://d.old.wanfangdata.com.cn/Periodical/zdycj201802028 张磊鑫, 龙晓鸿, 樊剑等, 2018.考虑碰撞的隔震桥梁易损性分析.工程力学, 34(S1):99-104. http://d.old.wanfangdata.com.cn/Thesis/D733882 赵宇翔, 2018.支座形式对简支梁桥地震反应的影响.震灾防御技术, 13(4):903-910. http://zzfy.eq-j.cn/zzfyjs/ch/reader/view_abstract.aspx?flag=1&file_no=20180417&journal_id=zzfyjs Aviran A., Mackie K. R., Stojadinovic B., 2008. Guidelines for nonlinear analysis of bridge structures in California. California: Pacific Earthquake Engineering Research Center. Billah A. H. M. M., Alam M. S., 2015. Seismic fragility assessment of highway bridges:A state-of-the-art review. Structure and Infrastructure Engineering, 11(6):804-832. doi: 10.1080/15732479.2014.912243 Bommer J. J., Acevedo A. B., 2004. The use of real earthquake accelerograms as input to dynamic analysis. Journal of Earthquake Engineering, 8(Spec001):43-91. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1080/13632460409350521 Caltrans, 2013. Seismic design criteria (Version 1.7). California Department of Transportation. Cornell C. A., Jalayer F., Hamburger R. O., et al., 2002. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines. Journal of Structural Engineering, 128(4):526-533. doi: 10.1061/(ASCE)0733-9445(2002)128:4(526) Nielson B. G., 2005. Analytical fragility curves for highway bridges in moderate seismic zones. Georgia Institute of Technology, Atlanta. 期刊类型引用(0)
其他类型引用(1)
-
下载:
点击查看大图
计量
- 文章访问数: 141
- HTML全文浏览量: 70
- PDF下载量: 4
- 被引次数: 1
