Research on Seismic Performance of Reactive Powder Concrete Square Columns Confined With FRP Tubes
-
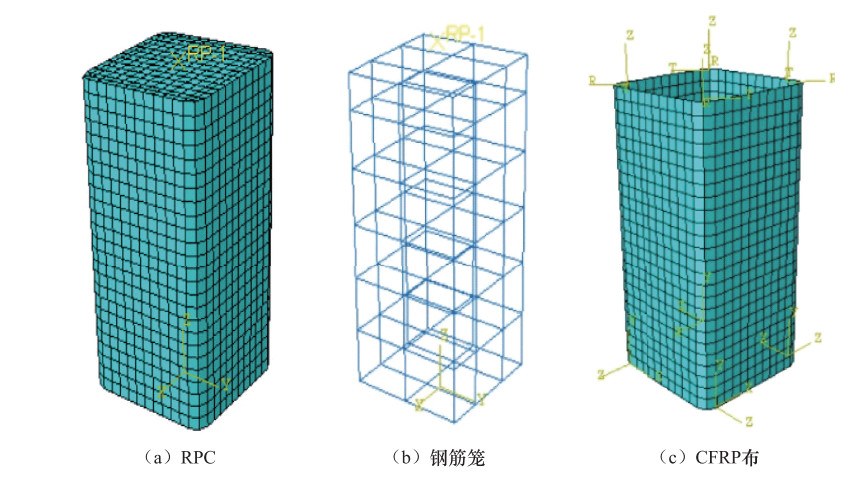
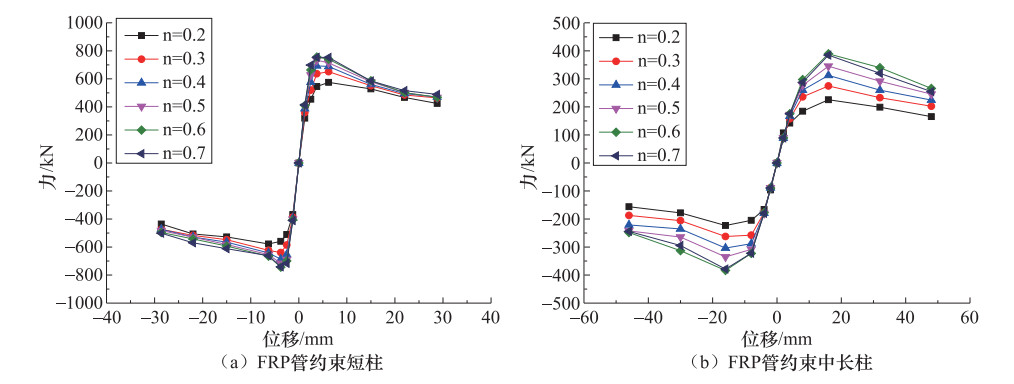
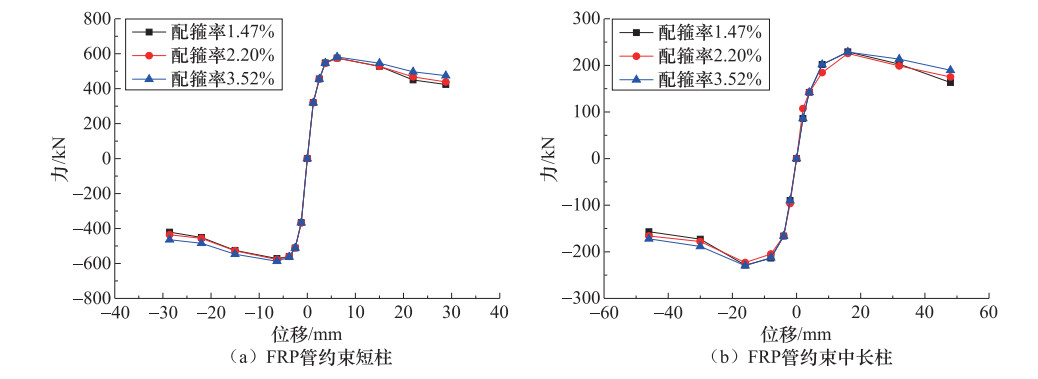
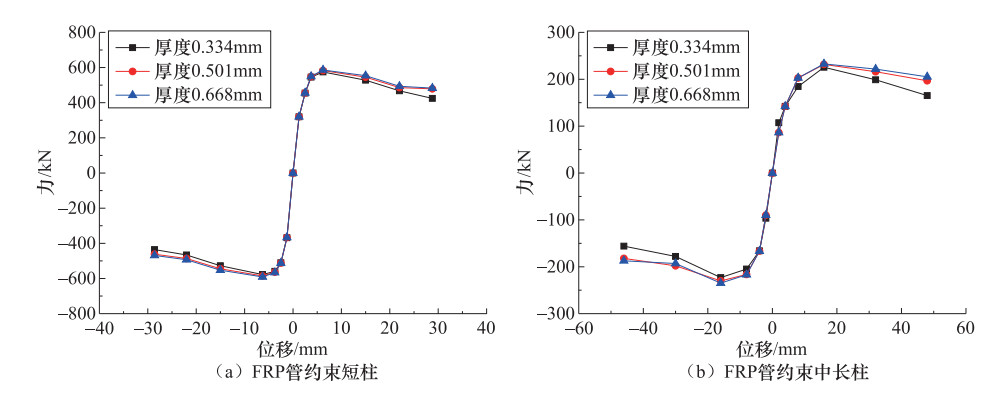
摘要: 为了探究纤维增强聚合物(fiber reinforced polymers,FRP)管约束活性粉末混凝土(reactive powder concrete,RPC)方柱在低周反复荷载作用下的抗震性能,利用有限元软件ABAQUS对FRP管约束RPC方柱进行了数值模拟,并对不同轴压比、配箍率和FRP管厚度条件下约束柱的抗震性能进行了分析。结果表明:采用有限元模型对FRP管约束RPC方柱进行模拟是可靠的,有限元模拟结果和试验结果吻合较好;轴压比为0.2~0.6时,峰值荷载随轴压比的增大而增大,轴压比为0.7时的峰值荷载较0.6时反而下降;配箍率、FRP管厚度的增加可以改善约束柱的抗震性能,延缓强度和刚度的退化;FRP管厚度为0.501mm时的约束效果最好。Abstract: To explore the seismic performance of reactive powder concrete square columns confined with fiber reinforced polymers tubes under low cyclic loading, the study analyzed RPC square columns confined with FRP tubes by finite element software ABAQUS and investigated the influences of axial compression ratio, stirrup ratio and FRP tubes thickness. The results are as follows:the finite element method is reliable, and the finite element simulation results are consistent with the experimental results; when the axial compression ratio is between 0.2 and 0.6, the peak loads increase with the axial compression ratio; when the axial compression ratio is 0.7, the peak load shows a downward trend; with the increase of stirrup ratio and FRP tubes thickness, the seismic performance of confined columns is improved, and the stiffness and capacity decrease slowly; the confinement works best when the thickness of FRP tubes is 0.501mm (number of layers is 3).
-
表 1 试件编号和约束方案
Table 1. Serial number and confining schemes of specimens
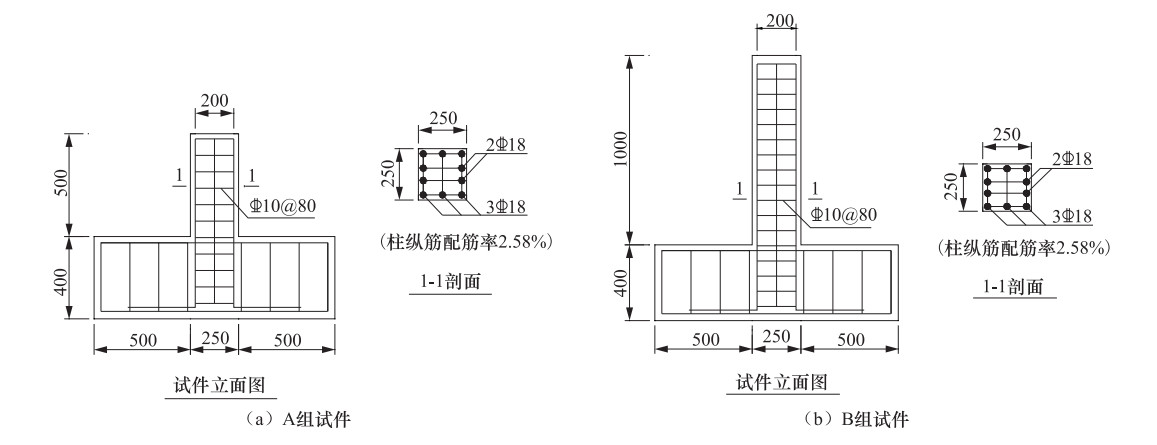
试件编号 剪跨比 纤维布粘贴方式 CFRP管层数 试验轴压比 箍筋 纵筋 A1 2 未约束 0 0.2 
10 
A2 2 全包500mm 2 0.2 
10 
B1 4 未约束 0 0.2 
10 
B2 4 全包1000mm 2 0.2 
10 
表 2 碳纤维布参数
Table 2. The parameters of carbon fiber sheets
抗拉强度/MPa 弹性模量/GPa 伸长率/% 层间剪切强度/MPa 理论厚度/mm 单位面积质量/g/m2 3400 230 1.67 46 0.167 295 表 3 RPC损伤模型参数
Table 3. Damage model parameters of RPC
膨胀角/(°) 偏心率 双轴受压极限强度
/单轴受压极限强度不变应力比 黏性系数 38 0.1 1.14 0.6667 0.005 表 4 钢筋材料参数
Table 4. Material parameters of reinforcement
种类 用途 屈服强度/MPa 极限强度/MPa 
箍筋 472 638 
纵筋 436 599 表 5 试验值与模拟值对比
Table 5. Values comparison between test and numerical calculation
试件编号 屈服荷载 峰值荷载 屈服位移 极限位移 试验值/kN 模拟值/kN 试验值/kN 模拟值/kN 试验值/kN 模拟值/kN 试验值/kN 模拟值/kN A1 458.12 476.05 549.11 566.67 5.29 5.26 18.12 17.35 A2 464.32 482.45 567.61 578.75 5.64 5.89 22.05 21.36 B1 162.32 179.51 218.32 224.95 7.56 8.12 33.26 34.45 B2 171.62 185.69 214.65 225.68 7.86 8.43 37.43 38.26 表 6 试件设计参数及有限元模拟结果
Table 6. Design parameters and finite element analysis results of specimens
试件编号 碳纤维布层数 FRP管厚度
/mm体积配箍率
/%轴压比
n峰值荷载
/kN屈服位移
/mm极限位移
/mm位移延性系数μ A2.20-0.20-2 2 0.334 2.20 0.20 578.75 5.89 22.05 3.74 A2.20-0.20-3 3 0.501 2.20 0.20 584.10 5.96 23.56 3.95 A2.20-0.20-4 4 0.668 2.20 0.20 588.70 5.91 23.89 4.04 A2.20-0.30-2 2 0.334 2.20 0.30 645.26 6.42 21.81 3.40 A2.20-0.40-2 2 0.334 2.20 0.40 690.03 6.57 19.69 3.00 A2.20-0.50-2 2 0.334 2.20 0.50 724.64 6.86 18.02 2.63 A2.20-0.60-2 2 0.334 2.20 0.60 749.77 6.92 17.53 2.53 A2.20-0.70-2 2 0.334 2.20 0.70 747.37 6.94 17.24 2.48 A1.47-0.20-2 2 0.334 1.47 0.20 573.66 5.91 21.81 3.69 A3.52-0.20-2 2 0.334 3.52 0.20 584.34 5.96 23.75 3.98 B2.20-0.20-2 2 0.334 2.20 0.20 225.68 8.43 38.26 4.54 B2.20-0.20-3 3 0.501 2.20 0.20 230.91 8.76 41.36 4.72 B2.20-0.20-4 4 0.668 2.20 0.20 233.83 8.68 41.85 4.82 B2.20-0.30-2 2 0.334 2.20 0.30 268.39 8.95 38.10 4.26 B2.20-0.40-2 2 0.334 2.20 0.40 308.02 9.12 37.45 4.11 B2.20-0.50-2 2 0.334 2.20 0.50 340.29 9.34 37.21 3.98 B2.20-0.60-2 2 0.334 2.20 0.60 386.46 9.42 36.88 3.92 B2.20-0.70-2 2 0.334 2.20 0.70 381.68 9.51 36.54 3.84 B1.47-0.20-2 2 0.334 1.47 0.20 228.87 8.46 38.94 4.60 B3.52-0.20-2 2 0.334 3.52 0.20 229.12 8.61 39.77 4.62 注:编号A开头代表以短柱试件A2为基础设计的试件,B开头代表以中长柱试件B2为基础设计的试件;试件A2.20-0.20-2中,2.20代表配箍率为2.20%,0.20代表轴压比为0.20,2代表FRP管的厚度为2层 -
邓宗才, 刘少新, 王海忠等, 2015.四种FRP管约束UHPC轴压特性的试验研究.北京工业大学学报, 41(5):728-734. http://d.old.wanfangdata.com.cn/Periodical/bjgydxxb201505013 李吴煜, 2009.RPC材料的塑性损伤本构模型参数识别及有限元验证.北京: 北京交通大学. 李忠献, 许成祥, 景萌等, 2002.碳纤维布加固钢筋混凝土短柱的抗震性能试验研究.建筑结构学报, 23(6):41-48. doi: 10.3321/j.issn:1000-6869.2002.06.006 肖建庄, 龙海燕, 石雪飞, 2004.纤维布加固高轴压混凝土柱抗震性能.同济大学学报, 32(8):990-995. doi: 10.3321/j.issn:0253-374X.2004.08.003 王吉忠, 王苏岩, 黄承逵, 2008.CFRP加固高强混凝土柱抗震性能和延性研究.大连理工大学学报, 48(5):708-714. http://d.old.wanfangdata.com.cn/Periodical/dllgdxxb200805016 吴有明, 2012.活性粉末混凝土(RPC)受压应力-应变全曲线研究.广州: 广州大学. 袁冰冰, 2018.活性粉末混凝土在工程中的应用与展望.科学技术创新, (5):105-106. doi: 10.3969/j.issn.1673-1328.2018.05.065 杨志慧, 2006.不同钢纤维掺量活性粉末混拟土的抗拉力学特性研究.北京: 北京交通大学. 朱伯龙, 姚振纲, 吕西林, 1989.结构抗震试验.北京:地震出版社. 赵树红, 叶列平, 张珂等, 2001.碳纤维布对混凝土柱抗震加固的试验分析.建筑结构, 31(12):17-19. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jzjg200112006 赵彤, 刘明国, 谢剑等, 2000.应用碳纤维布增强钢筋混凝土柱抗震能力的研究.地震工程与工程振动, 20(4):66-72. doi: 10.3969/j.issn.1000-1301.2000.04.010 赵彤, 刘明国, 谢剑, 2002.碳纤维布用于改善斜向受力高强混凝土柱抗震性能的研究.土木工程学报, 35(3):13-19. doi: 10.3321/j.issn:1000-131X.2002.03.003 赵悦, 2016.FRP管活性粉末混凝土柱抗震性能非线性分析.黑龙江: 黑龙江大学. Eshghi S, Zanjanizadeh V, 2008. Retrofit of slender square reinforced concrete columns with glass fiber-reinforced polymer for seismic resistance. Iranian journal of science & technology, 32(5):437-450. http://www.researchgate.net/publication/228511381_RETROFIT_OF_SLENDER_SQUARE_REINFORCED_CONCRETE_COLUMNS_WITH_GLASS_FIBER-REINFORCED_POLYMER_FOR_SEISMIC_RESISTANCE Krajcinovic D, Fonseka G, 1981. The continuous damage theory of brittle materials. Journal of applied mechanics, 48(4):809-815. doi: 10.1115/1.3157739 Saadatmanesh H, Ehsani M.R, JIN L, 1997. Repair of earthquake-damaged RC columns with FRP wraps. ACI structural journal, 94(2):206-214. http://www.researchgate.net/publication/291440828_Repair_of_earthquake-damaged_RC_columns_with_FRP_wraps Saadatmanesh H, Ehsani M.R, Li M., 1994. Strength and ductility of concrete columns externally reinforced with fiber composite strapes. ACI structual journal, 91(4):434-447. https://www.researchgate.net/publication/265287794_Strength_and_Ductility_of_Concrete_Columns_Externally_Reinforced_with_Fiber_Composite_Straps Saadatmanesh H, Ehsani M.R, Jin L, 1996. Seismic strengthening of circular bridge pier model with fiber composites. ACI structual journal, 93(6):639-647. https://www.researchgate.net/publication/279642878_Seismic_strengthening_of_circular_bridge_pier_models_with_fiber_composites Xiao Y, Wu H, Martin G, 1999. Prefabricated composite jacketing of RC columns for enhanced shear strength. Journal of structural engineering, ASCE, 125(3):255-264. https://www.researchgate.net/publication/239390774_Prefabricated_Composite_Jacketing_of_RC_Columns_for_Enhanced_Shear_Strength Zohrevand P, Mirmiran A, 2011. Behavior of ultra-high performance concrete confined by fiber-reinforced polymers. Journal of materials in civil engineering, 23(12):1727-1734. doi: 10.1061/(ASCE)MT.1943-5533.0000324 Zohrevand P, Mirmiran A, 2012.Cyclic behavior of hybrid columns made of ultra-high performance concrete and fiber reinforced polymers. Journal of composites for construction, 16(1):91-99 https://www.researchgate.net/publication/254593632_Cyclic_Behavior_of_Hybrid_Columns_Made_of_Ultra_High_Performance_Concrete_and_Fiber_Reinforced_Polymers Zohrevand P, Mirmiran A, 2013.Seismic response of ultra-High performance concrete-filled FRP tube columns. Journal of earthquake engineering, 17(1):155-170. doi: 10.1080/13632469.2012.713560 -




 下载:
下载: