Quantitative Analysis of the Observed Environmental Changes of Geomagnetic Stations in Mainland China from 1997 to 2016
-
摘要: 本文利用CHAOS-6地磁场模型计算1997—2016年中国大陆地区34个地磁台站模型值，分析比较模型计算值与台站实测值之间的差异，利用国际参考场模型IGRF12计算结果进行佐证。结果表明：地磁异常场模量△T作为地磁台站观测环境的一种标志，年变化显示：①中国大陆地区34个地磁基准台绝大部分位于地磁正常区或弱磁异常区，只有少数几个地磁台位于强磁异常区；②判断1个地磁台的地磁场环境，只测量总强度（F）是不够的，必须进行三分量绝对观测，利用地磁异常场模量△T评价地磁台的地磁场环境更全面、更科学合理。Abstract: Using CHAOS-6 geomagnetic field model, we calculated the model values of 34 geomagnetic stations between 1997-2016 in mainland China. By analyzing and comparing the model calculation value and the observation value, and the difference between using IGRF12 calculation results, we found that the geomagnetic anomalous field modulus(△T) is a good indicator of the geomagnetic station observation environment. Our results show that:①for the most part the geomagnetic normal area or weak magnetic anomaly area of 34 geomagnetic stations in mainland China, only a handful of geomagnetic station located in the strong magnetic anomaly zone, ②to judge the geomagnetic field environment of a geomagnetic platform, it is not enough to make the measurement of total strength (F) only, but to make the absolute observation of three components. Instead, it will be more comprehensive, more scientific and reasonable by using the modulus of geomagnetic anomalies (△T) in evaluating the geomagnetic field environment of a geomagnetic platform in future.
-
Key words:
- Geomagnetic field /
- CHAOS-6 model /
- Geomagnetic station /
- Modulus of geomagnetic anomaly /
- IGRF12 model
-
引言
1995年阪神地震中大开地铁车站的严重倒塌破坏在世界范围内引起了地震研究学者们对地下结构抗震问题的广泛关注。在地下结构地震反应特征和抗震设计方法等问题的研究过程中，逐渐形成了一系列实用抗震设计方法（刘晶波等，2010a；许成顺，2017）。其中，反应位移法与反应加速度法凭借理论明确、操作简便等优点，在实际工程设计中得到广泛应用，已被《城市轨道交通结构抗震设计规范》（GB 50909—2014）（中华人民共和国住房和城乡建设部，2014）和《地下结构抗震设计标准》（GB/T 51336—2018）（中华人民共和国住房和城乡建设部，2018）采纳。
反应加速度法通过将顶、底板相对位移最大时刻的自由场水平加速度施加于土-结模型上，计算地下结构变形与内力。与反应位移法相比，主要优势为：反应加速度法建立的土-结构模型可较准确地反映土-结构间相互作用，无须计算地基弹簧刚度系数，大大提高了计算效率与精度；反应位移法受限于地基弹簧与地震作用的施加方式，决定了其主要适用于矩形断面，而反应加速度法施加的地震作用为体积力，且模型采用土-结构整体模型，决定了其可适用于复杂断面地下结构的地震反应计算。总的来说，反应加速度法优于反应位移法（刘晶波等，2013；李新星等，2014）。
反应加速度法的应用关键在于地震输入荷载的确定。为简化计算过程，反应加速度法假设输入荷载为地震作用下自由场的反应加速度，然而，该假设忽略了结构的存在对自由场反应加速度的影响。基于此，刘如山等（2007）从一维自由土层反应的剪应力入手，首先对一维自由土层反应剪应力沿竖直方向进行微分，然后将其作为水平体荷载离散到有限元节点上，以此作为加载方法；董正方等（2014）运用柔度系数法中的结构变形和自由场变形之间的相互作用系数，修正了自由场地震反应加速度，近似考虑了结构的存在对反应加速度法的影响；Liu等（2018）通过理论解析方式推导了自由场模型与土-结模型之间场地反应加速度的关系，结果表明可通过2种模型场地相对位移修正场地反应加速度法；徐琨鹏等（2019）对比了反应加速度法和仅在土体施加加速度的简化方法，发现2种方法对侧边距取值不敏感；禹海涛等（2020）通过动力时程分析，提出地下结构附近存在动力响应增强区和衰减区，利用动力响应调整系数提高了反应加速度法的计算精度。
为考虑结构的存在对反应加速度法中地震输入荷载的影响，本文提出将土-结构模型转换为自由场模型的等效方式，采用等效后的土层参数进行自由场反应加速度计算，以此近似地反映结构的存在对地震输入荷载的影响，进而改进反应加速度法中地震输入荷载的计算过程。采用有限元软件ABAQUS对大开车站地震反应进行数值模拟分析，验证等效方式的有效性，并探讨等效模型宽度取值范围对结果的影响，初步给出等效模型宽度范围。
1. 反应加速度法
采用改进前反应加速度法对地下结构横断面进行抗震分析时，计算模型为图1所示的土-结构整体模型。一般地，土体采用二维平面应变单元模拟，结构采用梁单元模拟。将模型底边固定，模型两侧设置水平滑移边界。通过将地下结构顶、底板位置处土层相对位移最大时刻的各土层水平加速度或有效惯性加速度施加于土-结构整体模型上，获得地下结构变形与内力等反应。
反应加速度法主要计算步骤如下：
（1）一维土层地震反应分析。采用等效线性化程序EERA或SHAKE91对一维土层进行地震反应分析，记录结构顶、底板位置处土层最大相对位移时刻，各土层加速度及等效剪切模量Gi。《城市轨道交通结构抗震设计规范》建议，土层简单时地震输入荷载直接采用自由场水平加速度，土层复杂时地震输入荷载采用土层有效惯性加速度。
（2）建立土-结构模型。《城市轨道交通结构抗震设计规范》建议模型底面可取设计地震作用基准面，顶面取地表面，侧面边界到结构的距离宜取结构水平有效宽度的2～3倍，本文针对模型宽度对计算结果的影响展开进一步讨论。
（3）施加等效地震作用。将土层水平加速度或有效惯性加速度按各土层单元的位置施加于土-结构模型中的各土层上，结构部分按所在土层深度位置作用相应的加速度。
从反应加速度法计算模型和计算步骤可看出，该方法地震输入荷载采用的是自由场反应加速度，未考虑结构的存在对自由场加速度反应的影响，尤其是当地下结构刚度和周围土体刚度相差较大时，结构的存在可能会在较大程度上影响周围土体的地震反应。此外，在动力学理论方面，该方法忽略了阻尼因素的影响，仅是某种程度的近似，当土层反应仅有一阶振型发育时，该方法精度尚可，当遇到复杂土层时误差将增大。
2. 改进反应加速度法研究
2.1 等效思路
为考虑结构的存在对反应加速度法中地震输入荷载的影响，对反应加速度法中的加速度求解方法进行改进。首先，按结构周围土体的分层将土-结构模型中的结构与土体等效为自由场，计算等效自由场的土层参数；然后，采用等效线性化程序EERA将等效自由场土层参数进行处理，得到土层等效剪切模量，并计算等效自由场各土层反应加速度，如图2所示。
将图2所示土-结构模型等效为自由场模型时需进行结构等效和土层等效，其中Ki为等效后土体的刚度；K1i为结构的刚度；K2i为等效前土体的刚度。对于地下结构横断面，其顶、底板在断面水平方向上连续，侧墙、中柱在断面水平方向上间断，而土层为分层结构，在断面水平方向上连续。为便于土体与结构进行等效，将断面水平方向上间断的侧墙与中柱等效为连续结构，形成图3（a）所示的分层结构形式。在此基础上，按结构周围土层的划分，将分层结构与分层土体按照相对位置等效为分层的自由场，如图3（b）所示。
上述2个等效过程均包含等质量等效计算和等侧向刚度等效计算。自由场在地震作用下的反应加速度主要受场地质量分布与刚度分布的影响，等质量等效计算假设等效前后土-结构模型与自由场模型中各土层质量保持不变：
$$ {\rho _i}{V_i} = {\rho _{1i}}{V_{1i}} + {\rho _{2i}}{V_{2i}} $$ (1) 式中，
${\rho _i}$ 为等效后第i层土体密度；${V_i}$ 为采用土-结构模型总宽度计算的第i层土体体积；${\rho _{1i}}$ 为第i层土体对应的结构部分的密度；${V_{1i}}$ 为第i层土体中包含的结构体积；${\rho _{2i}}$ 为第i层土体密度；${V_{2i}}$ 为减去结构体积的第i层土体体积。等侧向刚度等效计算中，假设等效前后各土层侧向刚度保持不变，各土层与结构为短柱，进行侧向刚度的串并联叠加：
$$ {G_i}{b_i} = {G_{1i}}{b_{1i}} + {G_{2i}}{b_{2i}} $$ (2) 式中，
${G_i}$ 为等效后第i层土体剪切模量；${b_i}$ 为采用土-结构模型总宽度；${G_{1i}}$ 为结构剪切模量；${b_{1i}}$ 为第i层土体中结构的宽度；${G_{2i}}$ 为第i层土体剪切模量；${b_{2i}}$ 为减去结构宽度的第i层土体宽度。2.2 等效模型宽度的选取
为便于区分，将改进前反应加速度法称为反应加速度法-1（以下简称“RAM-1”），将改进后反应加速度法称为反应加速度法-2（以下简称“RAM-2”）。
采用图4所示土-结构模型边界至结构侧边的距离B表示模型宽度。在RAM-2计算过程中，反应加速度法拟静力计算时涉及土-结构模型宽度（以下简称“模型宽度-F”）、等效土-结构模型宽度（以下简称“模型宽度-B”）的选取。由前文可知，模型宽度-B不同，将直接改变等效自由场土层参数，影响等效自由场场地反应，从而影响反应加速度法计算结果。因此，本文针对不同模型宽度-B对反应加速度法计算结果的影响进行了探讨。
3. 实例分析
3.1 计算模型与参数选取
为验证等效方式的有效性，以大开车站为研究对象，进行了RAM-1、RAM-2与动力时程方法计算。结构断面尺寸如图5所示，结构埋深4.8 m，周围土层参数如表1所示（矢的照夫等，1996）。结构中柱沿车站纵向按3.5 m等间距分布，将其按一定原则等效为连续墙体，等效后中柱弹性模量为8.57 GPa，密度为714 kg/m3。顶、底板与侧墙弹性模量为30 GPa，密度为2 500 kg/m3。土-结构整体分析模型如图6所示，车站结构采用梁单元模拟，土体采用平面应变单元模拟。土体底边界固定，两侧边界设置水平滚轴边界。假设土体与结构之间接触良好，且不产生相对滑移，数值计算时土体与结构之间采用绑定约束。
表 1 土层参数表Table 1. Physical properties of soils分层 土质 厚度/m 密度/(t·m−3) 剪切波速/(m·s−1) 泊松比 1 填土 1 1.9 140 0.333 2 砂土 4.1 1.9 140 0.488 3 砂土 3.2 1.9 170 0.493 4 黏土 3.1 1.9 190 0.494 5 黏土 5.8 1.9 240 0.490 6 砂土 22 2.0 330 0.487 由于缺少大开车站周围土体动力参数，本文采用典型砂土和黏土剪切模量比、阻尼比与剪应变关系曲线（杜修力等，2018），如图7所示。考虑到地震动特性对地下结构地震反应的影响，基岩输入地震动选用Kobe地震动与El Centro地震动，地震动加速度时程曲线如图8所示，将加速度幅值调整为0.1、0.2、0.3 g。
验证等效思路有效性时，RAM-1与RAM-2模型宽度-F均取3倍结构宽度，RAM-2模型宽度-B取3倍结构宽度。动力时程分析共6种计算工况，反应加速度法共12种计算工况（包括RAM-1、RAM-2各6种计算工况）。
在探讨不同模型宽度-B对RAM-2计算结果的影响时，RAM-1与RAM-2模型宽度-F仍取为3倍结构宽度，RAM-2模型宽度-B分别取为1、2、3、4、5、7倍结构宽度。在0.1 g幅值的Kobe地震动作用下进行动力时程计算、RAM-1计算与不同模型宽度-B的RAM-2计算。
3.2 结果与分析
刘晶波等（2010b）和杜修力等（2017）指出地下结构中柱为抗震关键构件，在此基础上，计算不同地震作用下中柱与顶、底板位置处的相对位移、中柱底部弯矩、中柱底部剪力和侧墙底部弯矩，结果如表2所示，表中括号内为相应的误差。
表 2 不同地震作用下结构内力与变形Table 2. Internal force and deformation of structure under different earthquake load地震动 幅值 计算方法 顶、底板相对位移/mm 中柱底部弯矩/
[(kN·m)·m−1]中柱底部剪力/
(kN·m−1)侧墙底部弯矩/
[(kN·m)·m−1]Kobe 0.1 g 动力时程分析法 5.77 36.12 11.09 358.40 RAM-1 5.56(3.66%) 34.06(5.70%) 10.48(5.50%) 341.50(4.72%) RAM-2 5.71(1.04%) 35.00(3.10%) 10.78(2.80%) 351.20(2.01%) 0.2 g 动力时程分析法 16.93 102.70 30.88 887.30 RAM-1 16.17(4.47%) 99.31(3.30%) 30.80(0.26%) 879.50(0.88%) RAM-2 16.44(2.86%) 102.00(0.68%) 30.51(1.20%) 877.00(1.16%) 0.3 g 动力时程分析法 31.15 187.50 55.97 1476.00 RAM-1 30.30(2.76%) 181.70(3.09%) 54.43(2.75%) 1447.00(1.96%) RAM-2 30.94(0.67%) 185.50(1.07%) 55.44(0.95%) 1474.00(0.14%) EL Centro 0.1 g 动力时程分析法 14.12 86.02 26.09 771.40 RAM-1 13.41(5.02%) 81.68(5.05%) 25.04(4.02%) 741.00(3.94%) RAM-2 13.61(3.62%) 83.07(3.43%) 25.59(1.92%) 755.90(2.01%) 0.2 g 动力时程分析法 26.73 160.40 47.59 1288.00 RAM-1 25.36(5.15%) 151.70(5.42%) 45.47(4.45%) 1241.00(3.65%) RAM-2 26.12(2.30%) 156.30(2.56%) 46.82(1.62%) 1278.00(0.78%) 0.3 g 动力时程分析法 38.75 231.60 68.07 1755.00 RAM-1 35.48(8.44%) 210.60(9.07%) 62.24(8.56%) 1628.00(7.24%) RAM-2 37.51(3.22%) 222.10(4.10%) 65.35(4.00%) 1704.00(2.91%) 由表2可知，以动力时程为基准，不同工况下RAM-1计算的结构变形与内力最大误差为9%，不同工况下RAM-2计算的结构变形与内力最大误差为4.1%，等效方式将反应加速度法的计算误差由10%以内缩小至5%以内，提高了反应加速度法计算精度，表明了等效方式的有效性；RAM-2在不同幅值Kobe地震动作用下计算的结构变形与内力最大误差为3.1%，在不同幅值El Centro地震动作用下计算的结构变形与内力最大误差为4.1%，最大误差随地震动强度的改变未明显变化，说明该方法的计算结果较稳定。
以动力时程为基准计算的结构变形与内力、不同模型宽度-B 下 RAM-2 计算的结构变形与内力如表3所示，表中括号内为相应的误差。由表3、图9可知，与动力时程分析法相比，随着模型宽度-B的减小，RAM-2计算结果逐渐增加，逐渐接近动力时程计算结果，甚至大于动力时程计算结果；而RAM-1最大计算误差为5.7%，模型宽度-B为7、5、4、3倍结构宽度时，RAM-2最大计算误差分别为6.15%、4.51%、4.1%、3.1%，表明当模型宽度取值较大时，改进反应加速度法计算误差呈增大趋势，这是由于模型宽度越大，等效后的自由场模型更接近原始自由场模型，此时等效模型无法充分反映结构的存在造成的影响。结合表2所示不同工况下RAM-1计算的结构变形与内力最大误差为9%，不同工况下模型宽度-B为3倍结构宽度时，RAM-2最大计算误差为4.1%，若以计算误差减小50%为衡量标准，建议模型宽度-B取为1～3倍结构宽度。
表 3 不同模型宽度-B下结构内力与变形Table 3. Internal force and deformation of structure with different model width计算方法 模型宽度-B/
结构宽度顶、底板相对
位移/mm中柱底部弯矩/
[(kN·m)·m−1]中柱底部剪力/
(kN·m−1)侧墙底部弯矩/
[(kN·m)·m−1]动力时程分析法 — 5.77 36.12 11.09 358.40 RAM-1 — 5.56(3.66%) 34.06(5.70%) 10.48(5.50%) 341.50(4.72%) RAM-2 1 5.98(3.67%) 36.67(1.52%) 11.31(1.98%) 368.80(2.90%) 2 5.78(0.16%) 35.42(1.94%) 10.92(1.53%) 355.50(0.81%) 3 5.71(1.04%) 35.00(3.10%) 10.78(2.80%) 351.20(2.01%) 4 5.65(2.05%) 34.64(4.10%) 10.68(3.70%) 347.70(2.99%) 5 5.63(2.49%) 34.49(4.51%) 10.64(4.06%) 346.20(3.40%) 7 5.53(4.16%) 33.90(6.15%) 10.46(5.68%) 340.20(5.08%) 4. 结论
本文采用有限元分析软件ABAQUS对大开车站进行不同工况下的动力时程分析和改进前后反应加速度法分析，验证了等效方式对反应加速度法的有效性。在验证等效思路有效的基础上，进行了不同等效模型宽度的改进反应加速度法计算，初步给出了等效模型宽度的选取范围。
（1）在未改变RAM-1理论基础的前提下，对关键参数——地震输入荷载进行了修正。与动力时程分析法相比，修正后的反应加速度法使不同工况下的最大计算误差由10%以内缩小至5%以内，提高了反应加速度法计算精度。
（2）与动力时程分析结果相比，修正后的反应加速度法在不同工况下的最大计算误差未明显改变，说明修正结果具有稳定性。
（3）对不同等效模型宽度对反应加速度法计算结果的影响进行分析，根据结果建议等效模型边界至结构侧边的距离取为1～3倍结构宽度。
-
图 1 中国大陆地区34个地磁台站分布
Figure 1. Location map of 34 geomagnetic observatory stations in mainland china
图 3 1997—2016年中国大陆地区地磁台站地磁环境变化空间分布（IGRF12模型）
Figure 3. Spatial geomagnetic environment changes of the geomagnetic stations in mainland China between 1997 and 2016
表 1 地理坐标与地心坐标计算结果比较
Table 1. Comparison of calculation results between geographic coordinates and geocentric coordinates
测项 地理坐标下的模型值/nT 地心坐标下的模型值/nT 台站观测值/nT dif地理/nT dif地心/nT X红山 29305.2 29503.5 29547.2 -242.0 -43.7 Y红山 -2993.2 -2946.6 -3072.9 79.7 126.3 Z红山 44739.8 44523.6 44321.7 418.1 201.9 X昌黎 27768.7 28041.0 28045.4 -276.7 -4.4 Y昌黎 -3681.9 -3670.7 -3725.0 43.1 54.3 Z昌黎 46217.1 45889.4 45808.7 408.4 80.7 
下载: 导出CSV
表 2 地磁台的地磁异常场（CHAOS-6模型）
Table 2. The geomagnetic anomaly field of the observatories
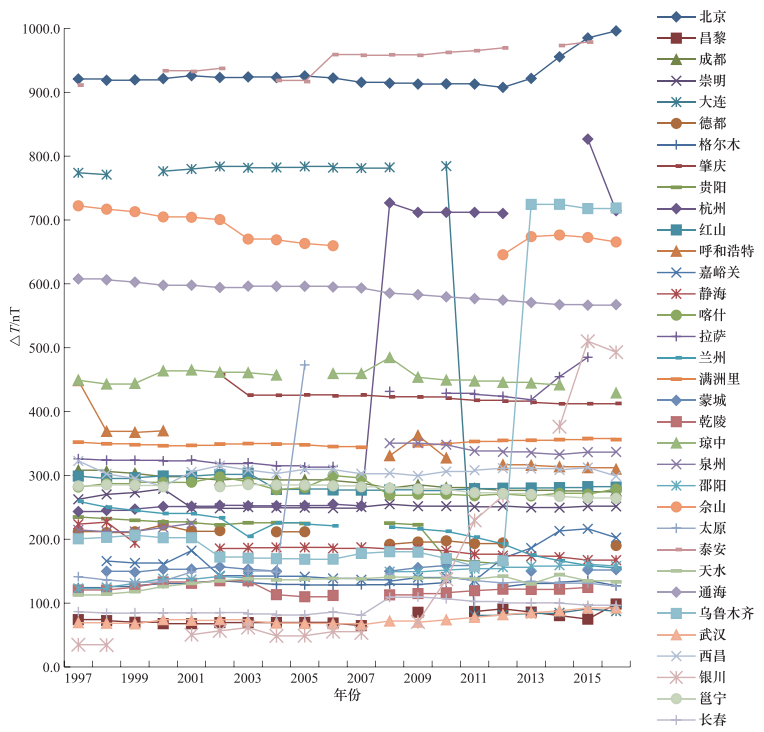
台站名称 △D/′ △I/° △H/nT △X/nT △Y/nT △Z/nT △F/nT △T/nT 北京 -18.6 -0.3 689.1 667.8 -231.5 592.0 865.4 928.0 昌黎 -6.6 0.0 -21.4 -27.9 -52.0 -45.3 -49.8 76.0 成都 3.9 0.3 -50.5 -49.4 40.0 280.80 172.10 288.6 崇明 14.8 0.1 72.0 84.7 136.7 197.3 193.3 254.7 大连 8.0 -0.5 323.6 329.4 25.8 -418.20 -177.10 548.4 德都 -13.1 -0.2 132.6 112.9 -112.3 -129.5 -64.0 204.9 格尔木 -7.6 -0.1 98.6 98.7 -66.9 50.1 97.4 129.7 肇庆 1.6 0.5 -50.4 -49.7 19.5 419.1 189.1 422.6 贵阳 -8.4 0.2 22.0 19.3 -90.0 184.8 135.3 213.8 杭州 -31.3 -0.3 96.3 66.3 -315.6 -233.4 -94.2 437.3 红山 -16.9 -0.2 51.4 37.7 -151.5 -239.2 -168.7 286.0 呼和浩特 -0.9 0.2 20.3 19.7 -9.2 343.8 308.1 345.2 嘉峪关 1.2 0.1 27.5 27.6 9.4 155.4 148.1 160.8 静海 -4.2 0.2 -76.2 -79.5 -27.4 165.8 98.3 186.0 喀什 7.1 0.1 30.9 27.2 58.1 272.8 249.7 280.8 台站名称 △D/′ △I/° △H/nT △X/nT △Y/nT △Z/nT △F/nT △T/nT 拉萨 -13.3 0.0 202.5 201.9 -134.3 235.8 309.7 368.8 兰州 -6.7 0.2 -62.6 -64.6 -57.9 193.8 121.4 212.8 满洲里 0.1 -0.1 -64.0 -63.1 10.7 -344.4 -343.7 350.4 蒙城 13.7 -0.1 65.7 54.4 -134.2 -49.1 4.3 153.1 乾陵 2.2 -0.1 51.5 52.6 17.6 -105.2 -51.9 121.6 琼中 -6.8 0.6 -65.0 -66.7 -76.5 441.6 129.6 453.3 泉州 -3.0 0.3 -29.5 -31.5 -29.5 271.2 138.8 296.2 邵阳 -1.4 -0.2 81.3 80.6 -18.6 -119.5 -17.6 145.7 佘山 -0.2 0.8 -323.1 -322.1 26.5 602.3 212.1 683.9 太原 -3.1 0.0 82.9 80.2 -33.2 93.1 123.4 158.9 泰安 23.9 -1.0 724.2 741.4 145.7 -573.6 -32.7 948.9 天水 1.8 -0.1 80.4 81.1 13.2 -103.1 -32.8 133.3 通海 -2.2 0.7 -99.1 -99.5 -22.0 578.8 254.6 587.8 乌鲁木齐 1.1 0.2 -124.5 -124.7 0.7 251.4 172.4 289.1 武汉 -0.1 -0.1 57.8 57.6 -5.2 -42.3 9.5 75.0 西昌 -19.9 0.0 146.0 140.9 -212.2 142.2 203.2 305.7 银川 -2.9 -0.1 79.2 77.8 -28.7 -127.1 -65.6 158.1 邕宁 -3.2 0.3 -31.0 -32.0 -34.3 274.1 123.7 278.2 长春 -7.7 0.0 6.2 -3.5 -58.4 3.5 6.2 92.2
下载: 导出CSV
表 3 地磁台的地磁异常场（IGRF12模型）
Table 3. The geomagnetic anomaly field of the observatories
台站名称 △D/′ △I/° △H/nT △X/nT △Y/nT △Z/nT △F/nT △T/nT 北京 -16.2 -0.4 724.2 704.8 -215.1 393.5 714.4 840.5 昌黎 -7.3 0.0 -65.7 -72.7 -52.1 -137.8 -151.7 165.3 成都 6.6 0.0 6.4 8.1 65.4 -30.0 -17.7 75.0 崇明 17.6 0.1 43.5 58.8 165.7 148.9 138.6 231.3 大连 10.5 -0.4 236.5 245.8 57.9 -373.3 -186.2 500.6 德都 -17.7 -0.1 17.6 -6.0 -120.9 -119.2 -101.5 170.5 格尔木 -4.3 0.1 -29.1 -29.1 -38.3 61.2 33.8 78.8 肇庆 4.8 0.0 -2.5 -0.6 53.1 38.2 19.2 67.5 贵阳 -6.2 0.0 10.5 8.5 -66.0 54.4 42.7 105.4 杭州 -32.1 -0.2 -2.9 -33.2 -315.4 -179.1 -125.3 392.5 红山 -13.9 0.0 -69.4 -80.2 -114.8 -157.1 -168.7 211.6 呼和浩特 4.2 0.1 -3.2 -0.3 34.1 255.3 219.6 258.5 嘉峪关 1.0 0.0 19.7 19.7 8.1 15.8 24.1 42.8 静海 1.8 0.1 -66.9 -64.6 22.0 48.7 5.0 85.6 喀什 8.7 0.2 -72.6 -76.9 64.4 239.9 168.1 260.6 拉萨 -13.6 0.0 159.1 158.5 -137.3 133.9 206.9 280.8 兰州 -1.9 -0.1 4.6 3.9 -17.1 -95.6 -75.2 98.7 满洲里 0.2 0.0 -163.7 -161.5 26.5 -336.0 -372.7 374.2 蒙城 -12.2 0.0 -24.2 -34.0 -113.2 -1.3 -16.4 120.8 乾陵 2.9 -0.1 -5.1 -3.7 27.1 -173.9 -140.9 177.2 琼中 -2.9 0.0 -7.6 -8.4 -33.2 -9.8 -11.8 41.7 泉州 1.3 -0.1 25.8 26.5 12.5 -70.1 -20.6 119.5 邵阳 -0.9 0.0 -15.2 -15.7 -8.7 -5.1 -14.9 32.7 佘山 4.0 0.4 -257.3 -253.0 61.5 256.8 8.8 367.1 太原 0.3 0.0 43.4 43.1 -0.9 19.2 39.9 85.9 泰安 22.2 -0.8 589.2 605.7 144.0 -497.5 -50.2 797.3 天水 6.2 -0.1 -2.5 -0.3 57.2 -109.5 -88.2 127.2 台站名称 △D/′ △I/° △H/nT △X/nT △Y/nT △Z/nT △F/nT △T/nT 通海 -1.2 0.2 -31.4 -31.6 -12.2 182.0 80.5 185.8 乌鲁木齐 1.6 0.2 -146.2 -146.7 3.8 151.3 72.9 214.2 武汉 1.7 -0.1 4.6 5.7 16.6 -63.4 -42.7 74.8 西昌 -20.2 -0.2 161.6 156.5 -215.6 -88.1 60.1 288.6 银川 -1.7 -0.1 -17.3 -18.2 -13.7 -139.1 -127.3 161.8 邕宁 -1.5 0.0 -9.5 -9.7 -16.4 9.3 -2.6 29.5 长春 -2.8 -0.1 31.8 27.7 -25.6 -109.3 -81.0 121.2
下载: 导出CSV
表 4 部分地磁台CHAOS-6和IGRF12模型的精度统计
Table 4. Accuracy from statistics of partial observatories by CHAO-6 and IGRF12 models
台站名称 △D/′ △I/° △H/nT △X/nT △Y/nT △Z/nT △F/nT △T/nT CHAOS-6 IGRF12 CHAOS-6 IGRF12 CHAOS-6 IGRF12 CHAOS-6 IGRF12 CHAOS-6 IGRF12 HAOS-6 IGRF12 CHAOS-6 IGRF12 CHAOS-6 IGRF12 琼中 -6.8 -2.9 0.6 0.0 -65.0 -7.6 -66.7 -8.4 -76.5 -33.2 441.6 -9.8 129.6 -11.8 453.3 41.7 通海 -2.2 -1.2 0.7 0.2 -99.1 -31.4 -99.5 -31.6 -22.0 -12.2 578.8 182.0 254.6 80.5 587.8 185.8 肇庆 1.6 4.8 0.5 0.0 -50.4 -2.5 -49.7 -0.6 19.5 53.1 419.1 38.2 189.1 19.2 355.0 67.5 邕宁 -3.2 -1.5 0.3 0.0 -31.0 -9.5 -32.0 -9.7 -34.3 -16.4 274.1 9.3 123.7 -2.6 278.2 29.5 成都 3.9 6.6 0.3 0.0 -50.5 6.4 -49.4 8.1 40.0 65.4 280.8 -30.0 172.1 -17.7 288.6 75.0 邵阳 -1.4 -0.9 -0.2 -0.0 81.3 -15.2 80.6 -15.7 -18.6 -8.7 -119.5 -5.1 -17.6 -14.9 113.0 32.7
下载: 导出CSV
-
安柏林, 康国发. 2017.基于CHAOS-5模型研究中国大陆地区地磁场长期变化.云南大学学报(自然科学版), 39(5):789-797.陈斌. 2011.自然正交分量方法在地震地磁监测中的应用.地震研究, 34(4):466-469. http://d.old.wanfangdata.com.cn/Periodical/yndxxb201705010 陈斌, 顾左文, 高金田等. 2012.IGR-11描述的2005-2010年中国地区地磁长期变化及其误差分析.地球物理学进展, 27(2):512-521. doi: 10.6038/j.issn.1004-2903.2012.02.014 丁鉴海, 索玉成, 余素荣. 2005.地磁场与电离层异常现象及其与地震的关系.空间科学学报, 25(6):536-542. doi: 10.3969/j.issn.0254-6124.2005.06.007 傅承义, 陈运泰, 祁贵仲. 1985.地球物理学基础.北京:科学出版社, 108-112. 顾春雷, 张毅, 徐如刚等. 2010.地震前后岩石圈磁场变化特征分析.地球物理学进展, 25(2):472-477. doi: 10.3969/j.issn.1004-2903.2010.02.013 顾左文, 张毅, 姚同起等. 2006.九江-瑞昌Ms5.7地震地磁异常的观测与分析.地震学报, 28(6):611-621. http://d.old.wanfangdata.com.cn/Periodical/dqwlxb200801020 李细顺, 高登平, 李琪等. 2015.CM4模型数据与台站实测数据的对比研究.震灾防御技术, 10(2):418-425. http://zzfy.eq-j.cn/zzfyjs/ch/reader/view_abstract.aspx?flag=1&file_no=20150223&journal_id=zzfyjs 李细顺, 高登平, 刘立申等. 2018.基于CM4模型的中国大陆地区地磁场时空分布特征分析.震灾防御技术, 13(1):98-113. http://zzfy.eq-j.cn/zzfyjs/ch/reader/view_abstract.aspx?flag=1&file_no=20180109&journal_id=zzfyjs 李琪, 杨星, 蔡绍平. 2015.极化方法应用于地磁台阵的震例分析.震灾防御技术, 10(2):412-417. http://zzfy.eq-j.cn/zzfyjs/ch/reader/view_abstract.aspx?flag=1&file_no=20150222&journal_id=zzfyjs 王振东, 顾左文, 陈斌等. 2017.CHAOS-6模型描述的中国地区地磁长期变化及误差分析.地震研究, 40(3):404-410. doi: 10.3969/j.issn.1000-0666.2017.03.015 徐文耀. 2002.地球主磁场的NOC模型.中国科学(D辑), 32(7):576-587. http://d.old.wanfangdata.com.cn/Periodical/zgkx-cd200207006 徐文耀. 2009.地球电磁现象物理学.合肥:中国科学技术大学出版社, 18-29. 杨云存, 高国明. 2014.1900-2010年地磁场水平分量梯度的全球变化.震灾防御技术, 9(S1):557-571. doi: 10.11899/zzfy2014s101 袁洁浩, 顾左文, 陈斌等. 2013.地震与火山电磁研究的国际学术交流与合作.地震研究, 36(1):132-140. doi: 10.3969/j.issn.1000-0666.2013.01.020 袁洁浩, 顾左文, 王粲等. 2016.2015年IUGG大会与世界华人地质大会的震磁研究进展.地震研究, 39(4):703-708. doi: 10.3969/j.issn.1000-0666.2016.04.022 Alldredge L. R.. 1987. On regional geomagnetic charts. Journal of Geomagnetism and Geoelectricity, 39(12):723-738. doi: 10.5636/jgg.39.723 Campbell W. H.. 2003. Introduction to geomagnetic fields. 2nd ed. New York:Cambridge University Press, 1-34. Finlay C. C., Olsen N., Tøffner-Clausen L.. 2015. DTU candidate field models for IGRF-12 and the CHAOS-5 geomagnetic field model. Earth, Planets and Space, 67:114. doi: 10.1186/s40623-015-0274-3 Finlay C. C., Olsen N., Kotsiaros S., et al.. 2016. Recent geomagnetic secular variation from Swarm and ground observatories as estimated in the CHAOS-6 geomagnetic field model. Earth, Planets and Space, 68:112. doi: 10.1186/s40623-016-0486-1 Haines G. V.. 1985. Spherical cap harmonic analysis. Journal of Geophysical Research:Solid Earth, 90(B3):2583-2591. doi: 10.1029/JB090iB03p02583 Hemant K., Maus S.. 2005. Geological modeling of the new CHAMP magnetic anomaly maps using a geographical information system technique. Journal of Geophysical Research:Solid Earth, 110(B12):B12103. doi: 10.1029/2005JB003837 Hemant K., Thébault E., Mandea M., et al.. 2007. Magnetic anomaly map of the world:merging satellite, airborne, marine and ground-based magnetic data sets. Earth and Planetary Science Letters, 260(1-2):56-71. doi: 10.1016/j.epsl.2007.05.040 Lesur V., Wardinski I., Rother M., et al.. 2008. GRIMM:the GFZ reference internal magnetic model based on vector satellite and observatory data. Geophysical Journal International, 173(2):382-394. doi: 10.1111/j.1365-246X.2008.03724.x Olsen N., Mandea M.. 2008. Rapidly changing flows in the Earth's core. Nature Geoscience, 1(6):390-394. doi: 10.1038/ngeo203 Olsen N., Mandea M., Sabaka T. J., et al.. 2009. CHAOS-2-a geomagnetic field model derived from one decade of continuous satellite data. Geophysical Journal International, 179(3):1477-1487. doi: 10.1111/j.1365-246X.2009.04386.x Olsen N., Mandea M., Sabaka T. J., et al.. 2010. The CHAOS-3 geomagnetic field model and candidates for the 11th generation IGRF. Earth, Planets and Space, 62:719-727. doi: 10.5047/eps.2010.07.003 Olsen N., Lühr H., Sabaka T. J., et al.. 2006. CHAOS-a model of the Earth's magnetic field derived from CHAMP, Ørsted, and SAC-C magnetic satellite data. Geophysical Journal International, 166(1):67-75. doi: 10.1111/j.1365-246X.2006.02959.x Olsen N., Lühr H., Finlay C. C., et al.. 2014. The CHAOS-4 geomagnetic field model. Geophysical Journal International, 197(2):815-827. doi: 10.1093/gji/ggu033 Thébault E., Finlay C. C., Beggan C. D., et al.. 2015. International geomagnetic reference field:the 12th generation. Earth, Planets and Space, 67:79 doi: 10.1186/s40623-015-0228-9 Wardinski I., Holme R.. 2006. A time-dependent model of the earth's magnetic field and its secular variation for the period 1980-2000. Journal of Geophysical Research:Solid Earth, 111(B12):B12101. http://cn.bing.com/academic/profile?id=14c7fcfc2d6313d7a31e469cc837b8e9&encoded=0&v=paper_preview&mkt=zh-cn 期刊类型引用(0)
其他类型引用(1)
-
下载:
点击查看大图
计量
- 文章访问数: 158
- HTML全文浏览量: 38
- PDF下载量: 1
- 被引次数: 1
