Identification and Analysis of Micro-earthquake Events in Open-pit Ore Area Based on Waveform Characters——A Case Study of Zhuozishan Molybdenum Mine
-
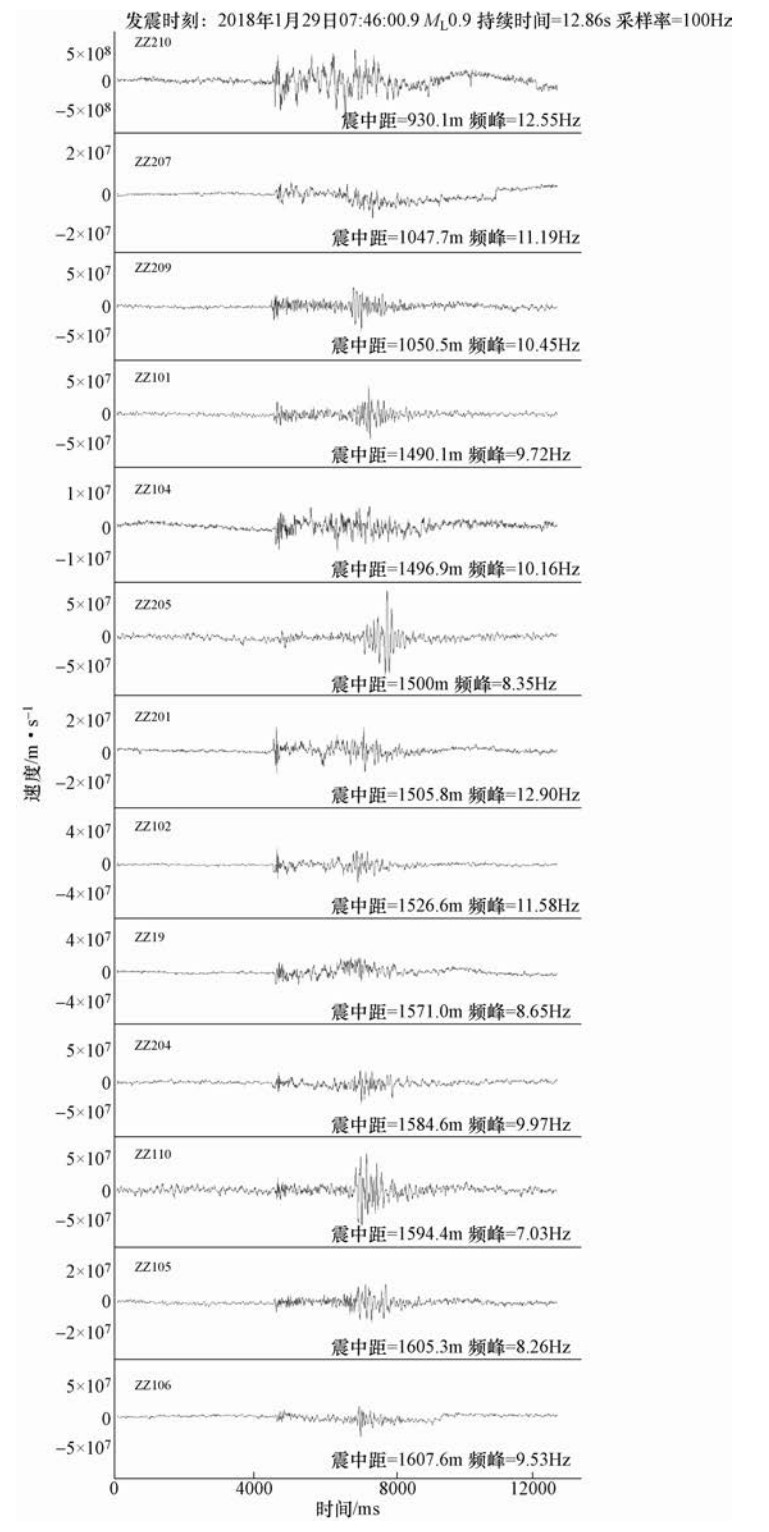
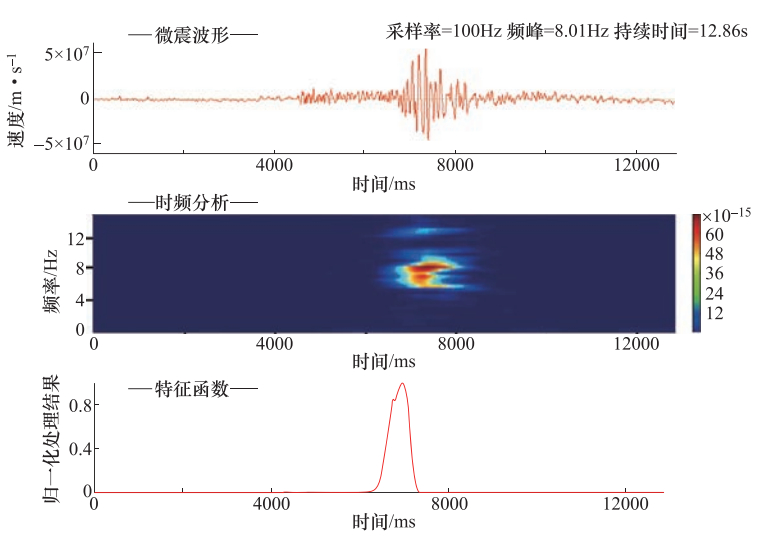
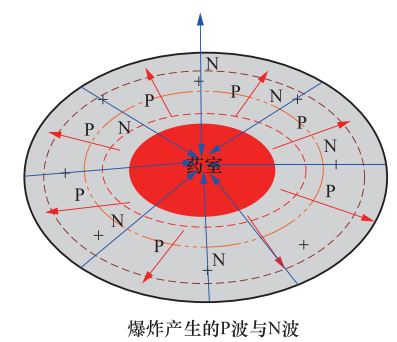
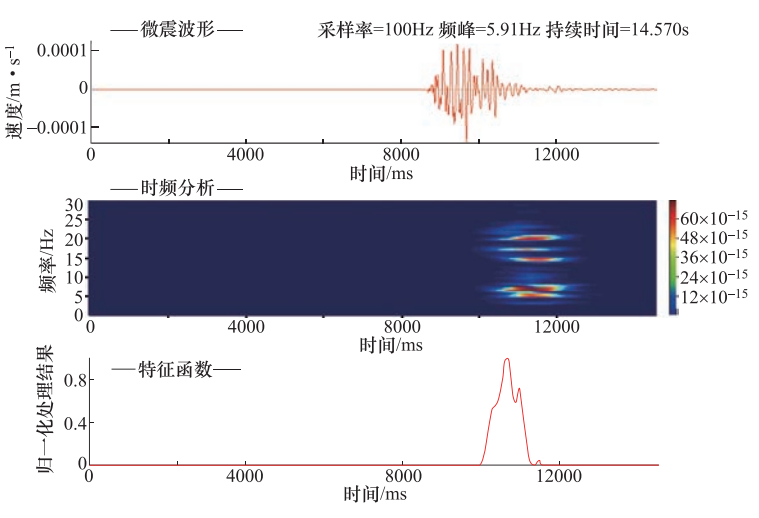
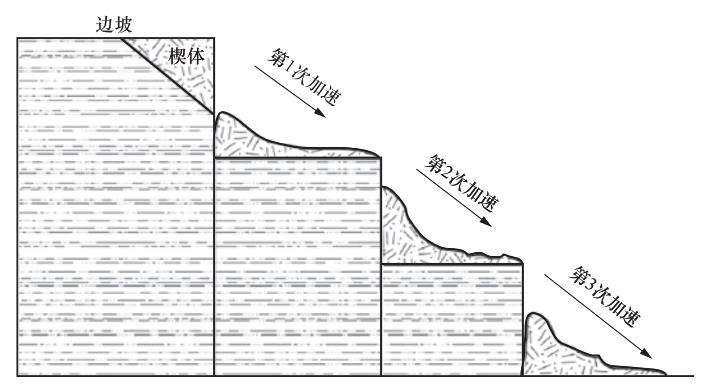
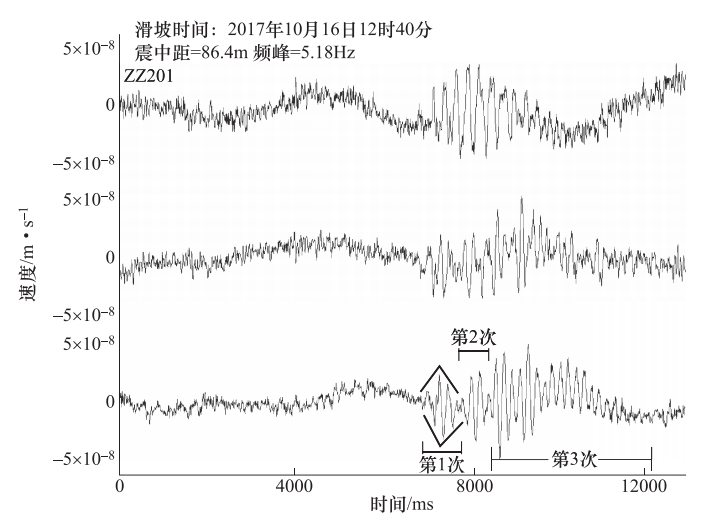
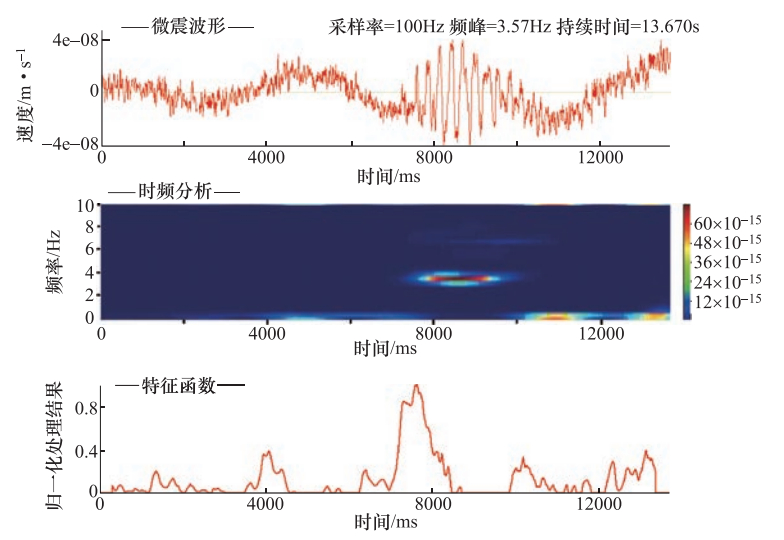
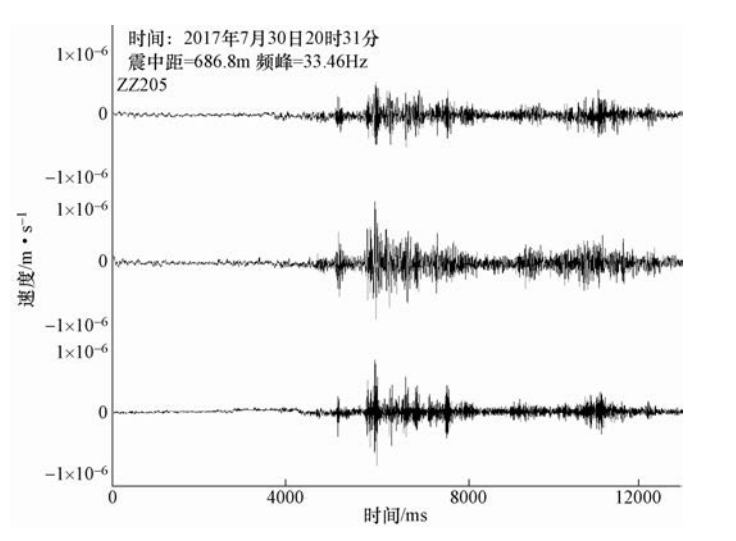
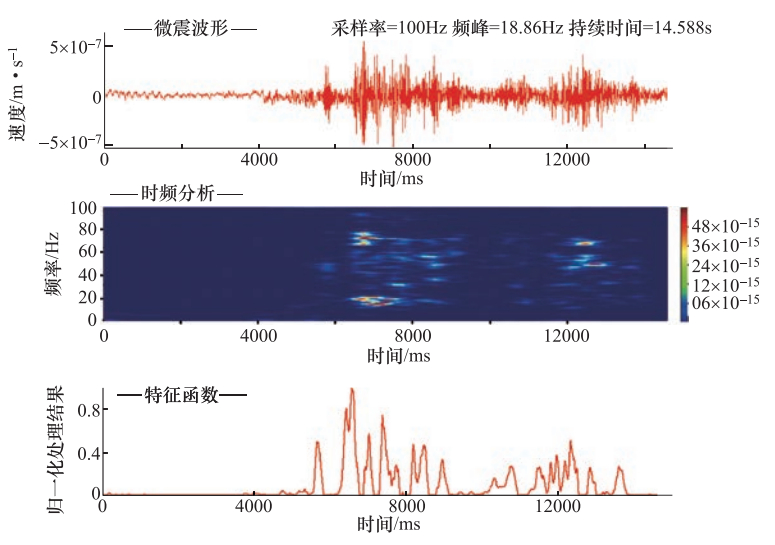
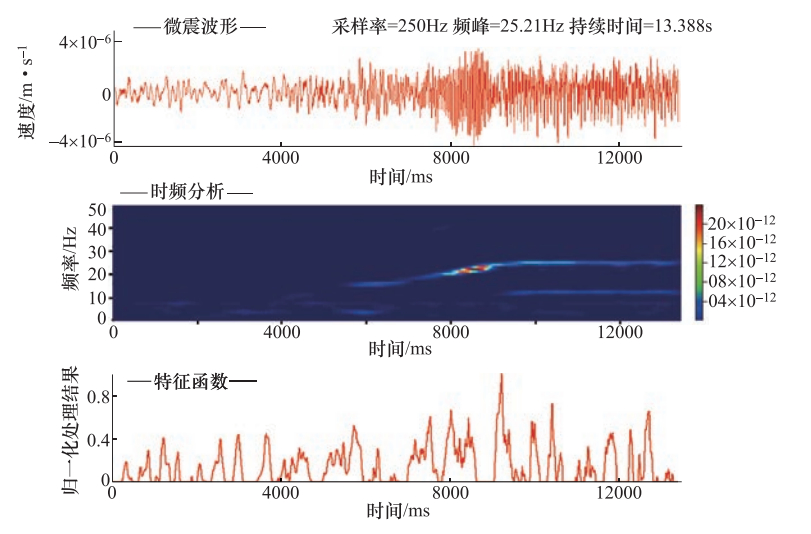
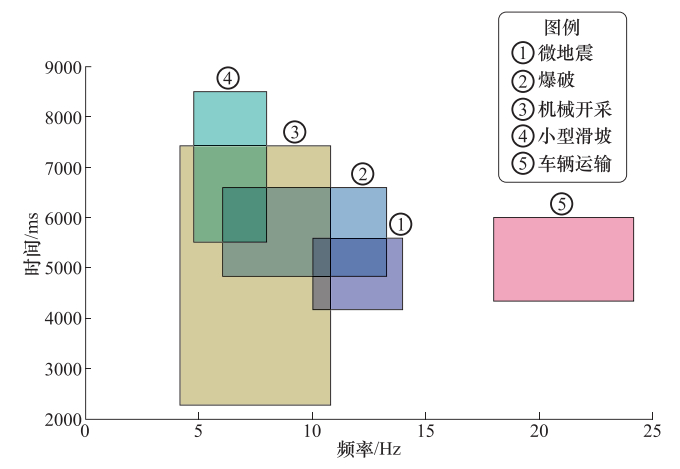
摘要: 基于前人研究成果以及现场的实测结果，采用卓资山露天钼矿微震监测项目产出资料，提取了5类微震事件的波形特征和时频特征。波形特征显示：微地震的振幅、辐射均匀性和频率变化特征表明微地震是由于岩层受到单力偶和剪切力作用破裂而产生；爆破具有P波初动方向向上、S波不易识别的特点，包含“初震段、主震段、尾波段”三段变化形态；小型边坡滑坡波事件属楔体滑坡，是由多个“加速—缓冲—终止”构成，波形是由包络线呈“V”字形的多组脉冲波列组成；机械开采震动事件具有自振能量不变、脉冲幅度相差很大、持续时间间隔不确定的特点；运输车辆波形振幅具有形态“弱—强—弱”、等频率、包络线呈多段纺锤形的特征。时频空间分布可以分为相对独立、界限分明的两类：一类包含微地震、爆破、机械开采、小型边坡滑坡事件，另一类只包含车辆运输事件。Abstract: Based on the previous research results and the field measurements, taking Zhuozishan open-pit molybdenum mine as an example, we analyzed the waveform and time-frequency characteristics of five kinds of micro-seismic events in the region. The amplitude, radiation uniformity and frequency variation of the microearthquakes show that the microearthquakes are caused by the single force couple and shear force. The blasting has a upward P wave initial direction, whereas the initial direction of S wave is not easy to identify, characterized with three section changes of initial earthquake, main shock and tail band". The event of small slope landslide belongs to wedge-body landslide, and the total process is composed of several so-called acceleration-buffer terminations, in which the waveform is composed of multiple sets of pulse wave trains with "V" shape of envelope line. The vibration event of mechanical mining is characterized by constant natural vibration energy, great difference in pulse amplitude and uncertain duration interval. The wave amplitude of the transport vehicle has the shape of "weak-strong-weak", equal frequency and multi-segment spindle shape. The time-frequency spatial distribution can be divided into two categories. The first contains micro-earthquakes, blasting, mechanical mining and small slope landslides, and the second contains only vehicle transport events. The research results provide a reference for the identification of microseismic events in open pit mines.
-
引言
众所周知，我国是地震频发的国家，地震可能造成高速铁路列车脱轨事故，为此，我国建立了相应的地震报警及紧急处置系统，力争在潜在破坏性地震到达之前发出报警，降低列车发生脱轨或倾覆的概率。目前广泛采用的地震报警参数主要为峰值加速度PGA，然而PGA主要体现地震波幅值，未考虑频谱及持时影响，对于无破坏性的高频小震可能产生误报现象。为避免这种干扰，郭恩栋等（2015）引入谱强度SI作为高速铁路地震报警参数，并给出相应的计算方法，SI从能量方面出发，考虑了幅值及频谱影响，忽略持时的影响，但相比PGA更合理。美国电力研究所EPRI（O'Hara 等，1991）在核电厂地震监测报警中引入累积绝对速度CAV作为报警参数，研究发现低频震动对CAV的贡献明显高于高频震动。我国三代核电站AP1000参考国外标准也引入了CAV作为地震报警参数（胡进军等，2013）。林宜娴（2002）提出CAV、PGA、PGV等参数可作为地震报警参数，其稳定性好，且确定性较高。Kostov（2005）根据欧洲几次强地震动数据，分析得出标准化累积绝对速度CAVSTD在预测地震动破坏能力方面明显优于PGA。伊斯坦布尔在地震预报警系统中利用累积绝对速度快速判别强地震动（Erdik等，2003）。Fahjan等（2011）在地震报警的触警算法中引入CAV，并提出新的用于报警系统的参数。黄俊等（2014）引入CAV作为报警参数，分析其在高速铁路报警中的适用性，研究发现CAV可有效排除破坏性小的高频小震对高速铁路列车地震报警的干扰。目前虽对CAV在地震报警中的应用有了深入研究，但在高速铁路列车地震报警中的研究较少，仅通过相关的地震波数据处理得出，未考虑车轨动力响应关系，且给出的计算参数为CAVSTD，为此，需探讨考虑车轨关系的基于相关起算阈值的CAV计算方法。
1. CAV相关参数
目前，地震工程界主要研究CAV、CAVSTD、CAV5。其中CAV于1988年由美国电力研究所（O'Hara等，1991）在核电厂报警中第2级判别标准中提出的，其概念为记录地震加速度数据的绝对值对记录时间进行积分，记为累积绝对速度CAV：
$${\rm{ CAV}} = \mathop \int \nolimits_0^{{{{t}}_{{\rm{max}}}}} \left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t$$ (1) 为提高CAV在核电厂报警中的准确度，EPRI在报告中引入标准化累积绝对速度CAVSTD，其可有效避免长持时记录的地震波尾部对应的幅值小且破坏性小的地震动对其数值的影响，其定义如下：将记录的加速度时程分成以1 s为时间间隔的N个小段，当1 s时间段内存在加速度绝对值≥0.025 g时，对该秒内加速度数值的绝对值进行积分，否则该秒内的积分值记为零，然后将整个记录时程进行相加求和，表达式为：
$$ {\rm{CA{V_{STD}}}} = \mathop \sum \limits_{{i=1}}^n \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\left| {{{a}}\left( {{t}} \right)} \right| < 0.025\;g}\\ {1,\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.025\;{{g}}} \end{array}} \right.$$ (2) Kramer等（2002）于2002年提出CAV5，用于场地液化判别，其概念为：将记录的加速度时程中对加速度数值的绝对值≥0.005 g进行积分求和，表达式为：
$${{\rm{ CAV}}_5} = \displaystyle\int \nolimits_0^\infty \left\langle {\rm{\chi }} \right\rangle \left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\left\langle {\rm{\chi }} \right\rangle = \left\{ {\begin{array}{*{20}{c}} {0\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.005\;g}\\ {1\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.005\;{{g}}} \end{array}} \right. $$ (3) 式中，a(t)为加速度时程，Wi为权重。
2. 改进的标准化累积绝对速度应用于高速铁路地震报警阈值中的计算方法
2.1 改进的标准化累积绝对速度起算阈值确定
本文引入31自由度的SY97477车辆模型（崔恩文，2014），结合车轨典型非线性接触关系，依据列车安全行驶的3项评判指标（脱轨系数、轮重减载率及横向力)，分析车体在轨道不平顺（我国高速铁路无砟轨道标准谱）与简谐波（仅考虑横向输入，与列车行驶方向垂直）共同激励下的动态响应，考虑95%的安全保证，引入2.55倍的动力放大系数（孙汉武等，2007），计算安全极限状态（超出3项指标任意1个限值）下不同车速对应的简谐波幅值随周期的变化关系，如图1所示。具体模型参数、车轨接触关系及评判标准可参考崔恩文（2014）的研究。
图 1 列车安全运行极限状态下不同车速对应的简谐波幅值随周期的变化关系Figure 1. The relationship between the amplitude of simple harmonic wave corresponding to different speeds and periods under the safe running limit state of the train由图1可知，车速一定时，即使幅值很小（<0.025 g）的低频简谐波也可能使列车脱轨，因此不能简单地套用标准化累积绝对速度CAVSTD计算公式，有必要研究改进的标准化累积绝对速度应用在高速铁路地震报警阈值中的计算方法。车速一定时，简谐波幅值随周期增加逐渐递减，最终趋于常数，且周期越大，不同车速对应的简谐波幅值之间的差值越小。车速为200 km/h时，当简谐波周期达2.2 s时，其幅值开始趋于常数，该常数约为0.008 g，本文规定此时的周期为简谐波幅值趋于常数对应的起始周期Tst，该常数记为Amin。不同车速下简谐波幅值趋于常数对应的起始周期及该常数的数值如表1所示。
表 1 不同车速下简谐波幅值趋于常数对应的起始周期及该常数的数值Table 1. The initial period of the simple harmonic wave amplitude tending to be constant at different speeds and the value of the constant项目 车速/（km·h−1） 200 250 300 350 400 起始周期Tst/s 2.2 2.3 2.1 2.0 1.7 Amin/g 0.008 0.004 0.004 0.004 0.004 由表1可知，车速为200 km/h与车速≥250 km/h时对应的Amin不同，车速≥250 km/h时Amin相同，但起始周期Tst随车速的增加呈递减趋势，说明车速越大，简谐波趋于常数所需的周期越小。
车速为200 km/h时，幅值低于0.008 g的简谐波对列车运行安全的影响可忽略不计。车速≥250 km/h时，幅值低于0.004 g的简谐波对列车运行安全的影响可忽略不计。由此可推算出改进的标准化累积绝对速度起算阈值，如表2所示。
表 2 不同车速下改进的标准化累积绝对速度起算阈值Table 2. Starting threshold of improved calculation of standardized cumulative absolute velocity at different speeds项目 车速/（km·h−1） 200 ≥250 改进的标准化累积绝对速度起算阈值/g 0.008 0.004 2.2 改进的标准化累积绝对速度应用在地震报警中的可行性分析
考虑改进的标准化累积绝对速度为累积过程的算法，其值对于加速度超过0.004 g或0.008 g的有限个数的高频小震会很小，因此，可较好地排除高速铁路沿线的高频小震，是较好的地震监测报警参数。
魏智祥（2015）分析了京武高速铁路线布置的强震仪监测到的列车运行时震动记录数据，发现列车运行产生的震动记录明显高于背景噪声，且发现东西、南北、垂直方向列车振动噪声幅值均≤0.002 g，由此可知本文设定的不同车速下改进的标准化累积绝对速度可有效排除列车振动的影响。
综上所述，本文给出改进的标准化累积绝对速度用于高速铁路地震报警是可行的。
2.3 改进的标准化累积绝对速度计算公式的确定
参照CAVSTD计算方法，本文给出车速为200 km/h时改进的标准化累积绝对速度CAV8计算公式如下：
$${{\rm{CAV}}_8} = \mathop \sum \limits_{i=1}^n \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.008\;g}\\ {1,\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.008\;{{g}}} \end{array}} \right.$$ (4) 当
$ a\left(t\right) $ $< 0.008\;g$ 时，${{W}}_{{i}}$ =0；当$\left|{a}\left({t}\right)\right|\geqslant 0.008\;g$ 时，${{W}}_{{i}}$ =1。本文给出的CAV8定义为：将加速度时程按1 s为时间间隔进行划分，如果在这1 s内加速度绝对值≥0.008 g，则对该秒内的加速度绝对值进行积分，否则忽略该秒内的积分值，然后将整个时程中每秒积分得到的数值进行累积求和。
车速为250 km/h时改进的标准化累积绝对速度CAV4计算公式如下：
$${ {\rm{CAV}}_4} = \mathop \sum \limits_{i=1}^{{n}} \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.004\;g}\\ {1,\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.004\;{{g}}} \end{array}} \right.$$ (5) 当
${a}\left({t}\right)$ $< 0.004\;g$ 时，${{W}}_{{i}}=0$ ；当$\left|{a}\left({t}\right)\right|\geqslant 0.004\;{g}$ 时，${{W}}_{{i}}$ =1。本文给出的CAV4定义为：将加速度时程按1 s为时间间隔进行划分，如果在这1 s内加速度绝对值≥0.004 g，则对该秒内的加速度绝对值进行积分，否则忽略该秒内的积分值，然后将整个时程中每秒积分得到的数值进行累积求和。
3. 高速铁路地震报警阈值确定
为确定基于改进的标准化累积绝对速度高速铁路地震报警阈值，本文从Peer数据库选取6条不同场地地震波（表3），对应的加速度反应谱如图2所示，对其进行归一化处理，分析加速度幅值与评判列车脱轨3项指标之间的关系，确定不同车速下影响行车安全的6条地震波加速度上限值，按照本文给出不同车速下改进的标准化累积绝对速度计算公式，给出6条地震波对应的改进的标准化累积绝对速度上限值，如表4所示。
表 3 地震波相关信息Table 3. Seismic wave information项目 地震波台站名称 Cape Mendocino TCU045 Capitola Hector EL Centro Imp. Co. Cent Poe Road 震级 7.01 7.62 6.93 7.13 6.54 6.54 峰值加速度/g 0.376 5 0.008 1 0.528 5 0.265 6 0.357 9 0.446 3 v30/（m·s−1） 567.78 704.64 288.62 726.00 192.05 316.64 加速度记录持时/s 36.0 45.0 39.9 45.3 40.0 22.3 表 4 不同车速下6条地震波加速度上限值与改进的标准化累积绝对速度上限值Table 4. The upper limit of acceleration amplitudes and upper limit improved calculation of standardized cumulative absolute velocity CAV of six seismic waves at different speeds地震波台站名称 车速200 km/h 车速250 km/h 车速300 km/h 车速350 km/h 车速400 km/h 加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-secCape Mendocino 0.074 0.17 0.070 0.17 0.055 0.13 0.040 0.09 0.039 0.09 TCU045 0.101 0.55 0.090 0.49 0.078 0.43 0.062 0.34 0.039 0.21 Capitola 0.109 0.34 0.078 0.25 0.062 0.20 0.054 0.17 0.039 0.11 Hector 0.101 0.27 0.070 0.19 0.062 0.17 0.054 0.14 0.047 0.12 EL Centro Imp. Co. Cent 0.078 0.16 0.070 0.18 0.054 0.13 0.039 0.08 0.027 0.05 Poe Road 0.074 0.19 0.054 0.14 0.043 0.11 0.039 0.10 0.035 0.08 由表4可知，车速相同时，即使地震波加速度相同，其对应的改进的标准化累积绝对速度不一定相同，如车速为200 km/h时，台站名称为Cape Mendocino与Poe Road的地震波加速度相同，但对应的改进的标准化累积绝对速度不同，且Cape Mendocino台站加速度记录持时较大，说明改进的标准化累积绝对速度与频谱紧密相关。车速≥250 km/h时，对于同一台站的地震波，峰值加速度越大其对应的改进的标准化累积绝对速度越大，如台站名称为Cape Mendocino的地震波，说明对于同一地震波而言，加速度影响累积绝对速度。根据改进的标准化累积绝对速度定义，加速度记录持时影响其数值。综上所述，改进的标准化累积绝对速度数值不仅与加速度幅值有关，还与频谱及加速度记录持时密切相关，可较好地反映地震动三要素。
选取6条地震波改进的标准化累积绝对速度最小值作为报警阈值，给出不同车速下基于改进的标准化累积绝对速度高速铁路地震报警阈值，如表5所示。由表5可知，改进的标准化累积绝对速度报警阈值与车速整体呈线性递减关系，中间车速对应的改进的标准化累积绝对速度可按线性插入计算。
表 5 不同车速下改进的标准化累积绝对速度高速铁路地震报警阈值Table 5. High-speed earthquake alarm threshold based on improved calculation of standardized cumulative absolute velocity thresholds at different vehicle speeds项目 车速/（km·h−1） 200 250 300 350 400 报警阈值/g-sec 0.16 0.14 0.11 0.08 0.05 4. 结论
（1）通过建立车轨模型，分析列车安全运行极限状态下简谐波幅值与周期的关系，得出不同车速下改进的标准化累积绝对速度起算阈值，并论证改进的标准化累积绝对速度在高速铁路地震报警中的可行性。
（2）参照标准化累积绝对速度CAVSTD计算公式，本文给出不同车速下改进的标准化累积绝对速度计算公式。
（3）根据本文给出的改进的标准化累积绝对速度计算公式，选取6条不同场地的地震波，分析列车在轨道不平顺及地震波共同激励下的动力响应，计算不同车速下改进的标准化累积绝对速度报警阈值，以供参考。
-
图 4 微地震波形（ML 0.9，震中距Δ=1050.5m）
Figure 4. The microseismic waveform (ML 0.9, epicentral distanceΔ=1050.5m)
图 5 微地震时频特征（ML 0.9，震中距Δ=1050.5m）
Figure 5. Time-frequency characteristics of microseismic(ML 0.9, epicentral distanceΔ=1050.5m)
图 11 ML 1.9小型边坡楔体滑坡波形
Figure 11. Waveform of ML 1.9 from the small slope wedge landslide
图 12 小型边坡滑坡事件时频特征曲线
Figure 12. Time-frequency characteristic curve of small slope and landslide events
图 13 ML 1.8的机械开采震动事件波形
Figure 13. Event waveform of ML 1.8 from the mechanical mining vibration
图 14 机械开采震动事件时频分析曲线
Figure 14. Time-frequency analysis curve of vibration events by mechanical mining
图 16 运输车辆事件时频分析特征曲线
Figure 16. The time-frequency characteristic curve of transport vehicle events
图 17 5类事件时频空间分布对比
Figure 17. Comparison of time-frequency spatial distribution of five typical events
表 1 5种类型事件波形特征统计表
Table 1. Statistical results of waveform characteristics of five typical events
事件类型 个数 震级范围
ML事件波形形态 频率集中度 持续时间
均值/s衰减
方式微地震 56 -0.5—1.9 包含P波、S波，面波发育，是能量较小的地震波 72×10-15 11.33 指数衰减，较快 爆破 79 -0.65—0.9 P波尖锐（初动向上）、S波不易识别，包含“初震”、“主震”、“尾波”三段 75×10-15 12.81 幂函数衰，减快 小型滑坡 23 1.5—1.9 由包络线呈“V”字型的波列组成 75×10-15 11.53 起伏不定，较慢 机械开采 206 -0.9—1.8 由“密集”、“尖锐”的波列组成 70×10-15 11.06 不规律 运输车辆 367 -0.6—1.0 由近似连续的、多组波形尖锐、包络线呈“纺缍”形的密集波列组成 30×10-15 10.70 不规律 
下载: 导出CSV
表 2 5种事件类型时频分布特征
Table 2. Time-frequency distribution characteristics of five typical events
事件类型 时间均值范围/ms 频率均值范围/Hz 微地震 4150—5583 10—14 爆破 4800—6600 6—13.3 小型边坡滑坡 5500—8500 4.8—8 机械开采 2250—7400 4.2—10.8 车辆运输 4333—6000 18—24.2
下载: 导出CSV
-
董世华, 2009, 基于微震监测技术在深井矿山地震波形的识别, 现代矿业, (7):129-131 doi: 10.3969/j.issn.1674-6082.2009.07.044 科恩, 1998, 时频分析: 理论与应用, 白居宪, 译.西安: 西安交通大学出版社 李夕兵, 李地元, 赵国彦等, 2006, 金属矿地下采空区探测、处理与安全评判, 采矿与安全工程学报, 23(1):24-29 doi: 10.3969/j.issn.1673-3363.2006.01.005 刘芳, 曹井泉, 赵蒙生等, 2005, 乌拉特前旗爆破与地震识别.高原地震, 17(2):22-27 doi: 10.3969/j.issn.1005-586X.2005.02.002 刘先锋, 张瑞明, 2013, 微震波形识别技术在监测边坡岩体中的应用.山西冶金, 36(6):27-29 doi: 10.3969/j.issn.1672-1152.2013.06.011 马举, 2014, 基于波形特征的矿山微震与爆破信号模式识别.长沙:中南大学. 宋维琪, 陈泽东, 毛中华, 2008, 水力压裂裂缝微地震监测技术.东营:中国石油大学出版社, 3-5. 姚家骏, 杨立明, 冯建刚. 2011.常用时频分析方法在数字地震波特征量分析中的应用.西北地震学报, 33(2):105-110. http://d.old.wanfangdata.com.cn/Periodical/xbdzxb201102001 张华, 姚宏, 陈鑫等. 2014.矿震识别及成因研究进展.国际地震动态, (3):4-12. doi: 10.3969/j.issn.0235-4975.2014.03.002 张萍, 高艳玲, 肖健等. 2001.辽宁台网记录爆破、矿震与地震的识别.地震地磁观测与研究, 22(5):29-34. doi: 10.3969/j.issn.1003-3246.2001.05.004 张青成, 王家磊, 李德璇等. 2013.露天矿山爆破振动影响因素分析研究.辽宁工程技术大学学报(自然科学版), 32(10):1334-1338. doi: 10.3969/j.issn.1008-0562.2013.10.008 赵淑红. 2006.时频分析方法及其在地震数据处理中的应用.西安:长安大学. 赵永, 刘卫红, 高艳玲. 1995.北京地区地震、爆破和矿震的记录图识别.地震地磁观测与研究, 16(4):48-54. http://www.cnki.com.cn/Article/CJFD1995-DZGJ504.006.htm Cohen L.1995. Time-frequency analysis. New York:Prentice - Hall. -
下载:
点击查看大图
计量
- 文章访问数: 117
- HTML全文浏览量: 34
- PDF下载量: 3
- 被引次数: 0
