Application of Infinite Element Method in Dynamic Analysis of Deep Overburden Earth-rock-fill Dam
-
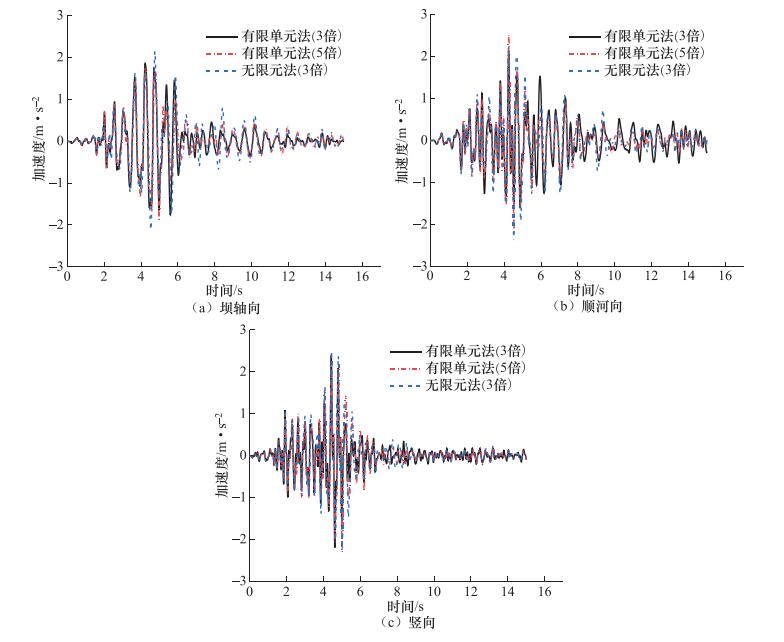
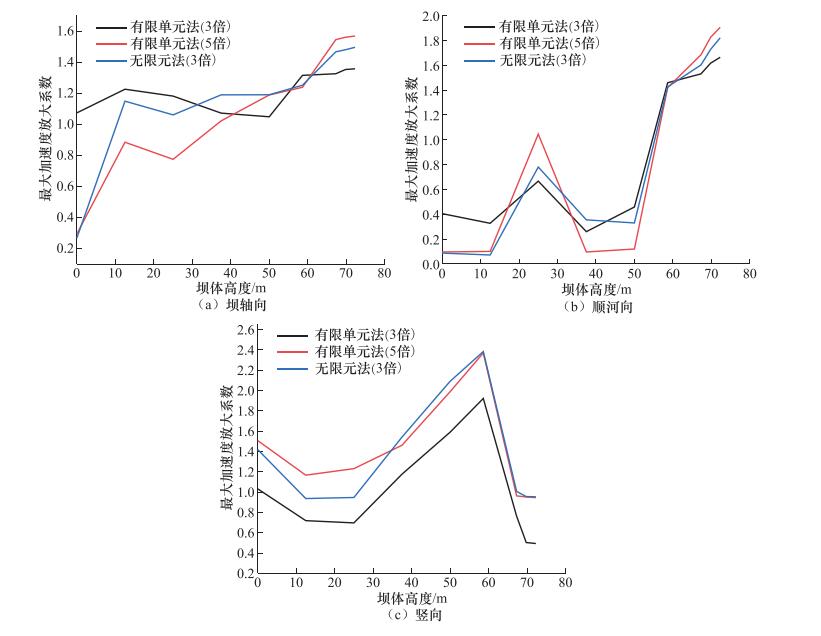
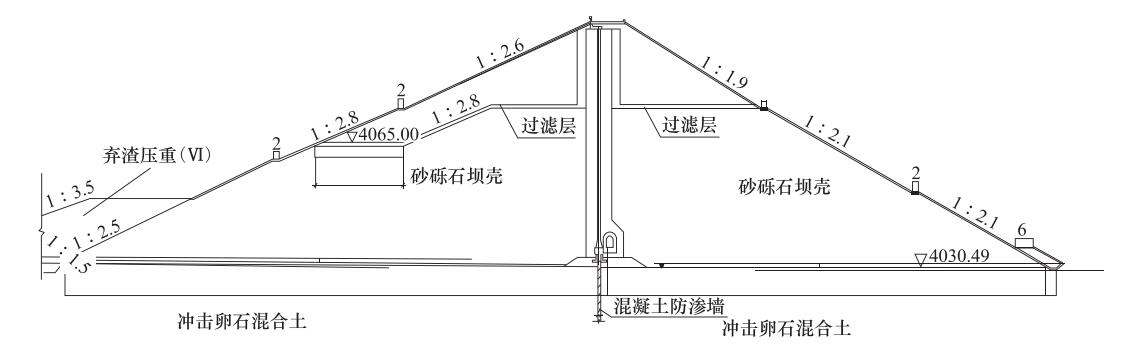
摘要: 以复杂地质条件的西藏高原地区旁多水电站实际工程为背景,探讨了有限元法与无限元法在深覆盖层悬挂式防渗墙土石坝结构非线性动力分析中的差异,分析和比较了无限元法和有限元法在西藏高原旁多水电站土石坝结构三维模型地震动响应的计算结果,验证了引入无限元法模拟西藏高原地区地基中复杂地质条件下的无限域或半无限域问题的可靠性和精确性。结果表明:在西藏高原地区复杂地质条件下,无限元法相比有限元法能量弥散现象较为明显。通过分析得到了西藏高原具有深覆盖层坝体结构地震动响应的规律性分析结果,为无限元法在西藏高原地区此类工程中的应用提供参考。Abstract: Taking the Tibetan plateau area of hydropower station with complex geological conditions as a case study, In this paper we analyze the nonlinear dynamic of deep soil layer hanged cut-off wall structure of earth-rock-fill dam by finite element method and the infinite element method, and compare the calculation results of seismic response of 3D model of earth-rock-fill dam structure of Pangduo hydropower station in Tibet plateau with infinite element method and finite element method, and verify the reliability and accuracy of infinite element method under complicated geological conditions in Tibet plateau foundation of infinite domain or semi-infinite domain. The results show that the infinite element method is more practical than the finite element method in the complex geological conditions of Tibet plateau. Our results of the seismic response of the dam structure with deep overburden on the Tibetan plateau will be significant in providing reference for the application of the infinite element method in such projects in the Tibetan plateau area in future.
-
表 1 材料等效线性模型参数
Table 1. Parameters of material equivalent linear model
材料 k1 k2 n λmax 坝壳料 20.43 2336 0.268 0.19 心墙 21.06 1106 0.556 0.25 地基 15.66 450 0.500 0.20 -
陈跃庆, 吕西林, 李培振等, 2006.不同土性的地基-结构动力相互作用振动台模型试验对比研究.土木工程学报, 39(5):57-64. doi: 10.3321/j.issn:1000-131X.2006.05.009 董光辉, 2011.深厚覆盖层上土石坝动力反应分析.大连: 大连理工大学. 沈珠江, 徐刚, 1996.堆石料的动力变形特性.水利水运科学研究, (2):143-150. http://d.old.wanfangdata.com.cn/Periodical/cjkxyyb201301009 孙萍, 2007.映射无限元在无限域问题中的模拟应用.广西水利水电, (2):10-13. doi: 10.3969/j.issn.1003-1510.2007.02.003 温立峰, 柴军瑞, 王晓, 2015.深覆盖层上面板堆石坝应力变形特性研究.岩土力学, 36(8):2386-2394. http://d.old.wanfangdata.com.cn/Periodical/ytlx201508035 向前, 2004.无限元参与地基基础-坝体动力相互作用分析.南宁: 广西大学. 燕柳斌, 2004.结构与岩土介质相互作用分析方法及其应用.南宁: 广西大学. 杨正权, 赵剑明, 刘小生等, 2016.超深厚覆盖层上土石坝动力分析边界处理方法研究.土木工程学报, 49(S2):138-143. 余翔, 孔宪京, 邹德高等, 2018.覆盖层上土石坝非线性动力响应分析的地震波动输入方法.岩土力学, 39(5):1858-1866. http://d.old.wanfangdata.com.cn/Periodical/ytlx201805039 赵崇斌, 2010.无限域中波传播问题的数值计算模拟.中国科学:物理学力学天文学, 40(7):828-837. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgkx-cg201007002 周小溪, 何蕴龙, 熊堃等, 2013.深厚覆盖层坝基防渗墙地震反应规律研究.长江科学院院报, 30(4):91-97, 102. doi: 10.3969/j.issn.1001-5485.2013.04.019 Bettess P., Zienkiewicz O. C., 1977. Diffraction and refraction of surface waves using finite and infinite elements. International Journal for Numerical Methods in Engineering, 11(8):1271-1290. doi: 10.1002/nme.1620110808 Chow Y. K., Smith I. M., 1981. Static and periodic infinite solid elements. International Journal for Numerical Methods in Engineering, 17(4):503-526. doi: 10.1002/nme.1620170403 Han H. Q., Chen S. S., Zheng C. F., et al., 2016. Study on the mechanical properties of deep overburden. In: Proceedings of 2015 International Conference on Intelligent Transportation, Big Data and Smart City. Halong Bay, Vietnam: IEEE, 791-796. Khalili N., Valliappan S., Yazdi J. T., et al., 1997. 1D infinite element for dynamic problems in saturated porous media. International Journal for Numerical Methods in Biomedical Engineering, 13(9):727-738. Noorzaie J., Mohammadian E., 2002. Seismic response of the Kavar concrete face rockfill dam (research note). International Journal of Engineering, - Transactions B:Applications, 15(4):333-346. Ungless R. F., 1973. An infinite finite element. UK: University of British Columbia. Yerli H. R., Kacin S., Kocak S., 2003. A parallel finite-infinite element model for two-dimensional soil-structure interaction problems. Soil Dynamics and Earthquake Engineering, 23(4):249-253. doi: 10.1016/S0267-7261(03)00022-8 Zhang C. H., Zhao C. B., 1987. Coupling method of finite and infinite elements for strip foundation wave problems. Earthquake Engineering and Structural Dynamics, 15(7):839-851. doi: 10.1002/eqe.4290150705 -



 下载:
下载: