Analysis of Seismic Performance of Q460 Steel Frame Columns under Low Cyclic Loading
-
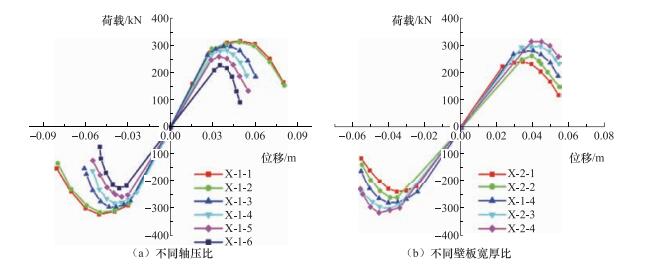
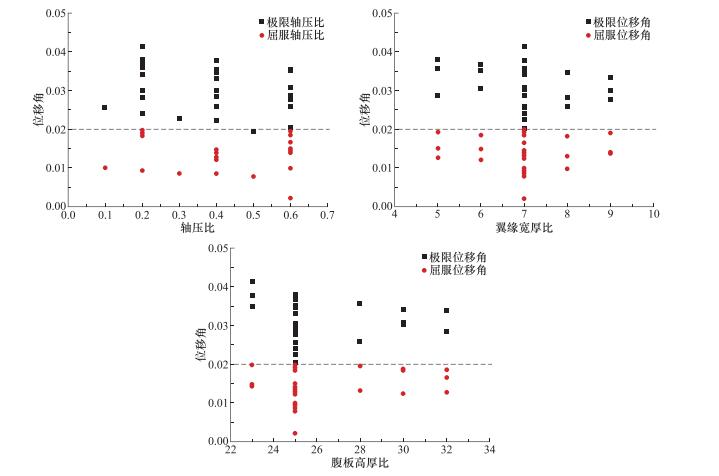
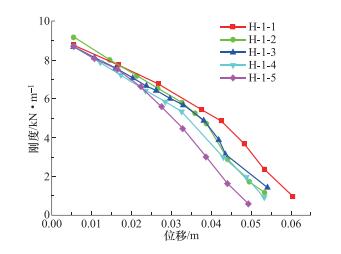
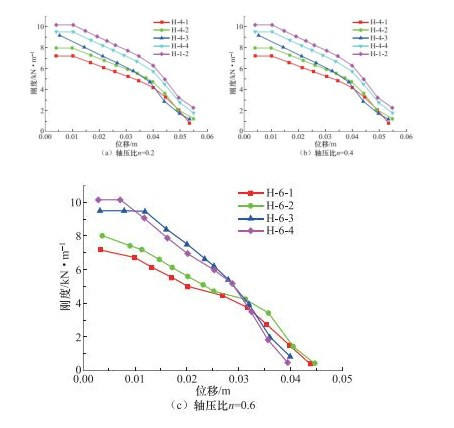
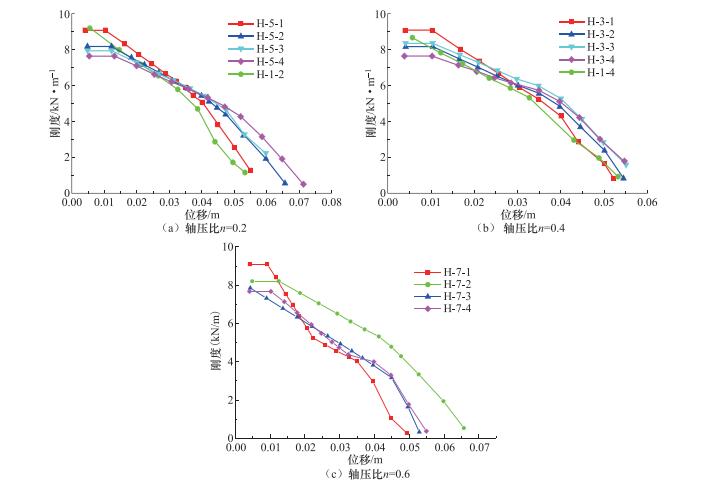
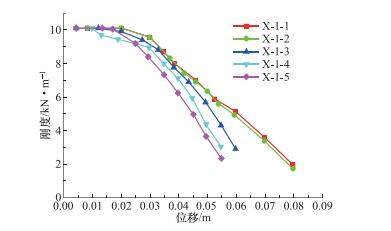
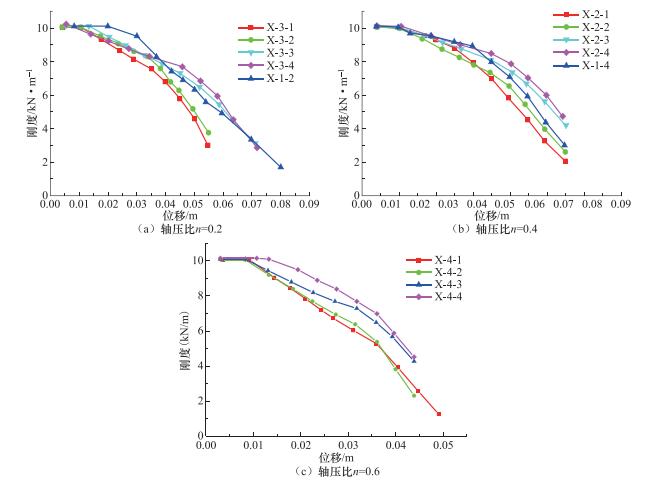
摘要: 为了进一步完善Q460钢材在抗震设计规范中相关限值的要求，本文利用有限元软件ABAQUS，以轴压比、翼缘宽厚比、腹板高厚比和壁板宽厚比为变量，建立了共48根“工”字型框架柱和“箱”型框架柱，分析了其抗震性能。结果表明：翼缘宽厚比对框架柱的能量耗散系数影响较小；能量耗散系数随轴压比、腹板高厚比（“工”字型）和壁板宽厚比（“箱”型）增大而明显减小；框架柱的极限承载力随轴压比的减小及壁板宽厚比和翼缘宽厚比的增大而逐渐增大，当腹板高厚比接近规范限值时，承载力下降趋势明显增大。与采用Q235钢材的框架柱相比，Q460钢材框架柱的延性较小，仅为2左右；当采用Q460钢材时，“工”字型框架柱的极限位移角限值建议取为0.03，“箱”型框架柱的极限位移角限值建议取为0.032。规范中对翼缘宽厚比限值的规定偏于保守，其值最大可取至9。无论是“工”字型框架柱还是“箱”型框架柱，其腹板高厚比均不宜过大。Q460钢材框架柱的刚度退化率随轴压比的增大而增强，且翼缘宽厚比越大，腹板高厚比越小，柱的初始刚度越大，刚度退化程度越明显。Abstract: In order to confirm the requirement of Q460 steel in seismic design better, the finite element software ABAQUS is used to simulate the seismic resistance of I-type and box-type bending members, with different axial compression ratios, flange width-to-thickness ratios, web height-to-thickness ratios and wall width-to-thickness ratio, under low cyclic repeated loading. The results showed that the difference in energy dissipation coefficient is not obvious for the members with different flange width-to-thickness ratio. The energy dissipation coefficient significantly reduces as the increase of the axial compression ratio, the web height-to-thickness ratio (I-type) and the wall width-to-thickness ratio (box-type). The ultimate bearing capacity of the specimens increases with the decrease of the axial compression ratio and the increase of width-thickness ratio of wall and flange. With the ratio of the web height-to-thickness approaches the standard limit, the downward trend of the bearing capacity exacerbates significantly. The ductility coefficient of Q235 steel column can reach 4, and that of Q460 steel column is only about 2. For the ultimate displacement angle of Q460 steel column, it is recommended to adopt 0.03 for the I-type column and 0.032 for the box-type column. In Chinese standard, the limit of the flange width-to-thickness ratio is conservative, and the value may be up to 9. The web height-to-thickness ratio should not be too large. The degree of stiffness degradation of Q460 steel column exacerbates with the increase of the axial compression ratio. The initial stiffness of the column is larger and the stiffness degradation is more severe when the flange width-to-thickness ratio increases and the ratio of the web height to thickness reduces.
-
引言
随着我国交通基础建设的持续深入发展，穿越黏滑断层的隧道不断涌现，如在建的雅康高速二郎山隧道穿越保凰活动断裂，成兰铁路诸隧道穿越龙门山活动断裂等。在2008年汶川地震中，都映高速部分隧道，其所穿越的黏滑断层在强震诱发下发生黏滑错动，造成错动段隧道结构和围岩严重破坏，甚至出现了隧道整体垮塌的严重震害（图 1），这对灾后救援和灾后重建工作造成了严重影响（四川省交通厅公路规划勘察设计研究院，2008；于海英等，2008）。如何提高断层黏滑错动时隧道结构的安全性和稳定性是亟待研究和解决的关键技术问题之一。
图 1 龙溪隧道黏滑断层段隧道整体垮塌Figure 1. Collapse of stick-slip fracture section in Longxi tunnel目前，黏滑断层隧道的减错措施主要有二衬设置减错缝和初支与二衬之间设置减错层2种。设置减错缝可减小隧道结构的纵向刚度，提高了隧道结构适应断层黏滑错动所产生相对变位的性能；设置减错层可减小隧道结构的横向刚度，消减了传递至二衬结构的强制位移。
国内外专家、学者对穿越黏滑断层隧道的减错技术做了部分研究，主要有：穿越活动断层隧道震害特征及震害机理（高孟潭等，2008；崔光耀等，2013a；何川等，2014）；断层错动下围岩与隧道结构的位移和应力变化（赵伯明等，2009；李玉江等，2013）；不同倾角、错距下断层黏滑错动对山岭隧道洞身结构的受力特性（熊炜等，2010；蒋建平等，2011；刘学增等，2014；张理平等，2017）；设置不同减错缝的减错效果（崔光耀等，2013b；李学峰等，2014；信春雷等，2015）；设置不同减错层的减错效果（崔光耀等，2013c）等。以上研究在穿越黏滑断层隧道断层错动机制，设置减错缝不同间距、减错层不同厚度减错效果方面做了部分工作，但均未对穿越黏滑断层隧道设置减错缝不同缝宽、减错层不同刚度的减错效果进行研究。本文依托都汶高速友谊隧道F1黏滑断层段，对黏滑断层隧道设置不同缝宽减错缝、不同刚度减错层的减错效果进行研究，以期能够促进穿越黏滑断层隧道减错技术的发展。
1. 研究情况
1.1 友谊隧道F1黏滑断层段工程概况
1.1.1 工程地质
隧址区位于纸厂沟与小桃沟之间的山体内，受断层和岩性影响，节理裂隙较发育，岩体较破碎。
F1黏滑断层为挤压性逆断层，隧道洞身穿F1黏滑断层而过，走向北东，倾向北西，倾角60°，破碎带宽度0.5—2.0m，断层破碎带主要由糜棱岩、碎块岩组成，Ⅴ级围岩。上下盘岩体均为Ⅴ级围岩。
1.1.2 支护结构设计
隧道支护结构为复合式衬砌，跨度×高度＝9.4m×8.0m；隧道初支采用C25喷射混凝土，厚度25cm，二衬采用C25模筑混凝土，厚度40cm。
1.2 计算情况
1.2.1 计算模型
以友谊隧道F1黏滑断层段为研究背景，利用FLAC3D有限差分数值模拟软件建立计算模型，隧道埋深为40m，隧底围岩厚40m，左右两侧宽度取5倍隧道跨度，约60m，纵向开挖长度100m。本次计算采用brick单元，其中围岩单元47550个，衬砌单元6820个。计算时围岩按弹塑性材料考虑，衬砌则按弹性材料考虑。减错缝采用12m设缝间距（崔光耀等，2013b），减错层厚度采用10cm（崔光耀等，2013c）。通过在上盘围岩施加位移荷载来模拟断层错动，位移荷载通过施加速度来实现，错距10cm。
1.2.2 计算参数
施工中减错缝主要采用止水带进行连接，减错层一般采用橡胶板（王帅帅等，2016），围岩根据勘测资料选取Ⅴ级围岩。计算模型物理力学参数如表 1所示。
表 1 计算模型参数Table 1. Parameters of calculation model参数 重度/kN·m-3 弹性模量/MPa 泊松比 黏聚力/MPa 内摩擦角/° 围岩 20 15000 0.40 0.10 24 C25喷射混凝土 22 23000 0.20 C25模注混凝土 25 28000 0.20 减错缝 6 10 0.45 减错层 10 0—2000 0.45 1.2.3 计算工况
本文主要研究减错缝不同缝宽、减错层不同刚度对减错效果的影响规律，计算工况如表 2所示。
表 2 计算工况Table 2. Calculation condition工况 计算内容 备注 1 无减错措施 2 施设减错缝 缝宽分别为：5cm、10cm、15cm、20cm 3 施设减错层 弹模分别为：2.5MPa、5MPa、10MPa、20MPa、50MPa、100MPa、200MPa、500MPa、1000MPa、2000MPa 1.2.4 监测布置
计算模型上盘设4个监测断面、下盘设3个监测断面，每个监测断面设置8个监测点，监测布置如图 2所示。
2. 减错缝宽度对减错效果的影响分析
2.1 结构内力
提取各工况错动完成时的各监测断面计算数据，以缝宽10cm为例进行内力分析。轴力、弯矩的计算按照公式（1）、（2）计算（中华人民共和国交通部，2004）。监测断面最大轴力值见表 3，监测断面最大弯矩值见表 4。
表 3 监测断面最大轴力（单位：kN）Table 3. Maximum axial force of monitoring section (unit: kN)工况 距断层距离/m -22 -10 -2 2 10 22 34 无减错措施 -6468 -9754 -14884 -13376 -13341 -9551 -3702 缝宽10cm -5917 -9133 -14857 -13395 -12558 -8646 -3153 注：距断层距离正值为上盘，负值为下盘，其它同理。 表 4 监测断面最大弯矩（单位：kN·m）Table 4. Maximum bending moment of monitoring section (unit: kN·m)工况 距断层距离/m -22 -10 -2 2 10 22 34 无减错措施 -60.2 -142.1 -217.6 -185.0 -121.9 -45.1 -126.7 缝宽10cm -61.3 -140.2 276.1 -200.5 -127.7 48.5 -116.6 轴力、弯矩计算公式为：
$$ N=\frac{1}{2}E({\varepsilon _内}+{\varepsilon _外})bh $$ (1) $$ M=\frac{1}{{12}}E({\varepsilon _内}-{\varepsilon _外})b{h^2} $$ (2) 式中，b为截面宽度（m），取1m；h为截面厚度（m）；E为弹性模量（MPa）；${\varepsilon _内}$、${\varepsilon _外}$为结构内、外侧应变；N为结构轴力（N）；M为弯矩（N·m）；后同。
由表 3可知，施设减错缝与无减错措施工况监测断面最大轴力值均呈现压应力状态，且沿隧道纵向分布趋势相似，最大值均出现在下盘靠近断层的断面，其中无减错措施工况值为-14884kN，施设减错缝工况值为-14857kN；随着监测断面与断层的距离增大，监测断面最大轴力呈下降趋势。由各监测断面最大轴力整体分析可知，施设减错缝工况监测断面最大轴力略小于无减错措施工况。
由表 4可知，无减错措施工况监测断面最大弯矩均表现为外侧受拉，施设减错缝改变了隧道结构受力，出现内侧受拉部位；监测断面最大弯矩值均出现在下盘靠近断层的断面，其中不设减错缝工况值为-217.6kN·m，施设减错缝工况值为276.1kN·m。由各监测断面最大弯矩整体分析可知，施设减错缝工况监测断面最大弯矩略大于无减错措施工况。
轴力、弯矩指标主要用于结构设计，单一分析轴力、弯矩不能综合体现结构的力学性能。隧道支护的结构安全性可由安全系数（综合考虑了轴力、弯矩等指标）体现。
2.2 结构安全系数
提取各工况错动完成时的内力计算数据进行安全系数分析，安全系数K按照公式（3）、（4）计算（中华人民共和国交通部，2004）。以缝宽10cm进行安全系数分析，监测断面最小安全系数见表 5。
$$ KN \le \varphi \alpha{R_{\rm{a}}}bh $$ (3) $$ KN \le \varphi \frac{{1.75{R_1}bh}}{{6{e_0}/h - 1}} $$ (4) 表 5 监测断面最小安全系数Table 5. Minimum safety factor of monitoring section工况 距断层距离/m -22 -10 -2 2 10 22 34 无减错措施 1.933 1.282 0.840 0.935 0.937 1.309 3.377 缝宽10cm 2.112 1.326 0.841 0.933 0.995 1.446 3.964 式中，Ra为混凝土抗压极限强度（MPa）；Rl为混凝土抗拉极限强度（MPa）；φ为构件纵向弯曲系数；α为轴向力偏心影响系数；e0为轴向力对截面的偏心距（m）。
由表 5可知，施设减错缝与无减错措施工况监测断面最小安全系数沿隧道纵向分布趋势相似，最小值均出现在下盘靠近断层监测断面，其中无减错措施工况安全系数最小值为0.840，施设减错缝工况安全系数最小值为0.841；随着监测断面与断层距离的增大，监测断面最小安全系数呈增大趋势，上盘安全系数整体较下盘小。由各监测断面最小安全系数整体分析可知，施设减错缝工况监测断面最小安全系数略大于无减错措施工况。
2.3 减错效果
根据安全系数分析各工况减错效果，减错效果可按式（5）进行计算，各工况减错效果如图 3所示。
$$ \lambda= \frac{{{K_1}-{K_0}}}{{{K_0}}} \times 100\% $$ (5) 式中：λ为减错效果；K0为无减错措施工况监测断面最小安全系数；K1为施设减错缝工况监测断面最小安全系数。
由图 3可知，各工况减错效果沿隧道纵向分布趋势相似，随着监测断面与断层的距离增大，上下盘减错效果整体呈上升趋势，且上盘减错效果较下盘整体更好，其中上盘减错效果最大为24.50%，下盘减错效果最大为9.26%。随着减错缝宽度的增加，隧道上盘减错效果变好，下盘缝宽10—15cm时减错效果最好，主要由于断层黏滑错动对上盘的影响远大于下盘。减错缝宽度的增加适应了断层黏滑错动造成的上盘强制位移，断层黏滑错动的能量得到一定程度的释放，从而提高了上盘隧道的结构安全性，可以设想，对于隧道上盘部分存在最优减错缝宽度；减错缝宽度的增加虽然适应了断层黏滑错动造成的下盘强制位移，但由于抵御断层黏滑错动对下盘影响所需减错缝缝宽为10—15cm，当缝宽增加到20cm时，下盘隧道整体刚度的下降对下盘隧道的结构安全性造成了不利影响，致使减错效果下降。
3. 减错层弹性模量对减错效果的影响分析
3.1 结构内力
提取各工况错动完成时各监测断面的计算数据，以减错层弹性模量为2.5MPa为例进行内力分析。监测断面最大轴力值见表 6，监测断面最大弯矩值见表 7。
表 6 监测断面最大轴力（单位：kN）Table 6. Maximum axial force of monitoring section (unit: kN)工况 距断层距离/m -21 -11 -2 2 11 21 32 无减错措施 -6515 -10663 -17049 -14062 -12114 -7572 -3777 减错层弹模（2.5MPa） -5557 -7014 -8375 -8981 -8490 -6154 -3788 表 7 监测断面最大弯矩（单位：kN·m）Table 7. Maximum bending moment of monitoring section (unit: kN·m)工况 距断层距离/m -21 -11 -2 2 11 21 32 无减错措施 -78.5 -155.9 -218 -187.2 -100.3 -46.8 -35.9 减错层弹模（2.5MPa） -173.4 -269 -254.1 -217.1 -108.0 -59.3 -42.7 由表 6可知，施设减错层与无减错措施工况监测断面最大轴力值均呈现压应力状态，且沿隧道纵向分布趋势相似，最大值均出现在上下盘靠近断层的断面，其中无减错措施工况值为-17049kN，施设减错层工况值为-8981kN；随着监测断面与断层距离的增大，监测断面最大轴力呈下降趋势。由各监测断面最大轴力整体分析可知，施设减错层工况监测断面最大轴力小于无减错措施工况。
由表 7可知，施设减错层与无减错措施工况监测断面最大弯矩值均表现为外侧受拉；无减错措施工况监测断面最大弯矩值出现在下盘靠近断层的断面，其值为-218kN·m，施设减错层监测断面最大弯矩值出现在下盘距离断层11m处，其值为-269kN·m。由各监测断面最大弯矩整体分析可知，施设减错层工况监测断面最大弯矩大于无减错措施工况。
3.2 结构安全系数
提取各工况错动完成时各监测断面的计算数据，以减错层弹性模量为2.5MPa为例进行安全系数分析，监测断面最小安全系数见表 8。
表 8 监测断面最小安全系数Table 8. Minimum safety factor of monitoring section工况 距断层距离/m -21 -11 -2 2 11 21 32 无减错措施 1.919 1.172 0.733 0.889 1.032 1.651 3.310 减错层弹模（2.5MPa） 2.455 1.798 1.505 1.583 1.592 2.031 3.399 由表 8可知，施设减错层与无减错措施工况监测断面最小安全系数沿隧道纵向分布趋势相似，最小值均出现在下盘靠近断层监测的断面，其中无减错措施工况最小安全系数最小值为0.733，施设减错层工况最小安全系数最小值为1.505；随着监测断面与断层距离的增大，监测断面最小安全系数呈增大趋势，上盘安全系数整体较下盘小。由各监测断面最小安全系数整体分析可知，施设减错层工况监测断面最小安全系数大于无减错措施工况。
3.3 减错效果
根据安全系数分析各工况减错效果，减错效果计算方法同式（5），各工况减错效果如图 4所示。
由图 4可知，各工况减错效果沿隧道纵向分布趋势相似，随着监测断面与断层距离的增大，上下盘减错效果整体呈下降趋势，且下盘减错效果较上盘整体略好，其中下盘减错效果最大为105.32%，上盘减错效果最大为78.07%；当减错层弹性模量增加到一定程度（约100MPa），减错效果趋于稳定。
4. 结论
（1）断层黏滑错动对隧道上盘的影响远大于下盘，上盘部分是黏滑断层隧道减错设防设计的重点段落。
（2）减错缝对上盘部分隧道结构的减错效果优于下盘，其中上盘减错效果最大为24.50%，下盘减错效果最大为9.26%；减错层对下盘部分隧道结构的减错效果略优于上盘，其中下盘减错效果最大为105.32%，上盘减错效果最大为78.07%。
（3）随着减错缝宽度的增加，隧道上盘减错效果变好，下盘缝宽10—15cm减错效果最好，主要是由于断层黏滑错动对上盘的影响远大于下盘。减错缝宽度的增加适应了断层黏滑错动造成的上盘强制位移，断层黏滑错动的能量得到一定程度的释放，从而提高了上盘隧道的结构安全性，可以设想，对于隧道上盘部分存在最优减错缝宽度；减错缝宽度的增加虽然适应了断层黏滑错动造成的下盘强制位移，由于抵御断层黏滑错动对下盘影响所需减错缝缝宽为10—15cm，当缝宽增加到20cm时，下盘隧道整体刚度的下降对下盘隧道的结构安全性造成了不利影响，致使减错效果下降。
（4）随着减错层弹性模量的增加，隧道上下盘减错效果降低；当减错层弹性模量增加到一定程度（约100MPa），减错效果趋于稳定。
-
图 3 “工”字型柱、“箱”型柱网格划分
Figure 3. Division diagram of I-type column and box-type column grid
图 16 “工”字型柱位移角的统计结果
Figure 16. Statistical results of displacement angle of I-type column
图 17 “箱”型柱位移角的统计结果
Figure 17. Statistical results of displacement angle of box-type column
图 18 “工”字型柱不同轴压比对应的刚度退化
Figure 18. Stiffness degradation of I-type column under different axial compression ratios
图 19 “工”字型柱不同翼缘宽厚比对应的刚度退化
Figure 19. Stiffness degradation of I-type column under different flange width-thickness ratio
图 20 “工”字型柱不同腹板高厚比对应的刚度退化
Figure 20. Stiffness degradation of I-type column under different web thickness ratio
图 21 “箱”型柱不同轴压比对应刚度退化
Figure 21. Stiffness degradation of box-type column under different axial compression ratios
图 22 “箱”型柱不同壁板宽厚比对应刚度退化
Figure 22. Stiffness degradation of box-type column under different panel wide heavy ratios
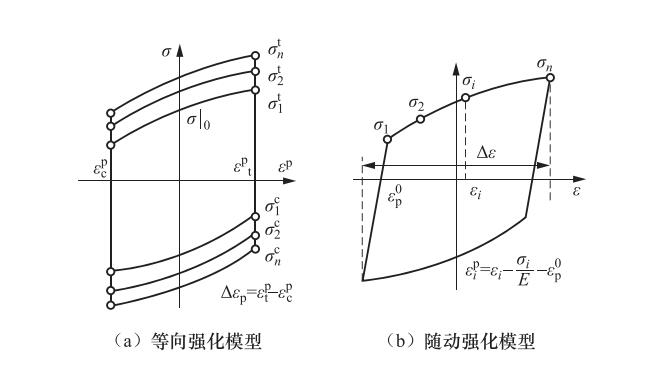
表 1 钢材本构模型参数
Table 1. Steel constitutive model parameters
钢材材性 $\sigma \left| {_0} \right.$/ N·mm-2 ${C_{{\rm{k}},1}}$/ N·mm-2 ${\gamma _1}$ ${C_{{\rm{k}},2}}$/ N·mm-2 ${\gamma _2}$ ${C_{{\rm{k}},3}}$/ N·mm-2 ${\gamma _3}$ ${C_{{\rm{k}},4}}$/ N·mm-2 ${\gamma _4}$ Q460 474 4797 156 3794 145 1498 107 Q345 429 7993 175 6773 116 2854 34 1450 29 Q235 407 6013 173 5024 120 3026 32 990 35 
下载: 导出CSV
表 2 试件参数
Table 2. Test piece parameters
试件编号 H/mm B/mm tf/mm tw/mm b/tf h0/tw [b/tf] [h0/tw] n N/kN H-0-1 200 150 12 10 5.8 17.6 7.1 30.7 0.2 493.1 H-0-2 300 180 12 10 7.1 27.6 7.1 30.7 0.2 651.4 H-0-3 300 220 12 10 8.8 27.6 7.1 30.7 0.2 739.7
下载: 导出CSV
表 3 试件的位移荷载
Table 3. Displacement load of specimen
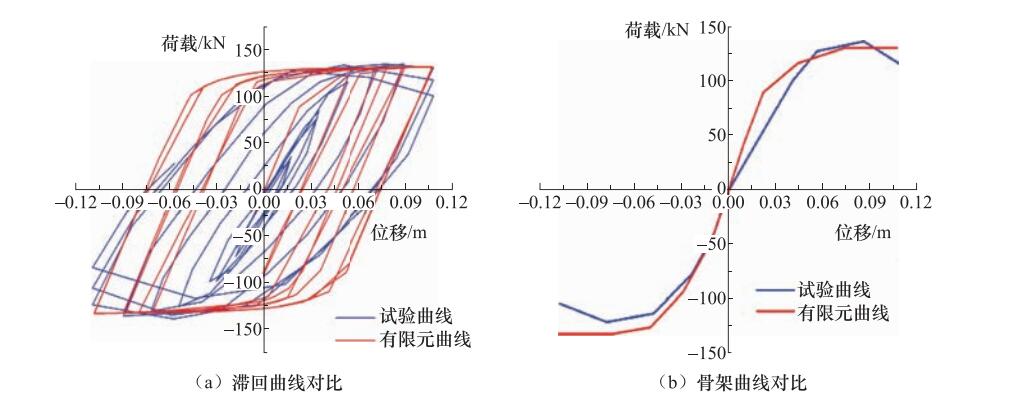
试件编号 ${\delta _1}$/mm ${\delta _2}$/mm ${\delta _3}$/mm ${\delta _4}$/mm ${\delta _5}$/mm ${\delta _6}$/mm ${\delta _7}$/mm H-0-1 9 18 36 54 72 90 108 H-0-2 6 12 24 36 48 60 72 H-0-3 6 12 24 36 48 60 72
下载: 导出CSV
表 4 ABAQUS计算与试验结果的最大承载力对比
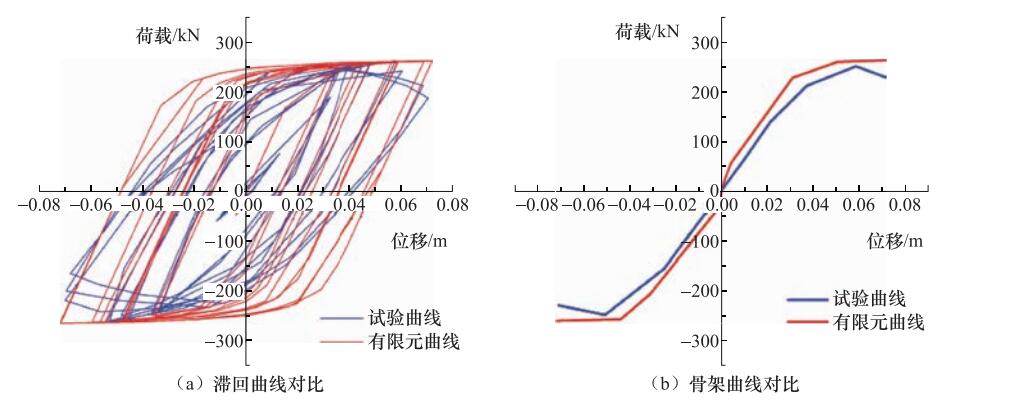
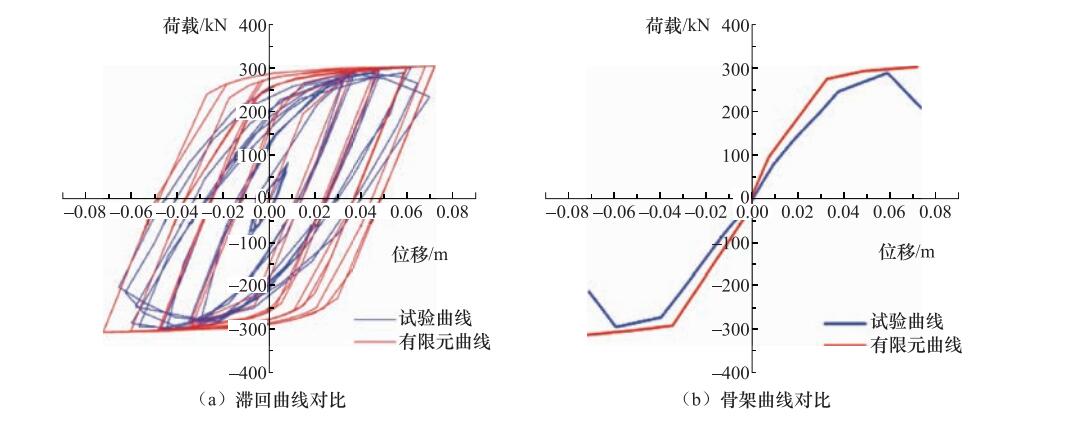
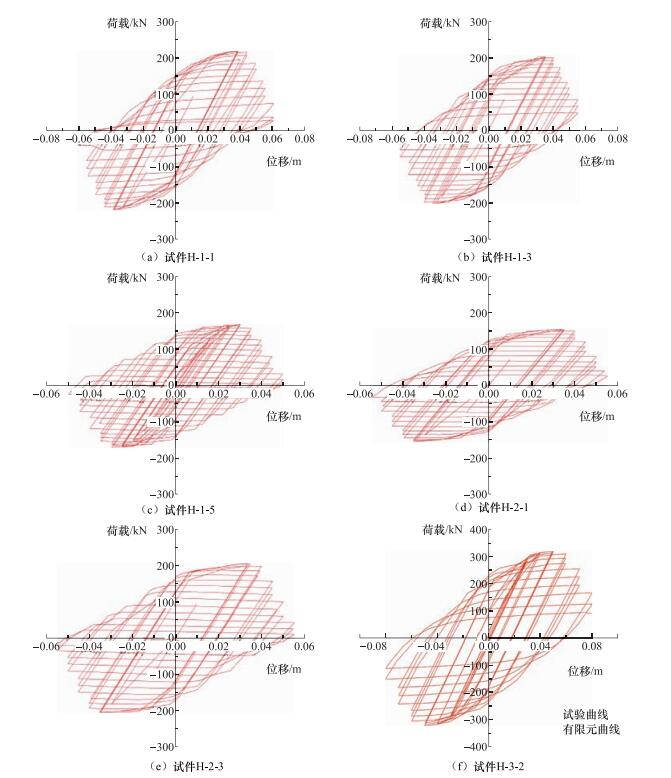
Table 4. Comparison of maximum bearing capacity between calculation and test
构件编号 ABAQUS结果/kN 试验结果/kN 相差/% H-0-1 132 139 -5 H-0-2 232 222 5.1 H-0-3 305 294 3.7
下载: 导出CSV
表 5 “工”字型截面试件设计参数
Table 5. Design parameters of I-type specimen
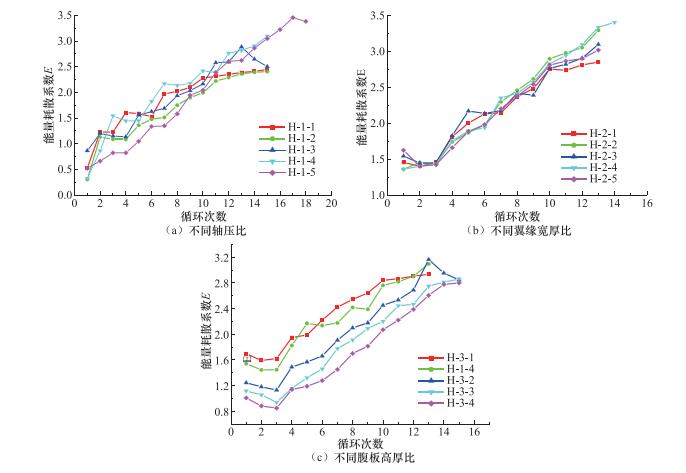
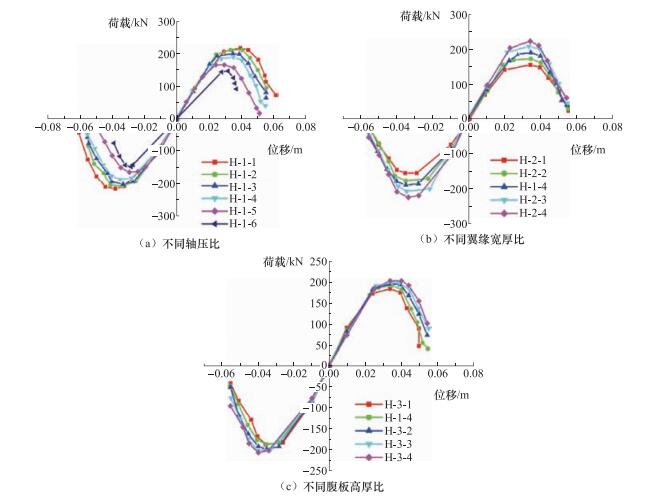
试件编号 b/mm h0/mm tw/mm tf/mm b/tf h0/tw λ L/mm n N/N H-1-1 178 250 10 12 7 25 30 1213 0.1 311.5 H-1-2 178 250 10 12 7 25 30 1213 0.2 623.0 H-1-3 178 250 10 12 7 25 30 1213 0.3 934.5 H-1-4 178 250 10 12 7 25 30 1213 0.4 1246.0 H-1-5 178 250 10 12 7 25 30 1213 0.5 1557.6 H-1-6 178 250 10 12 7 25 30 1213 0.6 1869.1 H-2-1 130 250 10 12 5 25 30 1183 0.4 1034.1 H-2-2 154 250 10 12 6 25 30 1199 0.4 1140.1 H-2-3 202 250 10 12 8 25 30 1224 0.4 1352.0 H-2-4 226 250 10 12 9 25 30 1234 0.4 1458.0 H-3-1 178 230 10 12 7 23 30 1088 0.4 1209.2 H-3-2 178 280 10 12 7 28 30 1700 0.4 1301.2 H-3-3 178 300 10 12 7 30 30 1524 0.4 1338.0 H-3-4 178 320 10 12 7 32 30 1648 0.4 1374.8 H-4-1 130 250 10 12 5 25 30 1183 0.2 517.0 H-4-2 154 250 10 12 6 25 30 1199 0.2 570.0 H-4-3 202 250 10 12 8 25 30 1524 0.2 676.0 H-4-4 226 250 10 12 9 25 30 1534 0.2 729.0 H-5-1 178 230 10 12 7 23 30 1088 0.2 604.6 H-5-2 178 280 10 12 7 28 30 1400 0.2 650.6 H-5-3 178 300 10 12 7 30 30 1524 0.2 669.0 H-5-4 178 320 10 12 7 32 30 1648 0.2 687.4 H-6-1 130 250 10 12 5 25 30 1183 0.6 1551.1 H-6-2 154 250 10 12 6 25 30 1199 0.6 1710.1 H-6-3 202 250 10 12 8 25 30 1224 0.6 2028.0 H-6-4 226 250 10 12 9 25 30 1234 0.6 2187.0 H-7-1 178 230 10 12 7 23 30 1088 0.6 1813.9 H-7-2 178 280 10 12 7 28 30 1400 0.6 1951.9 H-7-3 178 300 10 12 7 30 30 1524 0.6 2007.1 H-7-4 178 320 10 12 7 32 30 1648 0.6 2062.3
下载: 导出CSV
表 6 “箱”型截面试件设计参数
Table 6. Designing parameters of box-type specimen
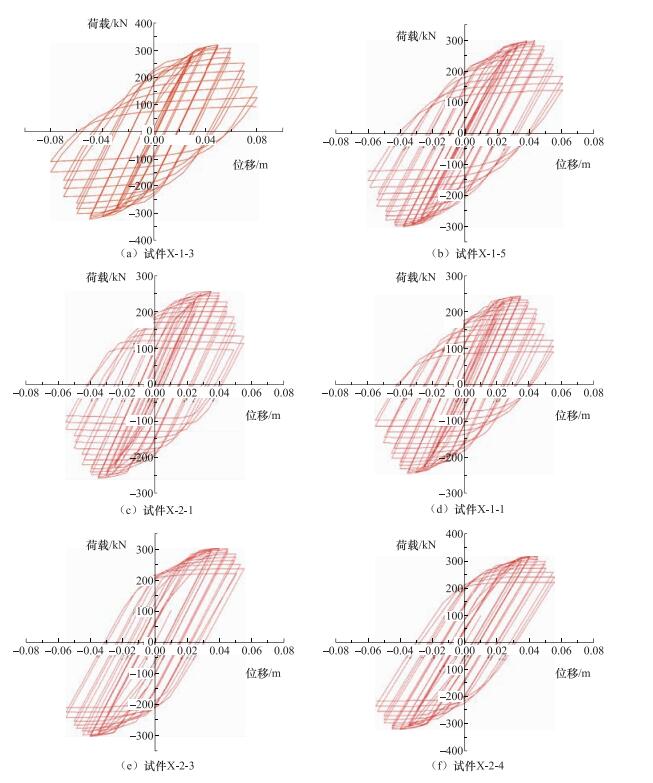
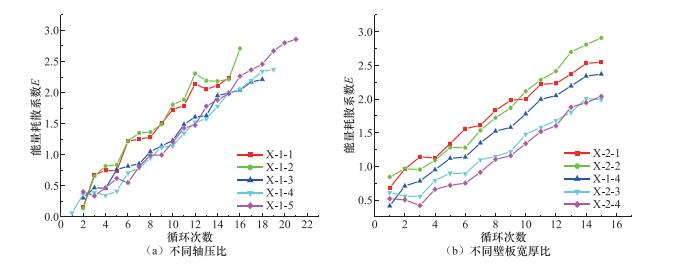
试件编号 B/mm D/mm t/mm B/t [B/t] λ L/mm n N/N X-1-1 300 300 20 15 23.6 30 1573 0.1 533.6 X-1-2 300 300 20 15 23.6 30 1573 0.2 1067.2 X-1-3 300 300 20 15 23.6 30 1573 0.3 1600.8 X-1-4 300 300 20 15 23.6 30 1573 0.4 2134.4 X-1-5 300 300 20 15 23.6 30 1573 0.5 2668 X-1-6 300 300 20 15 23.6 30 1573 0.6 3201.6 X-2-1 260 260 20 13 23.6 30 1288 0.4 1840 X-2-2 280 280 20 14 23.6 30 1430 0.4 1987.2 X-2-3 320 320 20 16 23.6 30 1716 0.4 2281.6 X-2-4 340 340 20 17 23.6 30 1859 0.4 2428.8 X-3-1 260 260 20 13 23.6 30 1288 0.2 920 X-3-2 280 280 20 14 23.6 30 1430 0.2 993.6 X-3-3 320 320 20 16 23.6 30 1716 0.2 1140.8 X-3-4 340 340 20 17 23.6 30 1859 0.2 1214.4 X-4-1 260 260 20 13 23.6 30 1288 0.6 2760 X-4-2 280 280 20 14 23.6 30 1430 0.6 2980.8 X-4-3 320 320 20 16 23.6 30 1716 0.6 3422.4 X-4-4 340 340 20 17 23.6 30 1859 0.6 3643.2
下载: 导出CSV
表 7 试件延性比计算结果
Table 7. Ductility ratio result of specimen from calculation
截面形状 试件编号 延性比 试件编号 延性比 试件编号 延性比 “工”字型 H-1-1 2.5256 H-3-1 2.5495 H-5-3 1.8175 H-1-2 2.5596 H-3-2 1.9412 H-5-4 1.8245 H-1-3 2.6382 H-3-3 2.4116 H-6-1 1.9092 H-1-4 2.5034 H-3-4 2.2301 H-6-2 2.0477 H-1-5 2.4784 H-4-1 1.9758 H-6-3 2.6084 H-1-6 1.3040 H-4-2 1.9735 H-6-4 1.9906 H-2-1 2.8007 H-4-3 1.5396 H-7-1 2.4463 H-2-2 2.8804 H-4-4 1.5725 H-7-2 1.8307 H-2-3 2.6508 H-5-1 2.0780 H-7-3 1.6720 H-2-4 2.3611 H-5-2 1.8176 H-7-4 1.7206 “箱”型 X-1-1 2.8794 X-2-1 2.4012 X-3-3 1.9370 X-1-2 2.7504 X-2-2 1.6506 X-3-4 1.8464 X-1-3 2.4262 X-2-3 1.8997 X-4-1 2.0211 X-1-4 2.1488 X-2-4 1.6812 X-4-2 1.8577 X-1-5 2.0218 X-3-1 2.0817 X-4-3 1.6825 X-1-6 1.6233 X-3-2 2.1513 X-4-4 1.9984
下载: 导出CSV
表 8 “工”字型柱位移角取值
Table 8. The recommended value of displacement angle of I-type column
n ${b_1}/{t_{\rm{f}}} \le 7\;且\;{h_0}/{t_{\rm{w}}} \le 28$ ${b_1}/{t_{\rm{f}}} > 7\;且\;{h_0}/{t_{\rm{w}}} > 28$ n≤0.2 θ＞0.035 0.035≥θ≥0.03 0.2＜n≤0.4 0.0375≥θ≥0.0325 0.035≥θ≥0.03 0.4＜n≤0.6 0.0325≥θ≥0.0275 0.03≥θ≥0.025 n＞0.6 0.03≥θ≥0.0275 0.0275≥θ≥0.025
下载: 导出CSV
表 9 “箱”型柱层间位移角的取值
Table 9. The recommended value of displacement angle of box-type column
n $B/t \le 15$ $B/t > 15$ n ≤0.2 θ＞0.035 0.035≥θ≥0.04 0.2＜n ≤0.4 0.04≥θ≥0.035 0.035≥θ≥0.03 0.4＜n ≤0.6 0.035≥θ≥0.03 0.03≥θ≥0.025 n＞0.6 0.03≥θ≥0.025 0.025≥θ≥0.02
下载: 导出CSV
-
班慧勇, 施刚, 刘钊等, 2011.Q420等边角钢轴压杆整体稳定性能试验研究.建筑结构学报, 32(2):60-67, 112. http://d.old.wanfangdata.com.cn/Periodical/jzjgxb201102009 郭子雄, 吕西林, 2004.高轴压比框架柱恢复力模型试验研究.土木工程学报, 37(5):32-38. http://d.old.wanfangdata.com.cn/Periodical/tmgcxb200405005 李国强, 王彦博, 陈素文等, 2013.Q460C高强度钢柱滞回性能有限元分析.建筑结构学报, 34(3):87-92. http://d.old.wanfangdata.com.cn/Periodical/jzjgxb201303011 施刚, 邓春森, 班慧勇等, 2012.Q460高强度钢材工字性压弯构件抗震性能的试验研究.土木工程学报, 45(9):53-61. 施刚, 邓春森等, 2012.Q460高强度钢材工形压弯构件抗震性能的试验研究.土木工程学报, 10(4):28-38. 王萌, 2013.强烈地震作用下钢框架的损伤退化行为.北京: 清华大学. 王萌, 石永久, 王元清, 2013.考虑累积损伤退化的钢材等效本构模型研究.建筑结构学报, 34(10):73-83. http://d.old.wanfangdata.com.cn/Periodical/jzjgxb201310009 中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局, 2010.GB 50011-2010建筑抗震设计规范(附条文说明)(2016年版).北京: 中国建筑工业出版社. Chaboche J. L., 1986. Time-independent constitutive theories for cyclic plasticity. International Journal of Plasticity, 2(2):149-188. doi: 10.1016/0749-6419(86)90010-0 Fukumoto Y., Kusama H., 1985. Local instability tests of plate elements under cyclic uniaxial loading. Journal of Structural Engineering, 111(5):1051-1067. doi: 10.1061/(ASCE)0733-9445(1985)111:5(1051) 国际桥梁与结构工程协会.高性能钢材在钢结构中的应用.中国建筑工业出版社, 2010. Rasmussen K. J. R., Hancock G. J., 1992. Plate slenderness limits for high strength steel sections. Journal of Constructional Steel Research, 23(1-3):73-96. doi: 10.1016/0143-974X(92)90037-F Rasmussen K. J. R., Hancock G. J., 1995. Tests of high strength steel columns. Journal of Constructional Steel Research, 34(1):27-52. doi: 10.1016/0143-974X(95)97296-A Usami T., Fukumoto Y., 1984. Welded box compression members. Journal of Structural Engineering, 110(10):2457-2470. doi: 10.1061/(ASCE)0733-9445(1984)110:10(2457) -
下载:
点击查看大图
计量
- 文章访问数: 126
- HTML全文浏览量: 41
- PDF下载量: 5
- 被引次数: 0
