Analysis and Application of Attenuation Relationships for Peak Accelerations of Ground Motion in Western China
-
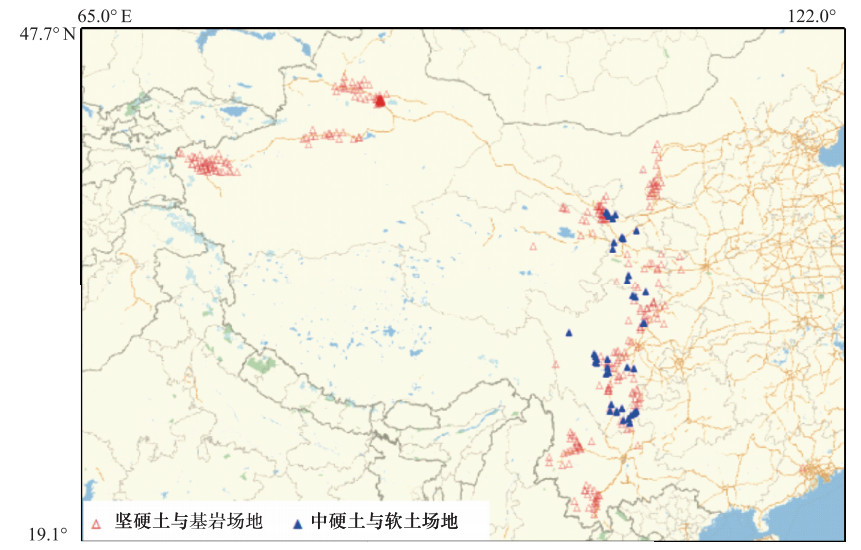
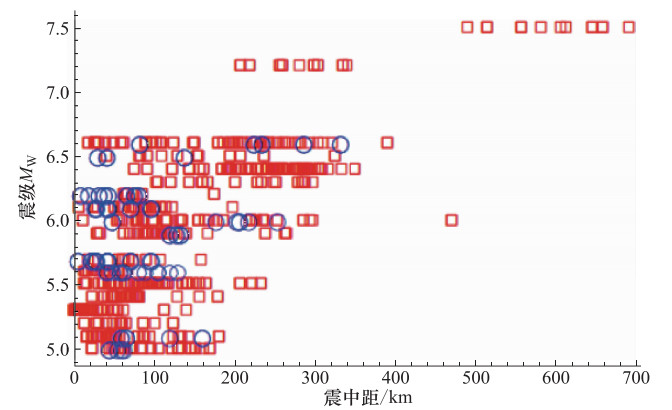
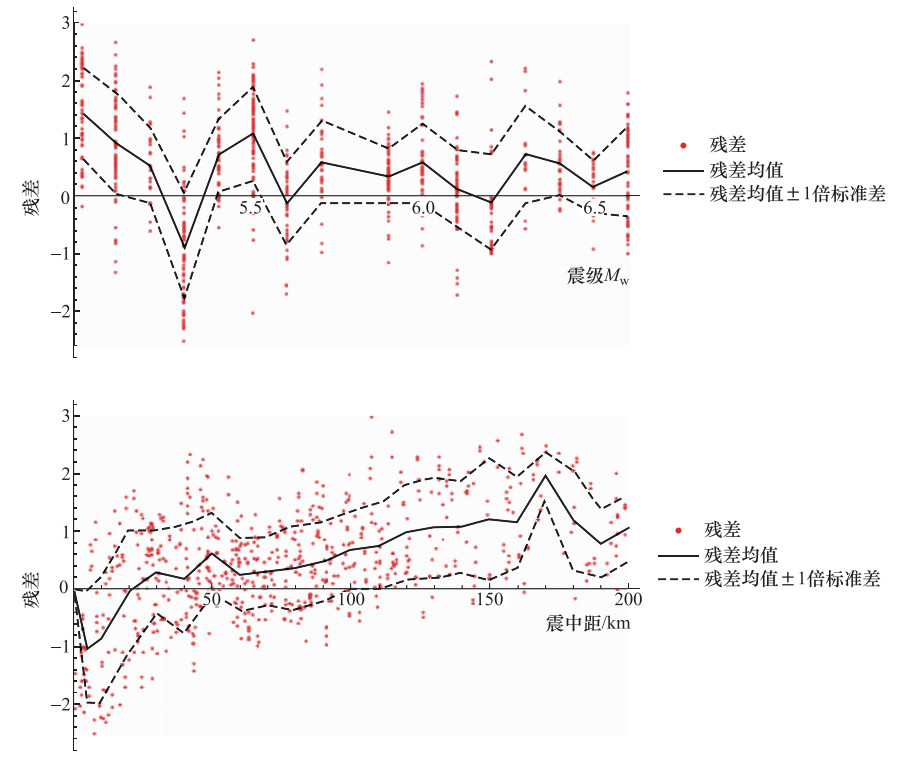
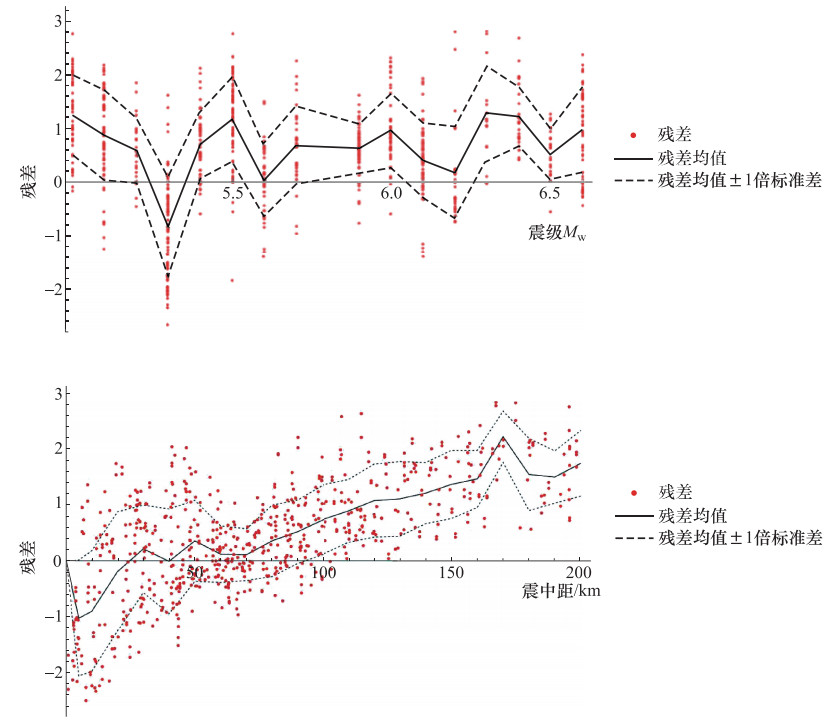
摘要: 地震动参数衰减关系描述了地震动参数随震级和距离等因素的变化情况，选取合适的地震动衰减关系是地震危险性分析中确定工程场地地震动参数的关键环节。本文收集、整理和分析了中国西部地区2012年3月9日—2017年9月16日间发生的42次地震事件中获取的强震动记录资料，并选择了3个国际上基于不同地区强震动记录数据建立的地震动加速度衰减关系(ASB11、SCEMY97和LLCS11)，开展了加速度衰减关系计算结果与中国西部强震动记录值的对比研究。比较了衰减关系峰值加速度的预测中值与实际记录值之间的差异，并分析了其残差随震级和距离的变化。得到了以下结论：①相比于SCEMY97和LLCS11，ASB11更适合于中国西部地区；②研究中国西部地区的衰减关系时，有必要考虑高频地震动的震级饱和现象。同时，对于如何修正已有衰减关系以使其更适合于中国西部地区给出了相应的建议。Abstract: The ground motion attenuation relationship depicts how ground motion parameters vary with factors such as magnitude and distance. It is critical to choose an appropriate attenuation relationship in determining the ground motion parameters for engineering sites in seismic hazard analysis. In this study, ground motion records from 42 earthquake events happened from 9 March 2012 to 16 September 2017 in western China were collected, sorted and analyzed. Three attenuation relationships for peak accelerations (ASB11, SCEMY97, LLCS11) worldwide, built with data from different regions, were compared with these record data. Through comparing the peak accelerations calculated by the three chosen attenuation relationships with the recorded peak accelerations, and analyzing the relationships between residuals and magnitude and distance, we conclude out that ① ASB11 works better for western China than SCEMY97 and LLCS11; ② the magnitude saturation of high-frequency ground motions needs to be considered in developing attenuation relationship for western China. Moreover, suggestions were made on the revision of the attenuation relationships so that they might work better for western China.
-
Key words:
- Western China /
- Attenuation relationship /
- Peak acceleration /
- MW /
- Epic-center distance
-
引言
剪切波速是表征场地土特性的重要参数，对于场地类别划分、砂土液化、软土震陷判别等至关重要。在实际工程建设中，受剪切波速测试环境、场地范围、经济等因素的影响，某些岩土中出现剪切波速数值缺失的情况，此时工程者往往采用经验统计模型进行剪切波速数值的补充。
目前学者已研究众多常规土类剪切波速与埋深间关系的经验统计模型，如王琦等（2018）基于天津地区地震安全性评价的实测剪切波速资料，采用幂函数模型，定性探讨了常见土类剪切波速与埋深的相关性；荣棉水等（2017）利用非线性最小二乘法，采用指数函数、一次函数、二次函数、幂函数、幂函数+常数函数、幂函数+一次函数6种回归模型对渤海海域7类土剪切波速和埋深的关系进行回归分析，指出最优模型为幂函数+一次函数模型；董菲蕃等（2013）基于福建沿海福州、泉州、漳州3个盆地大量的剪切波速实测资料，利用线性和二次多项式拟合得到各盆地5类土体等效剪切波速的空间分布特征；刘红帅等（2010）基于全国区域范围的实测钻孔资料，利用最小二乘法分别采用线性模型、指数模型和一元二次多项式模型建立分场地类别和不分场地类别下的常规土类（不包括淤泥质土）碎石土、砂土、粉土和黏性土剪切波速与埋深间的统计公式；战吉艳等（2009）利用苏州地区实测钻孔剪切波速资料进行研究，结果表明对于土层深度不大于50m的粘土和不小于40m的粉土，可采用幂函数形式模型的经验关系预测场地土剪切波速与土层深度的关系，对于粉质粘土和土层深度不小于40m的粉砂，可采用线性函数、幂函数分段形式模型的经验关系进行预测。经验公式受土层区域特性的影响显著，如乔峰等（2019）利用北京地区实测剪切波速资料建立的5种常见土类剪切波速与埋深之间关系的推荐模型，与利用全国数据建立的模型进行对比分析，指出区域性对剪切波速与深度之间的相关性存在影响；王琦等（2018）也研究指出剪切波速与埋深的经验公式受土层区域特性的影响显著。
由此可知，受地区土层差异性或模型关系影响，未统一给出相关的经验公式（荣棉水等，2017）。因此，选取合适的统计模型并建立合理的经验公式成为关键。
影响岩土剪切波速的主要因素为岩土类型、成因、物理状态和埋深（程祖锋等，1997）。很多学者也进行了相关性研究，如闫振军等（2019）通过华北地区10个城市928个钻孔的剪切波速从岩性条件、沉积环境等方面分析探讨了华北地区剪切波速随深度变化的特征；薛锋等（2014）给出考虑西安市地貌单元的细砂、中砂、粗砂、黄土、粉质粘土、古土壤、卵石等土类剪切波速与土层深度统计经验关系式；刘红帅等（2010）基于全国范围的实测钻孔资料，给出区分场地类别和不区分场地类别的情况下常规土类（不包括淤泥质土）碎石土、砂土、粉土和黏性土剪切波速与埋深之间的统计公式。
近年来，杭州作为长三角区域经济发展的重要城市，在城市建设中开展了大量地震安全性评价工作，积累了丰富的剪切波速资料。基于以上研究背景，考虑场地未明确土体物理状态的不利条件、建筑物场地类别在一定程度上反映了土的成因和物理状态以及国内学者在此方面的研究，本文利用现行3种最常规的剪切波速与埋深关系的经验模型进行分析，给出杭州市粉质粘土、淤泥质粉质粘土、粉砂、砂质粉土和粘质粉土5类典型土层在考虑场地分类和未考虑场地分类下的最优模型和相关系数，以供工程和研究参考。
1. 杭州市地质地貌概况
浙江省地貌单元可划分为浙西中山丘陵区、浙中盆地区、浙北平原区、浙东低山丘陵区、浙南中山区和浙东南沿海丘陵平原与岛屿区，杭州市位于浙西北地区，其西部（如临安和桐庐地区）属于浙西中山丘陵区；西南、西北山区属于中生代断块隆起；东部属于浙北平原区，地势低平，河流密集。杭州市工程地质单元主要以第四系地层为主，因新构造运动的影响，第四纪沉积成因类型繁多，沉积物的多次交替堆积和剥蚀，使得杭州地区覆盖层厚度变化较大（丁伯阳等，2012）。工程地质层主要包括前第四系和更新系统以来的第四系，前第四系（AnQ）主要由石灰岩、泥岩、砂岩等表征的基岩土层构成，第四系主要由中更新统、上更新统、全新统组成，成因类型主要有冲积相、冲湖积、湖沼积、冲海积、冲湖积、海积、冲积等，土类主要以稍密的砂质粉土、流塑的淤泥质土、硬塑或软塑的粘土和中密的粉细砂为主（浙江省住房和城乡建设厅，2019）。
2. 数据来源
本文收集了杭州市2011—2016年以来开展的地震安全性评价工作中98个项目报告的296个钻孔资料，钻孔分布示意如图 1所示。场地类别以Ⅱ、Ⅲ、Ⅳ类为主，场地分类方法参照《建筑抗震设计规范》（GB 50011—2010）（中华人民共和国住房和城乡建设部，2016）公式4.1.5和表4.1.6确定，场地土类型主要为中硬土、中软土和软弱土，中硬土场地主要分布于临安、富阳地区，覆盖层厚度以4—20m为主；中软土场地分布于主城区，覆盖层厚度约为30—60m，个别钻孔深度达100m；软弱土场地主要分布于钱塘江附近。因Ⅳ类场地钻孔数较少，本文未展开研究。本次场地钻孔土层剪切波速测试均采用单孔法，波速测试间距为1m。钻孔土类主要以粉质粘土、淤泥质粉质粘土、粉砂、砂质粉土和粘质粉土为主，因此，汇总上述5类土的土层埋深点与对应剪切波速值，分别研究场地未分类和分类（Ⅱ、Ⅲ）下的剪切波速随埋深变化的关系，不同土类剪切波速分布范围如表 1所示。
表 1 研究区不同土类剪切波速的分布范围Table 1. Distribution ranges of shear wave velocity of different soils in study area岩性 粉质粘土 淤泥质粉质粘土 粉砂 砂质粉土 粘质粉土 场地类别 总计 Ⅱ Ⅲ 总计 Ⅱ Ⅲ 总计 Ⅱ Ⅲ 总计 Ⅱ Ⅲ 总计 Ⅱ Ⅲ 测试点数 1915 324 1591 902 31 871 383 17 366 904 88 816 330 69 261 最小值/m·s-1 115 115 117 98 102 98 134 134 139 112 122 112 112 116 112 最大值/m·s-1 390 348 390 245 215 245 357 303 357 339 310 339 321 321 270 平均值/m·s-1 249.4 203.4 258.8 153.9 139.5 154.4 227.5 255.0 226.2 163.1 202.4 158.9 154.2 165.0 151.3 标准差/m·s-1 59.0 62.9 53.6 29.1 30.9 28.9 54.5 42.7 54.7 37.0 56.5 31.5 32.8 45.8 27.8 测试深度/m 2—78 2—44 2—78 2—46 4—24 2—46 1—56 1—30 5—56 1—57 1—34 1—57 2—44 2—36 2—44 3. 剪切波速与埋深关系模型
众多研究结果表明，剪切波速与埋深的关系可用线性函数、多项式函数、幂函数、幂函数+常函数等众多模型表示，本文选取常见的3种经验模型进行分析，分别为线性函数模型Vs=a+bH、二次函数模型Vs=a+bH+cH2、常函数+幂函数模型Vs=a+bHc，其中Vs为土体剪切波速，a、b、c分别为拟合系数。通过Origin统计分析功能，分别给出5类土的回归曲线及相关系数，最终采用拟合优度R2选出适合本地区的拟合模型，拟合优度为0＜R2＜1，R2越接近1时，拟合效果越佳。
4. 杭州市典型岩土层剪切波速与埋深关系模型分析
为更好地展示剪切波速与埋深的关系，首先绘制296个钻孔（不包括Ⅳ类场地）中粉质粘土、淤泥质粉质粘土、粉砂、砂质粉土和粘质粉土波速与埋深散点图，发现深度相近时剪切波速相差较大，总结原因为：剪切波速测试受环境和仪器精度的影响，出现个别坏点；因土体状态导致剪切波速相差较大，即受软硬夹层的影响。考虑回归分析仅能反映一般土质条件下的统计关系（董菲蕃等，2013；陈国兴等，1998），因此本文首先对于个别离散趋势较大的点和软硬夹层的剪切波速，参照董菲蕃等（2013）、陈国兴等（1998）的方法进行相关性处理，处理完成的数据如图 2所示。由图 2可知，总体上，剪切波速与埋深具有显著的相关性，即剪切波速随埋深具有明显的增长趋势。采用3种统计关系模型分别对不同场地分类情况下的5类土进行回归分析，拟合趋势如图 3—7所示，拟合优度如表 2所示，分布情况如图 8所示，为表达简洁，分别给出各土类在不同模型下的拟合工况编号，具体如表 2所示。
图 2 296个钻孔资料中5类常规土剪切波速与埋深散点图Figure 2. Scatter diagram of shear wave velocity and buried depth of five types of conventional soils in 296 borehole data
图 3 不同场地分类情况下粉质粘土剪切波速与埋深散点图Figure 3. Scatter diagrams of shear wave velocity and buried depth of silty clay under different site classifications
图 4 不同场地分类情况下淤泥质粉质粘土剪切波速与埋深散点图Figure 4. Scatter diagram of shear wave velocity and buried depth of mucky silty clay under different site classifications
图 5 不同场地分类情况下粉砂剪切波速与埋深散点图Figure 5. Scatter diagram of shear wave velocity and buried depth of silty sand under different site classifications
图 6 不同场地分类情况下砂质粉土剪切波速与埋深散点图Figure 6. Scatter diagram of shear wave velocity and buried depth of sandy silt under different site classifications
图 7 不同场地分类情况下粘质粉土剪切波速与埋深散点图Figure 7. Scatter diagram of shear wave velocity and buried depth of clayey silt under different site classifications表 2 不同场地分类情况下5类土拟合优度Table 2. Goodness of fitting of five types of soil under different site classification岩土类型 工况 R2 场地未分类 Ⅱ类场地 Ⅲ类场地 粉质粘土 FN1 0.86870 0.95298 0.86330 FN2 0.88890 0.95301 0.87860 FN3 0.89140 0.95284 0.88130 淤泥质粉质粘土 YN1 0.86130 0.87627 0.86470 YN2 0.86560 0.90946 0.86850 YN3 0.86460 0.90960 0.86770 粉砂 FS1 0.83000 0.95942 0.83480 FS2 0.84820 0.95659 0.84980 FS3 0.84140 0.95670 0.84540 砂质粉土 SF1 0.88030 0.97654 0.91490 SF2 0.88110 0.97672 0.91530 SF3 0.88020 0.97725 0.91550 粘质粉土 NF1 0.83070 0.95183 0.92820 NF2 0.83860 0.95568 0.92910 NF3 0.83520 0.95554 0.92810 
图 8 不同场地分类情况下5类土拟合优度Figure 8. Goodness of fitting of five types of soils under different site classification由图 8可知，总体上，Ⅱ类场地拟合优度均大于场地未分类和Ⅲ类场地，由图 2—7可知，Ⅱ类场地下各类土拟合数据样本量较少，这可能是导致拟合情况较好的原因。只有粘质粉土Ⅲ类场地的拟合优度明显优于场地未分类，淤泥质粉质粘土、粉砂和砂质粉土则相差不明显，而粉质粘土却相反，说明受岩土类型的影响，考虑场地分类因素并不一定减少误差或提高预测精度。考虑不同工程实际状况的需要，表 3给出场地未分类、Ⅱ类场地和Ⅲ类场地下5类常规土关系公式、残差标准差、适应范围和拟合优度，以供使用选择。
表 3 各场地类型下不同岩土类型的推荐模型Table 3. Recommended models for different geotechnical types under different site types岩土类型 场地类别 推荐模型 回归方程 残差标准差 R2 适应范围/m 粉质粘土 Ⅱ类 模型2 ${v_s} = 112.4398 + 5.9058H - 0.0077{H^2}$ 13.58 0.9530 2—44 Ⅲ类 模型3 ${v_s} = 86.5602 + 18.7249{H^{0.6352}}$ 18.45 0.8813 2—78 场地未分类 模型3 ${v_s} = 85.5503 + 21.3380{H^{0.6041}}$ 19.44 0.8914 2—78 淤泥质粉质粘土 Ⅱ类 模型2 ${v_s} = 104.8362 + 0.2524{H^{1.9230}}$ 8.83 0.9096 4—24 Ⅲ类 模型2 ${v_s} = 90.5189 + 4.1075H - 0.0227{H^2}$ 10.46 0.8685 2—46 场地未分类 模型2 ${v_s} = 89.9598 + 4.1857H - 0.0245{H^2}$ 10.65 0.8656 2—46 粉砂 Ⅱ类 模型1 ${v_s} = 130.5509 + 5.6417H$ 8.08 0.9594 1—30 Ⅲ类 模型2 ${v_s} = 100.2213 + 7.3496H - 0.0521{H^2}$ 18.79 0.8498 5—56 场地未分类 模型2 ${v_s} = 98.7936 + 7.5598H - 0.0558{H^2}$ 21.19 0.8482 1—56 砂质粉土 Ⅱ类 模型3 ${v_s} = 112.9768 + 4.1008{H^{1.1103}}$ 8.37 0.9773 1—34 Ⅲ类 模型3 ${v_s} = 120.9837 + 3.0980{H^{1.0546}}$ 18.45 0.9155 1—57 场地未分类 模型2 ${v_s} = 113.5888 + 4.5896H - 0.0079{H^2}$ 12.73 0.8811 1—57 粘质粉土 Ⅱ类 模型2 ${v_s} = 115.3530 + 4.2818H + 0.0461{H^2}$ 9.42 0.9551 2—36 Ⅲ类 模型2 ${v_s} = 121.1832 + 2.7579H + 0.0110{H^2}$ 7.39 0.9291 2—44 场地未分类 模型2 ${v_s} = 123.4666 + 2.4199H - 0.0354{H^2}$ 13.14 0.8386 2—44 5. 模型验证
为进一步验证本文推荐模型的可靠性和地区差异性，首先选取未进入统计的新建杭州至黄山铁路（Ⅱ类场地）和钱江新城二期连堡丰城项目（Ⅲ类场地）钻孔资料，将本文推荐模型预测的剪切波速与本地实测钻孔剪切波速进行对比分析，其中相对误差表示预测值与实测值之差占实测值的比值；然后选取国内学者发布的粉质粘土和粉砂剪切波速统计模型，将本文推荐模型与其他模型进行对比分析，以研究地区差异性影响，其中相对误差表示学者模型预测剪切波速与本文模型预测值之差占本文模型预测值的比值。
5.1 可靠性验证
（1）Ⅱ类场地对比分析结果如表 4所示，由表 4可知，Ⅱ类场地推荐模型和场地未分类推荐模型下的剪切波速预测值相对误差均在15%以内，最小相对误差仅为0.07%，最大相对误差为14.14%，具有良好的可靠性表现。且考虑场地分类与不考虑场地分类的剪切波速预测精度因岩土类型的不同产生了差异，相比其他土类，淤泥质粉质粘土明显表示出未考虑场地分类的剪切波速预测精度优于考虑场地类别，有别于回归分析中相差不大的规律，说明统计模型的实际预测精度也受岩土类型的影响。
表 4 Ⅱ类场地实测剪切波速与预测值的对比分析Table 4. Comparative analysis of measured shear wave velocity and predicted value of site Ⅱ岩土类型 钻孔编号 深度
/m实测剪切波速
/m·s-1Ⅱ类场地预测值
/m·s-1相对误差
/%场地未分类预测值
/m·s-1相对误差
/%粉质粘土 JZ1 3 130 130 0.07 127 -2.32 JZ1 5 143 142 -0.84 142 -0.72 JZ-Ⅳ 8 152 159 4.76 160 5.58 JZ-Ⅳ 24 222 250 12.68 231 4.09 JZ-Ⅳ 27 263 267 1.44 242 -8.06 粉砂 JZ1 29 278 278 -0.06 249 -10.54 JZ1 24 233 266 14.14 248 6.48 JZ1 26 286 277 -3.06 258 -9.92 淤泥质粉质粘土 JZ-Ⅳ 16 154 157 1.97 151 -2.17 JZ-Ⅳ 17 145 163 12.75 154 6.23 JZ-Ⅳ 19 159 177 11.62 161 1.03 （2）将推荐模型应用于Ⅲ类场中6个实测深度均超过50m的钻孔DZ1—DZ6场地。对Ⅲ类场地和场地未分类下的预测剪切波速与实测数据进行对比分析，结果如图 9所示。由图 9可知，除淤泥质粉质粘土在23m预测相对误差超过15%外，本文推荐模型预测出的剪切波速与实测剪切波速相对误差基本在15%以内，最小相对误差仅为0.02%，且各土类相对误差10%内的占比达90%以上，具有较高的预测可靠性；区别于Ⅱ类场地，Ⅲ类场中各岩土类型下考虑场地分类的剪切波预测值与未考虑场地分类的相对误差相差不大，但粉质粘土在整个预测深度范围内均表现出未考虑场地分类的预测值略优于考虑场地分类的预测值，而粉砂在25—27m、淤泥质粉质粘土在21—24m也表示出此规律，再次说明因岩土类型和预测深度的不同，考虑场地分类因素能否在实际工程中提高预测精度具有不确定性，应具体项目具体分析。
图 9 Ⅲ类场地实测剪切波速与预测值的对比分析图Figure 9. Comparative analysis of measured shear wave velocity and predicted value of site Ⅲ通过上述对Ⅱ、Ⅲ类场地实测剪切波速的验证，可知虽然个别土类相对误差将近20%（淤泥质粉质粘土），但超过90%的预测剪切波速相对误差在10%以内，因此用本文推荐模型预测出的剪切波速具有较高的可靠性。
5.2 地区差异性分析
为验证本文推荐模型与其他地区模型的差异，选取最常见的粉质粘土、粉砂，与国内学者研究的模型进行对比分析。选取模型主要包括荣棉水等（2017）基于渤海常见土类剪切波速资料统计分析给出的粉质粘土、粉砂模型，刘红帅等（2010）根据全国大量安全性评价实测钻孔资料统计给出的粉质粘土、粉砂模型及战吉艳等（2009）给出的苏州城区粉质粘土、粉砂模型。为表达简洁，分别用场地未分类、Ⅱ类场地和Ⅲ类场地代表本文推荐模型，渤海-Rong代表荣棉水等（2017）模型，用未分类-Liu、Ⅱ类-Liu和Ⅲ类-Liu代表刘红帅等（2010）模型中场地未分类、Ⅱ类场地和Ⅲ类场地下的经验模型，用苏州-Zhan代表战吉艳等（2009）模型。对比分析结果如图 10、11所示。
图 10 粉质粘土下本文模型与其他模型剪切波速对比分析图Figure 10. Comparative analysis of shear wave velocity of the model proposed in this paper and other models of silty clay
图 11 粉砂下本文模型与其他模型剪切波速对比分析图Figure 11. Comparative analysis of shear wave velocity of the model proposed in this paper and other models of silty sand由图 11（a）可知，总体上，在所有场地分类情况下，杭州地区粉质粘土推荐模型的剪切波速预测值明显低于刘红帅等（2010）模型，而与渤海-Rong、苏州-Zhan在部分深度上相差不明显，且在图 11（b）中也有体现：渤海-Rong与本文模型相对误差基本在5%以内，苏州-Zhan在2—29m和本模型相对误差在15%以内，而与刘红帅等（2010）模型在场地未分类情况下的相对误差为18%—51%、Ⅱ类场地下为17%—41%、Ⅲ类场地下为18%—41%，均体现了较大的差异性。说明受地区的影响，粉质粘土不同统计模型具有明显的地区差异性，因此建议应用者在选取模型时，应特别注意地区适应性。
由图 12可知，总体上，杭州地区粉砂剪切波速预测模型与粉质粘土相比表现出不同的规律性，即本文推荐粉砂模型与其他学者模型表现出更好的一致性，图 12（b）相对误差中也有所体现，即当预测深度超过10m后，各模型相对误差均在20%以内，说明受岩土类型的影响，不同岩土类型对地区的适应性不同。值得注意的是，在0—10m，渤海-Rong、未分类-Liu和Ⅲ类-Liu相对误差均较大，最大相对误差达39.1%，这也说明预测深范围会对模型的地区适应性产生影响。
综上可知，剪切波速与埋深间统计公式的地区差异性不仅受地区的影响显著，更与岩土类型、预测深度范围有关。
6. 结论
本文基于杭州市场地剪切波速资料，对杭州市粉质粘土、淤泥质粉质粘土、粉砂、砂质粉土和粘质粉土5类土的剪切波速与埋深经验关系进行相关性分析，主要结论如下：
（1）给出了杭州市5类土在考虑场地分类和未考虑场地分类情况下的最优拟合公式和适应范围，并对推荐模型进行了可靠性验证，对粉质粘土和粉砂进行了地区差异性分析。
（2）可靠性验证结果表明：本文剪切波速预测值与实测值相对误差均在20%以内，最小相对误差仅为0.02%，超90%的预测剪切波速相对误差在10%以内，具有较合理的可靠性。
（3）地区差异性分析结果表明：地区、岩土类型和预测深度均会对剪切波速预测模型的可靠性产生显著影响，故当地区无剪切波速资料时，应优先选用本地区统计模型，如若未有，则需选取已有资料，对选用模型进行岩土类型和适应预测深度范围验证，以保证所选模型的可靠性。
（4）预测模型回归分析结果表明：同一地区，场地分类并不一定提高经验模型的预测精度。受岩土类型和预测深度的影响，考虑场地分类因素能否在实际工程中提高预测精度也具有不确定性。
因本文统计模型未考虑土体的物理状态，所以仅适用于未确定土体物理状态的不利情况，需加强深入研究。
-
图 1 强震动记录的震级-震中距分布
Figure 1. The magnitude v.s. epic-center distance of strong ground motion records used in this study
图 4 ASB14计算峰值加速度与实际强震动记录的残差随震级和距离的分布
Figure 4. The distribution of residuals between peak ground acceleration calculated using ASB14 and recorded against magnitude and distance
图 5 SCEMY97计算峰值加速度与实际强震动记录的残差随距离和震级的分布
Figure 5. The distribution of residuals between peak ground acceleration calculated using SCEMY97 and recorded against magnitude and distance
图 6 LLCS11计算峰值加速度与实际强震动记录的残差随距离和震级的分布
Figure 6. The distribution of residuals between peak ground acceleration calculated using LLCS11 and recorded against magnitude and distance
表 1 地震事件基本信息
Table 1. Basic information of earthquake events
事件编号 地震时间 纬度/°N 经度/°E 矩震级MW 1 2012年3月9日6:50 39.4 81.3 5.9 2 2012年9月7日11:19 27.5 104 5.6 3 2013年1月18日20:42 31 99.4 5.6 4 2013年3月3日13:41 25.9 99.7 5.4 5 2013年3月11日11:01 40.2 77.5 5.2 6 2013年3月29日13:01 43.4 86.8 5.4 7 2013年4月17日9:45 26.9 99.8 5.3 8 2013年4月20日8:02 30.3 103 6.6 9 2013年7月22日7:45 34.5 104.2 6.0 10 2013年8月30日13:27 43.8 87.6 5.3 11 2013年9月20日5:37 37.7 101.5 5.1 12 2014年5月24日4:49 25 97.8 5.7 13 2014年5月30日9:20 25 97.8 5.9 14 2014年7月9日5:52 39.3 78.3 5.0 15 2014年8月3日16:30 27.1 103.3 6.2 16 2014年8月17日6:07 28.1 103.5 5.1 17 2014年10月2日23:56 36.4 97.8 5.2 18 2014年10月7日21:49 23.4 100.5 6.1 19 2014年11月22日16:55 30.26 101.69 6.1 20 2014年11月25日23:19 30.18 101.73 5.7 21 2014年12月6日2:43 23.31 100.5 5.6 22 2014年12月6日18:20 23.31 100.5 5.5 23 2015年1月10日13:21 40.2 77.3 5.1 24 2015年3月1日18:24 23.5 98.9 5.3 25 2015年4月15日15:39 39.8 106.3 5.5 26 2015年7月3日9:07 37.6 78.2 6.4 27 2015年10月26日17:09 36.5 70.8 7.5 28 2015年11月23日5:02 38 100.4 5.2 29 2015年12月7日15:50 38.2 72.9 7.2 30 2016年1月14日5:18 42.19 84.12 5.1 31 2016年1月21日1:13 37.71 101.7 5.9 32 2016年5月18日0:48 26.1 99.53 5.0 33 2016年6月26日16:17 39.43 73.4 6.4 34 2016年9月23日1:23 30.1 99.61 5.2 35 2016年11月25日22:24 39.27 74.04 6.6 36 2016年12月8日13:15 43.83 86.35 6.0 37 2017年3月27日7:55 25.89 99.8 5.1 38 2017年6月3日18:11 37.99 103.56 5 39 2017年8月8日21:19 33.2 103.82 6.5 40 2017年8月9日7:27 44.27 82.89 6.5 41 2017年9月16日18:11 42.11 83.43 5.5 42 2017年9月30日14:14 32.27 105 5.1 
下载: 导出CSV
表 2 所用地震动峰值加速度衰减关系及相关参数
Table 2. Peak acceleration attenuation relations and their parameters adopted in this study
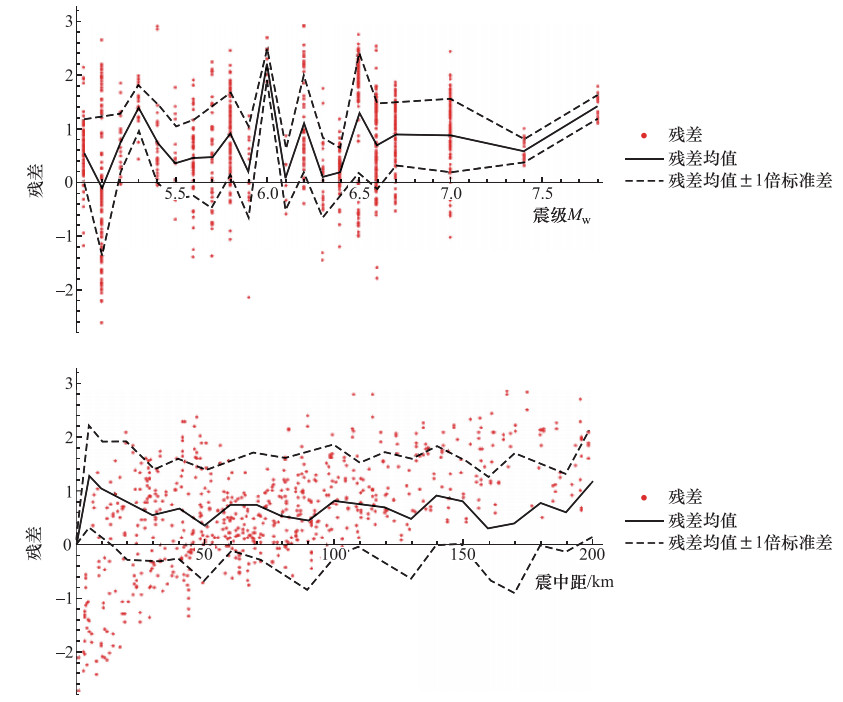
衰减关系编号 地区 震级MW 震中距/km 参数 ASB14(Akkar等，2014) 泛欧和中东 4.0—7.6 ＜200 RJB，Repi，Rhyp，MW，VS30，FN，FR SCEMY97(Sadigh等，1997) 美国西部 3.8—7.4 ＜200 Rrup(Repi)，MW，FN，FS LLCS11(Lin等，2011) 中国台湾 3.5—7.6 ＜240 Rrup(Repi)，MW
下载: 导出CSV
表 3 残差与震级、距离的相关系数
Table 3. Residual-magnitude and residual-distance correlation coefficients
衰减关系编号 残差与震级的相关系数 残差与距离的相关系数 ASB14 -0.121235 0.495025 SCEMY97 0.138204 0.64689 LLCS11 0.0942092 0.582699
下载: 导出CSV
-
姜治军, 2017.强震动台站的场地VS30估计及场地放大系数模型研究.哈尔滨: 中国地震局工程力学研究所. 司宏俊, 纐缬一起, 三宅弘惠等, 2014.基于基岩衰减公式的汶川·芦山地震强震动评价.地震工程与工程振动, 34(4):93-100. http://d.old.wanfangdata.com.cn/Conference/8421966 王继, 俞言祥, 龚飞等, 2008.中国西部地震动衰减关系的适用性分析——以部分新疆地震为例.中国地震, 24(2):126-133. doi: 10.3969/j.issn.1001-4683.2008.02.004 喻畑, 李小军, 2015.四川、甘肃地区VS30经验估计研究.地震工程学报, 37(2):525-533. doi: 10.3969/j.issn.1000-0844.2015.02.0525 袁一凡, 田启文, 2012.工程地震学.北京:地震出版社. Akkar S., Sandıkkaya M. A., Bommer J. J., 2014. Empirical ground-motion models for point- and extended-source crustal earthquake scenarios in Europe and the Middle East. Bulletin of Earthquake Engineering, 12(1):359-387. doi: 10.1007/s10518-013-9461-4 Campbell K. W., 2016. Comprehensive comparison among the Campbell-Bozorgnia NGA-West2 GMPE and three GMPEs from Europe and the Middle East. Bulletin of the Seismological Society of America, 106(5):2081-2103. doi: 10.1785/0120160024 Dangkua D. T., Rong Y. F., Harold M., 2018. Evaluation of NGA-West2 and Chinese Ground-motion prediction equations for developing seismic hazard maps of Mainland China. Bulletin of the Seismological Society of America, 108(5A):2422-2443. doi: 10.1785/0120170186 Douglas J., 2003. Earthquake ground motion estimation using strong-motion records:a review of equations for the estimation of peak ground acceleration and response spectral ordinates. Earth-Science Reviews, 61(1-2):43-104. doi: 10.1016/S0012-8252(02)00112-5 Dziewonski A. M., Chou T. A., Woodhouse J. H., 1981. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. Journal of Geophysical Research:Solid Earth, 86(B4):2825-2852. doi: 10.1029/JB086iB04p02825 Ekström G., Nettles M., Dziewoński A. M., 2012. The global CMT project 2004-2010:Centroid-moment tensors for 13, 017 earthquakes. Physics of the Earth and Planetary Interiors, 200-201:1-9. doi: 10.1016/j.pepi.2012.04.002 Lin P. S., Lee C. T., Cheng C. T., et al., 2011. Response spectral attenuation relations for shallow crustal earthquakes in Taiwan. Engineering Geology, 121(3-4):150-164. doi: 10.1016/j.enggeo.2011.04.019 Sadigh K., Chang C. Y., Egan J. A., et al., 1997. Attenuation relationships for shallow crustal earthquakes based on California strong motion data. Seismological Research Letters, 68(1):180-189. doi: 10.1785/gssrl.68.1.180 Zafarani H., Farhadi A., 2017. Testing ground-motion prediction equations against small-to-moderate magnitude data in Iran. Bulletin of the Seismological Society of America, 107(2):912-933. doi: 10.1785/0120160046 期刊类型引用(13)
1. 卢大伟，孙逸涵，刘红帅. 常规土类剪切波速与埋深经验公式的可靠性评价. 吉林大学学报(地球科学版). 2024(02): 546-557 . 
百度学术2. 易文星，李安，雷生学，郭长辉，原浩东. 天津市平原地区土层剪切波速与埋深间的关系. 华南地震. 2024(01): 52-62 . 百度学术3. 余松，吴建超，蔡永建，雷东宁，胡庆，杨钢. 湖北襄阳地区土体剪切波波速与深度的相关性研究. 大地测量与地球动力学. 2024(06): 618-623+629 . 百度学术4. 郭浩天，赵鑫竹，李向群. 长春市某建筑场地地质勘察及剪切波速特征研究. 路基工程. 2024(03): 8-14 . 百度学术5. 李志恒，谢俊举，李柯苇，温增平，李小军，王志才，许洪泰，赵晓芬，张娜. 山东地区场地剪切波速经验外推模型及其适用性. 地震地质. 2024(04): 934-954 . 百度学术6. 姚姜森，王珏，李圣，刘昌伟，宋晓春，陆斌斌. 昆明盆地常规土类剪切波速与埋深的关系研究. 华南地震. 2024(03): 40-50 . 百度学术7. 王金艳，陶小三，王琛，邵斌，徐烨. 盐城市城区土层剪切波速与土层深度相关性分析. 防灾减灾工程学报. 2024(05): 1193-1201 . 百度学术8. 孙洪新，左鹏. 地震剪切波速度测试在岩土工程勘察中的应用. 工程机械与维修. 2023(02): 105-107 . 百度学术9. 叶迎晨. 深厚覆盖层地区土层地震反应的不确定性分析. 地震科学进展. 2023(05): 193-202 . 百度学术10. 李敏，钟伟. 社区防震减灾工作指南建设探讨. 地震科学进展. 2023(12): 581-588 . 百度学术11. 李小军，任朋亮，王玉石，李再先，钟康明，董青. 不同形状三维凹陷地形场地对地震动影响比较分析. 岩土力学. 2023(11): 3327-3338 . 百度学术12. 张金欢，杨靖，夏雨波，田冀，苏玲，刘继东. 唐山市规划区土体剪切波速与深度的相关性分析. 科技和产业. 2023(22): 148-153 . 百度学术13. 蔡润，彭涛，罗东林，周亚东，尹欣欣，郭鹏，彭界超. 成都地区土层剪切波速与埋深的关系. 地震研究. 2022(03): 498-508 . 百度学术其他类型引用(1)
-
下载:
点击查看大图
计量
- 文章访问数: 162
- HTML全文浏览量: 41
- PDF下载量: 31
- 被引次数: 14
