An Improved Approach for Near-fault Pulse-like Ground Motion Simulation
-
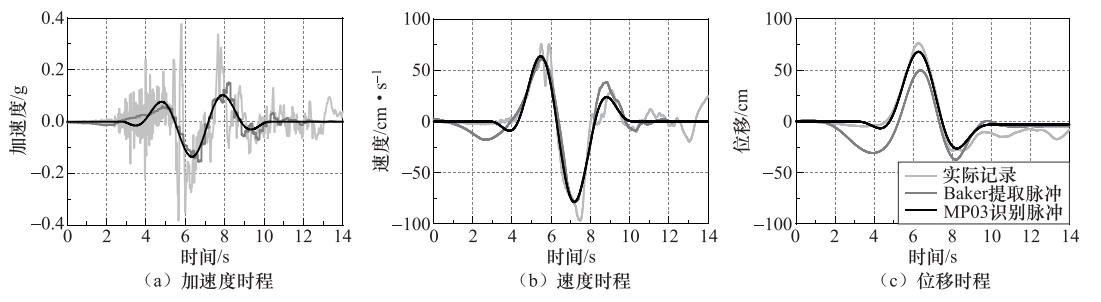
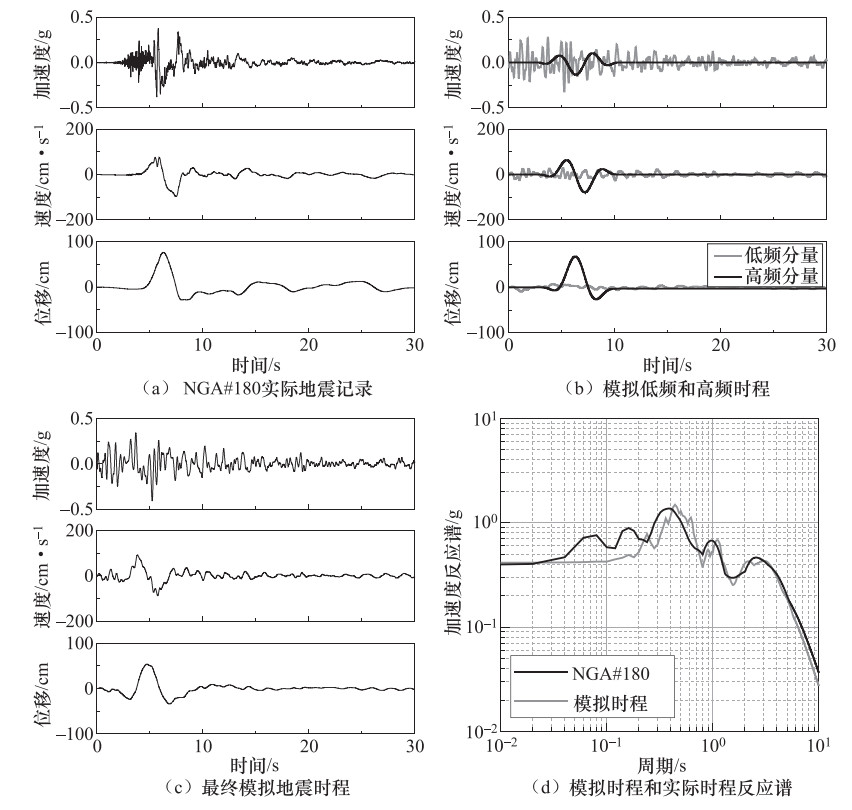
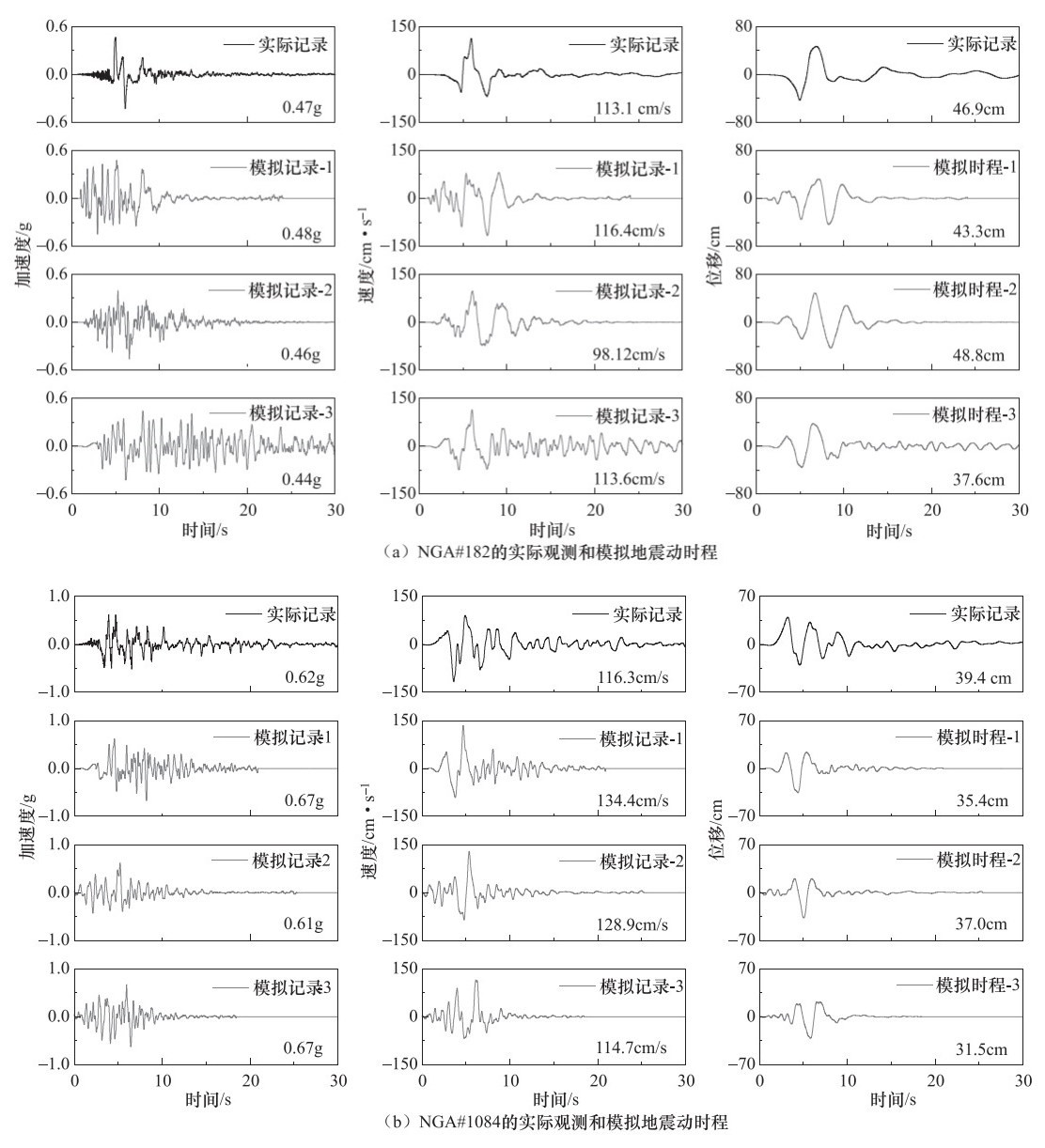
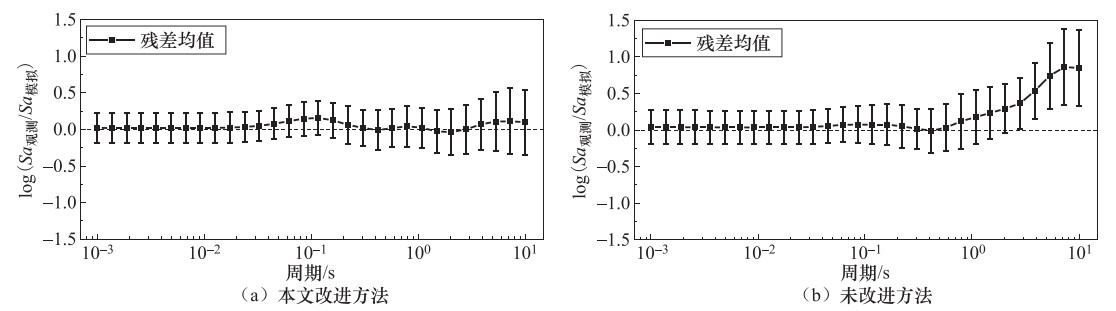
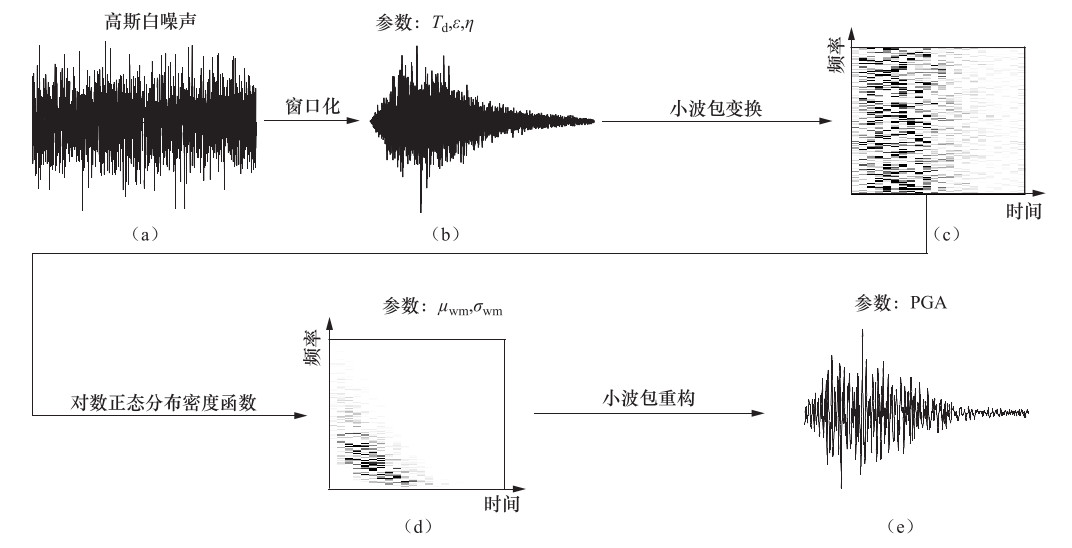
摘要: 本文基于小波包技术的随机地震动模拟方法，提出一种改进的参数化随机近断层脉冲型地震动模拟方法。然后，通过识别和提取近断层脉冲型地震动数据库中脉冲型地震动的特征参数，建立了基于震源、传播路径和场地特征等参数的脉冲模型参数预测方程。最后，通过模拟实际记录和误差分析检验了改进的模拟方法的有效性。结果表明：应用改进的模拟方法得到的地震动时程无论在波形、频率特性还是峰值上均与实际记录具有较好的一致性。改进的模拟方法在保留地震动时频非平稳性的基础上，能够有效地提高近断层脉冲型地震动的模拟效果，并且能够很好地体现脉冲型地震动的主要特征。Abstract: In this paper, an improved parameterized stochastic simulation method of near-fault pulse-like ground motion is proposed based on the stochastic ground motion simulation method using the wavelet packet method. Then, by identifying and extracting the characteristic parameters of pulse-like ground motions in a set near-fault ground motions database, the prediction equation of pulse model parameters in terms of the earthquake source, path and site characteristic parameters is established. Finally, the improved simulation method is verified by simulating recorded pulse-like ground motions and error analysis. Our results illustrate that simulated time histories of pulse-like ground motions by improved simulation method is well consistent with the recorded one in terms of waveform, frequency characteristic and peak value. The improved simulation method can effectively improve the simulation results of near-fault ground motion under retain time-frequency nonstationary of ground motion, and can also well reflect the main characteristics of pulse-like ground motion, which has very important engineering application value.
-
引言
地震动衰减关系是表征地震动参数随震级、距离和场地等因素变化规律的函数。地震动衰减关系作为工程地震学中最常用的估计或预测地震动的方法，被广泛用于工程地震学领域，包括地震危险性分析、地震区划、地震小区划和设计地震动确定等多方面(袁一凡等，2012)。地震动衰减关系通常采用相对固定的函数形式，大致由震源影响函数、距离影响函数、场地影响函数和修正项4个部分构成。衰减关系的系数值一般利用大量强震动记录资料统计确定。每个地区的地震构造环境、地壳介质以及地表和近地表局部场地条件等因素具有很大的差异性，因此，地震动衰减关系具有很强的地区性。欧洲(Akkar等，2014)、美国(Sadigh等，1997)、中国台湾(Lin等，2011)等国家和地区都获得基于强震动记录的适用于相应地区的地震动衰减关系。
何种地震动衰减关系更为适合1个特定的地区始终是研究的热点。Campbell(2016)利用NGA-West2中的数据，研究了3个针对欧洲和中东地区的地区性衰减关系和1个NGA衰减关系，分别比较了地震动衰减关系的预测中值和标准偏差，并进行了残差分析。认为Campbell-Bozorgnia衰减关系在更具有工程实用价值的大震和近场上优于另外3个衰减关系。Zafarani等(2017)为了找到更适合伊朗高原的小震和中震的地震动预测方程(GMPE)，使用3种不同的统计学方法，对8个GMPE进行了比较，其中只有Zafarani于2015年提出的衰减关系在全部的频率范围内均与数据较吻合。
虽然中国有很长的历史地震记载，但已获取强震动记录的地震事件不多，总体的强震动记录资料较少。因此，长久以来中国研究地震影响的分布往往采用烈度衰减关系。然而，地震烈度的空间分布虽然也能体现地震动强度的空间变化，反映其衰减特征，但它并非能直接反映地震动特性的相关物理量，甚至可能受到一些主观因素的干扰。经过多年来的发展，目前中国已经积累了一定量的强震动加速度记录，这或将使得我们有可能直接建立地震动加速度衰减关系(王继等，2008)。此外，也可以使用中国的强震动加速度记录，与目前国际上已有的衰减关系进行比较，找出其中较为适用的衰减关系，并进而研究对已有衰减关系进行修正处理的方法。司宏俊等(2014)比较了汶川地震和芦山地震中基岩和土层场地观测台站得到的加速度反应谱和基于日本强震动观测数据得出的基岩加速度反应谱衰减关系，发现两者有着相似的衰减特征，并通过拟合强震动记录加速度反应谱及其与衰减关系的残差，分析得到汶川地震和芦山地震的地震动记录台站的场地影响，与日本衰减关系中平均场地参数比较接近，VS30约为500m/s。Dangkua等(2018)考察了NGA-West2项目给出的地震动衰减关系对于中国地区的适用性，认为NGA-West2中的衰减关系对短周期地震动适用性较好，但在长周期范围结果偏高；此外，还利用对数最大似然法，为这些衰减关系分配了权重。
在地震动衰减关系中，峰值加速度(PGA)是主要被考虑的参数。地震动峰值加速度是指在一次特定地震事件中取得的1条加速度记录的绝对最大值，常被用于描述地震动的强度以及对结构反应的影响程度。虽然峰值加速度并非能完全控制结构反应的地震动参数，特别是对于较长自振周期的结构，但因为其是强震动记录中最容易取得的参数，且结构抗震设计规范中多采用标准形式的地震动反应谱与峰值加速度结合使用，因此，人们在进行衰减关系的研究时仍然十分关心且首先关注峰值加速度(Douglas，2003)。
1. 数据来源与分析
1.1 强震动记录
在地震动衰减关系研究中，为了关注有显著工程意义的地震动记录，同时也为了减小独立变量的误差，可以选取MW＞5地震的地震动记录进行研究(Douglas，2003)。因此，本文采用中国西部地区2012年3月9日—2017年9月16日间发生的42次MW＞5地震事件中共916条有效水平方向强震动记录(峰值加速度绝对值超过10gal)。震中位置和发震时间来自地震简报，震源机制和震级参考GCMT(Dziewonski等，1981；Ekström等，2012)，详细情况如表 1所示。研究中涉及的地震事件和地震台站的位置分别见图 2、图 3。
表 1 地震事件基本信息Table 1. Basic information of earthquake events事件编号 地震时间 纬度/°N 经度/°E 矩震级MW 1 2012年3月9日6:50 39.4 81.3 5.9 2 2012年9月7日11:19 27.5 104 5.6 3 2013年1月18日20:42 31 99.4 5.6 4 2013年3月3日13:41 25.9 99.7 5.4 5 2013年3月11日11:01 40.2 77.5 5.2 6 2013年3月29日13:01 43.4 86.8 5.4 7 2013年4月17日9:45 26.9 99.8 5.3 8 2013年4月20日8:02 30.3 103 6.6 9 2013年7月22日7:45 34.5 104.2 6.0 10 2013年8月30日13:27 43.8 87.6 5.3 11 2013年9月20日5:37 37.7 101.5 5.1 12 2014年5月24日4:49 25 97.8 5.7 13 2014年5月30日9:20 25 97.8 5.9 14 2014年7月9日5:52 39.3 78.3 5.0 15 2014年8月3日16:30 27.1 103.3 6.2 16 2014年8月17日6:07 28.1 103.5 5.1 17 2014年10月2日23:56 36.4 97.8 5.2 18 2014年10月7日21:49 23.4 100.5 6.1 19 2014年11月22日16:55 30.26 101.69 6.1 20 2014年11月25日23:19 30.18 101.73 5.7 21 2014年12月6日2:43 23.31 100.5 5.6 22 2014年12月6日18:20 23.31 100.5 5.5 23 2015年1月10日13:21 40.2 77.3 5.1 24 2015年3月1日18:24 23.5 98.9 5.3 25 2015年4月15日15:39 39.8 106.3 5.5 26 2015年7月3日9:07 37.6 78.2 6.4 27 2015年10月26日17:09 36.5 70.8 7.5 28 2015年11月23日5:02 38 100.4 5.2 29 2015年12月7日15:50 38.2 72.9 7.2 30 2016年1月14日5:18 42.19 84.12 5.1 31 2016年1月21日1:13 37.71 101.7 5.9 32 2016年5月18日0:48 26.1 99.53 5.0 33 2016年6月26日16:17 39.43 73.4 6.4 34 2016年9月23日1:23 30.1 99.61 5.2 35 2016年11月25日22:24 39.27 74.04 6.6 36 2016年12月8日13:15 43.83 86.35 6.0 37 2017年3月27日7:55 25.89 99.8 5.1 38 2017年6月3日18:11 37.99 103.56 5 39 2017年8月8日21:19 33.2 103.82 6.5 40 2017年8月9日7:27 44.27 82.89 6.5 41 2017年9月16日18:11 42.11 83.43 5.5 42 2017年9月30日14:14 32.27 105 5.1 1.2 观测台站场地VS30值的确定
VS30即场地地下30m深度内岩土层的平均剪切波速，是用于表征场地条件的重要物理参数。研究中涉及的强震动观测台站，其VS30值需要借助于已有的研究成果确定。因此，本文多数观测台站的VS30值采用了姜治军(2017)和俞畑等(2015)的研究成果，而对于已有研究成果中没有涉及的台站，其VS30值借助100km范围内最近台站的VS30或同类场地的VS30均值进行近似处理来确定。此外，本次研究还利用观测场地的VS30值对观测台站的场地类型进行划分。传统上将VS30=750m/s的场地作为基岩场地和土层场地的分界波速值，但因为VS30＞750m/s的台站十分缺乏，为此，本文以VS30=360m/s将场地划分两类，一类包括基岩和硬土场地，另一类包括中硬土和软土场地。这一场地分类处理与Sadigh等(1997)的做法一致。
文中选择的强震动记录大部分来自基岩和硬土场地，仅有少部分数据来自中硬土和软土场地(图 1)。
图 1 强震动记录的震级-震中距分布Figure 1. The magnitude v.s. epic-center distance of strong ground motion records used in this study2. 地震动峰值加速度衰减关系的比较
2.1 地震动衰减关系的选择
选择来自欧洲(Akkar等，2014)、美国(Sadigh等，1997)和中国台湾(Lin等，2011)的3个较有代表性的地区性地震动衰减关系。这些衰减关系的建立均未利用中国西部地区的强震动记录数据，在确定衰减关系系数时，是以当地的强震动记录数据为主，并加入其它地区发生的大地震的强震动记录进行补充。选择的衰减关系均采用浅层地壳地震的强震动记录进行推导，与本文采用的中国西部地区强震动记录的地震具有可比性。所选地震动衰减关系的具体情况见表 2。
表 2 所用地震动峰值加速度衰减关系及相关参数Table 2. Peak acceleration attenuation relations and their parameters adopted in this study衰减关系编号 地区 震级MW 震中距/km 参数 ASB14(Akkar等，2014) 泛欧和中东 4.0—7.6 ＜200 RJB，Repi，Rhyp，MW，VS30，FN，FR SCEMY97(Sadigh等，1997) 美国西部 3.8—7.4 ＜200 Rrup(Repi)，MW，FN，FS LLCS11(Lin等，2011) 中国台湾 3.5—7.6 ＜240 Rrup(Repi)，MW 表 2中，RJB为Joyner-Boore距离，Rhyp为震源距，Repi为震中距，Rrup为台站到破裂平面的距离(震级不太大时可近似为Repi)，MW为矩震级，VS30为30m处剪切波速，FN、FR和FS分别为正断层、逆冲断层和走滑断层的指标，一般为0；当且仅当震源机制为正断层时，FN=1；当且仅当震源机制为逆冲时，FR=1；当且仅当震源机制为走滑时，FS=1。
针对本文所用的地震动峰值加速度衰减关系的震级与震中距的适用范围，进一步将所采用的地震动记录限制在震级MW 5.0—7.5、震中距小于200km范围内，即只利用了震中距小于200km范围内的地震动记录，而不考虑震中距更大的那些地震动记录。
衰减关系LLCS11还考虑了断层上、下盘效应对地震动的影响，并分别为上、下盘给出了不同的系数。考虑到当地的地震构造背景，这种划分也许是有益的。但是，因为本文获得的地震动数据难以区分断层上、下盘，故本文将LLCS11中同种场地的上、下盘取平均使用。
本文采用的3个地震动衰减关系的峰值加速度衰减计算公式如下(峰值加速度单位为g)。
2.1.1 衰减关系ASB14
$$ \text{ln}(Y)=\text{ln}[{{Y}_{\text{REF}}}({{M}_{w}}, R, SoF)]+\text{ln}[S({{V}_{S30}}\text{, PG}{{\text{A}}_{\text{REF}}})]+\varepsilon \sigma $$ (1) $$ {\rm{ln}}({Y_{{\rm{REF}}}}) = \\ \left\{ \begin{array}{l} {a_1} + {a_2}({M_{\rm{W}}} - {c_1}) + {a_3}{(8.5 - {M_{\rm{W}}})^2} + [{a_4} + {a_5}({M_{\rm{W}}} - {c_1})]\ln (\sqrt {{R^2} + a_6^2}) + {a_8}{F_N} + {a_9}{F_R}, {M_{\rm{W}}} \le {c_{\rm{1}}}\\ {a_1} + {a_7}({M_{\rm{W}}} - {c_1}) + {a_3}{(8.5 - {M_{\rm{W}}})^2} + [{a_4} + {a_5}({M_{\rm{W}}} - {c_1})]\ln (\sqrt {{R^2} + a_6^2}) + {a_8}{F_N} + {a_9}{F_R}, {M_{\rm{W}}}{c_{\rm{1}}} \end{array} \right. $$ (2) $$ \ln \left( S \right) = \left\{ \begin{array}{l} {b_1}\ln \left( {{V_{{\rm{S}}30}}/{V_{{\rm{REF}}}}} \right) + {b_2}\ln \left[ {\frac{{{\rm{PG}}{{\rm{A}}_{{\rm{REF}}}} + c{{\left( {{V_{{\rm{S}}30}}/{V_{{\rm{REF}}}}} \right)}^n}}}{{\left( {{\rm{PG}}{{\rm{A}}_{{\rm{REF}}}} + c} \right){{\left( {{V_{{\rm{S}}30}}/{V_{{\rm{REF}}}}} \right)}^n}}}} \right],{V_{{\rm{S30}}}} \le {V_{{\rm{REF}}}}\\ {b_1}{\rm{ln}}\left[ {\frac{{{\rm{min}}\left( {{V_{{\rm{S}}30}},{V_{{\rm{CON}}}}} \right)}}{{{V_{{\rm{REF}}}}}}} \right],{V_{{\rm{S}}30}} > {V_{{\rm{REF}}}} \end{array} \right. $$ (3) 其中，PGAREF和VS30REF为参考场地的峰值地震动和VS30，参考场地的VS30为750m/s。YREF表示由衰减关系计算的参考场地的地震动变量，当计算参考场地的峰值地震动时，YREF=PGAREF。各系数取值为a1=2.52977，a2=0.0029，a3=-0.05496，a4=-1.31001，a5=0.2529，a6=7.5，a7=-0.5096，a8=-0.1091，a9=0.937，b1=-0.41997，b2=-0.28846，c=2.5，c1=6.75，n=3.2。
2.1.2 衰减关系SCEMY97
对于基岩场地：
$$ {\rm{ln}}(y) = {C_1} + {C_2}M + {C_3}{(8.5M)^{2.5}} + {C_4}\ln ({R_{rup}} + \exp ({C_5} + {C_6}M)) + {C_7}\ln ({R_{rup}} + 2) $$ (4) 其中，MW≤6.5：C1=-0.524，C2=1.0，C3=0.000，C4=-2.100，C5=1.29649，C6=0.250，C7=0.0；MW＞6.5：C1=-1.274，C2=1.1，C3=0.000，C4=-2.100，C5=-0.48451，C6=0.524，C7=0.0。
对于土层场地：
$$ {\rm{ln}}(y) = {C_1} + {C_2}M - {C_3}\ln ({R_{rup}} + {C_4}{e^{{C_5}M}}) + {C_6} + {C_7}{(8.5 - M)^{2.5}} $$ (5) 其中，对于走滑型地震，C1=-2.17；对于正断层地震和逆冲型地震，C1=-1.92；当MW≤6.5，C4=2.1861，C5=0.32；当MW＞6.5，C4=0.3825，C5=0.5882；C2=1.0，C3=1.70，C6=0.0，C7=0.0。
2.1.3 衰减关系LLCS11
对于基岩场地：
$$ \left\{ \begin{array}{l} {\rm{ln}}({\rm{PGA}}) = - 3.279 + 1.035M - 1.651\ln (R + 0.152{e^{0.623M}}), 上盘\\ {\rm{ln}}({\rm{PGA}}) = - 3.232 + 1.047M - 1.662\ln (R + 0.192{e^{0.630M}}), 下盘 \end{array} \right. $$ (6) 对于土层场地：
$$ \left\{ \begin{array}{l} {\rm{ln}}({\rm{PGA}}) = - 3.248 + 0.943M - 1.471\ln (R + 0.100{e^{0.648M}}), 上盘\\ {\rm{ln}}({\rm{PGA}}) = - 3.218 + 0.935M - 1.464\ln (R + 0.125{e^{0.650M}}), 下盘 \end{array} \right. $$ (7) 2.2 峰值加速度衰减关系计算值与实际记录比较
分别根据上述3个衰减关系公式计算峰值加速度，并与实际强震动记录中的峰值加速度进行比较，计算残差(R)。同时计算了残差在不同震中距和震级上的标准偏差(σ)，得到了残差随距离与震级的分布图像(图 4、图 5和图 6)。本文残差为实际记录中的峰值加速度减去衰减关系计算值，标准偏差为方差的平方根。
图 4 ASB14计算峰值加速度与实际强震动记录的残差随震级和距离的分布Figure 4. The distribution of residuals between peak ground acceleration calculated using ASB14 and recorded against magnitude and distance
图 5 SCEMY97计算峰值加速度与实际强震动记录的残差随距离和震级的分布Figure 5. The distribution of residuals between peak ground acceleration calculated using SCEMY97 and recorded against magnitude and distance
图 6 LLCS11计算峰值加速度与实际强震动记录的残差随距离和震级的分布Figure 6. The distribution of residuals between peak ground acceleration calculated using LLCS11 and recorded against magnitude and distance由图 4、图 5和图 6可以看出，大多数数据点的残差虽然不为0，但均位于[R-σ，R+σ]范围内，且残差的标准偏差与震级、距离关系不大，说明可能存在与距离和震级无关的误差。
SCEMY97和LLCS11整体上存在正的残差，即根据这2个衰减关系计算得到的峰值加速度小于中国西部地区的强震动记录值。这种趋势随距离和震级基本不变，可能意味着2个衰减关系需要引入1个常数项进行修正。ASB14虽然也有整体为正的残差，但残差随距离增大而增大，说明该衰减关系需要引入1个随距离增大而增大的项进行修正。总体来说，ASB14的残差小于SCEMY97和LLCS11。
此外，分别计算了ASB14、SCEMY97和LLCS11的残差与震级、距离的相关系数(表 3)，发现SCEMY97和LLCS11的残差与距离成中等相关，两者之间可能有中等程度的线性关系。这意味着若要对这些衰减关系进行修改，可以尝试引入线性项。考虑到相关系数的特点，这种线性关系可能需要更多的观测记录才能确定。
表 3 残差与震级、距离的相关系数Table 3. Residual-magnitude and residual-distance correlation coefficients衰减关系编号 残差与震级的相关系数 残差与距离的相关系数 ASB14 -0.121235 0.495025 SCEMY97 0.138204 0.64689 LLCS11 0.0942092 0.582699 3. 结论
观察上述3个地震动衰减(ASB14、SCEMY97和LLCS11)的残差与震级的关系，可以发现在地震动峰值加速度衰减关系中，考虑震级的平方项有重要的意义。衰减关系中震级的平方项与高频地震动的震级饱和现象有关，而这一现象在震级较大时表现更为明显。因为实际工程中更应关注的是震级较大的地震，所以在建立地震动峰值加速度衰减关系时，应该尽量采用具有震级的平方项的形式。
此外，上述3个地震动衰减关系的残差关于距离均存在一定程度的偏离。观察残差关于距离的分布，发现若对ASB14进行常数项的修正，对SCEMY97和LLCS11进行距离的线性项和常数项的修正，可能会使3个地震动衰减关系更适合于中国西部地区。
对于中国西部强震动记录数据，ASB14的表现优于SCEMY97和LLCS11，如果直接利用国外的地震动衰减关系，ASB14更适合于中国西部地区。然而总体来看，无论是随着震级还是距离的变化，采用3个衰减关系预测中国西部地区的地震动将会明显低估地震动峰值加速度。因此，发展强震动观测以积累更多的强震动记录，并基于中国不同区域的强震动记录资料直接统计确定相应的地震动衰减关系，仍然是需要努力的目标。
-
图 1 基于小波包的地震动模拟方法流程
Figure 1. Procedures for simulating ground motions using wavelet packet method
图 3 1979年Imperial Valley地震NGA#180水平向脉冲地震动模拟过程
Figure 3. Simulation process of NGA#180 horizontal pulse-like ground motions from Imperial Valley earthquake in 1979
图 4 NGA#182和NGA#1084的实际观测和模拟地震动时程
Figure 4. Acceleration, velocity and displacement time histories of observed and simulated ground motions
图 5 NGA#182和NGA#1084的实际观测和模拟地震动的加速度反应谱（5%阻尼比）
Figure 5. Acceleration response spectra at 5% damping ratio of observed and simulated ground motions
图 6 脉冲地震数据库中实际观测记录与模拟时程的加速度反应谱的残差均值及±1倍标准差
Figure 6. Mean residual bias and the±one standard deviation of near-fault stations observed and simulated in the pulse-like ground motions database
表 1 拟合参数γ和υ的分布系数和限定条件
Table 1. Boundary condition and coefficient of marginal distributions fitted to parameters γ and υ
参数 单位 符合分布 选定下限 选定上限 合适的分布参数 均值 标准差 γ burr 2.0 3.0 α=2.49，c=21.80，k=4.20 2.3 0.14 υ π uniform 0 2 1.0 0.58 
下载: 导出CSV
表 2 MP03脉冲模型参数的回归系数和标准差
Table 2. Regression coefficients and standard deviations of the MP03 model parameters
参数 α0 α1 α2 β1 β2 β3 β4 β5 ϕ τ σ Vp 1.6784 1.6152 1.6643 0.2201 -0.3060 -0.3230 -0.1231 0.0054 0.132 0.108 0.330 Tp -0.2312 -0.1828 0.1677 0.1762 -0.1295 0.0043 0.261 0.136 0.294 t0 -0.8739 -0.7214 -0.4478 0.2708 0.0551 -0.0455 0.0028 0.285 0.089 0.308
下载: 导出CSV
-
樊剑, 涂家祥, 吕超等, 2008.采用时频滤波技术的近断层脉冲地震人工模拟.华中科技大学学报(自然科学版), 36(11):116-119. http://www.cnki.com.cn/Article/CJFDTotal-HZLG200811044.htm 李亚楠, 2016.工程用地震动模拟随机性方法研究.大连: 大连理工大学. http://cdmd.cnki.com.cn/Article/CDMD-10141-1016204382.htm 罗全波, 陈学良, 高孟潭等, 2018.近断层速度脉冲与震源机制的关系浅析.震灾防御技术, 13(3):646-661. http://zzfy.eq-j.cn/zzfyjs/ch/reader/view_abstract.aspx?flag=1&file_no=20180316&journal_id=zzfyjs 田玉基, 杨庆山, 卢明奇, 2007.近断层脉冲型地震动的模拟方法.地震学报, 29(1):77-84. http://d.old.wanfangdata.com.cn/Periodical/dizhen200701009 Atkinson G. M., Assatourians K., Boore D. M., et al., 2009. A guide to differences between stochastic point-source and stochastic finite-fault simulations. Bulletin of the Seismological Society of America, 99(6):3192-3201. doi: 10.1785/0120090058 Baker J. W., 2007. Quantitative classification of near-fault ground motions using wavelet analysis. Bulletin of the Seismological Society of America, 97(5):1486-1501. doi: 10.1785/0120060255 Beresnev I. A., Atkinson G. M., 1997. Modeling finite-fault radiation from the ωn spectrum. Bulletin of the Seismological Society of America, 87(1):67-84. Boore D. M., 1983. Stochastic simulation of high-frequency ground motions based on seismological models of the radiated spectra. Bulletin of the Seismological Society of America, 73(6A):1865-1894. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=0aecda90-ca1d-4056-aa8d-57610c62fdb5 Bray J. D., Rodriguez-Marek A., 2004. Characterization of forward-directivity ground motions in the near-fault region. Soil Dynamics and Earthquake Engineering, 24(11):815-828. doi: 10.1016/j.soildyn.2004.05.001 Campbell K. W., 2008. Hybrid empirical ground motion model for PGA and 5% damped linear elastic response spectra from shallow crustal earthquakes in stable continental regions: Example for eastern North America. In: Proceeding of the 14th World Conference Earthquake Engineering. Beijing, China: WCEE. Dabaghi M. N., 2014. Stochastic modeling and simulation of near-fault ground motions for performance-based earthquake engineering. Berkeley: University of California. https://escholarship.org/uc/item/8db18756 Dabaghi M., Der Kiureghian A., 2017. Stochastic model for simulation of near-fault ground motions. Earthquake Engineering & Structural Dynamics, 46(6):963-984. http://cn.bing.com/academic/profile?id=080c7eb3415d4053e615dc23bd911f6a&encoded=0&v=paper_preview&mkt=zh-cn Joyner W. B., Boore D. M., 1993. Methods for regression analysis of strong-motion data. Bulletin of the Seismological Society of America, 83(2):469-487. http://cn.bing.com/academic/profile?id=862575101d927d3d6b3b88e6526957a0&encoded=0&v=paper_preview&mkt=zh-cn Li Y. N., Wang G. X., 2016. An improved approach for nonstationary strong ground motion simulation. Pure and Applied Geophysics, 173(5):1607-1626. doi: 10.1007/s00024-015-1189-4 Mavroeidis G. P., Papageorgiou A. S., 2003. A mathematical representation of near-fault ground motions. Bulletin of the Seismological Society of America, 93(3):1099-1131. doi: 10.1785/0120020100 Motazedian D., Atkinson G. M., 2005. Stochastic finite-fault modeling based on a dynamic corner frequency. Bulletin of the Seismological Society of America, 95(3):995-1010. doi: 10.1785/0120030207 Somerville P. G., Smith N. F., Graves R. W., et al., 1997. Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity. Seismological Research Letters, 68(1):199-222. doi: 10.1785/gssrl.68.1.199 Yamamoto Y., Baker J. W., 2013. Stochastic model for earthquake ground motion using wavelet packets. Bulletin of the Seismological Society of America, 103(6):3044-3056. doi: 10.1785/0120120312 Yang D. X., Zhou J. L., 2015. A stochastic model and synthesis for near-fault impulsive ground motions. Earthquake Engineering & Structural Dynamics, 44(2):243-264. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=720a58f1cf843d0534c204535de9022c -
下载:
点击查看大图
计量
- 文章访问数: 184
- HTML全文浏览量: 27
- PDF下载量: 13
- 被引次数: 0
