Study on the Flexural Bearing Capacity of Partially Unbonded Reinforced Concrete Beams at Beam Ends
-
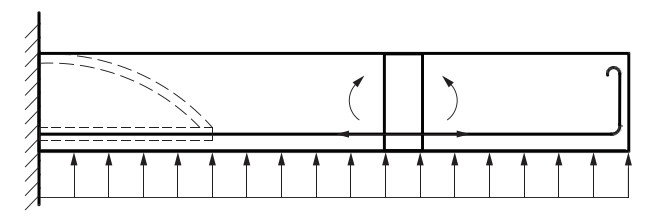
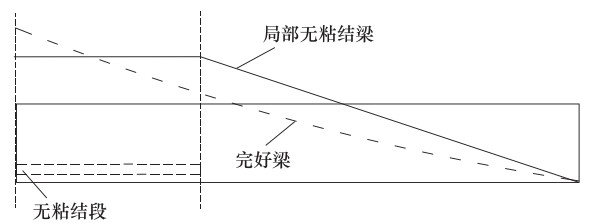
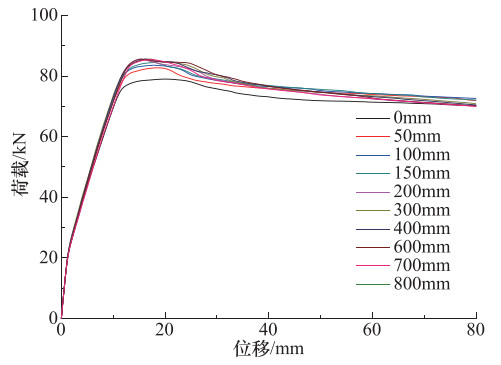
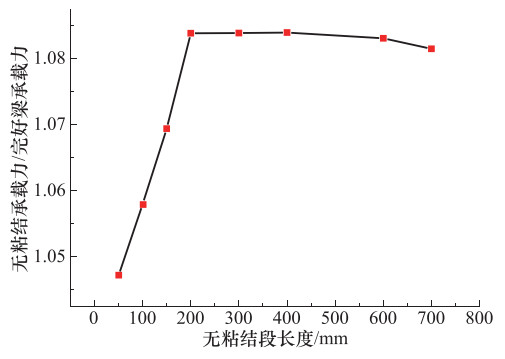
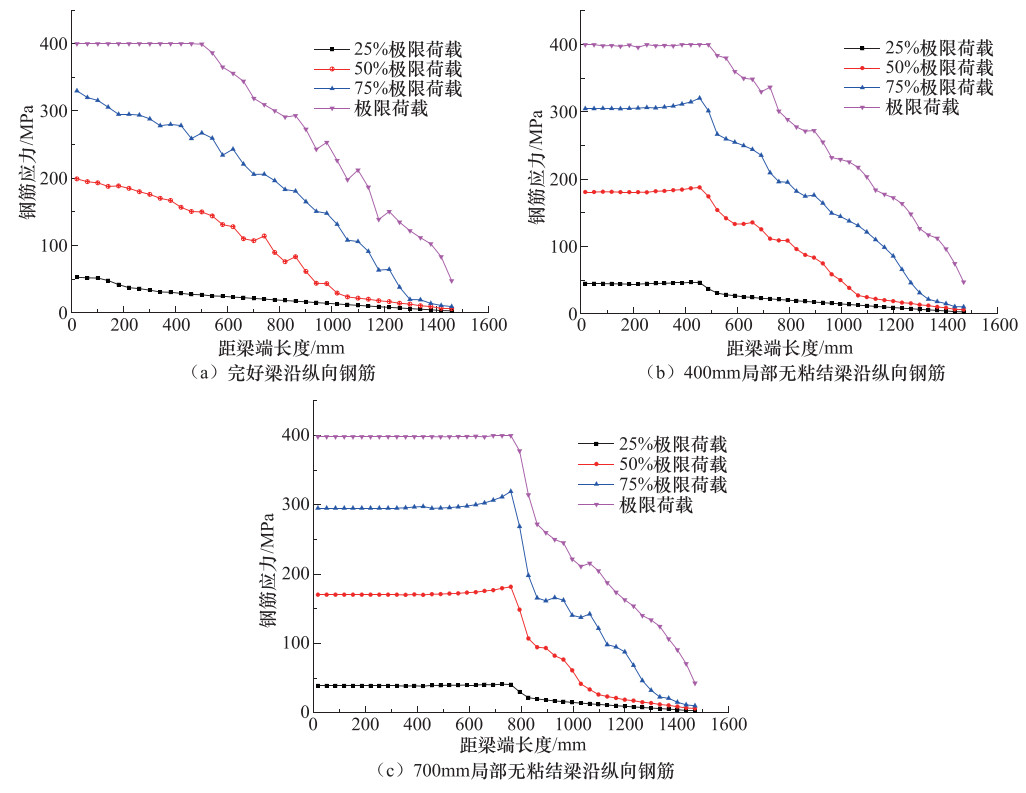
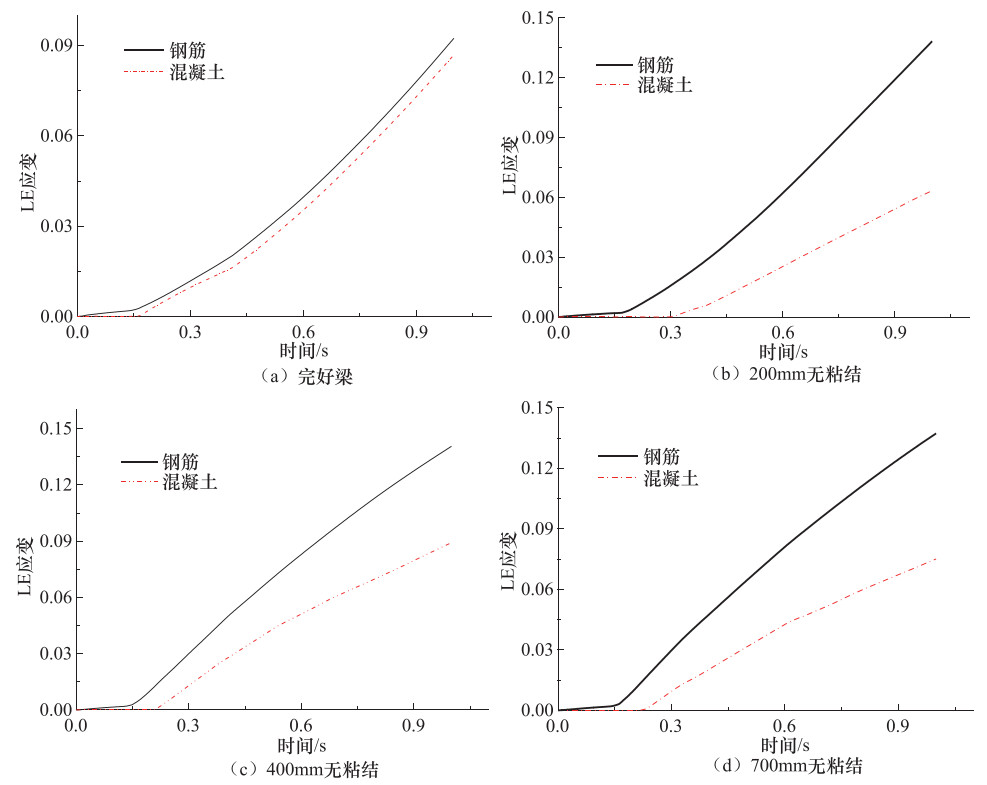
摘要: 为进一步研究梁端局部无粘结钢筋混凝土悬臂梁的抗弯承载力，在理论分析的基础上，使用ABAQUS有限元软件对局部无粘结梁与完好梁的承载力进行了仿真对比分析。结果表明，当局部无粘结梁与完好梁的配筋方式及材料力学性能一致、受拉纵筋锚固良好且可进入屈服阶段时，局部无粘结梁与完好梁的应变分布和应力历程有着明显的差异；局部无粘结梁的极限承载力高于完好梁；随着荷载的增加，无粘结梁的承载机理呈现出明显的“拱效应”。通过梁与拱的共同作用，建立了梁端局部无粘结钢筋混凝土梁抗弯承载力计算公式。Abstract: For the purpose of further studying the flexural capacity of partially unbonded RC cantilever beams at the end of beams, based on theoretical analysis, we used ABAQUS finite element software to simulate and to compare the bearing capacity of partially unbonded beams with that of intact beams. The results show that there exist obvious differences both in strain distribution and stress history between local unbonded beams and intact beams under the condition of that the reinforcement mode and material mechanical properties of local unbonded beams are the same as those of intact beams, and the anchorage of tensioned longitudinal bars is good and can enter the yield stage. We also found that the ultimate bearing capacity of local unbonded beams is slightly higher than that of intact beams. With the increase of load, the load-bearing mechanism of unbonded beams presents obvious "arch effect". Finally, through the interaction of beam and arch, the formulas for calculating the bending capacity of local unbonded reinforced concrete beams at the end of beams were established.
-
Key words:
- Reinforced concrete cantilever beam /
- Local unbond /
- Flexural capacity
-
图 2 梁端局部无粘结梁的受力特点示意图
Figure 2. Schematic diagram of the force characteristics of partially unbonded beam at the end of beam
图 3 受拉钢筋应力分布对比示意图
Figure 3. Schematic diagram of stress distribution in tension steel bar
图 6 局部无粘结钢筋混凝土梁有限元模型
Figure 6. Finite element model of partially unbonded reinforced concrete beams
图 8 不同无粘结段长度对承载力影响
Figure 8. Effect of different length of unbonded section on bearing capacity
图 9 完好梁和局部无粘结梁混凝土应变等值线
Figure 9. Strain contour map of intact beam and partially unbonded beam
图 12 钢筋与混凝土应变随加载时间变化关系
Figure 12. Relationship between strain of steel bar and concrete with loading time
表 1 数值模拟与试验结果对比
Table 1. Comparison between numerical simulation and experimental results
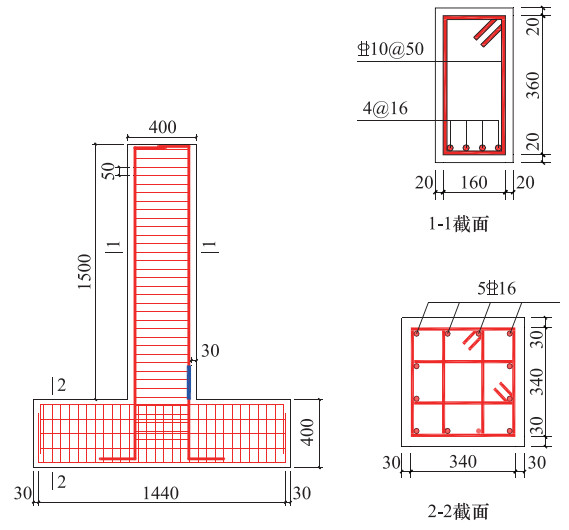
编号 受拉钢筋 配筋率 架立钢筋 无粘结长度/mm 极限荷载/kN 误差/% 试验结果 数值模拟 L-1A 2B10 0.73 2A6 0 30 29.55 1.50 L-1B 2B10 0.73 2A6 400 25 23.95 4.20 L-1C 2B10 0.73 2A6 800 24 24.25 1.04 L-1D 2B10 0.73 2A6 1400 26 24.73 4.88 L-2A 2B16 1.86 2A6 0 76 77.04 1.37 L-2B 2B16 1.86 2A6 400 70 69.18 1.17 L-2C 2B16 1.86 2A6 800 60 63.30 5.50 L-2D 2B16 1.86 2A6 1400 73 76.42 4.66 L-3A 2B20 2.91 2B8 0 101 98.72 2.28 L-3B 2B20 2.91 2B8 400 98 98.17 0.17 L-3C 2B20 2.91 2B8 800 100 89.69 10.31 L-3D 2B20 2.91 2B8 1400 79 75.13 4.90 均值 3.50 标准差 2.72 
下载: 导出CSV
表 2 混凝土本构模型参数
Table 2. Parameters of concrete constitutive model
参数 膨胀角/° 偏心率 初始等效双轴抗压屈服应力/初始单轴抗压屈服强度（${f_{b0}}/{f_{c0}}$） 受拉子午线与受压子午线常应力的比值K 粘性参数 取值 30 0.1 1.16 0.667 0.005
下载: 导出CSV
表 3 理论计算与姜新雨等（2018）试验结果对比
Table 3. Comparison between theoretical calculation and experimental results
无粘结段长度L/mm 理论计算弯矩/kN·m 试验弯矩/kN·m 计算弯矩/试验弯矩 400 119.93 126.85 0.945 200 118..82 120.22 0.988 0 109.69 112.00 0.979
下载: 导出CSV
表 4 本文计算公式与其它计算公式结果对比
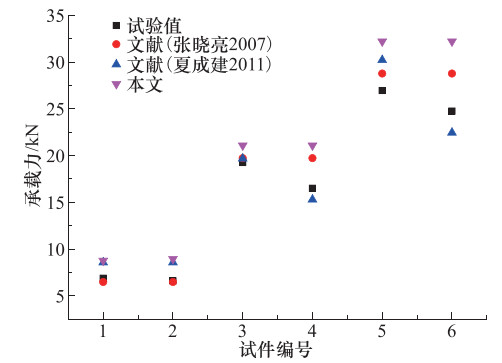
Table 4. Comparison of calculated results by the formulas in this paper to formulas by others
编号 试件 试验值 梁抗弯承载力计算结果 张晓亮等（2007）公式 夏成建（2011）公式 本文公式 1 L-1B 6.88 6.48 8.57 8.76 2 L-1C 6.60 6.48 8.57 5.69 3 L-2B 19.25 19.72 19.67 20.36 4 L-2C 16.50 19.72 15.29 17.84 5 L-3B 26.95 28.77 30.21 28.86 6 L-3C 24.75 28.77 22.45 28.29
下载: 导出CSV
-
曹双寅, 滕锦光, 陈建飞等, 2003.外贴纤维加固梁斜截面纤维应变分布的试验研究.土木工程学报, 36(11):6-11. http://d.old.wanfangdata.com.cn/Periodical/tmgcxb200311002 韩之江, 郭文龙, 韩颖异, 2016.粘贴钢板加固法试验研究分析.内蒙古公路与运输, (4):5-9. http://d.old.wanfangdata.com.cn/Periodical/nmgglyys201604002 姜新雨, 杨昌昆, 2018.纵筋局部无粘结RC梁受力性能研究.山西建筑, 44(6):51-52. doi: 10.3969/j.issn.1009-6825.2018.06.025 林旭川, 潘鹏, 叶列平等, 2009.汶川地震中典型RC框架结构的震害仿真与分析.土木工程学报, 42(5):13-20. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=tmgcxb200905002 刘九晏, 赵鹏, 赵娟等, 2017.全跨无粘结混凝土梁抗力性能仿真分析.水电能源科学, 35(1):145-148. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=sdnykx201701036 刘丽娜, 王伟超, 丁亚红, 2012.预应力加固法在土木工程中的研究应用.混凝土, (4):115-118. http://d.old.wanfangdata.com.cn/Periodical/hnt201204037 日本建筑学会, 1990.鉄筋コンクリート造建物の終局強度型耐震設計指針·同解説.日本建筑学会. 史庆轩, 王朋, 王秋维, 2013.桁架-拱模型用于钢筋混凝土梁的受剪承载力计算分析.土木建筑与环境工程, 35(4):7-12, 26. http://d.old.wanfangdata.com.cn/Periodical/cqjzdxxb201304002 王青, 徐港, 黄淳莹, 2008.锈蚀钢筋混凝土梁正截面承载力计算探讨.四川建筑科学研究, 34(2):101-103. doi: 10.3969/j.issn.1008-1933.2008.02.028 王庆霖, 池永亮, 牛荻涛, 2001.锈后无粘结钢筋混凝土梁的模拟试验与分析.建筑结构, 31(4):51-53, 63. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jzjg200104016 魏琏, 戴国莹, 1981.唐山地震作用下一座三层钢筋混凝土框架结构倒塌的分析.地震工程与工程振动, (1):34-40, 146. http://www.cnki.com.cn/Article/CJFD1981-DGGC198101004.htm 夏成建, 2011.局部粘结退化钢筋混凝土梁的抗弯承载力及变形分析.上海:上海交通大学. http://cdmd.cnki.com.cn/Article/CDMD-10248-1011268002.htm 张家广, 2015.防屈曲支撑加固钢筋混凝土框架抗震性能及设计方法.哈尔滨:哈尔滨工业大学. http://cdmd.cnki.com.cn/Article/CDMD-10213-1015957283.htm 中华人民共和国住房和城乡建设部, 2010.混凝土结构设计规范(GB 50010-2010).北京: 中国建筑工业出版社. 张晓亮, 陈晓晨, 宋晓冰, 2007.局部无粘结钢筋混凝土梁抗弯性能的试验研究.工业建筑, 37(S1):317-320, 446. http://d.old.wanfangdata.com.cn/Periodical/gyjz2007z1093 European Committee for Standardization, 2004. EN 1992-1-1 Eurocode 2: Design of concrete structures-Part 1-1: General rules and rules for building. Goitseone M., Mark A., Pilate M., 2010. Interaction between corrosion crack width and steel loss in RC beams corroded under load. Cement and Concrete Research, 40(9):1419-1428. doi: 10.1016/j.cemconres.2010.03.010 -
点击查看大图
计量
- 文章访问数: 123
- HTML全文浏览量: 16
- PDF下载量: 6
- 被引次数: 0
