Numerical Modeling Techniques of Rayleigh Wave Field and Its Application
-
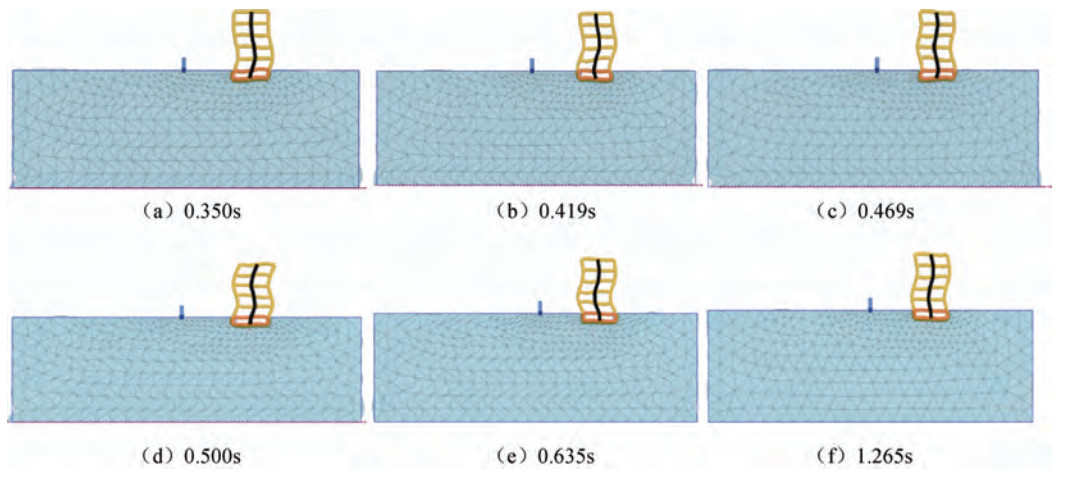
摘要: 本文总结了Rayleigh波场数值模拟的4种思路和各自特点，根据Lamb问题的理论分析成果提出了基于地表激振的Rayleigh波场数值模拟技术，论述了地表集中震源作用下引起地表波动场的特点及主要影响因素。在此基础上，利用Plaxis 2D有限元软件实现了Rayleigh波场的数值模拟，并结合算例验证了所提方法的可行性和结果的合理性。最后，针对多层建筑结构，研究了不同地震动输入模式下结构动力反应的特点。结果表明，Rayleigh波作用下结构的动力反应特性明显区别于在底部输入剪切波时的结果，不同地震动输入模式对结构的振动形态和破坏模式有着明显的影响。Abstract: Four different approaches about numerical modeling techniques of Rayleigh wave field were summarized. The techniques base on vertical harmonic point load on the free surface has been proposed in this paper. The main research achievements of Lamb issues, such as the characteristics of Rayleigh wave field under point load and its main influencing factors were discussed. On this basis the numerical modeling of Rayleigh wave field with Plaxis 2D was conducted and the effectiveness of the approach was verified with an example. The dynamic response of a multi-story building structure during propagation of Rayleigh wave was analyzed using the proposed method, and the results were compared to that from the traditional methods. Numerical analysis results show that different wave motion input methods have great effect on the dynamic response of building structures. The vibration shape and failure modes of the structure were greatly influenced by seismic input modes.
-
Key words:
- Rayleigh wave /
- Lamb issues /
- Plaxis 2D software /
- Numerical modeling /
- Wave motion input /
- Multi-story building
-
引言
关于场地地震反应的分析已有大量研究成果，研究表明土壤在地震作用下会表现出材料非线性效应ADDIN EN.CITE.DATA（Joyner等，1975；Huang等，2001；Arslan等，2006；Hosseini等，2012）。等效线性化方法ADDIN EN.CITE.DATA（Schnabel等，1972；Idriss等，1992；Bardet等，2000；王笃国等，2016）是一种频域方法，通过在不同土体应变条件下选择等效阻尼比和剪切模量，将非线性问题转化为线性问题。当采用材料非线性本构模型描述土体非线性时，需采用时间积分算法求解非线性动力有限元方程。时间积分算法可分为隐式方法和显式方法。隐式算法每时刻需求解线性代数方程组，计算效率相对较低，如Wilson-θ法和Newmark法等。显式算法无需求解线性代数方程组，适合于强非线性和自由度数目较大的问题。研究者已提出多种显式时间积分算法ADDIN EN.CITE.DATA（Chung等，1994；王进廷等，2002；Belytschko等，2014）。作者近期提出一种二阶精度的单步显式算法，该算法适合变时步问题，在线弹性范围内稳定性较好。本文将该算法推广至求解非线性动力有限元方程中，并将其应用于地震波垂直入射时非线性地震反应分析。
1. 非线性动力有限元方程的显式时间积分算法
设已知非线性体系第${t_i}$时步的受力状态，求解第${t_{i + 1}}$时步的非线性结构动力学方程：
$${\boldsymbol{M}}{{\boldsymbol{\ddot u}}_{i + 1}}{\boldsymbol{ + C}}{{\boldsymbol{\dot u}}_{i + 1}} + {\boldsymbol{f}}_{i + 1}^S{\boldsymbol{ = }}{{\boldsymbol{f}}_{i + 1}}$$ (1) 式中M、C、${{\boldsymbol{f}}^S}$和${\boldsymbol{f}}$分别表示非线性体系的质量矩阵、阻尼矩阵、内力向量和外荷载向量；u表示位移，点号对时间t求导，i+1表示第${t_{i + 1}}$时刻。第i+1时刻时间步长为：
$${\boldsymbol{\Delta }}{t_i} = {t_{i + 1}} - {t_i}$$ (2) 文献显式方法求解非线性方程（1）的过程如下，第i+1时刻位移${{\boldsymbol{u}}_{i + 1}}$为：
$${{\boldsymbol{u}}_{i + 1}} = {{\boldsymbol{u}}_i} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{t_i}{{\boldsymbol{\dot u}}_i} + \frac{{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{t_i}^2}}{2}{{\boldsymbol{\ddot u}}_i}$$ (3) 第i+1时刻位移增量$\mathit{\Delta }{{\boldsymbol{u}}_i}$、内力增量$\mathit{\Delta }{\boldsymbol{f}}_i^S$和内力全量${\boldsymbol{f}}_{i + 1}^S$分别为：
$$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\boldsymbol{u}}_i} = {{\boldsymbol{u}}_{i + 1}} - {{\boldsymbol{u}}_i}$$ (4) $$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{f}}_i^S = {\boldsymbol{f}}(\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\boldsymbol{u}}_i})$$ (5) $${\boldsymbol{f}}_{i + 1}^S = {\boldsymbol{f}}_i^S + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{f}}_i^S$$ (6) 第i+1时刻预估速度${{\boldsymbol{\dot {\tilde u}}}_{i + 1}}$、预估加速度${{\boldsymbol{\ddot {\tilde u}}}_{i + 1}}$、速度${{\boldsymbol{\dot u}}_{i + 1}}$和加速度${{\boldsymbol{\ddot u}}_{i + 1}}$分别为
$${{\boldsymbol{\dot {\tilde u}}}_{i + 1}} = {{\boldsymbol{\dot u}}_i} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{t_i}{{\boldsymbol{\ddot u}}_i}$$ (7) $${{\boldsymbol{\ddot {\tilde u}}}_{i + 1}} = {{\boldsymbol{M}}^{ - 1}}({{\boldsymbol{f}}_{i + 1}} - {\boldsymbol{C\dot {\tilde u}}}_{i + 1}^{} - {\boldsymbol{f}}_{i + 1}^S)$$ (8) $${{\boldsymbol{\dot u}}_{i + 1}} = {{\boldsymbol{\dot u}}_i} + \frac{{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{t_i}}}{2}({{\boldsymbol{\ddot u}}_i} + {{\boldsymbol{\ddot {\tilde u}}}_{i + 1}})$$ (9) $${{\boldsymbol{\ddot u}}_{i + 1}} = {{\boldsymbol{M}}^{ - 1}}({{\boldsymbol{f}}_{i + 1}} - {\boldsymbol{C\dot u}}_{i + 1}^{} - {\boldsymbol{f}}_{i + 1}^S)$$ (10) 式（3）—式（10）为求解式（1）的显式算法。算法中需由位移增量计算内力增量，目前常用的应力计算方法包括向前欧拉法、向后欧拉法和完全隐式计算法等ADDIN EN.CITE.DATA（Sloan等，1992；2001；Ahadi等，2003）。下面给出式（5）由位移增量计算内力增量的过程，即一种带误差控制的修正欧拉算法。
对于每个有限单元，由位移增量$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{u}}_i^e$计算应变增量$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e$的表达式为：
$$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e = {{\boldsymbol{B}}^e}\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{u}}_i^e$$ (11) 式中Be为应变矩阵。将ti时刻单元应变增量$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e$赋值给子步应变增量$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e$，ti时刻单元应力${\boldsymbol{ \pmb{\mathit{ σ}} }}_i^e$赋值给${\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e$，初始化子步应变增量和应力状态分别为：
$$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e \leftarrow \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e$$ (12) $${\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e \leftarrow {\boldsymbol{ \pmb{\mathit{ σ}} }}_i^e$$ (13) 每个子步中应力增量计算思路见图 1，具体计算公式如下：
$${\boldsymbol{D}}_1^e = {\boldsymbol{D}}({\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e)$$ (14) $$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_1^e = {\boldsymbol{D}}_1^e\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e$$ (15) $${\boldsymbol{D}}_2^e = {\boldsymbol{D}}({\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_1^e)$$ (16) $$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_2^e = {\boldsymbol{D}}_2^e\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e$$ (17) $$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_s^e = \frac{{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_1^e + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_2^e}}{2}$$ (18) 式中${{\boldsymbol{D}}^e}$为单元应力-应变关系矩阵。判断每个子步中应力增量$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\boldsymbol{ \pmb{\mathit{ σ}} }}_s}$是否符合精度要求的误差判断式为：
$${e_r} = \frac{{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_1^e - \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_2^e} \right\|}}{{\left\| {{\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_s^e} \right\|}}$$ (19) 判断误差er是否小于预先给定的判断值st，条件不满足时，缩小子步应变增量为：
$$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e \leftarrow A\sqrt {{{{s_t}} \mathord{\left/ {\vphantom {{{s_t}} {{e_r}}}} \right. } {{e_r}}}} \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e$$ (20) 式中A为误差峰值系数。采用缩小的子步应变增量重新进行式（14）—式（19）的计算与判断，循环直至满足精度要求，更新剩余应变增量和应力状态分别为：
$$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e \leftarrow \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e - \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e$$ (21) $${\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e \leftarrow {\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_s^e$$ (22) 利用更新剩余应变增量和应力状态循环执行式（14）—式（20），直至剩余应变增量小于等于零结束。
利用求得的第i+1时刻单元应力可得到单元应力增量和内力增量分别为：
$$ \Delta \boldsymbol{\sigma }_i^e = \boldsymbol{\sigma }_{i + 1}^e - \boldsymbol{\sigma }_i^e $$ (23) $$ \Delta {\boldsymbol{f}}_i^S{\rm{ = }}\sum\limits_e {\int {{{\boldsymbol{B}}^{e{\rm{T}}}}\boldsymbol{\Delta }{\boldsymbol{\sigma }}_i^e{\bf{d}}A} } $$ (24) 2. 地震波垂直入射时场地非线性地震反应分析
本节将上述非线性有限元方程的显式时间积分算法应用于地震波垂直入射时场地非线性地震反应分析中。假定基岩为线弹性半空间，考虑基岩上覆土层的材料非线性，不考虑土体阻尼。在土层下部设置黏性边界条件模拟半空间基岩的辐射阻尼，并在该处以等效结点力的方式实现地震动输入。
计算模型见图 2，选取A点作为观测点。土体非线性材料本构模型选取邓肯-张模型，土体线弹性参数见表 1，未给出配套的非线性参数，故算例中的非线性参数参考实际情况选取，后续研究中将使用更真实表现土体非线性行为的本构模型及真实工程场地参数。算例中的大气压参数取100kPa，内摩擦角增量取0°。入射地震动分别选取狄拉克脉冲和实测地震动（Gilroy Array #3，Coyote Lake, 1979）。入射狄拉克脉冲见图 3，观测点结果见图 4，实测地震动见图 5，观测点结果见图 6。图 4、图 6中给出采用中心差分法的计算结果作为参考解，由图 4、图 6可知，本文算法与中心差分法计算结果吻合较好，说明本文算法的有效性。
图 2 大开车站沿线土层纵断面构造Figure 2. Site condition of the Daikai subway station in vertical direction表 1 土层参数Table 1. Parameters of soils土质 深度/
m$\rho $/
（g/cm3）cs /
（m/s）v
-EN
-Rf
-c/
（MPa）θ/（°） D
-F
-人工填土 0—1.0 1.9 140 0.33 0.33 0.758 0.084 26.9 1.06 0.021 全新世砂土 1.0—5.1 1.9 140 0.32 0.33 0.758 0.084 26.9 1.06 0.021 全新世砂土 5.1—8.3 1.9 170 0.32 0.36 0.768 0.120 31.0 1.11 0.015 更新世粘土 8.3—11.4 1.9 190 0.40 0.44 0.822 0.188 28.4 1.01 0.012 更新世粘土 11.4—17.2 1.9 240 0.30 0.44 0.822 0.188 28.4 1.01 0.012 更新世砂土 17.2—22.2 2.0 330 0.26 0.51 0.840 0.300 30.0 1.02 0.011 基岩 ＞22.2 2.0 330 0.26 - - - - - - 
图 3 狄拉克脉冲速度和加速度时程图Figure 3. Velocity and acceleration time history of the Dirac pulse
图 4 狄拉克脉冲入射时场地反应分析结果Figure 4. Results of site analysis under the incident of Dirac pulse
图 5 实测地震动速度和加速度时程图Figure 5. Velocity and acceleration time history of the seismic motion
图 6 实测地震动入射时场地反应分析结果Figure 6. Results of site reaction analysis under the incident of the seismic motion表 1中ρ、cs、v、EN、Rf、c、θ为模型参数，分别表示密度、剪切波速、泊松比、无量纲幂次、破坏比、土的内聚力、土的摩擦角。D、F为试验常数。
3. 结论
本文发展一种求解材料非线性结构动力学方程的显式时间积分算法，并应用于地震波竖直入射时非线性地震反应分析中，通过算例验证了该方法的有效性。该显式算法具有无需对角阻尼矩阵、单步、稳定性良好等优点。本文考虑了邓肯-张非线性弹性本构模型，下步研究可考虑将该显式算法扩展到弹塑性本构模型及更能反映土层真实变形的本构模型中。
-
图 1 Rayleigh波场数值模拟的有限元网格划分
Figure 1. The finite element model for Rayleigh wave field simulation
图 2 不同时段有限元网格变形示意图
Figure 2. Illustration of deformation of finite element nets in different time domains
图 6 含建筑结构的场地有限元模型
Figure 6. The finite element model for soil-structure interaction analysis
图 7 Rayleigh波作用下不同时刻建筑物的振动形态
Figure 7. Deformation diagram by finite element model under Rayleigh wave
图 8 Rayleigh波作用下建筑物顶层两侧角点的水平和竖向位移时程
Figure 8. The displacement time histories in horizontal and vertical at the top of building under Rayleigh wave
图 9 剪切波作用下不同时刻建筑物的振动形态
Figure 9. Deformation diagram by finite element model under shear wave
图 10 剪切波作用下建筑物顶层两侧角点的水平和竖向位移时程
Figure 10. The displacement time histories in horizontal and vertical at the top of building under shear wave
图 11 剪切波与Rayleigh波联合作用下建筑物顶层两侧角点的水平和竖向位移时程
Figure 11. The displacement time histories in horizontal and vertical at the top of building under Rayleigh and shear wave
表 1 Plaxis 2D中土层材料参数
Table 1. Soil material parameters in the Plaxis 2D
材料模型 饱和重度 弹性模量 泊松比 线弹性 20kN/m3 5×104kN/m2 0.3 
下载: 导出CSV
表 2 Plaxis 2D中振动基础材料参数
Table 2. Foundation material parameters in the Plaxis 2D
材料模型 重度 弹性模量 泊松比 轴向刚度 线弹性，各向同性 5kN/m3 2.4×104kN/m2 0.2 7.6×106kN
下载: 导出CSV
表 3 建筑物材料属性（板单元）
Table 3. The material parameters of the building
材料类型 轴向刚度 抗弯刚度 重度 泊松比 上部结构：线弹性，各向同性 9.6×106kN 6.75×104kN·m2 10kN/m3 0.2 地下室：线弹性，各向同性 1.2×107kN 1.6×105kN·m2 20kN/m3 0.2
下载: 导出CSV
表 4 点对点锚杆材料属性
Table 4. The material parameters of the central pillar
材料类型 轴向刚度 平面外间距 线弹性 2.5×106kN 3.0m
下载: 导出CSV
-
巴振宁, 梁建文, 2014.瑞雷波斜入射下层状半空间中沉积谷地周围的三维散射研究.地震学报, 36(4):571-583. doi: 10.3969/j.issn.0253-3782.2014.04.004 崔杰, 张为, 张建国, 2008.Rayleigh波对浅地表地基震害的影响.华南地震, 28(2):10-18. doi: 10.3969/j.issn.1001-8662.2008.02.003 高广运, 1998.非连续屏障地面隔振理论与应用.杭州: 浙江大学. 梁建文, 魏新磊, Lee V.W., 2009.圆弧形沉积谷地对Rayleigh波三维散射解析解.天津大学学报, 42(1):24-34. http://d.old.wanfangdata.com.cn/Periodical/tianjdxxb200901005 刘广裕, 刘凯欣, 2007.区域脉冲载荷下二维Lamb问题的精确求解.固体力学学报, 28(4):341-346. doi: 10.3969/j.issn.0254-7805.2007.04.003 刘晶波, 李彬, 2006.Rayleigh波作用下地下结构的动力反应分析.工程力学, 23(10):132-135, 131. doi: 10.3969/j.issn.1000-4750.2006.10.025 刘晶波, 谭辉, 宝鑫等, 2018.土-结构动力相互作用分析中基于人工边界子结构的地震波动输入方法.力学学报, 50(1):32-43. http://d.old.wanfangdata.com.cn/Periodical/lxxb201801004 刘凯欣, 刘广裕, 2004.垂直点源问题的一个精确解.科学通报, 49(5):419-423. doi: 10.3321/j.issn:0023-074X.2004.05.003 刘志祥, 张海清, 2017.PLAXIS 2D基础教程.北京:机械工业出版社. 罗超, 2017.河谷地形及土-结构相互作用对大跨度桥梁地震反应的影响.上海:同济大学, 78-94. 萨瓦林斯基, 1981.地震波.段星北, 译.北京: 科学出版社. 佘德平, 2004.波场数值模拟技术.勘探地球物理进展, 27(1):16-21. http://d.old.wanfangdata.com.cn/Periodical/ktdqwljz200401003 施有志, 林树枝, 赵花丽, 2017a.瑞利阻尼参数对瑞利波作用下场地动力响应的影响.人民长江, 48(3):76-80. http://d.old.wanfangdata.com.cn/Periodical/rmcj201703016 施有志, 孙爱琴, 林树枝等, 2017b.Rayleigh波作用下地下综合管廊动力响应三维数值分析.世界地震工程, 33(4):196-210. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=sjdzgc201704023 苏传行, 2017.二维起伏地形瑞利面波数值模拟研究, 成都: 西南交通大学, 18-22. 王朝令, 刘争平, 2012.黏弹性边界条件在ANSYS有限元波场模拟中的实现.大地测量与地球动力学, 32(2):28-31. http://d.old.wanfangdata.com.cn/Periodical/dkxbydz201202007 王朝令, 刘争平, 黄云艳等, 2014.隧道地震预报波场的有限元数值模拟.吉林大学学报(地球科学版), 44(4):1369-1381. http://d.old.wanfangdata.com.cn/Periodical/cckjdxxb201404032 王贻荪, 1979.关于拉姆问题的精确解.湖南大学学报, 6(1):61-76. http://www.cnki.com.cn/Article/CJFDTOTAL-HNDX197901004.htm 王贻荪, 1980.半无限体表面在竖向集中谐和力作用下表面竖向位移的精确解.力学学报, 12(4):386-391. http://www.cnki.com.cn/Article/CJFDTOTAL-LXXB198004007.htm 王贻荪, 1982.地面波动分析若干问题.建筑结构学报, 3(2):56-67. 吴世明, 1997.土介质中的波.北京:科学出版社. 杨桂通, 张善元, 1988.弹性动力学.北京:中国铁道出版社. 杨先健, 徐建, 张翠红, 2013.土-基础的振动与隔振.北京:中国建筑工业出版社. 于文福, 2017.点源横向非均匀介质瑞利面波波场数值模拟研究.成都:西南交通大学, 66-72. http://d.old.wanfangdata.com.cn/Thesis/Y3324494 岳庆霞, 李杰, 2008.近似Rayleigh地震波作用下地下综合管廊响应分析.防灾减灾工程学报, 28(4):409-416. http://d.old.wanfangdata.com.cn/Periodical/dzxk200804002 Brinkgreve R. B. J., Kumarswamy S., Swolfs, W. M., 2016. PLAXIS 2D reference manual. Delft, The Netherlands: PLAXIS BV, 286-290. Kontoe S., Zdravkovic L., Potts D. M., 2009. An assessment of the domain reduction method as an advanced boundary condition and some pitfalls in the use of conventional absorbing boundaries. International Journal for Numerical and Analytical Methods in Geomechanics, 33(3):309-330. doi: 10.1002/nag.v33:3 Lamb H., 1904. On the propagation of tremors over the surface of an elastic solid. Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character, 203:1-42. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=J-STAGE_2074456 Woods R. D., 1968. Screening of surface waves in soils. Journal of Soil Mechanics and Foundations Division ASCE, 94(SM4):951-979. http://cn.bing.com/academic/profile?id=ede895a4b0901f507fc3cb2dde44587d&encoded=0&v=paper_preview&mkt=zh-cn Yu W. F., Liu Z. P., 2015. A numerical study of the Rayleigh wave particle motions excited by a point source and Poisson's ratio for lateral inhomogeneous half-spaces. Journal of Applied Geophysics, 123:242-255. doi: 10.1016/j.jappgeo.2015.09.009 -
下载:
点击查看大图
计量
- 文章访问数: 177
- HTML全文浏览量: 28
- PDF下载量: 20
- 被引次数: 0
