High Level Seismic Qualification Test of High Voltage Porcelain Insulator Disconnector in Chile High Earthquake Intensity Area
-
摘要: 为获取户外高压隔离开关的动态特性、研究瓷瓶破断力与地震载荷的关系以及验证隔离开关的抗震性能，开展了相关的考核试验。依据IEEE 693—2005标准的要求，试验前进行了应变计的校准试验、瓷瓶的弯曲破断试验和隔离开关的抗震性能试验。经过抗震试验，隔离开关完好无损且在抗震试验前后其共振频率变化不大，瓷瓶破断力大于地震载荷的2倍。结果表明隔离开关结构稳定，通过了抗震考核。Abstract: In order to obtain the dynamic characteristics of the outdoor high voltage disconnector and the relationship between the breaking force of the porcelain insulator and the earthquake load, and to verify the seismic performance of the disconnector, the calibration test of the strain gauge is carried out before the seismic test, the bending breaking test of the porcelain insulator is carried out on the basis of the requirements of the IEEE 693—2005 standard. Then the seismic performance test of the disconnector is conducted. After seismic testing, the disconnector is intact, and the resonance frequency of the porcelain insulator does not changed before and after the seismic test. The breaking force of the porcelain insulator is 2 times greater than that of the earthquake load. The result shows that the structure of the disconnector is stable to bear the seismic assessment.
-
引言
关于场地地震反应的分析已有大量研究成果，研究表明土壤在地震作用下会表现出材料非线性效应ADDIN EN.CITE.DATA（Joyner等，1975；Huang等，2001；Arslan等，2006；Hosseini等，2012）。等效线性化方法ADDIN EN.CITE.DATA（Schnabel等，1972；Idriss等，1992；Bardet等，2000；王笃国等，2016）是一种频域方法，通过在不同土体应变条件下选择等效阻尼比和剪切模量，将非线性问题转化为线性问题。当采用材料非线性本构模型描述土体非线性时，需采用时间积分算法求解非线性动力有限元方程。时间积分算法可分为隐式方法和显式方法。隐式算法每时刻需求解线性代数方程组，计算效率相对较低，如Wilson-θ法和Newmark法等。显式算法无需求解线性代数方程组，适合于强非线性和自由度数目较大的问题。研究者已提出多种显式时间积分算法ADDIN EN.CITE.DATA（Chung等，1994；王进廷等，2002；Belytschko等，2014）。作者近期提出一种二阶精度的单步显式算法，该算法适合变时步问题，在线弹性范围内稳定性较好。本文将该算法推广至求解非线性动力有限元方程中，并将其应用于地震波垂直入射时非线性地震反应分析。
1. 非线性动力有限元方程的显式时间积分算法
设已知非线性体系第${t_i}$时步的受力状态，求解第${t_{i + 1}}$时步的非线性结构动力学方程：
$${\boldsymbol{M}}{{\boldsymbol{\ddot u}}_{i + 1}}{\boldsymbol{ + C}}{{\boldsymbol{\dot u}}_{i + 1}} + {\boldsymbol{f}}_{i + 1}^S{\boldsymbol{ = }}{{\boldsymbol{f}}_{i + 1}}$$ (1) 式中M、C、${{\boldsymbol{f}}^S}$和${\boldsymbol{f}}$分别表示非线性体系的质量矩阵、阻尼矩阵、内力向量和外荷载向量；u表示位移，点号对时间t求导，i+1表示第${t_{i + 1}}$时刻。第i+1时刻时间步长为：
$${\boldsymbol{\Delta }}{t_i} = {t_{i + 1}} - {t_i}$$ (2) 文献显式方法求解非线性方程（1）的过程如下，第i+1时刻位移${{\boldsymbol{u}}_{i + 1}}$为：
$${{\boldsymbol{u}}_{i + 1}} = {{\boldsymbol{u}}_i} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{t_i}{{\boldsymbol{\dot u}}_i} + \frac{{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{t_i}^2}}{2}{{\boldsymbol{\ddot u}}_i}$$ (3) 第i+1时刻位移增量$\mathit{\Delta }{{\boldsymbol{u}}_i}$、内力增量$\mathit{\Delta }{\boldsymbol{f}}_i^S$和内力全量${\boldsymbol{f}}_{i + 1}^S$分别为：
$$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\boldsymbol{u}}_i} = {{\boldsymbol{u}}_{i + 1}} - {{\boldsymbol{u}}_i}$$ (4) $$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{f}}_i^S = {\boldsymbol{f}}(\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\boldsymbol{u}}_i})$$ (5) $${\boldsymbol{f}}_{i + 1}^S = {\boldsymbol{f}}_i^S + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{f}}_i^S$$ (6) 第i+1时刻预估速度${{\boldsymbol{\dot {\tilde u}}}_{i + 1}}$、预估加速度${{\boldsymbol{\ddot {\tilde u}}}_{i + 1}}$、速度${{\boldsymbol{\dot u}}_{i + 1}}$和加速度${{\boldsymbol{\ddot u}}_{i + 1}}$分别为
$${{\boldsymbol{\dot {\tilde u}}}_{i + 1}} = {{\boldsymbol{\dot u}}_i} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{t_i}{{\boldsymbol{\ddot u}}_i}$$ (7) $${{\boldsymbol{\ddot {\tilde u}}}_{i + 1}} = {{\boldsymbol{M}}^{ - 1}}({{\boldsymbol{f}}_{i + 1}} - {\boldsymbol{C\dot {\tilde u}}}_{i + 1}^{} - {\boldsymbol{f}}_{i + 1}^S)$$ (8) $${{\boldsymbol{\dot u}}_{i + 1}} = {{\boldsymbol{\dot u}}_i} + \frac{{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{t_i}}}{2}({{\boldsymbol{\ddot u}}_i} + {{\boldsymbol{\ddot {\tilde u}}}_{i + 1}})$$ (9) $${{\boldsymbol{\ddot u}}_{i + 1}} = {{\boldsymbol{M}}^{ - 1}}({{\boldsymbol{f}}_{i + 1}} - {\boldsymbol{C\dot u}}_{i + 1}^{} - {\boldsymbol{f}}_{i + 1}^S)$$ (10) 式（3）—式（10）为求解式（1）的显式算法。算法中需由位移增量计算内力增量，目前常用的应力计算方法包括向前欧拉法、向后欧拉法和完全隐式计算法等ADDIN EN.CITE.DATA（Sloan等，1992；2001；Ahadi等，2003）。下面给出式（5）由位移增量计算内力增量的过程，即一种带误差控制的修正欧拉算法。
对于每个有限单元，由位移增量$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{u}}_i^e$计算应变增量$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e$的表达式为：
$$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e = {{\boldsymbol{B}}^e}\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{u}}_i^e$$ (11) 式中Be为应变矩阵。将ti时刻单元应变增量$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e$赋值给子步应变增量$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e$，ti时刻单元应力${\boldsymbol{ \pmb{\mathit{ σ}} }}_i^e$赋值给${\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e$，初始化子步应变增量和应力状态分别为：
$$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e \leftarrow \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e$$ (12) $${\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e \leftarrow {\boldsymbol{ \pmb{\mathit{ σ}} }}_i^e$$ (13) 每个子步中应力增量计算思路见图 1，具体计算公式如下：
$${\boldsymbol{D}}_1^e = {\boldsymbol{D}}({\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e)$$ (14) $$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_1^e = {\boldsymbol{D}}_1^e\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e$$ (15) $${\boldsymbol{D}}_2^e = {\boldsymbol{D}}({\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_1^e)$$ (16) $$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_2^e = {\boldsymbol{D}}_2^e\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e$$ (17) $$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_s^e = \frac{{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_1^e + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_2^e}}{2}$$ (18) 式中${{\boldsymbol{D}}^e}$为单元应力-应变关系矩阵。判断每个子步中应力增量$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\boldsymbol{ \pmb{\mathit{ σ}} }}_s}$是否符合精度要求的误差判断式为：
$${e_r} = \frac{{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_1^e - \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_2^e} \right\|}}{{\left\| {{\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_s^e} \right\|}}$$ (19) 判断误差er是否小于预先给定的判断值st，条件不满足时，缩小子步应变增量为：
$$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e \leftarrow A\sqrt {{{{s_t}} \mathord{\left/ {\vphantom {{{s_t}} {{e_r}}}} \right. } {{e_r}}}} \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e$$ (20) 式中A为误差峰值系数。采用缩小的子步应变增量重新进行式（14）—式（19）的计算与判断，循环直至满足精度要求，更新剩余应变增量和应力状态分别为：
$$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e \leftarrow \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e - \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e$$ (21) $${\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e \leftarrow {\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_s^e$$ (22) 利用更新剩余应变增量和应力状态循环执行式（14）—式（20），直至剩余应变增量小于等于零结束。
利用求得的第i+1时刻单元应力可得到单元应力增量和内力增量分别为：
$$ \Delta \boldsymbol{\sigma }_i^e = \boldsymbol{\sigma }_{i + 1}^e - \boldsymbol{\sigma }_i^e $$ (23) $$ \Delta {\boldsymbol{f}}_i^S{\rm{ = }}\sum\limits_e {\int {{{\boldsymbol{B}}^{e{\rm{T}}}}\boldsymbol{\Delta }{\boldsymbol{\sigma }}_i^e{\bf{d}}A} } $$ (24) 2. 地震波垂直入射时场地非线性地震反应分析
本节将上述非线性有限元方程的显式时间积分算法应用于地震波垂直入射时场地非线性地震反应分析中。假定基岩为线弹性半空间，考虑基岩上覆土层的材料非线性，不考虑土体阻尼。在土层下部设置黏性边界条件模拟半空间基岩的辐射阻尼，并在该处以等效结点力的方式实现地震动输入。
计算模型见图 2，选取A点作为观测点。土体非线性材料本构模型选取邓肯-张模型，土体线弹性参数见表 1，未给出配套的非线性参数，故算例中的非线性参数参考实际情况选取，后续研究中将使用更真实表现土体非线性行为的本构模型及真实工程场地参数。算例中的大气压参数取100kPa，内摩擦角增量取0°。入射地震动分别选取狄拉克脉冲和实测地震动（Gilroy Array #3，Coyote Lake, 1979）。入射狄拉克脉冲见图 3，观测点结果见图 4，实测地震动见图 5，观测点结果见图 6。图 4、图 6中给出采用中心差分法的计算结果作为参考解，由图 4、图 6可知，本文算法与中心差分法计算结果吻合较好，说明本文算法的有效性。
图 2 大开车站沿线土层纵断面构造Figure 2. Site condition of the Daikai subway station in vertical direction表 1 土层参数Table 1. Parameters of soils土质 深度/
m$\rho $/
（g/cm3）cs /
（m/s）v
-EN
-Rf
-c/
（MPa）θ/（°） D
-F
-人工填土 0—1.0 1.9 140 0.33 0.33 0.758 0.084 26.9 1.06 0.021 全新世砂土 1.0—5.1 1.9 140 0.32 0.33 0.758 0.084 26.9 1.06 0.021 全新世砂土 5.1—8.3 1.9 170 0.32 0.36 0.768 0.120 31.0 1.11 0.015 更新世粘土 8.3—11.4 1.9 190 0.40 0.44 0.822 0.188 28.4 1.01 0.012 更新世粘土 11.4—17.2 1.9 240 0.30 0.44 0.822 0.188 28.4 1.01 0.012 更新世砂土 17.2—22.2 2.0 330 0.26 0.51 0.840 0.300 30.0 1.02 0.011 基岩 ＞22.2 2.0 330 0.26 - - - - - - 
图 3 狄拉克脉冲速度和加速度时程图Figure 3. Velocity and acceleration time history of the Dirac pulse
图 4 狄拉克脉冲入射时场地反应分析结果Figure 4. Results of site analysis under the incident of Dirac pulse
图 5 实测地震动速度和加速度时程图Figure 5. Velocity and acceleration time history of the seismic motion
图 6 实测地震动入射时场地反应分析结果Figure 6. Results of site reaction analysis under the incident of the seismic motion表 1中ρ、cs、v、EN、Rf、c、θ为模型参数，分别表示密度、剪切波速、泊松比、无量纲幂次、破坏比、土的内聚力、土的摩擦角。D、F为试验常数。
3. 结论
本文发展一种求解材料非线性结构动力学方程的显式时间积分算法，并应用于地震波竖直入射时非线性地震反应分析中，通过算例验证了该方法的有效性。该显式算法具有无需对角阻尼矩阵、单步、稳定性良好等优点。本文考虑了邓肯-张非线性弹性本构模型，下步研究可考虑将该显式算法扩展到弹塑性本构模型及更能反映土层真实变形的本构模型中。
-
图 1 样件总装图和应变片位置示意图
Figure 1. General assembly drawing of specimen and diagram of strain gauge position
图 2 瓷柱1纵向和横向力-应变校验图
Figure 2. Force and strain check diagram of porcelain column 1 in longitudinal and lateral direction
图 3 瓷柱2纵向和横向力-应变校验图
Figure 3. Force and strain check diagram of porcelain column 2 in longitudinal and lateral direction
图 7 抗震试验前、后测点T1的传递函数对比
Figure 7. Comparison of transfer function of T1 at three points before and after seismic test
表 1 样件参数
Table 1. Parameters of specimen
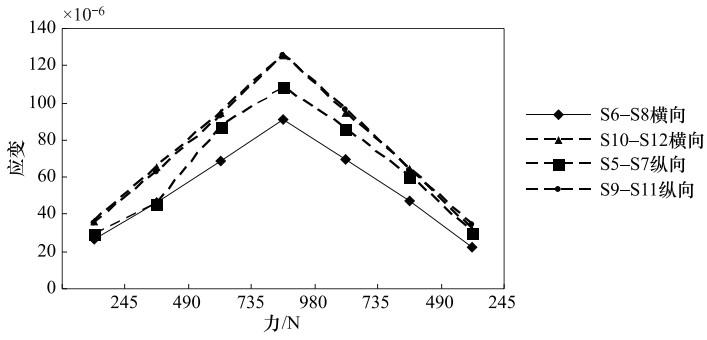
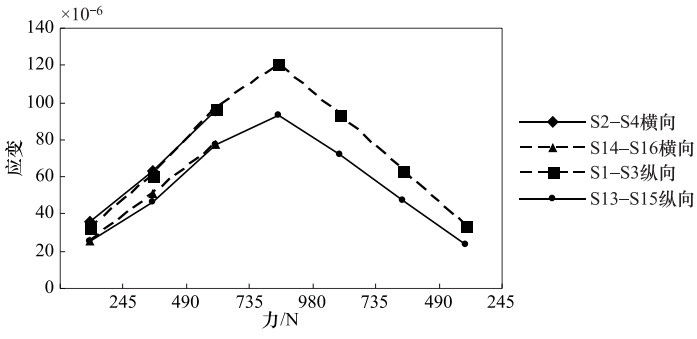
型号 额定电压 额定短时耐受电流 额定频率 额定电流 质量 GW4C-252D(G·W)/J4000-50 252kV 50kA 50Hz，60Hz 4000A 650kg 
下载: 导出CSV
表 2 力-应变测量结果
Table 2. Results of force and strain measurements
施加力/N 应变×10-6 S1—S3 S2—S4 S5—S7 S6—S8 S9—S11 S10—S12 S13—S15 S14—S16 245 25.16 25.16 29.15 26.21 35.07 36.19 32.12 35.77 490 45.75 50.58 45.92 46.48 63.00 65.06 59.89 62.41 735 76.44 76.29 86.32 68.88 92.62 94.45 95.41 94.45 980 92.00 95.60 108.51 91.38 125.33 125.15 119.51 119.12 735 71.07 85.60 69.75 95.98 94.85 92.52 490 47.04 60.43 46.81 63.85 64.26 62.56 245 23.51 29.65 22.33 34.61 31.44 33.06
下载: 导出CSV
表 3 瓷瓶绝缘子支柱样品的破断力
Table 3. Fracture force of the pillar sample of porcelain insulator
样品编号 1 2 3 4 5 6 7 8 破断力Fi/kN 10.71 9.95 11.57 10.86 10.49 9.13 11.12 9.65
下载: 导出CSV
表 4 主刀合、地刀分状态下振动响应探查结果
Table 4. The first order resonance frequency from vibration response detecting with the main cutter on and the ground cutter off
方向 一阶共振频率/Hz 测点T1 测点T2 测点T3 测点T4 横向 3.5 3.5 3.0 3.0 纵向 3.5 3.5 3.5 3.5 垂向 ＞33 ＞33 ＞33 ＞33
下载: 导出CSV
表 5 主刀分、地刀合状态下振动响应探查结果
Table 5. The first order resonance frequency from vibration response detecting with the main cutter off and the ground cutter on
方向 一阶共振频率/Hz 测点T1 测点T2 测点T3 测点T4 横向 3.5 3.5 3.5 3.5 纵向 3.5 3.5 3.0 3.0 垂向 ＞33 ＞33 ＞33 ＞33
下载: 导出CSV
表 6 主刀分、地刀分状态下振动响应探查结果
Table 6. The first order resonance frequency from vibration response detecting before seismic when the main cutter off and the ground cutter off
方向 一阶共振频率/Hz 测点T1 测点T2 测点T3 测点T4 横向 3.5 3.5 3.0 3.0 纵向 3.5 3.5 3.5 3.5 垂向 ＞33 ＞33 ＞33 ＞33
下载: 导出CSV
表 7 RRS考核试验过程中应变试验值
Table 7. Strain value in the process of RRS test
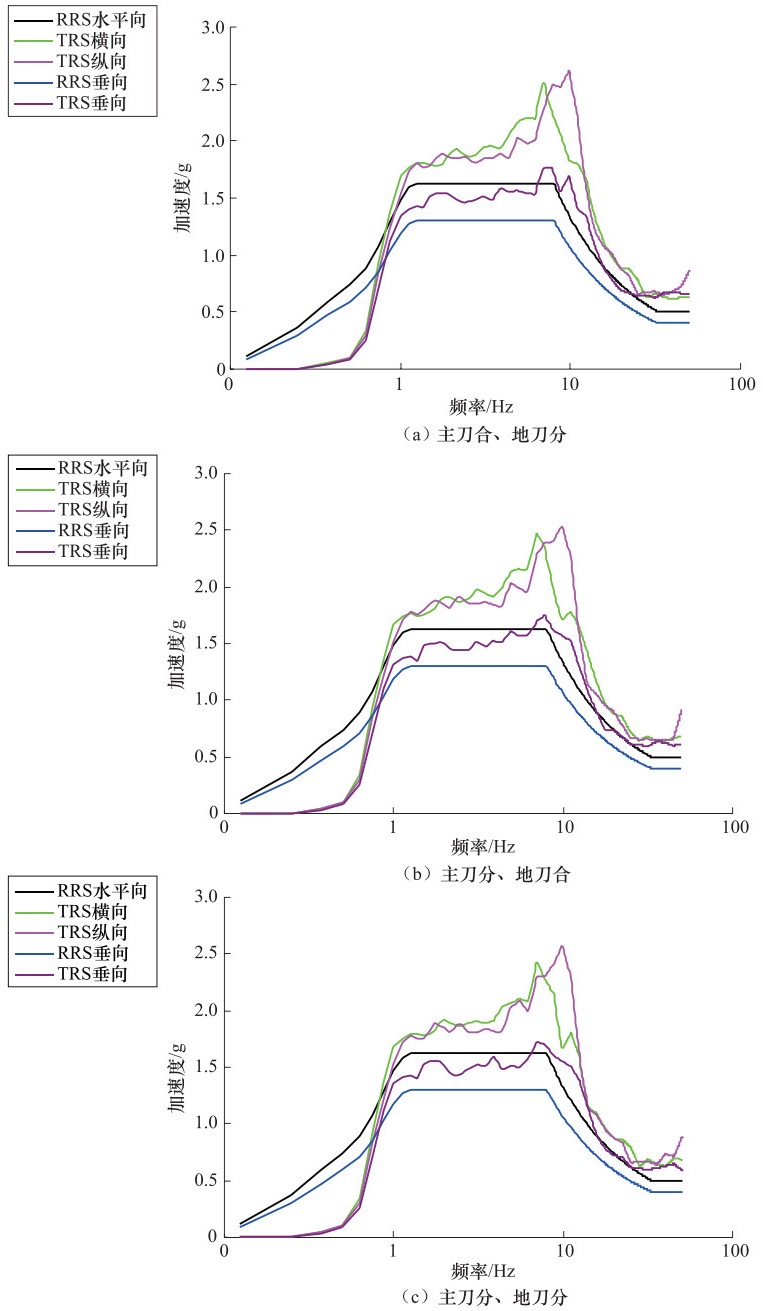
抗震考核试验 状态 应变×10-6 S1—S3 S2—S4 S5—S7 S6—S8 S9—S11 S10—S12 S13—S15 S14—S16 RRS1 主刀合、地刀分 62.90 109.34 65.60 87.11 130.95 168.98 159.85 176.66 RRS2 主刀分、地刀合 139.9 111.63 174.67 102.67 180.44 193.11 233.60 190.15 RRS3 主刀分、地刀分 99.83 116.71 169.71 102.66 165.25 184.20 170.38 186.64
下载: 导出CSV
表 8 RRS考核试验过程中加速度测量值
Table 8. The acceleration measurement value during the RRS assessment test
抗震考核试验 TT加速度/g T1加速度/g T2加速度/g T3加速度/g T4加速度/g X轴 Y轴 Z轴 X轴 Y轴 Z轴 X轴 Y轴 Z轴 X轴 Y轴 Z轴 X轴 Y轴 Z轴 RRS1 0.583 0.605 0.449 2.031 1.522 0.629 1.694 0.904 0.527 1.647 1.738 0.628 1.636 1.035 0.528 RRS2 0.587 0.633 0.426 1.756 2.069 0.566 1.064 1.678 0.507 2.063 1.939 0.563 1.236 1.537 0.592 RRS3 0.581 0.604 0.445 1.857 1.778 0.505 1.012 1.625 0.482 1.869 1.783 0.507 1.041 1.670 0.475 注：TT为台面加速度。
下载: 导出CSV
表 9 RRS考核试验中坐标轴的相关系数
Table 9. Correlation coefficient of three coordinate axes in RRS assessment test
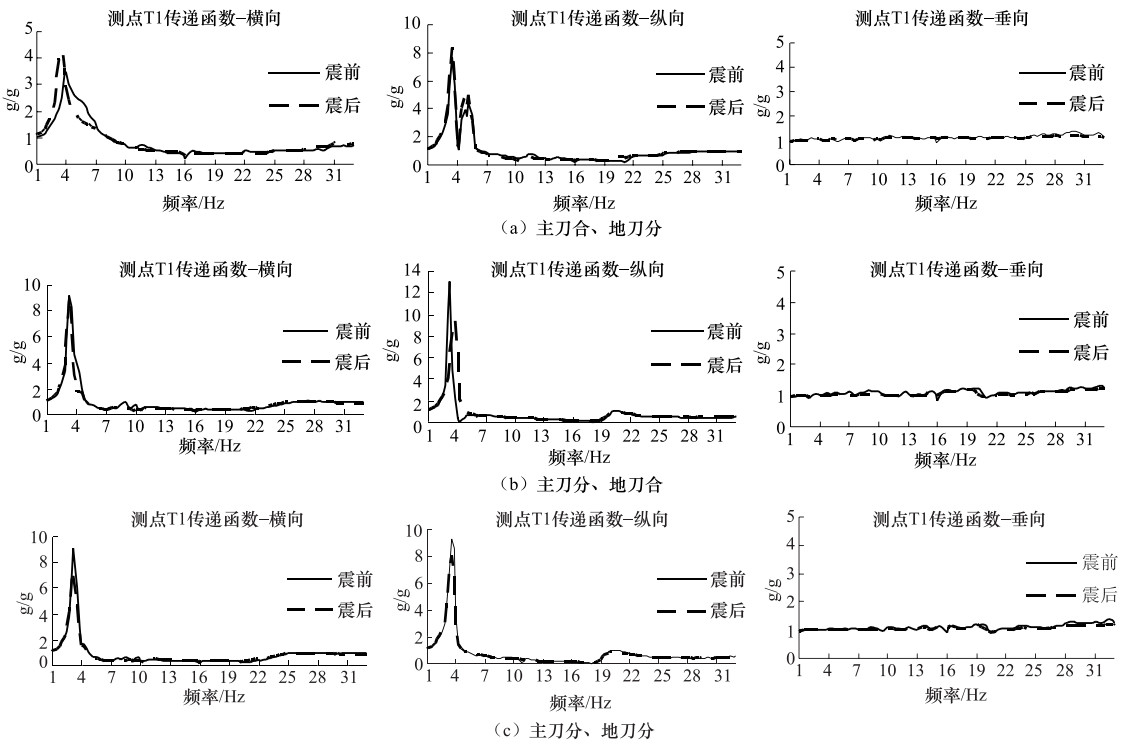
抗震考核试验 相关系数 X-Y轴 Y-Z轴 Z-X轴 RRS1 0.007 0.059 0.085 RRS2 0.007 0.059 0.085 RRS3 0.007 0.059 0.085
下载: 导出CSV
表 10 试后主刀合、地刀分状态下振动响应探查
Table 10. The first order resonance frequency from vibration response detecting after seismic with the main cutter on and the ground cutter off
方向 一阶共振频率/Hz 测点T1 测点T2 测点T3 测点T4 横向 3.0 3.0 3.0 3.0 纵向 3.5 3.5 3.5 3.5 垂向 ＞33 ＞33 ＞33 ＞33
下载: 导出CSV
表 11 试后主刀分、地刀合状态下振动响应探查
Table 11. The first order resonance frequency from vibration response detecting after seismic with the main cutter off and the ground cutter on
方向 一阶共振频率/Hz 测点T1 测点T2 测点T3 测点T4 横向 3.0 3.0 3.0 3.0 纵向 3.5 3.5 3.5 3.5 垂向 ＞33 ＞33 ＞33 ＞33
下载: 导出CSV
表 12 试后主刀分、地刀分状态下振动响应探查
Table 12. The first order resonance frequency from vibration response detecting after seismic with the main cutter off and the ground cutter off
方向 一阶共振频率/Hz 测点T1 测点T2 测点T3 测点T4 横向 3.0 3.0 3.0 3.0 纵向 3.5 3.5 3.5 3.5 垂向 ＞33 ＞33 ＞33 ＞33
下载: 导出CSV
表 13 地震载荷计算
Table 13. Calculation of seismic load
抗震试验 S1—S3和S2—S4中
应变较大者×10-6相应地震载荷
FS/NS5—S7和S6—S8中
应变较大者×10-6相应地震载荷
FS/NRRS1 109.34(S2—S4) 897 87.11(S6—S8) 936 RRS2 139.9(S1—S3) 1491 174.6(S5—S7) 1578 RRS3 116.71(S2—S4) 1196 169.7(S5—S7) 1533
下载: 导出CSV
表 14 瓷瓶绝缘子支柱样品的破断力(kN)
Table 14. Fracture force of the pillar sample of porcelain insulator (kN)
样品编号 破断力${F_i}$ 平均值$\bar F$ ${F_i} - \bar F$ ${({F_i} - \bar F)^2}$ 标准差$\sigma = \sqrt {\frac{{\sum {{{\left({{F_i} - \bar F} \right)}^2}} }}{{i - 1}}} $ 1 10.71 10.435 0.275 0.075 0.807 2 9.95 -0.485 0.235 3 11.57 1.135 1.29 4 10.86 0.425 0.180 5 10.49 10.435 0.055 0.003 0.807 6 9.13 -1.305 1.70 7 11.12 0.685 0.470 8 9.65 -0.785 0.616
下载: 导出CSV
表 15 K值与样品数关系
Table 15. The relation between the K-value and the number of the samples
样品数i 1 3 10 K值 0.66 0.8 1
下载: 导出CSV
-
国家核安全局, 1995. HAF·J0053-1995核设备抗震鉴定试验指南.北京:中国标准出版社. 韩军科, 朱全军, 杨风利等, 2008.基底隔震高压隔离开关抗震性能分析.电力建设, 29(6):39-42. doi: 10.3969/j.issn.1000-7229.2008.06.011 黄峰, 吕建国, 朱祝兵等, 2010.基于ANSYS的GW7-252隔离开关抗震减震性能分析.科技导报, 28(20):52-57. http://d.old.wanfangdata.com.cn/Periodical/kjdb201020012 金松安, 刘朝丰, 武胜斌等, 2013.高海拔隔离开关抗震分析研究.高压电器, 49(10):37-45. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gydq201310007 吕宝龙, 2007.高压隔离开关抗震可靠性研究.上海: 上海大学. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1149662 人民网, 2014.我国遥感卫星为智利地震监测提供服务.(2014-04-10). http://world.people.com.cn/n/2014/0410/c157278-24871427.html. 搜狐新闻, 2015.智利发生8.3级强震或出现危险海啸.(2015-09-17). http://news.sohu.com/20150917/n421334133.shtml. 王海菠, 程永锋, 孙宇晗等, 2018.特高压气体绝缘开关设备瓷套管抗震性能研究.地震工程学报, 40(3):406-412. doi: 10.3969/j.issn.1000-0844.2018.03.406 谢强, 朱瑞元, 周勇等, 2012. 220kV隔离开关地震模拟振动台试验.电网技术, 36(9):262-267. http://d.old.wanfangdata.com.cn/Periodical/dwjs201209044 新华网, 2010.智利地震死亡人数升至799人.(2010-03-04). http://news.sina.com.cn/w/2010-03-04/024019782435.shtml. 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会, 2010. GB/T 13540-2009高压开关设备和控制设备的抗震要求.北京:中国标准出版社. 中华人民共和国住房和城乡建设部, 2010. GB 50556-2010工业企业电气设备抗震设计规范.北京:中国计划出版社. 中华人民共和国住房和城乡建设部, 2013. GB 50260-2013电力设施抗震设计规范.北京:中国计划出版社. 朱全军, 高政国, 陈应禄等, 2018.基于随机反应谱理论的支柱类电气设备抗震性能评估方法研究.地震工程与工程振动, 38(2):194-200. http://d.old.wanfangdata.com.cn/Conference/9449584 IEEE, 2006. IEEE 693-2005 IEEE recommended practice for seismic design of substations. New York:IEEE. -
下载:
点击查看大图
计量
- 文章访问数: 174
- HTML全文浏览量: 46
- PDF下载量: 7
- 被引次数: 0
