Research on the Characteristics of Statistical Relationship between Shear Wave Velocity and Depth in North China
-
摘要: 剪切波速是区别土动力学和静力学的重要参数，其影响因素包括土层埋深、颗粒形状、颗粒比重、压缩模量、孔隙比、含水率和密度等，其中土层埋深对剪切波速的变化影响较大。本文搜集整理了华北地区10个城市的928个钻孔共10703个测点的剪切波速与土层埋深之间的经验统计关系，探讨华北地区剪切波速随深度变化的特征，并从岩性条件、沉积环境等方面分析其原因。通过对比分析，给出了华北地区黏性土和砂类土剪切波速随深度变化的最佳拟合经验统计关系，并进行实例验证，所得结果可为缺乏数据的区域提供一定参考。Abstract: Shear wave velocity is an important parameter to distinguish soil dynamics and statics. The influencing factors include soil depth, particle shape, particle specific gravity, compressive modulus, void ratio, water content and density, etc. Among them, the soil depth has a great influence on the change of shear wave velocity. Many scholars have given statistical relationships between soil depth and the shear wave velocity of different lithological soils such as clay, silt, sandy soil and gavel soil in different regions of the country. This paper collects and compiles the empirical statistical relationship between the shear wave velocity and soil depth of 16741 points in 753 holes in 11 cities of North China. The statistical relationship is summarized and the characteristics of shear wave velocity variation in North China are discussed from aspects of lithological conditions, sedimentary environment and so on. Through comparison and analysis, the best fitting empirical relationship between the shear wave velocity and the depth of clay soil and sand soil in North China is given and verified. The obtained results can provide certain reference for the areas lacking data, which has certain engineering practical significance.
-
Key words:
- North China region /
- Shear wave velocity /
- Statistical relationship /
- Soil depth /
- General model
-
图 2 黏性土剪切波速与深度变化关系的拟合模型曲线类型
Figure 2. Fitting model curve type of relationship between shear wave velocity and depth of clay soil
图 3 砂类土剪切波速与深度变化关系的拟合模型曲线类型
Figure 3. Fitting model curve type of relationship between shear wave velocity and depth of sand soil
图 4 剪切波速随深度变化冥函数统计模型及区域最优拟合曲线
Figure 4. The power function statistical model curve and regional optimal fitting curve of the relationship between shear wave velocity and depth
表 1 原始资料概况
Table 1. Overview of the original data
城市(地区) 总测点数/钻孔数 钻孔深度/m 北京 未知/173 0—100 天津 2212/78 0—120 唐山 未知/173 0—100 邯郸 1000/66 0—60 衡水 5696/82 0—91 阜阳 未知/50 0—60 烟台 未知/173 0—100 东营 未知/46 0—108 焦作 482/43 0—70 下辽河 1313/44 0—90 
下载: 导出CSV
表 2 城市(地区)地貌和主要地层岩性
Table 2. Overview of urban(regional) geomorphology and major strata lithology
城市(地区) 典型地貌 沉积类型 典型地层岩性 其他 北京 冲洪积平原 全新世冲洪积物(Q4fp) 粉质黏土、各类砂层 天津 冲积平原 全新世冲积物(Q4f) 粉土、粉质黏土 唐山 中低山丘陵地貌、滨海平原、三角洲地貌 全新世冲洪积物(Q4fp) 粉质黏土(黄土)、砂、卵石 邯郸 冲洪积平原 晚更新世滑积物(Q3dp) 粉土、粉质黏土、砂层和砾石 衡水 山前冲洪积平原、洪积湖积为主的中部平原 全新世冲积物(Q4f) 粉质黏土、粉土、砂层 阜阳 淮北冲积平原 全新世冲积物(Q4f) 粉土、粉质黏土、砂和砾石层 有古河道发育 烟台 低山丘陵、冲积
—海积平原全新世残坡积物(Q4eld) 黏性土、砂层 东营 黄河冲积三角洲地貌 全新世冲积物(Q4f) 黏性土、砂 黏土多含粉砂 焦作 山区与平原过渡带(统计区为冲洪积平原) 全新世冲洪积物(Q4fp) 黏性土、砂层 地貌复杂，冲洪积平原、低山丘陵、漫滩、洼地均有；黏性土中多夹砂或砾石 下辽河 河流冲洪积平原 全新世残坡积物(Q4eld) 粉质黏土、粉细砂层
下载: 导出CSV
表 3 黏性土剪切波速最优拟合经验关系统计
Table 3. The best fitting empirical and statistical formula for shear wave velocity of clay soil
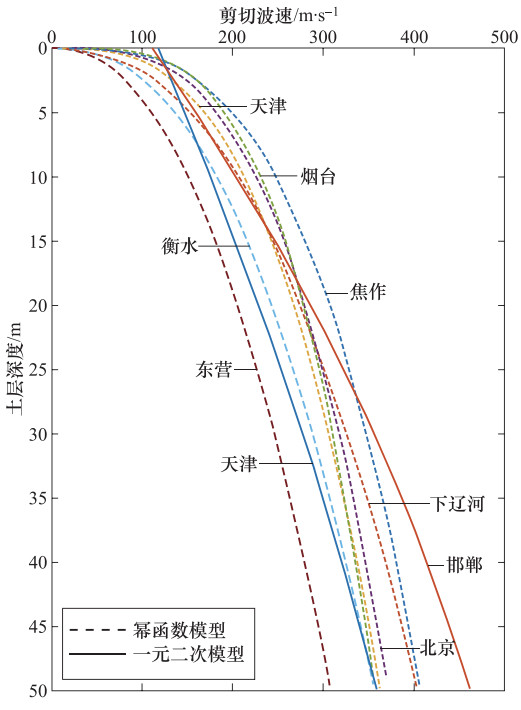
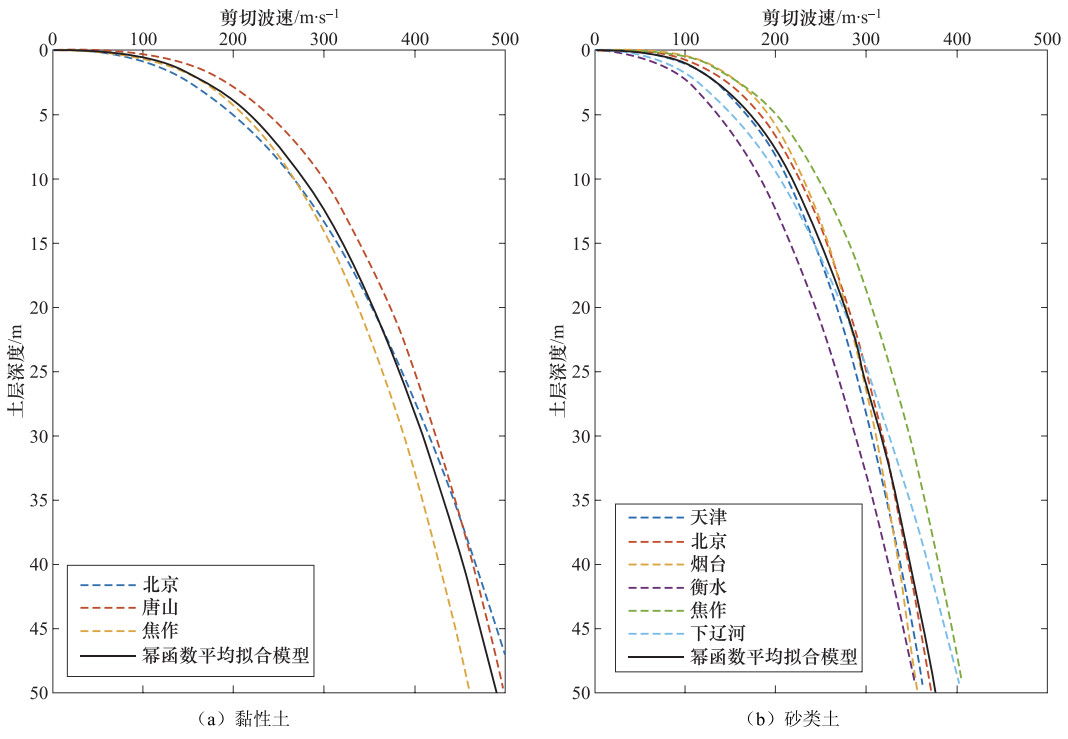
城市(地区) 经验关系式 拟合优度 钻孔深度/m 测点数 天津(侯颉等，2017) ${V_{\rm{s}}} = - 0.0148{H^2} + 5.0703H + 109.53$ 0.912 0—120 206 北京(王广军等，1986) ${V_{\rm{s}}} = 104.0{H^{0.407}}$ 未知 0—100 未知 唐山(王广军等，1986) ${V_{\rm{s}}} = 143.9{H^{0.317}}$ 未知 0—100 未知 烟台(王广军等，1986) ${V_{\rm{s}}} = 229.8{H^{0.142}}$ 未知 0—100 未知 邯郸(王帮圆等，2013) ${V_{\rm{s}}} = - 0.0173{H^2} + 7.4H + 129.9$ 0.848 0—50 ＞200 衡水(何仲太等，2014) ${V_{\rm{s}}} = 4.2529H + 134.42$ 0.937 0—100 281 阜阳(刘之雨等，2016) ${V_{\rm{s}}} = 0.0044{H^3} - 0.4836{H^2} + 18.5918H + 65.5488$ 0.825 0—60 未知 东营(齐静静，2011) ${V_{\rm{s}}} = \left\{ \begin{array}{l} 4.57H + 110.92, H < 30\\ 98.89{H^{0.286}}, H \ge 30 \end{array} \right.$ SD：0.784 0—108 ＞200 焦作(潘国营等，2000) ${V_{\rm{s}}} = 121.80{H^{0.34}}$ 0.940 0—43 82 下辽河(齐鑫等，2012) ${V_{\rm{s}}} = \left\{ \begin{array}{l} - 0.0665{H^2} + 9.944H + 99.729, H < 75\\ 84.261{H^{0.398}}, H \ge 75 \end{array} \right.$ 0.931 0—90 ＞150 注：SD(Standard Deviation)为标准差。
下载: 导出CSV
表 4 砂类土剪切波速最优拟合模型统计
Table 4. The best fitting model of shear wave velocity for sand soil
城市(地区) 经验关系式 拟合优度 钻孔深度/m 测点数 天津(侯颉等，2017) ${V_{\rm{s}}} = - 0.0244{H^2} + 6.0664H + 117.16$ 0.764 0—120 378 天津(王广军等，1986) ${V_{\rm{s}}} = 98.4{H^{0.334}}$ 未知 0—100 未知 北京(王广军等，1986) ${V_{\rm{s}}} = 111.0{H^{0.309}}$ 未知 0—100 未知 烟台(王广军等，1986) ${V_s} = 124.0{H^{0.270}}$ 未知 0—100 未知 邯郸(王帮圆等，2013) ${V_{\rm{s}}} = - 0.05783{H^2} + 9.896H + 111.2$ 0.747 0—50 70 衡水(何仲太等，2014) ${V_{\rm{s}}} = 69.816{H^{0.4166}}$ 0.756 0—91 834 东营(齐静静，2011) ${V_{\rm{s}}} = 53.89{H^{0.446}}$ SD：0.831 0—108 ＞150 焦作(潘国营等，2000) ${V_{\rm{s}}} = 121.19{H^{0.31}}$ 0.920 0—70 41 下辽河(齐鑫等，2012) ${V_{\rm{s}}} = 76.97{H^{0.4244}}$ 0.905 0—90 ＞200
下载: 导出CSV
表 5 黏性土剪切波速统计模型计算值、通用模型计算值与实测值对比
Table 5. Comparison of calculated values from statistical model, from general model, and measured values for the shear wave velocity of clay soil
深度H/m Vs实测值/m·s-1 统计模型 通用模型 Vs计算值/m·s-1 误差/% Vs计算值/m·s-1 误差/% 2 105 150 43.1 177 49.8 4 180 186 3.47 218 12.1 6 202 211 4.55 246 15.6 8 240 231 -3.8 268 7.88 10 260 247 -4.8 286 7.9 12 273 262 -4.1 302 9.72 28 425 340 -20 389 -4.4 32 340 355 4.37 405 25.3 34 370 362 -2.3 413 17.7 36 370 368 -0.5 420 20.2 38 380 374 -1.5 427 19.3
下载: 导出CSV
表 6 砂类土剪切波速统计模型计算值、通用模型计算值与实测值对比
Table 6. Comparison of calculated values from statistical model, from general model, and measured values for the shear wave velocity of sand soil
深度H/m Vs实测值/m·s-1 统计模型 通用模型 Vs计算值/m·s-1 误差/% Vs计算值/m·s-1 误差/% 4 160 124 -23 159 -0.6 8 176 166 -5.7 201 14.2 12 201 197 -2 231 14.9 16 210 222 5.71 255 21.4 20 237 243 2.53 275 16 24 265 262 -1.1 293 10.6 28 285 280 -1.8 309 8.42 56 378 373 -1.3 391 3.44 60 385 384 -0.3 400 3.9 64 402 395 -1.7 409 1.74 68 417 405 -2.88 418 0.24 72 431 415 -3.71 426 -1.2 76 470 424 -9.79 434 -7.7 80 476 433 -9.03 442 -7.1 84 496 442 -10.9 449 -9.5 88 510 451 -11.6 456 -11 92 525 459 -12.6 463 -12 96 532 467 -12.2 470 -12 100 571 476 -16.6 476 -17
下载: 导出CSV
-
陈国兴, 徐建龙, 袁灿勤, 1998.南京城区岩土体剪切波速与土层深度的关系.南京建筑工程学院学报, (2):32-37. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199800432323 程祖锋, 李萍, 李燕等, 1997.深圳地区部分岩土类型剪切波速与深度的关系分析.工程地质学报, 5(2):163-168. http://www.cnki.com.cn/Article/CJFDTotal-GCDZ702.010.htm 董菲蕃, 陈国兴, 金丹丹, 2013.福建沿海3个盆地的土层剪切波速与深度的统计关系.岩土工程学报, 35(S2):145-151. http://d.old.wanfangdata.com.cn/Conference/8211739 高飞, 孙小刚, 2005.上海地区场地剪切波速的特征分析.上海地质, (2):27-29, 36. doi: 10.3969/j.issn.2095-1329.2005.02.008 高玉峰, 刘汉龙, 2003.合肥膨胀土剪切波速的特征分析.岩土工程学报, 25(3):371-373. doi: 10.3321/j.issn:1000-4548.2003.03.027 何仲太, 马保起, 卢海峰, 2014.衡水市岩土体剪切波速与土层深度的关系.科学技术与工程, 14(35):90-96. doi: 10.3969/j.issn.1671-1815.2014.35.017 侯颉, 塔拉, 2017.利用深度回归分析天津市区土体剪切波速.华北地震科学, 35(2):48-53. doi: 10.3969/j.issn.1003-1375.2017.02.008 李守礼, 李迎春, 2005.东北与华北铁路工程地质特征与成就.铁道工程学报, (S1):140-150. http://d.old.wanfangdata.com.cn/Periodical/tdgcxb2005z1018 李铁飞, 陈学良, 高孟潭, 2016.玉溪盆地浅层土层颗粒特征与剪切波速的关系研究.地震学报, 38(6):934-941. http://d.old.wanfangdata.com.cn/Periodical/dizhen201606013 刘玉海, 陈志新, 倪万魁, 1998.地震工程地质学.北京:地震出版社. 刘之雨, 徐振霖, 2016.阜阳市颍东区剪切波速的特征分析.赤峰学院学报(自然科学版), 32(9):57-59. doi: 10.3969/j.issn.1673-260X.2016.09.026 潘国营, 许昭平, 赵元松, 2000.焦作市区岩土剪切波速和场地卓越周期研究.焦作工学院学报(自然科学版), 19(1):1-4. doi: 10.3969/j.issn.1673-9787.2000.01.001 齐静静, 2011.山东东营城区剪切波速回归分析及应用.勘察科学技术, (2):23-26. doi: 10.3969/j.issn.1001-3946.2011.02.006 齐鑫, 丁浩, 2012.下辽河平原区剪切波速与土层埋深关系分析.世界地震工程, 28(3):151-156. doi: 10.3969/j.issn.1007-6069.2012.03.027 荣棉水, 吕悦军, 蒋其峰等, 2017.渤海常见土类剪切波速与埋深关系分析.震灾防御技术, 12(2):288-297. http://zzfy.eq-j.cn/zzfyjs/ch/reader/view_abstract.aspx?flag=1&file_no=20170205&journal_id=zzfyjs 陶小三, 杨伟林, 高志兵等, 2009.南京河西地区岩土体剪切波速与土层深度的关系.防灾减灾工程学报, 29(3):320-324. http://d.old.wanfangdata.com.cn/Periodical/dzxk200903014 王帮圆, 李世峰, 王帮团等, 2013.邯郸市区场地土剪切波速与埋深相关性分析.河北工程大学学报(自然科学版), 30(3):92-95. doi: 10.3969/j.issn.1673-9469.2013.03.023 王广军, 苏经宇, 1986.连云港碱厂层状土剪切波速沿深度变化的推测.勘察科学技术, (3):35-38. http://www.cnki.com.cn/Article/CJFDTotal-KCKX198603007.htm 王金艳, 侯莹, 2017.常州市城区土层剪切波速与土层深度关系分析.地震工程学报, 39(S1):236-240. http://d.old.wanfangdata.com.cn/Periodical/xbdzxb2017z1041 王强, 王兰民, 吴志坚等, 2014.天水市岩土体剪切波速与埋深的变化关系.地震工程与工程振动, 34(S1):247-252. http://d.old.wanfangdata.com.cn/Conference/8707319 汪闻韶, 1994.土工地震减灾工程中的一个重要参量——剪切波.水利学报, (3):80-84. doi: 10.3321/j.issn:0559-9350.1994.03.012 温一波, 赵洞明, 陈尧, 2012.呈贡新区剪切波特征与分布.云南大学学报(自然科学版), 34(S2):221-226. http://d.old.wanfangdata.com.cn/Conference/7764855 张培震, 邓启东, 张国民等, 2003.中国大陆的强震活动与活动地块.中国科学(D辑), 33(S1):12-20. http://d.old.wanfangdata.com.cn/Periodical/zgkx-cd2003z1002 张小平, 马顺, 金源等, 2012.大连地区工程场地各类岩土剪切波速的变化特征分析.防灾减灾学报, 28(4):7-11. doi: 10.3969/j.issn.1674-8565.2012.04.002 中华人民共和国建设部, 国家质量监督检验检疫总局, 2004. GB 50011-2010建筑抗震设计规范(2008年版).北京:中国建筑工业出版社. -
点击查看大图
计量
- 文章访问数: 249
- HTML全文浏览量: 25
- PDF下载量: 30
- 被引次数: 0
