Comparison of Four Simplified Analytical Methods for Seismic Design of Underground Structures
-
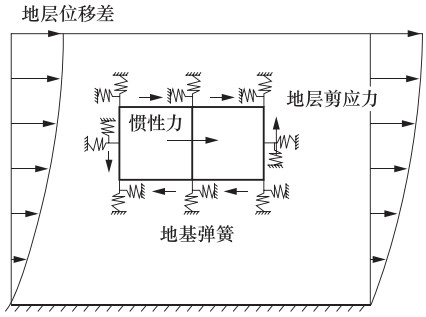
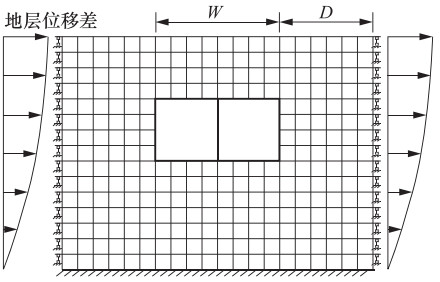
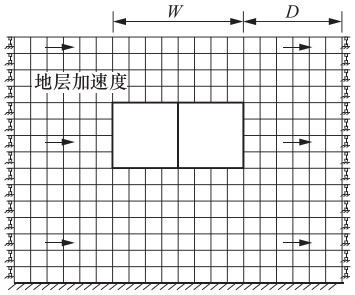
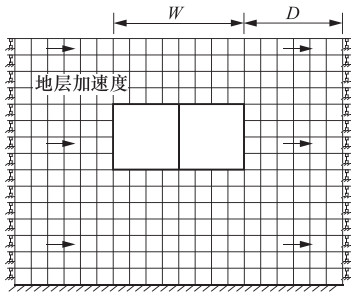
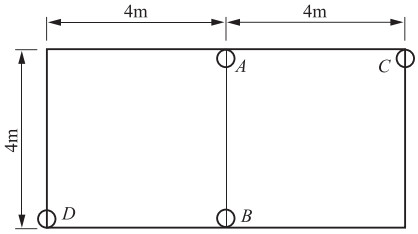
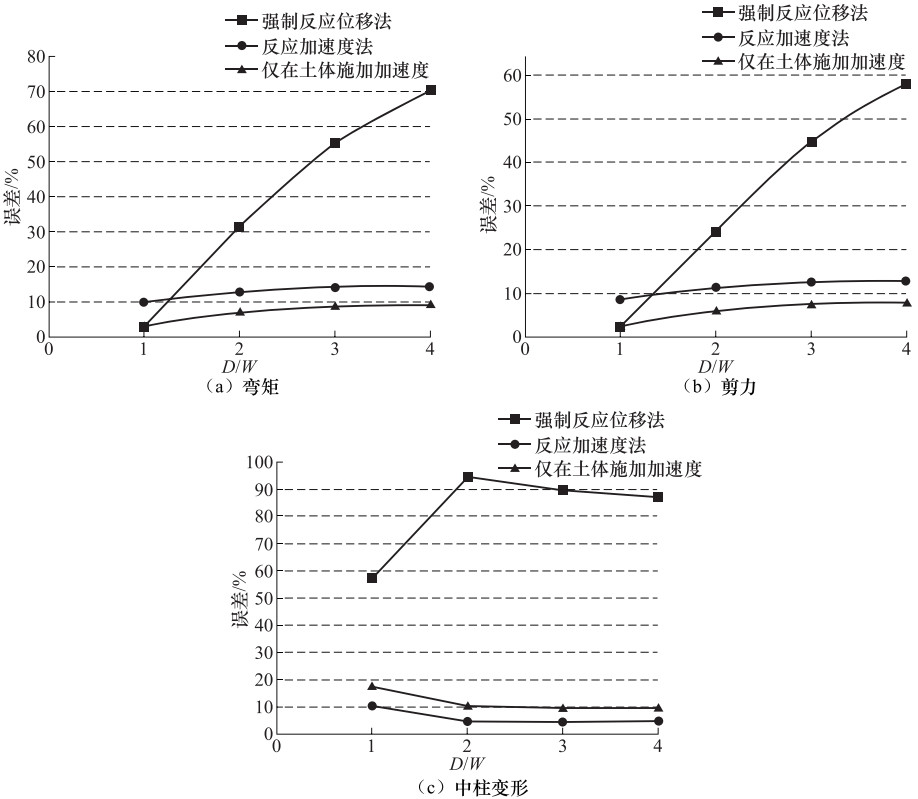
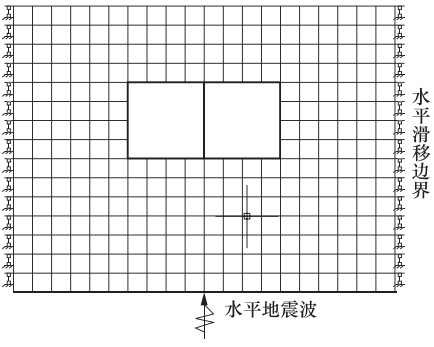
摘要: 在地下结构抗震设计简化分析方法中，强制反应位移法将土层变形施加在有限元模型侧边界模拟地震作用，反应加速度法将土层加速度施加到整个有限元模型上模拟地震作用，此外还有仅将土层加速度施加到土层模型上模拟地震作用的方法。上述方法均规避了反应位移法中关于弹簧刚度的取值问题，提高了计算效率。本文以1个双跨箱形结构为例，用动力时程分析的计算结果作为校核，分析了强制反应位移法、反应加速度法和仅将土层加速度施加到土体中的简化分析方法在不同侧边距条件下的计算精度，再结合常用的反应位移法，对比分析了4种简化分析方法的误差。分析结果表明：使用强制反应位移法时，侧边距取为1倍结构宽度导致的误差最小，反应加速度法和仅在土体施加加速度的简化方法对侧边距取值不敏感，反应位移法在角点造成的误差最大。Abstract: The theoretical basis of the simplified analytical method for seismic design of underground structure is that the deformation of underground structure depends on the deformation of foundation soil during earthquake, which fails to reflect the dynamic characteristics of the structure. Based on the most commonly used seismic displacement method, three kinds of simplified analytical methods are discussed in this paper. The forced displacement method is by applying the ground deformation to the boundary of the soil finite element model to simulate seismic load. The response acceleration method is by applying the ground acceleration to the integral finite element model to simulate seismic load. The third method is only by applying the ground acceleration to the soil finite element model to simulate seismic load. The above three simplified analytical methods can avoid calculating the value of the spring stiffness and improve the computational efficiency. Taking a double-span box structure as example, the calculations by applying three kinds of simplified analytical methods above with different lateral margins are carried out, and the analysis results are verified with the results of the dynamic time history method to calculate precisions. Combined with seismic displacement method, the error of four kinds of the simplified analytical methods is compared. The results show that the lateral margin should be equal to structure width when using the forced displacement method, and the response acceleration method and the method with only soil acceleration are not sensitive to the value of the lateral margin, and the error caused by the seismic displacement method reaches the maximum at the corner.
-
引言
剪切波速是土动力学和静力学的重要参数，在场地类别判定、砂土液化判别、场地卓越周期计算、土动剪切模量和阻尼比计算以及在地震安全性评价、地震小区划、土木工程抗震、岩土工程勘察、地震地质灾害评价等方面均有着重要应用(汪闻韶，1994；高玉峰等，2003；中华人民共和国建设部等，2004；王强等，2014)。在实际工程中，由于受塌孔、测试费用、测试时间、测试仪器以及场地条件等因素的影响，有时无法取得完整的波速资料或缺少波速资料，因此，关于剪切波速相关性的研究受到学者们的关注，也因此产生了很多经验公式。其中，剪切波速与深度统计关系的研究最多(程祖锋等，1997；陈国兴等，1998；高飞等，2005；陶小三等，2009；温一波等，2012；张小平等，2012；李铁飞等，2016；王金艳等，2017；荣棉水等，2017)，应用也最广泛。但是，现有的剪切波速随深度变化的经验统计关系式，大多是基于1个城市、开发区、甚至1个工程场地的测试资料，利用数理统计原理得到的。这些统计关系式的场地条件针对性强，但缺乏较大区域的普适性应用价值。
虽然地壳在横向和纵向的结构与物性方面均存在很强的非均匀性，但是影响中国大陆内部地貌格局和环境演变的构造运动具有分区性特征，成为构造分区的基础。因此，土质状态、地层结构、地形、地貌等地质条件也具有地区和区域性分布规律和特点(刘玉海等，1998；张培震等，2003)。因此，人们能够从更大范围的宏观上分析剪切波速随深度变化的统计关系，并从岩性条件、沉积环境等方面分析其变化规律特征，更好地服务工程建设。
根据资料的完整程度，并考虑地形地貌、地质构造条件，选择数据量相对较多、涉及区域相对较广的华北地区为研究对象，搜集整理了华北地区10个城市工程场地的928个钻孔共10703个测点剪切波速与土层埋深之间的经验统计模型关系。
通过对这些统计模型关系进行归纳梳理，探讨大华北地区各区域剪切波速随深度变化的特征，并从岩性条件、沉积环境等方面分析出现该特征的原因。通过对比分析，给出了大华北区主要岩性(黏性土和砂类土)剪切波速随深度变化的最佳拟合模型类型，且得出了华北地区黏性土和砂类土剪切波速随深度变化的最佳拟合经验统计关系的具体模型公式。经实例验证均取得较好的结果，所得结果能够为缺乏数据的区域提供一定参考。
1. 资料搜集与整理
本文共统计了北京、天津、唐山、邯郸、衡水、阜阳、烟台、东营、焦作、下辽河等10个城市(地区)的928个钻孔共10703个测点(图 1)，其中剪切波速测量所用仪器大部分为XG-I悬挂式波速测试仪，个别剪切波速的测量使用其它仪器，且所用方法均为单孔检层法。主要涉及的统计模型有5种，分别为线性函数${V_s} = a + bH$、指数函数${V_s} = a{H^b}$、一元二次多项式函数${V_s} = a + bH + c{H^2}$、一元三次多项式函数${V_s} = a + bH + c{H^2} + d{H^3}$和分段函数${V_s} = \left\{ \begin{array}{l} a + bH, H \le h\\ c{H^d}, H > h \end{array} \right.$。各城市的测点、钻孔数等资料的详细情况见表 1。
表 1 原始资料概况Table 1. Overview of the original data城市(地区) 总测点数/钻孔数 钻孔深度/m 北京 未知/173 0—100 天津 2212/78 0—120 唐山 未知/173 0—100 邯郸 1000/66 0—60 衡水 5696/82 0—91 阜阳 未知/50 0—60 烟台 未知/173 0—100 东营 未知/46 0—108 焦作 482/43 0—70 下辽河 1313/44 0—90 2. 统计分析
地貌及地层岩性是决定剪切波速大小的主要因素。在不同的地貌单元下，即使相同岩性的地层，因其沉积环境、沉积厚度等条件影响，剪切波速也会有较大差异(董菲蕃等，2013)。因此，分析剪切波速变化特征时主要考虑地貌及地层岩性2种因素，表 2为各统计区地貌和主要地层概况。
表 2 城市(地区)地貌和主要地层岩性Table 2. Overview of urban(regional) geomorphology and major strata lithology城市(地区) 典型地貌 沉积类型 典型地层岩性 其他 北京 冲洪积平原 全新世冲洪积物(Q4fp) 粉质黏土、各类砂层 天津 冲积平原 全新世冲积物(Q4f) 粉土、粉质黏土 唐山 中低山丘陵地貌、滨海平原、三角洲地貌 全新世冲洪积物(Q4fp) 粉质黏土(黄土)、砂、卵石 邯郸 冲洪积平原 晚更新世滑积物(Q3dp) 粉土、粉质黏土、砂层和砾石 衡水 山前冲洪积平原、洪积湖积为主的中部平原 全新世冲积物(Q4f) 粉质黏土、粉土、砂层 阜阳 淮北冲积平原 全新世冲积物(Q4f) 粉土、粉质黏土、砂和砾石层 有古河道发育 烟台 低山丘陵、冲积
—海积平原全新世残坡积物(Q4eld) 黏性土、砂层 东营 黄河冲积三角洲地貌 全新世冲积物(Q4f) 黏性土、砂 黏土多含粉砂 焦作 山区与平原过渡带(统计区为冲洪积平原) 全新世冲洪积物(Q4fp) 黏性土、砂层 地貌复杂，冲洪积平原、低山丘陵、漫滩、洼地均有；黏性土中多夹砂或砾石 下辽河 河流冲洪积平原 全新世残坡积物(Q4eld) 粉质黏土、粉细砂层 华北地区第四系覆盖层较厚(大于100m)，岩性主要为黏性土和砂类土，局部夹粉土和砂砾石互层(李守礼等，2005)。由于各地钻孔深度不一，为便于分析，钻孔深度统一取50m；模型关系仅考虑主要岩性，即黏性土和砂类土。根据统计归并得到了9个统计模型，见表 3、表 4以及图 2、图 3。
表 3 黏性土剪切波速最优拟合经验关系统计Table 3. The best fitting empirical and statistical formula for shear wave velocity of clay soil城市(地区) 经验关系式 拟合优度 钻孔深度/m 测点数 天津(侯颉等，2017) ${V_{\rm{s}}} = - 0.0148{H^2} + 5.0703H + 109.53$ 0.912 0—120 206 北京(王广军等，1986) ${V_{\rm{s}}} = 104.0{H^{0.407}}$ 未知 0—100 未知 唐山(王广军等，1986) ${V_{\rm{s}}} = 143.9{H^{0.317}}$ 未知 0—100 未知 烟台(王广军等，1986) ${V_{\rm{s}}} = 229.8{H^{0.142}}$ 未知 0—100 未知 邯郸(王帮圆等，2013) ${V_{\rm{s}}} = - 0.0173{H^2} + 7.4H + 129.9$ 0.848 0—50 ＞200 衡水(何仲太等，2014) ${V_{\rm{s}}} = 4.2529H + 134.42$ 0.937 0—100 281 阜阳(刘之雨等，2016) ${V_{\rm{s}}} = 0.0044{H^3} - 0.4836{H^2} + 18.5918H + 65.5488$ 0.825 0—60 未知 东营(齐静静，2011) ${V_{\rm{s}}} = \left\{ \begin{array}{l} 4.57H + 110.92, H < 30\\ 98.89{H^{0.286}}, H \ge 30 \end{array} \right.$ SD：0.784 0—108 ＞200 焦作(潘国营等，2000) ${V_{\rm{s}}} = 121.80{H^{0.34}}$ 0.940 0—43 82 下辽河(齐鑫等，2012) ${V_{\rm{s}}} = \left\{ \begin{array}{l} - 0.0665{H^2} + 9.944H + 99.729, H < 75\\ 84.261{H^{0.398}}, H \ge 75 \end{array} \right.$ 0.931 0—90 ＞150 注：SD(Standard Deviation)为标准差。 表 4 砂类土剪切波速最优拟合模型统计Table 4. The best fitting model of shear wave velocity for sand soil城市(地区) 经验关系式 拟合优度 钻孔深度/m 测点数 天津(侯颉等，2017) ${V_{\rm{s}}} = - 0.0244{H^2} + 6.0664H + 117.16$ 0.764 0—120 378 天津(王广军等，1986) ${V_{\rm{s}}} = 98.4{H^{0.334}}$ 未知 0—100 未知 北京(王广军等，1986) ${V_{\rm{s}}} = 111.0{H^{0.309}}$ 未知 0—100 未知 烟台(王广军等，1986) ${V_s} = 124.0{H^{0.270}}$ 未知 0—100 未知 邯郸(王帮圆等，2013) ${V_{\rm{s}}} = - 0.05783{H^2} + 9.896H + 111.2$ 0.747 0—50 70 衡水(何仲太等，2014) ${V_{\rm{s}}} = 69.816{H^{0.4166}}$ 0.756 0—91 834 东营(齐静静，2011) ${V_{\rm{s}}} = 53.89{H^{0.446}}$ SD：0.831 0—108 ＞150 焦作(潘国营等，2000) ${V_{\rm{s}}} = 121.19{H^{0.31}}$ 0.920 0—70 41 下辽河(齐鑫等，2012) ${V_{\rm{s}}} = 76.97{H^{0.4244}}$ 0.905 0—90 ＞200 
图 2 黏性土剪切波速与深度变化关系的拟合模型曲线类型Figure 2. Fitting model curve type of relationship between shear wave velocity and depth of clay soil
图 3 砂类土剪切波速与深度变化关系的拟合模型曲线类型Figure 3. Fitting model curve type of relationship between shear wave velocity and depth of sand soil2.1 黏性土
从表 3可以看出，华北区10个城市(地区)共分为5种拟合模型：线性函数(衡水)、冥函数(北京、唐山、烟台、焦作)、二次函数(天津、邯郸)、三次函数(阜阳)和分段函数(东营、下辽河)；拟合优度方面均较高(大于0.8)。而从图 2的曲线形状看出，虽然剪切波速的总体变化随深度增加而增大，但不同地区模拟曲线的变化趋势存在一定差异，除烟台、阜阳拟合模型曲线形状和变化趋势差异较大外，其它8条曲线的变化趋势以邯郸为界分为2部分：天津、衡水、东营和北京、唐山、焦作。
(1) 烟台、阜阳拟合模型曲线的形状接近，其变化趋势均与其它8条曲线明显不同，表现为随着深度增大，剪切波速起初增大较快，但在深度达10m和20m后增加较缓慢。说明该地区黏性土随深度增加，软硬程度变化较小。由于烟台地区地貌类型为冲积—海积平原，相应的沉积层类型为第四纪残坡积层(Q4eld)和冲海积层(Q4fm)，地层较软，因此剪切波速随深度变化较小。阜阳地区在地貌单元上属于淮北冲积平原，地层有第四系冲积层(Q4f)和晚更新世冲湖积层(Q3fl)，受古河道影响，地层较软，故剪切波速增大也较缓。
(2) 冥函数模型中，除烟台地区的模型曲线外，其它3条(北京、唐山、焦作)拟合模型非常接近，符合随深度增加、土层硬度逐渐增加的趋势。这与3个地方的沉积层成因均为第四系冲洪积层(Q4fp)有很大关系。
(3) 虽然衡水模型曲线为线性，但仅从曲线形状上看与天津(二次曲线)、东营(分段式曲线)非常接近，剪切波速随深度变化的趋势基本符合线性增大趋势。
由上述分析可知，沉积环境对剪切波速的变化影响较大，相同或相似的沉积环境，其模型曲线的形状和变化趋势均相近，如冲积—海积平原的烟台与冲湖积平原的阜阳，另外还有同为冲洪积的北京、唐山和焦作。
2.2 砂类土
与黏性土相比，华北地区砂类土拟合模型具有以下特点：
(1) 9条拟合曲线中只涉及冥函数模型和一元二次模型，其中一元二次曲线2条(天津、邯郸)，其余7条为冥函数，如图 3所示。
(2) 从图 3曲线分布可以看出，2种函数的变化趋势较一致，该区砂类土的拟合模型具有较好的规律性；邯郸砂类土统计拟合模型曲线的规律性与其它曲线差异较大，其原因与黏性土相同。
(3) 从拟合优度看，幂函数的拟合优度明显高于一元二次曲线，且模型曲线之间的差异值基本在50—150m/s，因此在该区域内砂类土的剪切波速随深度变化的拟合模型中，冥函数较为理想。
由上述分析可知，即使相同模型、相同岩性的土类，由于沉积环境相差大，其模型曲线的差异仍较大，如邯郸(位于滑积物组成的冲洪积平原)与天津(位于冲积物组成的冲积平原)的模型曲线。沉积环境越相近，模型曲线之间的差异性越小。
3. 最佳经验关系拟合
3.1 最佳经验关系
由上述统计对比分析可知，无论是黏性土还是砂类土，其剪切波速与深度之间的规律性较好且较一致的均为幂函数。黏性土与砂类土不同的是，黏性土幂函数模型的代表性区域较小(北京、唐山、焦作)，而砂类土的代表性区域相对较大(除东营外的其它地区)。
为了找出便于工程应用的通用冥函数模型，对3条黏性土和7条砂类土的冥函数曲线进一步优化拟合，分别得到2种类型土的区域通用拟合曲线(图 4)。其中黏性土的拟合关系式为y=122.6x0.3595，拟合优度R2=0.9765；砂类土拟合关系式为y=92.33x0.3525，拟合优度R2=0.9436。
图 4 剪切波速随深度变化冥函数统计模型及区域最优拟合曲线Figure 4. The power function statistical model curve and regional optimal fitting curve of the relationship between shear wave velocity and depth根据得到的拟合优度，认为上述拟合结果作为华北平原区冲洪积成因的黏性土和砂类土的剪切波速随深度变化通用计算公式是可行的。
3.2 实例验证
将得到的拟合函数应用于实际工程，并将钻孔的拟合剪切波速与实测剪切波速进行比较，以验证利用通用公式进行剪切波速与埋深关系回归分析的可靠性。
黏性土实例数据选自潘国营等(2000)给出的43个钻孔在50m范围内的不同深度(2m、4m、6m、8m、10m、12m、28m、32m、34m、36m和38m)的实测剪切波速，测试方法为单孔检层法；砂类土实例数据则选自何仲太等(2014)给出的82个钻孔在100m范围内的不同深度(4m、8m、12m、16m、20m、24m、28m、56m、60m、64m、68m、72m、76m、80m、84m、88m、92m、96m和100m)的实测剪切波速，该波速同样采用单孔检层法测试得到，采样间隔为1m。
黏性土实例采用焦作城区分布的主要岩土类型，包括人工填土、黏性土(粉土、粉质黏土和黏土)、砂类土和碎石土，选取黏土的实测剪切波速，分别用该统计区的拟合公式及区域通用拟合公式进行剪切波速拟合，并与实测剪切波速比较进行误差分析，结果见表 5。
表 5 黏性土剪切波速统计模型计算值、通用模型计算值与实测值对比Table 5. Comparison of calculated values from statistical model, from general model, and measured values for the shear wave velocity of clay soil深度H/m Vs实测值/m·s-1 统计模型 通用模型 Vs计算值/m·s-1 误差/% Vs计算值/m·s-1 误差/% 2 105 150 43.1 177 49.8 4 180 186 3.47 218 12.1 6 202 211 4.55 246 15.6 8 240 231 -3.8 268 7.88 10 260 247 -4.8 286 7.9 12 273 262 -4.1 302 9.72 28 425 340 -20 389 -4.4 32 340 355 4.37 405 25.3 34 370 362 -2.3 413 17.7 36 370 368 -0.5 420 20.2 38 380 374 -1.5 427 19.3 砂类土实例为衡水市某工程项目钻孔实测剪切波速，土层岩性主要为填土、黏性土(粉土、粉质黏土和黏土)、粉砂和细砂，选取粉砂进行验算，结果见表 6。
表 6 砂类土剪切波速统计模型计算值、通用模型计算值与实测值对比Table 6. Comparison of calculated values from statistical model, from general model, and measured values for the shear wave velocity of sand soil深度H/m Vs实测值/m·s-1 统计模型 通用模型 Vs计算值/m·s-1 误差/% Vs计算值/m·s-1 误差/% 4 160 124 -23 159 -0.6 8 176 166 -5.7 201 14.2 12 201 197 -2 231 14.9 16 210 222 5.71 255 21.4 20 237 243 2.53 275 16 24 265 262 -1.1 293 10.6 28 285 280 -1.8 309 8.42 56 378 373 -1.3 391 3.44 60 385 384 -0.3 400 3.9 64 402 395 -1.7 409 1.74 68 417 405 -2.88 418 0.24 72 431 415 -3.71 426 -1.2 76 470 424 -9.79 434 -7.7 80 476 433 -9.03 442 -7.1 84 496 442 -10.9 449 -9.5 88 510 451 -11.6 456 -11 92 525 459 -12.6 463 -12 96 532 467 -12.2 470 -12 100 571 476 -16.6 476 -17 (1) 砂类土通用模型的剪切波速拟合误差与统计模型差别不大，这与砂类土各区总体变化规律一致性较好有很大关系；也与实例数据与通用模型接近有关。
(2) 黏性土的通用模型计算结果与统计模型差别较大，由图 4(a)也可明显看出此差别，大部分测点的误差率小于20%，个别点的差值较大，但由此计算出的剪切波速不会使场地的软硬程度相差1级，故误差在可接受范围内。
4. 讨论与结论
虽然地貌条件与地层岩性是影响土体剪切波速大小的决定因素，但土的结构、状态、土体中存在的裂隙、孔隙度及孔隙中的充填物等也对剪切波速有一定影响，因此，在同一地貌单元内，相同土层的剪切波速也存在差别。由于地层岩性生成的地质环境不同，导致其土层密度、埋深、颗粒成分含量等物理性质各不相同，因此土层剪切波速具有明显的差异性。
通过上述统计分析可知，虽然华北地区黏性土和砂类土剪切波速随深度变化的拟合模型类型较多，但最佳模型类型均为幂函数模型，且砂类土相比于黏性土更具规律性。沉积环境相似的区域模型曲线形状和变化趋势更接近(如烟台和阜阳)，沉积环境相差较大的区域其曲线形状和变化趋势差异均较大(如邯郸和天津)，且沉积环境对黏性土的影响相比于砂类土更大。经实例验证，优化拟合后得到的华北区黏性土和砂类土的通用函数模型的误差均在合理范围之内，可作为该大区缺乏剪切波速资料时的估算公式。然而，通用模型也有一定的适用条件，黏性土的剪切波速受沉积环境影响较大，其通用模型的代表性有限，对于沉积条件接近的平原区适用性较强；砂类土的通用模型对于全新世堆积物、冲积层和冲洪积层的砂类土适用性较好。
由于统计数据量的不足，导致区域覆盖面不够广，因此今后还需要更多的数据统计分析，进一步充实和完善相关的研究工作。
-
图 10 自由场最不利水平相对位移分布
Figure 10. Least favorable displacement distributions of free-field
图 12 3种带土体简化分析方法的计算误差
Figure 12. Calculation errors of three simplified methods with soil model
表 1 土体与结构的物理力学参数
Table 1. Physical and mechanical parameters of soil and structure
类型 密度/g·cm-3 弹性模量/MPa 泊松比 内摩擦角/° 粘聚力/kPa 土体 1.9 30 0.3 30 30 结构 2.3 30000 0.167 
下载: 导出CSV
表 2 不同侧边距的弯矩计算结果
Table 2. Bending moment of structure with different lateral margins
D/W 使用方法 弯矩/kN·m 截面A 截面B 截面C 截面D 1倍 强制反应位移法 292.9 -291.3 280.8 353.9 反应加速度法 319.4 -324.5 294.0 367.1 仅在土体施加加速度 296.5 -300.6 278.4 351.8 2倍 强制反应位移法 179.5 -181.3 200.7 282.1 反应加速度法 328.1 -33.3 301.0 372.2 仅在土体施加加速度 309.3 -313.6 287.9 360.0 3倍 强制反应位移法 100.4 -101.3 147.7 224.7 反应加速度法 331.7 -336.9 303.8 374.9 仅在土体施加加速度 314.5 -18.9 291.8 363.9 4倍 强制反应位移法 50.2 -50.4 113.8 187.4 反应加速度法 332.6 -37.8 304.3 375.5 仅在土体施加加速度 316.2 -20.6 292.8 365.0 反应位移法 286.5 -290.1 201.0 199.8 动力分析 282.5 -89.1 272.3 345.2
下载: 导出CSV
表 3 不同侧边距的剪力计算结果
Table 3. Shear force of structure with different lateral margins
D/W 使用方法 剪力/kN 截面A 截面B 截面C 截面D 1倍 强制反应位移法 -182.6 -182.6 -213.5 -263.8 反应加速度法 -195.8 -204.0 -205.6 -271.7 仅在土体施加加速度 -186.6 -186.6 -196.8 -266.3 2倍 强制反应位移法 -112.8 -112.8 -169.0 -249.3 反应加速度法 -201.3 -209.4 -210.0 -274.3 仅在土体施加加速度 -194.7 -194.7 -202.0 -270.7 3倍 强制反应位移法 -63.0 -63.0 -144.4 -219.7 反应加速度法 -203.6 -211.7 -211.9 -276.2 仅在土体施加加速度 -198.0 -198.0 -204.2 -273.3 4倍 强制反应位移法 -31.4 -31.4 -128.2 -199.6 反应加速度法 -204.1 -212.3 -212.0 -276.4 仅在土体施加加速度 -199.0 -199.0 -204.5 -273.8 反应位移法 -174.8 -183.0 -106.2 -106.2 动力分析 -175.7 -180.6 -194.0 -266.7
下载: 导出CSV
表 4 不同侧边距的结构变形计算结果
Table 4. Deformation of structure with different lateral margins
D/W 使用方法 中柱顶、底相对位移/mm 1倍 强制反应位移法 2.396 反应加速度法 5.011 仅在土体施加加速度 4.636 2倍 强制反应位移法 0.302 反应加速度法 5.340 仅在土体施加加速度 5.026 3倍 强制反应位移法 0.584 反应加速度法 5.354 仅在土体施加加速度 5.071 4倍 强制反应位移法 0.722 反应加速度法 5.346 仅在土体施加加速度 5.077 反应位移法 3.628 动力分析 5.596
下载: 导出CSV
表 5 Kobe波下弯矩计算结果
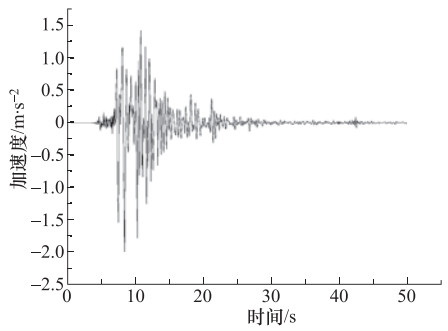
Table 5. Bending moment calculation results of structure under Kobe seismic wave
使用方法 弯矩/kN·m 平均误差/% 截面A 截面B 截面C 截面D 动力分析 375.3 -383.7 332.1 410.6 反应位移法 400.2 -403.7 284.3 276.0 10.5 强制反应位移法 298.8 -310.4 275.9 364.3 18.0 反应加速度法 341.9 -349.2 308.4 384.7 8.0 仅在土体施加加速度 312.4 -317.7 288.0 364.5 15.0
下载: 导出CSV
表 6 Kobe波下剪力计算结果
Table 6. Shear force calculation results of structure under Kobe seismic wave
使用方法 剪力/kN 平均误差/% 截面A 截面B 截面C 截面D 动力分析 -230.8 -242.9 -218.3 -299.0 反应位移法 -242.6 -257.5 -159.9 -139.9 13.7 强制反应位移法 -190.4 -190.4 -180.2 -290.7 27.0 反应加速度法 -207.4 -222.2 -209.8 -281.2 4.4 仅在土体施加加速度 -196.9 -196.9 -198.1 -275.4 5.6
下载: 导出CSV
表 7 Kobe波下结构变形计算结果
Table 7. Deformation calculation results of structure under Kobe seismic wave
使用方法 中柱顶、底相对位移/mm 平均误差/% 动力分析 5.808 反应位移法 4.768 17.9 强制反应位移法 3.232 44.4 反应加速度法 5.371 7.5 仅在土体施加加速度 4.900 15.6
下载: 导出CSV
-
陈国兴, 陈苏, 杜修力等, 2016.城市地下结构抗震研究进展.防灾减灾工程学报, 36(1):1-23. http://d.old.wanfangdata.com.cn/Periodical/jzgcjsysj2018063865 陈晓强, 钱七虎, 2010.我国城市地下空间综合管理的探讨.地下空间与工程学报, 6(4):666-671. http://d.old.wanfangdata.com.cn/Periodical/dxkj201004002 川岛一彦, 1994.地下构筑物の耐震设计.日本:鹿岛出版会. 林皋, 1990a.地下结构抗震分析综述(上).世界地震工程, (2):1-10. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000004586861 林皋, 1990b.地下结构抗震分析综述(下).世界地震工程, (3):1-10, 42. http://d.old.wanfangdata.com.cn/Periodical/dbdzyj201201005 刘晶波, 刘祥庆, 李彬, 2008.地下结构抗震分析与设计的Pushover分析方法.土木工程学报, 41(4):73-80. doi: 10.3321/j.issn:1000-131X.2008.04.011 刘晶波, 王文晖, 赵冬冬等, 2013.地下结构抗震分析的整体式反应位移法.岩石力学与工程学报, 32(8):1618-1624. http://d.old.wanfangdata.com.cn/Periodical/yslxygcxb201308014 刘如山, 胡少卿, 石宏彬, 2007.地下结构抗震计算中拟静力法的地震荷载施加方法研究.岩土工程学报, 29(2):237-242. doi: 10.3321/j.issn:1000-4548.2007.02.014 片山幾夫, 足立正信, 嶋田穰等, 1985.地下埋設構造物の実用的な準動的解析手法「応答震度法」の提案.土木学会年次学術講演会講演概要集, (40):737-738. 钱七虎, 2017.推进城市地下空间规划建设的思考.城乡建设, (18):60-65. doi: 10.3969/j.issn.1002-8455.2017.18.024 权登州, 王毅红, 井彦林等, 2015.黄土地区地铁地下结构抗震研究综述.震灾防御技术, 10(3):565-574. http://zzfy.eq-j.cn/zzfyjs/ch/reader/view_abstract.aspx?flag=1&file_no=20150310&journal_id=zzfyjs 同济大学, 2009.DG/TJ 08-2064-2009地下铁道建筑结构抗震设计规范.上海: 上海市建筑建材业市场管理总站. 杨智勇, 黄宏伟, 张冬梅等, 2012.盾构隧道抗震分析的静力推覆方法.岩土力学, 33(5):1381-1388. doi: 10.3969/j.issn.1000-7598.2012.05.016 中华人民共和国建设部, 2006.GB 50111-2006铁路工程抗震设计规范.北京:中国计划出版社. 中华人民共和国住房和城乡建设部, 2014.GB 50909-2014城市轨道交通结构抗震设计规范.北京:中国计划出版社. Hashash Y. M. A., Hook J. J., Schmidt B., et al., 2001. Seismic design and analysis of underground structures. Tunnelling and Underground Space Technology, 16(4):247-293. doi: 10.1016/S0886-7798(01)00051-7 Iida H., Hiroto T., Yoshida N., et al., 1996. Damage to daikai subway station. Soils and Foundations, 36(S):283-300. Penzien J., 2000. Seismically induced racking of tunnel linings. Earthquake Engineering Structural Dynamics, 29(5):683-691. doi: 10.1002/(ISSN)1096-9845 Tateishi A., 2005. A study on seismic analysis methods in the cross section of underground structures using static finite element method. Structural Engineering, 22(1):41-53. doi: 10.2208/jsceseee.22.41s Wang J. N., 1993. Seismic design of tunnels:a simple state-of-the-art design approach. New York:Parsons Brinckerhoff Quade and Douglas Inc. 期刊类型引用(7)
1. 张强，金鑫，刘英君. 浅埋地下结构反应位移法不同位置弹簧刚度系数的影响分析. 市政技术. 2023(02): 113-119 . 
百度学术2. 闫晓京，邢珏蕙，周忠发，朱忠义，孙枫然，周笋，段世昌，閤东东. 北京歌舞剧院大埋深地下结构设计. 建筑结构. 2023(18): 63-68+143 . 百度学术3. 程新俊，许翔，景立平，崔杰，梁海安. 一种基床系数计算方法及其在反应位移法中的应用. 岩土工程学报. 2023(12): 2604-2613 . 百度学术4. 刘春峰，屈永强，许紫刚. 用于地下结构地震反应分析的改进反应加速度法. 震灾防御技术. 2021(04): 710-716 . 本站查看5. 赵密，邵伟昂，黄景琦，杜修力，王媛. 圆形隧道横断面地震响应简化解析方法的数值验证. 工程力学. 2020(09): 84-93 . 百度学术6. 赵密，邵伟昂，黄景琦，杜修力，王媛. 衬砌厚度对隧道抗震简化解析方法精度的影响. 地震工程与工程振动. 2020(06): 47-60 . 百度学术7. 卜永红，权登州，祝河清，石晶. 砂土场地地铁车站抗震计算方法. 铁道建筑. 2019(11): 88-90+100 . 百度学术其他类型引用(8)
-
下载:
点击查看大图
计量
- 文章访问数: 228
- HTML全文浏览量: 30
- PDF下载量: 57
- 被引次数: 15
