Analysis of Precision of the Simplex Location Method in the Xinjiang Digital Seismic Network
-
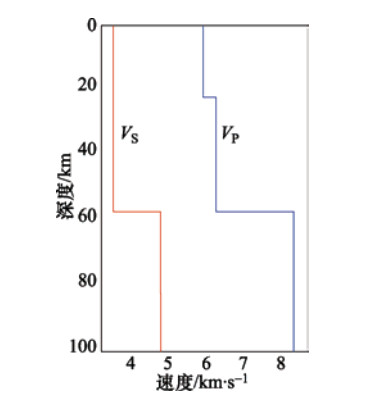
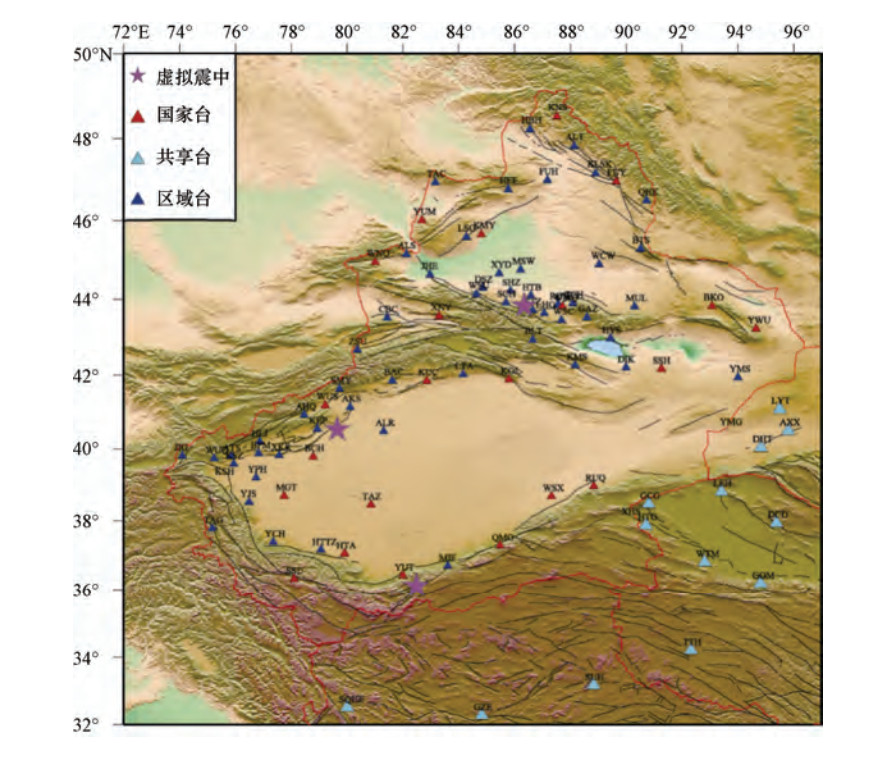
摘要: 地震定位是地震学中最基本的问题之一，现阶段大部分采用基于走时的方法。单纯形定位方法作为一种直接搜索类的方法，在新疆测震台网日常地震目录产出中发挥了重要作用。本文采用数值模拟的方法，利用新疆测震台网现有布局，结合“3400”走时表，分析单纯形定位方法在新疆测震台网的测定精度。研究表明，对于新疆测震台网网内浅源地震，单纯形定位方法能够得出较为精确的震中位置，而得出的网外地震震中位置存在一定偏差；初至折射波对震源深度有一定的控制能力，速度模型的准确性对震源深度和发震时刻的测定影响较大。Abstract: Seismic location is one of the most basic issues in seismology. Currently, most of earthquake location used a time-based approach. However, the simplex location method, as a direct search method, plays an important role in the daily earthquake catalog of the Xinjiang Digital Seismic Network. This paper applies numerical simulation methods, using the Xinjiang Digital Seismic Network and combing the "3400" travel timetable, and analyzes the measurement accuracy of the simplex location method in the Xinjiang Digital Seismic Network. The results show that for the shallow earthquakes in the Xinjiang Digital Seismic Network, the simplex location method can get a high-accurate epicenter location, However, there exists a certain deviation in outside the seismic network. The first arrival refracted wave has a certain ability to control the depth of the epicenter. The accuracy of the velocity model has a great influence on the depth of the epicenter and the determination of the time of earthquake occurrence.
-
Key words:
- Xinjiang region /
- Seismic location /
- Focal depth /
- Simplex location method
-
图 4 新疆测震台网分布及虚拟震中位置
Figure 4. Distribution of seismic station in Xinjiang and suppositional earthquake location
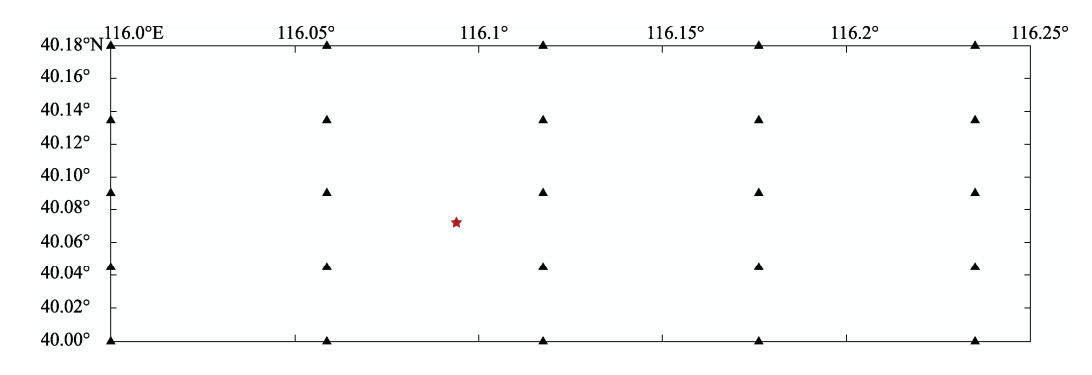
表 1 虚拟台网不同初始深度的定位结果
Table 1. Location results at different initial depths of the virtual network
虚拟震中 虚拟发震时刻 初始深度
/km定位结果 北纬/° 东经/° 深度/km 发震时刻 残差 40.0719°N
116.0939°E
H：13km2010-05-08
10:30:30.010 40.0839 116.0902 11 10:30:30.3 0.2 20 40.0672 116.0916 13 10:30:29.8 0.06 30 40.0713 116.0934 12 10:30:30.0 0.006 40 40.0713 116.0939 13 10:30:29.9 0.01 
下载: 导出CSV
表 2 各研究区域不同初始深度的定位结果
Table 2. Results of location in different regions at different initial depths of Xinjiang Digital Seismic Network
区域 虚拟震中 虚拟发震时刻 初始深度/km 定位结果 北纬/° 东经/° 深度/km 发震时刻 残差 南天山西段 40.54°N
79.65°E
H：10km2010-01-02
23:22:0310
20
30
4040.54
40.54
40.54
40.5479.65
79.65
79.65
79.659
9
10
923:22:3.0
23:22:3.0
23:22:3.1
23:22:3.00.21
0.22
0.25
0.21天山中段 43.83°N
86.35°E
H：10km2016-12-08
13:15:0310
20
30
4043.82
43.82
43.82
43.8286.35
86.35
86.35
86.3510
10
10
913:15:3.1
13:15:3.1
13:15:3.1
13:15:3.10.46
0.46
0.46
0.46西昆仑 36.12°N
82.49°E
H：10km2014-02-12
17:19:4810
20
30
4036.13
36.12
36.14
36.1382.49
82.49
82.51
82.498
9
10
917:19:48.3
17:19:48.4
17:19:48.5
17:19:48.40.37
0.38
0.47
0.38
下载: 导出CSV
表 3 加入随机误差后不同初始深度的定位结果
Table 3. Positioning results at different initial depths after adding random errrors
区域 虚拟震中 虚拟发震时刻 初始深度/km 定位结果 北纬/° 东经/° 深度/km 发震时刻 残差 南天山西段 40.54°N
79.65°E
H：10km2010-01-02
23:22:0310
20
30
4040.54
40.54
40.54
40.5479.64
79.65
79.66
79.6811
11
10
923:22:3.1
23:22:3.1
23:22:3.1
23:22:2.90.41
0.41
0.42
0.45天山中段 43.83°N
86.35°E
H：10km2016-12-08
13:15:0310
20
30
4043.83
43.83
43.82
43.8286.36
86.36
86.36
86.3512
12
10
1113:15:3.1
13:15:3.1
13:15:3.1
13:15:3.00.58
0.56
0.52
0.55西昆仑 36.12°N
82.49°E
H：10km2014-02-12
17:19:4810
20
30
4036.12
36.12
36.12
36.1382.49
82.49
82.51
82.517
8
9
817:19:48.3
17:19:48.3
17:19:48.2
17:19:48.40.49
0.42
0.46
0.46
下载: 导出CSV
表 4 不同数据源的定位结果
Table 4. Positioning results from different data source
处理方法 虚拟震中 虚拟发震时刻 初始深度/km 定位结果 北纬/° 东经/° 深度/km 发震时刻 残差 1 40.54°N
79.65°E
H：10km2010-01-02
23:22:0310
20
3040.54
40.54
40.5379.65
79.64
79.668
11
1223:22:2.9
23:22:3.2
23:22:2.00.4
0.43
0.412 40.54°N
79.65°E
H：10km2010-01-02
23:22:0310
20
3040.54
40.53
40.5479.65
79.66
79.638
8
923:22:3.0
23:22:2.8
23:22:3.00.4
0.38
0.253 40.54°N
79.65°E
H：10km2010-01-02
23:22:0310
20
3040.56
40.56
40.5579.64
79.63
79.6423
19
2123:22:2.0
23:22:1.5
23:22:1.71.3
1.3
1.24 40.54°N
79.65°E
H：10km2010-01-02
23:22:0310
20
3040.55
40.53
40.5179.64
79.70
79.6310
10
1023:22:2.9
23:22:2.0
23:22:3.40.35
0.65
0.535 40.54°N
79.65°E
H：10km2010-01-02
23:22:0310
20
3040.54
40.55
40.5579.60
79.64
79.635
4
923:22:2.8
23:22:2.9
23:22:3.60.27
0.28
0.196 40.54°N
79.65°E
H：10km2010-01-02
23:22:0310
20
3040.50
40.50
40.4979.39
79.38
79.375
6
623:22:4.5
23:22:5.8
23:22:5.70.69
0.6
0.54
下载: 导出CSV
表 5 虚拟震源位于下地壳时不同数据源的定位结果
Table 5. Positioning results from different data source in which the suppositional earthquake is located in the lower crust
处理方法 虚拟震中 虚拟发震时刻 初始深度
/km定位结果 北纬/° 东经/° 深度/km 发震时刻 残差 01 40.54°N
79.65°E
H：30km2010-01-02
23:22:0310
20
3040.54
40.54
40.5479.65
79.65
79.6530
29
2923:22:3.0
23:22:2.9
23:22:2.90.06
0.2
0.1202 40.54°N
79.65°E
H：30km2010-01-02
23:22:0310
20
3040.54
40.53
40.5479.65
79.65
79.6529
31
2923:22:2.9
23:22:3.0
23:22:2.90.31
0.29
0.281 40.54°N
79.65°E
H：30km2010-01-02
23:22:0310
20
3040.54
40.53
40.5479.67
79.66
79.6518
25
2723:22:2.3
23:22:2.8
23:22:2.80.9
0.4
0.52 40.54°N
79.65°E
H：30km2010-01-02
23:22:0310
20
3040.53
40.54
40.5479.66
79.65
79.6410
31
3023:22:3.4
23:22:2.9
23:22:3.00.6
0.3
0.23 40.54°N
79.65°E
H：30km2010-01-02
23:22:0310
20
3040.55
40.56
40.5479.64
79.63
79.6439
30
4123:22:1.6
23:22:1.0
23:22:1.80.9
1.4
1.04 40.54°N
79.65°E
H：30km2010-01-02
23:22:0310
20
3040.54
40.51
40.5679.61
79.59
79.6431
31
3123:22:3.4
23:22:3.9
23:22:2.90.3
0.3
0.35 40.54°N
79.65°E
H：30km2010-01-02
23:22:0310
20
3040.59
40.54
40.5579.70
79.62
79.6327
30
3323:22:1.8
23:22:3.3
23:22:3.20.5
0.2
0.36 40.54°N
79.65°E
H：30km2010-01-02
23:22:0310
20
3040.53
40.49
40.4779.46
79.45
79.3437
36
3623:22:4.0
23:22:4.3
23:22:4.90.4
0.5
0.7注：处理方法01未进行任何处理，处理方法02加入±0.5s随机误差，下同。
下载: 导出CSV
表 6 不同虚拟震源深度的定位结果（固定初始震源深度10km）
Table 6. Positioning results in different virtual source locations at a fixed initial depth of 10km
震源位置及发震时刻 处理方法 定位结果 北纬/° 东经/° 深度/km 发震时刻 残差 40.54°N
79.65°E
H：5km
2010-01-02
23:22:0301
02
1
2
3
4
5
640.54
40.54
40.53
40.53
40.54
40.57
40.53
40.5079.65
79.65
79.65
79.66
79.64
79.65
79.67
79.435
5
6
7
20
6
7
1923:22:3.1
23:22:3.1
23:22:3.0
23:22:3.0
23:22:2.9
23:22:2.8
23:22:2.7
23:22:4.90.2
0.3
0.5
0.6
1.6
0.5
0.1
0.640.54°N
79.65°E
H：15km
2010-01-02
23:22:0301
02
1
2
3
4
5
640.54
40.53
40.54
40.54
40.55
40.55
40.53
40.5279.65
79.65
79.65
79.66
79.63
79.64
79.65
79.5115
15
16
12
8
15
10
1523:22:3.0
23:22:3.0
23:22:3.1
23:22:3.0
23:22:1.7
23:22:3.0
23:22:3.2
23:22:3.90.2
0.3
0.2
0.4
1.9
0.3
0.2
0.640.54°N
79.65°E
H：20km
2010-01-02
23:22:0301
02
1
2
3
4
5
640.54
40.53
40.54
40.53
40.56
40.55
40.53
40.5279.65
79.65
79.65
79.66
79.64
79.62
79.63
79.4820
19
19
17
16
20
14
2423:22:2.9
23:22:3.0
23:22:3.0
23:22:3.1
23:22:2.0
23:22:3.2
23:22:3.2
23:22:4.20.3
0.47
0.4
0.3
1.7
0.4
0.2
0.7
下载: 导出CSV
-
蔡明军, 山秀明, 徐彦等, 2004.从误差观点综述分析地震定位方法.地震研究, 27(4):314-317. doi: 10.3969/j.issn.1000-0666.2004.04.005 陈向军, 上官文明, 宋秀青等, 2014.新疆全区和分区地壳速度模型的分析.中国地震, 30(2):178-187. doi: 10.3969/j.issn.1001-4683.2014.02.005 李艳永, 热依木江, 唐明帅等, 2016.利用震相方位角改善地震台网稀疏地区地震定位精度.地震地磁观测与研究, 37(2):57-62. http://d.old.wanfangdata.com.cn/Periodical/dzdcgcyyj201602010 田玥, 陈晓非, 2002.地震定位研究综述.地球物理学进展, 17(1):147-155. doi: 10.3969/j.issn.1004-2903.2002.01.022 田玥, 陈晓非, 2005.水平层状介质中的快速两点间射线追踪方法.地震学报, 27(2):147-154. doi: 10.3321/j.issn:0253-3782.2005.02.004 王桂丹, 2016.基于JOPENS/MSDP地震定位方法的定位结果分析.内陆地震, 30(1):74-80. http://www.cnki.com.cn/Article/CJFDTotal-LLDZ201601009.htm 夏仕安, 张佑龙, 隆爱军, 2011. MSDP在测震台网的应用.四川地震, (3):13-16. doi: 10.3969/j.issn.1001-8115.2011.03.003 谢辉, 金春华, 蔡新华等, 2011. MSDP单纯型和HYP2000定位方法对比分析.地震地磁观测与研究, 32(5):15-19. doi: 10.3969/j.issn.1003-3246.2011.05.003 新疆地震局分析预报室, 1982. "3000公里走时表"及其应用、新疆走时表工作的设想.地震地磁观测与研究, 3(4):25-30. http://www.cnki.com.cn/Article/CJFDTotal-DZGJ198204005.htm 曾融生, 滕吉文, 阚荣举等, 1965.我国西北地区地壳中的高速夹层.地球物理学报, 14(2):94-106. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX196502002.htm 张炳, 汪贵章, 戚浩等, 2012. HYPO2000与单纯形定位方法对比及作为速报算法的可行性分析.地震地磁观测与研究, 33(5-6):13-17. http://d.old.wanfangdata.com.cn/Periodical/dzdcgcyyj201205003 张诚, 张伶, 邓齐赞等, 1979.甘肃及邻近地区的地壳厚度.西北地震学报, 1(2):22-26. http://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ197902003.htm 张志斌, 朱浩清, 李艳永, 2015.基于地震波反演研究南天山中西段的震源深度.震灾防御技术, 10(S1):701-711. doi: 10.11899/zzfy2015s101 赵珠, 丁志峰, 易桂喜等, 1994.西藏地基定位-一种使用单纯形优化的非线性方法.地震学报, 16(2):212-219. http://www.cnki.com.cn/Article/CJFD1994-DZXB402.010.htm 赵仲和, 牟磊育, 2010.地震定位结果中误差描述的标准化.见: 中国地球物理学会第二十六届年会暨中国地震学会第十三次学术大会论文集.宁波: 中国地球物理学会, 中国地震学会, 299. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGEM201010001267.htm 中国地震局监测预报司, 2017.测震学原理与方法.北京:地震出版社. Geiger L., 1912. Probability method for the determination of earthquake epicenters from arrival time only. Bulletin of Saint Louis University, (8):60-71. Nelder J. A., Mead R., 1965. A simplex method for function minimization. The Computer Journal, 7(4):308-313. doi: 10.1093/comjnl/7.4.308 Prugger A. F., Gendzwill D. J., 1988. Microearthquake location:a nonlinear approach that makes use of a simplex stepping procedure. Bulletin of the Seismological Society of America, 78(2):799-815. -
点击查看大图
图(4) / 表(6)
计量
- 文章访问数: 92
- HTML全文浏览量: 21
- PDF下载量: 7
- 被引次数: 0
