New Activity of the Mingguang-Chihe Segmented of the Tanlu Fault Zone in Anhui Province
-
摘要: 郯庐断裂带南段淮河至女山湖段落已被证实具有晚第四纪活动性，为进一步追踪断裂带在女山湖以南的活动情况，选取明光至定远池河镇段落进行遥感解译、地质地貌调查、探槽开挖及年代样品测试等工作。研究发现，该段断裂在卫星影像上显示线性特征较差，发育断裂主要为池河-太湖断裂；断裂新活动主要表现为控制池河河谷的发育及沿明南土山村、池河石塘岳、池河周王等地展布的线性岗状地貌；在上述岗地边缘开挖探槽揭示断裂在该段最新活动方式具挤压逆冲性质，最新活动时代为中更新世，晚更新世以来不活动。上述结果初步表明，该段与其北侧相邻的淮河至女山湖段在第四纪活动性上存在差异，可能为郯庐断裂带在女山湖附近存在分段导致。Abstract: The section of Huaihe River to Nvshan Lake in the southern part of Tanlu fault zone has been beleived to be of late Quaternary activity. To trace further the activity of the fault to the south of the Nvshan Lake, we selected Mingguang south to Chihe Town section to conduct remote sensing interpretation, geological survey, trench excavation and age sample analysis. The results show that the linear features of this section are poor, and the main faults are the Chihe-Taihu fault. The new activities of the fault are mainly manifested as the control of the development of the valley of Chihe River and the hillock geomorphology along the Tushan Village in the Minguang Town, Shi Tangyue and Zhouwang Village in the Chihe Town. Excavation of trenches at the edge of the hillock revealed that the latest mode of activity of the fault in this segment is characterized by crushing and thrusting. The latest tectonic activity of the fault was the middle Pleistocene and inactivity since the late Pleistocene. The above preliminarily results show that exists the difference in Quaternary activity between this section and the Huaihe-Nvshan Lake section adjacent to the north side, possibly resulting from the subdivision of the Tanlu fault zone near the Nvshan Lake.
-
Key words:
- Tanlu fault zone /
- Chihe-Taihu fault /
- New activity /
- Trench /
- Nvshan lake
-
图 1 研究区构造
F1：嘉山-庐江断裂；F2：池河-太湖断裂；F3：石门山断裂；F4：五河-合肥断裂；F5：安丘-莒县断裂；F6：刘家铺-下马铺断裂；TWF：太和-五河断裂；LLF：临泉-刘府断裂；ZLF：自来桥-来安断裂；JXF：嘉山-响水断裂；Tc1：土山村探槽；Tc2：石塘岳2号探槽；Tc3：石塘岳1号探槽；Tc4：周王探槽
Figure 1. Distribution of faults in the study area
图 2 土山村探槽附近Google影像（a）、（b）及地貌（c）、（d）
Figure 2. Google images (a), (b) and geomorphology (c), (d) near the trench of the Tushan village
图 3 土山村探槽北壁照片（a）、局部照片（b）与剖面图（c）
Figure 3. The photo (a), local photo (b) and log (c) of the north wall of Tushan trenc
图 4 石塘岳附近Google影像（a）、1号探槽附近地貌（b）及2号探槽附近地貌（c）
Figure 4. Google image map (a) near Shitangyue, geomorphology near trench No. 1(b) and geomorphology near trench No. 2 (c)
图 5 石塘岳1号探槽北壁照片（a）与剖面（b）
Figure 5. The photo (a) and log (b) of the north wall of Shitangyue No. 1 trench
图 6 石塘岳2号探槽北壁（局部）照片（a）与剖面（b）
Figure 6. The photo (a) and log (b) of the north wall (partial) of Shitangyue No. 2 trench
图 7 周王探槽附近Google影像（a）及地貌（b）
Figure 7. Google images (a) and geomorphology (b) near the trench of the Zhouwang village
图 8 周王探槽北壁照片（a），局部照片（b）、（c）与剖面（d）
Figure 8. The photo (a), local photo (b), (c) and log (d) of the north wall of Zhouwang trench
图 9 周王探槽南壁照片（a）与剖面（b）
Figure 9. The photo (a) and log (b) of the south wall of Zhouwang trench
表 1 研究区中新生代地层
Table 1. A brief description of Mesozoic and Cenozoic strata in the study area
地质年代 岩石地层 主要岩性 第四纪 全新世（Qh） 丰乐镇组 灰黄色亚黏土、亚黏土 晚更新世（Q3） 戚咀组 褐黄色细粉砂、砂质黏土，含钙质结核和铁锰结核 中更新世（Q2） 泊岗组 上部棕黄、褐黄色粉砂质黏土；下部棕红色砂质黏土夹含砾砂质黏土 早更新世（Q1） 豆冲组 棕黄色、青灰色砂质含砾细砂，夹砂质黏土 新近纪 上新世（N2） 桂五组 玄武质火山岩沉积 中新世（N1） 下草湾组 灰绿色含砾粉砂质黏土岩，含砾黏土岩 古近纪 渐新世（E3） 明光组 褐黄、灰黄色粉砂质泥岩、灰色凝灰质砂岩互层 始新世（E2） 定远组 棕红、砖红、紫红色砂砾岩，泥质粉砂岩 古新世（E1） 白垩纪 晚白垩世（K2） 张桥组 砖红、棕红色细砾砂岩、含砾砂岩、粉砂岩 早白垩世（K1） 新庄组 上部黄绿、黄褐、灰红色砂岩、粉砂岩、泥岩和泥灰岩；下部灰紫色厚层砾岩、长石砂岩 
下载: 导出CSV
表 2 探槽剖面年龄样品测试结果
Table 2. Dating results of samples from the exploratory trench
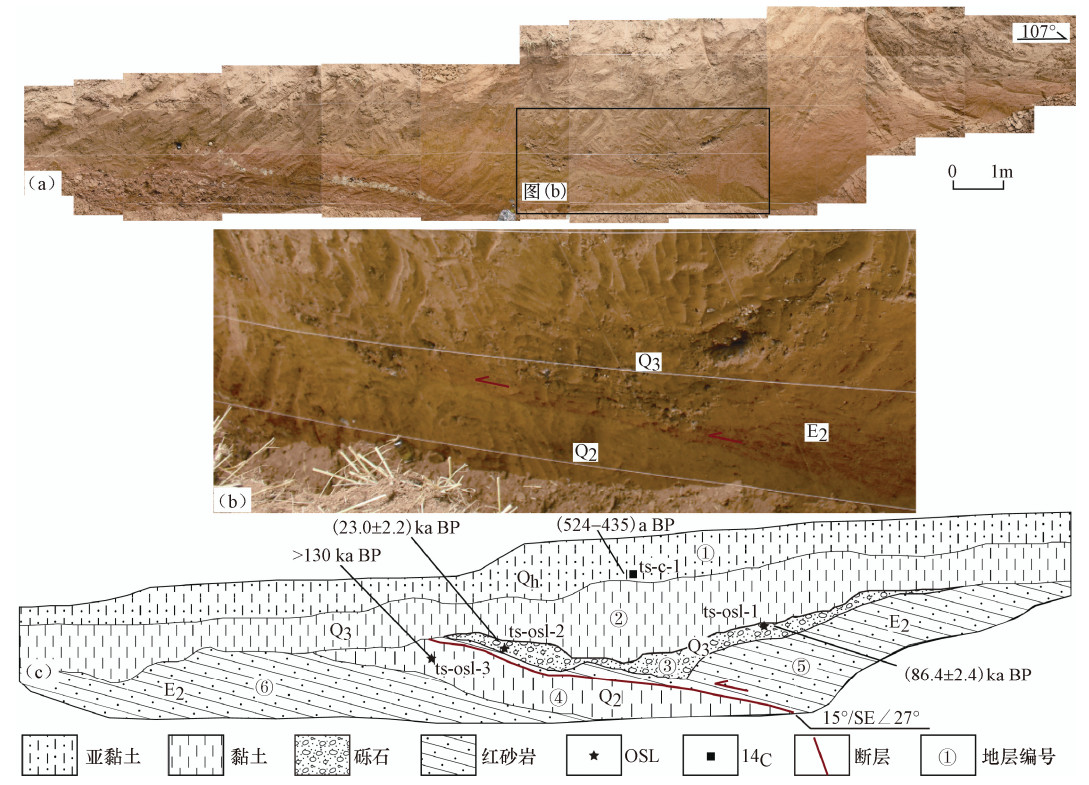
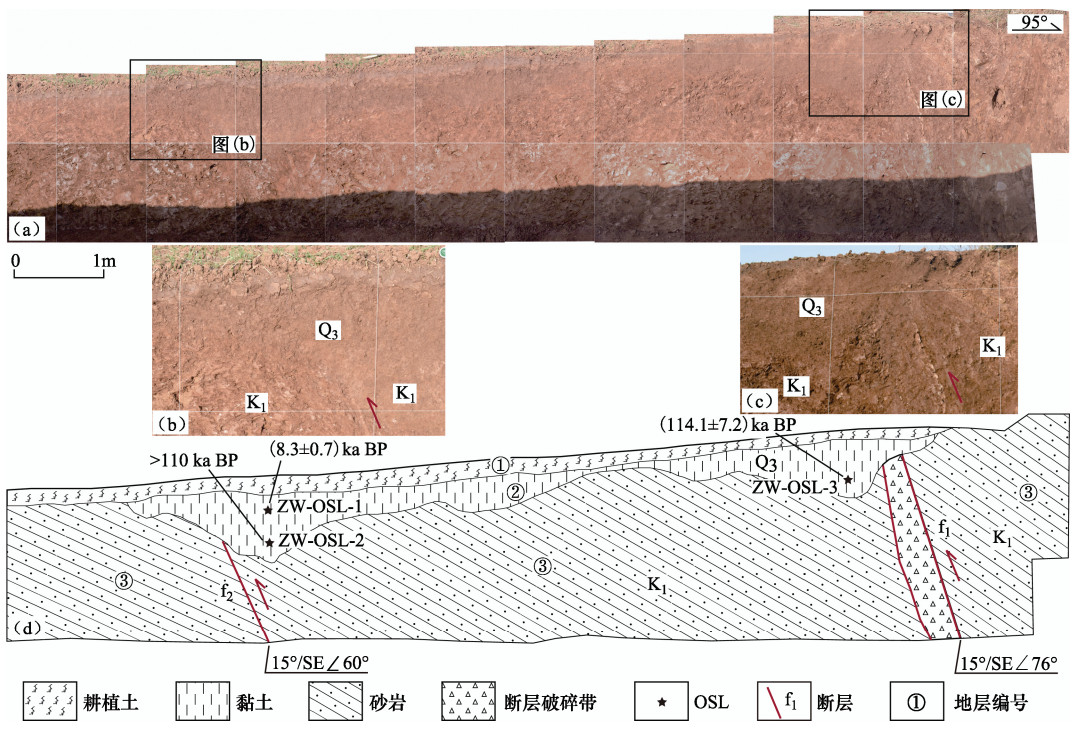
样品类型 编号 采样位置 地层岩性 测试方法 年龄/ka BP 14C ts-c-1 土山村探槽北壁层① 亚黏土 AMS加速质谱 0.524—0.435 OSL ts-osl-1 土山村探槽北壁层③ 砾石层夹黏土 SAR粗颗粒石英 86.4±2.4 ts-osl-2 土山村探槽北壁层③ 砾石层夹黏土 SAR粗颗粒石英 23.0±2.2 ts-osl-3 土山村探槽北壁层④ 黏土 SAR粗颗粒石英 ﹥130 ZW-OSL-1 周王探槽北壁层② 黏土 SAR粗颗粒石英 8.3±0.7 ZW-OSL-2 周王探槽北壁层② 黏土 SAR粗颗粒石英 ﹥110 ZW-OSL-3 周王探槽北壁层② 黏土 SAR粗颗粒石英 114.1±7.2 注：14C样品由美国BETA实验室测试；OSL样品由山东省地震局年代学实验室测试。
下载: 导出CSV
-
安徽省地质矿产局, 1987.安徽省区域地质志.北京:地质出版社. 曹筠, 许汉刚, 冉勇康等, 2017.郯庐断裂带沂水-汤头断裂南段晚第四纪活动新证及构造意义.地震地质, 39(2):287-303. doi: 10.3969/j.issn.0253-4967.2017.02.003 陈海云, 舒良树, 张云银等, 2004.合肥盆地中新生代构造演化.高校地质学报, 10(2):250-256. doi: 10.3969/j.issn.1006-7493.2004.02.011 方仲景, 丁梦林, 计凤桔等, 1980.郯城-庐江断裂带地震活动的地质分析.地震地质, 2(4):39-45. http://www.cnki.com.cn/Article/CJFDTotal-DZDZ198004004.htm 方仲景, 丁梦林, 向宏发等, 1986.郯庐断裂带的基本特征.科学通报, (1):52-55. http://cdmd.cnki.com.cn/Article/CDMD-10425-2007226415.htm 国家地震局地质研究所, 1987.郯庐断裂.北京:地震出版社. 刘备, 朱光, 翟明见等, 2015.郯庐断裂带安徽段活断层特征与成因.地质科学, 50(2):611-630. doi: 10.3969/j.issn.0563-5020.2015.02.017 刘国宏, 张云银, 贾洪义, 2003.合肥盆地构造演化及油气藏分析.油气地质与采收率, 10(3):1-3. doi: 10.3969/j.issn.1009-9603.2003.03.001 汤有标, 沈子忠, 林安培等, 1988.郯庐断裂带安徽段的展布及其新构造活动.地震地质, 10(2):46-50. http://www.cnki.com.cn/Article/CJFD1988-DZDZ198802006.htm 汤有标, 姚大全, 1990.郯庐断裂带南段新活动性的初步研究.地震研究, 13(2):155-165. http://www.cnki.com.cn/Article/CJFDTotal-DZYJ199002005.htm 吴海权, 江来利, 候明金等, 2004.安徽明光石坝地区新近纪地层层序的厘定.地层学杂志, 28(1):64-66, 96. doi: 10.3969/j.issn.0253-4959.2004.01.010 吴跃东, 刘家云, 汪德华, 2002.安徽明光盆地第三系层序地层学分析.现代地质, 16(4):374-381. doi: 10.3969/j.issn.1000-8527.2002.04.007 许世红, 钟建华, 柳忠泉, 2007.合肥盆地断层活动特征及其控制因素.大地构造与成矿学, 31(1):31-36. doi: 10.3969/j.issn.1001-1552.2007.01.004 许志琴, 1984.郯庐裂谷系概述.构造地质论丛, (3):39-46. 杨源源, 赵朋, 郑海刚等, 2017.郯庐断裂带安徽紫阳山段发现全新世活动证据.地震地质, 39(4):644-655. doi: 10.3969/j.issn.0253-4967.2017.04.002 姚大全, 1992.安徽明光隐伏活动断裂的发现及其意义.地震地质, 14(4):374-375. http://www.cnki.com.cn/Article/CJFDTotal-DZDZ199204018.htm 姚大全, 刘加灿, 2004.郯庐断裂带池河段的新活动.地震学报, 26(6):616-622. doi: 10.3321/j.issn:0253-3782.2004.06.007 姚大全, 郑海刚, 赵朋等, 2017.郯庐断裂带淮河南到女山湖段晚第四纪以来的新活动.中国地震, 33(1):38-45. doi: 10.3969/j.issn.1001-4683.2017.01.004 赵朋, 姚大全, 杨源源等, 2017.郯庐断裂带安徽浮山段晚第四纪以来活动新发现.地震地质, 39(5):889-903. doi: 10.3969/j.issn.0253-4967.2017.05.002 郑颖平, 翟洪涛, 李光等, 2012.郯庐断裂带江苏新沂-安徽宿松段地震危险性分析.华北地震科学, 30(2):48-51. doi: 10.3969/j.issn.1003-1375.2012.02.010 Zhu G., Niu M. L., Xie C. L., et al., 2010. Sinistral to normal faulting along the Tan-Lu fault zone:Evidence for geodynamic switching of the East China continental margin. The Journal of Geology, 118(3):277-293. doi: 10.1086/651540 Zhu G., Jiang D. Z., Zhang B. L., et al., 2012. Destruction of the eastern North China Craton in a backarc setting:Evidence from crustal deformation kinematics. Gondwana Research, 22(1): 86-103. doi: 10.1016/j.gr.2011.08.005 -
点击查看大图
计量
- 文章访问数: 65
- HTML全文浏览量: 7
- PDF下载量: 8
- 被引次数: 0
