引言

据研究，青藏高原及其周边地区历史上曾多次发生8级以上地震（Mugnier等，2013；张元生等，2015）。2015年4月25日，尼泊尔M_S 8.1地震发生于青藏高原南缘，属于典型的俯冲型地震。该地震所处的喜马拉雅断裂带中段是青藏高原及其周边地区热点地震研究区域。此次地震发生后，中国日喀则地区连续发生5.9级、5.3级地震，表明青藏高原周边地区的地震活动性在一定程度上受到了尼泊尔地震的影响。关于此次地震的孕震背景和过程、同震效应及其对中国大陆的影响等研究，已取得了一些有意义的成果，喜马拉雅断裂带上承载的汇聚作用，最终以喜马拉雅主逆冲断层上重复发生大地震永久变形的形式体现（刘静等，2015；盛书中等，2015；姚华建等，2015）。历史上，喜马拉雅断裂带至少发生过8次M_W 7.5以上的大地震（图 1）。

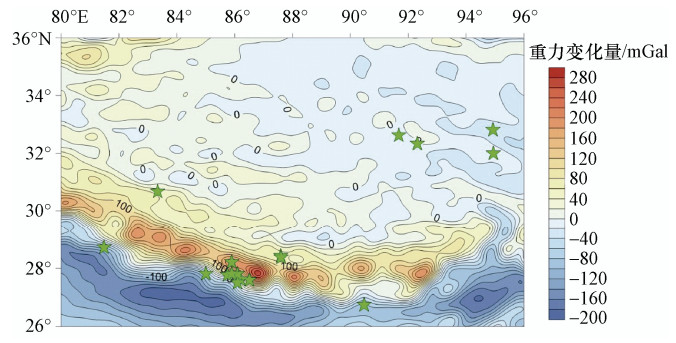
图 1  喜马拉雅主逆冲断裂带的历史地震和古地震事件的时空分布（据刘静等（2015））

Figure 1.  Distribution of historical earthquakes and palco-earthquakes along the Himalayan frontal thrust (after Liu et al., 2015)

下载: 全尺寸图片 幻灯片

布格重力异常通常反映了壳幔密度结构与正常地壳密度之间的差异性分布（薛典军等，2006；付广裕等，2015；康开轩等，2015；玄松柏等，2015），与地震孕育具有紧密联系，为研究地震孕育过程和发震机理提供地球动力学依据。随着卫星技术的发展，高精度测量全球重力场成为可能，继而构建了各种高分辨率的重力场模型。EGM2008（Earth Gravitational Model 2008）是近年来应用较为广泛的全球高阶重力场模型（Holmes等，2008），它的球谐展开阶次为2160，空间分辨率为5x（9km）（毕奔腾等，2016）。其前60阶、61—360阶、361—2160阶球谐系数分别由GRACE卫星数据、EGM96重力模型和剩余地形重力模型构建而成（郑增记等，2015；邹正波等，2010）。在青藏高原地区，EGM2008模型数据与实测地面重力数据之间存在约11.6mGal的误差（章传银等，2009），其异常的变化趋势大体一致（付广裕等，2013）。

根据前人研究，青藏高原许多地区的重力异常和构造活动之间有着密切的联系，构造活动较活跃的地区通常属于地壳不均衡或重力异常变化较快的地区。本文简述了青藏高原及其周边地区重力场细节信息特征，并结合尼泊尔M_S 8.1地震的均衡重力异常及GPS观测结果进行讨论。

1.   重力异常分析

重力异常通常反映地表下不同深度、不同规模及不同密度的地质体对应的重力异常叠加总效应。运用小波多尺度分析方法可将信号分解成各种不同频率成分，并且聚焦到任意细节上加以分析（侯遵泽等，1997）。本文通过小波多尺度的分析方法分离出反映其横向、纵向上不同尺度地质体产生的重力异常场（孟小红等，2012；Jiang等，2012），从而推测出目的地质体对应的重力特征。基于EGM2008重力场模型，并根据以上数据处理方法得到青藏高原及其周边地区的重力异常图，如图 2所示。由图可见其形态与地形图相似，在沿喜马拉雅山脉分布的高地势地区显示出明显的梯度带。该区域内布格重力异常以负值为主，约为-50mGal，由北向南逐渐增强。青藏高原布格重力异常在-300mGal以下，而在喜马拉雅山脉以南的印度板块则在-50mGal以上。在青藏块体与印度板块交界处有1条明显的重力梯度带，特别是在喜马拉雅山脉附近，重力值由北向南剧烈递增，在不到100km的范围内重力值增加了100mGal。

图 2  研究区重力异常图

Figure 2.  Gravity anomaly in the study areas

下载: 全尺寸图片 幻灯片

2.   小波多尺度分析

1984年，法国地球物理学家Crossman和Morlet提出小波分析方法。近年来，该方法被广泛应用于重力异常的处理。小波多尺度分析方法可以方便地将重力异常场分解成不同深度、规模、形态的信号成分，为解释深度、密度与重力场的变化关系提供了有效的依据（刘芳等，2013）。设函数f(t)∈L²(R)，定义其小波变换为：

其中，函数系

称为小波函数（Wavelet Function）。

φ(t)满足条件$\int_{ - \infty }^{ + \infty } {\varphi (t){\rm{d}}t = 0} $，令：

其中，φ(w)是φ(t)的傅里叶变换，得相应的小波逆变换公式为：

取a=a₀^j，b=ka₀^jb₀，a₀ > 1，b₀ > 0，则有小波变换的离散形式：

取a₀=2，b₀=1：

可以证明，$\int_{ - \infty }^{ + \infty } {{\varphi _{jk}}(X)} \overline {{\varphi _{mn}}(X)} {\rm{ d}}x = {\delta _{jm, kn}} = \left\{ \begin{array}{l} 1{\rm{ }}\;\;j = m, k = n\\ 0{\rm{ }}\;\;其他 \end{array} \right.$构成L²（R）空间的1组标准正交基。于是，有相应的小波逆变换：

利用Mallat算法，对青藏高原及周边地区重力场变化进行多尺度分解，通过功率谱分析原理计算每阶小波的径向功率谱，可估算出每阶异常的场源深度，所得结果如表 1所示。研究区布格重力异常1—6阶小波变换细节如图 3所示。由图可见，小波多尺度分解结果中1、2阶小波细节图像在喜马拉雅块体、川滇菱形块体等地区显示较为复杂，中上地壳浅层密度不均匀体的分布情况得以体现。三叠纪复理石沉积广泛分布在松潘—甘孜地块中巴颜喀拉和可可西里地区，厚度多在10km以上，由于后期构造活动强烈、基底褶皱变形，沉积物得到重新改造，其重力异常形态表现为略微杂乱的弱异常特征。3阶和4阶小波的细节异常图反映了青藏高原浅部的布格重力异常特征，由于许多弱小异常连片形成较大规模的重力异常，其内部布格重力异常呈条带状向东西延伸，贯穿整个青藏高原；异常呈有规律的高低相间分布，与地表断裂的分布位置相对应。沿青藏高原的南部喜马拉雅主边界断裂、北部阿尔金断裂及北昆仑断裂发育细长的高重力异常条带，推测是由地表浅部的火山岩条带引起的。在青藏高原四周边界断裂的位置均显示出低重力异常，将青藏高原与周边构造单元分开，明显地刻画出青藏高原的边界，其成因可能为青藏高原之下巨厚的地壳所引起的。青藏高原内部布格重力异常主要在-60—-20mGal（图 3（e）），其中雅鲁藏布江缝合带、羌塘地块中部呈低重力异常，而在主边界断裂、北昆仑断裂带、金沙江缝合带和班公湖-怒江缝合带则呈现出明显的条带状高重力异常，此异常由浅至深均存在，说明浅部火山岩不足以形成这些异常条带，主要还是由于高原地壳堆叠与莫霍褶皱所引起。喜马拉雅造山带以北则呈现负异常，推测是岩石受压力破碎或者存在地壳熔融物质。6阶小波细节图反映了该区域上地幔布格重力异常特征，对应的场源深度大约为56km。通过6阶小波变换后发现，深部物质有重新分配和调整的现象，青藏高原内部随着时代的推移有向东移动的迹象，而青藏高原壳幔物质挤入到川滇菱形块体，在这样1个狭小的空间内势必会积累巨大的应变能，从而造成该区地震活动性强。上地幔重力变化信号显示沿拉萨和喜马拉雅块体的重力变化信号呈现出不连续性，从而说明印度板块在俯冲过程中可能出现断裂。在喜马拉雅布格异常阶梯状陡变地带，中强地震频发，且地震震中的分布与喜马拉雅造山带的走向有一定的关系。推测由于陆-陆板块碰撞，挤压与能量的交换使该地带长期以来处于活动状态，从而孕育着大地震的发生。

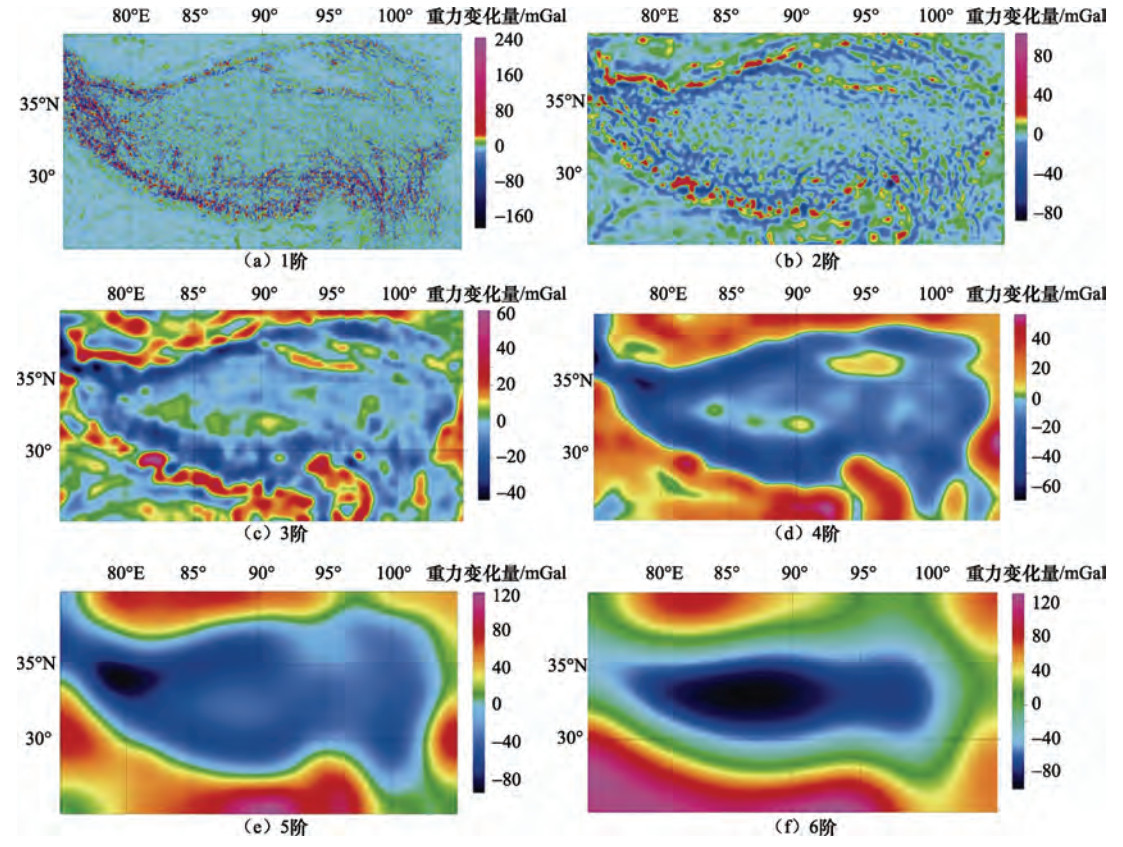
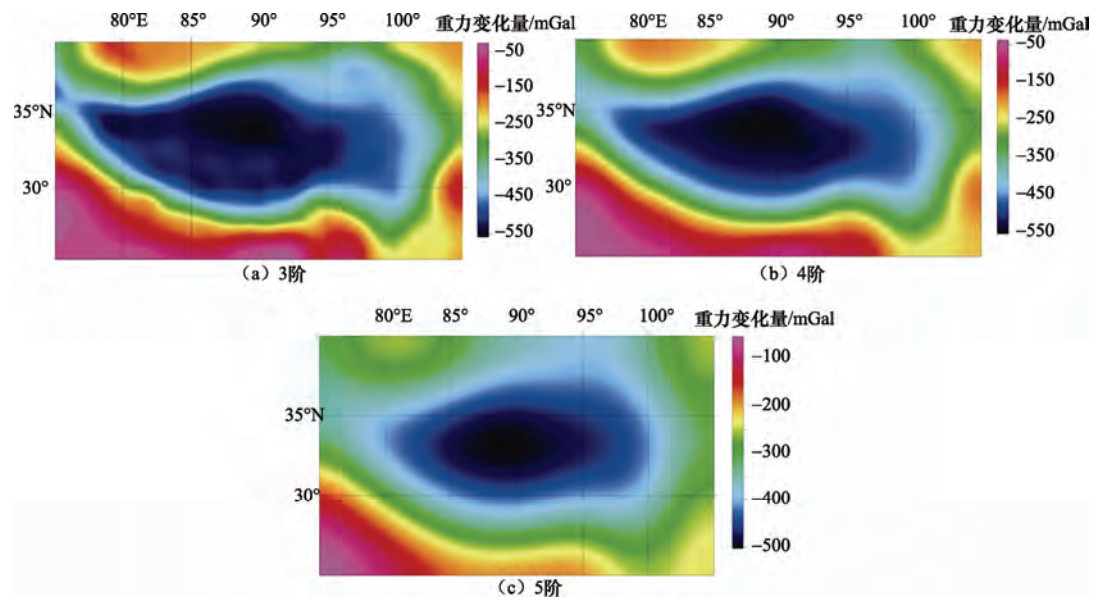
表 1  各阶小波细节反映的场源深度

Table 1.  Depth reflected by each of detail wavelet transform

阶次	1阶	2阶	3阶	4阶	5阶	6阶
近似场源深度/km	1	2	5	16	24	56

下载: 导出CSV 

| 显示表格

图 3  研究区布格重力异常1—6阶小波变换细节

Figure 3.  The detailed images of Bouguer gravity anomaly from 1^st to 6^th order multi-scale wavelet analysis

下载: 全尺寸图片 幻灯片

利用离散小波变换方法，将埋藏于不同尺度和深度的重力异常信息有效分离，从不同尺度和深度上分析此次地震的深部成因（祝意青，2007；褚庆忠等，2014）。研究区布格重力异常3—5阶小波变换逼近图（图 4）反映了下地壳至上地幔物质引起的重力效应，青藏高原块体为布格重力异常低值区，印度板块为布格重力异常高值区，其分界线与喜马拉雅断裂带一致。

图 4  研究区布格重力异常3—5阶小波逼近图

Figure 4.  The approximation of Bouguer gravity anomaly from 3^rd to 5^th multi-scale wavelet transform

下载: 全尺寸图片 幻灯片

据统计，2015年4月2日以来，该研究区的地震多发生在印度板块与欧亚板块的交界处（图 5）。该区的重力异常随空间变化异常剧烈，青藏高原块体与印度板块交界处则是1个高密度重力梯度带；5.0级以上地震在重力高低异常接触带上发生较为频繁。受印度板块与欧亚板块碰撞、挤压的作用，目前喜马拉雅地震带处于地震的强烈活动期，并孕育着7.0级以上大地震，危险性仍值得关注。

图 5  青藏高原及周边地区重力异常及5.0级以上地震分布

Figure 5.  Distribution of earthquakes with M≥5.0 and gravity anomalies over the Qinghai-Tibetan Plateau and its surrounding areas

下载: 全尺寸图片 幻灯片

3.   GPS及均衡重力异常分析

Ader等（2012）利用青藏高原及周边地区的GPS观测数据对喜马拉雅主断层面上的主要闭锁区进行定量分析，发现从喜马拉雅南缘到主前缘断裂之间为断层闭锁区主体，宽度达100km左右。通过分析GPS速度场，认为青藏高原存在近南北向挤压应变积累且喜马拉雅地区以北东向运动为主，而震源区周围的最大主压应变方向为NWW—SEE（孙文科等，2010；占伟等，2015；苏小宁等，2015），说明此次大震序列正是在印度板块与欧亚板块的强烈挤压作用下发生的。

喜马拉雅造山带南北两侧地区重力均衡异常变化显著，且重力异常呈现有规律的条带状展布（付广裕等，2015）。尼泊尔M_S 8.1地震以南地区的地壳均衡异常约为-100—0mGal，北部的喜马拉雅地震活动带地壳正均衡异常可达300—400mGal。该地震发生在地壳均衡负异常向正异常过渡的高梯度带上，即重力均衡与不均衡的耦合部位，雅鲁藏布江地带重力均衡异常趋近于零，表明2个陆-陆板块碰撞、挤压过渡带则完全处于非均衡状态，这与小波重力异常的分析结果一致，充分表明壳、幔物质再分配并进行强烈的物质交换，为强地震的孕育提供了良好的构造环境。

在巨大地震的孕育和发生过程中，震源区附近的物质发生迁移和质量再分布，重力场也会随之变化。GPS、重力均衡异常的结果与本文小波多尺度异常分析的结果一致，陆-陆板块的碰撞、挤压及物质交换导致了此次地震的发生。青藏高原及其周边地区岩石圈活动的动力学机制主要表现为地表隆升和地下深部物质迁移（卢占武等，2006；胡敏章等，2015），由此可以推断，基于EGM2008计算的青藏高原及周边地区的重力变化主要反映了该地区深部壳幔物质的迁移和质量再分布。

4.   结论与讨论

通过分析青藏高原及周边地区重力异常特征，结合GPS速度场和震源机制，初步探讨了青藏高原及其周边地区的重力变化，其主要反映了该地区深部壳幔物质的迁移和质量再分布，得到以下初步结论：

（1）该研究区（75°—105°E，25°—40°N）重力场变化平缓，且重力异常总体上属于负异常，而青藏高原块体与印度板块交界处则存在1个高密度重力梯度带，其异常随空间变化异常剧烈。

（2）震后的GPS速度场显示喜马拉雅主边界断裂存在大范围挤压应变积累，震源区处于近南北向挤压应变积累高值区的过渡区域，与重力异常所显示的过渡梯度带特征具有一致性。

（3）近年来5级以上地震多发于沿喜马拉雅山脉走向的重力异常负异常向正异常过渡的梯度带上，说明由于壳、幔物质强烈的物质交换使重力异常处于非均衡状态，从而使中强地震频发，因此该区地震危险性仍值得关注。