Ground Motion Simulations of Tangshan with Improved Empirical Green's Function
-
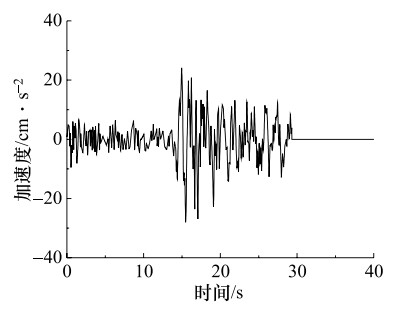
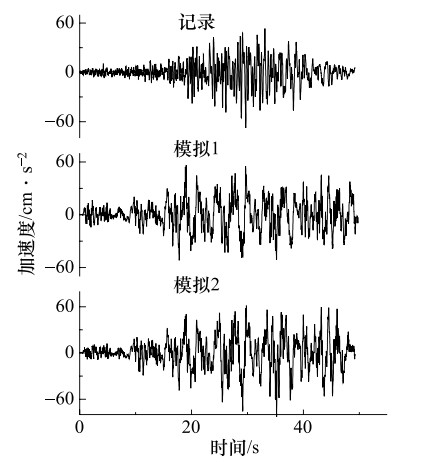
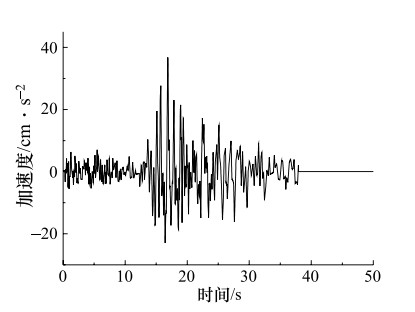
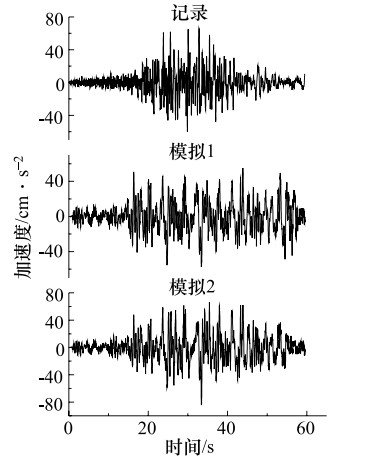
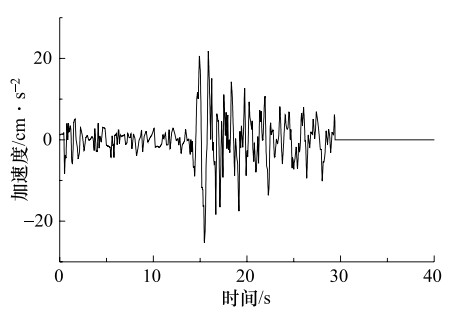
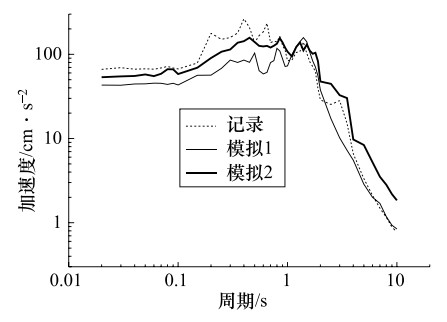
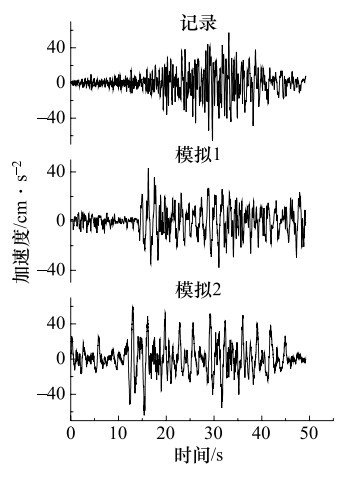
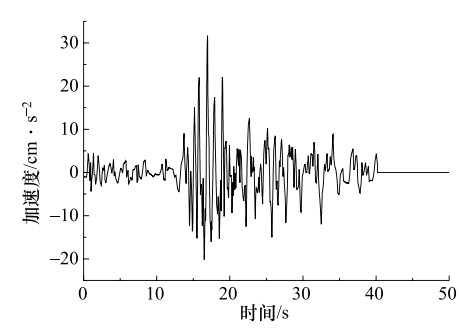
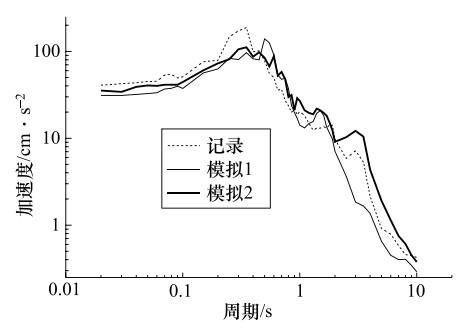
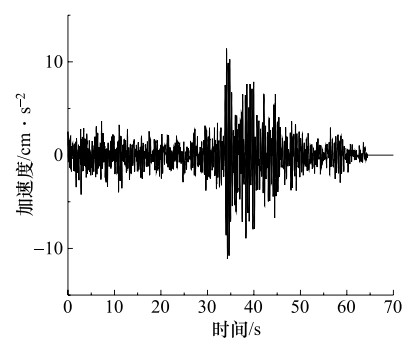
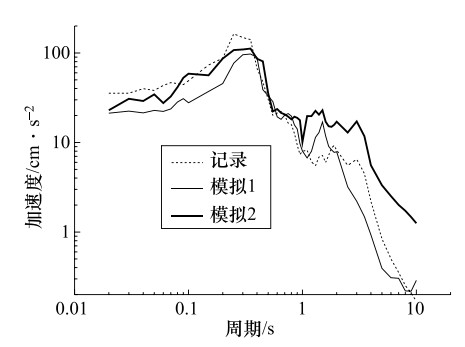
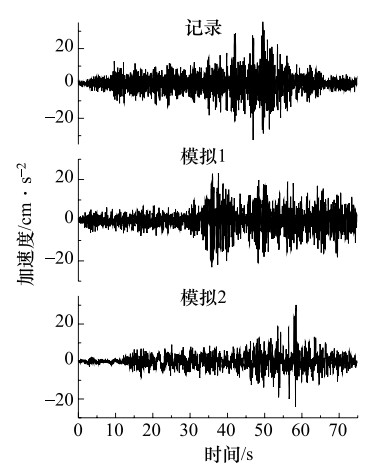
摘要: 建筑物的抗震设防需要尽可能地掌握未来大地震强震动记录信息，但大地震强震动记录的匮乏阻碍了抗震设防实践的发展。经验格林函数方法作为模拟地震动的主要方法，可以提供可靠的大地震强震动记录，但也存在着许多问题，如缺乏对大地震断层滑动分布不均匀的描述、用经验确定小震数目、模拟方法受到大小地震相似条件的限制等。文中对上述经验格林函数方法存在的问题进行了研究，改进的经验格林函数方法，有效地解决了上述问题。并用其对唐山大地震进行了模拟，并把模拟的地震动时程和反应谱与实际记录相比较，发现用改进方法模拟的地震动加速度反应谱比用未改进方法模拟结果更接近实际的地震动记录加速度反应谱。由此说明改进的经验格林函数可更准确的模拟地震动。Abstract: The seismic fortification of buildings needs to master the records of future large earthquakes as much as we can, but the lack of time histories of large earthquakes have hindered the progress of fortification for large earthquakes. Empirical Green's function method as the main method to simulate ground motions, can provide reliable strong ground motion records, but there are lack of descriptions that earthquake fault slip distribution is not uniform, the number of small earthquake is determined by experience, and simulation method is limited by similar condition. Therefore, the above situations are studied, and an improved empirical Green's function method is proposed to effectively solve the above problems effectively. We used to improved empirical Green's function method to simulate the Tangshan earthquake. The comparisons are made for the simulated seismic time histories, response spectra and the records. We found that the response spectra simulated by the improved method are closer to the seismic records than those obtained by the no-improved method. It is shown that the improved method is an effective method for simulation of ground motion.
-
引言
城市地球物理探测与传统的地球物理勘查差别很大，城市地质环境是被人类活动改造过的自然环境，实际情况会更加复杂。地下除地层、构造等天然地质体以外，还有地下管网系统、地下轨道交通、地下储存库等地下综合体。此外，城市地球物理场是动态演化的，在城市化前后甚至还会发生更加显著的变化（陈颙等，2003）。因此，城市地球物理探测具有探测深度浅、探测精度要求高、干扰因素多、场地受限等特点（李万伦等，2018）。目前国内外对目标层埋深仅有几十米（甚至十几米）的超浅层地震勘探经验不多，理论研究也不够深入。从地表至地下几十米的深度范围是各种人工地震勘探的盲区，但它对断层定位和活动性研究意义重大，近年来由于工程建设和防灾减灾的需要，已经开展了不少浅层地震勘探实践和技术研究（朱金芳等，2005）。在城市活断层探测中，用于第四纪覆盖区的活断层探测方法可分为地质学方法和地球物理方法，浅层或超浅层地震方法是地球物理方法调查城市活动断层研究中的重要手段之一（邓起东，2002；邓起东等，2003）。由于浅层地质条件以及新构造运动的特点，浅层或超浅层地震方法与常规地震勘探中采用的方法不完全相同。合理的数据采集方案是获得高分辨率地震剖面的重要基础；对浅层地震波传播速度的研究为数据处理中速度参考值的确定提供了理论依据。近年来，国内外浅层反射地震方法在城市活断层调查中的研究及其实例也相继发表，前人的研究成果反映了浅层地震方法的研究水平正在不断提高（Williams等，1995；潘纪顺等，2002；方盛明等，2002；刘保金等，2002；徐明才等，2005；段生全等，2005；杨晓平等，2007）。在利用浅层地震勘探方法确定隐伏活断层位置及其上断点埋深等工作中，一些地球物理工作者从地震波的激发、数据采集方法、室内资料处理与解释方法等方面进行了有益的探索，并取得了许多宝贵的经验，使得城市活断层浅层地震探测剖面质量和断层定位精度不断提高（何正勤等，2010；李大虎等，2010；杨歧焱等, 2015, 2016；许汉刚等，2016）。
青岛市地处胶东半岛西南部、黄海之滨，新构造运动以隆升为主，缺失第三系和第四系下部。第四纪晚期，受构造作用和海平面上升影响，接受十几米至二十余米厚以砂粘土为主的晚更新世—全新世河、海堆积物，直接覆盖于风化基岩（多为花岗岩）之上。东南部主要为花岗岩组成的低山丘陵，基岩在长期风化作用下形成了一定厚度的风化壳，并在山麓等和缓地带堆积有风化-坡积物，沿海港湾有第四纪晚期河海沉积；西北部主要是第四纪晚期的河海堆积平原或海湾，沉积有10—30m厚的第四系。因此，青岛市地震勘探属于超浅层地震勘探范畴。区域内发育若干北北东向断裂，活动性不甚强烈，地质地貌表现不很清楚，许多段落隐伏于第四系之下，断层的准确位置和活动性都不十分可靠（图 1）。与其他地区的有利探测环境相比，青岛市第四系很薄，横向物性变化大，垂向分层性差。对于不同的地震地质条件和探测目的，必须采用合理的野外采集方法和采集参数，因此，在一个新工区进行正式数据采集之前，应认真进行数据采集参数试验（何正勤等，2007）。本文通过在青岛王哥庄断裂上进行不同观测系统和采集参数的对比试验，获得了几米至二十几米深度范围内高分辨率的地震剖面，为隐伏活动断层位置及断层上断点的确定、钻孔剖面的布设和断层活动性的判定提供了可靠的科学依据。
图 1 青岛地区地质构造图Figure 1. Simplified geological map of the Qingdao areaF1：沧口断裂；F2：青岛山断裂；F3：劈石口断裂；F4：王哥庄断裂；F5：马山-王哥庄断裂1. 青岛地区地质构造概况
青岛及邻近地区在大地构造上属华北地台胶辽断隆，基底为元古代的变质岩系，经吕梁运动固结形成；古生代开始为地台发育时期，长期处于构造隆起状态，缺失古生代至三叠纪地层，致使结晶基底大面积出露。总体而言，青岛及邻近地区山势不高，以低山、丘陵和平原为主，海拔较高的山峰多为孤立分布，大致以沧口断裂为界划分为西北、东南2个不同的地貌分区。西北部地势较低，多为海湾、第四系冲洪积平原。由于新构造时期鲁东地区以隆升运动为主，青岛及邻近地区第四纪地层发育不良。许多地区基岩出露，部分地区沉积有晚更新世及全新世堆积物，局部地区发育有中更新世晚期的沉积物。市区东南部主要为花岗岩组成的低山丘陵，在山麓等和缓地带堆积有较厚的风化、坡积物，沿海港湾有第四纪晚期河海堆积；西北部是中生代地层组成的准平原和第四纪河海堆积平原（或海湾），沉积较厚的第四系，最大厚度近30米。
2. 超浅层地震勘探
2.1 青岛地区超浅层地震勘探的特点
（1）目的层比较浅，有效反射波大多在70ms以内，在反射波出现的时窗内，各种干扰波、特别是声波和面波很强，在接收反射波的后几道，出现折射波和反射波混合的情况，严重影响了有效反射波。
（2）在近震源处，震源干扰波条带内干扰严重，很难获取有效波，不同波阻抗界面形成的反射信号幅度远远小于干扰波振幅。
（3）青岛及附近地区沉积结构和地层厚度横向变化大，反射波速度和频率受此影响较大。
（4）青岛及附近地区覆盖层较薄，第四系底界面通常只有一个较强的风化界面，由于风化地层的风化程度是渐变的，风化基岩之间波阻抗差较小，第四系内部垂向分层差。基岩顶部常有数米厚的风化壳，有些基岩面甚至更浅，风化基岩与上覆地层之间的波阻抗差也不是很明显。
2.2 观测系统的设计和采集参数的选取
针对上述地震勘探特点，本文选取王哥庄断层（图 1中F4断裂）为实验对象，为了获得王哥庄断层从近地表至第四系底界面（深约30m）深度范围内的地震剖面，对同一深度范围按照探测精度由低到高的工作思路，在同一地震测线上采用不同的方法技术和探测参数，不同探测参数的地震剖面分别命名为TEST-a和TEST-b。地震数据采集使用德国DMT公司生产的SUMMIT数字地震仪，地震波激发采用了人工夯击和人工锤击，针对同一探测深度、不同精度的探测要求，采用的观测系统参数、地震波激发和数据采集参数见表 1。
表 1 观测系统参数和地震采集参数表Table 1. Survey parameters and seismic data acquisition details剖面编号 道间距/m 偏移距/m 接收道数 覆盖次数 激发震源 检波器固有频率/Hz 采样间隔/ms 记录长度/ms TEST-a 3 6 24 6 人工夯击 60 0.25 256 TEST-b 1 7 24 12 人工锤击 100 0.25 256 在不同道间距的超浅层地震记录上（图 2），图 2（a）、图 2（b）分别是TEST-a、TEST-b对应的超浅层地震共炮点记录。对比图 2（a）和图 2（b）可以看出，采用较大道间距、较小偏移距以及能量较大的震源可以获得一组很清楚的反射波组，但是近震源受干扰波影响严重，在超浅层不能获取有效反射波；采用较小道间距、较大偏移距以及能量较小震源，可以获取超浅层有效反射波，也可以减轻震源干扰波的影响，但是能量较弱，反射波信号相对变弱。
图 2 不同道间距的超浅层地震共炮点记录Figure 2. The common-shot gather of ultra-shallow seismic records in different trace intervals采用较小道间距和较弱震源，可以获取超浅层有效反射波，且垂向分层较好。由于采用小排列接收，道间距越小反射波能量衰减也越慢，因此受震源干扰波影响也变的越小，但是面波比较发育。由此可见，较小道间距和较小偏移距有利于保护反射波，延缓反射波的衰减，但是也带来了面波发育的问题；在保证探测深度要求的前提下，较弱的震源有利于避开震源干扰波的影响。
2.3 超浅层地震数据处理中的方法
采用Promax地震反射处理系统处理地震数据。在数据处理过程中，由于获得的原始记录的反射波近震源干扰严重，远震源反射波能量较强、干扰能量较弱等特点，因此选取记录信噪比高的远震反射波，可最大限度地提高地震资料的分辨率。其数据处理流程和方法主要包括：道编辑、静校正、真振幅恢复、地表一致性振幅处理、地表一致性反褶积、二维随机噪音衰减、f-k滤波、正常时差校正（NMO）、共中心点（CMP）叠加、叠后频率带通滤波和叠后剖面去噪等。
本文利用不同的滤波和处理方法来提高地震数据信噪比，图 3为同一记录数据在不同情况下进行f-k滤波获得的对比分析结果和频谱分析结果。其中，图 3（a）为原始数据和相对应的谱分析结果，可以看出在超浅层地震勘探中，地震反射波受浅层折射、面波和声波的影响，反射波信号相对较弱（图中红色圆圈），信噪比不高，通过频谱分析则显示地震数据主频有2个频段：50Hz和100Hz；图 3（b）为对原始数据应用f-k滤波后的结果及其频谱分析，由图可见应用f-k滤波后，数据中面波和声波得到有效减弱，反射波信号得到加强，信噪比也得到提高，频谱分析显示数据主频为100Hz，同时结果还显示面波频率范围与有效地震反射波接近，滤波困难，数据信噪比低；图 3（c）通过切除数据前几道信号，避免了近道面波对反射波的干扰，再进行f-k滤波，反射波信号明显增强，信噪比也得到进一步提高。对比结果表明，在浅层或超浅层地震勘探中，在取得信噪比较高的情况下，再对地震数据进行f-k滤波可以有效去除干扰波，提高地震反射波的信噪比。
图 3 原始数据及不同信噪比下的f-k滤波对比及其频谱分析图（一）Figure 3. Analysis between f-k filtering under different signal-to-noise ratio data and corresponding spectrum2.4 超浅层地震剖面特征
图 4、图 5分别是TEST-a、TEST-b测线经过数据处理后的地震反射时间及地质解释剖面（图中方向左西右东）。在图 4地震反射时间剖面中，丰富的地层界面反射波组出现在剖面100ms以上的时间范围内，存在1组起伏变化的反射波组，由2—3个强相位组成；在图 5地震反射时间剖面中，丰富的地层界面反射波组出现在剖面60ms以上的时间范围内，存在2组起伏变化的反射波组，分别由2—3个强相位组成。根据剖面上反射波同相轴的横向变化特征和上下反射波组关系，在该测线剖面上解释了1个断点，在图 4和图 5中标识为F。断层F位于TEST-a测线CDP423#和TEST-b测线CDP87#处，反射波同相轴出现了错动，断层为倾向西、高倾角逆断层，根据测区地质资料，判断该断层为王哥庄断裂。
图 4 TEST-a地震反射时间及地质解释剖面Figure 4. Stack time section of seismic reflection and the interpretation in TEST-a
图 5 TEST-b地震反射时间及地质解释剖面Figure 5. Stack time section of seismic reflection and the interpretation in TEST-b对比TEST-a、TEST-b测线的地震反射波叠加剖面发现，TEST-b测线在超浅层部分，特别是30ms以上部分有清晰的反射同相轴，说明小道距在超浅层地震勘探中，能揭示更多的断层结构细节。
3. 钻孔地质剖面及综合解
在王哥庄北TEST-a测线CDP423#和TEST-b测线CDP87#处的王哥庄断裂断点附近，布设了1组深19.1—23.5m、相邻孔距5—10m的钻孔（ZK1—ZK7），发现在ZK2与ZK6之间基岩顶面和第四系底部被断层错断4m左右，西升东降（图 6）。由图 6可见，除底部层位外，第四系各个层位均连续分布，未受断层构造变动，根据前期第四纪地层划分结果（包括测年结果），这套地层应为上更新统。因此，该处王哥庄断裂在晚更新世早期仍在活动。
图 6 TEST-a和TEST-b测线王哥庄断裂钻孔联合地质剖面Figure 6. The drilling geological section of WGZ fracture combined with the TEST-a and TEST-b survey lines4. 结论与讨论
（1）本文从城市活断层探测的角度出发，利用地质学、地球物理学等学科中的相关理论和方法，探讨超浅层地震在复杂地质构造背景下获得有效探测结果的前提条件。综合分析青岛地区地震勘探资料发现：①要依据扩展排列试验并参考观测系统参数选择原则，选好最小和最大偏移距，在超浅层探测中，近震源道记录中反射波与干扰波很难分辨，需要一定的偏移距才能将其分辨清楚；②最大偏移距不能过大，由于目标层埋深很浅，若排列长度过大，记录的多为折射波，所以需要采用短排列、小道间距进行数据采集。
（2）在对超浅层地震数据采集技术、资料处理与解释方法进行系统研究的基础上，以可清晰分辨出断层位置的典型剖面为例，证明在选择合适的观测系统和数据处理方法基础上，超浅层地震反射波法可以获取深度仅有十几米的地层反射信号，且大部分反射剖面都可较清楚地揭示出超浅部断层位置和断层特征。青岛王哥庄断裂地震勘探研究结果显示，超浅层地震反射方法在城市活断层探测中，特别是沿海覆盖层较浅的区域具有良好的应用前景。
（3）在对青岛王哥庄断裂超浅层地震反射时间剖面开展研究和解释的基础上，结合典型断点的钻孔联合剖面探测资料，研究了王哥庄断裂的准确位置、几何结构和活动性。研究表明，王哥庄断裂晚更新世以来可能也是活动的。
-
图 1 唐山主震断层划分和凹凸体位置
Figure 1. The fault division and the position of the convex and concave body of the Tangshan earthquak
图 2 在北京饭店一楼记录的宁河地震东西向加速度
Figure 2. The west-east acceleration of the Ninghe earthquake recorded at the first floor of the Beijing Hotel
图 3 3种方法获得的唐山大地震东西向反应谱比较
Figure 3. Comparison of the response spectra in west-east direction of the Tangshan earthquake from three methods
图 4 3种途径获得的唐山大地震东西向加速度时程
Figure 4. The west-east acceleration time histories of the Tangshan earthquake from the three approaches
图 5 北京饭店一楼记录到的宁河地震南北向加速度时程
Figure 5. the north-south acceleration record of the Ninghe earthquake received at the first floor of the Beijing Hotel
图 6 3种方法获得的南北向反应谱比较
Figure 6. Comparison of the response spectra in the north-south direction of the Tangshan earthquake from three methods
图 7 3种途径获得的唐山大地震南北向加速度时程
Figure 7. Acceleration time histories of the Tangshan earthquake in the direction of north-south recorded from the three approaches
图 8 北京饭店地下室记录的宁河地震东西向加速度记录
Figure 8. West-east acceleration time history of the Ninghe earthquake recorded at the basement of the Beijing Hotel
图 9 3种途径获得的唐山地震东西向反应谱比较
Figure 9. Comparison of the response spectra of the Tangshan earthquake in direction of west-east from three approaches
图 10 3种途径获得的唐山地震东西向加速度时程
Figure 10. The acceleration time histories of the Tangshan earthquake in the direction of west-east from the three approaches
图 11 北京饭店地下室记录的宁河地震南北向加速度记录
Figure 11. The north-south acceleration of the Ninghe earthquake recorded in the basement of the Beijing Hotel
图 12 3种途径获得的唐山地震南北向反应谱比较
Figure 12. Comparison of the response spectra of theTangshan earthquake in the direction of north-south at the Beijing Hotel basement from three approaches
图 13 3种途径获得的唐山地震南北向加速度时程
Figure 13. The acceleration time histories of the Tangshan earthquake in the direction of north-south from the three approaches
图 14 官厅水库记录的宁河地震南北向加速度记录
Figure 14. The north-south acceleration time history of the Ninghe earthquake recorded at the Guanting Reservoir
图 15 3种途径获得的唐山地震南北向反应谱比较
Figure 15. Comparison of the response spectra of the Tangshan earthquake in direction of South-North from three approaches
图 16 3种途径获得的唐山地震南北方向加速度时程
Figure 16. The north-south acceleration time histories of the Tangshan earthquake recorded from the three approaches
图 17 官厅水库记录的宁河地震竖直向加速度时程
Figure 17. The acceleration time history of the Ninghe earthquake recorded at the Guanting Reservoir in vertical direction
图 18 3种途径获得的唐山地震竖直向反应谱比较
Figure 18. Comparison of response spectra of the Tangshan earth quake vertical direction from the three approaches
图 19 3种途径获得的唐山地震竖方向加速度时程
Figure 19. The vertical acceleration time histories of the Tangshan earthquake from the three approaches
表 1 唐山大地震断层参数
Table 1. Fault parameters of the Tangshan earthquake
断层编号 走向/° 倾角/° M0/dyne·cm L×W/km2 D/m Δσ/bar 1 30 80 7.0×1026 57×20 1.38 20 2 50 80 7.0×1026 57×20 1.38 20 
下载: 导出CSV
表 2 宁河地震（MS 6.9）参数
Table 2. The Ninghe earthquake parameters (MS 6.9)
震中位置 震源深度/km 发震时刻 走向/° 倾角/° M0/dyne·cm L×W/km2 Δσ/bar D/m 39°17′N
118°47′E17 1976-11-9
21:53330 39 8.0×1025 18×9 35 0.672
下载: 导出CSV
表 3 大地震子断层含子事件个数
Table 3. The mumber of sub-events in the main earthquake
子断层编号 NL NW ND 1 4 3 3 2 4 3 3
下载: 导出CSV
-
国家地震局《一九七六年唐山地震》编辑组, 1982.一九七六年唐山地震.北京:地震出版社. 李启成, 2010.经验格林函数方法模拟地震动研究.哈尔滨:中国地震局工程力学研究所. 李启成, 孙颍川, 闫晓丹, 2016.用格林函数方法模拟卢龙地震.地球物理学进展, 31(5):1947-1952. http://d.old.wanfangdata.com.cn/Periodical/dzgcygczd200902003 罗奇峰, 1989.近场加速度的半经验合成.哈尔滨:国家地震局工程力学研究所. 王海云, 2004.近场强地震动预测的有限断层震源模型.哈尔滨:中国地震局工程力学研究所. http://d.old.wanfangdata.com.cn/Thesis/Y622304 吴迪, 2008.基于凹凸体模型的地震动半经验合成研究.上海:同济大学. 谢小碧, 1988.理论地震图方法及其在研究震源过程方面的应用.北京:中国科学院地球物理研究所. 药晓东, 章文波, 于湘伟, 2015.2008年汶川8.0级大地震近场强地面运动的模拟.地球物理学报, 58(3):886-903. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dqwlxb201503017 张之立, 李钦祖, 谷继成等, 1980.唐山地震的破裂过程及其力学分析.地震学报, 2(2):111-129. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=HY000001790762 周蕙兰, 1985.浅源走滑大震震源过程的某些特征.地球物理学报, 28(6):579-587. doi: 10.3321/j.issn:0001-5733.1985.06.004 朱传镇, 1985.唐山及其邻区的地震活动.见: 刘恢先主编, 唐山大地震震害.北京: 地震出版社, 1-16. Beresnev I. A., Atkinson G. M., 1998. Stochastic finite-fault modeling of ground motions from the 1994 northridge, California, earthquake. Ⅰ. Validation on rock sites. Bulletin of the Seismological Society of America, 88 (6):1392-1401. Boore D. M., 2003. Simulation of ground motion using the stochastic method. Pure and Applied Geophysics, 160 (3-4):635-676. http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_773ad1cbf1dcba3266bb060c1201c3cd Irikura K., 1983. Semi-empirical estimation of strong ground motions during large earthquakes. Bull Disas Prev Res Inst, Kyoto University, 33:63-104. https://repository.kulib.kyoto-u.ac.jp/dspace/handle/2433/124917 Irikura K., 1986. Prediction of strong acceleration motion using empirical Green's function. In: Proceedings of the 7th Japan Earthquake Engineering Symposium. December 8, Tokyo, 151-156. Irikura K., 1989. Prediction of strong ground motion using empirical Green's function-some problems of synthetic procedure of ground motion. Disaster prevention research institute annuals, Kyoto University, 32 (B-1):41-52. https://ci.nii.ac.jp/naid/120001178494/en/ Irikura K., Kamae K., 1994. Estimation of strong ground motion in broad-frequency band based on a seismic source scaling model and an empirical Green's function technique. Annals of Geophysics, 37 (6):1721-1743. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=Doaj000000629618 Irikura K., 2000. Prediction of strong motions from future earthquakes caused by active faults-case of the Osaka basin. In: Proceedings of the 12th World Conference on Earthquake Engineering. Auckland: IAEE. Irikura K., Miyake H., Iwata T., 2004. Recipe for predicting strong ground motions from future large earthquakes. Disaster prevention research institute annuals, Kyoto University, 47 (A), 25-45. Irikura K., 2006. Predicting strong ground motions with a "recipe". Bull disas prev res inst Univ Tokyo, 81:341-352. James M., 2002, Earthquake Source Studies Related to Strong Ground Motion Estimates. Report of Japan's Ministry of Culture, Science and Technology, 664-670. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=77d433887077f8d263b928df128a284e -
下载:
点击查看大图
计量
- 文章访问数: 117
- HTML全文浏览量: 57
- PDF下载量: 5
- 被引次数: 0
