Preliminary Analysis of Long-period Ground Motion in Xingtai
-
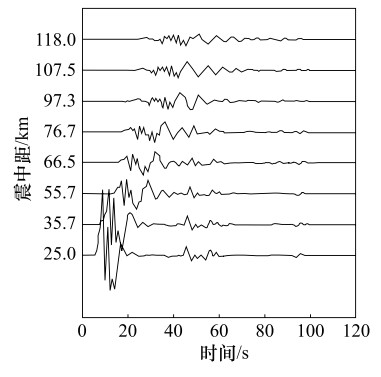
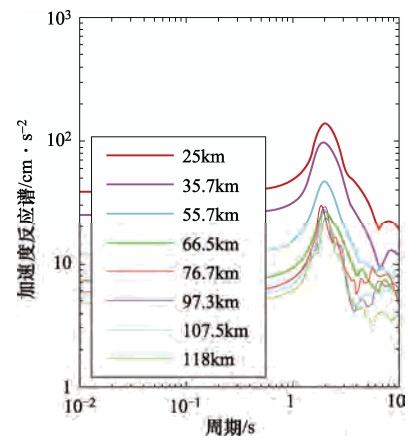
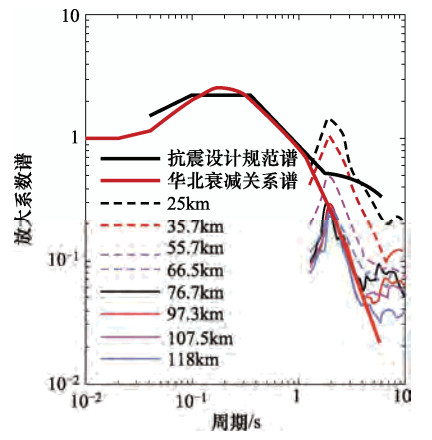
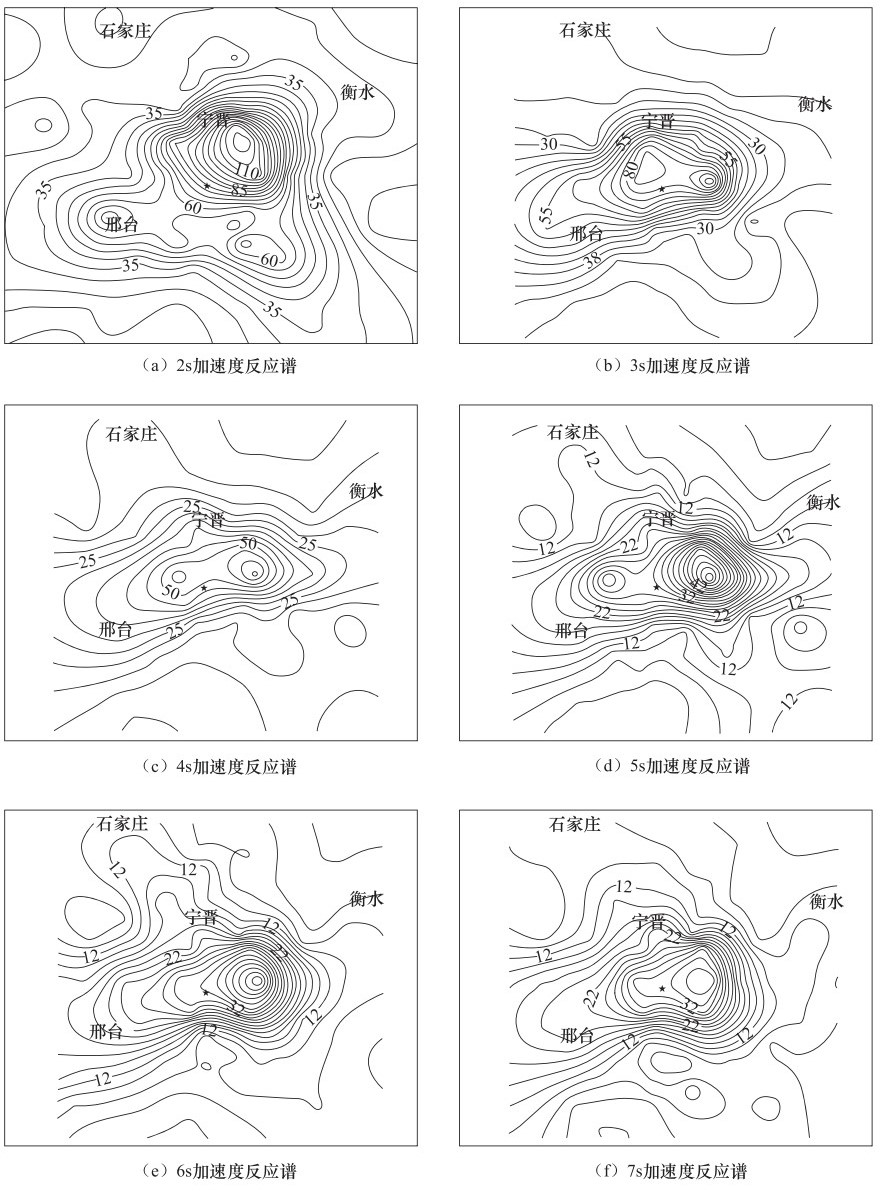
摘要: 沉积平原中存在地表低速沉积层是长周期地震动产生的关键因素，而长周期地震动会对长周期建筑物造成严重威胁和震害。本文基于邢台地震的历史地震震源模型和含地表沉积层的地壳速度模型，采用离散波数有限元法，对邢台地区进行了长周期地震动的计算分析。研究表明，邢台平原地区在大震中会产生长周期地震波，邢台地震中反应谱峰值区域位于宁晋南，与极震区基本重合。震中距小于55km区域内的周期1.5—4s的放大系数谱超过了抗震设计规范谱，反应谱放大系数值在周期2s附近达到峰值。因此，邢台地区因存在地表软弱沉积层，该区抗震设防可能对长周期地震动估计不足，建议应予以特别考虑。Abstract: The low velocity sediment on the plain is the main factor which generates the strong long-period waves. And the long-period ground motion may cause severe damage to high-rise buildings. We obtain crustal velocity structure including shallow part and historical earthquake source, and discrete wavenumber finite element method is used to calculate synthetic seismogram. Our results show that long-period ground motion will appear in strong earthquakes due to the existence of low velocity sediment in the Xingtai region. Then, the peak area we calculate and the meizoseismal area in the Xingtai earthquake appear to overlap. The amplification coefficient is larger than the seismic design code in 1.5-4s when epicentral distance is less than55 km, and amplification coefficient reaches peaks on 2s. The long-period part of the seismic design codes of Xingtai plain may exist shortage, more attention should be paid in the future.
-
引言
高速铁路的快速发展给人们出行带来便捷的同时，也会产生振动和噪声，影响着人们的生活环境（王逢朝等，1999；夏禾等，2004；刘厚毅等，2018；郁雯等，2021）。不同于传统列车，高速列车运行引起的振动对铁路沿线建筑物等具有更显著的影响（尹皓等，2010；王金凤等，2012）。因此，高速列车运行引起的环境振动问题受到了广泛关注。
现场测试是研究高速列车运行引起的环境振动特征的主要有效方法之一。Connolly等（2014）分别对比利时高速铁路网中平地、路堤、路堑和高架4种路基形式下列车经过产生的环境振动进行实测，并对不同条件下的测试结果进行对比分析，通过研究车速与地面振动的关系，提出了二者之间呈弱正相关的关系，研究结果表明，当高速列车经过时，接近轨道处振动的垂直分量占主导，而远离轨道处振动的水平分量与垂直分量相当，甚至占主导，其中路堑段的环境振动水平最高，且频带范围最宽。Zhai等（2015）于2014年对我国京沪高速铁路运行速度300～410 km/h的CRH380AL和CRH380BL动车组车型经过路堤段引起的环境振动进行了现场测试，并对实测数据进行频谱分析，得到距轨道中心线不同距离的各测点频谱特征，拟合了不同行车速度下振动衰减规律曲线，研究结果表明，运行速度超过300 km/h高速列车引起的环境振动主频主要集中在20～60 Hz，且与列车几何特征密切相关。Degrande等（2001）依托布鲁塞尔至巴黎的高速铁路沿线工程，对运行速度223～314 km/h高速列车引起的环境振动进行测试，并利用实测数据验证了数值预测模型，研究结果表明，随着列车车速的增加，地面振动高频部分逐渐增加。Ju等（2009）对我国台湾中部运行速度270 km/h的HSR-700T型高速列车在路堤和隧道中运行时进行了自由场地试验，试验结果与现场测试研究得到的衰减特征相似。Galvín等（2009）测试了西班牙有砟轨道运行速度151～298 km/h高速列车引起的环境振动，测试结果与数值模拟结果具有较好的一致性。葛勇等（2010）为研究列车运行引起的振动加速度衰减特征，对渝遂线CRH2型和谐号动车组列车运行的场地振动进行了实测，提出了一阶指数衰减公式和二次多项式衰减公式，并与测试结果进行对比，对测试结果进行了频谱分析，研究结果表明，一阶指数衰减公式误差较小，Hilbert边际谱可更好地反映场地振动特性。Connolly等（2015）于2014年对欧洲7个国家17个高速铁路观测点进行了大量环境振动观测，对观测得到的约1 500组振动实测数据进行分析，通过数据拟合，针对3个国际度量标准参数（VdB、KBFmax和PPV）分别提出地面振动预测公式，并与先前提出的预测公式进行比较修正，研究结果表明，土层性质对地面振动强度的影响较大，振动评价应充分考虑其带来的影响。Kouroussis等（2016）于2015年分别对比利时高速铁路路堑段、路堤段和平地段进行现场测试，探究不同地基条件对高速铁路振动产生和传播的影响，在标定现场土层参数的基础上，分别建立三维有限元模型以重现3个测试场地，模拟结果表明，路堤段和平地段模拟结果与实测结果吻合较好，下伏土层刚度对振动产生和传播的影响最大，因此进行振动评价时需考虑路基形式和地下土层刚度情况。贺玉龙等（2012）为研究高架段环境振动的衰减特性，对京津城际高速列车运行在天津市武清区杨村特大桥247号桥墩时的环境振动进行测试，测试结果表明，软土地区高速铁路通过高架段引起的环境振动符合对数衰减规律，且在距轨道中心线30 m范围内衰减较快，随后衰减趋于平缓，然而测试结果与我国现有环境振动预测公式有明显差异，说明我国现有环境振动预测公式仍有缺陷，需在大量测试数据的基础上对现有预测公式进行适当修正。王玉石等（2014）通过对哈大铁路客运专线4个地震监测点附近的测试发现，列车运行引起的地震动幅值较大，但随距离的增加衰减较快。刘厚毅等（2018）通过现场实测分析了高速列车引起的地基土不同深度处振动响应及其随深度的衰减规律。
目前国内外已有研究通过现场测试分析了高速列车引起的地表振动随距轨道中心线距离的变化特征及环境振动主要影响频带，但高速列车引起的振动响应与场地条件、路基形式等密切相关，深入开展不同场地条件和不同路基形式下高速铁路地表处振动响应现场测试研究，分析地表振动响应随距轨道中心线距离的变化特征，对路线两侧环境管理、工程设计和防震措施等具有一定意义。本文针对不同场地条件下高墩高架式、低墩高架式、路堤式及路堑式高速铁路地基土距轨道中心线不同距离地表处三分量振动响应开展现场测试研究，分析了不同工程场地高速列车引起的振动响应随水平距离的变化特征，该变化特征总体表现为：不同场地条件与路基形式下，随着距轨道中心线距离的增加，振动峰值加速度总体呈衰减趋势，且距轨道近距离处振动峰值加速度衰减较快，远距离处振动峰值加速度衰减较慢，这与已有研究结论一致。然而，不同场地条件与路基形式下，地表处三分量振动峰值加速度随距轨道中心线距离的增加衰减速度不同，在距轨道中心线一定距离处振动峰值加速度随距离的增加而增大，表明路基形式与场地条件对高速铁路车辆运行引起的地基振动具有显著影响。
1. 现场测试
1.1 测试场地选择与测试仪器一致性试验
高速列车运行引起的环境振动现场测试沿京沪高速铁路线开展，在昆山市、无锡市、南京市、宿州市、徐州市、济宁市、枣庄市、德州市各选取1个适宜的试验场地，对Ⅰ、Ⅱ、Ⅲ、Ⅳ类建筑场地GB 50011—2010《建筑抗震设计规范》（中华人民共和国住房和城乡建设部等，2010））条件下的高架式、路堤式和路堑式高速铁路地基土振动响应进行现场测试，主要内容如表1所示。
表 1 高速铁路环境振动影响现场测试工况Table 1. High-speed rail environmental vibration impact field test conditions information路基形式 场地类型 测试地点 测试内容 高墩高架式（桥墩高度≥10 m） Ⅱ类 南京市浦口区（桥墩高约12 m） 地表不同距离处振动加速度 Ⅲ类 无锡市锡山区（桥墩高约10.5 m） Ⅳ类 苏州市昆山市（桥墩高约10.5 m） 低墩高架式（桥墩高度≤7 m） Ⅱ类 宿州市埇桥区（桥墩高约6.5 m） Ⅲ类 德州市齐河县（桥墩高约5 m） 路堤式 Ⅱ类 枣庄市峄城区 Ⅰ类 徐州市贾汪区 路堑式 Ⅱ类 济宁市邹城市 现场测试仪器为ETNA2型数字强震动加速度仪，该仪器具有宽频带、动态范围大、噪声水平低、分辨率高等特点。现场测试前对投入现场测试的仪器进行了一致性试验，结果表明测试仪器具有较好的稳定性和一致性。
1.2 测点布设
对不同场地条件和不同路基形式下高速铁路沿线地面振动进行现场测试，测得距轨道中心线不同距离处高速列车引起的地表三分量振动加速度，以分析高速列车引起的地面振动随距离的变化特征。测试地表距轨道中心线不同距离处的振动加速度响应时，设置7个测点，测试仪器为7台ETNA2型数字强震动加速度仪，将仪器分别置于距轨道中心线（高架桥路基形式）或铁路外侧防护栏（路堤形式和路堑形式）0、5、10、20、30、50、70 m位置处，如图1～图3所示。测试路基形式包括高架式（高墩、低墩）、路堤式和路堑式路基。在高架式路基测试场地，第1台仪器放置于轨道中心线正下方靠近桥墩处；在路堤和路堑式路基测试场地，第1台仪器放置于紧靠轨道外侧护栏处。按照统一规定方向（垂直轨道方向为水平x向，平行轨道方向为水平y向，竖向为z向）将测试仪器置于不同距离处并调平、固定。
图 2 路堤式路基试验场地仪器布置示意图Figure 2. Embankment subgrade test site instrument layout diagram
图 3 路堑式路基试验场地仪器布置示意图Figure 3. Cutting type subgrade test site instrument layout diagram1.3 现场测试
现场测试用高速动车组均为设计运行速度300 km/h以上的高速列车。测试距轨道中心线不同距离地表处高速列车引起的振动响应时，每个测试场地一般测试3～4次，每次测试记录时间为2 h，采样率为200 Hz，记录方式为定时触发记录，以确保每台测试仪器同步记录。为便于分析，现场测试中记录了触发时间及每组高速列车通过测试场地的时刻，并利用激光测速仪测试各组列车通过测试现场的速度，同时观察了列车类型，便于后期数据处理。
2. 高速列车引起的地表振动测试结果分析
鉴于测试得到的各原始加速度记录存在一定的零位漂移，为此对原始振动加速度记录a（t）进行了零阶基线校正，具体处理步骤如下：
（1）依据无列车通过时间段内的加速度记录，计算得到加速度平均值a0；
（2）从有列车经过时记录的加速度记录a（t）中减去加速度平均值a0，得到无零位漂移的加速度记录时程。
依据经基线校正的列车通过时各振动加速度记录，可确定列车通过时距轨道中心线不同距离地表处测点垂直轨道水平向、平行轨道水平向与竖向峰值加速度。在此基础上，依据不同场地条件、不同路基形式、不同测点的不同方向加速度峰值进行算术平均，得到相应的平均加速度峰值进行分析。
在现场测试结果的基础上筛选运行速度约为300 km/h、车型为CRH380AL、以16节车厢编组运行的列车经过南京市浦口区测试场地时记录的振动加速度数据，如图4、图5所示。
图 4 南京市浦口区测试场地距轨道中心线不同距离地表三分量振动加速度时程曲线Figure 4. Three component vibration acceleration time history of the surface at different distances from the center line of the orbit in Pukou District, Nanjing
图 5 南京市浦口区测试场地距轨道中心线不同距离地表三分量振动加速度频谱曲线Figure 5. Three component vibration acceleration spectrum of the surface at different distances from the center line of the orbit in Pukou District, Nanjing由图4可知，地表竖向与水平向振动加速度基本随距轨道中心线距离的增加而衰减，近轨道处衰减较快。由图5可知，近轨道处的频带明显较宽，随着距轨道中心线距离的增加，频带逐渐变窄且优势频率变低，高频振动逐渐减小。
对现场测试数据进行处理，得到Ⅱ、Ⅲ、Ⅳ类场地高墩高架式路基条件下高速列车引起的地表振动峰值加速度随距轨道中心线距离的变化曲线如图6所示，Ⅱ、Ⅲ类场地低墩高架式路基条件下高速列车引起的地表振动峰值加速度随距轨道中心线距离的变化曲线如图7所示，Ⅰ、Ⅱ类场地路堤式路基条件下高速列车引起的地表振动峰值加速度随距轨道中心线距离的变化曲线如图8所示，Ⅱ类场地路堑式路基条件下高速列车引起的地表振动峰值加速度随距轨道中心线距离的变化曲线如图9所示。
图 6 高墩高架式路基条件下高速列车引起的地表振动峰值加速度随距轨道中心线距离的变化曲线Figure 6. Variation curves of peak acceleration of ground vibration caused by high-speed train under high pier elevated subgrade with distance from track centerline
图 7 低墩高架式路基条件下高速列车引起的地表振动峰值加速度随距轨道中心线距离的变化曲线Figure 7. Variation curves of peak acceleration of ground vibration caused by high-speed train under low pier elevated subgrade with distance from track centerline
图 8 路堤式路基条件下高速列车引起的地表振动峰值加速度随距轨道中心线距离的变化曲线Figure 8. Variation curves of peak acceleration of ground vibration caused by high-speed train under embankment with distance from the center line of track
图 9 路堑式路基条件下高速列车引起的地表振动峰值加速度随距轨道中心线距离的变化曲线Figure 9. Variation curves of peak acceleration of ground vibration caused by high-speed train under cutting subgrade with distance from the center line of track由图6可知，对于高速列车引起的高墩高架式路基地表振动响应，Ⅱ类场地条件下，三分量振动峰值加速度在距轨道中心线0～20 m范围内衰减速度较快，随后衰减速度迅速变缓；而Ⅲ、Ⅳ类场地条件下，三分量振动峰值加速度在距轨道中心线5 m处均较0 m处放大，在距轨道中心线5～10 m范围内三分量振动峰值加速度迅速衰减，随后衰减速度变缓。Ⅲ类场地条件下，三分量振动峰值加速度衰减最快，其次为Ⅱ类场地，最后为Ⅳ类场地。
由图7可知，对于高速列车引起的低墩高架式路基地表振动响应，Ⅱ类场地条件下，三分量振动峰值加速度在距轨道中心线0～20 m范围内衰减速度较快，随后衰减速度迅速变缓，且垂直轨道水平向振动峰值加速度在距轨道中心线10 m和30 m处略有放大，平行轨道水平向振动峰值加速度在距轨道中心线30 m处也略有放大；而Ⅲ类场地条件下，三分量振动峰值加速度在距轨道中心线0～5 m范围内迅速衰减，距离超过5 m后三分量振动峰值加速度衰减趋势明显变缓，其中垂直轨道水平向振动峰值加速度在距轨道中心线10 m处略有放大。Ⅲ类场地较Ⅱ类场地而言，三分量振动峰值加速度在更短距离内衰减至较小值，随后开始缓慢衰减。
由图8（a）可知，对于Ⅰ类场地条件下的路堑式路基，高速列车引起的水平向振动峰值加速度均随距轨道中心线距离的增大呈先增大后减小的趋势，竖向振动峰值加速度在距轨道中心线12～22 m范围内减小，随后在距轨道中心线22～62 m范围内放大，当距离超过62 m时，峰值加速度开始减小；高速列车引起的垂直轨道水平向振动峰值加速度在距轨道中心线42 m处达最大值，平行轨道水平向和竖向振动峰值加速度在距轨道中心线62 m处达最大值；垂直轨道水平向振动峰值加速度在距轨道中心线42 m处较12 m处增大约446%，平行轨道水平向振动峰值加速度在距轨道中心线62 m处较12 m处增大约105%，竖向振动峰值加速度在距轨道中心线62 m处较12 m处增大约37%，可知垂直轨道水平向振动峰值加速度放大速度大于平行轨道水平向和竖向；随着距轨道中心线距离进一步增加，三分量振动峰值加速度衰减速度基本相同。
由图8（b）可知，对于Ⅱ类场地条件下的路堑式路基，高速列车引起的垂直轨道水平向、平行轨道水平向和竖向振动峰值加速度均随距轨道中心线距离的增加呈衰减趋势。当距轨道中心线16～46 m时，垂直轨道水平向振动峰值加速度随距轨道中心线距离的增加先增大后减小，在距轨道中心线21、26 m处均较16 m处大，当距轨道中心线距离超过26 m后，峰值加速度迅速衰减，在距轨道中心线46 m处较16 m处衰减约84%；平行轨道水平向振动峰值加速度随距轨道中心线距离的增加呈先增大后减小的趋势，在距轨道中心线21、26、36 m处均较16 m处大，当距轨道中心线距离超过36 m后，峰值加速度迅速衰减，在距轨道中心线46 m处较16 m处衰减约64%；竖向振动峰值加速度随距轨道中心线距离的增加逐渐衰减，距轨道中心线16～26 m时的衰减速度大于距轨道中心线26～46 m时，在距轨道中心线46 m处较16 m处衰减约88%；在距轨道中心线46～86 m范围内，三分量振动峰值加速度随距轨道中心线距离的增加衰减速度变缓，且衰减速度基本相同。
由图9可知，对于路堑式路基，高速列车引起的垂直轨道水平向、平行轨道水平向和竖向振动峰值加速度均随距轨道中心线距离的增加呈先衰减后增大再衰减的趋势，在距轨道中心线30 m和40 m处有所放大；当距轨道中心线10～20 m时，三分量振动峰值加速度均快速衰减，其中垂直轨道水平向振动峰值加速度减小约72%，平行轨道水平向振动峰值加速度减小约56%，竖向振动峰值加速度减小约75%；当距轨道中心线20～40 m时，三分量振动峰值加速度均出现放大，其中垂直轨道水平向振动峰值加速度增大约61%，平行轨道水平向振动峰值加速度增大约63%，竖向振动峰值加速度增大约28%，水平向振动峰值加速度增大速度大于竖向振动峰值加速度；当距轨道中心线距离超过40 m时，三分量振动峰值加速度均逐渐衰减，且水平向振动峰值加速度衰减速度大于竖向振动峰值加速度。
3. 结论
本文选择8个不同场地类型及路基形式的工程场地进行高速列车运行引起的地表振动加速度测试，分析地表处振动峰值加速度随距轨道中心线距离的变化特征，主要得出以下结论：
（1）高墩高架式路基轨道中心线正下方三分量振动峰值加速度总体略小于低墩高架式路基，说明振动传播过程中，高桥墩对振动能量有一定削减作用。定性分析认为，这是由于高速列车运行引起的振动高频成分丰富，而低墩较高墩固有振动频率高，低墩对高频振动的衰减作用相对较小。
（2）不同场地条件下，地表处三分量振动峰值加速度随距轨道中心线距离的增加衰减速度不同，总体表现为Ⅲ类场地条件下三分量振动峰值加速度衰减最快，Ⅱ类场地次之，Ⅳ类场地衰减最慢。定性分析认为，这是由于不同场地条件下振动频率特性存在差异。
（3）Ⅱ、Ⅲ、Ⅳ类场地条件下，随着距轨道中心线距离的增加，三分量振动峰值加速度均呈衰减趋势，且距轨道近距离处峰值加速度衰减较快，远距离处峰值加速度衰减较慢；Ⅰ类场地条件下，高速列车引起的地表处振动响应随距轨道中心线距离的增加呈先增大后减小的趋势，垂直轨道水平向振动峰值加速度在距轨道中心线42 m处达最大值，平行轨道水平向和竖向振动峰值加速度在距轨道中心线62 m处达最大值。定性分析认为，近路基振动水平衰减较快，这是由高频振动衰减快引起的，随着距轨道中心线距离的增加，其振动主要为低频振动，衰减相对较慢。Ⅰ类场地条件下，不同方向的振动峰值加速度最大值出现的位置不同，分析认为这是由振动频率特性差异引起的。
（4）随着距轨道中心线距离的增加，不同路基形式的工程场地三分量振动峰值加速度在不同位置处有所增大，高墩高架式路基条件下三分量振动峰值加速度多在距轨道中心线5 m处较0 m大，低墩高架式路基条件下三分量振动峰值加速度多在距轨道中心线10 m处较5 m大。定性分析认为，振动峰值加速度在一定距离处出现增大是由振动波经反射叠加所致，与场地条件密切相关。
（5）在距轨道中心线一定距离处，振动峰值加速度随着距轨道中心线距离的增加出现变大现象，Ⅰ、Ⅱ、Ⅲ类场地条件下，垂直轨道水平向振动峰值加速度放大效应均大于平行轨道水平向和竖向，而在Ⅳ类场地条件下，竖向振动峰值加速度放大效应大于水平向。定性分析认为，这是由振动频率特性与局部场地条件共同作用引起的。
（6）高速列车运行引起的地表振动峰值加速度傅里叶谱分析结果表明，近轨道处频带明显较宽，随着距轨道中心线距离的增加，频带逐渐变窄且优势频率变低，高频振动逐渐减小。
-
图 1 邢台地震震源机制及邢台地区断层分布
F1：新河断裂；F2：晋县断裂；F3：隆尧断裂；F4：衡水断裂；
F5：元氏断裂；F6：邯郸断裂；F7：明化镇断裂；F8：鸡泽断裂Figure 1. Focal mechanism of the Xingtai earthquake and fault distribution
图 2 实际速度模型模拟速度记录波形
Figure 2. Velocity waveforms simulated with actual velocity structure
图 3 Crust 2.0速度模型速度记录波形
Figure 3. Velocity waveforms simulated with Crust 2.0 velocity structure
图 6 加速度反应谱分布（单位：cm/s2）
Figure 6. Distribution of acceleration response spectrum (unit: cm/s2)
表 1 966年邢台宁晋东南7.2级地震震源参数
Table 1. Source parameter of the 1966 Xingtai MS 7.2 earthquake
参数 数值 断裂 新河断裂 地震矩M0 2.87×1027dyne·cm 应力降Δσ 32.3bar 断层长度 50km 断层宽度 17km 上升时间 1s 破裂速度 2km/s 震中经度 115.03°E 震中纬度 37.32°N 震源深度 9km 走向 NNE30° 滑动角 162° 倾角 45°NWW向正断层 
下载: 导出CSV
表 2 邢台地区含地表浅部的速度结构模型
Table 2. Crustal velocity structure including shallow part in the Xingtai region
层数 深度/km 厚度/km vp/km·s-1 vs/km·s-1 ρ/g·cm-3 1 0.25 0.25 2.5 1.4 2.0 2 0.5 0.25 3.0 1.7 2.2 3 0.75 0.25 3.4 1.8 2.35 4 1 0.25 3.5 2.0 2.45 5 2 1 4.05 2.2 2.55 6 3 1 4.1 2.25 2.6 7 4 1 4.15 2.3 2.6 8 5 1 5.0 2.9 2.7 9 8 3 5.7 3.4 2.7 10 12 4 6.1 3.6 2.75 11 16 4 6.3 3.7 2.75 12 20 4 6.4 3.8 2.8 13 25 5 6.5 3.8 2.8 14 30 5 6.8 3.8 2.8 15 35 5 7.0 4.1 2.9 16 40 5 8.0 4.7 3.0
下载: 导出CSV
-
陈运泰, 林邦慧, 林中洋等, 1975.根据地面形变的观测研究1966年邢台地震的震源过程.地球物理学报, 18(3):164-182. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX197503002.htm 付长华, 高孟潭, 陈鲲, 2012.北京盆地结构对长周期地震动反应谱的影响.地震学报, 34(3):374-382. doi: 10.3969/j.issn.0253-3782.2012.03.009 郭金萍, 陈学良, 高孟潭等, 2015.运动学震源模型对近断层长周期地震动模拟研究综述.世界地震工程, 31(4):226-235. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=sjdzgc201504032 龙锋, 闻学泽, 徐锡伟, 2006.华北地区地震活断层的震级-破裂长度、破裂面积的经验关系.地震地质, 28(4):511-535. doi: 10.3969/j.issn.0253-4967.2006.04.001 吕作勇, 吴建平, 2010.华北地区地壳上地幔三维P波速度结构.地震学报, 32(1):1-11. http://d.old.wanfangdata.com.cn/Periodical/dizhen201001001 梅世蓉, 1999.邢台地震孕育发生模型及其前兆机理探讨.地震, 19(1):1-10. http://d.old.wanfangdata.com.cn/Periodical/diz199901001 彭小波, 2011.汶川地震强震动记录分析及应用.哈尔滨:中国地震局工程力学研究所. 邵学钟, 张家茹, 章思亚等, 1993.邢台地震区深部构造背景的地震转换波探测和研究.地球物理学报, 36(5):609-620. doi: 10.3321/j.issn:0001-5733.1993.05.008 王亚楠, 杜永峰, 胡高兴等, 2018.远场长周期地震下基于规范设计隔震结构的抗震性能研究.地震工程学报.40(2):219-224. doi: 10.3969/j.issn.1000-0844.2018.02.219 徐锡伟, 吴卫民, 张先康等, 2002.首都圈地区地壳最新构造变动与地震.北京:科学出版社. 叶迎晨, 2014.厚沉积层对长周期地震动的影响研究.北京:中国地震局地球物理研究所. 叶迎晨, 俞言祥, 高孟潭, 2014.台湾西部滨海平原地震面波的长周期反应谱及其与规范谱的比较研究.地震工程与工程振动, 34(S1):225-231. http://d.old.wanfangdata.com.cn/Conference/8707322 张怀, 周元泽, 吴忠良等, 2009.福州盆地强地面运动特征的有限元数值模拟.地球物理学报, 52(5):1270-1279. doi: 10.3969/j.issn.0001-5733.2009.05.016 中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局, 2010.GB 50011-2010建筑抗震设计规范(附条文说明)(2016年版).北京: 中国建筑工业出版社. Aki K., 1968. Seismic displacements near a fault. Journal of Geophysical Research, 73 (16):5359-5376. doi: 10.1029/JB073i016p05359 Boore D. M., 2001. Comparison of ground motions from the 1999 Chi-Chi earthquake with empirical predictions largely based on data from California. Journal of Geophysical Research, 91 (5):1212-1217. http://adsabs.harvard.edu/cgi-bin/nph-data_query?bibcode=2004BuSSA..94.2198W&db_key=PHY&link_type=ABSTRACT Kawase H., Aki K., 1989. A study on the response of a soft basin for incident S, P, and Rayleigh waves with special reference to the long duration observed in Mexico City. Bulletin of the Seismological Society of America, 79 (5):1361-1382. https://pubs.geoscienceworld.org/ssa/bssa/article-abstract/79/5/1361/119226/a-study-on-the-response-of-a-soft-basin-for?redirectedFrom=fulltext Koketsu K., Miyake H., 2008. A seismological overview of long-period ground motion. Journal of Seismology, 12 (2):133-143. doi: 10.1007/s10950-007-9080-0 Lee W. H. K., Kanamori H., Jennings P. C., et al., 2002. International handbook of earthquake and engineering seismology. New York:Academic Press. Olson A. H., Orcutt J. A., Frazier G. A., 1984. The discrete wavenumber/finite element method for synthetic seismograms. Geophysical Journal International, 77 (2):421-460. doi: 10.1111/j.1365-246X.1984.tb01942.x Shapiro N. M., Campillo M., Paul A., et al., 1997. Surface-wave propagation across the Mexican Volcanic Belt and the origin of the long-period seismic-wave amplification in the Valley of Mexico. Geophysical Journal International, 128 (1):151-166. doi: 10.1111/gji.1997.128.issue-1 Stidham C., Antolik M., Dreger D., et al., 1999. Three-dimensional structure influences on the strong-motion wavefield of the 1989 Loma Prieta earthquake. Bulletin of the Seismological Society of America, 89 (5):1184-1202. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=47a5ec8642569d3eca87824ae94570bc -
下载:
点击查看大图
计量
- 文章访问数: 154
- HTML全文浏览量: 18
- PDF下载量: 5
- 被引次数: 0
