Shear Capacity Calculation Method of Reinforced Concrete Frame Spatial Exterior Joints Using Softened Strut and Tie Model
-
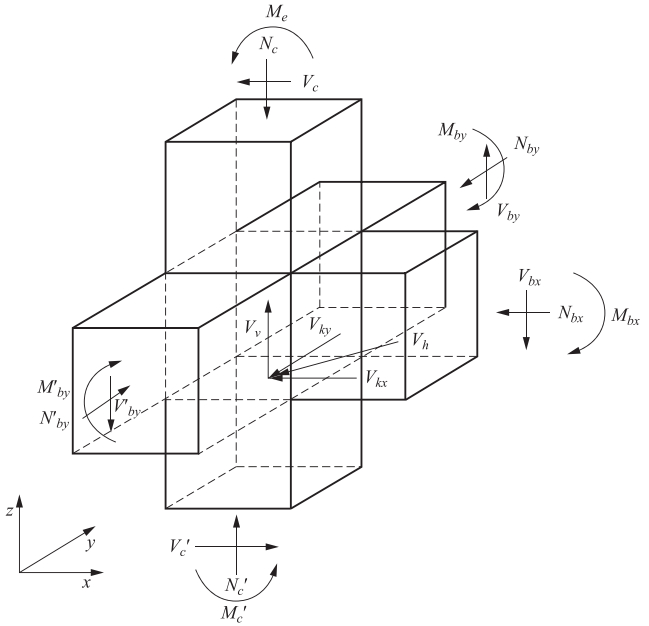
摘要: 实际地震作用是多维的、随机的，框架节点在2个方向同时受力，其抗震能力相比于单向地震作用会降低。目前，对节点核心区在2个方向同时受力时抗剪承载力的研究尚未完善。在双向受力下，节点核心区2个方向传来的剪力形成合剪力作用面，在节点核心区内部形成不同于单向受力下的斜向斜压杆。本文基于软化拉-压杆模型，针对水平双向受力相同的空间边节点，在合剪力作用面内建立抗剪承载力计算模型，确定空间边节点核心区斜压杆以及钢筋拉杆的计算方法。利用有限元软件建立不同参数空间边节点模型，并收集部分空间节点试验数据，将剪力计算值与模拟值或试验值进行对比。结果表明，基于软化拉-压杆模型建立的双向受力下钢筋混凝土框架，其边节点抗剪承载力计算值与模拟值或试验值吻合良好。Abstract: In practice, earthquake action is multi-dimensional and random, in which panel zone in frame structure is subjected to bidirectional loading.Under such case the anti-seismic capability may be lower than the designed capability based on unidirectional earthquake action.So far, the detailed calculation methods of shear capability for panel zone in reinforced concrete (RC) frame subjected to bidirectional loading has not been studied well.In this paper, we take reinforced concrete frame exterior joints under bidirecitional loading as a subject, and study the mechanical properties and shear mechanism of spatial exterior joints, in order to establish a calculation method of spatial exterior joints base on softened strut-and-tie model (SSTM), and to verify the accuracy of the calculation method.Obtained by the analysis, a synthetic shear force is imposed on panel zone and the inclined compression zone is formed at the end of column under bidirecitional loading, which is different from the shear mechanism under unidirectional loading.The spatial exterior joint models with different variables are established and analyzed with the software of ABAQUS, then we compare the simulated values to calculated values.The result shows that the calculation method of reinforced concrete frame exterior joints under bidirecitional loading based on SSTM is useful in providing calculated results with high accuracy.
-
引言
地震前兆观测主要关注观测数据随时间的相对变化，装置系数误差不影响观测数据的相对变化，但不正确的装置系数可能导致地电阻率观测结果出现系统误差（王兰炜等，2014），因此，正确的装置系数有利于不同区域观测数据的对比和地震前兆数据的研究。自2009年起，河北大柏舍台，甘肃天水台、武都台、平凉台，陕西合阳台实施了井下地电阻率垂直观测试验，井孔深100—225m，供电极距60—120m，测量极距20—60m（刘君等，2015；王兰炜等，2015）。上述台站地电阻率垂向观测通常为1个钻孔，供电电极和测量电极均布设于1个钻孔中，部分垂向观测的供电电极A接近地表，如天水台、武都台、合阳台的供电电极A埋深仅4—5m；部分垂向观测的供电电极A埋深为40m左右，如大柏舍台。垂向地电阻率观测中的装置系数与电流的空间分布及电极位置有关，现有垂向观测装置系数计算方法依据地下点、地表点电流源产生的电场计算得出，忽略了供电电极A的埋深。江宁台深井垂向地电阻率观测装置为在2口深井进行垂向观测的试验装置，与传统垂向地电阻率观测装置不同。本文根据地下点电流源产生的电场讨论装置系数计算方法，并比较计算方法对江宁台垂向地电阻率观测的影响。
1. 台址概况
江宁台地处南京市江宁区禄口街道水荆墅村，地形开阔平坦，周围无大中型工矿企业，测区位于南京-湖熟断裂南西盘和方山-小丹阳断裂西盘的楔形地块上，东距茅山断裂带30km，西北距长江36km。测区内现有垂向地电阻率观测装置为在2口深井进行垂向观测的试验装置，井距5.17m，供电电极A、测量电极M分别布设在深275m的2号井内200m和275m处，供电电极B、测量电极N分别布设在深400m的1号井内400m和325m处（图 1）。该垂向观测系统采用ZD8BI型地电仪，根据《地震台站建设规范（地电台站第1部分）》（DB/T.18.1—2006）中关于地电阻率台站的技术要求，对新建垂向观测装置的场地进行高密度电法、电测深等测试。高密度电法探测和电测深报告中NW—SE和NS测线结果表明，观测区域电测深曲线具有K形特征，电性结构等效为3层（樊晓春等，2018），场地电性层参数见表 1。
表 1 江宁台场地电性层参数Table 1. The underground electrical structure of Jiangning geoelectric stationNW—SE测线 NS测线 层厚/m 电阻率/Ω·m 层厚/m 电阻率/Ω·m 29.40 39.29 24.56 18.71 220.94 143.06 203.42 274.52 ∞ 60.39 ∞ 54.79 2. 点电流源在非全空间产生的电场
点电流处于不完全全空间时，对点电流源位于地下和地表 2种情况进行讨论。地下点电流源产生的电场指点电流源的电流I在地下一定深度时流入地下介质中产生的电场，为不完全全空间。假设地下介质电性均匀，介质电阻率为ρ，电流I从地下A点流入（图 2），采用镜像法计算（刘昌谋等，1994；刘国兴，2005），见式（1）。地表点电流源产生的电场指地表点电流源电流I流入地下介质，从无限远处流出时在介质中产生的电场，为半无限空间。假设地下介质电性均匀，介质电阻率为ρ，电流I从地表A点流入地下，电流线的分布以A为中心向周围呈辐射状，该情况为图 2的特例（王兰炜等，2014），见式（2）。
图 2 地下点电源产生的电场示意图Figure 2. The schematic diagram of the electric field generated by underground point power supply（1）地下点电流源产生的电场（不完全全空间）
$$ {V_{{\rm{MN}}}} = \frac{{\rho I}}{{4{\rm{ \mathsf{ π} }}}}\left({\frac{1}{{\overline {AM} }} + \frac{1}{{\overline {{A_1}M} }} - \frac{1}{{\overline {{A_1}N} }} - \frac{1}{{\overline {AN} }}} \right) $$ (1) （2）地表点电流源产生的电场（半无限空间）
$$ {V_{{\rm{MN}}}} = \frac{{\rho I}}{{2{\rm{ \mathsf{ π} }}}}\left({\frac{1}{{\overline {AM} }} - \frac{1}{{\overline {AN} }}} \right) $$ (2) 3. 装置系数计算方法
装置系数是地电阻率观测中特有的参数，通常用K表示，与观测装置中电极分布情况有关，表征地电阻率是视电阻率（王兰炜等，2014）。当测区区域介质电阻率均匀分布时，地电阻率ρs与介质真实的电阻率ρ数值相同。
根据奥斯定理和镜像原理（钱家栋等，1985），假设测区为均匀介质，垂向观测中的装置系数计算方法如下：
（1）方法Ⅰ：传统垂向观测装置系数计算方法（王兰炜等，2014）
传统方法井下垂向观测装置忽略电极A的埋深，在点电源B与地面对称的位置设镜像点B1，见图 3（a）。根据式（1）和式（2），则K为：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\left({\frac{2}{{\overline {AM} }} - \frac{2}{{\overline {AN} }}} \right) - \left({\frac{1}{{\overline {BM} }} + \frac{1}{{\overline {{B_1}M} }} - \frac{1}{{\overline {{B_1}N} }} - \frac{1}{{\overline {BN} }}} \right)}} $$ (3) 不考虑江宁台垂向观测电极A埋深时，因江宁台垂向观测AM=BN，AN=BM，则：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\frac{3}{{\overline {AM} }} - \frac{3}{{\overline {AN} }} - \frac{1}{{\overline {{B_1}M} }} + \frac{1}{{\overline {{B_1}N} }}}} $$ (4) （2）方法Ⅱ：采用全空间方式的装置系数计算方法（钱家栋等，1985；王兰炜等，2014）
当电极埋深h远大于供电极长度AB时，为全空间，则K为地表观测装置系数的2倍，即：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\frac{1}{{\overline {AM} }} - \frac{1}{{\overline {AN} }} - \frac{1}{{\overline {BM} }} + \frac{1}{{\overline {BN} }}}} $$ (5) （3）方法Ⅲ：采用不完全全空间方式的装置系数计算方法
江宁台垂向观测的电极A、M、N、B分别位于埋深200m、275m、325m、400m处，应按地下点电源产生的电场模型计算（不完全全空间），如图 3（b）所示。在点电源A、B与地面对称的位置设镜像点A1、B1，忽略1号井和2号井的水平距离l，根据式（1），则供电电流I（+I和-I）在M、N间产生的电位差为：
$$ {V_{MN}} = \frac{{\rho I}}{{4{\rm{ \mathsf{ π} }}}}\left[ {\left({\frac{1}{{\overline {AM} }} + \frac{1}{{\overline {{A_1}M} }} - \frac{1}{{\overline {{A_1}N} }} - \frac{1}{{\overline {AN} }}} \right) - \left({\frac{1}{{\overline {BM} }} + \frac{1}{{\overline {{B_1}M} }} - \frac{1}{{\overline {{B_1}N} }} - \frac{1}{{\overline {BN} }}} \right)} \right] $$ (6) 则K为：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\left({\frac{1}{{\overline {AM} }} + \frac{1}{{\overline {{A_1}M} }} - \frac{1}{{\overline {AN} }} - \frac{1}{{\overline {{A_1}N} }}} \right) - \left({\frac{1}{{\overline {BM} }} + \frac{1}{{\overline {{B_1}M} }} - \frac{1}{{\overline {BN} }} - \frac{1}{{\overline {{B_1}N} }}} \right)}} $$ (7) 因江宁台垂向观测AM=BN，AN=BM，则：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\frac{2}{{\overline {AM} }} - \frac{2}{{\overline {AN} }} + \frac{1}{{\overline {{A_1}M} }} - \frac{1}{{\overline {{A_1}N} }} - \frac{1}{{\overline {{B_1}M} }} + \frac{1}{{\overline {{B_1}N} }}}} $$ (8) （4）方法Ⅳ：采用不完全全空间方式（考虑井距l）的装置系数计算方法
按照地下点电源产生电场的模型计算（不完全全空间），在点电源A、B与地面对称的位置设镜像点A1、B1，h1、h2、h3表示供电电极A、B、M的电极埋深，井距l表示2口井孔水平距离（图 3（c）），则：
$$ \overline {AM} = {h_3} - {h_1} $$ (9) $$ \overline {AN} = \sqrt {{l^2} + {{({h_2} - {h_3})}^2}} $$ (10) $$ \overline {{A_1}M} = {h_1} + {h_3} $$ (11) $$ \overline {{A_1}N} = \sqrt {{l^2} + {{({h_2} + 2{h_1} - {h_3})}^2}} $$ (12) $$ \overline {{B_1}M} = \sqrt {{l^2} + {{({h_2} + {h_3})}^2}} $$ (13) $$ \overline {{B_1}N} = 2{h_2} - {h_3} + {h_1} $$ (14) 将式（9）至式（14）代入式（8），则K变为：
$$ K = \frac{{4\pi }}{{\frac{2}{{{h_3} - {h_1}}} - \frac{2}{{\sqrt {{l^2} + {{({h_2} - {h_3})}^2}} }} + \frac{1}{{{h_1} + {h_3}}} - \frac{1}{{\sqrt {{l^2} + {{({h_2} + 2{h_1} - {h_3})}^2}} }} - \frac{1}{{\sqrt {{l^2} + {{({h_2} + {h_3})}^2}} }} + \frac{1}{{2{h_2} - {h_3} + {h_1}}}}} $$ (15) 4. 江宁台垂向地电阻率观测装置系数计算
采用方法Ⅰ—Ⅳ分别计算江宁台垂向地电阻率观测的装置系数K，结果见表 2。考虑江宁台垂向地电阻率观测的电极布设不同于传统垂向观测装置，所有电极埋深均在200m以上，本文认为应以方法Ⅳ为参考值，采用式（16）计算不同装置系数计算方法的相对误差。方法Ⅰ、Ⅱ、Ⅲ相对误差分别为-32.01%、1.37%、0.43%，可知方法Ⅰ不适用于江宁台垂向地电阻率观测，该计算方法通常仅适用于供电电极A埋深小于5m的垂向观测，如天水台、合阳台。方法Ⅱ相对误差较小，江宁台垂向观测于2018年4月25日至2018年11月22日曾采用该方法。考虑仅当电极埋深远大于供电极距时称为全空间，而江宁台垂向装置最小电极埋深仅与供电极距相当，因此，方法Ⅱ同样不适用于江宁台垂向观测。除江宁台外，大部分台站观测装置电极埋深明显小于供电极距，均不宜采用方法Ⅱ。方法Ⅲ相对误差最小，江宁台垂向地电阻率观测于2018年11月23日至2019年10月30日曾采用该方法，2018年11月出现的台阶是由调整装置系数导致的（图 4）。由于江宁台垂向地电阻率观测为多孔观测，须考虑井距才能准确计算其装置系数，因而最终采用方法Ⅳ进行计算。
$$ \sigma = \frac{{k_{方法}} - {k_{方法Ⅳ}}}{{{k_{方法Ⅳ}}}} $$ (16) 表 2 江宁台垂向观测的装置系数Table 2. The configuration coefficient of vertical geo-resistivity observation in Jiangning earthquake station计算方法 AM/m AN/m B1M/m B1N/m A1M/m A1N/m 装置系数K Ⅰ 75.000 125.000 675.000 725.000 — — 790.000 Ⅱ 75.000 125.000 — — — — 1178.000 Ⅲ 75.000 125.000 675.000 725.000 475.000 525.000 1167.000 Ⅳ 75.000 125.374 675.020 725.000 475.000 525.292 1162.000 
图 4 江宁台垂向观测整点值曲线Figure 4. The hourly observational value curves of vertical geo-resistivity observation at Jiangning Seismic Station5. 结论
本文以江宁台垂向地电阻率观测为例，提出2种以不完全全空间方式计算的新方法，并与现有垂向观测装置计算方法进行比较。研究结果表明，方法Ⅳ最符合江宁台垂向地电阻率观测装置。考虑方法Ⅳ中部分参数存在小数部分，认为保留小数点后三位能满足装置系数精度要求。方法Ⅳ除适用于2口井垂向观测装置外，同样适用于忽略井距时供电电极A埋深超过5m的单口井垂向观测装置。
致谢: 衷心感谢中国地震局地壳应力研究所王兰炜研究员对本文提出的建议和意见。 -
图 5 荷载位移曲线模拟值与试验值对比
Figure 5. Comparison of load-displacement curve between test results and simulated results
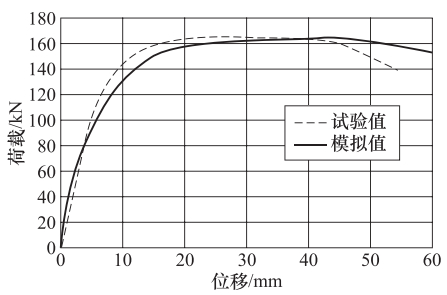
表 1 有限元模拟值与试验值对比
Table 1. Comparison of simulated results and test results
对比项 屈服荷载/kN 屈服位移/mm 峰值荷载/kN 峰值位移/mm 极限荷载/kN 极限位移/mm 试验值 139.9 13 163.9 45 152.8 60 模拟值 148.4 11.5 161.8 41.8 137.6 54.6 
下载: 导出CSV
表 2 空间边节点参数及计算值与模拟值对比
Table 2. Comparison of spatial joints between calculated results and simulated results
模型编号 节点形式 hb/mm hc/mm fck/MPa 轴压比 柱纵筋配筋 箍筋配筋 计算值Vjh, c/kN 模拟值Vjh, a/kN Vjh, c/Vjh, a B-1 边节点 450 400 27.9 0.1 12C18+4C22 A10@50 474.17 550.09 0.862 B-2 边节点 450 400 27.9 0.1 12C18+4C22 A12@50 484.77 573.71 0.845 B-3 边节点 450 400 27.9 0.15 12C18+4C22 A10@50 486.51 552.99 0.879 B-4 边节点 450 400 27.9 0.3 12C18+4C22 A10@50 524.57 589.44 0.890 B-5 边节点 450 400 27.9 0.3 12C18+4C22 A12@50 535.17 602.73 0.888 B-6 边节点 450 400 27.9 0.45 12C18+4C22 A10@50 564.20 616.74 0.915 SP1 角节点 250 220 34.3 0.2 16D13 A6@80 216.18 262* 0.825 SP2 角节点 250 220 29.1 0.6 16D13 A6@80 225.73 247.8* 0.911 SP3 角节点 250 220 29.1 0.6 16D13 A10@80 253.41 275.8* 0.919 注：fck为混凝土轴心抗压强度标准值；Vjh, a值中上标*的为试验值。
下载: 导出CSV
-
陈永春, 高红旗, 马颖军等, 1995.双向反复荷载下钢筋砼空间框架梁柱节点受剪承载力及梁筋粘结锚固性能的试验研究.建筑科学, (2):13-20, 32. http://www.cnki.com.cn/Article/CJFDTOTAL-JZKX502.001.htm 崔建宇, 车轶, 孙建刚等, 2014.高层钢筋混凝土框架底层角节点抗震性能.重庆大学学报, 37(2):98-105. http://d.old.wanfangdata.com.cn/Periodical/cqdxxb201402014 傅剑平, 2002.钢筋混凝土框架节点抗震性能与设计方法研究.重庆:重庆大学. 框架节点专题研究组, 1983.低周反复荷载作用下钢筋混凝土框架梁柱节点核心区抗剪强度的试验研究.建筑结构学报, (6):1-17. 雷远德, 曲哲, 王涛, 2014.钢筋混凝土空间框架底层梁柱节点双向往复加载试验研究.土木工程学报, 47(12):64-72, 106. http://d.old.wanfangdata.com.cn/Conference/8608664 唐九如, 冯纪寅, 庞同和, 1985.钢筋混凝土框架梁柱节点核心区抗剪强度试验研究.南京工学院学报, (4):61-75. http://cdmd.cnki.com.cn/Article/CDMD-10710-1017869266.htm 王玉雷, 2010.低周反复荷载作用下混凝土框架边节点性能试验研究.哈尔滨:哈尔滨工业大学. 中华人民共和国建设部, 2010.《混凝土结构设计规范》GB 50011-2010.北京:中国建筑工业出版社. Euro-International Concrete Committee, 1993.CEB-FIP Model Code 1990.Lausanne. Ghobarah A., El-Amoury T., 2005.Seismic rehabilitation of deficient exterior concrete frame joints.Journal of Composites for Construction, 9 (5):408-416. doi: 10.1061/(ASCE)1090-0268(2005)9:5(408) Hwang S.J., Lee H.J., 2000.Analytical model for predicting shear strengths of interior reinforced concrete beam-column joints for seismic resistance.Structural Journal, 97 (1):35-44. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=e5d75e7b6798950c6649221c6db989e0 Hwang S.J., Lee H.J., 2002.Strength prediction for discontinuity regions by softened strut-and-tie model.Journal of Structural Engineering, 128 (12):1519-1526. doi: 10.1061/(ASCE)0733-9445(2002)128:12(1519) -
下载:
点击查看大图
计量
- 文章访问数: 88
- HTML全文浏览量: 26
- PDF下载量: 4
- 被引次数: 0
