Design and Implementation of High-performance Computing Platform Accounting Service System in Key Laboratory of Earthquake Prediction
-
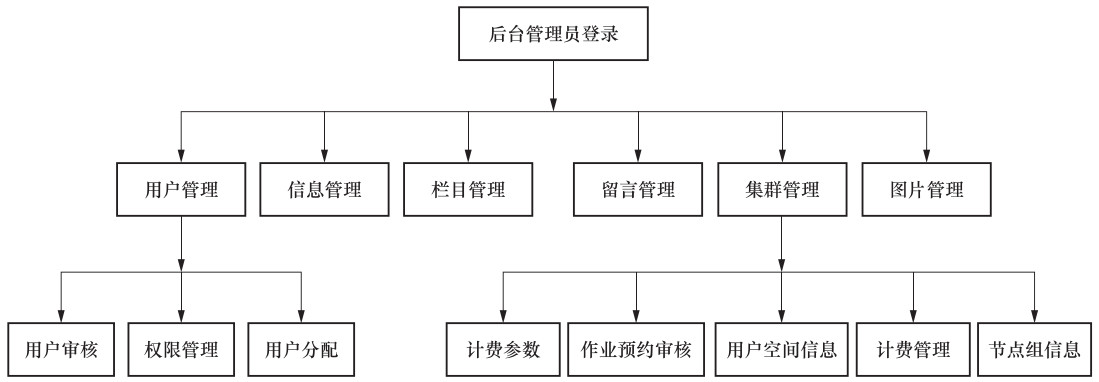
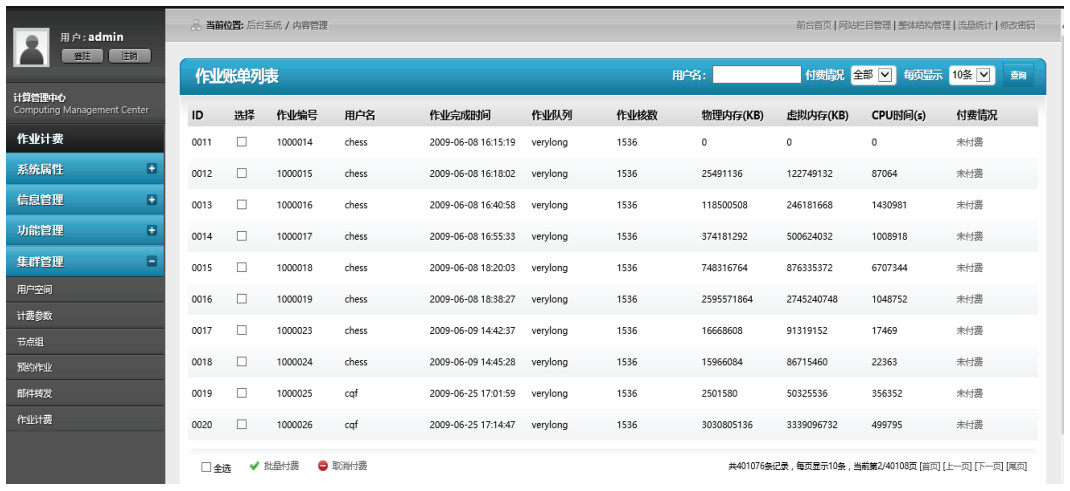
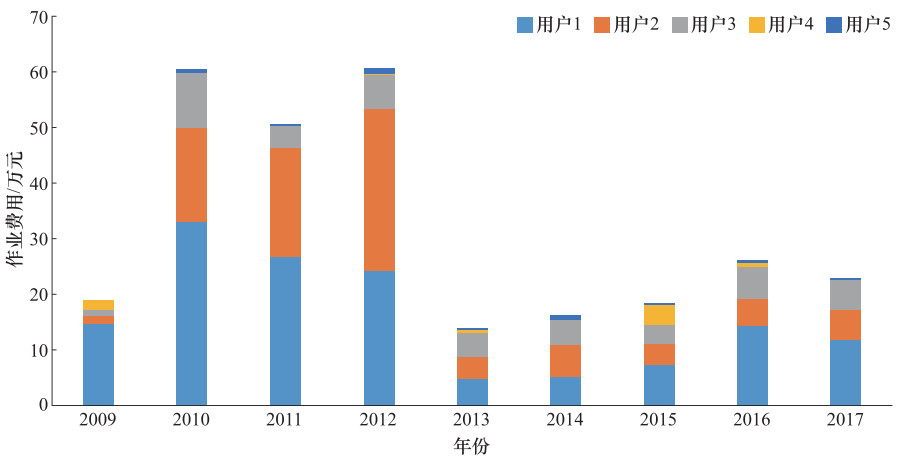
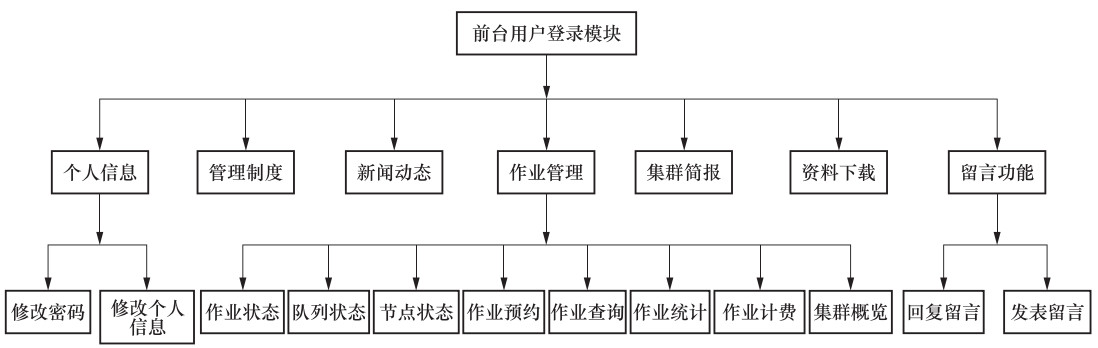
摘要: 本文简要回顾了高性能计算在地震研究中的应用,介绍了中国地震局地震预测重点实验室高性能计算平台及其应用情况,并指出作业计费的必要性。其次,详细介绍了1种高性能计算平台计费服务系统的设计与实现。该系统基于TORQUE和LSF集群作业管理系统日志信息的分析处理,具备作业查询、作业统计、作业计费、作业预约、信息管理、留言管理等功能,有益于解决高性能计算平台计算收费和运维支出平衡的问题,提高了平台的透明度和利用率,促进信息共享和技术交流,并具有较好的扩展性和应用前景。最后,对高性能计算过渡到高性能云计算进行了展望。Abstract: This paper briefly reviews the application of high-performance computing in seismic research, introduces the high-performance computing platform and its application in the key laboratory of earthquake prediction of China Earthquake Administrator, and points out the necessity of cluster accounting. The design and implementation of a high-performance computing platform accounting service system is presented in detail. Based on job log analysis and processing of TORQUE and LSF cluster management system, the system provides with such functions as job query, job statistics, job accounting, job order function and online information sharing and exchange. The system is beneficial to solve the problem of calculating fee and platform cost balance on high-performance computing platform, improves the transparency and utilization of platform, promotes information sharing and technology exchange, and has better expansibility and application prospect. Finally, the development prospect of high-performance computing transition to high-performance cloud computing is briefly described.
-
Key words:
- Seismic research /
- High-performance computing /
- Job log /
- Accounting system
-
表 1 计算资源价格及权重赋值
Table 1. The price and weight value of computing resoureces
资源指标 价格/元 权重/% CPU时 0.3 70 物理内存/GB 1.0 20 虚拟内存/GB 1.0 10 -
陈振娅, 杨英, 陈丽娟等, 2009.基于OpenPBS的高性能计算平台计费系统.山东科学, 22(5):98-102. http://d.old.wanfangdata.com.cn/Periodical/sdkx200905022 郭婷婷, 徐锡伟, 2011.有限元法在构造应力场与地震预测研究中的应用与发展.地震研究, 34(2):246-253. doi: 10.3969/j.issn.1000-0666.2011.02.023 何戈, 董小社, 钱德沛, 2003.网络计算环境下一种计费方法的研究与实现.计算机工程与应用, 39(17):185-187. doi: 10.3321/j.issn:1002-8331.2003.17.060 李惠欢, 杨敏, 吴汝明, 2016.基于TORQUE的高性能计算平台记账系统.计算机应用与软件, 33(8):126-130, 205. doi: 10.3969/j.issn.1000-386x.2016.08.028 李闽峰, 李圣强, 王斌等, 2009.地震预测研究所高性能集群计算系统.见: 中国地球物理2009.合肥: 中国地球物理学会. 李圣强, 李闽峰, 刘桂平等, 2012.高性能集群计算系统的构建.地震, 32(1):144-149. doi: 10.3969/j.issn.1000-3274.2012.01.014 廖凯宁, 郝永伟, 2015.地震数据处理和地震动力学仿真平台的优化研究.计算机工程与科学, 37(4):663-669. doi: 10.3969/j.issn.1007-130X.2015.04.007 林皎, 张武生, 徐伟平等, 2012.高性能计算平台预付费管理系统的研制与应用.实验技术与管理, 29(12):104-105, 128. doi: 10.3969/j.issn.1002-4956.2012.12.030 刘明良, 2008.基于校园网格系统计费方案研究.计算机系统应用, (3):60-63, 91. http://d.old.wanfangdata.com.cn/Periodical/jsjxtyy200803016 龙桂华, 赵宇波, 李小凡等, 2011.三维交错网格有限差分地震波模拟的GPU集群实现.地球物理学进展, 26(6):1938-1949. doi: 10.3969/j.issn.1004-2903.2011.06.007 陆新征, 卢啸, 许镇等, 2014.基于高性能计算的工程抗震与防灾: 从单体到城市.见: 徐正安, 任伟新, 丁克伟主编, 第六届结构工程新进展国际论坛文集.北京: 中国建筑工业出版社. 陆新征, 陈磊, 曾翔等, 2015.基于云计算的工程结构地震响应数值模拟.沈阳建筑大学学报(自然科学版), 31(5):769-777. http://www.cnki.com.cn/Article/CJFDTOTAL-SYJZ201505002.htm 吕弋培, 徐锐, 田文洪等, 2009.基于中国国家高性能计算与网格系统的抗震减灾应用平台.中国科技纵横, (12):472-476. doi: 10.3969/j.issn.1671-2064.2009.12.347 马新生, 谢志南, 王延伟等, 2010.高性能集群系统在地震波数值模拟中的应用.地震工程与工程振动, 30(6):43-48. http://d.old.wanfangdata.com.cn/Periodical/dzgcygczd201006007 牛铁, 朱鹏, 赵毅等, 2010.超级计算环境计算配额系统设计和实现.计算机应用, 30(S2):8-9, 39. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201003007085 沈瑜, 李娟, 常飚等, 2014.高性能计算机统一资源管理系统的设计与实现.计算技术与自动化, 33(1):83-90. http://d.old.wanfangdata.com.cn/Periodical/jsjsyzdh201401018 盛乐标, 周庆林, 2014.利用LSF API实现高性能计算机集群的机时统计.实验科学与技术, 12(2):50-52, 117. doi: 10.3969/j.issn.1672-4550.2014.02.017 王洪涛, 谢礼立, 2009.考虑楼板作用的钢筋混凝土框架有限元模型及并行计算效率.地震工程与工程振动, 29(1):63-69. http://d.old.wanfangdata.com.cn/Periodical/dzgcygczd200901008 王伟, 杨利, 刘建锋, 2008.一种高性能计算环境中的计费系统.计算机工程与科学, 30(1):148-150. doi: 10.3969/j.issn.1007-130X.2008.01.042 占昌宝, 罗川, 丁振坤等, 2016.高层建筑抗震性能预测仿真研究.计算机仿真, 33(8):397-402. doi: 10.3969/j.issn.1006-9348.2016.08.086 张军华, 臧胜涛, 单联瑜等, 2010.高性能计算的发展现状及趋势.石油地球物理勘探, 45(6):918-925. http://d.old.wanfangdata.com.cn/Periodical/zggckx200001016 赵毅, 朱鹏, 迟学斌等, 2007.浅析高性能计算应用的需求与发展.计算机研究与发展, 44(10):1640-1646. http://d.old.wanfangdata.com.cn/Periodical/jsjyjyfz200710002 -



 下载:
下载: