Analysis of Influence of Floor Lateral Stiffness Ratio on Seismic Vulnerability of Masonry Structures
-
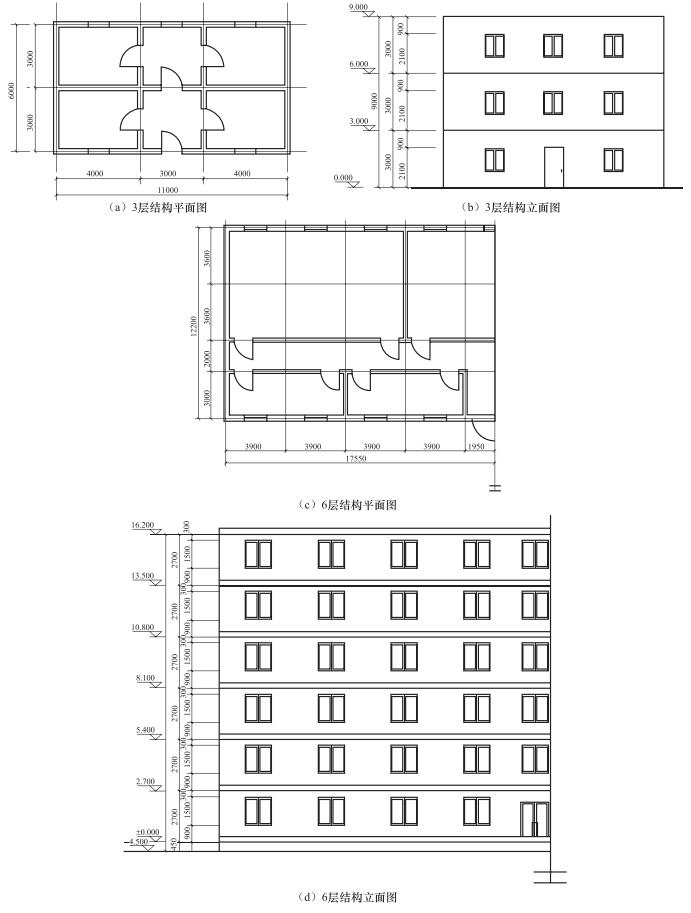
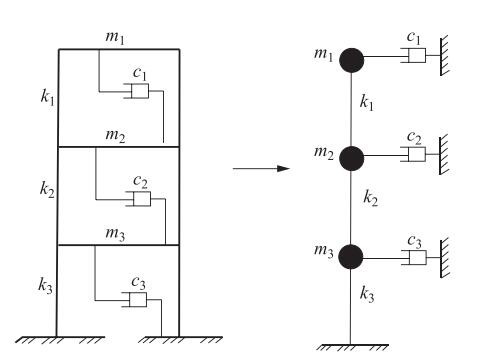
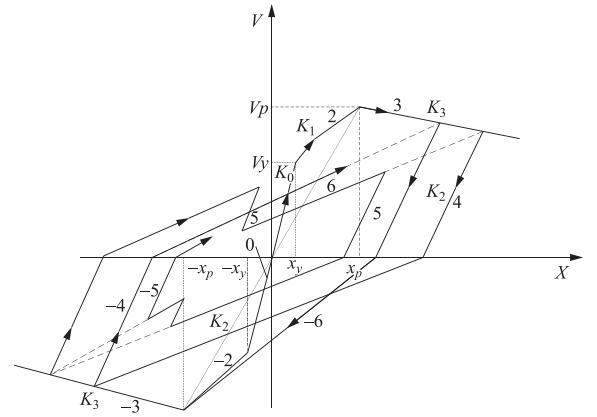
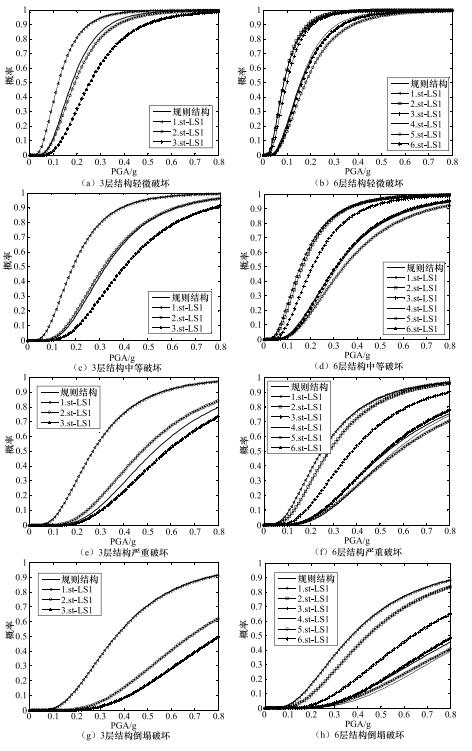
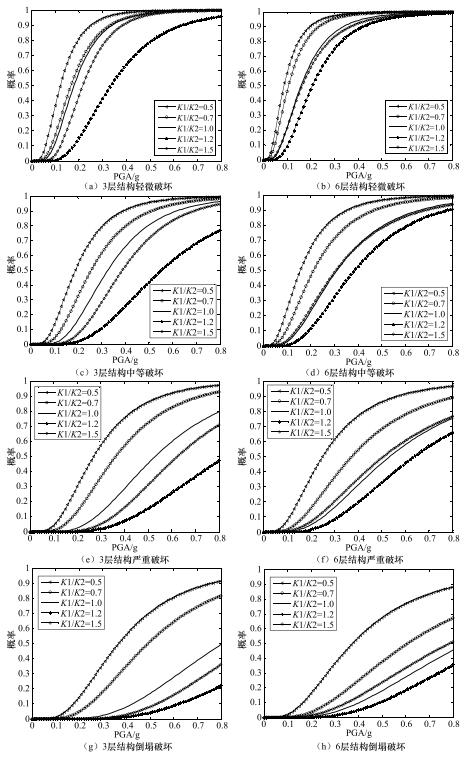
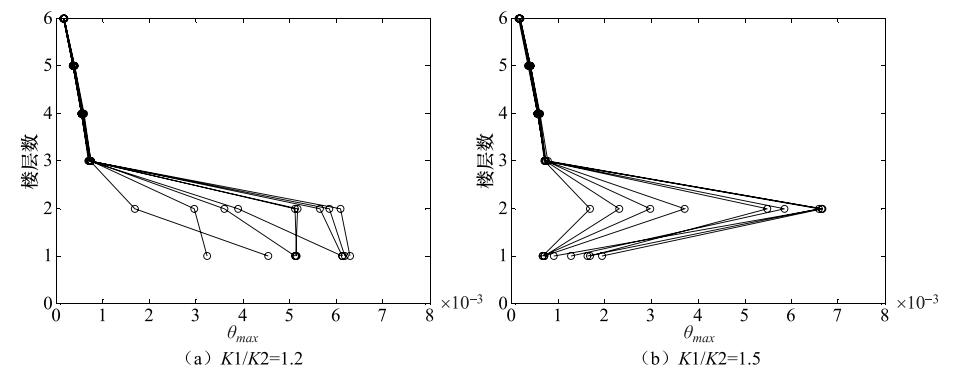
摘要: 砌体结构的震害现象表明楼层侧向刚度不均匀分布是造成其破坏的重要原因之一。本文开展楼层侧向刚度变化对结构易损性的影响分析。以3层和6层砌体结构为例，采用等效多自由度层间剪切模型，基于非线性动力时程分析，定量研究了竖向刚度不规则性对砌体结构易损性的影响。以结构最大层间位移角为地震反应参数，借助增量动力分析及回归拟合方法，建立了基于峰值加速度的结构易损性曲线。通过改变楼层的侧向刚度值来模拟薄弱层，研究了楼层刚度变化对结构不同破坏状态超越概率的影响。通过改变底层与二层的侧向刚度比，分析了底部刚度突变对结构不同破坏状态超越概率分布的影响。研究表明：与规则结构相比，当刚度突变位于结构底层时，在地震作用下结构易损性相对较高；随着底层与二层的侧向刚度比从0.5增大至1.2，结构易损性逐渐降低。当刚度比为1.5时，结构薄弱层由底层转移至二层，结构整体易损性增加；当底层与二层侧向刚度比小于1时，结构倒塌易损性要显著高于规则结构。Abstract: Earthquake damage investigations have shown that the irregular vertical stiffness is one of the important causes of the serious destruction of masonry structures. In this paper, based on multi-degree-of-freedom shear type models, we take the vertical stiffness irregular masonry structure of three-story and six-story as example to evaluate structural behavior through change the position of irregulars tiffness from story drift ratios obtained through nonlinear time history analysis. Then, the structural response was obtained through incremental dynamic analysis, and the vulnerability curve of masonry structure based on the peak ground acceleration was established. At last, the influence of the stiffness change on the probability of the structure beyond the different damage states is analyzed. Meanwhile, the different lateral stiffness ratio of two adjacent structures is analyzed. The results show that under a given ground motion, in contrast to regular tifness, it could be found that the greater the change of the structure bottom stiffness, the more severe the structural damage in the earthquake. When the lateral stiffness ratio of the bottom two layers increase from 0.5 to 1.2, the earthquake resistance capacity of the structure increase, but when the lateral stiffness ratio increase to 1.5, structural weak-layer has been transferred, and its seismic capacity decreased. This study can be used to estimate the probability of vertical stiffness irregular masonry structures exceeding different damage states in future earthquakes.
-
Key words:
- Masonry structure /
- Incremental dynamic analysis /
- Stiffness ratio /
- Seismic vulnerability /
- Weak-layer
-
图 1 挑选的地震动的加速度反应谱
Figure 1. The acceleration response spectrum of selected ground motion
图 3 砌体结构动力反应值与地震参数对数拟合结果
Figure 3. Logarithmic fitting results of dynamic response and seismic parameters of masonry structure
图 7 震害资料统计结果与砌体结构基于PGA的易损性曲线对比
Figure 7. Comparison of statistical data of earthquake disasters and fragility curves of masonry structure based on PGA
图 9 不同刚度比对应的结构易损性曲线
Figure 9. Fragility curves of masonry structure corresponding to different stiffness ratios
图 10 PGA输入为0.4g时各楼层最大层间位移角
Figure 10. Maximum interstory drift with the input of PGA is 0.4g
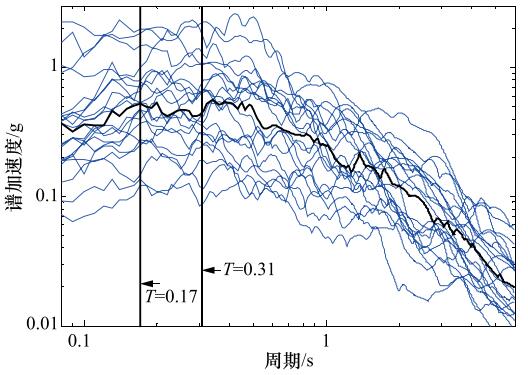
表 1 选择的地震动记录
Table 1. Selected records of ground motion
地点 台站 年份 Mw 断层距/km VS30/m·s-1 美国，圣费尔南多 Buena Vista–Taft 1971 6.61 111.37 386 伊朗，曼吉尔 Abhar 1990 7.37 75.58 303 美国，旧金山 El Centro Imp. Co. Cent 1987 6.54 18.2 292 美国，旧金山 Poe Road (temp) 1987 6.54 11.16 317 土耳其，迪兹杰 Bolu 1999 7.14 12.02 294 美国，兰德斯 Coolwater 1992 7.28 19.74 353 美国，兰德斯 Desert Hot Springs 1992 7.28 21.78 359 中国台湾，集集 HWA033 1999 7.62 39.55 379 中国台湾，集集 CHY046 1999 7.62 24.1 442 美国，阿拉斯加德纳利 Carlo (temp) 2002 7.9 49.94 399 美国，摩根山丘 Gilroy Array #3 1984 6.19 13.01 350 美国，赫克托矿 Hesperia - 4th & Palm 1999 7.13 89.87 358 意大利，伊尔皮纳 Calitri 1980 6.2 8.81 456 土耳其，科贾埃利 Goynuk 1999 7.51 31.74 348 土耳其，科贾埃利 Iznik 1999 7.51 30.73 477 美国，洛马普雷塔 Anderson Dam (L Abut) 1989 6.93 19.9 489 日本，阪神 Kakogawa 1995 6.9 22.5 312 美国，帝国谷 Cerro Prieto 1979 6.53 15.19 472 美国，帝国谷 Delta 1979 6.53 22.03 242 美国，帝国谷 El Centro Array #9 1940 6.95 6.09 213 日本，阪神 Shin-Osaka 1995 6.9 19.15 256 
下载: 导出CSV
表 2 层间位移角限值
Table 2. Allowable value of story drift ratios
破坏状态 层间位移角均值（${\mu _{{\theta _{\max }}|DS}}$） 变异系数（${\delta _{{\theta _{\max }}|DS}}$） 层间位移角中值（${\eta _{{\theta _{\max }}|DS}}$） 对数标准差（${\beta _{{\theta _{\max }}|DS}}$） 轻微破坏（LS1） 1/1600（0.000625） 0.35 0.00059 0.34 中等破坏（LS2） 1/700（0.00143） 0.35 0.00135 0.34 严重破坏（LS3） 1/350（0.0028） 0.35 0.00264 0.34 接近倒塌（LS4） 1/200（0.005） 0.35 0.0047 0.34
下载: 导出CSV
表 3 规则结构回归系数A、B
Table 3. Regression coefficients A, B of regular structures
砌体结构 A B $ {\beta _{{\theta _{{\rm{max|PGA}}}}}}$ 3层 -5.003 1.379 0.589 6层 -5.105 1.234 0.569
下载: 导出CSV
表 4 设防砖混结构震害矩阵
Table 4. Earthquake damage matrix of fortified masonry structures
破坏等级 设防烈度 Ⅵ Ⅶ Ⅶ Ⅸ Ⅹ 基本完好 85 50 22 8 1 轻微破坏 14 36 37 13 3 中等破坏 1 13 30 24 11 严重破坏 0 1 9 42 50 毁坏 0 0 2 13 35
下载: 导出CSV
表 5 回归系数A、B的值
Table 5. Regression coefficients A, B
结构 刚度变化位置 A B $ {\beta _{{\theta _{{\rm{max|PGA}}}}}}$ 3层 第1层 -3.419 1.877 1.011 第2层 -4.67 1.636 0.775 第3层 -4.903 1.804 0.851 6层 第1层 -3.896 1.429 0.845 第2层 -4.264 1.274 0.680 第3层 -4.799 1.116 0.544 第4层 -5.21 1.169 0.525 第5层 -5.19 1.273 0.665 第6层 -5.038 1.288 0.631
下载: 导出CSV
-
高小旺, 钟益村, 1990.底层全框架砖房震害预测方法.建筑科学, (2):47-53. http://d.old.wanfangdata.com.cn/Conference/188058 李小军, 于爱勤, 甘朋霞等, 2008.汶川8.0级地震北川县城区灾害调查与分析.震灾防御技术, 3(4):352-362. doi: 10.3969/j.issn.1673-5722.2008.04.004 林旭川, 陆新征, 叶列平, 2008.砌体结构的地震倒塌模拟与分析.见: 2008年汶川地震建筑震害分析与重建研讨会论文集.北京: 中国土木工程学会, 中国建筑学会, 中国工程院. 刘红彪, 郭迅, 2012.极震区典型砌体结构的振动台倒塌对比试验分析.土木工程学报, 45(12):18-28. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QKV20122013041200077994 刘锡荟, 张鸿熙, 刘经伟等, 1981.用钢筋混凝土构造柱加强砖房抗震性能的研究.建筑结构学报, 2(6):47-55. doi: 10.1016-j.hrthm.2009.06.009/ 刘砚山, 童丽萍, 2013.抗侧刚度比对底框砌体房屋抗震性能的影响.工程抗震与加固改造, 35(4):15-21, 31. doi: 10.3969/j.issn.1002-8412.2013.04.003 孙柏涛, 陈洪富, 闫培雷等, 2014.南北地震带房屋建筑抗震能力分区特征研究——以四川省为例.土木工程学报, 47(S1):6-10. http://d.old.wanfangdata.com.cn/Conference/8608721 孙柏涛, 邓宏宇, 2015.底框结构房屋抗震性能研究.建筑结构学报, 36(S2):131-137. http://d.old.wanfangdata.com.cn/Periodical/jzjgxb2015z2020 孙柏涛, 梅云弟, 2012.竖向变刚度约束砌体结构抗震能力研究.地震工程与工程振动, 32(2):1-13. http://d.old.wanfangdata.com.cn/Periodical/dzgcygczd201202001 孙雷, 刘福胜, 王少杰等, 2013.短周期村镇砌体建筑振动特性实测与抗震性能分析.土木工程学报, 46(S2):57-62. http://d.old.wanfangdata.com.cn/Conference/7986632 温增平, 徐超, 陆鸣等, 2009.汶川地震重灾区典型钢筋混凝土框架结构震害现象.北京工业大学学报, 35(6):753-760. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=SciencePaper201303040000222922 夏敬谦, 丁世文, 周四骏等, 1988.水平荷载下砖墙恢复力特性及能量耗损特性的研究.世界地震工程, (2):5-14. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000002726787 熊立红, 夏锦江, 2003.新型混凝土空心砌块房屋抗震性能研究.地震工程与工程振动, 23(3):132-137. doi: 10.3969/j.issn.1000-1301.2003.03.021 熊立红, 2004.多层混凝土砌块结构性态抗震研究.北京: 中国地震局工程力学研究所. http://cdmd.cnki.com.cn/Article/CDMD-85406-2005127949.htm 徐超, 陈波, 李小军等, 2013.芦山MS7.0地震建筑结构震害特征.地震学报, 35(5):749-758. doi: 10.3969/j.issn.0253-3782.2013.05.013 杨玉成, 杨柳, 高云学等, 1982.现有多层砖房震害预测的方法及其可靠度.地震工程与工程振动, 2(3):75-86. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000000199313 张令心, 江近仁, 刘洁平, 2002.多层住宅砖房的地震易损性分析.地震工程与工程振动, 22(1):49-55. doi: 10.3969/j.issn.1000-1301.2002.01.009 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会, 2009.中国地震烈度表(GB/T 17742-2008).北京: 中国标准出版社. 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会, 2009.建(构)筑物地震破坏等级划分(GB/T 24335-2009).北京: 中国标准出版社. 中华人民共和国建设部, 1994.设置钢筋混凝土构造柱多层砖房抗震技术规程(JGJT13-1994).北京: 中国建筑工业出版社. 中华人民共和国住房和城乡建设部, 2012.砌体结构设计规范(GB 50003-2011).北京: 中国计划出版社. 周强, 孙柏涛, 2010.汶川地震中极震区砌体结构教学楼典型震害分析.震灾防御技术, 5(4):467-476. doi: 10.3969/j.issn.1673-5722.2010.04.009 庄一舟, 谢狄敏, 1999.砌体结构抗震可靠度分析方法.工程力学, (S1):920-925. http://d.old.wanfangdata.com.cn/Conference/75229 Shinozuka M., Feng M. Q., Lee J., et al., 2000. Statistical analysis of fragility curves. Journal of Engineering Mechanics, 126 (12):1224-1231. doi: 10.1061/(ASCE)0733-9399(2000)126:12(1224) Shome N., 1999. Probabilistic seismic demand analysis of nonlinear structures. California: Stanford University. Singhal A., Kiremidjian A. S., 1996. Method for probabilistic evaluation of seismic structural damage. Journal of Structural Engineering, 122 (12):1459-1467. doi: 10.1061/(ASCE)0733-9445(1996)122:12(1459) Vamvatsikos D., Cornell C. A., 2002. Incremental dynamic analysis. Earthquake Engineering & Structural Dynamics, 31 (3):491-514. http://d.old.wanfangdata.com.cn/Periodical/tjdxxb201002006 Xiong C., Lu X. Z., Lin X. C., et al., 2016. Parameter determination and damage assessment for THA-based regional seismic damage prediction of multi-story buildings. Journal of Earthquake Engineering, 21(3):461-485. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1080/13632469.2016.1160009 -
点击查看大图
计量
- 文章访问数: 53
- HTML全文浏览量: 6
- PDF下载量: 2
- 被引次数: 0
